The Estimation of Risk Premia with Omitted Variable Bias: Evidence from China

Abstract

The Chinese stock market is replete with numerous omitted variables that can introduce biases in the standard estimation of risk premiums when traditional linear asset pricing models are applied. The three-pass method enables the estimation of risk premiums for observable factors even when not all relevant factors are explicitly specified or observed within the model. Accordingly, we have applied this method to construct portfolios with stocks from China’s A-share market as the test assets. Empirical research findings indicate that the three-pass method could be more effective than traditional linear asset pricing models in estimating risk premiums.

1. Introduction

Asset pricing has a rich historical background that dates back to the early 20th century when scholars first began to investigate the behavior of financial markets and factors that shape asset prices. This led to the development of the Capital Asset Pricing Model (CAPM) in the 1950s and 1960s, which established a theoretical framework for comprehending the relationship between risk and return in financial markets. In the 1970s, the Efficient Market Hypothesis (EMH) gained prominence, positing that financial markets are efficient and that asset prices always reflect all available information. Since then, several alternative models have been proposed, such as the Fama-French Three-Factor Model, which incorporates additional risk factors beyond just market risk.

Since Fama and MacBeth’s (1973) seminal work, there has been a vast body of literature examining empirical asset pricing. According to Harvey et al. (2016), of the existing literature, approximately 316 factors have explanatory power in the cross-section of stocks1. Most of these studies use a linear model that consists of tradable factors, non-tradable factors, or a combination of the two to explain excess returns. Non-tradable factors are risks that cannot be directly represented by portfolios, such as consumption, inflation, and liquidity risks (Burmeister and McElroy 1988; Jagannathan and Wang 1998). A general way to test for the non-tradable factors is by constructing a tradable portfolio that isolates that non-tradable risk. Such a mimicking portfolio approach usually only consists of a small set of portfolios (e.g., portfolios sorted by size and book-to-market ratio) to project the factor of interest (Giglio and Xiu 2021). As such, the linear model of asset pricing is prone to the problem of omitted variables since it is difficult to explicitly account for all relevant factors in the model.

The fundamental theory of econometrics suggests that omitted variables can lead to a violation of the assumption of no autocorrelation in the error term, which is necessary for unbiased and efficient estimation. If there are omitted variables that are correlated with the included factors, the error term may be serially correlated, resulting in biased and inefficient estimates of the model parameters.

In the case of China, the issue of omitted variables is even more prevalent for three reasons. Firstly, there is a significant difference between the accounting standards used in China and the United States. The use of Chinese Accounting Standards (CAS) in China instead of International Financial Reporting Standards (IFRS) can result in discrepancies in financial reporting and lead to omitted variables. Consequently, there is a lack of measures for several intangible factors such as the advertising expense ratios, labor expense ratios (labor expenses/sales), management quality, brand reputation, or corporate culture (e.g., the advertising factor by Chemmanur and Yan 2019; the labor factor by Kozak et al. 2020). Moreover, the Chinese stock market is less developed. Restrictions on events such as derivative trading, options trading, and share repurchasing of the firms lead to the lack of such microstructure factors (e.g., the option-to-stock volume ratio factor by Johnson and So 2012; the share repurchases factor by Ikenberry et al. 1995, among others). Last but not least, the stock market in China is intensively intervened by the government (Brunnermeier et al. 2022; Dang et al. 2023), which also contributes to the cross-sectional return of the stock. Since government intervention is unobservable2, such a factor is also inevitably omitted. Overall, the Chinese stock market is particularly susceptible to the problem of omitted variable bias due to a higher prevalence of non-tradable factors being overlooked. This results in a greater adverse impact on asset pricing in the Chinese capital market.

Giglio and Xiu (2021) propose a three-pass methodology that can correctly estimate the risk premium of the given factor with the presence of omitted variables. This three-pass methodology is based on (1) the high dimensionality of the test assets and (2) its rotation invariance property. The rotation invariance property of the linear asset pricing model refers to the fact that the order of the control factors in the model does not affect the estimation of the risk premium of the factor of interest. This property suggests that as long as the entire factor space is recovered, the risk premium of the factor of interest can be identified even when other factors are neither observed nor included in the model. As such, to recover the factor space, the first step is to use the principal component analysis to determine the relevant factors and their weights from a large panel of test asset returns. Then, estimate the risk premia of these components by running a cross-sectional regression with all the principal components (except for the factor in interest) subtracted from the first step. Third, run a time series regression of the factor of interest on the principal components to estimate the relationship between them ($\beta$). This step also corrects the measurement error of the factor of interest. The corrected risk premium of the factor of interest in the asset pricing model can be recovered by the product of $\beta$ estimated in the third step and their risk premia in the second step. This three-pass methodology can be interpreted as an alternative version of the conventional mimicking portfolio approach in the sense that the factor of interest is projected onto the principal components of returns rather than to a chosen set of portfolios.

To account for the unique characteristics of the Chinese market and the prevalent issue of omitted variables, we first verified the presence of omitted variables in the Chinese market according to Guermat (2014) and re-estimated the risk premiums using the three-pass method proposed by Giglio and Xiu (2021). Traditional linear asset pricing models often exhibit biases in estimating standard risk premiums, primarily due to the omission of certain factors. In contrast, the three-pass method enables the estimation of risk premiums for observable factors, even in scenarios where not all relevant factors are explicitly identified or observed within the model. By applying this method to construct portfolios with stocks from China’s A-share market and conducting empirical analysis, we are able to compare the outcomes with those from traditional models. Our findings suggest that the three-pass method provides more accurate estimations of risk premiums, thus offering a more effective approach for asset pricing in the Chinese market where omitted variables are a significant concern.

The rest of the paper is organized as follows. Section 2 gives a brief description of the methodology. Section 3 describes the data we use. Section 4 compares and discusses the results of the conventional two-pass regression and the three-pass regression for both the tradable factors and the non-tradable factors. Section 5 provides a conclusion.

2. Methodology

In this section, we briefly introduce the three-pass methodology of asset pricing (Giglio and Xiu 2021) that we use to test the cross-sectional returns in China. Assume that there are $p$ risk factors in the asset pricing model:

$$\overline{R}=\beta \overline{V}+\overline{U}$$

(1)

In Equation (1), $COV(U,V)=0$ holds because of exogeneity, $R$ is an $nT$ matrix of excess returns, $V$ is an $pT$ matrix of risk factors. $U$ is an $nT$ matrix of idiosyncratic errors, $\beta$ is a vector of risk premiums of the factors $\overline{R},\overline{V},\overline{U}$ are the matrices of the demean variables. Since the true matrix $V$ is not completely observable, only a portion of the factors are able to be included in the model. We denote these observable risk factors as $G$, which can be expressed by a function of V:

$$\overline{G}=\eta \overline{V}+\overline{Z}$$

(2)

In Equation (2), $E(Z)=0$ and $COV(Z,V)=0$ hold because of exogeneity, $G$ is a $dT$ matrix that consists of all the observable risk factors at the given time interval T, $Z$ is a $dT$ matrix of the measurement error, $\eta$ is the loadings of the observable risk factors on the true risk factors $V$.

From Equations (1) and (2), it is intuitive that if the matrix $V$ is not fully observable, then both $\eta$ (the loadings of $G$ to $V$) and $\gamma$ (the risk premia of the factors in $V$) cannot be estimated. However, the rotation invariance property of the asset pricing model allows us to be able to estimate $\eta \gamma$ without knowing the true $V_t$ since $\widehat{V}=H\overline{V}$, where $H$ is some $p\times p$ full-ranked matric, can be recovered.

Hence, we can rewrite Equations (1) and (2) as

$$\overline{R}=\beta H^{-1}H\overline{V}+\overline{U}$$

(3)

$$\overline{G}=\eta H^{-1}H\overline{V}+\overline{Z}$$

(4)

If we define $\widehat{\eta }=\eta H^{-1}$, $\widehat{\gamma }=H\gamma$, and $\widehat{\beta }=\beta H^{-1}$, then Equations (3) and (4) can be expressed as

$$\overline{R}=\widehat{\beta }\widehat{V}+\overline{U}$$

(5)

$$\overline{G}=\widehat{\eta }\widehat{V}+\overline{Z}$$

(6)

As long as $\widehat{V}$ can be estimated, we are able to recover $\widehat{\eta }=\eta H^{-1}$ from Equation (6) and $E(Z)=0$. $\widehat{\gamma }$ can also be recovered by the cross-sectional regression of $\widehat{V}$ to $R$. Although we cannot recover either $\eta$ or $\gamma$ separately due to the unknown value of $H$, we can still identify $\widehat{\eta }\widehat{\gamma }$ as the risk premium of $g_t$ since

$$\widehat{\eta }\widehat{\gamma }=\eta H^{-1}H\gamma =\eta \gamma$$

According to Bai and Ng (2002) and Bai (2003), by conducting principal component analysis on the panel of observed returns $\overline{R}$, we can recover $\beta$ and $\overline{V}$ on some invertible matrix $H$ as long as $n,T\to \infty$. Therefore, for a given set of observable returns $R$ and the factors of interest $G$, we can tackle the problem of omitted variable bias by employing the three-pass estimator by Giglio and Xiu (2021).

In the first step, we conduct the principal component analysis of the matrix $n^{-1}{T}^{-1}{\overline{R}}^T\overline{R}$. We define $\widehat{V}=T^{1/2}{({\xi }_1:{\xi }_2:\dots :{\xi }_{\widehat{p}})}^T$ as the factors of the linear asset pricing model and $\widehat{\beta }=T^{-1}\overline{R}{\widehat{V}}^T$ as their loadings, where ${\xi }_1,{\xi }_2,\dots ,{\xi }_{\widehat{p}}$ are the normalized eigenvectors (of length 1) corresponding to the largest $\widehat{p}$ eigenvalues of the matrix $n^{-1}{T}^{-1}{\overline{R}}^T\overline{R}$, and $\widehat{p}$ is a consistent estimator of the number of the risk factors in $\widehat{V}$.

Then, by conducting cross-sectional ordinary least-square regression of the demeaned return $\overline{R}$ onto the weights of the factors $\widehat{\beta }$ obtained from the first step to estimate the risk premia

$$\widehat{\gamma }=({\widehat{\beta }}^T\widehat{\beta }{)}^{-1}{\widehat{\beta }}^T\overline{R}$$

In the last step, we run a time-series regression of the risk factors of interest $g_t$ onto the principal components (the risk factors extracted from the first step) $\widehat{V}$ to recover $\widehat{\eta }$ and the fitted value of the observed factor $\widehat{G}$:

$$\widehat{\eta }=\overline{G}{\widehat{V}}^T(\widehat{V}{\widehat{V}}^T{)}^{-1}$$

$$\widehat{G}=\widehat{\eta }\widehat{V}$$

As previously stated, combining the estimates from the second and third steps yields an estimation of the risk premium ($\widehat{\eta }\widehat{\gamma }$) for the observable factor in matrix G. Equivalently, the three-pass estimator can also be written as

$$\widehat{\eta }\widehat{\gamma }=\overline{G}{\widehat{V}}^T(\widehat{V}{\widehat{V}}^T{)}^{-1}({\widehat{\beta }}^T\widehat{\beta }{)}^{-1}{\widehat{\beta }}^T\overline{r}$$

(7)

3. Data

The data we use in this paper are collected from the financial statements of A-share listed companies (including the main board, Growth Enterprise Market, and Science and Technology Innovation Board) from the CSMAR database between 2006 and 2020. We calculated various financial indicators to serve as the basis for constructing investment portfolios and tradable factors. In total, we constructed 125 investment portfolios, comprising 25 portfolios sorted by market-to-book ratio, 25 portfolios sorted by market capitalization and free float, 25 portfolios sorted by market capitalization and investment, 25 portfolios sorted by market capitalization and momentum, and 25 portfolios sorted by market capitalization and beta.

To test our hypothesis, we constructed seven tradable factors and seven non-tradable factors. The tradable factors are constructed by long-short portfolios based on the relevant financial indicators. These tradable factors include the market risk premium factor (MKT), the market capitalization factor (SMB), the market-to-book ratio factor (HML), the profitability factor (RMW), the investment factor (CMA), the beta factor (BAB), and the idiosyncratic volatility factor (STD). Additionally, we select seven non-tradable risk factors to test their risk premia. These non-tradable factors include residuals from an AR(1) model of industrial growth (IP) (Ludvigson and Ng 2016), the three principal components extracted from 249 macroeconomic indicators in China (Resid1, Resid2, Resid3), El Niño index per year (NINO), number of sunspots (SUN), and annual average temperature in Shanghai (where the Shanghai Stock Exchange is located) (TEMP) following Novy-Marx (2014). All results were generated using Matlab 2022b.

4. Empirical Results

The first step involves examining the pricing model for any omitted variables. According to Guermat (2014), we use both OLS and GLS methods to test for the presence of omitted variables within the CAPM model. This involves conducting OLS and GLS regressions with our constructed 125 investment portfolios as the dependent variable and the market risk premium factor (MKT) as the explanatory variable. Guermat (2014) states that R-squared values obtained from OLS and GLS regressions can only both equal 1 if the assumption of no omitted variables is correct. If the R-squared values from both OLS and GLS regressions are not equal to 1, the hypothesis that omitted variables exist cannot be rejected. The R-squared values reported in

Table 1. R² of the OLS regressions and the GLS regressions.

	(1)	(2)
	${\mathit{R}}_{\mathit{O}\mathit{L}\mathit{S}}^2$	${\mathit{R}}_{\mathit{G}\mathit{L}\mathit{S}}^2$
Tradable Risk Factors
MKT	0.9221	0.9188
SMB	0.0423	0.1072
HML	0.0225	0.0240
RMW	0.0654	0.1429
CMA	0.0060	0.0628
BAB	0.1343	0.0807
STD	0.0841	0.0102
Non-tradable Risk Factors
IP	0.0290	0.0334
Resid1	0.0358	0.0279
Resid2	0.0066	0.0054
Resid3	0.0125	0.0111
NINO	0.0474	0.0341
SUN	0.0314	0.1795
TEMP	0.0406	0.2047

, obtained from testing with both OLS and GLS regressions, are less than 1, confirming the presence of omitted variables in the CAPM model. Moreover, when replacing the market risk premium factor (MKT) with the remaining 13 factors, the R-squared values from both regression methods still remain less than 1 and show a significant decrease from 1, validating Guermat’s (2014) assertion that R-squared values decrease with the increasing significance of omitted variables.

We build on Guermat (2014) and use OLS and GLS methods to analyze the regression R-squared in scenarios with omitted variables, not only identifying the presence of omitted variables in the pricing process but also showing that the accuracy of regressions on the market risk premium factor (MKT) is impacted when omitted variables are present. The three-pass method employed in this paper effectively mitigates this issue.

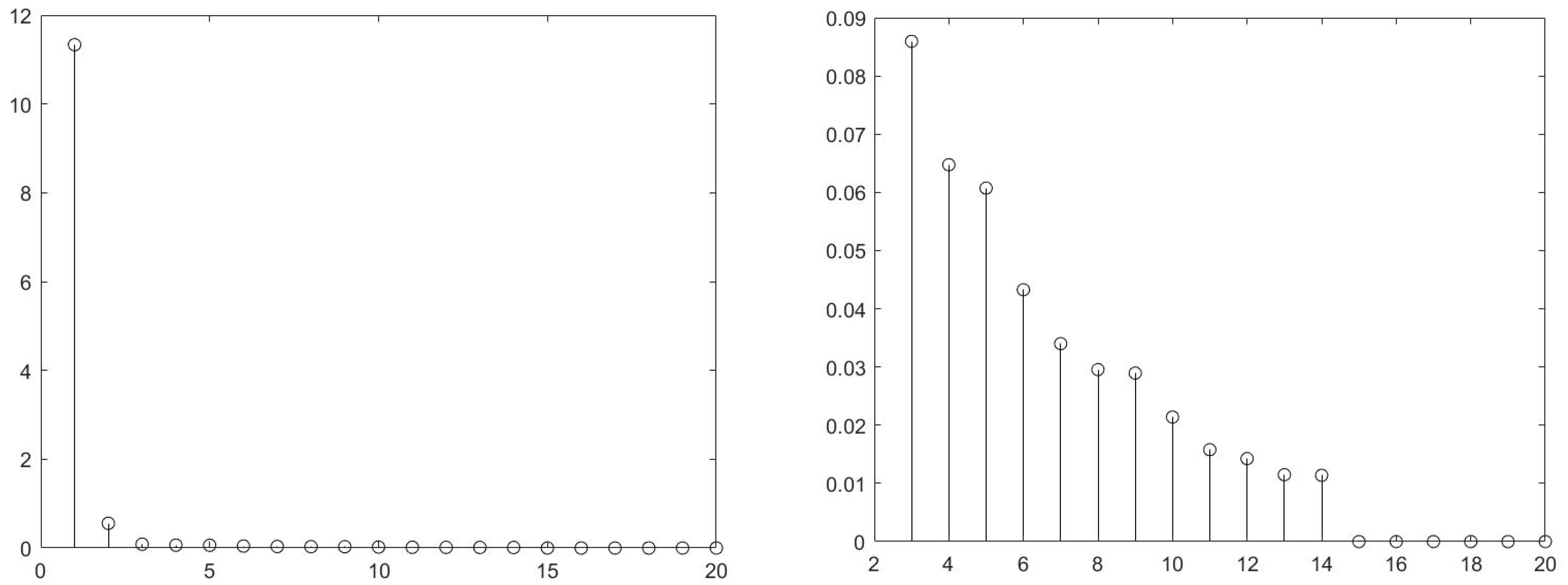
The second step in estimating the risk premium of observable factors is to determine the dimensionality of the latent factor model or the number of the risk factors in $\widehat{V}$ denoted by $\widehat{p}$. Figure 1 displays the first 20 eigenvalues of the covariance matrix of the returns panel for the 125 investment portfolios we constructed. Consistent with the general characteristics of large panels, the first eigenvalue significantly surpasses the others in magnitude, as shown in the left panel of Figure 1. The right panel focuses on the 3rd–20th eigenvalues, and we observe a clear drop-off in eigenvalues after the third one, suggesting a recommendation of $p=3$. The cross-sectional R-squared of the model with three principal components is 84%, indicating that it explains a substantial portion of the expected cross-sectional variation in returns among the 125 test portfolios.

We next compare the risk premia of these factors, estimated using several prevalent methods. Column (1) in

Table 2. Comparison of the risk premia estimated via different methods.

	(1)	(2)	(3)	(4)	(5)
	Average Return	Two-Pass Regression	Three-Pass Regression	R2	Ridge
Tradable Risk Factors
MKT	0.1346 *** (0.0053)	0.1566 *** (0.0062)	0.1538 *** (0.0054)	99.95	0.1555
SMB	0.1488 *** (0.0037)	0.1420 *** (0.0035)	0.1412 *** (0.0036)	98.08	0.1396
HML	0.0299 *** (0.0010)	0.0494 *** (0.0016)	0.0361 *** (0.0006)	73.11	0.0459
RMW	0.0504 *** (0.0007)	0.0351 *** (0.0010)	0.0519 *** (0.0002)	32.37	0.0382
CMA	0.0556 *** (0.0003)	0.0031 *** (0.0006)	0.0150 *** (0.0002)	38.36	0.0063
BAB	0.0093 *** (0.0004)	−0.0129 *** (0.0008)	−0.0135 *** (0.0003)	50.13	−0.0182
STD	0.0784 *** (0.0010)	−0.0515 *** (0.0009)	−0.0533 *** (0.0008)	63.28	−0.0518
Non-tradable Risk Factors
IP		0.9321 (2.2164)	0.1324 (1.2197)	12.89	−0.4393
Resid1		0.0035 *** (0.0003)	−0.0005 ** (0.0002)	47.63	0.0011
Resid2		−0.1946 *** (0.0604)	0.0846 *** (0.0304)	14.37	−0.1145
Resid3		0.0986 *** (0.0150)	0.1433 *** (0.0034)	22.81	0.0919
NINO		−0.0141 (0.0242)	−0.1766 *** (0.0119)	34.60	−0.0580
SUN		21.7967 (96.5508)	18.2258 (184.9851)	41.02	19.9921
TEMP		0.0410 *** (0.0105)	−0.0832 *** (0.0068)	22.82	−0.0003

Note: Each column in Table 2 provides an estimated coefficient $\gamma$ for the risk premium and its corresponding standard error. The first column shows the time-series average excess return for the tradable factor. The second column shows the estimated risk premium for the factor obtained through two-pass cross-sectional regression. The third column shows the estimated risk premium for the factor obtained through three-pass estimation. The fourth column shows the factor’s time-series regression for potential factors. The fifth column shows the risk premium estimated by ridge regression for the factor. *, **, and *** represent significance at the 10%, 5%, and 1% confidence levels, respectively. Standard errors are listed in the parathesis.

reports the time series average return of the tradable factor, representing the model-free estimate of the risk premium for the observable factors. Column (2) shows the risk premium obtained via the conventional Fama–MacBeth two-pass regression, along with the corresponding standard errors. Column (3) presents the risk premium estimates for factors obtained via the three-pass method from Equation (7), along with the corresponding standard errors. Column (4) shows the coefficients of each factor in the time-series regression against the latent factors. Column (5) reports the risk premium estimates obtained via ridge regression for each factor. Generally, for tradable factors, we can see that the results generated by the three-pass methodology are closer to the time-series average excess returns of the factors. For example, for the value factor (HML), the time-series average excess return is 2.99 basis points per year, with a standard error of 0. The risk premium estimate obtained via the two-pass method produces a highly significant estimate of 4.94 basis points per year, while the three-pass method yields a statistically significant estimate of 3.61 basis points per year for the value factor (HML). As this factor is tradable, we expect any consistent estimates to be close to the risk premium of 2.99 basis points. Consequently, the results of the three-pass method are more accurate than those of the two-pass method.

As shown in column (3) of Table 2, the risk premia generated from the three-pass method are, in general, closer to the excess returns of the mimicking portfolio of the corresponding tradable risk factors. For the group of non-tradable risk factors, we can see that the risk premia of IP and SUN estimated using the three-pass method (and the two-pass method) are statistically insignificant. The risk premium of the first macro principal component from Ludvigson and Ng (2016) Resid1 is significant at a 95% confidence level, but it is extremely small in magnitude (−0.0005) and negative. Other than these, other non-tradable risk factors seem to have statistically significant risk premia estimated using the three-pass method.

We try to provide some explanations for the insignificance and magnitude of risk premia of the three non-tradable factors NINO, Resid1, and TEMP based on the unique features of the Chinese stock market and the behavior of the Chinese investors.

The risk premia estimated by the three-pass regression involving the El Niño index and average temperature become statistically significant, in contrast to the results from the two-pass regression. Novy-Marx (2014) suggests that El Niño events typically correspond to reduced global agricultural production, which consequently leads to increased costs for many firms in terms of food and raw materials. Therefore, during El Niño episodes, companies with higher gross profit margins and less dependence on raw materials tend to display relatively stronger performance. Consequently, investments in stocks based on gross profit margin are likely to outperform during El Niño periods, thereby affecting the risk premium of stocks. Novy-Marx (2014) posits a positive association between the El Niño phenomenon and stock performance in the US market. However, our three-pass regression analysis using Chinese data reveals a contrasting predictive effect. This discrepancy may be attributed to the global temperature anomalies observed during El Niño events from December to February, such as warmer-than-average conditions in China and cooler-than-average temperatures along the Gulf Coast of the United States (Zhai et al. 2016).

The temperature in Shanghai (where the Shanghai Stock Exchange is located), denoted as TEMP, is also a source of risk that negatively affects the returns of assets in China. In line with Kang et al. (2010) and Cao and Wei (2005), domestic investors in Shanghai demonstrate greater sensitivity to local weather conditions than foreign investors. Weather-driven variations in investors’ decision-making and risk preferences can lead to changes in stock returns and volatility, with lower temperatures potentially encouraging more assertive trading strategies and higher risk-adjusted returns.

On the other hand, the three principal components extracted from 249 macroeconomic indicators in China (Resid1, Resid2, Resid3) have statistically significant risk premia estimated by the three-pass regression. This can be explained by China’s accession to the WTO in 2001, which has brought about a growing prominence of China’s macroeconomic fundamentals and volatility in asset pricing within its market. The effects of these factors have been observed in the risk premiums of China’s stock market, as they contribute significantly to the explanation of the risk–return relationship (Girardin and Joyeux 2013).

Column (4) in Table 2 displays the R-square of the time-series regressions of each risk factor on the. In the presence of measurement errors, the observed factors will not perfectly capture the variation in the true or latent factors, leading to a reduction in the R-squared value of the regression. Therefore, the R-square will be less than 100% when measurement errors are present in the factors. The R-squares of some tradable factors, such as MKT and SMB, are remarkably close to 100%, which indicates that the measurement errors of these factors are sufficiently small. Comparing the tradable factors with the non-tradable factors, we can see that the average R-squares for tradable factors is approximately 65.04%, while the average R-squares for non-tradable factors is around 28.02%. This result strongly suggests that the measurement accuracy of tradable factors in estimating risk premiums is generally higher than that of non-tradable factors.

Last but not least, in column (5) of Table 2, we report the estimation results of the first step of the three-pass approach using ridge regression instead of principal component analysis. Our findings reveal that the point estimates obtained from ridge regression are generally highly consistent with the baseline results from the three-pass approach using principal component analysis. This finding also supports the reliability of the three-pass approach.

Liu et al. (2019) introduce a three-factor model for the Chinese stock market. Their regression coefficients were not significant, suggesting that the market risk premium factor (MKT), the market capitalization factor (SMB), and the market-to-book ratio factor (HML) did not exhibit significant risk premiums. Compared with Liu et al. (2019), our findings indicate the existence of risk premiums for these factors in China. We surmise that the discrepancy arises because their analysis did not account for the more extensive omitted variable biases that affect the Chinese stock market. The prevalent three-factor pricing model suffers from substantial omitted variable bias, making the application of the three-pass method to alleviate this issue significantly valuable.

5. Conclusions

In this paper, we start by discussing the problem of measurement error and omitted variables in the Chinese market. The issue of omitted variable bias is a daunting obstacle in asset pricing modeling due to the impossibility of perfectly and comprehensively including all relevant factors in a model. Researchers must utilize economic theory and empirical evidence to identify the most crucial and pertinent factors to incorporate into the model and employ statistical tests to assess the significance of additional factors beyond the baseline model. Nevertheless, in the context of the Chinese stock market, the problem of omitted variables is further exacerbated by distinctive characteristics. These characteristics encompass restricted data availability, discrepancies in financial reporting arising from the adoption of Chinese Accounting Standards, and the challenging measurement of government intervention in the stock market. To tackle these challenges, researchers may resort to alternative data sources and advanced statistical techniques, such as machine learning algorithms, and forge partnerships with policymakers and regulatory agencies to gain valuable insights into the impact of government intervention. Ultimately, the objective is to construct a model that accurately captures the unique features of the Chinese stock market and yields dependable estimates of asset pricing parameters, notwithstanding the complexities of omitted variable bias. We next follow the three-pass methodology by Giglio and Xiu (2021) to re-examine the risk premia of several tradable factors and non-tradable factors using data from the Chinese stock market. By comparison, the risk premia estimated by the three-pass methodology outperforms the ones from the conventional two-pass methodology. Our results suggest that the three-pass procedure typically generates estimates that are more closely aligned with the average excess returns of the tradable factors, and it also yields regression coefficients that are more statistically significant for non-tradable factors. We provide some plausible explanations for the statistical significance of non-tradable factors that align with the unique features of the Chinese stock market. However, we have only assessed the risk premiums of observable factors. The influence of unobservable factors on asset prices warrants further investigation in future research.