Methodology for Economic Analysis of Highly Uncertain Innovative Projects of Improbability Type

Abstract

Modern conditions for real investment are generally associated with increasing uncertainty, which is even more relevant when evaluating innovative projects. Current innovation analysis methods using a linear model are outdated. At the same time, an open interactive model of the innovation process, formed due to digitalization, allows to connect to innovations at almost any stage of their life cycle. The aim of the study is to form a methodology for the economic analysis of innovative projects implemented in the context of an open innovation model. To achieve the goal, the study defines approaches to innovation projects differentiation. The approach to the analysis methods selection is based on the decision matrix. The developed decision matrix allows to determine the location of each project as its element and to select analysis methods, considering the project’s uncertainty characteristics. The logic of the analysis methods transformation under the influence of a changing uncertainty level determines the combination of the fuzzy-set approach and the concept of real options. The implementation of the project analysis algorithm leads to the choice of an appropriate method for evaluating effectiveness and ensures that the flexible risk response concept under conditions of improbable uncertainty is taken into account when implementing the option model.

1. Introduction

In the context of the new economy, the concept of economic growth as an increase in the production and consumption of goods over time has been replaced by the concept of economic development associated with the process of introducing innovations. At the same time, the development of information and communication technologies in the direction of global digitalization has determined the global trend of industrial innovation policy Industry 4.0. The development of the innovation sector as a key driver for the growth of the industrial sector (which is the foundation of the economy) has become a global trend. The innovative development of economic systems involves a qualitatively new level of investment, through a continuous process of innovative project implementation.

Innovative projects are classified as investment projects. Developments in the field of analysis of innovative projects are discussed in many scientific works. Kolk M. and Eagar R. investigated the return on investment in innovation (Kolk and Eagar 2014). Koskinen Y. and Maeland J. considered the relationship between innovation, competition and the investment start (Koskinen and Maeland 2016). Research in the field of evaluation of innovations and innovative projects is highlighted in the works of various scientists (Demidenko et al. 2019; Alekseev and Khlebnikov 2018; Lyubushin and Brikach 2014). Analyzing the content of the above works, we can conclude that they cover detailed forecast models for all parameters of the project, which implies the implementation of innovations and provides quantitative economic estimates for the innovation project. Thus, they can be used as a methodological document for the analysis of a certain category of investment projects in innovation. However, a significant part of these studies is devoted to finding approaches to determining the results and costs, taking into account the characteristics of innovative projects. A common feature is the assumption that the forecast of the project indicators that determine the integral efficiency is carried out at the time of the analysis. It should be noted that this assumption does not take into account a number of key features of innovation and investment projects implemented in the digital economy. Today, real investment conditions are generally associated with increasing uncertainty (in particular, due to globalization and rapid technical development), and therefore are accompanied by a high level of risk, which affects the ongoing projects. This problem becomes more relevant in the evaluation of innovative projects, which causes additional uncertainty.

The signs of innovation defined in the Oslo Guide (2018) determine the following main features of innovation and investment projects, structured by Antokhina and Voroshin (Antokhina et al. 2019):

-

Increased risk level, which is caused by additional uncertainty due to: long-term character; specificity or uniqueness of the generated results and/or resources expended; ambiguity in the structure of the project, that is, in the composition and sequence of actions performed and their relationships.

-

Expressed phasing, which determines the variability: duration of innovative projects; start time of investment; project results.

The peculiarities of investments in innovations affect not only the methodology for calculating indicators that determine the values of the integral efficiency criterion, but also modify the tools for analyzing and evaluating the economic efficiency of innovative projects, transforming the general methodological approach.

Risk in economic activity is understood as the probability of a deviation of the result from the expected value. This definition of risk defines at least two approaches regarding the sign of this deviation. The main one understands risk as the probability of an undesirable event (deviation of the expected result in a negative direction). A systematic review of publications on the issue of innovation uncertainty in terms of generating risk as a threat is presented in (Jalonen 2012). According to this approach, risk is a kind of threat that should be avoided or minimized by creating the stable environment in which the likelihood of change is minimized. The proposed methods of evasion and neutralization, which reflect the principle of moderate pessimism, provide a reduction in losses in an unfavorable development scenario. At the same time, their implementation limits the possibility of obtaining additional effects if the deviations from the expected values are positive.

This interpretation of risk in modern research on the innovative economy is replaced by an approach that expands the concept of risk. Risk is understood not only as the probability of negative events, but also as the probability of a positive deviation of the result (which means an opportunity rather than a threat). Researchers have obtained evidence that under these conditions, it is effective to use risk management methods that allow to maintain the possibility of favorable deviations (Lamberts-Van Assche and Compernolle 2022). This is especially important in the framework of innovative projects, for which changes are a source of efficiency rather than a threat.

The concept of real options, which combines both approaches, makes it possible to calculate its specific economic indicators even in conditions of increased risks and phased project implementation. The development of this concept in relation to the analysis of investment projects is contained, in particular, in the work of Damodaran A. (Damodaran 2019), Kornilova S.V. (Kornilova 2021), Harikae, S (Harikae et al. 2021), Chandra, A (Chandra et al. 2022). The specificity of the use of real options in the field of innovative projects was studied by Muñoz, J.I. et al. (Muñoz et al. 2011), Panchenko A.V. and Abrakhmanov A.A. (Panchenko and Abrakhmanov 2014), Baranov et al. (Baranov et al. 2018), Deeney P. et al. (Deeney et al. 2021). Detailed literature reviews of studies on the applyication of real options in green innovations are presented by Casper Boongaling A. (Casper Boongaling 2021), Ginbo, T. (Ginbo et al. 2021), as well as Nadajarah, S. and Secomandi, N. (Nadajarah and Secomandi 2022).

It should be noted that a significant share of the uncertainty of innovative projects implemented in the digital economy arises due to the impact of various weakly structured factors, which means that it is not measurable and belongs to the category of estimates. In this situation, it is difficult to use probabilistic methods, since the lack of available information does not allow us to choose an adequate probabilistic model due to the lack of statistical data (Kotov 2019). As a result, there is a need for non-probability approaches to assessing uncertainty.

The problems of applying the fuzzy-set approach to the analysis of economic processes in general, and investment projects, in particular, are discussed in scientific works (Carlsson et al. 2010; Hassanzadeh et al. 2011; Lee and Lee 2011; Wang et al. 2015; Baranov et al. 2018).

It should be noted that the search for methods of economic analysis of innovative projects is carried out in terms of an outdated linear model of the innovation process, which assumes that most stages of the innovation commercialization process are implemented within the framework of one innovator enterprise. At the same time, the open interactive model of the innovation process, which is being formed in the context of digitalization the implementation of Industry 4.0, allows us to observe the commercialization process at almost any stage. The processes and features of an open interactive process innovation model in industry are discussed here (Kvasha et al. 2021) and here (Kvasha and Malevskaia-Malevich 2021). This situation requires taking into account the heterogeneity of the array of subjects of innovative projects in the developed methodological approaches. In particular, it is necessary to take into account both the heterogeneity of the array of innovation projects subjects and the types of innovations implemented within the project.

This study is aimed at developing approaches to substantiate the methodological apparatus for analyzing the economic efficiency of a wide range of innovative projects of industrial enterprises implemented in an open interactive model of the innovation process. Thus, the object of the study is the projects of industrial enterprises that implement the entire range of product innovations. The purpose of the study is to form a methodology for the economic analysis of innovative projects implemented under conditions of increased uncertainty of the Industry 4.0 industrial policy. To achieve this goal, the following tasks are formulated:

• Determine approaches to the differentiation of industrial projects of product innovations, since their heterogeneity causes different levels of implementation uncertainty.
• Establish the logic of transformation of methods for analyzing industrial innovation projects, taking into account the specifics of implementation in conditions of increased uncertainty.
• Select methods that can be applied to the economic analysis of industrial innovation projects.
• Form an approach to the choice of methods depending on the level of uncertainty of the innovation project.
• Develop a methodology for the analysis of industrial innovation projects for the conditions of an open interactive model.
• Develop tools for a fuzzy-multiple approach to the economic analysis of innovative projects, taking into account the conditions of increased uncertainty of the improbability type.
• Test the algorithm as part of an industrial innovation project implemented under conditions of increased uncertainty of the improbability type.

2. Results

2.1. Project Type Differenciation

Projects for the implementation of product innovations, based on the level of novelty, are differentiated into projects basic innovations, i.e., innovations based on major inventions associated with the emergence of a new or globally modified product based on new scientific principles; improving innovations, i.e., innovations that develop as part of basic innovations are much less novel and have a shorter life cycle (for example, a new generation of products); and microinnovations, i.e., minor improvements that do not have a major impact on the properties and/or cost of the products.

According to the type of the subject of innovation, depending on the stage of connection to the interactive innovation process, projects are differentiated into implemented ones

• Early recipients: subjects joining from the earliest stages of the innovation process;
• Early majority: subjects joining from the production development stage (startup stage);
• Majority: subjects joining at the end of the rapid growth stage;
• Laggards: subjects joining at the end of the expansion stage.

2.2. Factors and Directions of Transformation of Economic Analysis Methods of Investment Projects

Factors and directions of transformation of economic analysis methods of investment projects related to innovation were established. The features of these projects determine the emergence of such transformation factors for analytical tools as a higher level and type of uncertainty, as well as the likelihood of changes in project parameters during its implementation. The effect of the first factor lies in the fact that a significant share of uncertainty is of a non-statistical estimative nature, which determines the need for improbability approaches. The effect of the second factor lies, firstly, in the fact that, in relation to innovative projects, there is an expansion of the risk array with speculative risks, which are also characterized by the possibility of deviations in a positive direction. The risk in this case is considered rather not as a danger, but as an opportunity, which determines the expediency of methods of acceptance. Secondly, the use of classical approaches limits the analysis to the exclusion of possible project modifications from the field of view. Accordingly, for a number of innovative projects, there is a need for approaches that include the ability to respond to changes, in particular, the option approach.

2.3. Conditions of an Open Model of the Innovation Process

Since we are considering the conditions of an open model of the innovation process, various projects for the implementation of product innovations are characterized by different levels of specificity and uncertainty: from almost zero relative to traditional investment projects to the maximum. Thus, it was concluded that for the purposes of economic analysis of innovative projects, the entire considered pool of methods can be used:

(1).

Traditional dynamic methods;

(2).

Traditional dynamic methods, taking into account the specifics of innovation forecasts;

(3).

Real options method;

(4).

Fuzzy set approach;

(5).

Qualitative methods/Static quantitative methods.

The higher the specificity and uncertainty of an innovative project, the greater the number of adequate methods for economic analysis.

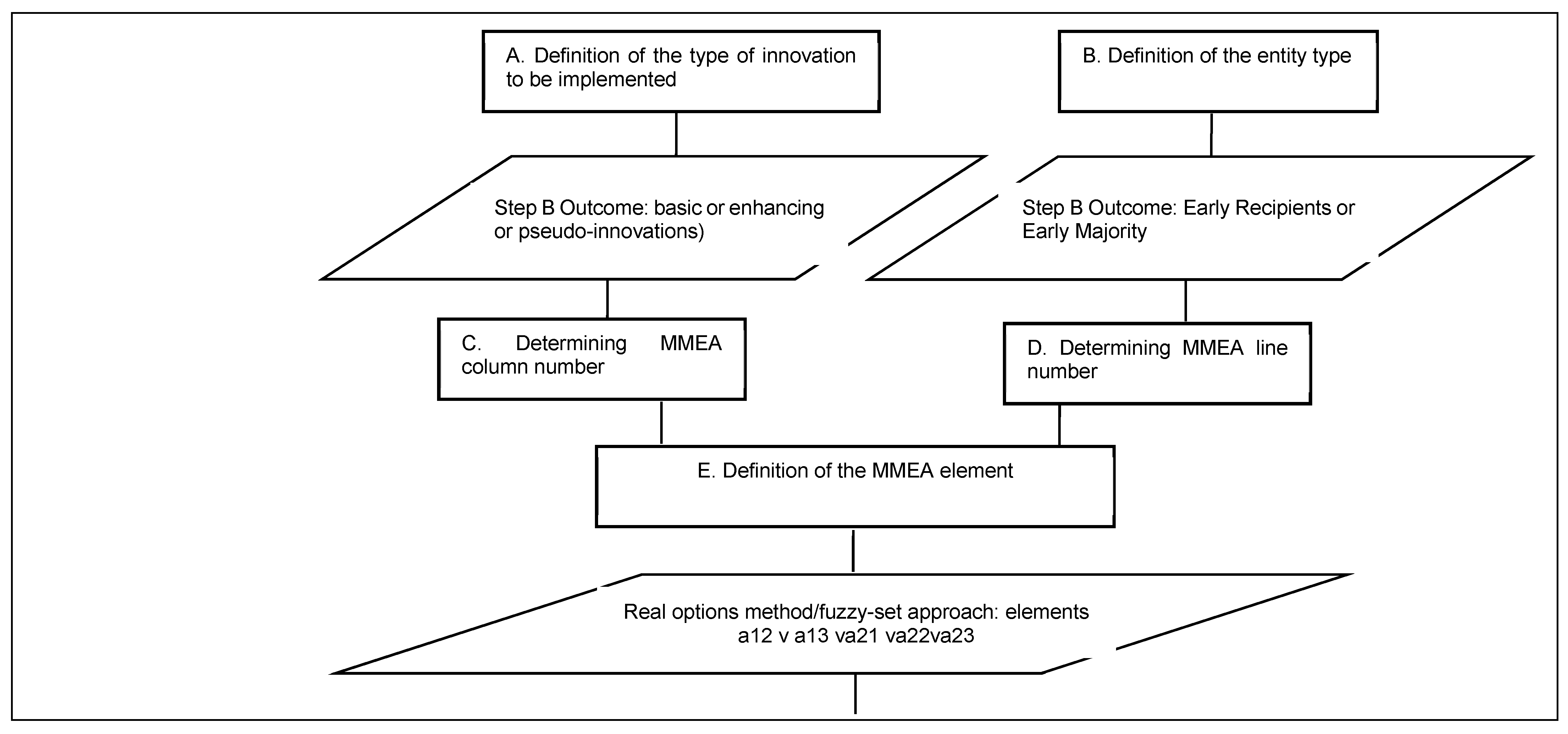
2.4. Matrix Method of Economic Analysis

Based on the decision matrix method, a choice matrix of methods of economic analysis (MMEA) of innovative projects in the conditions of an interactive innovation process be formed. If the columns of the matrix are represented by types of innovations, then the number of columns of the matrix will be equal to n = 3. Arranging innovations in the descending order of the level of novelty, we obtain the following groups of matrix elements:

• Column 1—Basic innovations (elements a_m1).
• Column 2—Improving innovations (elements a_m2).
• Column 3—Microinnovations (elements a_m3).

When the matrix rows are represented by types of subjects, the number of matrix rows will be equal to m = 4. Arranging the subjects of innovation in the order of the distance between the stages of connection to the innovation process, we obtain the following groups of matrix elements:

• Line 1—Early recipients (elements a_1n).
• Line 2—Early majority (elements a_2n).
• Line 3—Majority (elements _3n).
• Line 4—Laggards (elements a_4n).

Thus, the more to the right and higher the matrix element is located, the higher the level of specificity and uncertainty of the innovative project relative to traditional investments.

Taking into account the results obtained regarding the methods for analyzing the effectiveness of innovative projects based on the type of implementing entity with the type of innovations implemented by it, the following values of the elements of the matrix being developed can be obtained:

• a₁₁—Qualitative methods/Static quantitative methods.
• a₁₂—Real options method/Fuzzy set approach.
• a₁₃—Real options method/Fuzzy set approach.
• a₂₁—Real Options Method/Fuzzy Set Approach.
• a₂₂—Real options method/Fuzzy set approach.
• a₂₃—Traditional dynamic methods, taking into account the specifics of innovation forecasts.
• a₃₁—Traditional dynamic methods, taking into account the specifics of innovation forecasts.
• a₃₂—Traditional dynamic methods, taking into account the specifics of innovation forecasts.
• a₃₃—Traditional dynamic methods.
• a₄₁—Traditional dynamic methods.
• a₄₂—Traditional dynamic methods.
• a₄₃—Traditional dynamic methods.

Thus, when the parameter of the type of implementing entities is combined with the parameters of the types of implemented innovations in the conditions of an interactive innovation process, the MMEA of innovative projects will look like this:

2.5. The Implementation of the Option Model

The implementation of the option model of an innovation and investment project determines the features of accounting for uncertainty and risk in its assessment, in terms of including the following additional elements of effective management in the algorithm for analyzing and evaluating the effectiveness of innovative projects implemented in the digital economy:

• analysis of opportunities to make changes to the internal indicators of an innovation-investment project when implementing risky situations (determining the composition of real options) and building an option model of the project;
• assessment of real options for an innovation-investment project;
• definition of parameters of uncertainty and risk, causing favorable and unfavorable deviations for the project, as well as triggering the process of changes and exercise of options.

As a result of applying the fuzzy-multiple approach, the financial model of the project and its integral performance indicators take on fuzzy values. Therefore, there is a need to supplement the analysis results with assessments of the reliability (plausibility) of the obtained indicators. It may be proposed to include the following assessments of the reliability (plausibility) of fuzzy indicators of the innovation-investment project in the analysis:

-

Most plausible (reliable) value $k_j$ of the indicator of the innovation-investment project (j is the ordinal number of the indicator).

-

The level of plausibility (reliability) of achieving the reference value of the j-th indicator of the innovation-investment project ($K_j$).

-

The level of reliability of the most plausible (reliable) value of the indicator of the innovation-investment project ($k_j^P$).

-

The level of reliability of the effective values $k_j$ indicator of the innovation-investment project.

An algorithm for analyzing the effectiveness of innovative projects based on the concept of real options and a fuzzy-multiple approach is shown in Figure 1.

Thus, the concept of real options allows us to consider the increased uncertainty that is characteristic of innovative projects implemented in the digital economy, and the risk associated with it, not as a threat, but as an opportunity to obtain additional benefits. At the same time, real options represent, on the one hand, a way to analyze and evaluate the effectiveness of investments in a significant array of innovative projects, and on the other hand, a tool for accounting for uncertainty and risk adequate to the method of risk acceptance. This method, together with a fuzzy-multiple approach that offers tools for working with non-statistical (estimated) uncertainty, takes into account the peculiarities of investing in innovation.

2.6. Fuzzy-Multiple Approach

In order to apply a fuzzy-multiple approach to the economic analysis of innovative projects, taking into account the conditions of increased uncertainty of the probabilistic type, the following tools have been developed:

-

Method for determining the most plausible (reliable) value of the indicator of the innovation-investment project (K_j).

Since the set of the integral indicator$K_j=\left(k_j{}_1,k_j{}_2,k_j{}_3\right)$, as a rule, is defined as a triangular fuzzy number and is calculated on the basis of subnormal fuzzy sets of income, costs, and investments, then it is also subnormal. Calculation of the most plausible (reliable) value of the indicator $K_j$ is possible with a normal symmetric triangular number with a vertex ${\mu }_A\left(K_j\right)=1$. Then, the most plausible value $k_j^P$:

$$k_j^P=\raisebox{1ex}{$\left(k_j{}_1+k_j{}_3\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$$

(1)

-

Method for determining the level of plausibility (reliability) of achieving the reference value of the j-th indicator of the innovation-investment project ($K_j$).

The level of credibility (reliability) of the indicator$K_j$ can be achieved on the basis of the function ${\mu }_A\left(K_j\right)$. In this case, reaching a point to the left of the top of the function ${\mu }_A\left(K_j\right)$ is a favorable factor.

-

Method for determining the level of reliability of the most plausible (reliable) value of the indicator of the innovation-investment project ($k_j^P$).

For triangular fuzzy numbers, the reliability value of the indicator $k_j^P$ can be defined as the ratio of the area under the graph of the function ${\mu }_A\left(K_j\right)$ to the total area under the graph of the plausibility function ${\mu }_A\left(k_j^P\right)$. The value obtained can be estimated using the Harrington scale

-

Method for determining the level of reliability of the effective values $k_j$ indicator of the innovation-investment project.

As an approach to assessing the level of reliability, it can be proposed to determine the reliability of hitting the $k_j$ indicator in the effective area based on the analysis of the ratio of the total area under the membership function graph, the analyzed indicator, and the area under the membership function graph to the right of the reference line.

Thus, the method for graphical assessment of the reliability of achieving effective values $k_j$ of the indicator of an innovation-investment project under the conditions of applying a fuzzy-multiple approach includes the following sequence of steps:

-

Determination of the reference value of the j-th indicator of the innovation project ($K_j$).

-

Determination of effective and ineffective ranges of values of the j-th indicator of the innovation-investment project based on the j-th benchmark. In most cases, when $k_j\ge K_j$ the value of the j-th indicator is effective.

-

Determination of areas of effective ($S_M$) and ineffective ($S_P$) confidence zones.

-

Determination of the area of values of the j-th indicator of the innovation-investment project according to the Formula (4):

$$S=S_P+S_M$$

(2)

-

The value of the indicator of reliability of achieving effective values of the j-th indicator of the innovation-investment project according to the Formula (5):

$$R=\frac{S_M}{S_P+S_M}$$

(3)

-

Evaluation of the value of the indicator of reliability of achieving effective values of the j-th indicator of the innovation-investment project using the Harrington scale.

2.7. Results of Applying the Proposed Economic Analysis Algorithm

Let us present the results of applying the proposed economic analysis algorithm as part of an industrial innovation project implemented under conditions of increased uncertainty of the improbability type.

Step A. Definition of the type of innovation to be implemented.

To ensure further economic development, a project is being considered to develop, test, and market a new series of wireless addressable optical-electronic detectors belonging to the type of improving innovations (a_m2).

Step B. Definition of the entity type of the innovation process.

The enterprise under consideration implements its innovative projects, relying on the research developments of the partner SIE, being an innovator in this niche, a “pioneer” (early recipient).

Step C. Determining the MMEA column number.

MMEA a_m2 are improving innovations.

Step D. Determining the MMEA line number.

MMEA elements a_1n are early recipients.

Step E. Definition of the MMEA element.

According to the results of the previous analysis steps, this element is defined as a₁₂. In accordance with the MMEA innovation projects presented in

Table 1. Matrix of methods for economic analysis of innovative projects.

Type of Organization	Type of Innovation	Basic Innovations		Improving Innovations		Microinnovations
Early recipients		a11	Qualitative Methods/static quantitative methods	a12	Real Options Method / Fuzzy-Set Approach	a13	Real Options Method/Fuzzy-Set Approach
Early majority		a21	Real Options Method/Fuzzy-Set Approach	a22	Real Options Method / Fuzzy-Set Approach	a23	Traditional dynamic methods, taking into account the specifics of innovation forecasts
Majority		a31	Traditional dynamic methods, taking into account the specifics of innovation forecasts	a32	Traditional dynamic methods, taking into account the specifics of innovation forecasts	a33	Traditional Dynamic Methods
Laggards		a41	Traditional Dynamic Methods	a42	Traditional Dynamic Methods	a43	Traditional Dynamic Methods

, with a given combination of the parameter of the type of innovation being implemented with the parameter of the group of subjects of the innovation process, the methods of real options in combination with the fuzzy-multiple approach are appropriate.

Step F. Evaluation of the effectiveness of the innovation project.

F1. Development of an option model of the project

An innovative project for the introduction into production and market launch of a new category of wireless addressable optoelectronic detectors at the time of analysis has a high degree of uncertainty, due to the fact that it is impossible to predict precisely the development not only of the economy as a whole, but also of the market impact on the sales parameters of the product being developed.

The disclosure of this uncertainty should occur in the next 12 months, when it becomes clear how the consequences of the current crisis have affected the complementary construction industry. If there is the evidence of negative factors, then after 12 months it is possible to complete the project after the prototyping stage, transferring the assets used in it to other projects. This opportunity represents a real option to abandon the project. The value of these assets at the time of possible abandonment of the project is estimated at CU500,000 (strike price of the option).

F2. Building a financial model of the project using a fuzzy-multiple approach

The total volume of investments before the production development stage is forecasted at the level of 1,300,000 (c.u.).1

Given the innovativeness and speed of development of innovations in this product category, the total project time for the development, production, and launch of a new series of wireless addressable optoelectronic detectors is T = 5. The forecast period of the innovation project is determined at the level of 5 years.

For each year t of the forecast period, the cash flow of the project is given as a set of triangular fuzzy numbers$C{F}_{}^t=\left(C{F}_1^t,C{F}_2^t,C{F}_3^t\right) \left(c.u.\right)$. $C{F}_2^t$ is determined on the basis of the forecasted at the time of the analysis of sales revenues and costs for the production and sale of wireless addressable optoelectronic detectors for the next 5 years. In addition, the lower and upper threshold values of cash flow indicators ($C{F}_1^t$ and $C{F}_3^t$ respectively) were calculated by expert methods. The lower threshold is set based on the assumption that sales revenues may fall below the forecast by no more than 10%, and costs will not exceed forecasts by more than 10%. The upper threshold is set based on the assumption that sales revenues will not exceed the forecast by more than 5%, and costs will not fall from forecasts by more than 5%.

Extended cash flow outside the forecast period is also a triangular fuzzy number determined by cash flow $C{F}_{}^6$, the rate of decline in cash flow by 10% in period 6, and the increase in the rate of decline by 30% per year.

For each year t, discounted cash flow of the project is defined as a set of triangular fuzzy numbers $DC{F}_{}^t=\left(DC{F}_1^t,DC{F}_2^t,DC{F}_3^t\right)$ (c.u.) calculated based on their fuzzy value of the cash flow of year t and the discount rate set at 15.45% per year.

The financial model with fuzzy values of cash flows for the considered innovative project is presented in

Table 2. Financial model of the innovation project.

Year	Number of Stage	Investments, c.u.	CF, c.u.			DCF, c.u.
			Low	Forecast	High	Low	Forecast	High
2021	0	1,300,000
2022	1		−31,207	−8370	3049	−27,031	−7250	2641
2023	2		179,650	246,500	279,925	134,784	184,939	210,017
2024	3		326,650	404,500	443,425	212,276	262,867	288,163
2025	4		346,259	419,690	456,406	194,906	236,240	256,907
2026	5		257,848	308,080	333,196	125,717	150,208	162,454
2027	6		197,600	247,000	271,700	83,449	104,312	114,743
2028	7		177,840	222,300	244,530	65,054	81,317	89,449
2029	8		154,721	193,401	212,741	49,023	61,278	67,406
2030	9		128,573	160,716	176,788	35,286	44,108	48,518
2031	10		100,326	125,407	137,948	23,849	29,811	32,793
2032	11		71,672	89,589	98,548	14,758	18 447	20,292
2033	12		45,060	56,325	61,958	8037	10,046	11,050
2034	13		23,311	29,138	32,052	3601	4501	4951
2035	14		8684	10,854	11,940	1162	1452	1598
2036	15		1600	2000	2200	185	232	255
Index
TV				1,136,732		284,404	355,504	391,055
∑		1,300,000	1,988,585	2,507,132	2,766,405	925,056	1,182,509	1,311,236
NPV						−374,944	−117,491	11,236
i						15.45%	15.45%	15.45%
IRR						7.96%	13.20%	15.66%

.

F3. Valuation of the real option of the project

The opt-out option identified in the project is a European put option. Its evaluation is possible on the basis of a combination of such financial analysis tools as the Black–Scholes model and the option parity principle.

The spot price (the present value of the project’s cash flow) is a triangular fuzzy number $C_0^{}=\left(925056,1182509,1311236\right) \left(c.u.\right)$.

The calculation results for the predicted spot price value for the model are shown in Figure 2.

The value of the real option of the considered innovative project is a fuzzy number $V_{ROV}^{}=\left(208999,185329,175524\right)\left(c.u.\right)$.

F4. Analysis of project efficiency taking into account real options and fuzzy-multiple approach

The net present value of the considered innovation project is $NP{V}_{}^{}=\left(NP{V}_1,NP{V}_2,NP{V}_3\right)=\left(-374944,-117491,11236\right)$ (c.u.) (Table 2). This set is subnormal. Figure 3 is a graph of the membership function ${\mu }_A\left(NPV\right)$.

The net current effect of the project, excluding the value of the option held, is mainly in the ineffective area, as also evidenced by the relative indicators of interest rates (expected return (i) and return on the project (IRR)).

Since the set $NP{V}_{}^{}=\left(NP{V}_1,NP{V}_2,NP{V}_3\right)=\left(-374944,-117491,11236\right)$ (c.u.) is subnormal, in order to establish the most plausible (reliable) the value of the indicator NPV, a normal triangular fuzzy number is determined with a vertex ${\mu }_A\left(NPV\right)=1$. Then, the most plausible value of NPV can be determined by the Formula (2) $NP{V}_{}^P=\raisebox{1ex}{$\left(NP{V}_1+NP{V}_3\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=\raisebox{1ex}{$\left(-374944+11236\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=-181854$ (c.u.).

The confidence level of positive NPV values is below 8.7%, which is a very low value according to the Harrington scale. The reliability indicators of positive NPV values are also very low (shaded figure in Figure 3).

Taking into account the cost of the available option, the integral effect of the considered innovative project is: $NP{V}_{ROV}=\left(NP{V}_{RO{V}_1},NP{V}_{RO{V}_2}.NP{V}_{RO{V}_3}\right)=\left(-165945,67838,186759\right)$ (c.u.).

Figure 4 is a graph of the membership function ${\mu }_A\left(NP{V}_{ROV}\right)$.

The most plausible (reliable) value of $NP{V}_{ROV}$ is positive:

$$\begin{array}{c}NP{V}_{ROV}^P=\raisebox{1ex}{$\left(NP{V}_{RO{V}_1}+NP{V}_{RO{V}_3}\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=\raisebox{1ex}{$\left(-165945+186759\right)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=10407 \\ (\mathrm{c}.\mathrm{u}.)\end{array},$$

i.e., taking into account the value of the existing real option, according to this criterion, the project can be recognized as effective. The reliability of this indicator can be defined as the ratio of the area under the membership function graph$NP{V}_{ROV}$ to the total area under the plausibility function graph $NP{V}^P{}_{ROV}$ and is 67.4%, which, in accordance with the Harrington scale, characterizes a high level of reliability.

The level of plausibility of achieving a non-negative value of the indicator $NP{V}_{ROV}$ is 47.87%, while this point is located to the left of the top of the membership function of the indicator $NP{V}_{ROV}$, which is a favorable factor.

To determine the reliability of positive values of $NP{V}_{ROV}$, it is necessary to determine the reliability of this indicator falling into the effective area (shaded area in Figure 4). The following steps of the proposed methodology for graphical assessment of the reliability of achieving effective values when applying the fuzzy-multiple approach were performed:

-

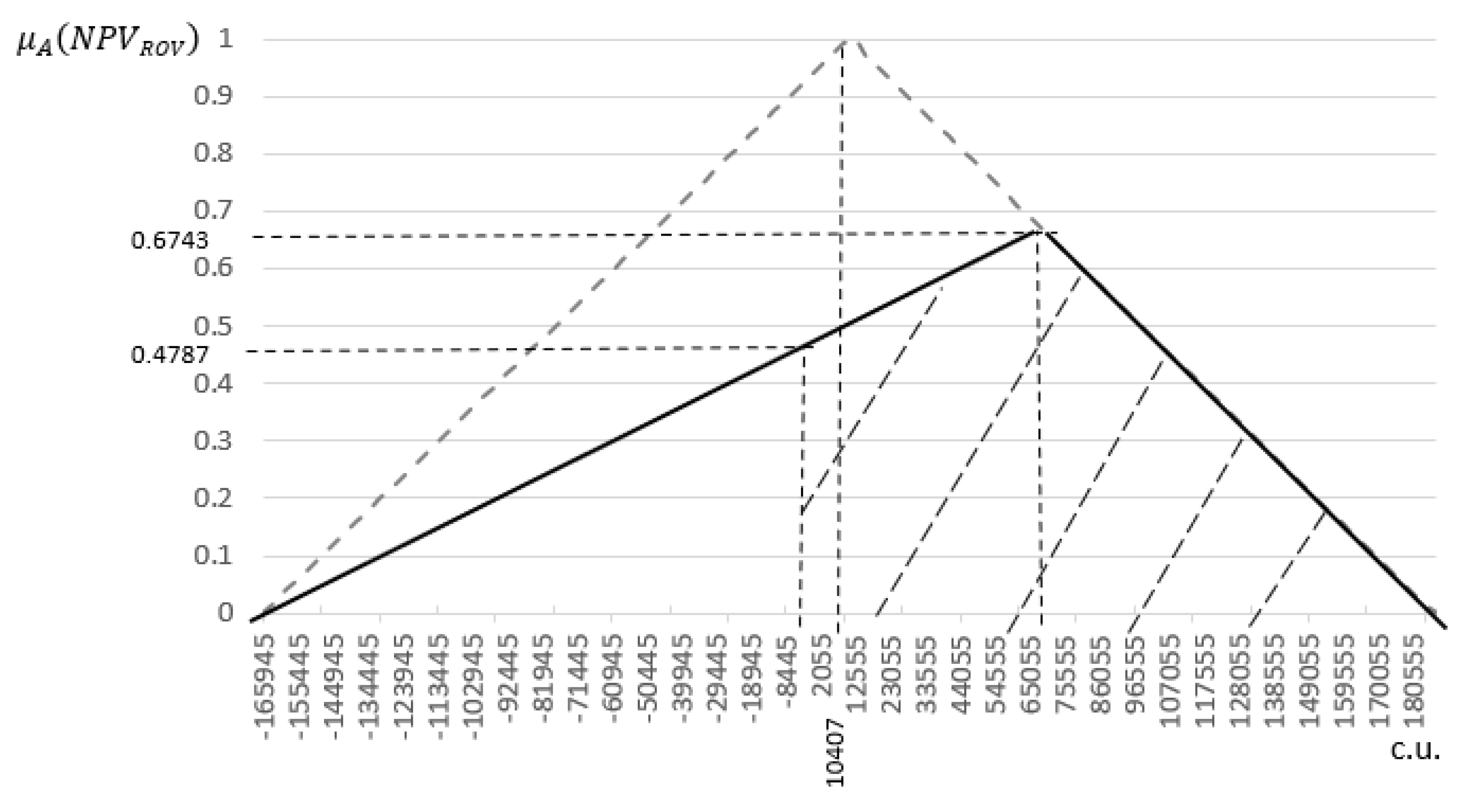
Reference value of indicator $NP{V}_{ROV}$ = 0.

-

The effective range of values of the efficiency indicator of the considered project $NP{V}_{ROV}>0$.

-

The area of the effective region is $S_M=79205$ (c.u.), the area of the ineffective region is $S_P=39716$ (c.u.).

-

The area of fuzzy values of the indicator $NP{V}_{ROV}$ is S $=79205+39716=118921$ (c.u.).

-

The value of the reliability indicator for achieving effective values $NP{V}_{ROV}$ is $R=\frac{79205}{118921}=0.667$.

-

In accordance with the Harrington scale, the reliability of achieving the effective values of the integral indicator of the project is high.

-

Fixing real options in the project and determining the factors that trigger the process of changes and the exercise of options.

In accordance with the estimates obtained, the indicators of the innovative project under consideration are effective, plausible, and reliable. Thus, the option to abandon the project should be fixed. The factors are determined for the option to be exercised.

3. Materials and Methods

3.1. Criteria for Projects Differentiation

Differentiation of projects for the implementation of product innovations was carried out according to two criteria.

-

The level of innovation novelty. The level differentiation was based on the approach (Mensch 1975) without taking into account the fake innovations group. Taking into account that the improving innovations group is not homogeneous, a subgroup of micro-innovations is singled out in it.

-

Types of subjects of innovation. The distinction between the types of innovative projects subjects was based on the approach (Schumpeter 1989).

3.2. Choice of a Method for Analyzing an Innovation Project

The heterogeneity of innovations, as well as the diverse coverage of the stages of the innovation process, cause differences in the level of specificity of various innovation projects relative to traditional innovative projects. Thus, the choice of a method for analyzing an innovation project (under the conditions of an interactive model of the innovation process) depends on the assessment level of its specificity, which can be determined by comparing the type of implemented innovations with the type of implementing subject.

3.3. Methods of Innovative Projects Analysis

Since innovative projects have all the characteristics of traditional investment projects (associated with real investment), the methods of their economic analysis should be based on the principles of investment project management.

3.3.1. Traditional Dynamic Methods

From the point of view of economic efficiency analysis, investment projects are considered as a series of positive (inflows) and negative (outflows) cash flows generated by the project. In other words, the main factors of economic efficiency are the size and temporal distribution of payment flows (positive and negative), which in turn are determined by the size of income, as well as current and investment costs, respectively. In addition, a significant factor in economic efficiency is the ratio of the return on the project and the return on alternative investments, that is, the rate of return required by the market.

This approach maximally characterizes the economic effect of the implementation of investment projects, which determines a significant number of methods for assessing the feasibility of projects based on it. The base method is the discounted cash flow method, which involves the calculation of net present value (NPV), i.e., a cumulative cash flow, of payments at different times reduced to a single time point by discounting at a rate equal to the required market return. If the NPV indicator is positive, the project is considered cost-effective and can be accepted for financing.

Traditional methods of analysis and evaluation of the effectiveness of investment projects under the principle of risk acceptance use the method of risk premium to the discount rate. The basis for determining this premium is the application of the CAPM model, which consists in adding the risk-free rate to the risk premium of the project, which is determined as the product of the beta coefficient of the project and the market risk premium.

The considered methodological approach is classical in the current practice of analyzing investment projects and does not take into account the peculiarities of innovative projects of the digital economy, as well as conditions of increased uncertainty in their implementation.

3.3.2. Traditional Dynamic Methods, Taking into Account the Specifics of Innovation Forecasts

Kossov V.V. et al. developed Guidelines for the evaluation of investment projects (2008), clause 4.3 of Appendix 4 of which contains fairly detailed models for predicting the parameters of innovative project projects. From our point of view, the proposed approach does not take into account the entire array of specific characteristics of innovative projects. The main disadvantage of the proposed methodology is its static nature, since, like the traditional methodology, it forecasts all indicators for the project at the time of analysis. Exact forecasting before the start of the project, which does not reflect the characteristic of increased uncertainty (all directions) nor the staging of innovative projects implemented in the context of digitalization, does not provide for the possibility of changes in the project during its implementation.

Thus, these recommendations can be used as a methodological document for the analysis of only a certain category of innovation investment projects.

3.3.3. Real Options Method

This approach can become one of the key ones in the field of accounting for uncertainty and risk in the evaluation of innovative projects of the digital economy, as it allows us to minimize losses in case of an unfavorable situation and obtain additional benefits if the economic dynamics is positive. The flexibility of innovative projects (the level of which is characterized by the availability of real options) becomes one of the main factors of efficiency in conditions of increased uncertainty (Antokhina et al. 2019).

In the case of using the option approach, the risk of the project ceases to be symmetrical. An option can be exercised in case of the favorable outcome and left behind in case of an undesirable development of events. In other words, in this case, losses can be limited, but the potential for positive effects is unlimited. As a result, under the conditions of effective management within the concept of risk acceptance, an asymmetric risk function is formed (losses are limited, positive effects are unlimited) (Kvasha et al. 2021). In other words, the increase in uncertainty causes an increase in the cost of project flexibility ($V_G)$. Therefore, the cost of innovative projects ($V_I$), characterized by an increased level of uncertainty, will be higher than that of the projects without an innovative component.

$$V_I=V+V_G,$$

(4)

where $V_{ROV}$ is the economic evaluation of the innovation project taking flexibility level into account; $V$ is the static economic evaluation of the innovation project without taking flexibility level into account.

In other words, the concept of risk acceptance is based on the consideration of uncertainty as a source of additional value, determined as flexibility, which can be defined as the total value of real options$V_G=\sum V_{ROV}$. The set of options for an innovative project includes real options of three main types: an option to expand, an option to refuse, and an option to delay the implementation of the project.

The problem of estimating the value of real options is solved by using approaches to the valuation of financial options, which involve two basic methods of valuation, the Black–Scholes model and the Cox–Ross–Rubinstein model (binomial model) (Brayley 2019).

The development of options pricing models in the direction of accounting for flexibility, which is relevant for the evaluation of real options for innovative projects, is mainly associated with the division of the investment process into stages. So, a significant array of innovative investment projects can also be considered as a set of real options that provide an opportunity after each stage to either start implementing the next one or refuse to invest in order to maintain the liquidation value if the continuation of the project is not economically feasible (option for successive investments). An option for successive investments in the classification of financial options is a compound structured option. When the option term T is split into several stages, the current value of the investment will depend on the value of the external European call option and the internal binary options. In this case, the vanilla option is treated as the underlying asset, with compound structured options having multiple prices and multiple expiration dates. Approaches to the valuation of a compound option are based on the works of Geske (1979).

Binary options contain only two outcomes: the investor receives nothing, or the investor receives a predetermined amount if the current price of the asset at the exercise date is higher than the strike price of the option if a binary call option is being considered. In this case, the value of the binary call option is determined by the current value of the strike price. To evaluate a multi-stage compound option, the model obtained by V.T. Lin can be used.

The Black–Scholes and Geske models use the assumption of constant volatility in the value of the underlying asset. In general, different stages of innovative projects are characterized by different levels of uncertainty (for example, at the R&D stage, the uncertainty is much higher than at the stage of production development).

There are studies that develop the Geske model in the direction of accounting for different volatility at different stages of the investment process. J.-V. Hsu obtained a modification of the Geske formula for estimating the value of a composite European call option, taking into account the different volatility of investment stages.

To evaluate a multi-stage compound option and take into account different levels of volatility, R. Hong, V.-V. Khe, and J.-L. Meng have developed the model proposed by W.T. Lin.

It should be noted that the use of finance theoretical models results in certain limitations in the application of the option approach to the analysis of real investments. The main problem is that financial models assume the existence of an efficient market for financial assets, whose prices directly depend on the incoming information, also including a large number of players. The conditions for investing in real assets are characterized by a small number of players, so the use of probabilistic approaches results in large inaccuracies in estimates. In addition, the flow of information in the process of real investment occurs discretely, that is, the adjustment of project parameters is not carried out continuously.

A significant part of the uncertainty of innovative projects implemented in the digital economy arises as a result of the impact of various weakly structured factors, i.e., it is not measurable and belongs to the category of estimates. In this situation, the use of probabilistic methods is difficult, since the lack of available information does not allow us to choose an adequate probabilistic model due to the lack of statistical data (Oslo Guide 2018).

Not only is there little information available regarding the future results and costs of the project, but it may not be available at the time of the analysis at all. As a result, there is a need for non-probability approaches to assessing uncertainty, one of which is based on the use of fuzzy set theory, whose tools allow us to use and process information of any kind.

3.3.4. Fuzzy Set Approach

The use of the option approach to the analysis of real investments and innovative projects is associated with limitations in the use of probabilistic approaches due to the lack of necessary statistics. To solve these problems, the researchers propose to use non-probability methods of working with uncertainty, namely the methods of options theory, i.e., to combine the option approach with the methodology of fuzzy sets.

Based on the fuzzy-set approach, a new theory of analysis in the conditions of uncertainty has arisen, which is not related to probabilistic assessment—the theory of possibilities. The theory of possibilities makes it possible to establish fairly strict regularities, the parameters of which are set according to certain linguistic rules, even in the absence of the necessary number of observations to obtain a probabilistic distribution law.

The translation of linguistic descriptions into a fuzzy quantitative form allows us to model processes that are heterogeneous and limited in scope of observations, taking into account the estimated uncertainty and analyzing the impact of uninsurable risks on project indicators. In other words, unlike the theory of probability, the theory of possibilities allows us to make more rough estimates, which ensures its applicability when information is limited (Nedosekin 2003).

When calculating the integral indicators of an investment project, it is assumed that the cash flow for the project can be determined. However, in the case of analyzing a large array of projects related to innovation in the context of digitalization, the exact value of the cash flow cannot be determined. Only expert characteristics of the project parameters are available, often representing a tripartite assessment of the predictive low and high development scenarios. As a result, the project cash flow model is formed as a fuzzy triangular number.

3.3.5. Qualitative Methods/Static Quantitative Methods

The polar approach rejects using quantitative indicators, replacing them with selection based on qualitative or expert methods, most of which mainly rely on intuition. This approach eliminates the need to carry out forecasting under conditions of significant uncertainty, but instead does not offer criteria for making decisions on projects. The approach can be supplemented by calculating short-term performance indicators that do not take into account the time factor, based on the concept of CVP analysis (e.g., Lulaj and Iseni 2018).

3.4. Decision Matrix Aproach

To select analysis methods depending on the level of uncertainty of a particular innovative project, an approach based on a decision matrix was used. This approach works well when it is necessary to make a choice from a set of alternatives, taking into account several factors. The approach involves compiling a table where the columns contain the options from which the choice is made, and the rows contain the factors that need to be taken into account. Each variant/factor combination is discussed below.

3.5. Algorithmization Method

The methodology for analyzing industrial innovation projects for the conditions of an open interactive model is formalized on the basis of the algorithmization of this process. In other words, the methodology is a coded sequence of actions leading to obtaining economic estimates of an innovative project based on selected analysis methods, taking into account the level of project uncertainty. Encoding is based on pseudocode in a natural, partially formalized language. As formal constructions, block diagrams are used, using certain geometric shapes with connection lines indicating the order in which instructions are executed.

3.6. Fuzzy-Set Approach Metodology

The starting characteristic of the fuzzy-set approach is some arbitrary set X, to which all the results of observations refer. Then the fuzzy set A is a set of values X, which is given by the membership function $0\le {\mu }_A\left(x\right)\le 0$. The value ${\mu }_A\left(x\right)$ is a number between 0 and 1, characterizing the degree of membership of the element $x\in X$ in the fuzzy set A. In the range $0\le {\mu }_A\left(x\right)<1$, $x$belongs to the set A with different degrees of confidence, the higher ${\mu }_A\left(x\right)$, the higher the degree of membership of x in the set A. A fuzzy set A is called normal if its height is equal to 1. Otherwise, it is called subnormal.

If X belongs to the set of real numbers, then one speaks of fuzzy numbers. In the analysis of innovative projects, triangular ($A=\left(a_1,a_2,a_4\right)$) numbers are used, where the values characterize moderate, pessimistic, and optimistic development scenarios. The membership function of triangular fuzzy numbers can be determined by Formula (2):

$${\mu }_A\left(x,a_1,a_2,a_4\right)=\{\begin{array}{c}\begin{array}{c}0, x\ge a_1\\ \frac{x-a_1}{a_2-a_1},a_1\le x\le a_2\\ \frac{a_4-x}{a_4-a_2}, a_2\le x\le a_4\end{array}\\ 0, x\ge a_4\end{array}$$

(5)

Operations can be carried out on fuzzy numbers, which are reduced to operations with ordinary numbers at a certain reliability interval (level of membership) (Nedosekin 2003). The value obtained can be estimated using the Harrington scale, characterizing the degree of approximation to some ideal:

-

0.81–1.0 very high;

-

0.64–0.80 high;

-

0.37–0.63 average;

-

0.20–0.36 low;

-

0–0.19 very low.

3.7. Calculating the Performance Indicators

The developed methodological approach was tested in the process of analyzing the innovation project in the field of development and production of optical-electronic detectors. The enterprise, the subject of the innovative project, is a high-tech industrial enterprise of a patent type, concentrated in the niche of security detectors intended for residential, commercial, industrial, office, warehouse, and other premises. The enterprise has been developing in its market niche since 1993 and is one of the leading enterprises in the country in this area, which is due to high innovation activity. As a result of long-term partnership with one of the university SIEs, the enterprise is included in the innovation cycle from the earliest stages. High scientific potential of employees, developed experimental base, professional level of mass production organization, as well as modern technological measuring and testing equipment allow the enterprise to develop and master new products in a short time and at a high technical level.

Let us present some sources and models that were involved in the process of calculating the performance indicators of the analyzed innovation project. For calculations, a ready-made model in Microsoft spreadsheets from Damodaran A. was used (Damodaran 2019). An important factor in the calculations is the discount rate, which, as noted, is usually estimated based on the CAPM model. At the same time, the capital of the enterprise under consideration is not circulated on the open market, which makes it difficult to apply this model. In this case, the way out will be to use a similar cumulative approach, when the risk-free rate is aggregated with the risk premium based on the analysis of the profitability of peer enterprises. The yield of national government bonds was used as the risk-free rate, which was 9.31% as of the settlement date (http://www.cbr.ru/hd_base/zcyc_params/ (accessed on 10 February 2022).

The main cost factor of a real option is the standard deviation of the project, which in practice, as a rule, is replaced by the standard deviation of the enterprise implementing the project. Due to the lack of industry-average domestic data, it is proposed to use the available data on the standard deviation of the equity of foreign companies in countries characterized by high innovative activity (in particular, the United States) (Damodaran 2019). To apply the indicator in domestic conditions, the standard deviation indicator is adjusted for country risk calculated by comparing the dispersion of returns of foreign and national market indices.

4. Discussion

Thus, as a result of the study, a comprehensive methodological approach to the analysis of innovative projects was formed, taking into account the features of increased uncertainty and open economic systems, including Industry 4.0.

4.1. Thedependence of Uncertainty Level of a Product Innovation Project

It is shown that the level of uncertainty of a product innovation project increases with an increase in the level of novelty (from micro-innovation to basic), depending on the stage from which the subject implementing the project joins the innovation process. At the same time, projects implementing process innovations have not been studied. Moreover, they were not included in the analysis of differentiation of innovations by other classification criteria, which, in our opinion, should not affect the result.

4.2. Influende of Different Factors

The logic of transformation of the methods of analysis of innovative projects under the influence of such factors as the changing level and type of uncertainty, as well as the associated increase in possible changes in the parameters of the project during the implementation process, has been established. The specified impact determines the unification of the fuzzy-set approach and the concept of real options as the basis of the methodological toolkit for the economic analysis of innovative projects. These methods are already quite actively proposed by researchers. The new result is an established causal chain from the identified features of innovative projects to analysis methods that take them into account.

4.3. Investmnent Analysis Method

It is shown that under the conditions of an open model of the innovation process, projects for the implementation of product innovations are characterized by different levels of specificity and uncertainty: from almost zero relative to traditional investment projects to the maximum. This circumstance determines the possibility of using the entire pool of methods for economic analysis of projects up to the calculation of traditional dynamic performance indicators (NPV, IRR, etc.).

4.4. Decision Matrix

A decision matrix has been developed, on the basis of which the location of each project can be determined as an element of the matrix and, accordingly, the selection of methods for economic analysis of innovative projects has been carried out. The proposed methodology links all known methods of analysis of project efficiency and correlates with them the features of ongoing innovation projects, taking into account the specific characteristics of a particular project in an interactive model of the innovation process.

4.5. Algoritm for Effective Rael Option Model Implementation

A methodology for the analysis of industrial innovation projects for the conditions of an open interactive model is formed, which is solved in the form of an algorithm. The passage of this algorithm leads to the choice of an adequate method for analyzing the effectiveness and, in the case of the implementation of the option model, ensures that the concept of flexible response to risk is taken into account and work with improbable uncertainty inherent in the conditions of digitalization by methods of a fuzzy-multiple approach.

4.6. Development of the Fuzzy-Set Approach

In the development of the fuzzy-set approach in relation to the analysis of innovative projects of increased uncertainty of the probabilistic type, methods are proposed for assessing the levels of credibility and reliability of the main parameters of innovative projects with high uncertainty.

4.7. Algorithm Testing

The proposed algorithm has been successfully tested in the process of analyzing an industrial innovation project, which is characterized by the maximum level of uncertainty of the improbability type, for which quantitative methods are applicable. Approaches to the analysis of uncertain projects, for which only qualitative (mainly expert) methods are applicable, have not been studied here. Another limitation is the use of the quantitative value of the standard deviation of the project, determined at the time of the analysis. At the same time, under conditions of increased uncertainty of the improbability type, the standard deviation in many cases is a fuzzy variable, which should be taken into account in further research.