Abstract
Crediting represents one of the biggest risks faced by the banking sector, and especially by commercial banks. In the literature, there have been a number of studies concerning credit risk management, often involving credit scoring systems making use of machine learning (ML) techniques. However, the specificity of individual banks’ datasets means that choosing the techniques best suited to the needs of a given bank is far from straightforward. This study was motivated by the need by Credins Bank in Tirana for a reliable customer credit scoring tool suitable for use with that bank’s specific dataset. The dataset in question presents two substantial difficulties: first, a high degree of imbalance, and second, a high level of bias together with a low level of confidence in the recorded data. These shortcomings are largely due to the relatively young age of the private banking system in Albania, which did not exist as such until the early 2000s. They are shortcomings not encountered in the more conventional datasets that feature in the literature. The present study therefore has a real contribution to make to the existing corpus of research on credit scoring. The first important question to be addressed is the level of imbalance. In practice, the proportion of good customers may be many times that of bad customers, making the impact of unbalanced data on classification models an important element to be considered. The second question relates to bias or incompleteness in customer information in emerging and developing countries, where economies tend to function with a large amount of informality. Our objective in this study was identifying the most appropriate ML methods to handle Credins Bank’s specific dataset, and the various tests that we performed for this purpose yielded abundant numerical results. Our overall finding on the strength of these results was that this kind of dataset can best be dealt with using balanced random forest methods.
1. Introduction
The banking sector is constantly exposed to various types of risk, including strategic risk, cybersecurity risk, market risk, liquidity risk, credit risk, and operational risk. Among these, credit risk is arguably the most significant, especially for commercial banks. A credit score is a numeric expression measuring a person’s creditworthiness. Service suppliers sometimes need to evaluate a customer’s credit history in order to determine whether or not to provide a particular service. The term credit scoring is generally used in relation to the computing of credit scores. Traditional credit scores may incorporate a dozen or so variables, but in the age of big data, a customer might have hundreds of data items to be taken into consideration.
Various methods have been developed for credit scoring based on machine learning (ML) techniques. These methods are suitable for dealing with large sets of data, since they allow a deeper data analysis. In this work, our focus was on meeting a specific need, namely a reliable credit scoring system for a relatively new bank (established in 2003). We note that the private banking system in Albania is quite new, and there is little feedback available to inform the design of tools most suitable for Albanian customers. Until now, private Albanian banks have had almost no resources at their disposal that are tailored to their specific needs. Our ultimate aim is the development of a web application tool that the bank can use for customer credit scoring.
When it comes to credit scoring, the best performing machine learning (ML) classification algorithms vary according to the specifics of datasets, of feature selection, along with other factors. Support vector machines (SVM), gradient boosting, and tree-based algorithms (e.g., random forest (RF)) are recognized as valuable methods. However, certain limitations appear to be endemic when applying ML algorithms to credit scoring. These limitations are not due to the poor performance or the lack of sophistication in the algorithms themselves, but rather, they arise from biased data, interpretability, regulations, and scalability. In this work, we focus on the application of these methods in the context of a specific case study in a developing country, Albania. The dataset provided by Credins Bank contains a high degree of imbalance and/or inconsistency, and a large amount of information that is either biased or incomplete. Another closely connected problem is linked to the typology of the customers. Customers in developed countries with well-established economies and financial systems tend to be different in a number of respects from customers in emerging and developing countries such as Albania, where the economy exhibits a high level of informality. Questions relating to data analysis and influencing factors in emerging countries have been investigated in the context of different economic sectors (see, for example, Yang and Li (2018) and Yang et al. (2022)), and not only the commercial banking sector, which is our focus here.
This paper is organized as follows. In Section 2, we present the state of the art of ML methods used in credit scoring. Section 3 focuses on the data sample used in this study. We describe its composition and how data cleaning and transformation are carried out. Section 4 reports on the training and the testing process. In particular, we provide numerical results for two ML methods tested in depth, namely SVM and RF. In Section 5, we give our concluding remarks. The main contribution of this work is that it provides one of the very first detailed studies based on real data from an Albanian bank. Its secondary contribution is testing a wide range of ML methods and showing that balanced random forest methods are able to deal effectively with imbalanced and biased customer datasets. This is a new contribution in relation to the use of ML methods for credit scoring.
2. State of the Art
There have been a large number of studies on customer credit scoring, and reviews of works in this area are also published quite regularly. We report first on the main review studies, before focusing in particular on support vector machine (SVM) and random forest (RF) methods.
Among the ML methods commonly used in credit scoring, discriminant analysis was one of the earliest classification methods to be used (Dinca and Bociu 2015; Ortuño et al. 1994). Subsequently, regression methods (linear and logistic regression) have also frequently been employed (Banasik et al. 2003; Karlis and Rahmouni 2007; Laitinen and Laitinen 2000). K-nearest-neighbor (KNN) is a non-parametric statistical technique that is often used as a measure for more complex classifiers (Mukid et al. 2018). Artificial neural networks (ANN) fall into the category of nonlinear regression and discrimination methods (Lee et al. 2002; Pang et al. 2002; West 2000). Issues relating to credit scoring were also addressed in some interesting recent works: Brygała (2022) looks in particular at imbalance, Kil et al. (2021) addresses specific cases including cooperative banks, and Ampountolas et al. (2021) examines micro-credit scoring. However, to the best of our knowledge, there have been no studies specifically concerned with what concerns us here, that is to say, bank customer datasets that exhibit a high level of both imbalance and information incompleteness. Our strategy was, therefore, based on a review of the literature to test experimentally all the possibly relevant methods in order to determine which perform best with this kind of data. We are interested in a specific case of datasets impacted by both imbalanced and biased information.
2.1. Review of Comparative Studies
The credit scoring literature is substantial, and there have been various comparative studies relating to the state of the art. In Yu et al. (2008), Yu compared credit scoring methods using the following metrics: accuracy, interpretability, simplicity, and flexibility. He found that SVM has high accuracy and flexibility, together with a better interpretability than neural networks. Yu’s study also conducted a review of 32 articles relating to the implementation of machine learning methods for credit scoring. The datasets in question were mostly from Germany and Australia, i.e., rich, industrialized countries, although one or two of the studies were based on datasets from elsewhere: for example, Galindo and Tamayo (2000) analyzed data from Mexican banks.
More recent papers have compared different algorithms for credit scoring where datasets are imbalanced. It was shown in De Melo Junior et al. (2019) that RF and extreme gradient boosting perform well with extremely unbalanced data. However, that study considered only the standard SVM algorithm, rather than optimized versions of it, such as fuzzy SVM (Lin and Wang 2002), fuzzy SVM for class imbalance learning (Batuwita and Palade 2010), weighted LSSVM (Suykens et al. 2002), or LS-fuzzy SVM (Yu 2014).
Finally, two other works worth citing are Baesens et al. (2003) and Lessmann et al. (2015). The first of these, Baesens et al. (2003) provides valuable insights into various classification techniques. Apart from the well-known traditional algorithms used for credit scoring (linear regression, logistic regression, linear discriminant analysis), other ML algorithms, including decision trees, KNN, SVM, and neural networks, were all applied in an evaluation of credit risk. The second work mentioned, Lessmann et al. (2015) was essentially an update of Baesens et al. (2003) to include studies realized between 2003 and 2014. These two works confirm the interest of SVM and neural methods. Below, we will be focusing on two ML methods, namely SVM and RF. Our choice of these two methods derives from a careful study of the literature and from our own analysis of the case in hand, as we will explain in the remainder of the paper.
2.2. Support Vector Machines (SVM)
SVM is a classification algorithm widely used for solving two-group classification problems. It consists in finding the optimal hyperplane for separating the data points into two classes. SVM was first introduced in Boser et al. (1992), and its applications in the financial field, and in particular in credit scoring, started to appear after 2000. Implementations have been described in various works, including Baesens et al. (2003), Schebesch and Stecking (2005), and Brown and Mues (2012). SVM works very well with balanced datasets, but it is less effective in the case of imbalanced data because of its sensitivity to noise and outliers. This issue of sensitivity may, to some extent, be overcome through the use of fuzzy SVM (FSVM), first proposed in Lin and Wang (2002). Subsequently, Batuwita and Palade (2010) proposed fuzzy SVM–class imbalance (FSVM–CIL) as a way of addressing both imbalanced data and sensitivity to noise/outliers. In addition, a new version of fuzzy SVM, bilateral-weighted fuzzy SVM, was proposed in Yu et al. (2008). This method constructs two instances from the original instance, one for the positive class and one for the negative class, assigning members to them with different membership weights. For example, an instance detected as an outlier is considered to be a member of the class that it belongs to with a large membership weight, and at the same time, it is considered to be a member of the opposing class but with a small membership weight. This model offers a better generalization ability and a more efficient use of the training sample.
Other advanced SVM methods, including least squares fuzzy SVM (LS-FSVM) and least squares bilateral fuzzy SVM (LS-BFSVM) are also described in Yu et al. (2008).
2.3. Random Forest (RF)
RF methods are defined as a group of unpruned classification or regression trees generated using random feature selection. Once a large number of trees has been generated, each tree votes for the most popular class (Breiman 2001). The class that obtains the most votes is the decision tree majority class. This process is also termed majority voting, i.e., every individual classifier votes for a class, and the majority wins.
A decision tree is a tree-like structure which separates a set of input samples into a number of smaller sets according to certain characteristics of their attributes. The decision tree algorithm comprises three phases:
- Feature selection. This is intended to filter out features that are highly correlated with classification results.
- Decision tree generation.
- Decision tree pruning. The main purpose of pruning is to reduce the risk of overfitting by actively removing some branches.
In RF, three important hyperparameters require tuning. These are the number of trees, the number of features used to build each tree, and the number of samples for each tree. In this regard, we should mention De Melo Junior et al. (2019), where RF is successfully used in credit scoring with imbalanced datasets.
3. Handling Data
In practice, addressing the credit scoring problem means following a working methodology in two steps, the first step being data preparation or preprocessing, and the second step data training and testing.
3.1. Working Methodology Outline
Each of the two steps mentioned above is composed of several tasks. The first step, preprocessing, includes tasks such as data cleaning, data transformation, and data reduction. The purpose of this first step is to improve the quality of the data so that the ML algorithms can perform with higher accuracy and with better generalization capabilities. The second step is composed of two tasks: training, and then testing. The training task corresponds to a process in which an algorithm is “taught” to recognize patterns in a dataset, and the testing task assesses the model’s accuracy. Performing these two tasks involves separating the dataset into training and testing datasets. The testing task is closely linked to a task of performance measurement. In our study, we use metrics such as specificity, sensitivity, total accuracy, and area under the ROC1 curve (AUC) to evaluate the performance of the learning algorithms.
An additional consideration is the interpretability of decisions. When working with banking applications, attention must be paid to interpretability, given that there are generally strict regulations about interpretability in force. Applications must be able to provide information on the reason for a particular decision. This can also be helpful in determining appropriate interest rates for different customers. Here, there are two important elements that can prove useful: one is the application’s global evaluation of attribute weights, and the other is its measurement of the precise weight of each specific attribute when scoring a new customer. In our study, we opted for a recent method, SHAP (Shapley additive explanations). Lundberg and Lee (2017), which originated in coalitional game theory and is used to compute the contribution of each feature in individual predictions. The feature values of a data instance act like players in a game, with Shapley values indicating how a ”payout” may be distributed fairly among the features.
3.2. The Dataset
The dataset contains information about the bank’s Albanian customers. There are 10,215 samples in this data, of which 9737 samples are labeled good customers and 478 samples bad customers. After the removal of unsuitable samples and outliers, 10,114 samples are left, corresponding to 9652 good customers and 462 bad customers.
3.2.1. Imbalance
The ratio of good customers to bad customers is about 22:1, meaning that the dataset is heavily imbalanced. The danger here is that the supervised learning algorithm will pay too much attention to the majority class, with a deterioration in the classification performance for the minority class, even though the overall accuracy ratio remains high. In order to address this issue, we looked at some oversampling and undersampling methods for the respective processing of the majority and minority classes.
3.2.2. Feature Engineering
Features contain a customer’s personal information, including age, gender, information about education and employment history, credit specifications, such as approved loan amount and duration, information about credit history, and other relevant details, such as objectives and references. In total, there are 14 quantitative and 11 qualitative features. The qualitative features need to be processed by coding methods that render them quantitative, and the three coding methods that we tested for our purposes are one-hot encoding, ordinal encoding, and additive encoding. The differences between these coding methods are not significant for SVM-based models. Nevertheless, for computing the distance between features, one-hot encoding gives better results that the two others. One-hot encoding increases the number of features, which makes the use of principal component analysis (PCA) necessary, and PCA is advantageous in improving the performance of SVM-based models.
PCA, as a dimensionality-reduction method, helps to reduce the number of interesting dimensions in the data space. For our purposes, if we consider the number of principal components whose eigenvalues are greater than 1, the screen plot suggests a choice of fewer than 30 components. The cumulative sum of explained variance ratio, accounting for more than 80% of the explained variance, shows that taking only 30 components is sufficient, although it should be noted that the overall number of components remains high. We tested the impact of PCA on several representative SVM- and RF-based methods. Since PCA radically alters the data space, the performance of the algorithms used may be affected. Thus, we see that the changes in the data structure significantly improve the performance of LSFSVM, but that this is not the case for the RF model; consequently, in our experiments, we decided not to apply PCA in association with the RF model.
4. Data Training and Testing
The second step in our credit scoring methodology corresponds to data training and testing. In assessing the performance of the various methods tested in this paper, we used four metrics: specificity, sensitivity, total accuracy, and AUC. Specificity, sensitivity and total accuracy are calculated using Equations (1)–(3), respectively, while AUC measures the degree of separability between the two classes.
It is important to measure both specificity and sensitivity since each of these plays a role in determining a bank’s credit policy. If specificity is very low, the bank will end up lending to bad customers, with a resulting loss of profit. At the same time, improving the specificity should not be at the expense of sensitivity. Given that good customers are the majority class, even a fraction of a percentage decrease in sensitivity will be significant, representing a lost opportunity to lend to good customers.
4.1. Testing Main ML Methods
We tested the performance of a number of classical ML algorithms on our dataset, in order to subsequently look more closely at those that performed best. Each of the algorithms was found to have its own advantages and disadvantages in building a credit risk evaluation model, but no single one stood out as the overall best performer across all criteria. We can see from Table 1 that the SVM classifier and the random forest classifier have a high total accuracy, while specificity and sensitivity remain acceptable. We therefore proceeded to study the main variants of the SVM and RF methods in some detail.

Table 1.
Results for standard ML methods.
4.2. Testing SVM Methods
SVM-based models include fuzzy SVM (FSVM), bilateral fuzzy SVM (BFSVM), least squares SVM (LSSVM), least squares fuzzy SVM (LSFSVM), weighted least squares SVM (WLSSVM), least squares bilateral fuzzy SVM (LSBFSVM), SVM and bagging, fuzzy SVM and bagging, and least squares fuzzy SVM and bagging.
We see from Table 2 that FSVM and BFSVM have higher specificity than other methods, but sensitivity is low. LSSVM, LSFSVM, WLSSVM and LSBFSVM have higher total accuracy. Considering the trade-off between specificity and sensitivity, LSFSVM and LSBFSVM perform better. The results obtained are acceptable, but as we show below, leveraging RF-based methods may lead to even better numerical results.

Table 2.
Results for SVM-based methods.
4.3. Testing Random Forest Based Models
Alongside SVM, we also tested several RF-based models. Random forest methods are known to be less sensitive to outliers, given that the estimation of a given point is influenced only by local points (i.e., the points located in the same leaf node). Their tree structure means that RF methods are not affected by feature scaling methods, such as normalization or standardization. RF methods also have their own feature selection methods, providing high accuracy and low overfitting. To address the issue of imbalance, we investigated specific random forest methods, as described below.
4.3.1. Weighted Random Forest
Weighted random forest (WRF) is an optimized version of random forest for imbalanced data, based on the principle of cost-sensitive learning. Since the RF classifier tends to be biased toward the majority class, a heavier penalty is placed on misclassifying the minority class. Weighted random forest assigns a weight to each class, with the minority class given a larger weight (i.e., a higher misclassification cost). In our tests, we set “Bad customers weight = 4” and “Good customers weight = 0.2”.
4.3.2. Balanced Random Forest
Balanced random forest (BRF) randomly undersamples each bootstrap sample, artificially altering the class distribution so that classes are represented equally in each tree. Where there is a large imbalance in data, BRF is computationally more efficient since each tree uses only a small portion of the training set to grow. In contrast, WRF needs to use the entire training set. WRF assigns a weight to the minority class, possibly making it more vulnerable to noise than BRF. A majority case that is mislabeled as belonging to the minority class may have a larger impact on the prediction accuracy of the majority class in WRF than in BRF.
4.3.3. Smote and Random Forest
The synthetic minority oversampling technique (SMOTE) is a method used for sampling data. The principle is as follows: for a minority class sample x, randomly choose a K nearest neighbor sample . Generate the new sample with , where is a random value between 0 and 1.
Borderline SMOTE is an improved SMOTE method which divides the minority samples into three categories, namely safe, danger and noise. The method then consists of assigning different weights to these three categories and generating different numbers of samples.
From Table 3, we remark that random forest classifiers perform better as regards specificity and AUC. Balanced random forest (BRF) has higher specificity than weighted random forest (WRF). Borderline SMOTE RF has better sensitivity than random forest. We conclude that BRF performs well with extremely imbalanced data and could be a good candidate for our purposes. In the following subsection, we describe a model that is designed to solve this problem by leveraging prediction probability and thresholds in BRF.

Table 3.
Results for RF-based methods.
5. Going Further—Using Graphic Distribution Analysis
5.1. Graphic Distribution
Graphic distribution of performance (good and bad) across the predicted probabilities of default is a way to visually evaluate the performance of a model. The greater the separation between these distributions, the more accurate the model.
Comparing Figure 1 and Figure 2, we observe that the LSFSVM model fails to clearly separate the two classes. Most of the good customers have a high predicted probability close to 95%, while for the bad customers, probabilities are spread across the whole probability range. Consequently, we conclude that least squares fuzzy SVM does not perform well in relation to our requirements.
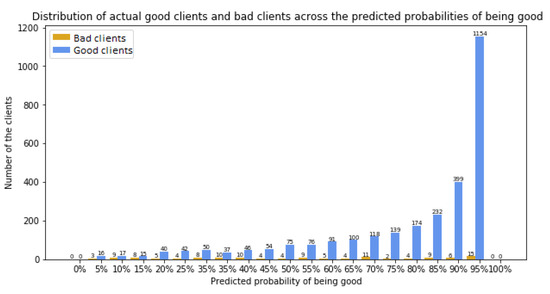
Figure 1.
Distribution of good and bad customers with a least squares fuzzy SVM model.
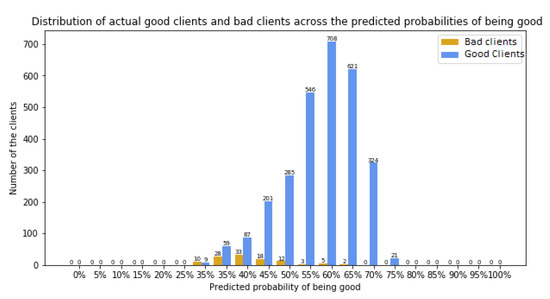
Figure 2.
Distribution of good and bad customers with a balanced random forest model.
In Figure 2, the predicted “bad customers” are to be found mainly in the interval [25%, 50%], and there are no “bad customers” beyond a predicted default of 70%. The predicted “good customers” occur in the interval [45%, 75%]. We can therefore set the predicted probability interval [0%, 70%] as “uncertain”. Figure 2 suggests that the prediction performance might potentially be improved via the use of a graphic distribution. This is our focus in the following section.
5.2. Improved Balanced Random Forest
We now focus on the balanced random forest (BRF) model, and describe an “improved” variant of BRF that draws heavily on the graphic distribution. We note that above a certain threshold, almost all the “good” customers are correctly predicted. We can therefore remove the samples whose probability occurs within [threshold, 1] and who are “certain” (for a high threshold). Next, a new round of classification is run by interchanging the training set with the testing one. Then, the balanced random forest is used on the remaining samples. This is the principle of the method we used to obtain the results below. In our tests, we also considered both high thresholds, intended to remove good customers with a high probability, and low thresholds, to deal with bad customers. All this gave rise to three different versions of the algorithm: a first version in which only good customers are removed in each round; a second version in which only bad customers are removed; and a third version in which some bad and some good customers are removed in each round. Results for the three versions are shown below.
Typically, the first version tries to remove as many good customers as possible who are “certain”, in order to converge to a more balanced dataset and obtain a good classifier. In our model, initially the training set (50% of the whole dataset) trains the model, and the threshold is selected according to the graphic distribution of the training set. The test set (50% of the dataset) is processed by three classifiers in turn. For Classifier 1 we set = . For Classifier 2 we set and . For Classifier 3, where both high and low thresholds are used, we set , , , and .
With respect to the results given in Table 4, and in comparison with the results with BRF, our improved BRF performs better in terms of sensitivity (Classifier 1) and in terms of specificity (Classifier 2), while for Classifier 3, the performance is almost the same as for BRF. BRF can be considered to be a generally effective method, while our improved BRF has the potential to become interesting when a particular focus is placed on dealing with bad customers.

Table 4.
Results for improved BRF.
Looking at the improved BRF method, there is a risk on overfitting if the same training sets are used. In order to overcome this, as already mentioned above, we propose training two models in parallel at each step of the improved BRF algorithm. More specifically, we first split the dataset into two complementary datasets, A and B, then train a model on A which is used to test B, following which we perform training on (remaining) B and use it to test A.
6. Concluding Remarks
The intention behind this study was the creation of an operational credit scoring tool for a bank in Albania. We tested a number of ML methods and found that SVM- and RF-based methods gave promising results. Although SVM-based methods perform well in general, we noticed that precision in relation to the minority class remains less good that what might have been hoped. RF, on the other hand, appears to achieve much better results with our dataset. This is especially true when using the balanced random forest method, which has a good balance among different criteria. Going further, for the case in hand where the main goal is to identify bad customers with a high degree of precision, our improved BRF method could potentially be very useful. To recapitulate our findings, we now have two effective methods, namely balanced random forest and improved balanced random forest. The first performs well overall, while the second is able to detect a large proportion of bad customers, but remains quite “conservative” in identifying good customers. The take-home message from this study is that RF methods are good candidates for dealing with the kind of unbalanced, biased, or incomplete datasets that may be encountered in the case of local banks in developing countries.
Author Contributions
Conceptualization D.N. and O.K.; methodology, D.F. and D.N.; software, D.F.; validation, D.F., D.N. and O.K.; resources, O.K.; data curation, D.F. and O.K., writing, review and editing D.N. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Credins Bank, Tirana, Albania.
Data Availability Statement
Data available on request due to restrictions privacy.
Acknowledgments
The authors wish to thank Zinan Zhou for the support provided in the computation part.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | ROC: Receiver Operating Characteristic. |
References
- Ampountolas, Apostolos, Titus Nyarko Nde, Paresh Date, and Corina Constantinescu. 2021. A machine learning approach for micro-credit scoring. Risks 9: 50. [Google Scholar] [CrossRef]
- Baesens, Bart, Tony Van Gestel, Stijn Viaene, Maria Stepanova, Johan Suykens, and Jan Vanthienen. 2003. Benchmarking state-of-the-art classification algorithms for credit scoring. Journal of the Operational Research Society 54: 627–35. [Google Scholar] [CrossRef]
- Banasik, John, Jonathan Crook, and Lyn Thomas. 2003. Sample selection bias in credit scoring models. Journal of the Operational Research Society 54: 822–32. [Google Scholar] [CrossRef]
- Batuwita, Rukshan, and Vasile Palade. 2010. Fsvm-cil: Fuzzy support vector machines for class imbalance learning. IEEE Transactions on Fuzzy Systems 18: 558–71. [Google Scholar] [CrossRef]
- Boser, Bernhard E., Isabelle M. Guyon, and Vladimir N. Vapnik. 1992. A training algorithm for optimal margin classifiers. Paper presented at Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, July 27–29; pp. 144–52. [Google Scholar]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef] [Green Version]
- Brown, Iain, and Christophe Mues. 2012. An experimental comparison of classification algorithms for imbalanced credit scoring data sets. Expert Systems with Applications 39: 3446–53. [Google Scholar] [CrossRef] [Green Version]
- Brygała, Magdalena. 2022. Consumer bankruptcy prediction using balanced and imbalanced data. Risks 10: 24. [Google Scholar] [CrossRef]
- De Melo Junior, Leopoldo Soares, Franco Maria Nardini, Chiara Renso, and José Antônio Fernandes de Macêdo. 2019. An empirical comparison of classification algorithms for imbalanced credit scoring datasets. Paper presented at 18th IEEE International Conference On Machine Learning And Applications (ICMLA), Boca Raton, FL, USA, December 16–19; pp. 747–54. [Google Scholar]
- Dinca, Gheorghita, and Madalina Bociu. 2015. Using discriminant analysis for credit decision. Bulletin of the Transilvania University of Brasov. Economic Sciences. Series V 8: 277. [Google Scholar]
- Galindo, Jorge, and Pablo Tamayo. 2000. Credit risk assessment using statistical and machine learning: Basic methodology and risk modeling applications. Computational Economics 15: 107–43. [Google Scholar] [CrossRef]
- Karlis, Dimitris, and Mohieddine Rahmouni. 2007. Analysis of defaulters’ behaviour using the Poisson-mixture approach. IMA Journal of Management Mathematics 18: 297–311. [Google Scholar] [CrossRef]
- Kil, Krzysztof, Radosław Ciukaj, and Justyna Chrzanowska. 2021. Scoring models and credit risk: The case of cooperative banks in poland. Risks 9: 132. [Google Scholar] [CrossRef]
- Laitinen, Erkki K., and Teija Laitinen. 2000. Bankruptcy prediction: Application of the Taylor’s expansion in logistic regression. International Review of Financial Analysis 9: 327–49. [Google Scholar] [CrossRef]
- Lee, Tian-Shyug, Chih-Chou Chiu, Chi-Jie Lu, and I-Fei Chen. 2002. Credit scoring using the hybrid neural discriminant technique. Expert Systems with Applications 23: 245–54. [Google Scholar] [CrossRef]
- Lessmann, Stefan, Bart Baesens, Hsin-Vonn Seow, and Lyn C. Thomas. 2015. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research 247: 124–36. [Google Scholar] [CrossRef] [Green Version]
- Lin, Chun Fu, and Sheng De Wang. 2002. Fuzzy support vector machines. IEEE Transactions on Neural Networks 13: 464–71. [Google Scholar] [CrossRef]
- Lundberg, Scott M., and Su-In Lee. 2017. A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems. Long Beach: The MIT Press, pp. 4765–74. [Google Scholar]
- Mukid, M. A., T. Widiharih, A. Rusgiyono, and A. Prahutama. 2018. Credit scoring analysis using weighted k nearest neighbor. Journal of Physics: Conference Series 1025: 12114. [Google Scholar] [CrossRef]
- Ortuño, M. Artís, Montserrat Guillén, and JOSÉ Ma Martínez. 1994. A model for credit scoring: An application of discriminant analysis. Qüestiió: Quaderns D’estadística i Investigació Operativa 18. [Google Scholar]
- Pang, Su-Lin, Yan-Ming Wang, and Yuan-Huai Bai. 2002. Credit scoring model based on neural network. Paper presented at International Conference on Machine Learning and Cybernetics, Beijing, China, November 4–5; Volume 4, pp. 1742–46. [Google Scholar]
- Schebesch, Klaus B., and Ralf Stecking. 2005. Support vector machines for classifying and describing credit applicants: Detecting typical and critical regions. Journal of the Operational Research Society 56: 1082–88. [Google Scholar] [CrossRef]
- Suykens, Johan A. K., Jos De Brabanter, Lukas Lukas, and Joos Vandewalle. 2002. Weighted least squares support vector machines: Robustness and sparce approximation. Neurocomputing 48: 85–105. [Google Scholar] [CrossRef]
- West, David. 2000. Neural network credit scoring models. Computers & Operations Research 27: 1131–52. [Google Scholar]
- Yang, Weixin, and Lingguang Li. 2018. Efficiency evaluation of industrial waste gas control in china: A study based on data envelopment analysis (dea) model. Journal of Cleaner Production 179: 1–11. [Google Scholar] [CrossRef]
- Yang, Weixin, Hao Gao, and Yunpeng Yang. 2022. Analysis of influencing factors of embodied carbon in china’s export trade in the background of “carbon peak” and “carbon neutrality”. Sustainability 14: 3308. [Google Scholar] [CrossRef]
- Yu, Lean. 2014. Credit risk evaluation with a least squares fuzzy support vector machines classifier. Discrete Dynamics in Nature and Society 2014: 564213. [Google Scholar] [CrossRef]
- Yu, Lean, Shouyang Wang, Kin Keung Lai, and Ligang Zhou. 2008. Bio-Inspired Credit Risk Analysis: Computational Intelligence with Support Vector Machines. Berlin: Springer. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).