1. Introduction
Sensitivity analysis is indispensable for model building, model interpretation, and model validation, as it provides insight into the relationship between model inputs and outputs. A key tool used for sensitivity analysis are sensitivity measures, that assign to each model input a score, representing an input factor’s ability to explain the variability of a model output’s summary statistic; see
Saltelli et al. (
2008) and
Borgonovo and Plischke (
2016) for an in-depth review. One of the most widely used output summary statistic is the variance, which gives rise to sensitivity measures, e.g., the Sobol indices, that apportion the uncertainty in the output’s variance to input factors. In many applications, such as reliability management and financial and insurance risk management, however, the variance is not the output statistic of concern and instead quantile-base measures are used; indicatively, see
Asimit et al. (
2019);
Fissler and Pesenti (
2022);
Maume-Deschamps and Niang (
2018);
Tsanakas and Millossovich (
2016). Furthermore, typical for financial risk management applications is that model inputs are subject to distributional uncertainty. Probabilistic (or global) sensitivity measures, however, tacitly assume that the model’s distributional assumptions are correctly specified; indeed, sensitivity measures based on the difference between conditional (on a model input) and unconditional densities (of the output) are termed “common rationale”
Borgonovo et al. (
2016). Examples include indices, such as Borgonovo’s sensitivity measures
Borgonovo (
2007), the
f-sensitivity index
Rahman (
2016), and sensitivity indices based on the Cramér–von Mises distance
Gamboa et al. (
2018), we also refer to
Plischke and Borgonovo (
2019) for a detailed overview and to
Gamboa et al. (
2020) for estimation of these sensitivity measures. Recently,
Plischke and Borgonovo (
2019) define sensitivity measures that depend only on the copula between input factors, whereas
Pesenti et al. (
2021) propose a sensitivity measure based on directional derivatives that take dependence between input factors into account. Estimating these sensitivities, however, may render difficult in application where joint observations are scarce, e.g., insurance portfolios, and their interpretation may be limited as dependence structures are commonly specified by expert opinions
Denuit et al. (
2006).
We consider an alternative sensitivity analysis framework proposed in
Pesenti et al. (
2019) that (a) considers statistical summaries relevant to risk management, (b) applies to models subject to distributional uncertainty, thus instead of relying on correctly specified distributions from which to calculate sensitivity measures we derive alternative distributions that fulfil a specific probabilistic stress and are “closest” to the baseline distribution; and (c) studies reverse sensitivity measures. Differently to the framework proposed in
Pesenti et al. (
2019) who use the Kullback–Leibler divergence to quantify the closedness of probability measures, in this work we consider the Wasserstein distance of order two to measure the distance between distribution functions. The Wasserstein distance allows for more flexibility in the choice of stresses including survival probabilities (via quantiles) used in reliability analysis, risk measures employed in finance and insurance, and utility functions relevant for decision under ambiguity.
Central to the reverse sensitivity analysis framework is a
baseline model, the 3-tuple
, consisting of random input factors
, an aggregation function
mapping input factors to a univariate output
, and a probability measure
. The methodology has been termed
reverse sensitivity analysis by
Pesenti et al. (
2019) since it proceeds in a reverse fashion to classical sensitivity analysis where input factors are perturbed and the corresponding altered output is studied. Indeed, in the reverse sensitivity analysis proposed by
Pesenti et al. (
2019) a stress on the output’s distribution is defined and changes in the input factors are monitored. The quintessence of the sensitivity analysis methodology is, however, not confined to stressing the output’s distribution, it is also applicable to stressing an input factor and observing the changes in the model output and in the other inputs. Throughout the exposition, we focus on the reverse sensitivity analysis that proceeds via the following steps:
- (i)
Specify a stress on the baseline distribution of the output;
- (ii)
Derive the unique stressed distribution of the output that is closest in the Wasserstein distance and fulfils the stress;
- (iii)
The stressed distribution induces a canonical Radon–Nikodym derivative ; a change of measures from the baseline to the stressed probability measure ;
- (iv)
Calculate sensitivity measures that reflect an input factors’ change in distribution from the baseline to the stressed model.
Sensitivity testing using divergence measures–in the spirit of the reverse sensitivity methodology–has been studied by
Cambou and Filipović (
2017) using
f-divergences on a finite probability space; by
Pesenti et al. (
2019) and
Pesenti et al. (
2021) using the Kullback–Leibler divergence; and
Makam et al. (
2021) consider a discrete sample space combined with the
-divergence. It is however known that the set of distribution functions with finite
f-divergence, e.g., the Kullback–Leibler and
divergence–around a baseline distribution function depends on the baseline’s tail-behaviour, thus the choice of
f-divergence should be chosen dependent on the baseline distribution
Kruse et al. (
2019). The Wasserstein distance on the contrary, automatically adapts to the baseline distribution function in that the Wasserstein distance penalises dissimilar distributional features such as different tail behaviour
Bernard et al. (
2020). The Wasserstein distance has enjoyed numerous applications to quantify distributional uncertainty, see, e.g.,
Blanchet and Murthy (
2019) and
Bernard et al. (
2020) for applications to financial risk management. In the context of uncertainty quantification,
Moosmüeller et al. (
2020) utilise the Wasserstein distance to elicit the (uncertain) aggregation map
g from the distributional knowledge of the inputs and outputs.
Fort et al. (
2021) utilises the Wasserstein distance to introduce global sensitivity indices for computer codes whose output is a distribution function. In this manuscript we use the Wasserstein distance as it allows for different stresses compared to the Kullback–Leibler divergence. Indeed, the Wasserstein distance allows for stresses on any distortion risk measures, while the Kullback–Leibler divergence only allow for stresses on risk measures which are Value-at-Risk (VaR) and VaR and Expected Shortfall jointly, see
Pesenti et al. (
2019).
This paper is structured as follows: In
Section 2, we state the notation and definitions necessary for the exposition.
Section 3 introduces the optimisation problems and we derive the unique stressed distribution function of the output which has minimal Wasserstein distance to the baseline output’s distribution and satisfies a stress. The considered stresses include constraints on risk measures, quantiles, expected utilities, and combinations thereof. In
Section 4, we characterise the canonical Radon–Nikodym derivative, induced by the stressed distribution function, and study how input factors’ distributions change when moving from the baseline to the stressed model. An application of the reverse sensitivity analysis is demonstrated on a mixture model in
Section 5.
3. Deriving the Stressed Distribution
Throughout this section we assume that the modeller’s
baseline model is the 3-tuple
consisting of a random vector of input factors
, an aggregation function
mapping input factors to a (for simplicity) univariate output
, and a probability measure
. The baseline probability measure
reflects the modeller’s (statistical and expert) knowledge of the distribution of
and we denote the distribution function of the output by
. The modeller then performs reverse sensitivity analysis, that is tries to understand how prespecified stresses/constraints on the output distribution
F, e.g., an increase in jointly its mean and standard deviation or a risk measures such as the Value-at-Risk (VaR) or Expected Shortfall (ES), affects the baseline model, e.g., the joint distribution of the input factors. For this, we first define the notion of a
stressed distribution. Specifically, for given constraints we call a solution to the optimisation problem
a stressed distribution. In problem (
1), the baseline distribution
F is fixed and we seek over all alternative distributions
the one who satisfies the stress(es) and which has smallest Wasserstein distance to
F. The solution to problem (
1)–the stressed distribution–may be interpreted as the most “plausible” distribution function arising under adverse circumstances. Examples of stresses and constraints considered in this work include an increase (decrease), compared to their corresponding values under the reference probability
, in e.g., the mean, mean and standard deviation, distortion risk measures, and utility functions, and combinations thereof.
Next, we recall the concept of weighted isotonic projection which is intrinsically connected to the solution of optimisation problem (
1); indeed the stressed quantile functions can be uniquely characterised via weighted isotonic projections.
Definition 2 (Weighted Isotonic Projection
Barlow et al. (
1972))
. The weighted isotonic projection of a function with weight function , , is its weighted projection onto the set of non-decreasing and left-continuous functions in . That is, the unique function satisfying When the weight function is constant, i.e.,
,
, we write
, as in this case the isotonic projection is indeed independent of
c. The weighted isotonic projection admits not only a graphical interpretation as the non-decreasing function that minimises the weighted
-distance from
ℓ but has also a discrete counterpart: the weighted isotonic regression
Barlow et al. (
1972). Numerically efficient algorithms for calculating weighted isotonic regressions are available, e.g., the
R package
isotone De Leeuw et al. (
2010).
In the next sections, we solve problem (
1) for different choices of constraints. Specifically, for risk measures constraints (
Section 3.1), integral constraints (
Section 3.2), Value-at-Risk constraints (
Section 3.3), and expected utility constraint (
Section 3.4), and in
Section 3.5 we consider ways to smooth stressed distributions. Using these stressed distributions, we derive the stressed probability measures in
Section 4 and study how a stress on the output is reflected on the input distribution(s).
3.1. Risk Measure Constraints
This section considers stresses on distortion risk measures, that is we derive the unique stressed distribution that satisfies an increase and/or decrease of distortion risk measures while minimising the Wasserstein distance to the baseline distribution F.
Definition 3 (Distortion Risk Measures)
. Let be a square-integrable function with and . Then the distortion risk measure with distortion weight function γ is defined as The above definition of distortion risk measures makes the assumption that positive realisations are undesirable (losses) while negative realisations are desirable (gains). The class of distortion risk measures includes one of the most widely used risk measures in financial risk management, the Expected Shortfall (ES) at level
(also called Tail Value-at-Risk), with
, see, e.g.,
Acerbi and Tasche (
2002). The often used risk measure Value-at-Risk (VaR), while admitting a representation given in (
2), has a corresponding weight function
that is not square-integrable. We derive the solution to optimisation problem (
1) with a VaR constraint in
Section 3.3.
Theorem 1 (Distortion Risk Measures)
. Let , be a distortion risk measure with weight function and assume there exists a distribution function satisfying for all . Then, the optimisation problemhas a unique solution given by where the Lagrange multipliers are such that the constraints are fulfilled, that is for all . In the above theorem, and also in later results, we assume that there exists a distribution function which satisfies all constraints. This assumption is not restrictive and requires that, particularly, multiple constraints are chosen carefully, e.g., imposing that for , i.e., the mean being larger than the , cannot be fulfilled by any distribution function; thus, a combination of stresses not of interest to a modeller.
We observe that the optimal quantile function is the isotonic projection of a weighted linear combination of the baseline’s quantile function
and the distortion weight functions of the risk measures. A prominent group of risk measures is the class of coherent risk measures, that are risk measures fulfilling the properties of monotonicity, positive homogeneity, translation invariance, and sub-additivity; see
Artzner et al. (
1999) for a discussion and interpretation. It is well-known that a distortion risk measure is coherent, if and only if, its distortion weight function
is non-decreasing
Kusuoka (
2001). For the special case of a constraint on a coherent distortion risk measure that results in a larger risk measure compared to the baseline’s, we obtain an analytical solution without the need to calculate an isotonic projection.
Proposition 1 (Coherent Distortion Risk Measure)
. If is a coherent distortion risk measure and , then optimisation problem (3) with has a unique solution given by We illustrate the stressed distribution functions for constraints on distortion risk measures in the next example. Specifically, we look at the - risk measures which are a parametric family of distortion risk measures.
Example 1 (
-
Risk Measure)
. The α-β risk measure, , is defined bywhere and is the normalising constant. This parametric family contains several notable risk measures as special cases: for we obtain , and for the conditional lower tail expectation (LTE) at level β.Moreover, if the α-β risk measure emphasises losses (gains) relative to gains (losses). For and , the risk measure is equivalent to , where and .
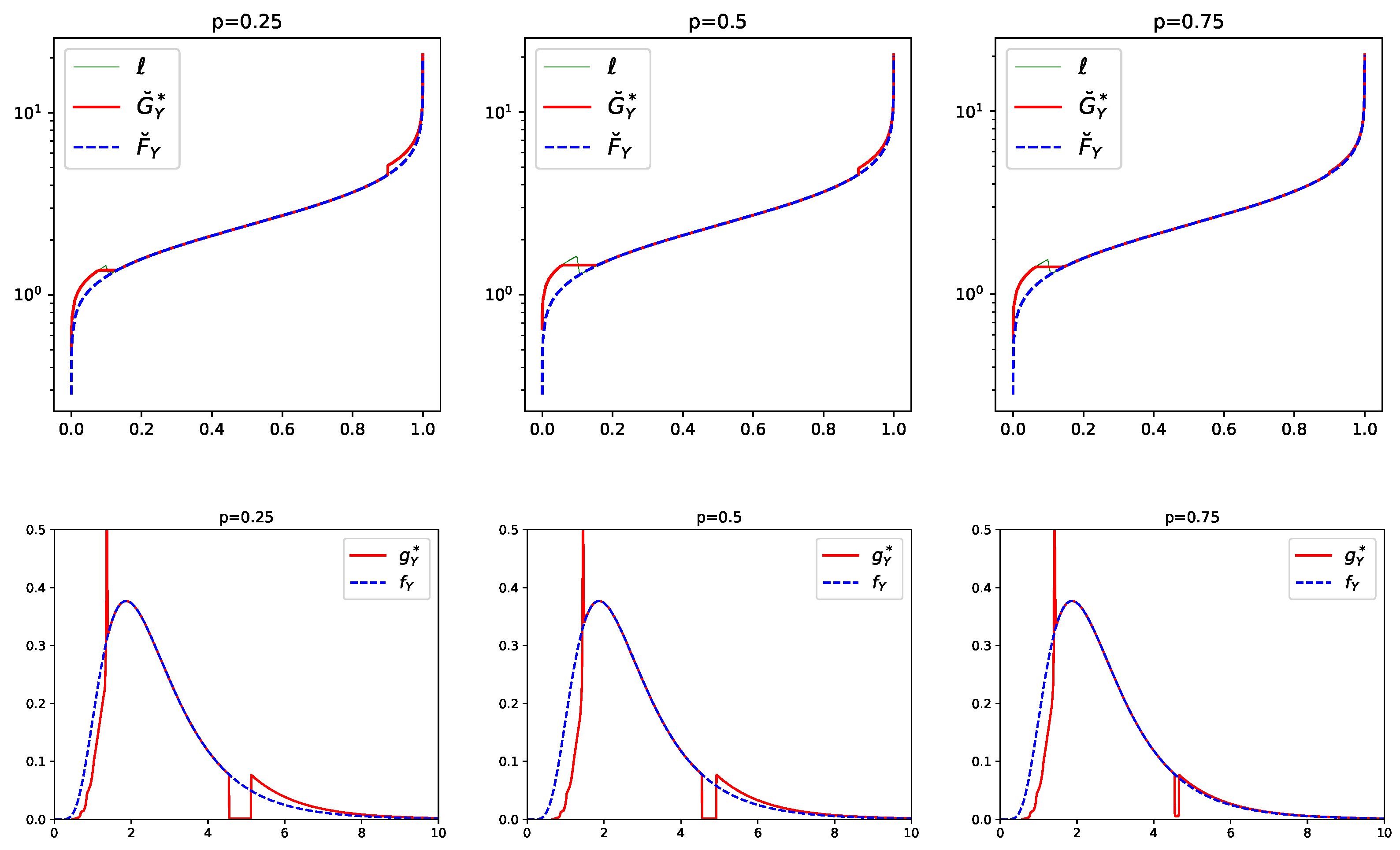
Figure 1 displays the baseline and the stressed quantile functions of a random variable Y under a 10% increase on the α-β risk measure with , , and various . The baseline distribution is chosen to be is with parameters and . We observe in Figure 1 that the stressed quantile functions have, in all three plots, a flat part which straddles and a jump at . The length of the flat part is increasing with increasing p while the size of the jump is decreasing with increasing p. This can also be seen in the stressed densities which have, for all values of p, a much heavier right albeit a much lighter left tail than the density of the baseline model. Thus, under this stress, both tails of the baseline distribution are altered. 3.2. Integral Constraints
The next results are generalisations of stresses on distortion risk measures to integral constraints, and include as a special case a stress jointly on the mean, the variance, and distortion risk measures.
Theorem 2 (Integral)
. Let be square-integrable functions and assume there exists a distribution function satisfying and for all , and . Then the optimisation problemhas a unique solution given by where and the Lagrange multipliers and are non-negative and such that the constraints are fulfilled. A combination of the above theorems provides stresses jointly on the mean, the variance, and on multiple distortion risk measures.
Proposition 2 (Mean, Variance, and Risk Measures).
Let , , , and distortion risk measures , . Assume there exists a distribution function with mean , standard deviation , and which satisfies , for all . Then the optimisation problemhas a unique solution given byand the Lagrange multipliers with are such that the constraints are fulfilled. Example 2 (Mean, Variance, and ES)
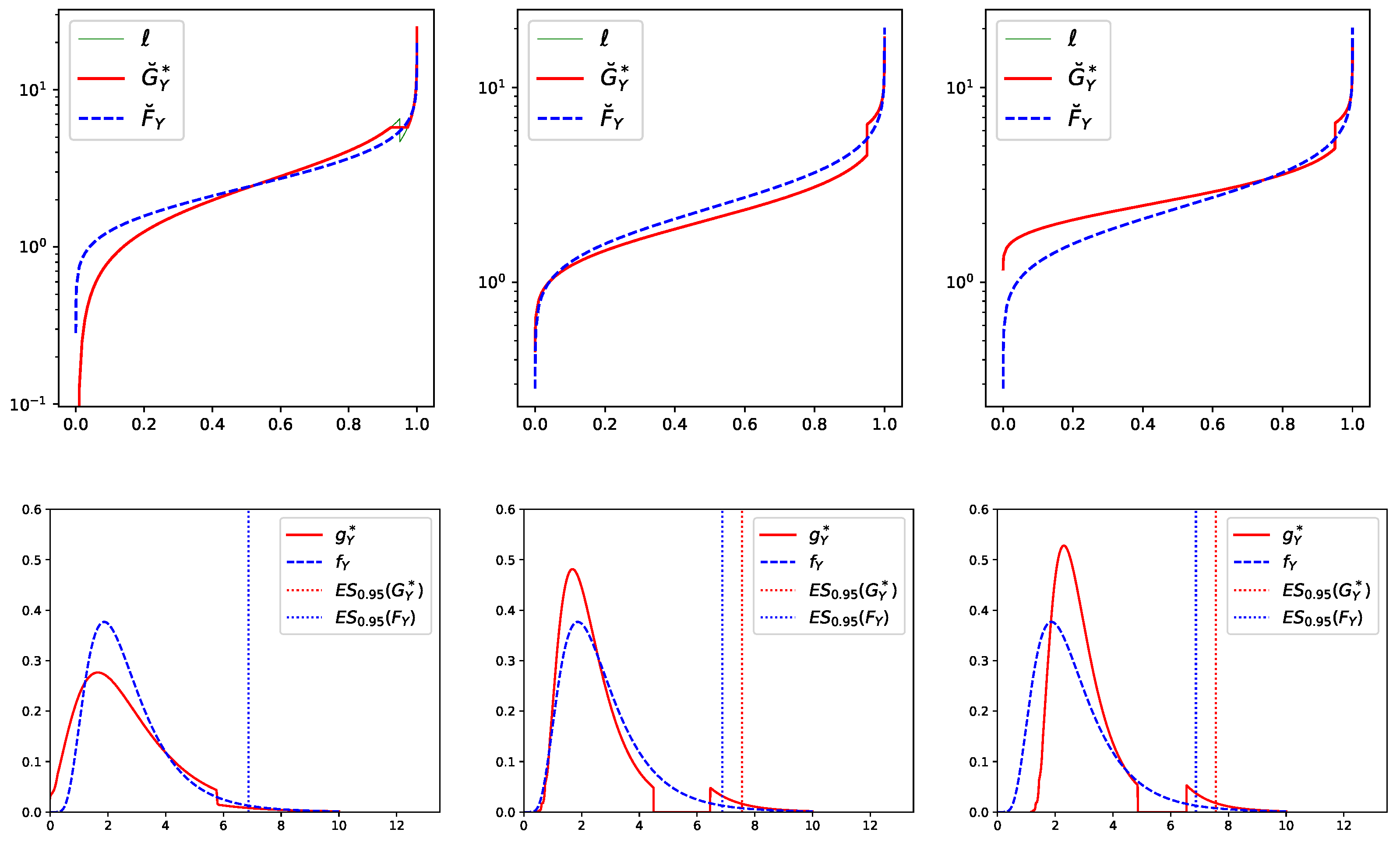
. Here, we illustrate Proposition 2 with the ES risk measure and three different stresses. The top panels of Figure 2 display the baseline quantile function and the stressed quantile function of Y, where the baseline distribution of Y is again with parameters and . The bottom panels display the corresponding baseline and stressed densities. The left panels correspond to a stress, where, under the stressed model, the and the mean are kept fixed at their corresponding values under the baseline model, while the standard deviation is increased by 20%. We observe, both in the quantile and density plot, that the stressed distribution is more spread out indicating a larger variance. Furthermore, at the stressed density drops to ensure that . This drop is due to the fact that a stress composed of a 20% increase in the standard deviation while fixing the mean (i.e., without a constraint on ) results in an ES that is larger compared to the baseline’s. Indeed, under this alternative stress (without a constraint on ES) we obtain that compared to .The middle panels correspond to a 10% increase in and a 10% decrease in the mean, while keeping the standard deviation fixed at its value under the baseline model. The density plot clearly indicates a general shift of the stressed density to the left, stemming from the decrease in the mean, and a single trough which is induced by the increase in ES. The right panels correspond to a 10% increase in , a 10% increase in the mean, and a 10% decrease in the standard deviation. The stressed density still has the trough from the increase in ES; however, the density is less spread out (reduction in the standard deviation) and generally shifted to the right (increase in the mean).
3.3. Value-at-Risk Constraints
In this section we study stresses on the risk measure Value-at-Risk (VaR). The VaR at level
of a distribution function
is defined as its left-continuous quantile function evaluated at
, that is
We further define the right-continuous
, that is the right-continuous quantile function of
evaluated at
, by
Theorem 3 (
)
. Let and consider the optimisation problemand define such that . Then, the following holds- (i)
under constraint (a), if , then the unique solution is given by if , then there does not exist a solution.
- (ii)
under constraint (b), if , then the unique solution is given by if , then there does not exist a solution.
The above theorem states that if the optimal quantile function exists it is either the baseline quantile function or constant equal to q. Moreover, the stressed quantile function (if it exists) jumps at which implies that the existence of a solution hinges on the careful choice of the stress. For a stress on (constraint (a)) for example, a solution exists if and only if the constraint satisfies ; a decrease in the from the baseline to the stressed model. The reason for the non-existence of a solution when stressing VaR upwards is that the unique increasing function that minimises the Wasserstein distance and satisfies the constraint is not left-continuous and thus not a quantile function.
Alternatively to stressing VaR or
, and in particularly in the case when a desired stressed solution does not exist, one may stress instead the distortion risk measure Range-Value-at-Risk (RVaR)
Cont et al. (
2010). The RVaR at levels
is defined by
and belongs to the class of distortion risk measures. The
attains as limiting cases the VaR and
. Indeed, for any
it holds
The solution to stressing is provided in Theorem 1.
3.4. Expected Utility Constraint
This section considers the change from the baseline to the stressed distribution under an increase of an expected utility constraint. In the context of utility maximisation, the next theorem provides a way to construct stressed models with a larger utility compared to the baseline.
Theorem 4 (Expected Utility and Risk Measures)
. Let be a differentiable concave utility function, , and be distortion risk measures, for . Assume there exists a distribution function satisfying and for all . Then the optimisation problemhas a unique solution given by where is the left-inverse of , and , are such that the constraints are fulfilled. The utility function in Theorem 4 need not be monotone, indeed the theorem applies to any differentiable concave function, without the need of an utility interpretation. Moreover, Theorem 4 also applies to differentiable convex (disutility) functions and constraint ; a situation of interest in insurance premium calculations. In this case, the solution is given by (5) with .
Example 3 (HARA Utility & ES)
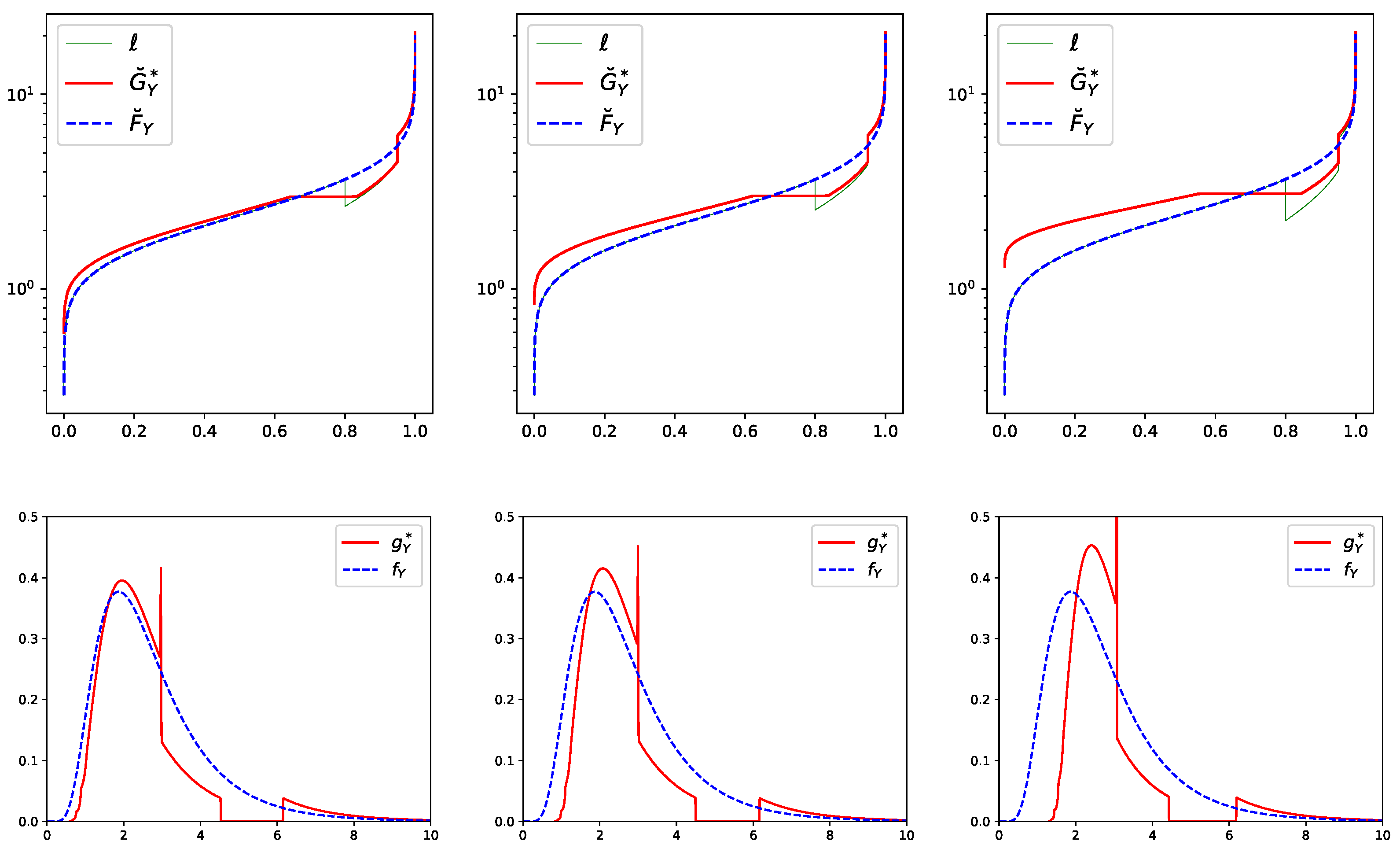
. The Hyperbolic absolute risk aversion (HARA) utility function is defined bywith parameters , , and where guarantees concavity.We again choose the baseline distribution of Y to be with and and consider utility parameters , , and . Figure 3 displays the baseline and the stressed quantile functions and , respectively, for a combined stress on the HARA utility and on at levels 0.8 and 0.95. Specifically, for all three stresses we decreasing by 10% and increasing by 10% compared to their values under the baseline model. Moreover, the HARA utility is increased by 0%, 1%, and 3%, respectively, corresponding to the panels from the left to the right. The flat part in the stressed quantile function around , visible in all top panels of Figure 3, is induced by the decrease in while the jump at is due to the increase in . From the left to the right panel in Figure 3, we observe that the larger the stress on the HARA utility, the more the stressed quantile function shifts away from the baseline quantile function . 3.5. Smoothing of the Stressed Distribution
We observe that the stressed quantile functions derived in
Section 3 generally contain jumps and/or flat parts even if the baseline distribution is absolutely continuous. In situation where this is not desirable, one may consider a smoothed version of the stressed distributions. For this, we recall that the isotonic regression, the discrete counterpart of the weighted isotonic projection, of a function
ℓ evaluated at
with positive weights
, is the solution to
There are numerous efficient algorithms that solve (6) most notably the pool-adjacent-violators (PAV) algorithm
Barlow et al. (
1972). It is well-known that the solution to the isotonic regression contains flat parts and jumps. A smoothed isotonic regression algorithm, termed smooth pool-adjacent-violators (SPAV) algorithm, using an
regularisation was recently proposed by
Sysoev and Burdakov (
2019). Specifically, they consider
where
,
, are prespecified smoothing parameters. Using a probabilitistic reasoning,
Sysoev and Burdakov (
2019) argue that
may be chosen proportional to a (e.g., quadratic) kernel evaluated at
and
, that is
The choice of smoothing parameter
correspond to the original isotonic regression larger values of
correspond to a greater degree of smoothness of the solution.
can either be prespecified or estimated using cross-validation, see e.g.,
Sysoev and Burdakov (
2019).
To guarantee that the smoothed quantile function still fulfils the constraint, one may replace in every step of the optimisation for finding the Lagrange parameter the PAV with the SPAV algorithm. Thus, the Lagrange parameter are indeed found such that the constraints are fulfilled.
Remark 1. There are numerous works proposing smooth versions of isotonic regressions. Approaches include kernel smoothers, e.g., Hall and Huang (2001), and spline techniques, e.g., Meyer (2008). These algorithms, however, are computationally heavy in that their computational cost is , where n is the number of data points. Furthermore, these algorithm require a careful choice of the kernel or the spline basis which is in contrast to the SPAV. We refer the reader to Sysoev and Burdakov (2019) for a detailed discussion and references to smooth isotonic regression algorithms. 4. Analysing the Stressed Model
Recall that a modeller is equipped with a baseline model, the 3-tuple
, consisting of a set of input factors
, a univariate output random variable of interest,
, and a probability measure
. For a stress on the output’s baseline distribution
, we derived in
Section 3 the corresponding unique stressed distribution function, denoted here by
. Thus, to fully specify the stressed model we next define a stressed probability measure
that is induced by
.
4.1. The Stressed Probability Measures
A stressed distribution
induces a canonical change of measure that allows the modeller to understand how the baseline model including the distributions of the inputs changes under the stress. The Radon–Nikodym (RN) derivative of the baseline to the stressed model is
where
and
denote the densities of the baseline and stressed output distribution, respectively. The RN derivative is well-defined since
,
-a.s. The distribution functions of input factors under the stressed model – the stressed distributions – are then given, e.g., for input
,
, by
and for multivariate inputs
by
where
denotes the expectation under
. Note that under the stressed probability measure
, the input factors’ marginal and joint distributions may be altered.
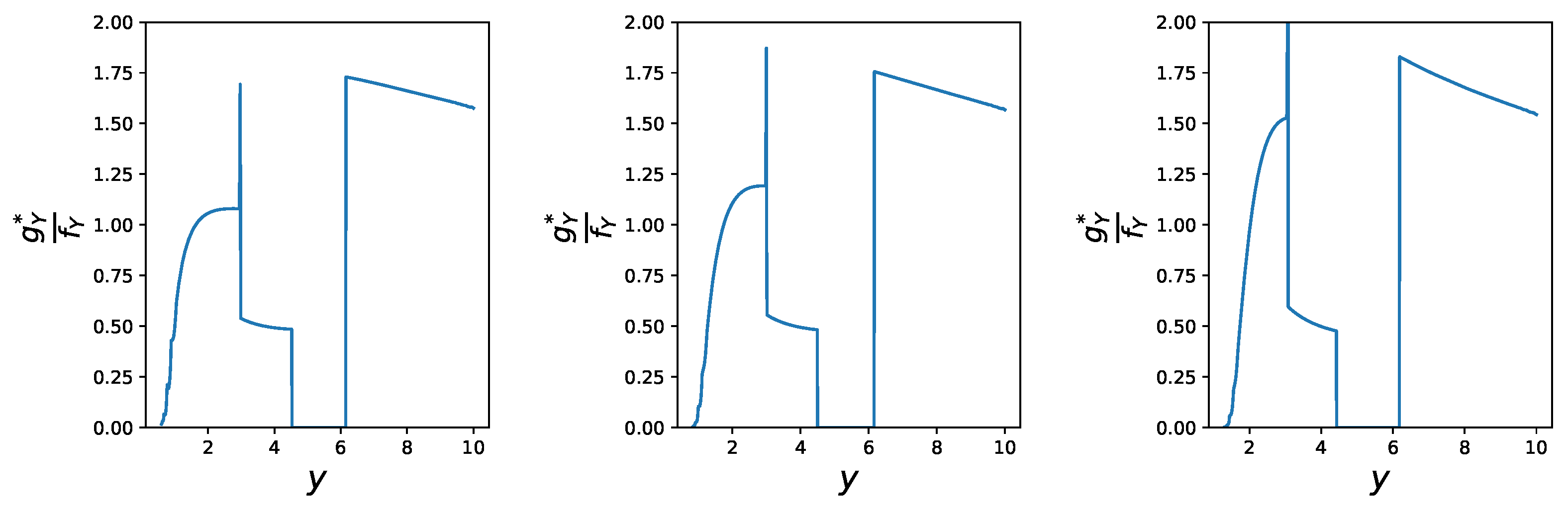
Example 4 (HARA Utility & ES continued). We continue Example 3 and illustrate the RN-densities for the following three stresses (from the left to the right panel): a 10% decrease in and a 10% increasing for all three stresses, and a 0%, 1%, and 3% increase in the HARA utility, respectively.
We observe in Figure 4, that for all three stresses large realisations of Y obtain a larger weight under the stressed probability measures compared to the baseline probability . Indeed, for all three stresses it holds that whenever and . This is in contrast to small realisations of Y which obtain a weight smaller than 1. The impact of the different levels of stresses of the HARA utility (0%, 1%, and 3%, from the left to the right panel) can be observed in the left tail of ; a larger stress on the utility induces larger weights. The length of the trough of is increasing from the left panel (approx. ()) to the right panel (approx. ()), and corresponds in all cases to the constant part in (see Figure 3, top panels) which is induced by the decrease in under the stressed model. 4.2. Reverse Sensitivity Measures
Comparison of the baseline and a stressed model can be conducted via different approaches depending on the modeller’s interest. While probabilistic sensitivity measures underlie the assumption of a fixed probability measure and quantify the divergence between the conditional (on a model input) and the unconditional output density
Saltelli et al. (
2008), the proposed framework compares a baseline and a stressed model, i.e., distributions under different probability measures. Therefore, to quantify the distributional change in input factor
from the baseline
to the stressed
probability, a sensitivity measure introduced by
Pesenti et al. (
2019) may be suitable which quantifies the variability of an input factor’s distribution from the baseline to the stressed model. A generalisation of the reverse sensitivity measure is stated here.
Definition 4 (Marginal Reverse Sensitivity Measure
Pesenti et al. (
2019))
. For a function , the reverse sensitivity measure to input with respect to a stressed probability measure is defined by where is the set of all probability measures whose RN-derivative have the same distribution as under . We adopted the convention that and . The sensitivity measure is called “reverse”, as the stress is applied to the output random variable
Y and the sensitivity monitors the change in input
. The definition of 4 applies, however, also to stresses on input factors, in which case the RN-density
is a function of the stressed input factor and we refer to
Pesenti et al. (
2019) for a discussion. Note, that the reverse sensitivity measure can be viewed as a normalised covariance measure between the input
and the Radon Nikodym derivative
.
The next proposition provides a collection of properties that the reverse sensitivity measure possesses, we also refer to
Pesenti et al. (
2019) for a detailed discussion of these properties. For this, we first recall the definition of comonotonic and counter-monotonic random variables.
Definition 5. Two random variables and are comonotonic under , if and only if, there exists a random variable W and non-decreasing functions , such that the following equalities hold in distribution underThe random variables and are counter-monotonic under , if and only if, (7) holds with one of the functions being non-increasing, and the other non-decreasing. If two random variables are (counter) comonotonic under one probability measure, then they are also (counter) comonotonic under any other absolutely continuous probability measure, see, e.g., Proposition 2.1 of
Cuestaalbertos et al. (
1993). Thus, we omit the specification of the probability measure when discussing counter- and comonotonicity.
Proposition 3 (Properties of Reverse Sensitivity Measure). The reverse sensitivity measure possesses the following properties:
- (i)
;
- (ii)
if are independent under ;
- (iii)
if and only if are comonotonic;
- (iv)
if and only if are counter-comonotonic.
The function provides the flexibility to create sensitivity measures that quantify changes in moments, e.g., via , , or in the tail of distributions, e.g., via , for .
Next, we generalise Definition 4 to a sensitivity measure that accounts for multiple input factors. While measures the change of the distribution of from the baseline to the stressed model the sensitivity introduced below, quantifies how the joint distribution of changes when moving from to .
Definition 6 (Bivariate Reverse Sensitivity Measure)
. For a function , the reverse sensitivity measure to inputs with respect to a stressed probability measure is defined by where is given in Definition 4. The bivariate sensitivity measure satisfies all the properties in Proposition 3 when is replaced by . The bivariate sensitivity can also be generalised to k input factors by choosing a function .
Remark 2. Probabilistic sensitivity measures are typically used for importance measurement and take values in ; with 1 being the most important input factor and 0 being (desirably) independent from the output Borgonovo et al. (2021). This is in contrast to our framework where lives in and e.g., a negative dependence, such as negative quadrant dependence between and implies that , see Pesenti et al. (2019) [Proposition 4.3]. Thus, the proposed sensitivity measure is different in that it allows for negative sensitivities where the sign of indicates the direction of the distributional change. 5. Application to a Spatial Model
We consider a spatial model for modelling insurance portfolio losses where each individual loss occurs at different locations and the dependence between individual losses is a function of the distance between the locations of the losses. Mathematically, denote the locations of the insurance losses by , where are the coordinates of location , . The insurance loss at location m, denoted by , follows a distribution with location parameter 25. Thus, the minimum loss at each location is 25 and locations with larger mean also exhibit larger standard deviations. The losses have, conditionally on , a Gaussian copula with correlation matrix given by , where denotes the Euclidean distance. Thus, the further apart the locations and are the smaller the correlation between and . The parameter takes values with probabilities that represent different regimes. Indeed, corresponds to a correlation of 1 between all losses, independently of their location. Larger values of correspond to smaller albeit still positive correlation. Thus, regime with can be viewed as, e.g., circumstances suitable for natural disasters. We further define the total loss of the insurance company by .
We perform two different stresses on the total loss
Y detailed in
Table 1. Specifically, we consider as a first stress a 0% change in HARA utility, a 0% change in
, and a 1% increase in
from the baseline to the stressed model. The second stress is composed of a 1% increase in HARA utility, a 1% increase in
, and a 3% increase in
compared to the baseline model. As the second stress increases all three metrics it may be viewed as a more severe distortion of the baseline model.
Next, we calculate reverse sensitivity measures for the losses
for both stresses
and
.
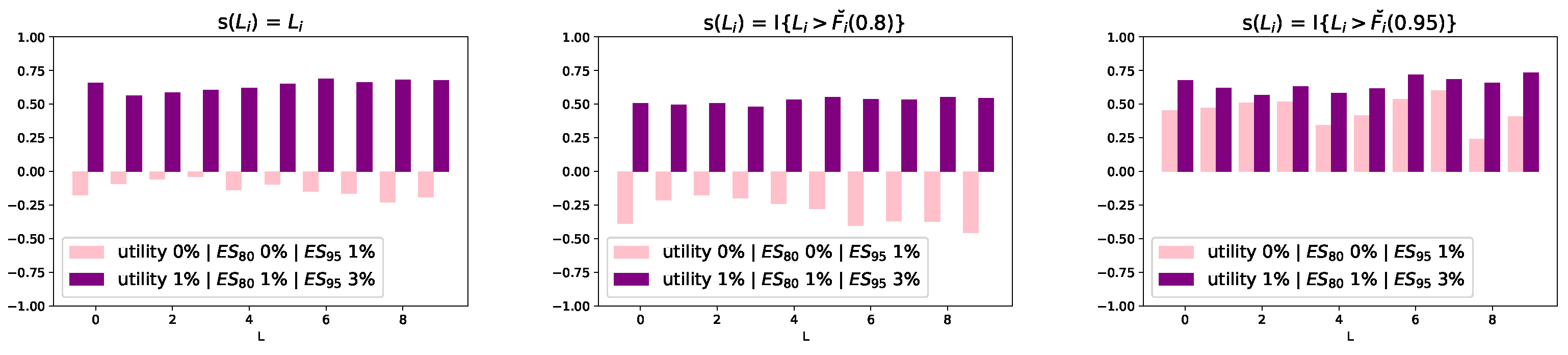
Figure 5 displays the reverse sensitivity measures for functions
,
, and
, from the left to the right panel, and where
, denotes the
-quantile function of
,
.
We observe that for stress 2, the reverse sensitivities to all losses and all choices of function are positive. This contrasts the reverse sensitivities for stress 1. Indeed, for stress 1 the reverse sensitivities with both and are negative, with the former values being smaller indicating a smaller change in the distributions of the ’s. By definition of the reverse sensitivity, the left panel corresponds to the (normalised) difference between the expectation under the stressed and baseline model. The middle and right panels correspond to the (normalised) change in the probability of exceeding and , respectively. Thus, as seen in the plots, while the expectations and probabilities of exceeding the 80% -quantile are smaller under the stressed model, the probabilities of exceeding the 95% -quantile are increased substantially. The first stress increases the at level 0.95 while simultaneously fixes the utility and at level 0.8 to its values under the baseline model. This induces under the stressed probability measure a reduction of the mean and of the probability of exceeding the 80% -quantile while the probability of exceeding the 95% -quantile increases. Thus, the reverse sensitivity measures provide a spectrum of measures to analyse the distributional change of the losses from the baseline to the stressed model.
Next, for a comparison we calculate the delta sensitivity measure of introduced by
Borgonovo (
2007). For a probability measure
the delta measure of
is defined by
where
and
are the densities of
Y and
under
, respectively, and where
is the conditional density of the total portfolio loss
Y given
under
.
Table 2 reports the delta measures under the baseline model
and the two stresses, i.e.,
and
. We observe that the delta measures are similar for all losses
and do not change significantly under the different probability measures. As the delta sensitivity measure quantifies the importance of input factors under a probability measure, having similar values for
,
, and
, means that the importance ranking of the
’s under different stresses does not change. We also report, in the first two columns of
Table 2, the reverse sensitivity measures with
. The reverse sensitivity measures provide, in contrast to the delta measure, insight into the change in the distributions of the
’s from
and
.
Alternatively to considering the change in the marginal distributions
from the baseline to the stressed model, we can study the change in the dependence between the losses when moving from the baseline to a stressed model. For this, we consider the bivariate reverse sensitivity measures for the pairs
and
for the second stress
, that is a 1% increase in HARA utility and
, and a 3% increase in
. Specifically, we look at the function
, where
and
are the
-quantile functions of
and
respectively. This bivariate sensitivity measures quantifies the impact a stress has on the probability of joint exceedances with values
and
indicating that the probabilities of joint exceedances increase more for stress 2. This can also be seen in
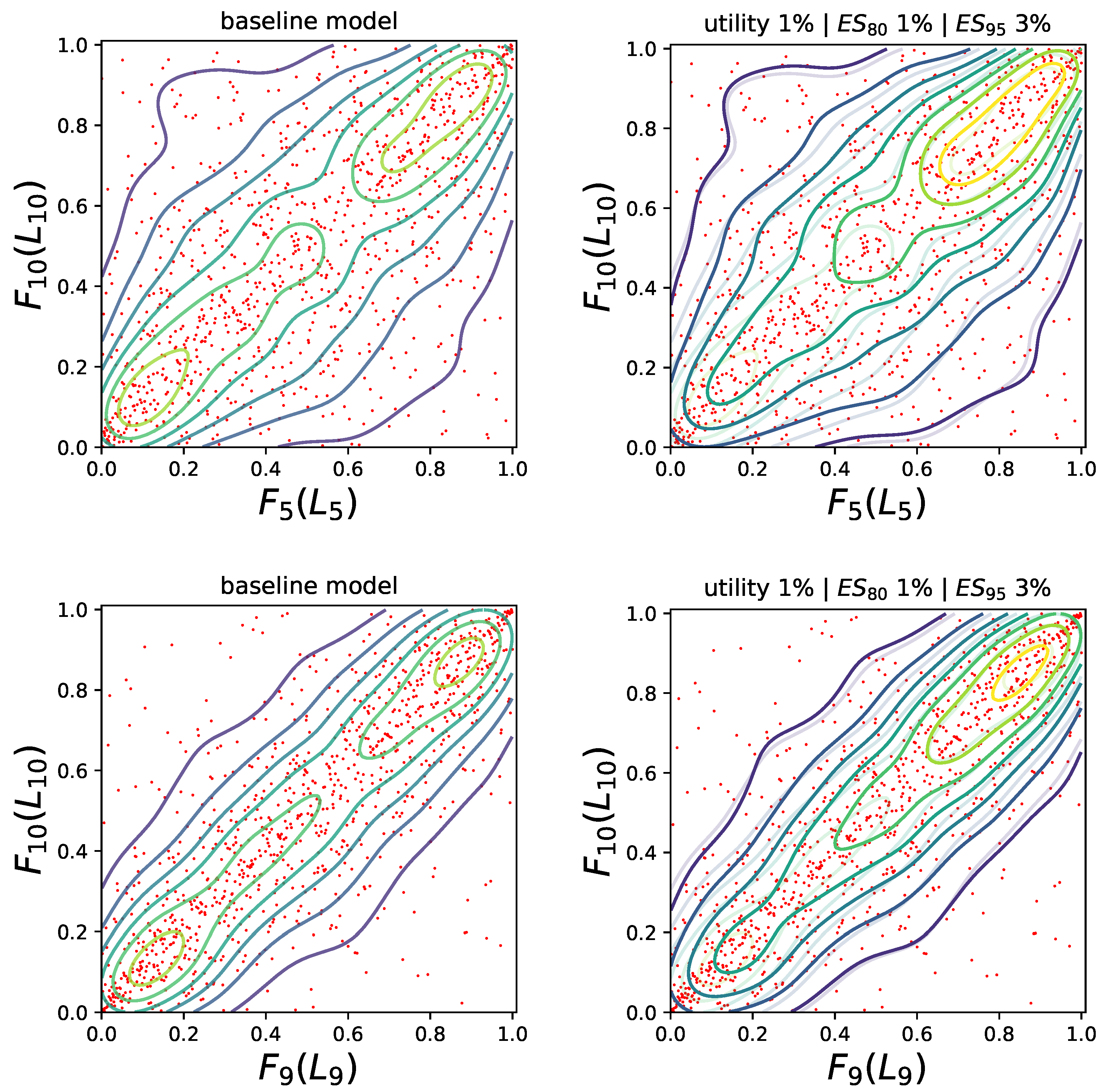
Figure 6 which shows the bivariate copulae contours of
(top panels) and
(bottom panels). The left contour plots correspond to the baseline model
whereas the right panels display the contours under the stress model
(solid lines) together with the baseline contours (reported using partially transparent lines). The red dots are the simulated realisations of the losses
and
, respectively (which are the same for the baseline and stressed model). We observe that for both pairs
and
the copula under the stressed model admits larger probabilities of joint large events, which is captured by the bivariate reverse sensitivity measure admitting positive values close to 1.