Performance Comparison of Systemic Inflammatory Response Syndrome with Logistic Regression Models to Predict Sepsis in Neonates
Abstract
:1. Introduction
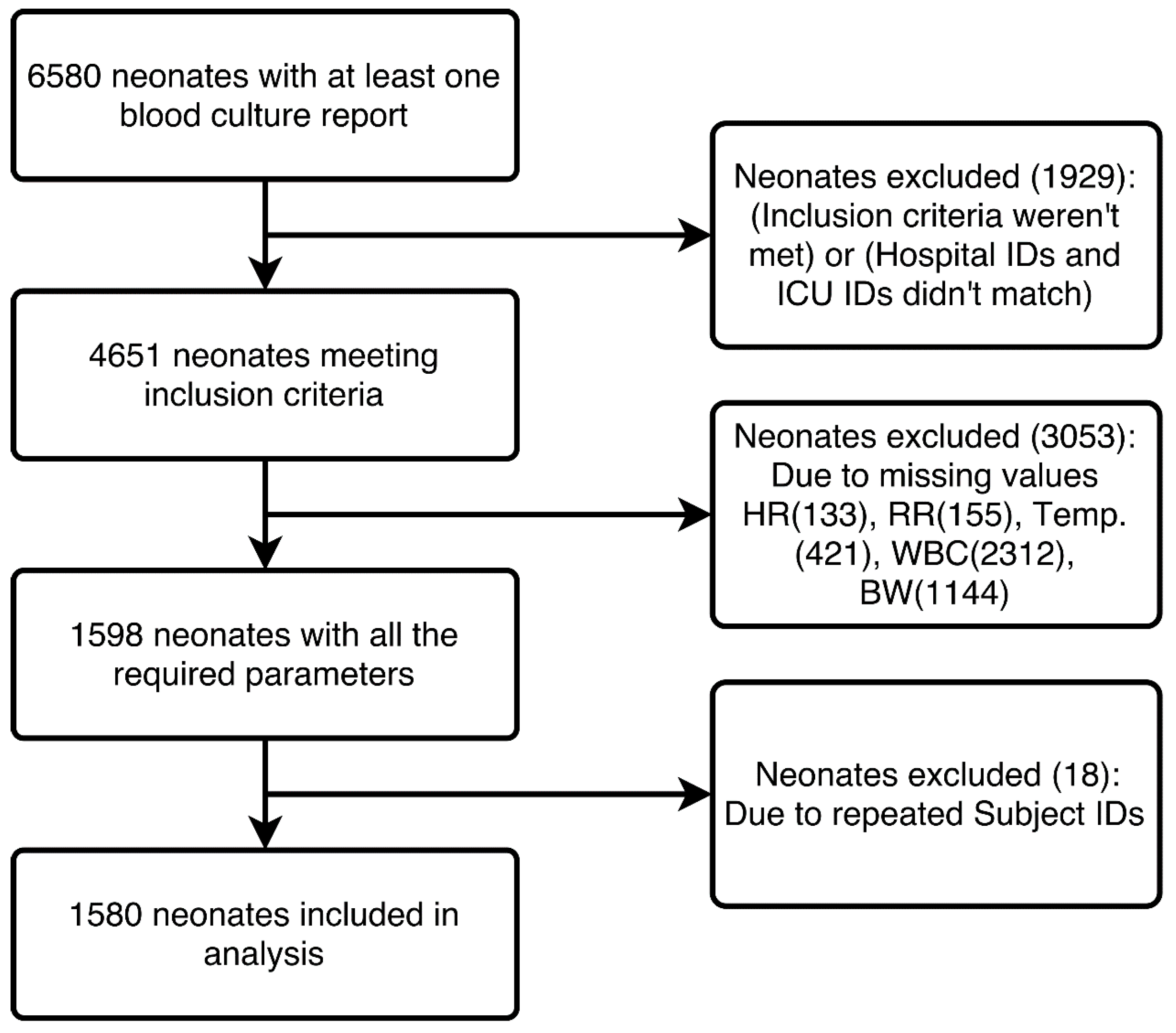
2. Materials and Methods
2.1. Study Design
2.2. Definitions
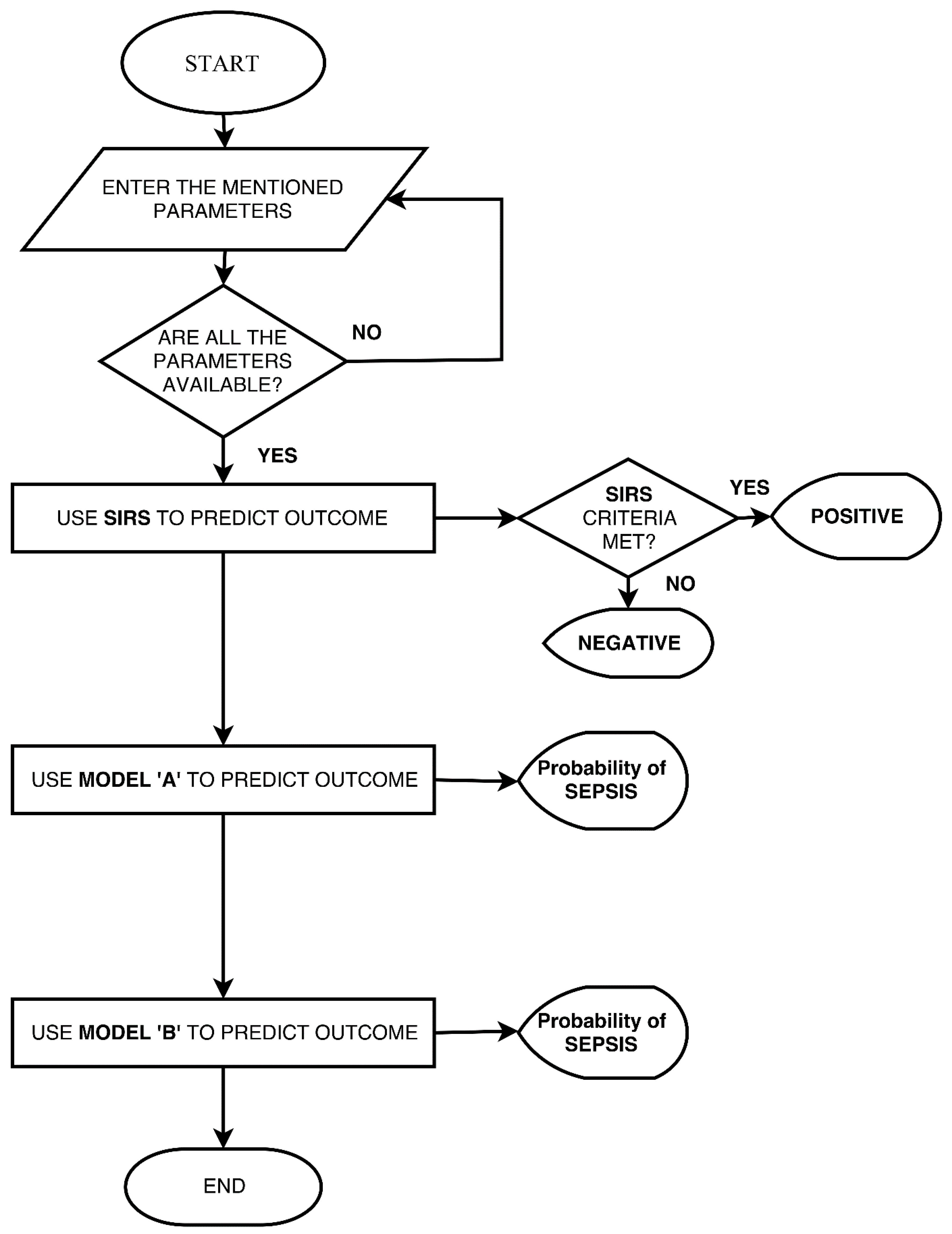
2.3. SIRS
2.4. Statistical Analysis
3. Results
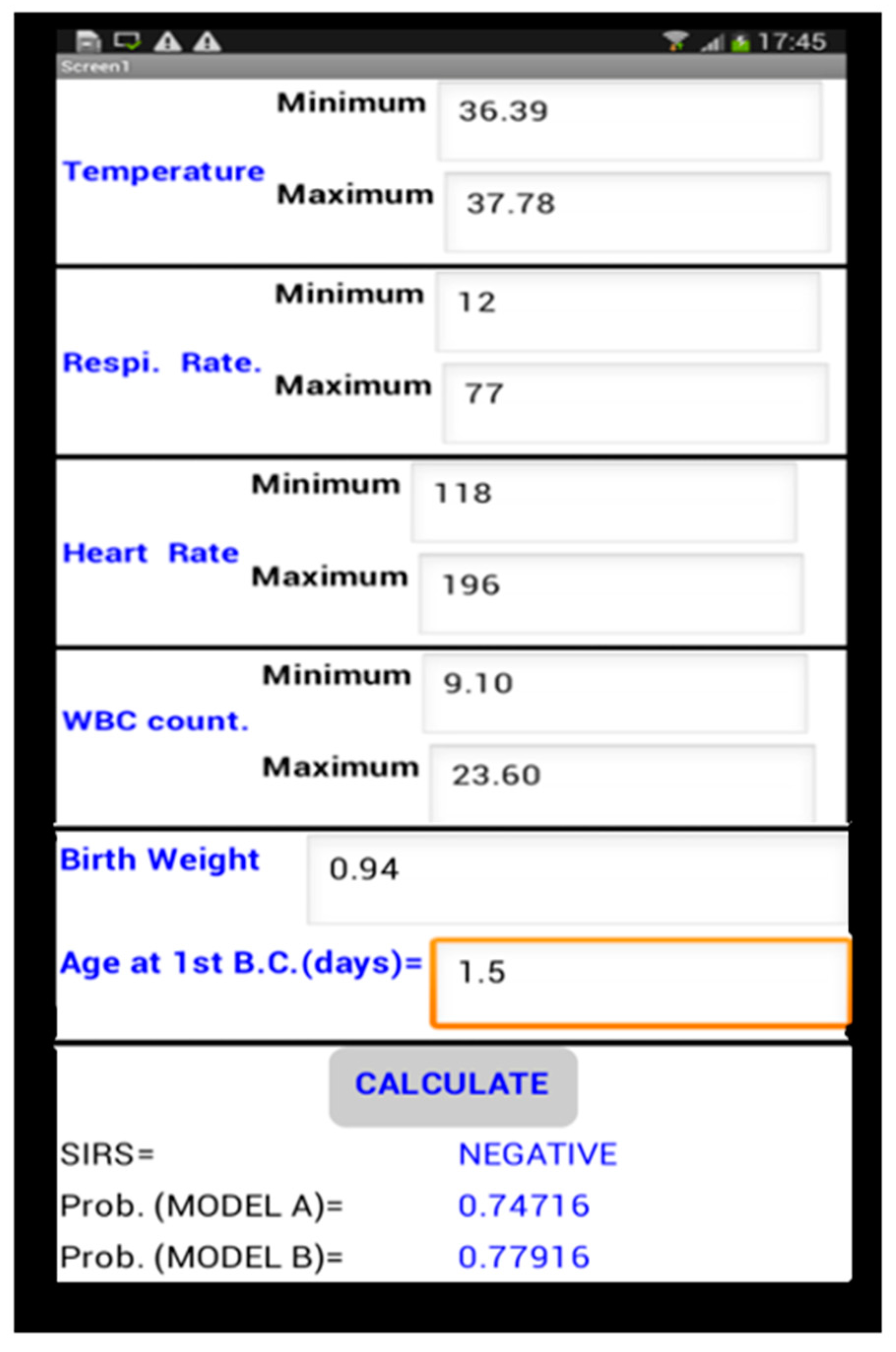
Mobile Application
- Step 1:where β0, β1, ...., βn are the logistic regression coefficients and X1, X2, ..., Xn are the independent predictor variables.
- Step 2:where L is the Logit calculated in step 1.
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Lawn, J.E.; Wilczynska-Ketende, K.; Cousens, S.N. Estimating the Causes of 4 Million Neonatal Deaths in the Year 2000. Int. J. Epidemiol. 2006, 35, 706–718. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Johnson, H.L.; Cousens, S.; Perin, J.; Scott, S.; Lawn, J.E.; Rudan, I.; Campbell, H.; Cibulskis, R.; Li, M.; et al. Global, Regional, and National Causes of Child Mortality: An Updated Systematic Analysis for 2010 with Time Trends since 2000. Lancet 2012, 379, 2151–2161. [Google Scholar] [CrossRef]
- Kurlat, I.; Stoll, B.J.; McGowan, J.E., Jr. Time to Positivity for Detection of Bacteremia in Neonates. J. Clin. Microbiol. 1989, 27, 1068–1071. [Google Scholar] [PubMed]
- Squire, E.; Favara, B.; Todd, J. Diagnosis of Neonatal Bacterial Infection: Hematologic and Pathologic Findings in Fatal and Nonfatal Cases. Pediatrics 1979, 64, 60–64. [Google Scholar] [CrossRef] [PubMed]
- Neal, P.R.; Kleiman, M.B.; Reynolds, J.K.; Allen, S.D.; Lemons, J.A.; Yu, P.L. Volume of Blood Submitted for Culture from Neonates. J. Clin. Microbiol. 1986, 24, 353–356. [Google Scholar] [PubMed]
- Schelonka, R.L.; Chai, M.K.; Yoder, B.A.; Hensley, D.; Brockett, R.M.; Ascher, D.P. Volume of Blood Required to Detect Common Neonatal Pathogens. J. Pediatr. 1996, 129, 275–278. [Google Scholar] [CrossRef]
- Gerdes, J.S.; Polin, R.A. Sepsis Screen in Neonates with Evaluation of Plasma Fibronectin. Pediatr. Infect. Dis. J. 1987, 6, 443–446. [Google Scholar] [CrossRef] [PubMed]
- Hammerschlag, M.R.; Klein, J.O.; Herschel, M.; Chen, F.C.J.; Fermin, R. Patterns of Use of Antibiotics in Two Newborn Nurseries. N. Engl. J. Med. 1977, 296, 1268–1269. [Google Scholar] [CrossRef] [PubMed]
- Maramba-lazarte, C.C.; Bunyi, M.A.C.; Gallardo, E.E.; Lim, J.G.; Lobo, J.J.; Aguilar, C.Y.; Maramba-lazarte, C.C. Etiology of Neonatal Sepsis in Five Urban Hospitals in the Philippines. PIDSP J. 2011, 12, 75–85. [Google Scholar]
- Huskins, W.C.; Goldmann, D.A.; Hamer, D.H. Impact of Enhanced Infection Control at Two Neonatal Intensive Care Units in the Philippines. Clin. Infect. Dis. 2013, 48, 13–21. [Google Scholar]
- Bone, R.C.; Balk, R.A.; Cerra, F.B.; Dellinger, R.P.; Fein, A.M.; Knaus, W.A.; Schein, R.M.; Sibbald, W.J. Definitions for Sepsis and Organ Failure and Guidelines for the Use of Innovative Therapies in Sepsis. The ACCP/SCCM Consensus Conference Committee. American College of Chest Physicians/Society of Critical Care Medicine. Chest 1992, 101, 1644–1655. [Google Scholar] [CrossRef] [PubMed]
- Levy, M.M.; Fink, M.P.; Marshall, J.C.; Abraham, E.; Angus, D.; Cook, D.; Cohen, J.; Opal, S.M.; Vincent, J.-L.; Ramsay, G.; et al. 2001 SCCM/ESICM/ACCP/ATS/SIS International Sepsis Definitions Conference. Intensive Care Med. 2003, 29, 530–538. [Google Scholar] [CrossRef] [PubMed]
- Seymour, C.W.; Liu, V.X.; Iwashyna, T.J.; Brunkhorst, F.M.; Rea, T.D.; Scherag, A.; Rubenfeld, G.; Kahn, J.M.; Shankar-Hari, M.; Singer, M.; et al. Assessment of Clinical Criteria for Sepsis For the Third International Consensus Definitions for Sepsis and Septic Shock (Sepsis-3). JAMA 2016, 315, 762. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, B.; Giroir, B.; Randolph, A.; International Consensus Conference on Pediatric Sepsis. International Pediatric Sepsis Consensus Conference: Definitions for Sepsis and Organ Dysfunction in Pediatrics. Pediatr. Crit. Care Med. 2005, 6, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Hofer, N.; Zacharias, E.; Müller, W.; Resch, B. Performance of the Definitions of the Systemic Inflammatory Response Syndrome and Sepsis in Neonates. J. Perinat. Med. 2012, 40, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Stoll, B.J.; Hansen, N.; Fanaroff, A.A.; Wright, L.L.; Carlo, W.A.; Ehrenkranz, R.A.; Lemons, J.A.; Donovan, E.F.; Stark, A.R.; Tyson, J.E.; et al. Late-Onset Sepsis in Very Low Birth Weight Neonates: The Experience of the NICHD Neonatal Research Network. Pediatrics 2002, 110, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Stoll, B.J.; Hansen, N.; Fanaroff, A.A.; Wright, L.L.; Carlo, W.A.; Ehrenkranz, R.A.; Lemons, J.A.; Donovan, E.F.; Stark, A.R.; Tyson, J.E.; et al. Changes in Pathogens Causing Early-Onset Sepsis in Very-Low-Birth-Weight Infants. N. Engl. J. Med. 2002, 347, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Johnson, A.E.W.; Pollard, T.J.; Shen, L.; Lehman, L.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Anthony Celi, L.; Mark, R.G. MIMIC-III, a Freely Accessible Critical Care Database. Sci. Data 2016, 3, 160035. [Google Scholar] [CrossRef] [PubMed]
- Pollard, T.J.; Johnson, A.E.W. The MIMIC III Clinical Database. Version 1.4. Available online: https://physionet.org/physiobank/database/mimic3cdb/ (accessed on 25 April 2017).
- Thompson, P.J.; Greenough, A.; Gamsu, H.R.; Nicolaides, K.H.; Philpott-Howard, J. Congenital Bacterial Sepsis in Very Preterm Infants. J. Med. Microbiol. 1992, 36, 117–120. [Google Scholar] [CrossRef] [PubMed]
- DaSilva, O.; Hammerberg, O. Diagnostic Value of Leukocyte Indices in Late Neonatal Sepsis. Pediatr. Infect. Dis. J. 1994, 13, 409–411. [Google Scholar] [PubMed]
- Fowlie, P.W.; Schmidt, B. Diagnostic Tests for Bacterial Infection from Birth to 90 Days-a Systematic Review. Arch. Dis. Child. Fetal Neonatal Ed. 1998, 78, F92–F98. [Google Scholar] [CrossRef] [PubMed]
- Modi, N.; Dore, C.J.; Saraswatula, A.; Richards, M.; Bamford, K.B.; Coello, R.; Holmes, A. A Case Definition for National and International Neonatal Bloodstream Infection Surveillance. Arch. Dis. Child. Fetal Neonatal Ed. 2008, 94, F8–F12. [Google Scholar] [CrossRef] [PubMed]
- MIT App Inventor. Massachusetts Institute of Technology: Cambridge, MA, USA. Available online: http://appinventor.mit.edu/explore/ (accessed on 20 August 2017).
- Wynn, J.L.; Wong, H.R.; Shanley, T.P.; Bizzarro, M.J.; Saiman, L.; Polin, R.A. Time for a Neonatal-Specific Consensus Definition for Sepsis. Pediatr. Crit. Care Med. 2014, 15, 523–528. [Google Scholar] [CrossRef] [PubMed]
| Neonatal Variables | Cut-off Values According to Age | |
|---|---|---|
| Age 0 Days to 1 Week | Age 1 Week to 1 Month | |
| Heart Rate (Beats/min) | >180 or <100 | >180 or <100 |
| Respiratory Rate (Breaths/min) | >50 | >40 |
| Leukocyte Count (×103/mm3) | >34 | >19.5 or <5 |
| Temperature (°C) | >38.5 or <36 | >38.5 or <36 |
| Sex (Male/Female) | (915/665) | |
| Mean | Range | |
| Birth Weight (kg) | 2.18 | (0.36–5.4) |
| Gestational Age (weeks) | 32.99 | (18–43) |
| Features | Present In | |
| N | % | |
| Blood Culture (BC) | (204/1376) † | (12.91/87.08) † |
| Cerebrospinal fluid (CSF) culture | (10/1570) † | (0.63/99.36) † |
| BC and/or CSF culture | (204/1376) † | (12.91/87.08) † |
| Mortality | 28 | 1.77 |
| Abnormal Heart Rate * | 291 | 18.41 |
| Abnormal Respiratory Rate * | 1456 | 92.15 |
| Abnormal Leukocyte count * | 26 | 1.64 |
| Abnormal Temperature * | 74 | 4.68 |
| Sr. No. | Name of the Parameter | Function 1 |
|---|---|---|
| 1 | Birth Weight | 0.633 |
| 2 | Heart Rate (Maximum) | −0.625 |
| 3 | Respiratory Rate (Minimum) | 0.495 |
| 4 | Temperature (Minimum) | 0.403 |
| 5 | WBC (Maximum) | −0.285 |
| 6 | WBC (Minimum) | 0.256 |
| 7 | Age at first Blood culture draw | −0.135 |
| 8 | Heart Rate (Minimum) | −0.100 |
| Chi-Square | df | Sig. | ||
|---|---|---|---|---|
| Step 1 | Step | 26.961 | 1 | 0.000 |
| Block | 26.961 | 1 | 0.000 | |
| Model | 252.869 | 8 | 0.000 |
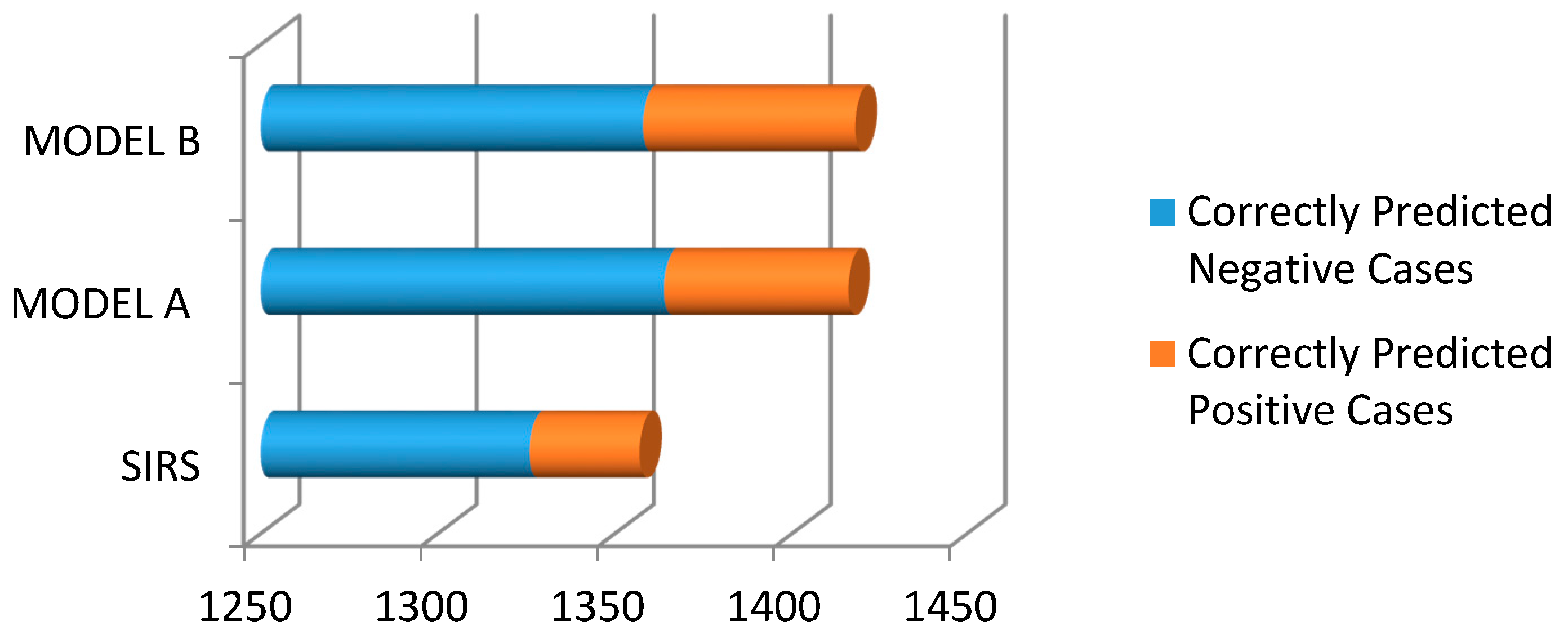
| Sensitivity | Specificity | PPV | NPV | PLR | NLR | |
|---|---|---|---|---|---|---|
| SIRS | 16.15 | 95.53 | 33.33 | 89.17 | 3.61 | 0.88 |
| 95% CI | (11.24–22.13) | (94.31–96.56) | (25.03–42.82) | (88.55–89.77) | (2.41–5.41) | (0.82–0.93) |
| Model A † | 29.17 | 97.82 | 66.67 | 90.22 | 13.36 | 0.72 |
| 95% CI | (21.90–37.32) | (96.68–98.64) | (54.97–76.62) | (89.25–91.11) | (8.16–21.89) | (0.65–0.80) |
| Model A * | 20.83 | 99.30 | 76.92 | 91.76 | 29.58 | 0.80 |
| 95% CI | (10.47–34.99) | (97.96–99.85) | (48.72–92.12) | (90.59–92.79) | (8.43–103.80) | (0.69–0.92) |
| Model B † | 31.25 | 97.30 | 63.38 | 90.43 | 11.56 | 0.71 |
| 95% CI | (23.79–39.50) | (96.06–98.23) | (52.46–73.08) | (89.43–91.35) | (7.37–18.13) | (0.63–0.79) |
| Model B * | 31.25 | 99.06 | 78.95 | 92.75 | 33.28 | 0.69 |
| 95% CI | (18.66–46.25) | (97.61–99.74) | (56.46–91.56) | (91.35–93.93) | (11.51–96.24) | (0.57–0.84) |
| Value | df | Significance | |
|---|---|---|---|
| SIRS ‡ | 41.530 | 1 | <0.001 |
| Model A †,‡ | 169.774 | 1 | <0.001 |
| Model B †,‡ | 169.912 | 1 | <0.001 |
| Model A *,¥ | - | - | <0.001 |
| Model B *,¥ | - | - | <0.001 |
| Cut-Off | Prediction Performance (%) | ||||
|---|---|---|---|---|---|
| Training Set | Testing Set | ||||
| Sn | Sp | Sn | Sp | ||
| Model A | 0.1 | 81.94 (74.67–87.85) | 72.45 (69.51–75.26) | 75.00 (60.40–86.36) | 78.17 (73.94–82.00) |
| 0.2 | 67.36 (59.06–74.93) | 89.60 (87.50–91.46) | 68.75 (53.75–81.34) | 92.02 (89.03–94.41) | |
| 0.3 | 44.44 (36.17–52.95) | 93.66 (91.93–95.12) | 33.33 (20.40–48.41) | 95.07 (92.56–96.92) | |
| 0.4 | 34.72 (26.99–43.10) | 95.95 (94.50–97.10) | 25.00 (13.64–39.60) | 98.83 (97.28–99.62) | |
| 0.5 | 29.17 (21.90–37.32) | 97.82 (96.68–98.64) | 20.83 (10.47–34.99) | 99.30 (97.96–99.85) | |
| 0.6 | 22.22 (15.72–29.90) | 98.75 (97.83–99.35) | 16.67 (7.48–30.22) | 99.30 (97.96–99.85) | |
| 0.7 | 16.67 (10.98–23.78) | 98.96 (98.10–99.50) | 4.17 (0.51–14.25) | 99.53 (98.31–99.94) | |
| Model B | 0.1 | 82.64 (75.45–88.44) | 74.95 (72.08–77.66) | 77.08 (62.69–87.97) | 79.58 (75.43–83.31) |
| 0.2 | 68.75 (60.50–76.21) | 88.67 (86.50–90.60) | 66.67 (51.59–79.60) | 91.08 (87.96–93.61) | |
| 0.3 | 56.25 (47.74–64.49) | 93.45 (91.70–94.93) | 50.00 (35.23–64.77) | 94.37 (91.73–96.36) | |
| 0 4 | 41.67 (33.52–50.17) | 95.43 (93.91–96.66) | 41.67 (27.61–56.79) | 97.65 (95.73–98.87) | |
| 0.5 | 31.25 (23.79–39.50) | 97.30 (96.06–98.23) | 31.25 (18.66–46.25) | 99.06 (97.61–99.74) | |
| 0.6 | 24.31 (17.55–32.15) | 98.44 (97.44–99.12) | 18.75 (8.95–32.63) | 99.30 (97.96–99.85) | |
| 0.7 | 16.67 (10.98–23.78) | 98.96 (98.10–99.50) | 14.58 (6.07–27.76) | 99.53 (98.31–99.94) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakur, J.; Pahuja, S.K.; Pahuja, R. Performance Comparison of Systemic Inflammatory Response Syndrome with Logistic Regression Models to Predict Sepsis in Neonates. Children 2017, 4, 111. https://doi.org/10.3390/children4120111
Thakur J, Pahuja SK, Pahuja R. Performance Comparison of Systemic Inflammatory Response Syndrome with Logistic Regression Models to Predict Sepsis in Neonates. Children. 2017; 4(12):111. https://doi.org/10.3390/children4120111
Chicago/Turabian StyleThakur, Jyoti, Sharvan Kumar Pahuja, and Roop Pahuja. 2017. "Performance Comparison of Systemic Inflammatory Response Syndrome with Logistic Regression Models to Predict Sepsis in Neonates" Children 4, no. 12: 111. https://doi.org/10.3390/children4120111
APA StyleThakur, J., Pahuja, S. K., & Pahuja, R. (2017). Performance Comparison of Systemic Inflammatory Response Syndrome with Logistic Regression Models to Predict Sepsis in Neonates. Children, 4(12), 111. https://doi.org/10.3390/children4120111




