Experimentally Constrained Mechanistic and Data-Driven Models for Simulating NMDA Receptor Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. ExperimentallyConstrained Data
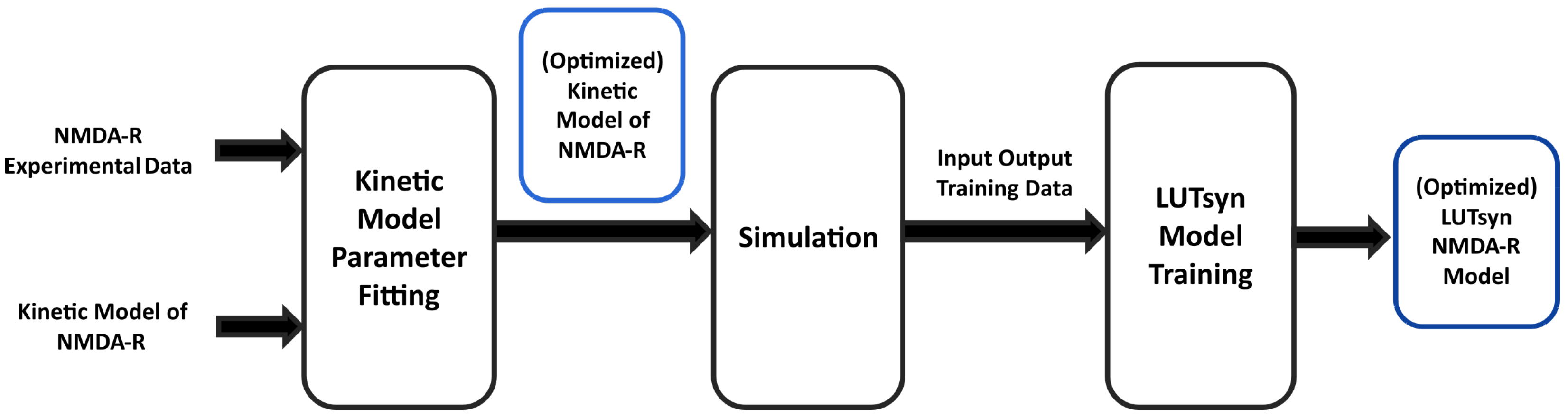
2.2. Computational and Simulation Methods
2.3. Kinetic Synapse Model of NMDA-R
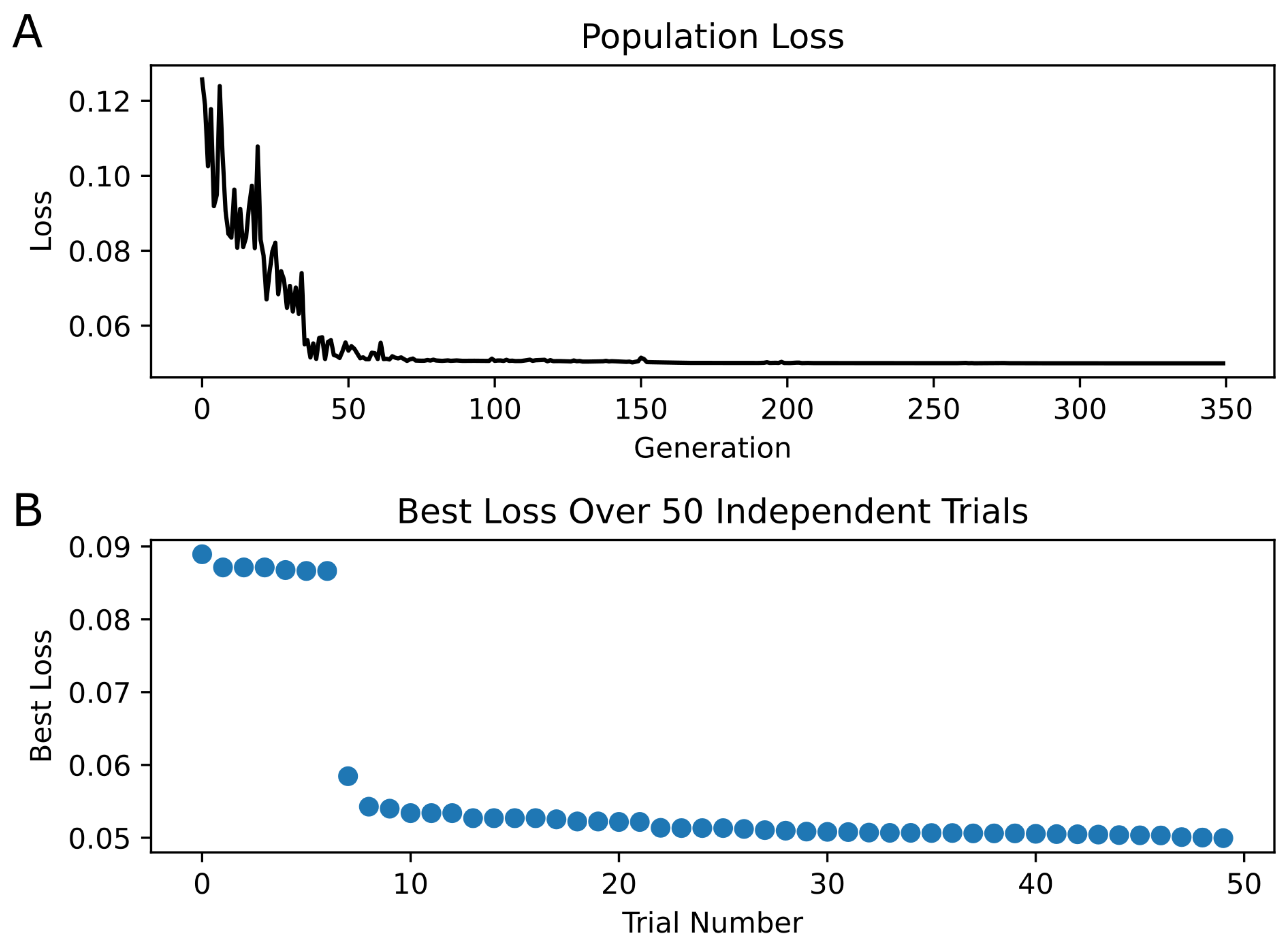
2.4. Kinetic Model Parameter Fitting
- 1
- In response to three 1 ms square pulses of 1mM glutamate delivered at 10 Hz;
- 2
- In response to three 1 ms square pulses of 1mM glutamate delivered at 100 Hz;
- 3
- In response to a synaptic-like pulse of glutamate.
2.5. LUTsyn Model
2.6. LUTsyn Model Training
- 1
- Generate a Poisson pulse train of synaptic events.
- 2
- Generate the NMDA-R response to the pulse train using the kinetic model.
- 3
- Categorize each response’s waveform as 1st–5th order.
- 4
- Calculate the mean response of each order.
- 5
- Estimate the time constants of a triple exponential that best fit the mean response of each order using PSO.
3. Results
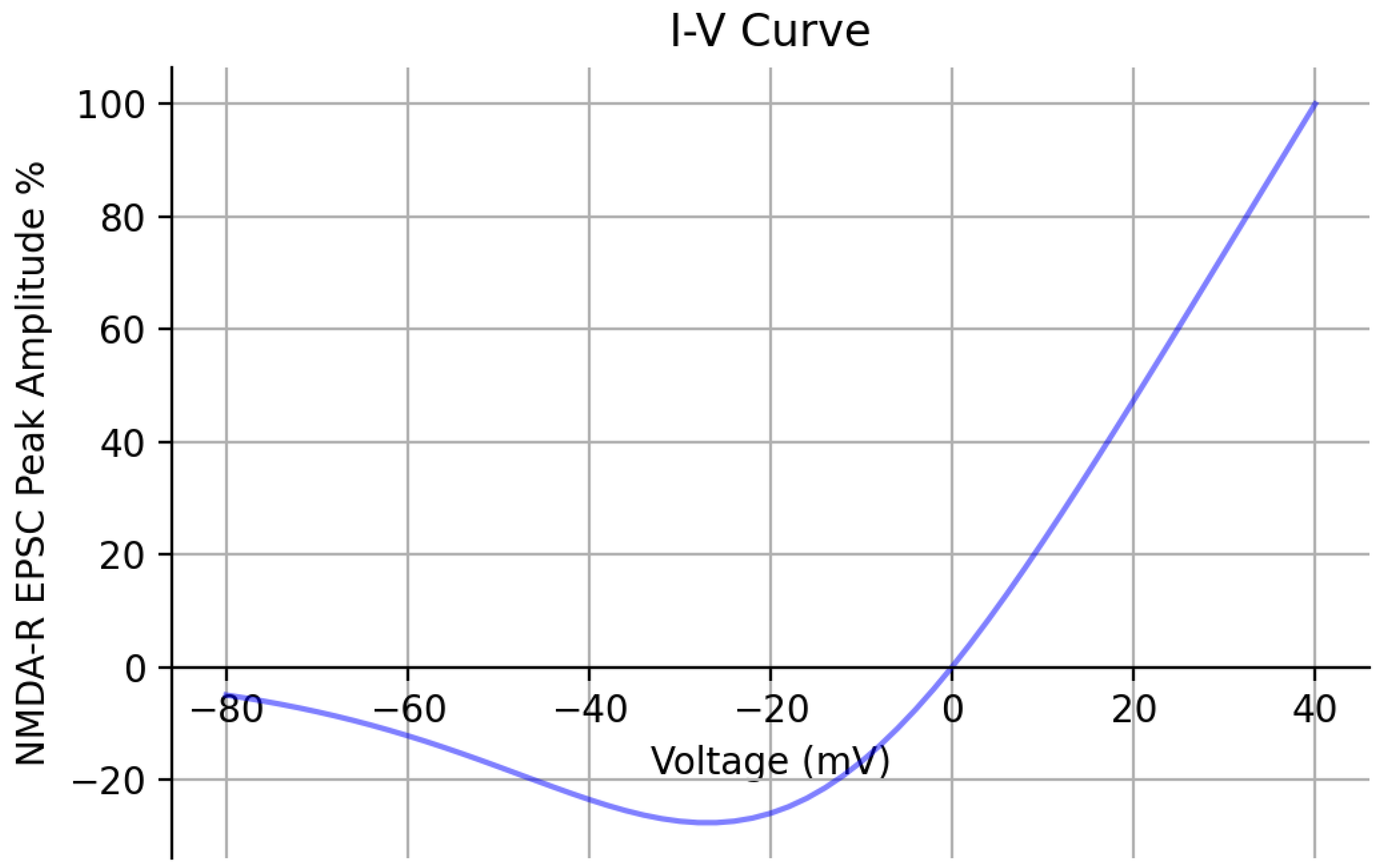
3.1. Validation of Kinetic Model
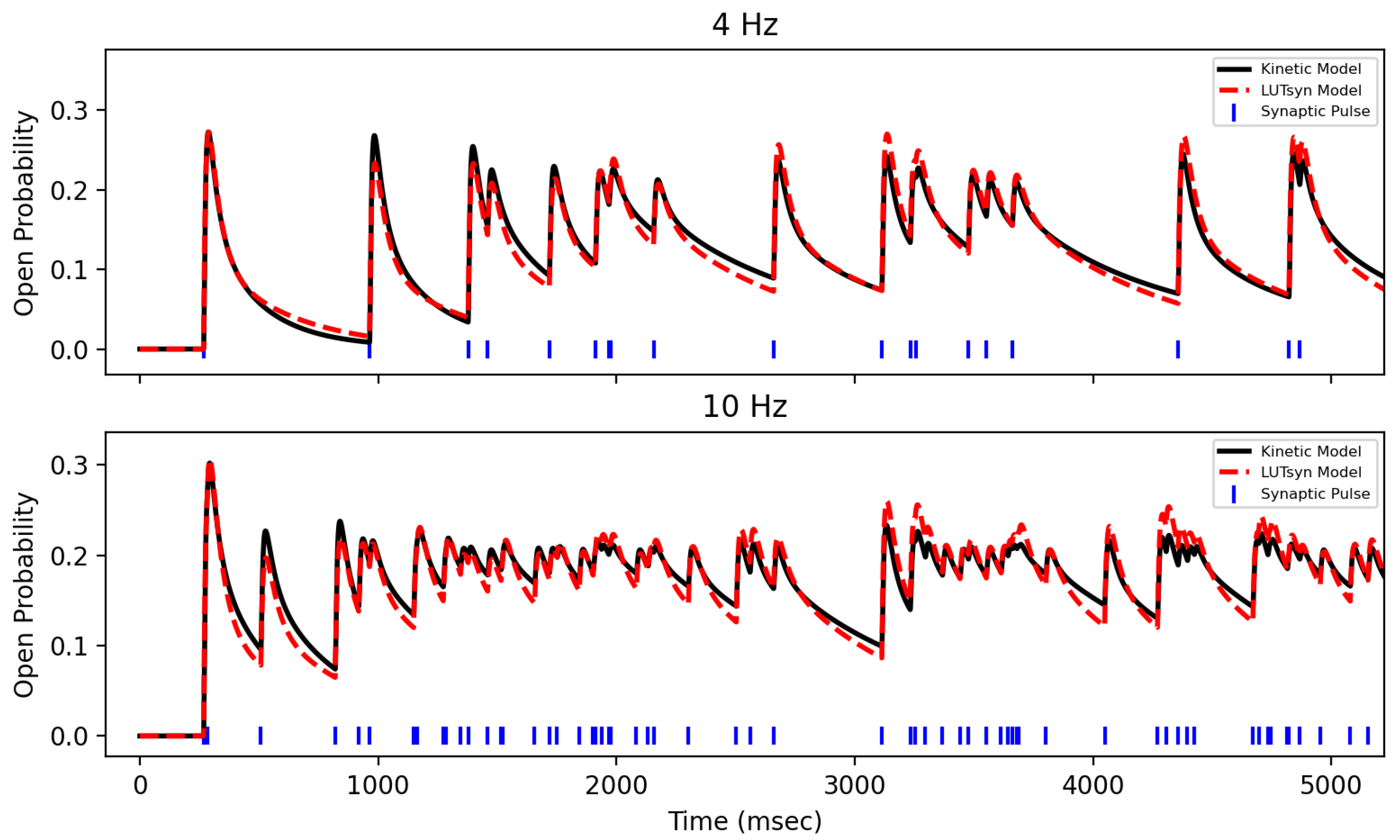
3.2. Validation of LUTsyn Model
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NMDA-R | N-methyl-D-aspartate Receptor |
| LUTsyn | Look-Up Table Synapse |
| PSO | Particle Swarm Optimization |
| NRMSE | Normalized Root Mean Squared Error |
| EPSC | Excitatory Postsynaptic Current |
References
- Hansen, K.B.; Yi, F.; Perszyk, R.E.; Furukawa, H.; Wollmuth, L.P.; Gibb, A.J.; Traynelis, S.F. Structure, function, and allosteric modulation of NMDA receptors. J. Gen. Physiol. 2018, 150, 1081–1105. [Google Scholar] [CrossRef]
- Paoletti, P.; Bellone, C.; Zhou, Q. NMDA receptor subunit diversity: Impact on receptor properties, synaptic plasticity and disease. Nat. Rev. Neurosci. 2013, 14, 383–400. [Google Scholar] [CrossRef]
- Vicini, S.; Wang, J.F.; Li, J.H.; Zhu, W.J.; Wang, Y.H.; Luo, J.H.; Wolfe, B.B.; Grayson, D.R. Functional and pharmacological differences between recombinant N- methyl-D-aspartate receptors. J. Neurophysiol. 1998, 79, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Iacobucci, G.J.; Popescu, G.K. NMDA receptors: Linking physiological output to biophysical operation. Nat. Rev. Neurosci. 2017, 18, 236–249. [Google Scholar] [CrossRef] [PubMed]
- Tian, M.; Stroebel, D.; Piot, L.; David, M.; Ye, S.; Paoletti, P. GluN2A and GluN2B NMDA receptors use distinct allosteric routes. Nat. Commun. 2021, 12, 4709. [Google Scholar] [CrossRef]
- Popescu, G.; Robert, A.; Howe, J.R.; Auerbach, A. Reaction mechanism determines NMDA receptor response to repetitive stimulation. Nature 2004, 430, 790–793. [Google Scholar] [CrossRef]
- Zhang, W.; Howe, J.R.; Popescu, G.K. Distinct gating modes determine the biphasic relaxation of NMDA receptor currents. Nat. Neurosci. 2008, 11, 1373–1375. [Google Scholar]
- Kussius, C.L.; Kaur, N.; Popescu, G.K. Pregnanolone sulfate promotes desensitization of activated NMDA receptors. J. Neurosci. 2009, 29, 6819–6827. [Google Scholar] [CrossRef]
- Robert, A.; Howe, J.R. How AMPA receptor desensitization depends on receptor occupancy. J. Neurosci. 2003, 23, 847–858. [Google Scholar] [CrossRef]
- Schorge, S.; Elenes, S.; Colquhoun, D. Maximum likelihood fitting of single channel NMDA activity with a mechanism composed of independent dimers of subunits. J. Physiol. 2005, 569, 395–418. [Google Scholar] [CrossRef]
- Allam, S.L.; Ghaderi, V.S.; Bouteiller, J.M.C.; Legendre, A.; Ambert, N.; Greget, R.; Bischoff, S.; Baudry, M.; Berger, T.W. A computational model to investigate Astrocytic glutamate uptake influence on synaptic transmission and neuronal spiking. Front. Comput. Neurosci. 2012, 6, 70. [Google Scholar] [CrossRef]
- Ambert, N. Computational studies of NMDA receptors: Differential effects of neuronal activity on efficacy of competitive and non-competitive antagonists. Rev. Argent. Cardiol. 2010, 79, 246–250. [Google Scholar] [CrossRef]
- Pham, D.t.J.; Yu, G.J.; Bouteiller, J.m.C.; Berger, T.W. Bridging Hierarchies in Multi-Scale Models of Neural Systems: Look-Up Tables Enable Computationally Efficient Simulations of Non-linear Synaptic Dynamics. Front. Comput. Neurosci. 2021, 15, 733155. [Google Scholar] [CrossRef]
- Booker, S.A.; Sumera, A.; Kind, P.C.; Wyllie, D.J. Contribution of nmda receptors to synaptic function in rat hippocampal interneurons. eNeuro 2021, 8, ENEURO.0552-20.2021. [Google Scholar] [CrossRef] [PubMed]
- Choi, K.; Medley, J.K.; König, M.; Stocking, K.; Smith, L.; Gu, S.; Sauro, H.M. Tellurium: An extensible python-based modeling environment for systems and synthetic biology. BioSystems 2018, 171, 74–79. [Google Scholar] [CrossRef]
- Hines, M.L.; Carnevale, N.T. The NEURON Simulation Environment. Neural Comput. 1997, 9, 1179–1209. [Google Scholar] [CrossRef]
- Garrett, A. inspyred: Bio-inspired Algorithms in Python. 2023. Available online: https://aarongarrett.github.io/inspyred/ (accessed on 30 June 2025).
- Berger, A.J.; Dieudonné, P.; Ascher, P. Glycine uptake governs glycine site occupancy at NMDA receptors of excitatory synapses. J. Neurophysiol. 1998, 80, 3336–3340. [Google Scholar] [CrossRef]
- Bakkar, W.; Ma, C.L.; Pabba, M.; Khacho, P.; Zhang, Y.L.; Muller, E.; Martina, M.; Bergeron, R. Chronically saturating levels of endogenous glycine disrupt glutamatergic neurotransmission and enhance synaptogenesis in the CA1 region of mouse hippocampus. Synapse 2011, 65, 1181–1195. [Google Scholar] [CrossRef]
- Cummings, K.A.; Popescu, G.K. Glycine-dependent activation of NMDA receptors. J. Gen. Physiol. 2015, 145, 513–527. [Google Scholar] [CrossRef]
- Jahr, C.E.; Stevens, C.F. Voltage Dependence of NMDA-Activated Predicted by Single-Channel Kinetics. J. Neurosci. 1990, 10, 3178–3182. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Savtchenko, L.P.; Rusakov, D.A. The optimal height of the synaptic cleft. Proc. Natl. Acad. Sci. USA 2007, 104, 1823–1828. [Google Scholar] [CrossRef]
- Anchisi, D.; Scelfo, B.; Tempia, F. Postsynaptic currents in deep cerebellar nuclei. J. Neurophysiol. 2001, 85, 323–331. [Google Scholar] [CrossRef][Green Version]



| Variable Name | Description | Notes |
|---|---|---|
| Open probability of NMDA-R at time t | - | |
| EPSC mediated by a population of NMDA-Rs at time t | Derived from Ohm’s Law | |
| N | Number of NMDA-Rs present | - |
| V | Membrane potential | Units of mV |
| Reversal potential of NMDA-R | Set to 0 mV | |
| Expected value of single-channel conductance of NMDA-R at time t | Units of pS | |
| Single-channel conductance of NMDA-R when factoring the voltage-dependent magnesium block | Equation (3) was derived from [21] (units of pS) | |
| Single-channel conductance of NMDA-R when magnesium is absent | Equation (4) was derived from [12] (units of pS) | |
| Open-state conductance with 1 glutamate molecule bound | From [12] (units of pS) | |
| Open-state conductance with 2 glutamate molecules bound | From [12] (units of pS) | |
| External magnesium concentration | Units of mM | |
| Equilibrium constant of magnesium | Value set to 3.57 from [21] | |
| Steepness of voltage-dependent transition from to | from [12] | |
| Holding potential | Units of mV |
| Rate Constant (Units) | Original Value | New Value |
|---|---|---|
| (M−1 s−1) | 17 | 46 |
| (s−1) | 60 | 86 |
| (s−1) | 127 | 208 |
| (s−1) | 161 | 152 |
| (s−1) | 580 | 1200 |
| (s−1) | 2610 | 5000 |
| (s−1) | 2508 | 1130 |
| (s−1) | 2167 | 4823 |
| (s−1) | 3449 | 6998 |
| (s−1) | 662 | 278 |
| (M−1 s−1) | 5 | 1 |
| (s−1) | 12 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, D.-T.J.; Bouteiller, J.-M.C. Experimentally Constrained Mechanistic and Data-Driven Models for Simulating NMDA Receptor Dynamics. Biomedicines 2025, 13, 1674. https://doi.org/10.3390/biomedicines13071674
Pham D-TJ, Bouteiller J-MC. Experimentally Constrained Mechanistic and Data-Driven Models for Simulating NMDA Receptor Dynamics. Biomedicines. 2025; 13(7):1674. https://doi.org/10.3390/biomedicines13071674
Chicago/Turabian StylePham, Duy-Tan J., and Jean-Marie C. Bouteiller. 2025. "Experimentally Constrained Mechanistic and Data-Driven Models for Simulating NMDA Receptor Dynamics" Biomedicines 13, no. 7: 1674. https://doi.org/10.3390/biomedicines13071674
APA StylePham, D.-T. J., & Bouteiller, J.-M. C. (2025). Experimentally Constrained Mechanistic and Data-Driven Models for Simulating NMDA Receptor Dynamics. Biomedicines, 13(7), 1674. https://doi.org/10.3390/biomedicines13071674






