Mutational Slime Mould Algorithm for Gene Selection
Abstract
:1. Introduction
- (1)
- An improved slime mould algorithm (ISMA) is proposed to solve continuous global optimization problems and high-dimensional gene selection problems.
- (2)
- The performance of the ISMA algorithm is verified by comparing it with several famous optimization algorithms.
- (3)
- Different transfer functions are used to transform the proposed ISMA into a discrete version of BISMA, and they are compared to choose the most suitable transfer function for the binary ISMA optimizer.
- (4)
- The optimal BISMA version was selected as a gene selection optimizer to select the optimal gene subset from the gene expression data set.
- (5)
- The performance of the selected method is verified by comparing it with several other advanced optimizers.
2. Related Works
2.1. Machine Learning for Gene Selection
2.2. Swarm Intelligence for Gene Selection
3. The Proposed ISMA
3.1. SMA
| Algorithm 1: Pseudo-code of SMA |
| Begin Initialize the parameters: , Initialize slime mould population While t ≤ Calculate the fitness of each individual in the slime mould Update best fitness and the Calculate the weight according to Equation (3) Calculate according to Equation (4) Calculate according to Equation (5) For (each search agent) Update according to Equation (2) Update , based on and , respectively Update the positions according to Equation (1) EndFor iteration = iteration + 1 EndWhile Return the best fitness and End |
3.2. The Cauchy Mutation Operator
3.3. The Mutation and Crossover Strategy in DE
- A.
- Mutation
- B.
- Crossover
3.4. The Hybrid Structure of the Proposed ISMA
| Algorithm 2: Pseudo-code of ISMA |
| Begin Initialize of the parameters: , Initialize of slime mould population While Calculate the fitness for each individual in slime mould Update and the best fitness Calculate the weight ,a,b according to Equations (3)–(5) For Update using Equation (2) Update , based on and , respectively Update the positions by Equation (1) EndFor Use Cauchy mutation strategy to update the best individual and the best fitness Adopt MC strategy to update the best individual and the best fitness iteration = iteration + 1 EndWhile Return the best fitness and as the best solution End |
3.5. Computational Complexity
4. Experimental Design and Analysis of Global Optimization Problem
4.1. Comparison between SMA Variant and Original SMA and DE Algorithm
4.2. Comparison with Advanced Algorithms
5. The Proposed Technique for Gene Selection
5.1. System Architecture of Gene Selection Based on ISMA
5.2. Fitness Function
5.3. Implementation of Discrete BSSMA
6. Experimental Design and Discussion on Gene Selection
6.1. Experimental Design
6.2. The Proposed BISMA with Different TFs
6.3. Comparative Evaluation with Other Optimizers
7. Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| + | 30 | [−10, 10] | 0 |
| 30 | [−100, 100] | 0 | |
| { | 30 | [−100, 100] | 0 |
| + ] | 30 | [−30, 30] | 0 |
| 30 | [−100, 100] | 0 | |
| + random[0,1) | 30 | [−128, 128] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| − | 30 | [−500, 500] | −418.9829 × 30 |
| cos(2 + 10] | 30 | [−5.12, 5.12] | 0 |
| −20 exp{−0.2{)} + 20 + e | 30 | [−32, 32] | 0 |
| 30 | [−600, 600] | 0 | |
| {10sin()+ [1+10()]+ + | 30 | [−50, 50] | 0 |
| (3)+[1+(3)]+ [1+(2)]+ | 30 | [−50, 50] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| + 10(1 − )cos | 2 | [−5, 5] | 0.398 |
| [1 + (19 − 14 + 3)] × [30 + ×(18 − 32 + 48 − 36 + 27 | 2 | [−2, 2] | 3 |
| 3 | [1, 3] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 |
| Function | Class | Functions | Optimum |
|---|---|---|---|
| F24 | Hybrid | Hybrid Function 5 (N = 5) | 2100 |
| F25 | Hybrid Function 6 (N = 5) | 2200 | |
| F26 | Composition | Composition Function 1 (N = 5) | 2300 |
| F27 | Composition Function 2 (N = 3) | 2400 | |
| F28 | Composition Function 3 (N = 3) | 2500 | |
| F29 | Composition Function 4 (N = 5) | 2600 | |
| F30 | Composition Function 5 (N = 5) | 2700 | |
| F31 | Composition Function 6 (N = 5) | 2800 | |
| F32 | Composition Function 7 (N = 3) | 2900 | |
| F33 | Composition Function 8 (N = 3) | 3000 |
| F1 | F2 | F3 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| SMA | 3.2559 × 10−44 | 1.7833 × 10−43 | 1.7856 × 10−44 | 3.2559 × 10−44 | 1.7833 × 10−43 | 1.7856 × 10−44 |
| CSMA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| MCSMA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| DE | 1.8673 × 10−159 | 4.1198 × 10−159 | 1.3001 × 10−94 | 1.8673 × 10−159 | 4.1198 × 10−159 | 1.3001 × 10−94 |
| F4 | F5 | F6 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 0.0000 × 100 | 0.0000 × 100 | 1.5210 × 10−20 | 0.0000 × 100 | 0.0000 × 100 | 1.5210 × 10−20 |
| SMA | 9.1947 × 10−44 | 5.0362 × 10−43 | 4.5273 × 10−1 | 9.1947 × 10−44 | 5.0362 × 10−43 | 4.5273 × 10−1 |
| CSMA | 0.0000 × 100 | 0.0000 × 100 | 1.0735 × 100 | 0.0000 × 100 | 0.0000 × 100 | 1.0735 × 100 |
| MCSMA | 5.5509 × 10−247 | 0.0000 × 100 | 3.7675 × 100 | 5.5509 × 10−247 | 0.0000 × 100 | 3.7675 × 100 |
| DE | 6.3804 × 10−15 | 1.3750 × 10−14 | 3.2827 × 101 | 6.3804 × 10−15 | 1.3750 × 10−14 | 3.2827 × 101 |
| F7 | F8 | F9 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 5.2004 × 10−5 | 4.4680 × 10−5 | 6.5535 × 104 | 5.2004 × 10−5 | 4.4680 × 10−5 | 6.5535 × 104 |
| SMA | 1.8109 × 10−3 | 1.9112 × 10−3 | −1.256 × 104 | 1.8109 × 10−3 | 1.9112 × 10−3 | −1.256 × 104 |
| CSMA | 1.0466 × 10−5 | 7.1026 × 10−6 | 6.5535 × 104 | 1.0466 × 10−5 | 7.1026 × 10−6 | 6.5535 × 104 |
| MCSMA | 2.8153 × 10−4 | 1.4821 × 10−4 | −1.256 × 104 | 2.8153 × 10−4 | 1.4821 × 10−4 | −1.256 × 104 |
| DE | 2.4715 × 10−3 | 4.9474 × 10−4 | −1.244 × 104 | 2.4715 × 10−3 | 4.9474 × 10−4 | −1.244 × 104 |
| F10 | F11 | F12 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| SMA | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| CSMA | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| MCSMA | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| DE | 7.7568 × 10−15 | 9.0135 × 10−16 | 0.0000 × 100 | 7.7568 × 10−15 | 9.0135 × 10−16 | 0.0000 × 100 |
| F13 | F14 | F15 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 |
| SMA | 4.8249 × 10−3 | 7.4218 × 10−3 | 1.3350 × 100 | 4.8249 × 10−3 | 7.4218 × 10−3 | 1.3350 × 100 |
| CSMA | 4.3078 × 10−3 | 6.3340 × 10−3 | 1.2955 × 100 | 4.3078 × 10−3 | 6.3340 × 10−3 | 1.2955 × 100 |
| MCSMA | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 |
| DE | 1.3498 × 10−32 | 5.5674 × 10−48 | 1.0311 × 100 | 1.3498 × 10−32 | 5.5674 × 10−48 | 1.0311 × 100 |
| F16 | F17 | F18 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −1.032 × 100 | 1.2770 × 10−8 | 3.9838 × 10−1 | −1.032 × 100 | 1.2770 × 10−8 | 3.9838 × 10−1 |
| SMA | −8.2436 × 10−1 | 4.1923 × 10−1 | 4.1640 × 10−1 | −8.2436 × 10−1 | 4.1923 × 10−1 | 4.1640 × 10−1 |
| CSMA | −1.031 × 100 | 1.1109 × 10−3 | 4.1829 × 10−1 | −1.031 × 100 | 1.1109 × 10−3 | 4.1829 × 10−1 |
| MCSMA | −1.031 × 100 | 6.5572 × 10−4 | 3.9865 × 10−1 | −1.031 × 100 | 6.5572 × 10−4 | 3.9865 × 10−1 |
| DE | −1.031 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 | −1.031 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 |
| F19 | F20 | F21 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −3.863 × 100 | 1.1037 × 10−4 | −3.163 × 100 | −3.863 × 100 | 1.1037 × 10−4 | −3.163 × 100 |
| SMA | −3.782 × 100 | 9.4398 × 10−2 | −2.958 × 100 | −3.782 × 100 | 9.4398 × 10−2 | −2.958 × 100 |
| CSMA | −3.795 × 100 | 7.9965 × 10−2 | −2.901 × 100 | −3.795 × 100 | 7.9965 × 10−2 | −2.901 × 100 |
| MCSMA | −3.861 × 100 | 1.9880 × 10−3 | −3.042 × 100 | −3.861 × 100 | 1.9880 × 10−3 | −3.042 × 100 |
| DE | −3.862 × 100 | 2.7101 × 10−15 | −3.321 × 100 | −3.862 × 100 | 2.7101 × 10−15 | −3.321 × 100 |
| F22 | F23 | F24 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −1.040 × 101 | 3.3560 × 10−6 | −1.054 × 101 | −1.040 × 101 | 3.3560 × 10−6 | −1.054 × 101 |
| SMA | −1.032 × 101 | 9.7684 × 10−2 | −1.044 × 101 | −1.032 × 101 | 9.7684 × 10−2 | −1.044 × 101 |
| CSMA | −9.877 × 100 | 1.2268 × 100 | −1.041 × 101 | −9.877 × 100 | 1.2268 × 100 | −1.041 × 101 |
| MCSMA | −1.040 × 101 | 6.2358 × 10−6 | −1.054 × 101 | −1.040 × 101 | 6.2358 × 10−6 | −1.054 × 101 |
| DE | −1.040 × 101 | 1.8067 × 10−15 | −1.053 × 101 | −1.040 × 101 | 1.8067 × 10−15 | −1.053 × 101 |
| F25 | F26 | F27 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 3.4989 × 103 | 2.2734 × 102 | 2.5000 × 103 | 3.4989 × 103 | 2.2734 × 102 | 2.5000 × 103 |
| SMA | 1.0429 × 104 | 2.8215 × 104 | 2.5169 × 103 | 1.0429 × 104 | 2.8215 × 104 | 2.5169 × 103 |
| CSMA | 4.7397 × 103 | 1.2900 × 103 | 2.5000 × 103 | 4.7397 × 103 | 1.2900 × 103 | 2.5000 × 103 |
| MCSMA | 3.6251 × 103 | 1.8988 × 102 | 2.5000 × 103 | 3.6251 × 103 | 1.8988 × 102 | 2.5000 × 103 |
| DE | 2.3554 × 103 | 8.2085 × 101 | 2.6152 × 103 | 2.3554 × 103 | 8.2085 × 101 | 2.6152 × 103 |
| F28 | F29 | F30 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 2.7000 × 103 | 0.0000 × 100 | 2.7147 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7147 × 103 |
| SMA | 2.7000 × 103 | 0.0000 × 100 | 2.7732 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7732 × 103 |
| CSMA | 2.7000 × 103 | 0.0000 × 100 | 2.7172 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7172 × 103 |
| MCSMA | 2.7000 × 103 | 0.0000 × 100 | 2.7788 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7788 × 103 |
| DE | 2.7066 × 103 | 8.5796 × 10−1 | 2.7003 × 103 | 2.7066 × 103 | 8.5796 × 10−1 | 2.7003 × 103 |
| F31 | F32 | F33 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 |
| SMA | 4.1186 × 103 | 1.9606 × 103 | 2.8989 × 107 | 4.1186 × 103 | 1.9606 × 103 | 2.8989 × 107 |
| CSMA | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 |
| MCSMA | 5.4386 × 103 | 1.1178 × 103 | 4.0742 × 107 | 5.4386 × 103 | 1.1178 × 103 | 4.0742 × 107 |
| DE | 3.6286 × 103 | 2.4807 × 101 | 1.2080 × 105 | 3.6286 × 103 | 2.4807 × 101 | 1.2080 × 105 |
| Function | SMA | CSMA | MCSMA | DE |
|---|---|---|---|---|
| F1 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 |
| F2 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 |
| F3 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 |
| F4 | 1.7344 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F5 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.3438 × 10−2 | 1.7344 × 10−6 |
| F6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 |
| F7 | 2.3534 × 10−6 | 4.0715 × 10−5 | 2.6033 × 10−6 | 1.7344 × 10−6 |
| F8 | 1.6503 × 10−1 | 1.2720 × 10−1 | 1.3851 × 10−1 | 1.6268 × 10−1 |
| F9 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 5.0000 × 10−1 |
| F10 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 1.0135 × 10−7 |
| F11 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 |
| F12 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 |
| F13 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 |
| F14 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.0000 × 100 |
| F15 | 2.8786 × 10−6 | 2.6033 × 10−6 | 6.7328 × 10−1 | 3.5888 × 10−4 |
| F16 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F17 | 1.2381 × 10−5 | 8.4661 × 10−6 | 9.5899 × 10−1 | 1.7344 × 10−6 |
| F18 | 7.3433 × 10−1 | 4.0483 × 10−1 | 1.1973 × 10−3 | 1.7344 × 10−6 |
| F19 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.6033 × 10−6 | 1.7344 × 10−6 |
| F20 | 6.3391 × 10−6 | 6.3391 × 10−6 | 2.6033 × 10−6 | 1.7344 × 10−6 |
| F21 | 1.7344 × 10−6 | 1.7344 × 10−6 | 9.0993 × 10−1 | 3.1123 × 10−5 |
| F22 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.9569 × 10−2 | 1.7344 × 10−6 |
| F23 | 1.7344 × 10−6 | 1.7344 × 10−6 | 4.2843 × 10−1 | 1.7344 × 10−6 |
| F24 | 6.9838 × 10−6 | 2.5967 × 10−5 | 3.1618 × 10−3 | 1.7344 × 10−6 |
| F25 | 3.1123 × 10−5 | 1.1265 × 10−5 | 4.2767 × 10−2 | 1.7344 × 10−6 |
| F26 | 2.5000 × 10−1 | 1.0000 × 100 | 1.0000 × 100 | 4.3205 × 10−8 |
| F27 | 5.0000 × 10−1 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 |
| F28 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 |
| F29 | 6.5213 × 10−6 | 1.8326 × 10−3 | 1.6789 × 10−5 | 1.7344 × 10−6 |
| F30 | 3.7896 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F31 | 4.8828 × 10−4 | 1.0000 × 100 | 2.5631 × 10−6 | 1.7344 × 10−6 |
| F32 | 7.8125 × 10−3 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F33 | 3.7896 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| +/=/− | 25/8/0 | 16/16/1 | 15/18/1 | 16/7/10 |
| Algorithm | ISMA | SMA | CSMA | MCSMA | DE |
|---|---|---|---|---|---|
| AVR | 2.256060606 | 3.847979798 | 3.202525253 | 2.90959596 | 2.783838384 |
| rank | 1 | 5 | 4 | 3 | 2 |
| F1 | F2 | F3 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| MPEDE | 5.6838 × 10−223 | 0.0000 × 100 | 2.0352 × 10−109 | 5.6838 × 10−223 | 0.0000 × 100 | 2.0352 × 10−109 |
| LSHADE | 8.6954 × 10−203 | 0.0000 × 100 | 2.6224 × 10−85 | 8.6954 × 10−203 | 0.0000 × 100 | 2.6224 × 10−85 |
| ALCPSO | 4.5530 × 10−186 | 0.0000 × 100 | 1.0128 × 10−6 | 4.5530 × 10−186 | 0.0000 × 100 | 1.0128 × 10−6 |
| CLPSO | 2.7917 × 10−34 | 2.0632 × 10−34 | 5.6730 × 10−21 | 2.7917 × 10−34 | 2.0632 × 10−34 | 5.6730 × 10−21 |
| CESCA | 1.0264 × 103 | 7.6509 × 102 | 7.2069 × 100 | 1.0264 × 103 | 7.6509 × 102 | 7.2069 × 100 |
| IGWO | 0.0000 × 100 | 0.0000 × 100 | 5.4179 × 10−260 | 0.0000 × 100 | 0.0000 × 100 | 5.4179 × 10−260 |
| BMWOA | 8.7826 × 10−4 | 1.9389 × 10−3 | 8.5362 × 10−3 | 8.7826 × 10−4 | 1.9389 × 10−3 | 8.5362 × 10−3 |
| OBLGWO | 2.6476 × 10−281 | 0.0000 × 100 | 5.6311 × 10−142 | 2.6476 × 10−281 | 0.0000 × 100 | 5.6311 × 10−142 |
| F4 | F5 | F6 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 0.0000 × 100 | 0.0000 × 100 | 5.6931 × 10−12 | 0.0000 × 100 | 0.0000 × 100 | 5.6931 × 10−12 |
| MPEDE | 1.3923 × 10−5 | 2.6447 × 10−5 | 1.1960 × 100 | 1.3923 × 10−5 | 2.6447 × 10−5 | 1.1960 × 100 |
| LSHADE | 1.3040 × 10−4 | 2.3249 × 10−4 | 5.3155 × 10−1 | 1.3040 × 10−4 | 2.3249 × 10−4 | 5.3155 × 10−1 |
| ALCPSO | 2.6029 × 10−5 | 3.4443 × 10−5 | 2.5603 × 101 | 2.6029 × 10−5 | 3.4443 × 10−5 | 2.5603 × 101 |
| CLPSO | 1.3451 × 100 | 2.6110 × 10−1 | 6.5461 × 10−1 | 1.3451 × 100 | 2.6110 × 10−1 | 6.5461 × 10−1 |
| CESCA | 2.0286 × 101 | 7.5303 × 100 | 2.4759 × 105 | 2.0286 × 101 | 7.5303 × 100 | 2.4759 × 105 |
| IGWO | 7.5149 × 10−26 | 4.1158 × 10−25 | 2.3186 × 101 | 7.5149 × 10−26 | 4.1158 × 10−25 | 2.3186 × 101 |
| BMWOA | 3.6139 × 10−3 | 3.9430 × 10−3 | 3.9781 × 10−3 | 3.6139 × 10−3 | 3.9430 × 10−3 | 3.9781 × 10−3 |
| OBLGWO | 2.7133 × 10−157 | 1.4861 × 10−156 | 2.6112 × 101 | 2.7133 × 10−157 | 1.4861 × 10−156 | 2.6112 × 101 |
| F7 | F8 | F9 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 9.4873 × 10−5 | 6.6385 × 10−5 | 6.5535 × 104 | 9.4873 × 10−5 | 6.6385 × 10−5 | 6.5535 × 104 |
| MPEDE | 3.2148 × 10−3 | 1.6021 × 10−3 | −1.187 × 104 | 3.2148 × 10−3 | 1.6021 × 10−3 | −1.187 × 104 |
| LSHADE | 6.5393 × 10−3 | 5.0546 × 10−3 | −1.895 × 103 | 6.5393 × 10−3 | 5.0546 × 10−3 | −1.895 × 103 |
| ALCPSO | 9.6181 × 10−2 | 3.9035 × 10−2 | −1.147 × 104 | 9.6181 × 10−2 | 3.9035 × 10−2 | −1.147 × 104 |
| CLPSO | 2.6752 × 10−3 | 7.7407 × 10−4 | −1.256 × 104 | 2.6752 × 10−3 | 7.7407 × 10−4 | −1.256 × 104 |
| CESCA | 5.3895 × 10−1 | 3.4475 × 10−1 | −3.901 × 103 | 5.3895 × 10−1 | 3.4475 × 10−1 | −3.901 × 103 |
| IGWO | 2.7827 × 10−4 | 2.2936 × 10−4 | −7.436 × 103 | 2.7827 × 10−4 | 2.2936 × 10−4 | −7.436 × 103 |
| BMWOA | 1.1610 × 10−3 | 8.5016 × 10−4 | −1.257 × 104 | 1.1610 × 10−3 | 8.5016 × 10−4 | −1.257 × 104 |
| OBLGWO | 2.3640 × 10−5 | 2.4037 × 10−5 | −1.253 × 104 | 2.3640 × 10−5 | 2.4037 × 10−5 | −1.253 × 104 |
| F10 | F11 | F12 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| MPEDE | 2.0353 × 100 | 6.7054 × 10−1 | 1.5065 × 10−2 | 2.0353 × 100 | 6.7054 × 10−1 | 1.5065 × 10−2 |
| LSHADE | 3.3455 × 10−14 | 3.7417 × 10−15 | 1.2274 × 10−2 | 3.3455 × 10−14 | 3.7417 × 10−15 | 1.2274 × 10−2 |
| ALCPSO | 8.3257 × 10−1 | 8.5957 × 10−1 | 1.7674 × 10−2 | 8.3257 × 10−1 | 8.5957 × 10−1 | 1.7674 × 10−2 |
| CLPSO | 1.2138 × 10−14 | 2.4831 × 10−15 | 0.0000 × 100 | 1.2138 × 10−14 | 2.4831 × 10−15 | 0.0000 × 100 |
| CESCA | 6.7169 × 100 | 1.9070 × 100 | 1.0700 × 101 | 6.7169 × 100 | 1.9070 × 100 | 1.0700 × 101 |
| IGWO | 4.6777 × 10−15 | 9.0135 × 10−16 | 0.0000 × 100 | 4.6777 × 10−15 | 9.0135 × 10−16 | 0.0000 × 100 |
| BMWOA | 4.6994 × 10−3 | 5.2250 × 10−3 | 1.7612 × 10−3 | 4.6994 × 10−3 | 5.2250 × 10−3 | 1.7612 × 10−3 |
| OBLGWO | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 | 8.8818 × 10−16 | 0.0000 × 100 | 0.0000 × 100 |
| F13 | F14 | F15 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 |
| MPEDE | 3.2626 × 10−1 | 9.4775 × 10−1 | 9.9800 × 10−1 | 3.2626 × 10−1 | 9.4775 × 10−1 | 9.9800 × 10−1 |
| LSHADE | 1.1303 × 10−1 | 4.0369 × 10−1 | 9.9800 × 10−1 | 1.1303 × 10−1 | 4.0369 × 10−1 | 9.9800 × 10−1 |
| ALCPSO | 1.1403 × 10−2 | 3.4415 × 10−2 | 9.9800 × 10−1 | 1.1403 × 10−2 | 3.4415 × 10−2 | 9.9800 × 10−1 |
| CLPSO | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 | 1.3498 × 10−32 | 5.5674 × 10−48 | 9.9800 × 10−1 |
| CESCA | 4.2932 × 105 | 6.0065 × 105 | 3.0471 × 100 | 4.2932 × 105 | 6.0065 × 105 | 3.0471 × 100 |
| IGWO | 1.6832 × 10−2 | 3.2997 × 10−2 | 9.9800 × 10−1 | 1.6832 × 10−2 | 3.2997 × 10−2 | 9.9800 × 10−1 |
| BMWOA | 1.7335 × 10−4 | 5.7395 × 10−4 | 9.9800 × 10−1 | 1.7335 × 10−4 | 5.7395 × 10−4 | 9.9800 × 10−1 |
| OBLGWO | 2.4316 × 10−2 | 3.9405 × 10−2 | 9.9800 × 10−1 | 2.4316 × 10−2 | 3.9405 × 10−2 | 9.9800 × 10−1 |
| F16 | F17 | F18 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −1.032 × 100 | 6.9699 × 10−9 | 3.9808 × 10−1 | −1.032 × 100 | 6.9699 × 10−9 | 3.9808 × 10−1 |
| MPEDE | −1.032 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 | −1.032 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 |
| LSHADE | −1.032 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 | −1.032 × 100 | 6.7752 × 10−16 | 3.9789 × 10−1 |
| ALCPSO | −1.032 × 100 | 5.6082 × 10−16 | 3.9789 × 10−1 | −1.032 × 100 | 5.6082 × 10−16 | 3.9789 × 10−1 |
| CLPSO | −1.032 × 100 | 6.4539 × 10−16 | 3.9789 × 10−1 | −1.032 × 100 | 6.4539 × 10−16 | 3.9789 × 10−1 |
| CESCA | −1.026 × 100 | 5.9057 × 10−3 | 7.0892 × 10−1 | −1.026 × 100 | 5.9057 × 10−3 | 7.0892 × 10−1 |
| IGWO | −1.032 × 100 | 2.2583 × 10−13 | 3.9789 × 10−1 | −1.032 × 100 | 2.2583 × 10−13 | 3.9789 × 10−1 |
| BMWOA | −1.031 × 100 | 4.4024 × 10−16 | 3.9789 × 10−1 | −1.031 × 100 | 4.4024 × 10−16 | 3.9789 × 10−1 |
| OBLGWO | −1.032 × 100 | 9.0832 × 10−9 | 3.9801 × 10−1 | −1.032 × 100 | 9.0832 × 10−9 | 3.9801 × 10−1 |
| F19 | F20 | F21 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −3.863 × 100 | 9.7215 × 10−5 | −3.159 × 100 | −3.863 × 100 | 9.7215 × 10−5 | −3.159 × 100 |
| MPEDE | −3.863 × 100 | 2.7101 × 10−15 | −3.271 × 100 | −3.863 × 100 | 2.7101 × 10−15 | −3.271 × 100 |
| LSHADE | −3.863 × 100 | 1.3042 × 10−4 | −1.952 × 100 | −3.863 × 100 | 1.3042 × 10−4 | −1.952 × 100 |
| ALCPSO | −3.862 × 100 | 2.5243 × 10−15 | −3.274 × 100 | −3.862 × 100 | 2.5243 × 10−15 | −3.274 × 100 |
| CLPSO | −3.863 × 100 | 2.7101 × 10−15 | −3.322 × 100 | −3.863 × 100 | 2.7101 × 10−15 | −3.322 × 100 |
| CESCA | −3.610 × 100 | 1.6803 × 10−1 | −2.176 × 100 | −3.610 × 100 | 1.6803 × 10−1 | −2.176 × 100 |
| IGWO | −3.863 × 100 | 1.0500 × 10−9 | −3.251 × 100 | −3.863 × 100 | 1.0500 × 10−9 | −3.251 × 100 |
| BMWOA | −3.863 × 100 | 1.5134 × 10−14 | −3.290 × 100 | −3.863 × 100 | 1.5134 × 10−14 | −3.290 × 100 |
| OBLGWO | −3.863 × 100 | 1.3281 × 10−6 | −3.223 × 100 | −3.863 × 100 | 1.3281 × 10−6 | −3.223 × 100 |
| F22 | F23 | F24 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | −1.040 × 101 | 5.9774 × 10−6 | −1.054 × 101 | −1.040 × 101 | 5.9774 × 10−6 | −1.054 × 101 |
| MPEDE | −9.542 × 100 | 2.2747 × 100 | −9.817 × 100 | −9.542 × 100 | 2.2747 × 100 | −9.817 × 100 |
| LSHADE | −1.023 × 101 | 9.6292 × 10−1 | −1.053 × 101 | −1.023 × 101 | 9.6292 × 10−1 | −1.053 × 101 |
| ALCPSO | −9.876 × 100 | 1.6093 × 100 | −9.997 × 100 | −9.876 × 100 | 1.6093 × 100 | −9.997 × 100 |
| CLPSO | −1.040 × 101 | 5.7155 × 10−9 | −1.054 × 101 | −1.040 × 101 | 5.7155 × 10−9 | −1.054 × 101 |
| CESCA | −1.091 × 100 | 4.2964 × 10−1 | −1.172 × 100 | −1.091 × 100 | 4.2964 × 10−1 | −1.172 × 100 |
| IGWO | −9.166 × 100 | 2.2815 × 100 | −1.018 × 101 | −9.166 × 100 | 2.2815 × 100 | −1.018 × 101 |
| BMWOA | −1.040 × 101 | 9.4634 × 10−11 | −1.054 × 101 | −1.040 × 101 | 9.4634 × 10−11 | −1.054 × 101 |
| OBLGWO | −1.040 × 101 | 3.5332 × 10−5 | −1.054 × 101 | −1.040 × 101 | 3.5332 × 10−5 | −1.054 × 101 |
| F25 | F26 | F27 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 3.4696 × 103 | 1.5041 × 102 | 2.5000 × 103 | 3.4696 × 103 | 1.5041 × 102 | 2.5000 × 103 |
| MPEDE | 2.5483 × 103 | 2.1545 × 102 | 2.6152 × 103 | 2.5483 × 103 | 2.1545 × 102 | 2.6152 × 103 |
| LSHADE | 2.4214 × 103 | 1.2400 × 102 | 2.6152 × 103 | 2.4214 × 103 | 1.2400 × 102 | 2.6152 × 103 |
| ALCPSO | 2.6317 × 103 | 1.8339 × 102 | 2.6153 × 103 | 2.6317 × 103 | 1.8339 × 102 | 2.6153 × 103 |
| CLPSO | 2.4055 × 103 | 8.0140 × 101 | 2.6152 × 103 | 2.4055 × 103 | 8.0140 × 101 | 2.6152 × 103 |
| CESCA | 5.5650 × 103 | 9.4857 × 102 | 3.0675 × 103 | 5.5650 × 103 | 9.4857 × 102 | 3.0675 × 103 |
| IGWO | 2.5661 × 103 | 1.8331 × 102 | 2.6206 × 103 | 2.5661 × 103 | 1.8331 × 102 | 2.6206 × 103 |
| BMWOA | 2.9003 × 103 | 1.9433 × 102 | 2.5005 × 103 | 2.9003 × 103 | 1.9433 × 102 | 2.5005 × 103 |
| OBLGWO | 2.6973 × 103 | 2.3782 × 102 | 2.6188 × 103 | 2.6973 × 103 | 2.3782 × 102 | 2.6188 × 103 |
| F28 | F29 | F30 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 2.7000 × 103 | 0.0000 × 100 | 2.7181 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7181 × 103 |
| MPEDE | 2.7112 × 103 | 4.6410 × 100 | 2.7202 × 103 | 2.7112 × 103 | 4.6410 × 100 | 2.7202 × 103 |
| LSHADE | 2.7056 × 103 | 3.3938 × 100 | 2.7104 × 103 | 2.7056 × 103 | 3.3938 × 100 | 2.7104 × 103 |
| ALCPSO | 2.7124 × 103 | 5.0481 × 100 | 2.7553 × 103 | 2.7124 × 103 | 5.0481 × 100 | 2.7553 × 103 |
| CLPSO | 2.7072 × 103 | 9.5781 × 10−1 | 2.7004 × 103 | 2.7072 × 103 | 9.5781 × 10−1 | 2.7004 × 103 |
| CESCA | 2.7206 × 103 | 8.6833 × 100 | 2.7123 × 103 | 2.7206 × 103 | 8.6833 × 100 | 2.7123 × 103 |
| IGWO | 2.7107 × 103 | 2.5492 × 100 | 2.7007 × 103 | 2.7107 × 103 | 2.5492 × 100 | 2.7007 × 103 |
| BMWOA | 2.7000 × 103 | 1.1250 × 10−2 | 2.7006 × 103 | 2.7000 × 103 | 1.1250 × 10−2 | 2.7006 × 103 |
| OBLGWO | 2.7000 × 103 | 0.0000 × 100 | 2.7005 × 103 | 2.7000 × 103 | 0.0000 × 100 | 2.7005 × 103 |
| F31 | F32 | F33 | ||||
| mean | std | mean | mean | std | mean | |
| ISMA | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 | 3.0000 × 103 | 0.0000 × 100 | 3.1000 × 103 |
| MPEDE | 3.9778 × 103 | 3.4239 × 102 | 1.6519 × 106 | 3.9778 × 103 | 3.4239 × 102 | 1.6519 × 106 |
| LSHADE | 3.7470 × 103 | 8.7552 × 101 | 2.9248 × 105 | 3.7470 × 103 | 8.7552 × 101 | 2.9248 × 105 |
| ALCPSO | 4.4793 × 103 | 5.0276 × 102 | 2.8922 × 106 | 4.4793 × 103 | 5.0276 × 102 | 2.8922 × 106 |
| CLPSO | 3.7271 × 103 | 8.5165 × 101 | 3.8465 × 103 | 3.7271 × 103 | 8.5165 × 101 | 3.8465 × 103 |
| CESCA | 5.4621 × 103 | 2.9312 × 102 | 1.6432 × 107 | 5.4621 × 103 | 2.9312 × 102 | 1.6432 × 107 |
| IGWO | 3.7942 × 103 | 1.0332 × 102 | 8.4824 × 105 | 3.7942 × 103 | 1.0332 × 102 | 8.4824 × 105 |
| BMWOA | 3.0001 × 103 | 1.8250 × 10−1 | 3.8977 × 105 | 3.0001 × 103 | 1.8250 × 10−1 | 3.8977 × 105 |
| OBLGWO | 3.5344 × 103 | 4.8730 × 102 | 3.4895 × 106 | 3.5344 × 103 | 4.8730 × 102 | 3.4895 × 106 |
| Function | MPEDE | LSHADE | ALCPSO | CLPSO | CESCA | IGWO | BMWOA | OBLGWO |
|---|---|---|---|---|---|---|---|---|
| F1 | 1.7344 × 10−6 | 1.7333 × 10−6 | 1.7333 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.0000 × 100 |
| F2 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.5000 × 10−1 |
| F4 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 3.7896 × 10−6 |
| F5 | 8.1806 × 10−5 | 5.9829 × 10−2 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F6 | 3.5657 × 10−4 | 2.4414 × 10−4 | 1.7333 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F7 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 5.7924 × 10−5 | 1.7344 × 10−6 | 3.1123 × 10−5 |
| F8 | 1.4831 × 10−3 | 1.4591 × 10−3 | 1.4835 × 10−3 | 1.3642 × 10−3 | 1.4557 × 10−3 | 1.4839 × 10−3 | 1.4839 × 10−3 | 1.4839 × 10−3 |
| F9 | 1.7300 × 10−6 | 5.0136 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.0000 × 100 |
| F10 | 1.7203 × 10−6 | 8.7824 × 10−7 | 1.7041 × 10−6 | 1.0651 × 10−6 | 1.7344 × 10−6 | 1.0135 × 10−7 | 1.7344 × 10−6 | 1.0000 × 100 |
| F11 | 1.9472 × 10−4 | 3.9586 × 10−5 | 1.3163 × 10−4 | 1.0000 × 100 | 1.7333 × 10−6 | 1.0000 × 100 | 1.7333 × 10−6 | 1.0000 × 100 |
| F12 | 2.6499 × 10−5 | 1.7948 × 10−5 | 1.7311 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F13 | 5.2772 × 10−5 | 4.0204 × 10−4 | 1.7062 × 10−6 | 1.0000 × 100 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F14 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 1.0000 × 100 | 1.7344 × 10−6 | 4.1722 × 10−7 | 3.9063 × 10−3 | 1.7344 × 10−6 |
| F15 | 1.4795 × 10−2 | 1.9209 × 10−6 | 2.7653 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 5.9836 × 10−2 | 2.7653 × 10−3 | 1.8519 × 10−2 |
| F16 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.1748 × 10−2 |
| F17 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.1827 × 10−2 |
| F18 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.3059 × 10−1 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F19 | 1.7344 × 10−6 | 3.1123 × 10−5 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.3534 × 10−6 |
| F20 | 3.8822 × 10−6 | 1.9152 × 10−1 | 3.8822 × 10−6 | 1.7344 × 10−6 | 1.9209 × 10−6 | 8.4661 × 10−6 | 6.3391 × 10−6 | 2.2248 × 10−4 |
| F21 | 6.4352 × 10−1 | 1.6503 × 10−1 | 1.4795 × 10−2 | 7.7309 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F22 | 1.4795 × 10−2 | 3.1123 × 10−5 | 2.7653 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 4.9498 × 10−2 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F23 | 2.7653 × 10−3 | 1.7344 × 10−6 | 2.7653 × 10−3 | 1.7344 × 10−6 | 1.7344 × 10−6 | 6.8836 × 10−1 | 1.7344 × 10−6 | 2.6033 × 10−6 |
| F24 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.6033 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F25 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.9209 × 10−6 | 1.7344 × 10−6 |
| F26 | 4.3205 × 10−8 | 6.7988 × 10−8 | 1.7344 × 10−6 | 1.7333 × 10−6 | 1.7333 × 10−6 | 1.7333 × 10−6 | 1.7333 × 10−6 | 1.7344 × 10−6 |
| F27 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 |
| F28 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.0000 × 100 |
| F29 | 7.8647 × 10−2 | 1.4839 × 10−3 | 1.4139 × 10−1 | 1.7344 × 10−6 | 2.5637 × 10−2 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F30 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.5000 × 10−1 |
| F31 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 2.9305 × 10−4 |
| F32 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| F33 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 | 1.7344 × 10−6 |
| +/=/− | 22/3/8 | 20/4/9 | 23/2/8 | 16/6/11 | 30/1/2 | 19/5/9 | 21/0/12 | 16/8/9 |
| Algorithm | ISMA | MPEDE | LSHADE | ALCPSO | CLPSO | CESCA | IGWO | BMWOA | OBLGWO |
|---|---|---|---|---|---|---|---|---|---|
| AVR | 3.7075758 | 4.0257576 | 4.1979798 | 5.1949495 | 3.8792929 | 8.8474747 | 5.0984848 | 5.080303 | 4.9681818 |
| rank | 1 | 3 | 4 | 8 | 2 | 9 | 7 | 6 | 5 |
| S-Shaped Family | ||
|---|---|---|
| Name | TFs | Graphs |
| TFS1 | 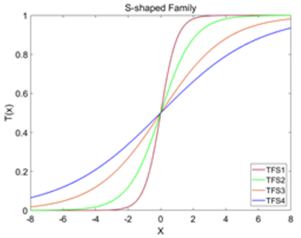 | |
| TFS2 | ||
| TFS3 | ||
| TFS4 | ||
| V-Shaped Family | ||
| Name | TFs | Graphs |
| TFV1 |  | |
| TFV2 | ||
| TFV3 | ||
| TFV4 | ||
| Datasets | Samples | Genes | Categories |
|---|---|---|---|
| Colon | 62 | 2000 | 2 |
| SRBCT | 83 | 2309 | 4 |
| Leukemia | 72 | 7131 | 2 |
| Brain_Tumor1 | 90 | 5920 | 5 |
| Brain_Tumor2 | 50 | 10,367 | 4 |
| CNS | 60 | 7130 | 2 |
| DLBCL | 77 | 5470 | 4 |
| Leukemia1 | 72 | 5328 | 5 |
| Leukemia2 | 72 | 11,225 | 3 |
| Lung_Cancer | 203 | 12,601 | 3 |
| Prostate_Tumor | 102 | 10,509 | 2 |
| Tumors_9 | 60 | 5726 | 9 |
| Tumors_11 | 174 | 12,533 | 11 |
| Tumors_14 | 308 | 15,009 | 26 |
| Datasets | Metrics | BISMA_S1 | BISMA_S2 | BISMA_S3 | BISMA_S4 | BISMA_V1 | BISMA_V2 | BISMA_V3 | BISMA_V4 |
|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 143.6448 | 157.4435 | 173.4187 | 162.0243 | 0.4216 | 0.9718 | 0.6992 | 0.6992 |
| avg | 307.5000 | 464.5000 | 476.5000 | 498.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| SRBCT | std | 138.2114 | 95.9528 | 156.2727 | 154.4375 | 2.9515 | 2.9364 | 1.9322 | 1.4337 |
| avg | 376.5000 | 465.5000 | 566.0000 | 565.0000 | 4.0000 | 5.0000 | 4.5000 | 4.5000 | |
| Leukemia | std | 589.3556 | 296.6164 | 135.8554 | 64.6241 | 0.9487 | 1.2517 | 0.3162 | 0.3162 |
| avg | 1595.5000 | 1359.0000 | 1738.5000 | 1755.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Brain_Tumor1 | std | 926.7275 | 778.2962 | 44.3653 | 560.9920 | 147.6392 | 8.0939 | 11.1679 | 19.3724 |
| avg | 1050.0000 | 1319.5000 | 1451.5000 | 1461.5000 | 2.0000 | 3.0000 | 2.5000 | 2.5000 | |
| Brain_Tumor2 | std | 755.7944 | 978.0951 | 955.6762 | 430.0868 | 1.7512 | 0.9944 | 1.2293 | 0.4831 |
| avg | 1938.0000 | 2509.5000 | 2510.0000 | 2529.5000 | 1.0000 | 2.0000 | 1.5000 | 1.0000 | |
| CNS | std | 504.4472 | 867.2775 | 732.4766 | 489.2598 | 2.2136 | 0.5164 | 0.0000 | 0.4216 |
| avg | 1685.0000 | 1720.5000 | 1805.0000 | 1935.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| DLBCL | std | 292.2214 | 169.4024 | 129.8839 | 79.6573 | 0.0000 | 0.6750 | 0.3162 | 0.6325 |
| avg | 490.5000 | 1295.0000 | 1334.5000 | 1371.5000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Leukemia1 | std | 348.2874 | 536.8715 | 66.7750 | 77.7810 | 1.3499 | 1.8135 | 1.1005 | 1.2472 |
| avg | 1163.0000 | 1271.5000 | 1283.0000 | 1328.5000 | 2.0000 | 2.0000 | 2.0000 | 2.0000 | |
| Leukemia2 | std | 731.5217 | 497.7822 | 232.6141 | 929.4172 | 3.7357 | 1.6633 | 1.4142 | 1.4181 |
| avg | 1255.5000 | 2532.5000 | 2673.5000 | 2737.5000 | 3.0000 | 2.5000 | 1.5000 | 3.0000 | |
| Lung_Cancer | std | 1191.4138 | 1241.8645 | 1162.5447 | 623.9975 | 19.8161 | 16.1593 | 29.0746 | 93.8666 |
| avg | 3066.0000 | 3122.0000 | 3111.0000 | 3162.0000 | 23.5000 | 19.0000 | 16.5000 | 15.5000 | |
| Prostate_Tumor | std | 1573.8463 | 1270.5976 | 1119.6290 | 1279.6201 | 6.2405 | 37.9867 | 1.0750 | 1.8529 |
| avg | 2540.0000 | 2709.0000 | 2631.5000 | 2760.5000 | 3.5000 | 2.0000 | 2.5000 | 2.5000 | |
| Tumors_9 | std | 785.7851 | 856.2383 | 533.6090 | 595.3492 | 243.1681 | 42.0502 | 595.2484 | 139.8144 |
| avg | 1376.5000 | 1409.5000 | 1698.0000 | 1421.0000 | 1.0000 | 2.0000 | 2.5000 | 4.0000 | |
| Tumors_11 | std | 1040.6752 | 1660.6726 | 1391.3213 | 1285.5454 | 108.9483 | 288.1741 | 948.9861 | 248.4647 |
| avg | 3118.5000 | 4607.0000 | 4642.0000 | 3287.0000 | 210.0000 | 304.5000 | 374.5000 | 233.0000 | |
| Tumors_14 | std | 2353.3411 | 1657.2601 | 974.4708 | 1551.2076 | 1520.8509 | 930.6287 | 618.4779 | 966.3795 |
| avg | 4920.0000 | 7469.0000 | 7450.0000 | 6775.0000 | 1143.5000 | 760.5000 | 540.5000 | 569.5000 | |
| ARV | 5.7143 | 6.3893 | 6.8143 | 7.0393 | 2.5286 | 2.6536 | 2.4464 | 2.4143 | |
| Rank | 5 | 6 | 7 | 8 | 3 | 4 | 2 | 1 | |
| Datasets | Metrics | BISMA_S1 | BISMA_S2 | BISMA_S3 | BISMA_S4 | BISMA_V1 | BISMA_V2 | BISMA_V3 | BISMA_V4 |
|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 1.305 × 10−1 | 1.399 × 10−1 | 1.620 × 10−1 | 1.042 × 10−1 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.1429 | 0.1667 | 0.1667 | 0.1548 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| SRBCT | std | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Leukemia | std | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Brain_Tumor1 | std | 5.463 × 10−2 | 5.604 × 10−2 | 7.147 × 10−2 | 5.520 × 10−2 | 3.162 × 10−2 | 3.162 × 10−2 | 3.162 × 10−2 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0500 | 0.0500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Brain_Tumor2 | std | 9.088 × 10−2 | 8.051 × 10−2 | 1.370 × 10−1 | 8.051 × 10−2 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| CNS | std | 8.794 × 10−2 | 1.466 × 10−1 | 8.607 × 10−2 | 1.528 × 10−1 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.1548 | 0.0000 | 0.0000 | 0.1548 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| DLBCL | std | 3.953 × 10−2 | 4.518 × 10−2 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Leukemia1 | std | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Leukemia2 | std | 0.000 × 100 | 4.518 × 10−2 | 4.518 × 10−2 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Lung_Cancer | std | 2.528 × 10−2 | 2.561 × 10−2 | 2.491 × 10−2 | 3.310 × 10−2 | 0.000 × 100 | 1.506 × 10−2 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0238 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Prostate_Tumor | std | 6.449 × 10−2 | 5.020 × 10−2 | 7.071 × 10−2 | 5.182 × 10−2 | 3.162 × 10−2 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0909 | 0.0000 | 0.0455 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Tumors_9 | std | 7.313 × 10−2 | 1.315 × 10−1 | 6.325 × 10−2 | 1.406 × 10−1 | 5.271 × 10−2 | 0.000 × 100 | 0.000 × 100 | 0.000 × 100 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Tumors_11 | std | 4.353 × 10−2 | 4.395 × 10−2 | 5.206 × 10−2 | 4.678 × 10−2 | 2.886 × 10−2 | 2.413 × 10−2 | 2.975 × 10−2 | 1.757 × 10−2 |
| avg | 0.0556 | 0.0590 | 0.0572 | 0.0572 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Tumors_14 | std | 4.856 × 10−2 | 1.028 × 10−1 | 5.861 × 10−2 | 4.875 × 10−2 | 4.411 × 10−2 | 7.900 × 10−2 | 3.750 × 10−2 | 6.582 × 10−2 |
| avg | 0.2952 | 0.2540 | 0.2971 | 0.2833 | 0.2500 | 0.2374 | 0.2457 | 0.2379 | |
| ARV | 5.1107 | 5.1107 | 5.0429 | 5.0571 | 4.9857 | 4.0429 | 3.9571 | 3.9429 | |
| Rank | 8 | 8 | 6 | 7 | 5 | 4 | 3 | 2 | |
| Datasets | Metrics | BISMA_S1 | BISMA_S2 | BISMA_S3 | BISMA_S4 | BISMA_V1 | BISMA_V2 | BISMA_V3 | BISMA_V4 |
|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 1.2251 × 10−1 | 1.3115 × 10−1 | 1.5248 × 10−1 | 9.9228 × 10−2 | 1.0500 × 10−5 | 2.4300 × 10−5 | 1.7500 × 10−5 | 1.7500 × 10−5 |
| avg | 0.14415 | 0.16695 | 0.16966 | 0.16554 | 2.50 × 10−5 | 2.50 × 10−5 | 2.50 × 10−5 | 2.50 × 10−5 | |
| SRBCT | std | 2.9942 × 10−3 | 2.0787 × 10−3 | 3.3855 × 10−3 | 3.3457 × 10−3 | 6.3900 × 10−5 | 6.3600 × 10−5 | 4.1900 × 10−5 | 3.1100 × 10−5 |
| avg | 0.0081564 | 0.010084 | 0.012262 | 0.01224 | 8.67 × 10−5 | 0.00010832 | 9.75 × 10−5 | 9.75 × 10−5 | |
| Leukemia | std | 4.1329 × 10−3 | 2.0801 × 10−3 | 9.5270 × 10−4 | 4.5318 × 10−4 | 6.6500 × 10−6 | 8.7800 × 10−6 | 2.2200 × 10−6 | 2.2200 × 10−6 |
| avg | 0.011189 | 0.0095302 | 0.012191 | 0.012307 | 7.01 × 10−6 | 7.01 × 10−6 | 7.01 × 10−6 | 7.01 × 10−6 | |
| Brain_Tumor1 | std | 5.1602 × 10−2 | 5.4124 × 10−2 | 6.7843 × 10−2 | 5.1574 × 10−2 | 2.9920 × 10−2 | 3.0033 × 10−2 | 3.0031 × 10−2 | 1.6362 × 10−4 |
| avg | 0.018758 | 0.018163 | 0.059215 | 0.06541 | 1.69 × 10−5 | 2.53 × 10−5 | 2.11 × 10−5 | 2.11 × 10−5 | |
| Brain_Tumor2 | std | 8.4413 × 10−2 | 7.4520 × 10−2 | 1.3015 × 10−1 | 7.6131 × 10−2 | 8.4500 × 10−6 | 4.8000 × 10−6 | 5.9300 × 10−6 | 2.3300 × 10−6 |
| avg | 0.012262 | 0.015231 | 0.012441 | 0.013635 | 4.82 × 10−6 | 9.65 × 10−6 | 7.23 × 10−6 | 4.82 × 10−6 | |
| CNS | std | 8.4987 × 10−2 | 1.3856 × 10−1 | 8.0292 × 10−2 | 1.4740 × 10−1 | 1.5500 × 10−5 | 3.6200 × 10−6 | 0.0000 × 100 | 2.9600 × 10−6 |
| avg | 0.1548 | 0.018712 | 0.023061 | 0.1594 | 7.01 × 10−6 | 7.01 × 10−6 | 7.01 × 10−6 | 7.01 × 10−6 | |
| DLBCL | std | 3.7662 × 10−2 | 4.3039 × 10−2 | 1.1875 × 10−3 | 7.2826 × 10−4 | 0.0000 × 100 | 6.1700 × 10−6 | 2.8900 × 10−6 | 5.7800 × 10−6 |
| avg | 0.0044844 | 0.012009 | 0.012201 | 0.012539 | 9.14 × 10−6 | 9.14 × 10−6 | 9.14 × 10−6 | 9.14 × 10−6 | |
| Leukemia1 | std | 3.2691 × 10−3 | 5.0392 × 10−3 | 6.2676 × 10−4 | 7.3006 × 10−4 | 1.2700 × 10−5 | 1.7000 × 10−5 | 1.0300 × 10−5 | 1.1700 × 10−5 |
| avg | 0.010916 | 0.011934 | 0.012042 | 0.012469 | 1.88 × 10−5 | 1.88 × 10−5 | 1.88 × 10−5 | 1.88 × 10−5 | |
| Leukemia2 | std | 3.2584 × 10−3 | 4.3716 × 10−2 | 4.3135 × 10−2 | 4.1399 × 10−3 | 1.6600 × 10−5 | 7.4100 × 10−6 | 6.3000 × 10−6 | 6.3200 × 10−6 |
| avg | 0.0055924 | 0.011281 | 0.011909 | 0.012194 | 1.34 × 10−5 | 1.11 × 10−5 | 6.68 × 10−6 | 1.34 × 10−5 | |
| Lung_Cancer | std | 2.3808 × 10−2 | 2.2944 × 10−2 | 2.2084 × 10−2 | 3.1035 × 10−2 | 7.8600 × 10−5 | 1.4293 × 10−2 | 1.1538 × 10−4 | 3.7249 × 10−4 |
| avg | 0.018605 | 0.04004 | 0.022837 | 0.013115 | 9.33 × 10−5 | 8.73 × 10−5 | 6.55 × 10−5 | 6.15 × 10−5 | |
| Prostate_Tumor | std | 6.2632 × 10−2 | 4.4868 × 10−2 | 6.4827 × 10−2 | 4.9589 × 10−2 | 3.0037 × 10−2 | 1.8073 × 10−4 | 5.1100 × 10−6 | 8.8200 × 10−6 |
| avg | 0.018427 | 0.098843 | 0.024919 | 0.06217 | 2.85 × 10−5 | 9.52 × 10−6 | 1.19 × 10−5 | 1.19 × 10−5 | |
| Tumors_9 | std | 7.3201 × 10−2 | 1.2925 × 10−1 | 6.0930 × 10−2 | 1.3705 × 10−1 | 5.1706 × 10−2 | 3.6719 × 10−4 | 5.1978 × 10−3 | 1.2209 × 10−3 |
| avg | 0.012256 | 0.012308 | 0.014827 | 0.012408 | 8.73 × 10−6 | 1.75 × 10−5 | 2.18 × 10−5 | 3.49 × 10−5 | |
| Tumors_11 | std | 4.0291 × 10−2 | 4.4019 × 10−2 | 4.8341 × 10−2 | 4.3815 × 10−2 | 2.7431 × 10−2 | 2.2469 × 10−2 | 2.7845 × 10−2 | 1.7275 × 10−2 |
| avg | 0.0646 | 0.074911 | 0.071693 | 0.06889 | 0.0013903 | 0.0019768 | 0.0046557 | 0.00092955 | |
| Tumors_14 | std | 4.2144 × 10−2 | 9.9535 × 10−2 | 5.5160 × 10−2 | 4.2749 × 10−2 | 4.2056 × 10−2 | 7.3598 × 10−2 | 3.5842 × 10−2 | 6.0899 × 10−2 |
| avg | 0.30311 | 0.26614 | 0.30706 | 0.28783 | 0.24017 | 0.22696 | 0.23548 | 0.22735 | |
| ARV | 5.9786 | 5.9786 | 6.2214 | 6.6214 | 6.6929 | 2.7036 | 2.7536 | 2.6036 | |
| Rank | 5 | 5 | 6 | 7 | 8 | 3 | 4 | 2 | |
| Datasets | Metrics | BISMA_S1 | BISMA_S2 | BISMA_S3 | BISMA_S4 | BISMA_V1 | BISMA_V2 | BISMA_V3 | BISMA_V4 |
|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 1.2191 | 1.3052 | 2.4355 | 1.4757 | 1.1938 | 1.4909 | 1.2686 | 1.3287 |
| avg | 85.9626 | 90.0505 | 121.3363 | 89.5739 | 94.0297 | 84.1583 | 82.0512 | 82.549 | |
| SRBCT | std | 1.5885 | 1.8773 | 2.8525 | 1.084 | 1.8508 | 2.45 | 3.0216 | 2.414 |
| avg | 102.6595 | 105.9233 | 153.5824 | 106.7198 | 110.4927 | 101.3722 | 94.9202 | 98.0153 | |
| Leukemia | std | 4.6463 | 7.1863 | 8.4485 | 4.176 | 5.6477 | 8.9345 | 7.1624 | 5.6551 |
| avg | 288.1026 | 369.0878 | 418.859 | 300.3361 | 312.7438 | 281.3737 | 263.277 | 262.0363 | |
| Brain_Tumor1 | std | 15.0486 | 5.518 | 5.9123 | 3.6483 | 6.5985 | 7.0206 | 5.2887 | 9.7095 |
| avg | 257.1141 | 329.2853 | 355.1649 | 265.6545 | 268.0102 | 235.1687 | 226.2937 | 221.4106 | |
| Brain_Tumor2 | std | 26.0923 | 16.4663 | 5.829 | 5.9109 | 5.7821 | 6.9892 | 8.4514 | 4.4363 |
| avg | 394.7483 | 557.1407 | 417.7936 | 408.0532 | 429.047 | 378.0446 | 403.66 | 366.1612 | |
| CNS | std | 18.5258 | 8.2571 | 4.9416 | 4.7855 | 5.2549 | 5.1788 | 6.3485 | 2.5764 |
| avg | 282.115 | 399.2233 | 297.2468 | 292.9844 | 305.7291 | 270.9286 | 305.3575 | 257.4227 | |
| DLBCL | std | 13.4459 | 7.3986 | 3.7698 | 3.2965 | 6.6934 | 6.881 | 5.9037 | 6.3564 |
| avg | 229.0604 | 318.173 | 239.9178 | 235.4501 | 243.1863 | 222.2096 | 206.4178 | 207.6545 | |
| Leukemia1 | std | 13.0915 | 7.1145 | 4.2194 | 3.5637 | 4.3786 | 5.3226 | 3.4246 | 4.1366 |
| avg | 221.6625 | 306.661 | 230.06 | 226.9516 | 236.7801 | 206.948 | 201.3261 | 199.8014 | |
| Leukemia2 | std | 27.9557 | 27.8952 | 7.3565 | 6.2185 | 9.6514 | 10.0649 | 7.2691 | 9.5984 |
| avg | 454.5811 | 626.5679 | 467.8857 | 467.3684 | 482.2521 | 424.8834 | 411.641 | 408.7297 | |
| Lung_Cancer | std | 40.0181 | 14.4133 | 21.3431 | 26.7837 | 47.3963 | 37.8825 | 48.654 | 32.9511 |
| avg | 835.7816 | 1064.939 | 847.6348 | 828.0133 | 677.3208 | 558.4493 | 534.8904 | 521.5364 | |
| Prostate_Tumor | std | 25.1417 | 10.4573 | 6.7311 | 10.3808 | 19.9367 | 16.2087 | 12.0796 | 24.8174 |
| avg | 470.1901 | 659.3352 | 485.7299 | 477.1534 | 464.5947 | 415.6169 | 390.0605 | 389.1298 | |
| Tumors_9 | std | 13.5588 | 8.8614 | 3.2316 | 4.0011 | 2.6109 | 4.0259 | 4.3268 | 3.487 |
| avg | 231.0626 | 333.3597 | 240.6433 | 238.7621 | 246.7118 | 220.015 | 208.5856 | 206.8161 | |
| Tumors_11 | std | 39.8624 | 15.6572 | 18.8506 | 15.9373 | 46.4145 | 36.5902 | 20.4801 | 15.6274 |
| avg | 744.1785 | 985.7713 | 758.463 | 752.3035 | 630.7326 | 555.8758 | 502.5768 | 483.1388 | |
| Tumors_14 | std | 73.1984 | 62.0491 | 69.1097 | 103.7124 | 77.7274 | 74.0669 | 49.1133 | 57.7599 |
| avg | 1560.365 | 1901.44 | 1556.638 | 1541.604 | 1087.476 | 880.2872 | 760.1826 | 723.8812 | |
| ARV | 4.7 | 7.5143 | 6.4071 | 5.0571 | 5.8929 | 2.8643 | 2.1357 | 1.4286 | |
| Rank | 4 | 8 | 7 | 5 | 6 | 3 | 2 | 1 | |
| Optimizers | Parameters | Value |
|---|---|---|
| bGWO | 2 | |
| 0 | ||
| BPSO | Min inertia weight | 0.4 |
| Min inertia weight | 0.9 | |
| 0.2 | ||
| bWOA | 2 | |
| 0 |
| Datasets | Metrics | BISMA | BSMA | bGWO | BGSA | BPSO | bALO | BBA | BSSA | bWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 0.5164 | 29.5727 | 15.9753 | 23.2178 | 18.7901 | 26.9081 | 57.2076 | 413.9399 | 1.6499 |
| avg | 1 | 46 | 153.5 | 769 | 899 | 876 | 818 | 424.5 | 2 | |
| SRBCT | std | 1.2649 | 20.5721 | 15.2567 | 28.0515 | 17.2321 | 21.7348 | 88.7612 | 234.9426 | 1.8974 |
| avg | 3 | 33.5 | 192 | 898.5 | 1023 | 996 | 936 | 1073.5 | 4 | |
| Leukemia | std | 0.42164 | 21.9699 | 41.075 | 22.2264 | 31.8531 | 27.3595 | 180.2885 | 1254.8997 | 0.91894 |
| avg | 1 | 36 | 791.5 | 3106 | 3354 | 3288 | 2850 | 3427 | 2 | |
| Brain_Tumor1 | std | 3.1429 | 78.3272 | 37.8001 | 45.6636 | 31.3739 | 42.0132 | 104.9288 | 1333.051 | 1.2649 |
| avg | 3.5 | 65 | 631 | 2559 | 2766 | 2737 | 2449.5 | 2646.5 | 3 | |
| Brain_Tumor2 | std | 1.7029 | 240.6062 | 75.5373 | 55.0019 | 55.9691 | 46.9871 | 135.9838 | 2454.5883 | 1.1785 |
| avg | 2.5 | 156 | 1148.5 | 4672.5 | 4914.5 | 4864.5 | 4209 | 2946.5 | 2.5 | |
| CNS | std | 0.31623 | 136.7067 | 42.7265 | 96.6304 | 35.9623 | 50.9117 | 198.0223 | 1551.1952 | 3.2335 |
| avg | 1 | 87.5 | 852 | 3171 | 3386.5 | 3344.5 | 2985 | 3293 | 2 | |
| DLBCL | std | 0.42164 | 33.4865 | 23.7957 | 48.9182 | 24.6162 | 37.7601 | 156.4013 | 833.0272 | 0.99443 |
| avg | 1 | 40.5 | 571.5 | 2329.5 | 2522.5 | 2489 | 2245 | 2625.5 | 2 | |
| Leukemia1 | std | 0.8165 | 25.3588 | 33.1832 | 39.1324 | 20.8017 | 31.6665 | 190.6413 | 1124.43 | 1.2649 |
| avg | 2 | 40 | 550.5 | 2303 | 2473.5 | 2419 | 2132 | 2538.5 | 3.5 | |
| Leukemia2 | std | 1.2649 | 22.3617 | 46.4113 | 57.6102 | 51.1196 | 42.9973 | 252.5475 | 2534.8708 | 1.1972 |
| avg | 2.5 | 55 | 1245.5 | 5021.5 | 5320.5 | 5272.5 | 4592 | 5412.5 | 3 | |
| Lung_Cancer | std | 27.247 | 240.5198 | 66.0041 | 77.9308 | 42.3663 | 48.9689 | 688.2611 | 2587.9333 | 13.898 |
| avg | 10 | 172 | 1504 | 5750.5 | 6030 | 5947.5 | 5097.5 | 6092 | 5.5 | |
| Prostate_Tumor | std | 1.4181 | 234.6364 | 63.2583 | 109.3395 | 83.1836 | 39.8112 | 191.4855 | 2202.9629 | 1.792 |
| avg | 2 | 181.5 | 1262.5 | 4772.5 | 5029 | 4955.5 | 4401.5 | 5041 | 3 | |
| Tumors_9 | std | 102.7665 | 812.1526 | 43.0834 | 71.0286 | 45.3878 | 37.3722 | 171.1166 | 1120.278 | 3.0258 |
| avg | 8 | 174 | 674 | 2529 | 2732.5 | 2655.5 | 2376.5 | 2750 | 3 | |
| Tumors_11 | std | 231.5253 | 558.048 | 45.2396 | 142.4798 | 102.5773 | 88.8522 | 190.7012 | 1889.8508 | 113.9361 |
| avg | 235.5 | 497 | 1596.5 | 5776.5 | 6080.5 | 5968.5 | 5281.5 | 6134.5 | 110.5 | |
| Tumors_14 | std | 681.716 | 2562.6438 | 127.5985 | 132.4234 | 80.2649 | 77.5818 | 187.6832 | 61.4366 | 664.218 |
| avg | 682 | 1469 | 2382.5 | 7337.5 | 7401 | 7357.5 | 6349.5 | 7426.5 | 565 | |
| ARV | 1.4643 | 3.1357 | 4.1714 | 6.2643 | 8.175 | 7.5107 | 5.5286 | 7.1286 | 1.6214 | |
| Rank | 1 | 3 | 4 | 6 | 9 | 8 | 5 | 7 | 2 | |
| Datasets | Metrics | BISMA | BSMA | bGWO | BGSA | BPSO | bALO | BBA | BSSA | bWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 0.0000 | 0.0527 | 0.1162 | 0.1925 | 0.1229 | 0.2222 | 0.1592 | 0.1554 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0833 | 0.1667 | 0.0833 | 0.2262 | 0.0714 | 0.0000 | |
| SRBCT | std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0901 | 0.0000 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.1056 | 0.0000 | 0.0000 | |
| Leukemia | std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0707 | 0.0000 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Brain_Tumor1 | std | 0.0316 | 0.0502 | 0.0560 | 0.0546 | 0.0564 | 0.0735 | 0.0881 | 0.0574 | 0.0351 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0500 | 0.0000 | 0.1111 | 0.0000 | 0.0000 | |
| Brain_Tumor2 | std | 0.0000 | 0.0000 | 0.0777 | 0.0831 | 0.0866 | 0.1235 | 0.1454 | 0.1235 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.2083 | 0.0000 | 0.0000 | |
| CNS | std | 0.0000 | 0.0883 | 0.0703 | 0.1179 | 0.1194 | 0.0856 | 0.1315 | 0.1365 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0714 | 0.3333 | 0.0714 | 0.0000 | |
| DLBCL | std | 0.0000 | 0.0000 | 0.0000 | 0.0395 | 0.0395 | 0.0395 | 0.1111 | 0.0000 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0625 | 0.0000 | 0.0000 | |
| Leukemia1 | std | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0602 | 0.0000 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Leukemia2 | std | 0.0000 | 0.0000 | 0.0000 | 0.0395 | 0.0395 | 0.0527 | 0.0979 | 0.0452 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0625 | 0.0000 | 0.0000 | |
| Lung_Cancer | std | 0.0158 | 0.0206 | 0.0234 | 0.0341 | 0.0363 | 0.0248 | 0.0463 | 0.0359 | 0.0151 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0476 | 0.0732 | 0.0238 | 0.0000 | |
| Prostate_Tumor | std | 0.0000 | 0.0483 | 0.0422 | 0.0701 | 0.0844 | 0.0699 | 0.1589 | 0.0787 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0500 | 0.3000 | 0.0955 | 0.0000 | |
| Tumors_9 | std | 0.0000 | 0.0703 | 0.0904 | 0.0000 | 0.0703 | 0.0811 | 0.2532 | 0.1309 | 0.0000 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.3667 | 0.0000 | 0.0000 | |
| Tumors_11 | std | 0.0223 | 0.0614 | 0.0211 | 0.0570 | 0.0488 | 0.0508 | 0.0638 | 0.0586 | 0.0369 |
| avg | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0263 | 0.0557 | 0.1144 | 0.0588 | 0.0263 | |
| Tumors_14 | std | 0.0599 | 0.0516 | 0.0603 | 0.0719 | 0.0368 | 0.0559 | 0.0818 | 0.1008 | 0.0682 |
| avg | 0.2624 | 0.2808 | 0.1759 | 0.2028 | 0.2713 | 0.2379 | 0.3906 | 0.2583 | 0.2284 | |
| ARV | 4.0786 | 4.625 | 4.35 | 4.8393 | 5.0964 | 5.1571 | 7.4357 | 5.2857 | 4.1321 | |
| Rank | 1 | 4 | 3 | 5 | 6 | 7 | 9 | 8 | 2 | |
| Datasets | Metrics | BISMA | BSMA | bGWO | BGSA | BPSO | bALO | BBA | BSSA | bWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 1.2910 × 10−5 | 5.0206 × 10−2 | 1.1035 × 10−1 | 1.8282 × 10−1 | 1.1702 × 10−1 | 2.1096 × 10−1 | 1.3282 × 10−1 | 1.4476 × 10−1 | 4.1248 × 10−5 |
| avg | 2.5000 × 10−5 | 1.1500 × 10−3 | 4.3875 × 10−3 | 9.8642 × 10−2 | 1.8077 × 10−1 | 1.0080 × 10−1 | 1.7705 × 10−1 | 8.0020 × 10−2 | 5.0000 × 10−5 | |
| SRBCT | std | 2.7403 × 10−5 | 4.4567 × 10−4 | 3.3052 × 10−4 | 6.0770 × 10−4 | 3.7331 × 10−4 | 4.7086 × 10−4 | 5.4394 × 10−2 | 5.0897 × 10−3 | 4.1104 × 10−5 |
| avg | 6.4991 × 10−5 | 7.2574 × 10−4 | 4.1594 × 10−3 | 1.9465 × 10−2 | 2.2162 × 10−2 | 2.1577 × 10−2 | 1.9757 × 10−2 | 2.3256 × 10−2 | 8.6655 × 10−5 | |
| Leukemia | std | 2.9568 × 10−6 | 1.5407 × 10−4 | 2.8804 × 10−4 | 1.5587 × 10−4 | 2.2337 × 10−4 | 1.9186 × 10−4 | 3.8230 × 10−2 | 8.8001 × 10−3 | 6.4442 × 10−6 |
| avg | 7.0126 × 10−6 | 2.5245 × 10−4 | 5.5505 × 10−3 | 2.1781 × 10−2 | 2.3520 × 10−2 | 2.3058 × 10−2 | 1.6518 × 10−2 | 2.4032 × 10−2 | 1.4025 × 10−5 | |
| Brain_Tumor1 | std | 3.0044 × 10−2 | 4.7527 × 10−2 | 5.3069 × 10−2 | 5.1816 × 10−2 | 5.3452 × 10−2 | 6.9773 × 10−2 | 6.3670 × 10−2 | 4.9713 × 10−2 | 3.3378 × 10−2 |
| avg | 2.9561 × 10−5 | 9.4172 × 10−4 | 5.6841 × 10−3 | 2.2204 × 10−2 | 7.1128 × 10−2 | 2.3408 × 10−2 | 1.2274 × 10−1 | 2.4928 × 10−2 | 2.5338 × 10−5 | |
| Brain_Tumor2 | std | 8.2133 × 10−6 | 1.1604 × 10−3 | 7.3988 × 10−2 | 7.9166 × 10−2 | 8.2304 × 10−2 | 1.1744 × 10−1 | 1.3429 × 10−1 | 1.2498 × 10−1 | 5.6840 × 10−6 |
| avg | 1.2057 × 10−5 | 7.5239 × 10−4 | 5.5899 × 10−3 | 2.2574 × 10−2 | 2.3715 × 10−2 | 2.3488 × 10−2 | 2.3165 × 10−2 | 1.4332 × 10−2 | 1.2057 × 10−5 | |
| CNS | std | 2.2179 × 10−6 | 8.3687 × 10−2 | 6.6773 × 10−2 | 1.1206 × 10−1 | 1.1335 × 10−1 | 8.1427 × 10−2 | 1.5272 × 10−1 | 1.3596 × 10−1 | 2.2679 × 10−5 |
| avg | 7.0136 × 10−6 | 2.2373 × 10−3 | 6.0843 × 10−3 | 2.3320 × 10−2 | 2.4165 × 10−2 | 9.1574 × 10−2 | 1.8163 × 10−1 | 9.2401 × 10−2 | 1.4027 × 10−5 | |
| DLBCL | std | 3.8548 × 10−6 | 3.0615 × 10−4 | 2.1755 × 10−4 | 3.7526 × 10−2 | 3.7505 × 10−2 | 3.7552 × 10−2 | 6.1711 × 10−2 | 7.6159 × 10−3 | 9.0915 × 10−6 |
| avg | 9.1424 × 10−6 | 3.7027 × 10−4 | 5.2249 × 10−3 | 2.1348 × 10−2 | 2.3149 × 10−2 | 2.2820 × 10−2 | 1.9112 × 10−2 | 2.4003 × 10−2 | 1.8285 × 10−5 | |
| Leukemia1 | std | 7.6638 × 10−6 | 2.3802 × 10−4 | 3.1146 × 10−4 | 3.6730 × 10−4 | 1.9525 × 10−4 | 2.9723 × 10−4 | 3.6838 × 10−3 | 1.0554 × 10−2 | 1.1873 × 10−5 |
| avg | 1.8772 × 10−5 | 3.7545 × 10−4 | 5.1671 × 10−3 | 2.1616 × 10−2 | 2.3217 × 10−2 | 2.2705 × 10−2 | 1.9378 × 10−2 | 2.3827 × 10−2 | 3.2852 × 10−5 | |
| Leukemia2 | std | 5.6343 × 10−6 | 9.9607 × 10−5 | 2.0673 × 10−4 | 3.7572 × 10−2 | 3.7745 × 10−2 | 4.9938 × 10−2 | 5.3561 × 10−2 | 4.6911 × 10−2 | 5.3328 × 10−6 |
| avg | 1.1136 × 10−5 | 2.4499 × 10−4 | 5.5479 × 10−3 | 2.2367 × 10−2 | 2.3699 × 10−2 | 2.3510 × 10−2 | 1.9595 × 10−2 | 2.4109 × 10−2 | 1.3363 × 10−5 | |
| Lung_Cancer | std | 1.5004 × 10−2 | 1.9354 × 10−2 | 2.2153 × 10−2 | 3.2336 × 10−2 | 3.4492 × 10−2 | 2.3622 × 10−2 | 3.1687 × 10−2 | 4.1718 × 10−2 | 1.4294 × 10−2 |
| avg | 5.1587 × 10−5 | 1.1885 × 10−3 | 6.1905 × 10−3 | 2.3317 × 10−2 | 2.4093 × 10−2 | 6.8815 × 10−2 | 6.3121 × 10−2 | 4.6873 × 10−2 | 2.5794 × 10−5 | |
| Prostate_Tumor | std | 6.7472 × 10−6 | 4.6054 × 10−2 | 4.0020 × 10−2 | 6.6461 × 10−2 | 8.0247 × 10−2 | 6.6461 × 10−2 | 1.1415 × 10−1 | 7.7648 × 10−2 | 8.5258 × 10−6 |
| avg | 9.5157 × 10−6 | 2.0126 × 10−3 | 6.1828 × 10−3 | 2.3454 × 10−2 | 2.4241 × 10−2 | 7.1027 × 10−2 | 1.0987 × 10−1 | 9.3377 × 10−2 | 1.4273 × 10−5 | |
| Tumors_9 | std | 8.9737 × 10−4 | 6.7888 × 10−2 | 8.5899 × 10−2 | 6.2023 × 10−4 | 6.6747 × 10−2 | 7.7087 × 10−2 | 1.9970 × 10−1 | 1.2797 × 10−1 | 2.6422 × 10−5 |
| avg | 6.9857 × 10−5 | 1.5194 × 10−3 | 5.8854 × 10−3 | 2.2083 × 10−2 | 2.4162 × 10−2 | 2.3411 × 10−2 | 2.3214 × 10−2 | 2.4703 × 10−2 | 2.6196 × 10−5 | |
| Tumors_11 | std | 2.1319 × 10−2 | 5.7197 × 10−2 | 1.9912 × 10−2 | 5.4119 × 10−2 | 4.6341 × 10−2 | 4.8083 × 10−2 | 5.9891 × 10−2 | 5.7273 × 10−2 | 3.4943 × 10−2 |
| avg | 1.3923 × 10−3 | 6.6026 × 10−3 | 6.4171 × 10−3 | 2.3604 × 10−2 | 4.9392 × 10−2 | 7.6599 × 10−2 | 1.2055 × 10−1 | 6.7590 × 10−2 | 2.6123 × 10−2 | |
| Tumors_14 | std | 5.5130 × 10−2 | 5.3345 × 10−2 | 5.7317 × 10−2 | 6.8032 × 10−2 | 3.5029 × 10−2 | 5.2960 × 10−2 | 7.0141 × 10−2 | 9.5849 × 10−2 | 6.4709 × 10−2 |
| avg | 2.5180 × 10−1 | 2.7576 × 10−1 | 1.7527 × 10−1 | 2.1745 × 10−1 | 2.8210 × 10−1 | 2.5053 × 10−1 | 3.1859 × 10−1 | 2.7012 × 10−1 | 2.2178 × 10−1 | |
| ARV | 1.6964 | 1.6964 | 3.7571 | 4.2286 | 5.9 | 7.1286 | 6.8143 | 6.8071 | 6.6429 | |
| Rank | 1 | 1 | 3 | 4 | 5 | 9 | 8 | 7 | 6 | |
| Datasets | Metrics | BISMA | BSMA | bGWO | BGSA | BPSO | bALO | BBA | BSSA | bWOA |
|---|---|---|---|---|---|---|---|---|---|---|
| Colon | std | 0.93215 | 0.55407 | 0.098098 | 0.11018 | 0.076472 | 0.069336 | 0.19183 | 0.23189 | 0.4158 |
| avg | 79.1933 | 35.9194 | 14.2079 | 7.2215 | 4.2471 | 4.1295 | 13.9446 | 23.2622 | 26.0384 | |
| SRBCT | std | 2.1619 | 0.51149 | 0.15702 | 0.11402 | 0.13534 | 0.16851 | 0.25667 | 0.3163 | 0.37599 |
| avg | 93.6061 | 41.244 | 16.2856 | 8.8596 | 5.4073 | 5.2877 | 16.3119 | 27.1393 | 29.9446 | |
| Leukemia | std | 7.2303 | 1.8022 | 0.3074 | 0.42745 | 0.27052 | 0.35454 | 0.51794 | 0.93854 | 1.2515 |
| avg | 256.4992 | 122.7257 | 44.8501 | 23.5815 | 12.5313 | 12.2151 | 45.0914 | 79.2949 | 89.7865 | |
| Brain_Tumor1 | std | 6.9684 | 1.0527 | 0.278 | 0.45035 | 0.47769 | 0.32493 | 0.49618 | 1.069 | 1.2276 |
| avg | 220.5351 | 103.2569 | 38.7039 | 21.6636 | 13.2493 | 12.7106 | 40.4449 | 68.416 | 74.6861 | |
| Brain_Tumor2 | std | 4.4718 | 2.0085 | 0.40876 | 0.4924 | 0.4705 | 0.34669 | 0.57963 | 1.4683 | 1.9697 |
| avg | 354.245 | 176.7797 | 63.4666 | 29.9924 | 13.3176 | 12.3337 | 60.1049 | 110.4912 | 131.5993 | |
| CNS | std | 4.7455 | 1.4788 | 0.51911 | 0.26787 | 0.19856 | 0.2563 | 0.6056 | 0.94437 | 1.1606 |
| avg | 248.504 | 122.8625 | 44.5969 | 22.0423 | 10.8899 | 10.3101 | 43.5037 | 77.9093 | 89.9202 | |
| DLBCL | std | 5.3919 | 0.93684 | 0.23064 | 0.16063 | 0.29357 | 0.16353 | 0.47267 | 0.61759 | 1.1042 |
| avg | 200.6234 | 94.9785 | 35.3048 | 18.7326 | 10.6001 | 10.3269 | 35.7383 | 61.9793 | 69.2286 | |
| Leukemia1 | std | 4.3623 | 1.1156 | 0.31638 | 0.35829 | 0.27141 | 0.19161 | 0.52207 | 0.86822 | 0.85614 |
| avg | 194.386 | 92.0658 | 34.0793 | 17.7135 | 9.9582 | 9.5621 | 34.4391 | 60.048 | 66.7794 | |
| Leukemia2 | std | 7.374 | 3.0726 | 0.49382 | 0.61819 | 0.5241 | 0.50114 | 0.61738 | 1.9491 | 2.7261 |
| avg | 399.2129 | 192.557 | 69.7935 | 36.9327 | 19.1668 | 18.0316 | 69.7835 | 123.9545 | 144.0557 | |
| Lung_Cancer | std | 41.6799 | 4.5389 | 1.0736 | 3.7226 | 4.3019 | 3.6112 | 4.3848 | 2.089 | 2.7099 |
| avg | 515.1456 | 233.6435 | 99.2504 | 93.316 | 77.8452 | 75.9999 | 127.7409 | 190.8128 | 167.6969 | |
| Prostate_Tumor | std | 17.4231 | 2.7956 | 0.56853 | 0.55518 | 0.82953 | 0.5596 | 1.1379 | 1.3348 | 1.8037 |
| avg | 383.2946 | 183.4421 | 68.6138 | 42.0024 | 25.8001 | 25.2016 | 72.0151 | 122.9783 | 133.436 | |
| Tumors_9 | std | 2.9367 | 1.1039 | 0.25397 | 0.356 | 0.42194 | 0.23273 | 0.39294 | 0.77615 | 1.0106 |
| avg | 203.6074 | 98.814 | 36.386 | 18.1879 | 9.237 | 8.8404 | 35.6073 | 62.8321 | 71.9579 | |
| Tumors_11 | std | 11.6164 | 3.5569 | 1.045 | 2.7062 | 2.8401 | 3.2718 | 3.7758 | 1.9198 | 1.6793 |
| avg | 465.5284 | 226.3375 | 93.2904 | 78.8383 | 61.7486 | 60.114 | 113.7264 | 175.511 | 163.5641 | |
| Tumors_14 | std | 78.3081 | 9.9354 | 2.1979 | 13.6846 | 7.0692 | 10.4616 | 8.8472 | 4.4011 | 5.6434 |
| avg | 664.032 | 309.3361 | 159.1758 | 202.5748 | 176.6571 | 176.1249 | 235.2403 | 308.2242 | 212.441 | |
| ARV | 9 | 7.95 | 4.1857 | 3.1 | 1.8929 | 1.2571 | 4.6643 | 6.2643 | 6.6857 | |
| Rank | 9 | 8 | 4 | 3 | 2 | 1 | 5 | 6 | 7 | |
References
- Ye, M.; Wang, W.; Yao, C.; Fan, R.; Wang, P. Gene Selection Method for Microarray Data Classification Using Particle Swarm Optimization and Neighborhood Rough Set. Curr. Bioinform. 2019, 14, 422–431. [Google Scholar] [CrossRef]
- Wang, S.; Kong, W.; Zeng, W.; Hong, X. Hybrid Binary Imperialist Competition Algorithm and Tabu Search Approach for Feature Selection Using Gene Expression Data. Biomed Res. Int. 2016, 2016, 9721713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uthayan, K. A novel microarray gene selection and classification using intelligent dynamic grey wolf optimization. Genetika 2019, 51, 805–828. [Google Scholar] [CrossRef] [Green Version]
- Shukla, A.; Singh, P.; Vardhan, M. Gene selection for cancer types classification using novel hybrid metaheuristics approach. Swarm Evol. Comput. 2020, 54, 100661. [Google Scholar] [CrossRef]
- Sharma, A.; Rani, R. C-HMOSHSSA: Gene selection for cancer classification using multi-objective meta-heuristic and machine learning methods. Comput. Methods Programs Biomed. 2019, 178, 219–235. [Google Scholar] [CrossRef]
- Mohamad, M.; Omatu, S.; Deris, S.; Yoshioka, M.; Abdullah, A.; Ibrahim, Z. An enhancement of binary particle swarm optimization for gene selection in classifying cancer classes. Algorithms Mol. Biol. 2013, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Mabu, A.; Prasad, R.; Yadav, R. Gene Expression Dataset Classification Using Artificial Neural Network and Clustering-Based Feature Selection. Int. J. Swarm Intell. Res. 2020, 11, 65–86. [Google Scholar] [CrossRef]
- Jin, C.; Jin, S. Gene selection approach based on improved swarm intelligent optimisation algorithm for tumour classification. Iet Syst. Biol. 2016, 10, 107–115. [Google Scholar] [CrossRef]
- Dabba, A.; Tari, A.; Meftali, S.; Mokhtari, R. Gene selection and classification of microarray data method based on mutual information and moth flame algorithm. Expert Syst. Appl. 2021, 166, 114012. [Google Scholar] [CrossRef]
- Dabba, A.; Tari, A.; Meftali, S. Hybridization of Moth flame optimization algorithm and quantum computing for gene selection in microarray data. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 2731–2750. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Chen, H.-L. Enhanced support vector machine using parallel particle swarm optimization. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014. [Google Scholar]
- Alshamlan, H.; Badr, G.; Alohali, Y. mRMR-ABC: A Hybrid Gene Selection Algorithm for Cancer Classification Using Microarray Gene Expression Profiling. Biomed Res. Int. 2015, 2015, 604910. [Google Scholar] [CrossRef] [Green Version]
- Alshamlan, H.; Badr, G.; Alohali, Y. Genetic Bee Colony (GBC) algorithm: A new gene selection method for microarray cancer classification. Comput. Biol. Chem. 2015, 56, 49–60. [Google Scholar] [CrossRef]
- Liu, B.; Tian, M.; Zhang, C.; Li, X. Discrete Biogeography Based Optimization for Feature Selection in Molecular Signatures. Mol. Inform. 2015, 34, 197–215. [Google Scholar] [CrossRef]
- Best, M.; Sol, N.; In’t Veld, S.G.J.G.; Vancura, A.; Muller, M.; Niemeijer, A.N.; Fejes, A.V.; Tjon Kon Fat, L.A.; Huis In’t Veld, A.E.; Leurs, C.; et al. Swarm Intelligence-Enhanced Detection of Non-Small-Cell Lung Cancer Using Tumor-Educated Platelets. Cancer Cell 2017, 32, 238. [Google Scholar] [CrossRef]
- Best, M.; In’t Veld, S.; Sol, N.; Wurdinger, T. RNA sequencing and swarm intelligence-enhanced classification algorithm development for blood-based disease diagnostics using spliced blood platelet RNA. Nat. Protoc. 2019, 14, 1206–1234. [Google Scholar] [CrossRef]
- Ang, J.; Mirzal, A.; Haron, H.; Hamed, H. Supervised, Unsupervised, and Semi-Supervised Feature Selection: A Review on Gene Selection. IEEE-Acm Trans. Comput. Biol. Bioinform. 2016, 13, 971–989. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, C.; Li, X. The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection. Genes 2018, 9, 258. [Google Scholar] [CrossRef] [Green Version]
- Mundra, P.; Rajapakse, J. SVM-RFE With MRMR Filter for Gene Selection. IEEE Trans. Nanobioscience 2010, 9, 31–37. [Google Scholar] [CrossRef]
- Li, J.; Su, L.; Pang, Z. A Filter Feature Selection Method Based on MFA Score and Redundancy Excluding and It∙s Application to Tumor Gene Expression Data Analysis. Interdiscip. Sci.-Comput. Life Sci. 2015, 7, 391–396. [Google Scholar] [CrossRef]
- Kim, Y.; Yoon, Y. A genetic filter for cancer classification on gene expression data. Bio-Med. Mater. Eng. 2015, 26, S1993–S2002. [Google Scholar] [CrossRef] [Green Version]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Bolon-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A. A review of feature selection methods on synthetic data. Knowl. Inf. Syst. 2013, 34, 483–519. [Google Scholar] [CrossRef]
- Lee, S.; Xu, Z.; Li, T.; Yang, Y. A novel bagging C4.5 algorithm based on wrapper feature selection for supporting wise clinical decision making. J. Biomed. Inform. 2018, 78, 144–155. [Google Scholar]
- Al-Thanoon, N.; Qasim, O.; Algamal, Z. Tuning parameter estimation in SCAD-support vector machine using firefly algorithm with application in gene selection and cancer classification. Comput. Biol. Med. 2018, 103, 262–268. [Google Scholar] [CrossRef]
- Yang, A.; Cao, T.; Li, R.; Liao, B. A Hybrid Gene Selection Method for Cancer Classification Based on Clustering Algorithm and Euclidean Distance. J. Comput. Theor. Nanosci. 2012, 9, 611–615. [Google Scholar] [CrossRef]
- Wang, L.; Han, B. Hybrid feature selection method for gene expression analysis. Electron. Lett. 2014, 50, 1269–1270. [Google Scholar]
- Sungheetha, A.; Sharma, R. Extreme Learning Machine and Fuzzy K-Nearest Neighbour Based Hybrid Gene Selection Technique for Cancer Classification. J. Med. Imaging Health Inform. 2016, 6, 1652–1656. [Google Scholar] [CrossRef]
- Lu, H.; Chen, J.; Yan, K.; Jin, Q.; Xue, Y.; Gao, Z. A hybrid feature selection algorithm for gene expression data classification. Neurocomputing 2017, 256, 56–62. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Lv, Z.; Yang, P. Diversified personalized recommendation optimization based on mobile data. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2133–2139. [Google Scholar] [CrossRef]
- Cao, B.; Fan, S.; Zhao, J.; Tian, S.; Zheng, Z.; Yan, Y.; Yang, P. Large-scale many-objective deployment optimization of edge servers. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3841–3849. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Susilo, W. PPO-CPQ: A privacy-preserving optimization of clinical pathway query for e-healthcare systems. IEEE Internet Things J. 2020, 7, 10660–10672. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Chang, Q. Feature selection methods for big data bioinformatics: A survey from the search perspective. Methods 2016, 111, 21–31. [Google Scholar] [CrossRef]
- Prasartvit, T.; Banharnsakun, A.; Kaewkamnerdpong, B.; Achalakul, T. Reducing bioinformatics data dimension with ABC-kNN. Neurocomputing 2013, 116, 367–381. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. -Int. J. Escience 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Dong, J.S.; Lewis, A. Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer: Berlin/Heidelberg, Germany, 2019; Volume 811. [Google Scholar]
- Chen, X.; Tianfield, H.; Mei, C.; Du, W.; Liu, G. Biogeography-based learning particle swarm optimization. Soft Comput. 2017, 21, 7519–7541. [Google Scholar] [CrossRef]
- Liang, J.; Qin, A.; Suganthan, P.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Cai, Z.; Gu, J.; Luo, J.; Zhang, Q.; Chen, H.; Pan, Z.; Li, Y.; Li, C. Evolving an optimal kernel extreme learning machine by using an enhanced grey wolf optimization strategy. Expert Syst. Appl. 2019, 138, 112814. [Google Scholar] [CrossRef]
- Reddy, K.; Panwar, L.; Panigrahi, B.; Kumar, R. Binary whale optimization algorithm: A new metaheuristic approach for profit-based unit commitment problems in competitive electricity markets. Eng. Optim. 2019, 51, 369–389. [Google Scholar] [CrossRef]
- Kouadri, R.; Slimani, L.; Bouktir, T. Slime mould algorithm for practical optimal power flow solutions incorporating stochastic wind power and static var compensator device. Electr. Eng. Electromechanics 2020, 45–54. [Google Scholar] [CrossRef]
- Mostafa, M.; Rezk, H.; Aly, M.; Ahmed, E. A new strategy based on slime mould algorithm to extract the optimal model parameters of solar PV panel. Sustain. Energy Technol. Assess. 2020, 42, 100849. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.; Premkumar, M. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Mohamed, R. HSMA_WOA: A hybrid novel Slime mould algorithm with whale optimization algorithm for tackling the image segmentation problem of chest X-ray images. Appl. Soft Comput. 2020, 95, 106642. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Jia, H.; Li, Y.; Jiang, Z. Hybrid improved slime mould algorithm with adaptive beta hill climbing for numerical optimization. J. Intell. Fuzzy Syst. 2021, 40, 1667–1679. [Google Scholar] [CrossRef]
- Zubaidi, S.; Abdulkareem, I.H.; Hashim, K.S.; Al-Bugharbee, H.; Ridha, H.M.; Gharghan, S.K.; Al-Qaim, F.F.; Muradov, M.; Kot, P.; Al-Khaddar, R. Hybridised Artificial Neural Network Model with Slime Mould Algorithm: A Novel Methodology for Prediction of Urban Stochastic Water Demand. Water 2020, 12, 2692. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Heidari, A.A.; Wang, X.; Chen, Y.; Wang, M.; Chen, H. Towards augmented kernel extreme learning models for bankruptcy prediction: Algorithmic behavior and comprehensive analysis. Neurocomputing 2021, 430, 185–212. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, W. An Efficient Parameter Adaptive Support Vector Regression Using K-Means Clustering and Chaotic Slime Mould Algorithm. IEEE Access 2020, 8, 156851–156862. [Google Scholar] [CrossRef]
- Baliarsingh, S.; Vipsita, S. Chaotic emperor penguin optimised extreme learning machine for microarray cancer classification. Iet Syst. Biol. 2020, 14, 85–95. [Google Scholar] [CrossRef]
- Banu, P.; Azar, A.; Inbarani, H. Fuzzy firefly clustering for tumour and cancer analysis. Int. J. Model. Identif. Control. 2017, 27, 92–103. [Google Scholar] [CrossRef]
- Chen, L.; Li, J.; Chang, M. Cancer Diagnosis and Disease Gene Identification via Statistical Machine Learning. Curr. Bioinform. 2020, 15, 956–962. [Google Scholar] [CrossRef]
- Mahendran, N.; Vincent, P.; Srinivasan, K.; Chang, C. Machine Learning Based Computational Gene Selection Models: A Survey, Performance Evaluation, Open Issues, and Future Research Directions. Front. Genet. 2020, 11, 603808. [Google Scholar] [CrossRef]
- Tan, M.; Chang, S.; Cheah, P.; Yap, H. Integrative machine learning analysis of multiple gene expression profiles in cervical cancer. Peerj 2018, 6, e5285. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Lin, J.; Guo, H. Feature subset selection via an improved discretization-based particle swarm optimization. Appl. Soft Comput. 2021, 98, 106794. [Google Scholar] [CrossRef]
- Sadeghian, Z.; Akbari, E.; Nematzadeh, H. A hybrid feature selection method based on information theory and binary butterfly optimization algorithm. Eng. Appl. Artif. Intell. 2021, 97, 104079. [Google Scholar] [CrossRef]
- Coleto-Alcudia, V.; Vega-Rodriguez, M. Artificial Bee Colony algorithm based on Dominance (ABCD) for a hybrid gene selection method. Knowl.-Based Syst. 2020, 205, 106323. [Google Scholar] [CrossRef]
- Lee, J.; Choi, I.; Jun, C. An efficient multivariate feature ranking method for gene selection in high-dimensional microarray data. Expert Syst. Appl. 2021, 166, 113971. [Google Scholar] [CrossRef]
- Khani, E.; Mahmoodian, H. Phase diagram and ridge logistic regression in stable gene selection. Biocybern. Biomed. Eng. 2020, 40, 965–976. [Google Scholar] [CrossRef]
- Chen, K.; Wang, K.; Wang, K.; Angelia, M. Applying particle swarm optimization-based decision tree classifier for cancer classification on gene expression data. Appl. Soft Comput. 2014, 24, 773–780. [Google Scholar] [CrossRef]
- Mohamad, M.; Omatu, S.; Deris, S.; Yoshioka, M. A Modified Binary Particle Swarm Optimization for Selecting the Small Subset of Informative Genes From Gene Expression Data. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 813–822. [Google Scholar] [CrossRef] [Green Version]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. -Int. J. Escience 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Gandomi, A.H.; Chu, X.; Chen, H. RUN Beyond the Metaphor: An Efficient Optimization Algorithm Based on Runge Kutta Method. Expert Syst. Appl. 2021, 181, 115079. [Google Scholar] [CrossRef]
- Tu, J.; Chen, H.; Wang, M.; Gandomi, A.H. The Colony Predation Algorithm. J. Bionic Eng. 2021, 18, 674–710. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Heidari, A.A.; Noshadian, S.; Chen, H.; Gandomi, A.H. INFO: An Efficient Optimization Algorithm based on Weighted Mean of Vectors. Expert Syst. Appl. 2022, 195, 116516. [Google Scholar] [CrossRef]
- Hussien, A.G.; Heidari, A.A.; Ye, X.; Liang, G.; Chen, H.; Pan, Z. Boosting whale optimization with evolution strategy and Gaussian random walks: An image segmentation method. Eng. Comput. 2022. [Google Scholar] [CrossRef]
- Yu, H.; Song, J.; Chen, C.; Heidari, A.A.; Liu, J.; Chen, H.; Zaguia, A.; Mafarja, M. Image segmentation of Leaf Spot Diseases on Maize using multi-stage Cauchy-enabled grey wolf algorithm. Eng. Appl. Artif. Intell. 2022, 109, 104653. [Google Scholar] [CrossRef]
- Lai, X.; Zhou, Y. Analysis of multiobjective evolutionary algorithms on the biobjective traveling salesman problem (1, 2). Multimed. Tools Appl. 2020, 79, 30839–30860. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Heidari, A.A.; Wang, M.; Zhang, X.; Chen, Y.; Pan, Z. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowl.-Based Syst. 2021, 213, 106684. [Google Scholar] [CrossRef]
- Hu, J.; Gui, W.; Heidari, A.A.; Cai, Z.; Liang, G.; Chen, H.; Pan, Z. Dispersed foraging slime mould algorithm: Continuous and binary variants for global optimization and wrapper-based feature selection. Knowl.-Based Syst. 2022, 237, 107761. [Google Scholar] [CrossRef]
- Chen, H.; Wang, M.; Zhao, X. A multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Appl. Math. Comput. 2020, 369, 124872. [Google Scholar] [CrossRef]
- Yu, H.; Qiao, S.; Heidari, A.A.; Bi, C.; Chen, H. Individual Disturbance and Attraction Repulsion Strategy Enhanced Seagull Optimization for Engineering Design. Mathematics 2022, 10, 276. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, K.; Li, W.; Zhao, N.; Chen, W.; Huang, C.; Chen, H.; Wang, M. Improved Butterfly Optimizer-Configured Extreme Learning Machine for Fault Diagnosis. Complexity 2021, 2021, 6315010. [Google Scholar] [CrossRef]
- Han, X.; Han, Y.; Chen, Q.; Li, J.; Sang, H.; Liu, Y.; Pan, Q.; Nojima, Y. Distributed Flow Shop Scheduling with Sequence-Dependent Setup Times Using an Improved Iterated Greedy Algorithm. Complex Syst. Modeling Simul. 2021, 1, 198–217. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving fuzzy job-shop scheduling problem using DE algorithm improved by a selection mechanism. IEEE Trans. Fuzzy Syst. 2020, 28, 3265–3275. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gao, D.; Pedrycz, W. Solving multi-objective fuzzy job-shop scheduling problem by a hybrid adaptive differential evolution algorithm. IEEE Trans. Ind. Inform. 2022. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, X.; Zhou, Y.; Liu, Y.; Zhou, X.; Chen, H.; Zhao, H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022, 585, 441–453. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, Q.; Hao, K.; Jin, Y. A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems With Irregular Pareto Fronts. IEEE/CAA J. Autom. Sin. 2021, 8, 303–318. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 9512741. [Google Scholar] [CrossRef]
- Cai, Z.; Gu, J.; Wen, C.; Zhao, D.; Huang, C.; Huang, H.; Tong, C.; Li, J.; Chen, H. An Intelligent Parkinson’s Disease Diagnostic System Based on a Chaotic Bacterial Foraging Optimization Enhanced Fuzzy KNN Approach. Comput. Math. Methods Med. 2018, 2018, 2396952. [Google Scholar] [CrossRef]
- Dong, R.; Chen, H.; Heidari, A.A.; Turabieh, H.; Mafarja, M.; Wang, S. Boosted kernel search: Framework, analysis and case studies on the economic emission dispatch problem. Knowl.-Based Syst. 2021, 233, 107529. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G.; Ding, J. Knee-based decision making and visualization in many-objective optimization. IEEE Trans. Evol. Comput. 2020, 25, 292–306. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G.; Lv, J. Evolutionary multiobjective optimization with robustness enhancement. IEEE Trans. Evol. Comput. 2019, 24, 494–507. [Google Scholar] [CrossRef]
- Ye, X.; Liu, W.; Li, H.; Wang, M.; Chi, C.; Liang, G. Modified Whale Optimization Algorithm for Solar Cell and PV Module Parameter Identification. Complexity 2021, 2021, 8878686. [Google Scholar] [CrossRef]
- Chen, H.L.; Yang, B.; Wang, S.J.; Wang, G.; Li, H.Z.; Liu, W.B. Towards an optimal support vector machine classifier using a parallel particle swarm optimization strategy. Appl. Math. Comput. 2014, 239, 180–197. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar]
- Piotrowski, A. L-SHADE optimization algorithms with population-wide inertia. Inf. Sci. 2018, 468, 117–141. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, J.; Lin, Y.; Chen, N.; Zhan, Z.H.; Chung HS, H.; Li, Y.; Shi, Y.H. Particle Swarm Optimization with an Aging Leader and Challengers. IEEE Trans. Evol. Comput. 2013, 17, 241–258. [Google Scholar] [CrossRef]
- Lin, A.; Wu, Q.; Heidari, A.A.; Xu, Y.; Chen, H.; Geng, W.; Li, C. Predicting Intentions of Students for Master Programs Using a Chaos-Induced Sine Cosine-Based Fuzzy K-Nearest Neighbor Classifier. IEEE Access 2019, 7, 67235–67248. [Google Scholar] [CrossRef]
- Heidari, A.; Aljarah, I.; Faris, H.; Chen, H.; Luo, J.; Mirjalili, S. An enhanced associative learning-based exploratory whale optimizer for global optimization. Neural Comput. Appl. 2020, 32, 5185–5211. [Google Scholar] [CrossRef]
- Heidari, A.; Abbaspour, R.; Chen, H. Efficient boosted grey wolf optimizers for global search and kernel extreme learning machine training. Appl. Soft Comput. 2019, 81, 105521. [Google Scholar] [CrossRef]
- Wang, S.; Guo, H.; Zhang, S.; Barton, D.; Brooks, P. Analysis and prediction of double-carriage train wheel wear based on SIMPACK and neural networks. Adv. Mech. Eng. 2022, 14, 16878132221078491. [Google Scholar] [CrossRef]
- Lv, Z.; Li, Y.; Feng, H.; Lv, H. Deep learning for security in digital twins of cooperative intelligent transportation systems. IEEE Trans. Intell. Transp. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Lv, Z.; Chen, D.; Feng, H.; Zhu, H.; Lv, H. Digital twins in unmanned aerial vehicles for rapid medical resource delivery in epidemics. IEEE Trans. Intell. Transp. Syst. 2021, 1–9. [Google Scholar] [CrossRef]
- Zou, Q.; Xing, P.; Wei, L.; Liu, B. Gene2vec: Gene subsequence embedding for prediction of mammalian N6-methyladenosine sites from mRNA. RNA 2019, 25, 205–218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Zhou, L.; Fan, Q.; Huang, X.; Liu, Y. Weak and strong convergence analysis of Elman neural networks via weight decay regularization. Optimization 2022, 1–23. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, Z.; Huang, X. Parameter Conjugate Gradient with Secant Equation Based Elman Neural Network and its Convergence Analysis. Adv. Theory Simul. 2022, 2200047. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Xu, Q.; Zeng, Y.; Tang, W.; Peng, W.; Xia, T.; Li, Z.; Teng, F.; Li, W.; Guo, J. Multi-task joint learning model for segmenting and classifying tongue images using a deep neural network. IEEE J. Biomed. Health Inform. 2020, 24, 2481–2489. [Google Scholar] [CrossRef]
- Li, J.; Xu, K.; Chaudhuri, S.; Yumer, E.; Zhang, H.; Guibas, L. Grass: Generative recursive autoencoders for shape structures. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, C.; Xu, X.; Huang, H.; Xu, K. Learning practically feasible policies for online 3D bin packing. Sci. China Inf. Sci. 2022, 65, 1–17. [Google Scholar] [CrossRef]
- Emary, E.; Zawba, H.; Hassanien, A. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2010, 9, 727–745. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.; Hassanien, A. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Yang, X. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Reddy, K.; Panwar, L.; Panigrahi, B.; Kumar, R. A New Binary Variant of Sine-Cosine Algorithm: Development and Application to Solve Profit-Based Unit Commitment Problem. Arab. J. Sci. Eng. 2018, 43, 4041–4056. [Google Scholar] [CrossRef]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Örnek, B.N.; Aydemir, S.B.; Düzenli, T.; Özak, B. A novel version of slime mould algorithm for global optimization and real world engineering problems: Enhanced slime mould algorithm. Math. Comput. Simul. 2022, 198, 253–288. [Google Scholar] [CrossRef]
- Gürses, D.; Bureerat, S.; Sait, S.M.; Yıldız, A.R. Comparison of the arithmetic optimization algorithm, the slime mold optimization algorithm, the marine predators algorithm, the salp swarm algorithm for real-world engineering applications. Mater. Test. 2021, 63, 448–452. [Google Scholar] [CrossRef]
- Cai, Z.; Xiong, Z.; Wan, K.; Xu, Y.; Xu, F. A node selecting approach for traffic network based on artificial slime mold. IEEE Access 2020, 8, 8436–8448. [Google Scholar] [CrossRef]
- Li, D.; Zhang, S.; Ma, X. Dynamic Module Detection in Temporal Attributed Networks of cancers. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 19, 2219–2230. [Google Scholar] [CrossRef]
- Ma, X.; Sun, P.G.; Gong, M. An integrative framework of heterogeneous genomic data for cancer dynamic modules based on matrix decomposition. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 19, 305–316. [Google Scholar] [CrossRef]
- Huang, L.; Yang, Y.; Chen, H.; Zhang, Y.; Wang, Z.; He, L. Context-aware road travel time estimation by coupled tensor decomposition based on trajectory data. Knowl.-Based Syst. 2022, 245, 108596. [Google Scholar] [CrossRef]
- Wu, Z.; Li, R.; Xie, J.; Zhou, Z.; Guo, J.; Xu, X. A user sensitive subject protection approach for book search service. J. Assoc. Inf. Sci. Technol. 2020, 71, 183–195. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, S.; Lian, X.; Su, X.; Chen, E. A dummy-based user privacy protection approach for text information retrieval. Knowl.-Based Syst. 2020, 195, 105679. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, S.; Zhou, H.; Li, H.; Lu, C.; Zou, D. An effective approach for the protection of user commodity viewing privacy in e-commerce website. Knowl.-Based Syst. 2021, 220, 106952. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.X.; Hong, J.J.; Wang, Y.X.; Fu, J.B.; Yang, H.; Yu, C.Y.; Li, F.C.; Hu, J.; Xue, W.W.; et al. Clinical trials, progression-speed differentiating features and swiftness rule of the innovative targets of first-in-class drugs. Brief. Bioinform. 2020, 21, 649–662. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.; Li, X.; Yang, S.; Chen, Y. Clinical success of drug targets prospectively predicted by in silico study. Trends Pharmacol. Sci. 2018, 39, 229–231. [Google Scholar] [CrossRef]
- Cao, X.; Sun, X.; Xu, Z.; Zeng, B.; Guan, X. Hydrogen-Based Networked Microgrids Planning Through Two-Stage Stochastic Programming with Mixed-Integer Conic Recourse. IEEE Trans. Autom. Sci. Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Wang, T.; Jiang, R. Hierarchical feature fusion with mixed convolution attention for single image dehazing. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 510–522. [Google Scholar] [CrossRef]
- Wu, Z.; Li, G.; Shen, S.; Cui, Z.; Lian, X.; Xu, G. Constructing dummy query sequences to protect location privacy and query privacy in location-based services. World Wide Web 2021, 24, 25–49. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, R.; Li, Q.; Lian, X.; Xu, G. A location privacy-preserving system based on query range cover-up for location-based services. IEEE Trans. Veh. Technol. 2020, 69, 5244–5254. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Zeng, B. A Study on the Strong Duality of Second-Order Conic Relaxation of AC Optimal Power Flow in Radial Networks. IEEE Trans. Power Syst. 2022, 37, 443–455. [Google Scholar] [CrossRef]
- Tian, Y.; Su, X.; Su, Y.; Zhang, X. EMODMI: A multi-objective optimization based method to identify disease modules. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 5, 570–582. [Google Scholar] [CrossRef]
- Su, Y.; Li, S.; Zheng, C.; Zhang, X. A heuristic algorithm for identifying molecular signatures in cancer. IEEE Trans. NanoBioscience 2019, 19, 132–141. [Google Scholar] [CrossRef]
- Wang, D.; Liang, Y.; Xu, D.; Feng, X.; Guan, R.J.K.-B.S. A content-based recommender system for computer science publications. Knowl.-Based Syst. 2018, 157, 1–9. [Google Scholar] [CrossRef]
- Li, J.; Chen, C.; Chen, H.; Tong, C. Towards Context-aware Social Recommendation via Individual Trust. Knowl.-Based Syst. 2017, 127, 58–66. [Google Scholar] [CrossRef]
- Li, J.; Lin, J. A probability distribution detection based hybrid ensemble QoS prediction approach. Inf. Sci. 2020, 519, 289–305. [Google Scholar] [CrossRef]
- Li, J.; Zheng, X.-L.; Chen, S.-T.; Song, W.-W.; Chen, D.-R. An efficient and reliable approach for quality-of-service-aware service composition. Inf. Sci. 2014, 269, 238–254. [Google Scholar] [CrossRef]
- Qiu, S.; Zhao, H.; Jiang, N.; Wang, Z.; Liu, L.; An, Y.; Zhao, H.; Miao, X.; Liu, R.; Fortino, G. Multi-sensor information fusion based on machine learning for real applications in human activity recognition: State-of-the-art and research challenges. Inf. Fusion 2022, 80, 241–265. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, C.; Xiao, Z.; Zhao, L.; Chen, H.; Chang, X. Random Reconstructed Unpaired Image-to-Image Translation. IEEE Trans. Ind. Inform. 2022, 1. [Google Scholar] [CrossRef]
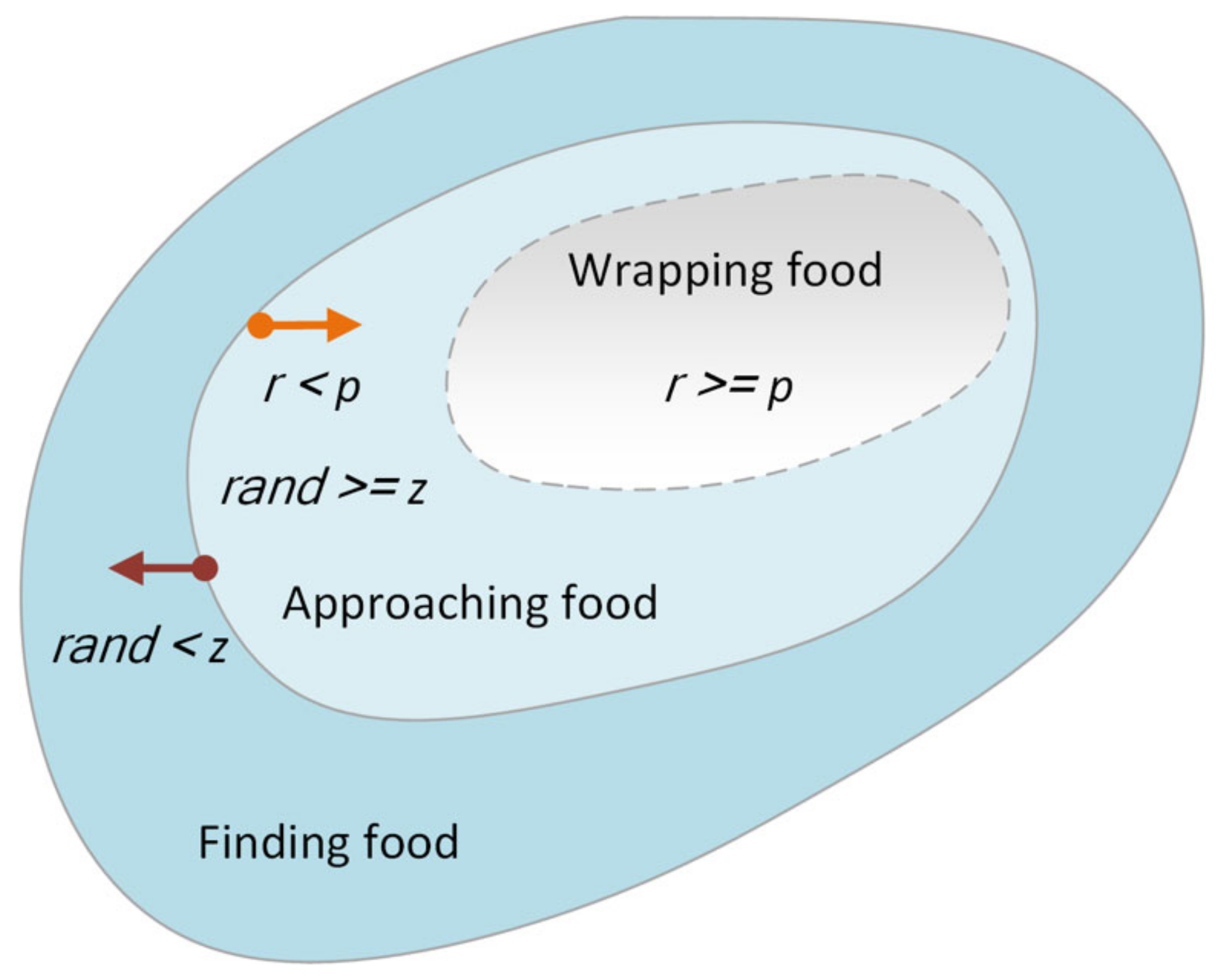
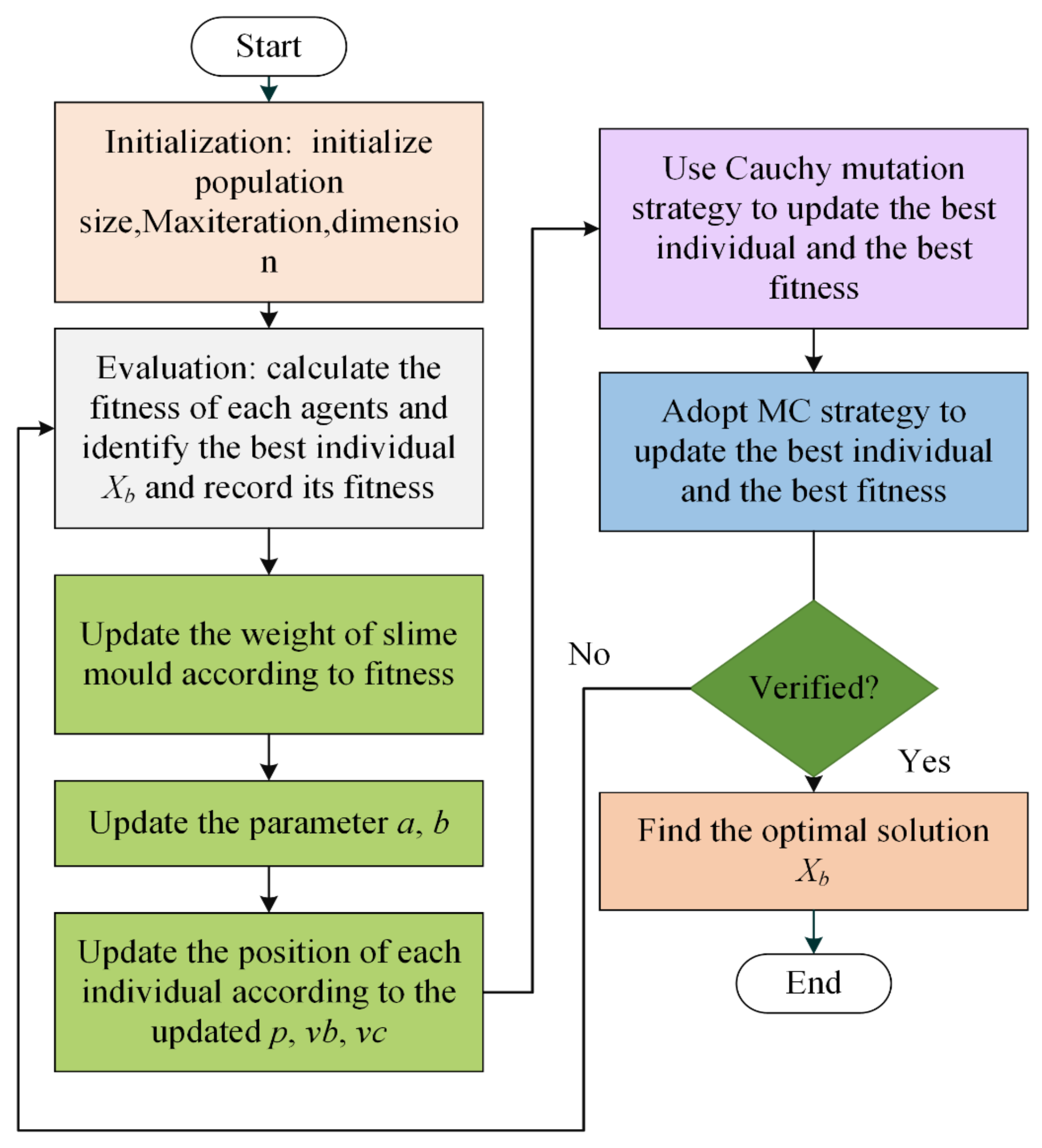
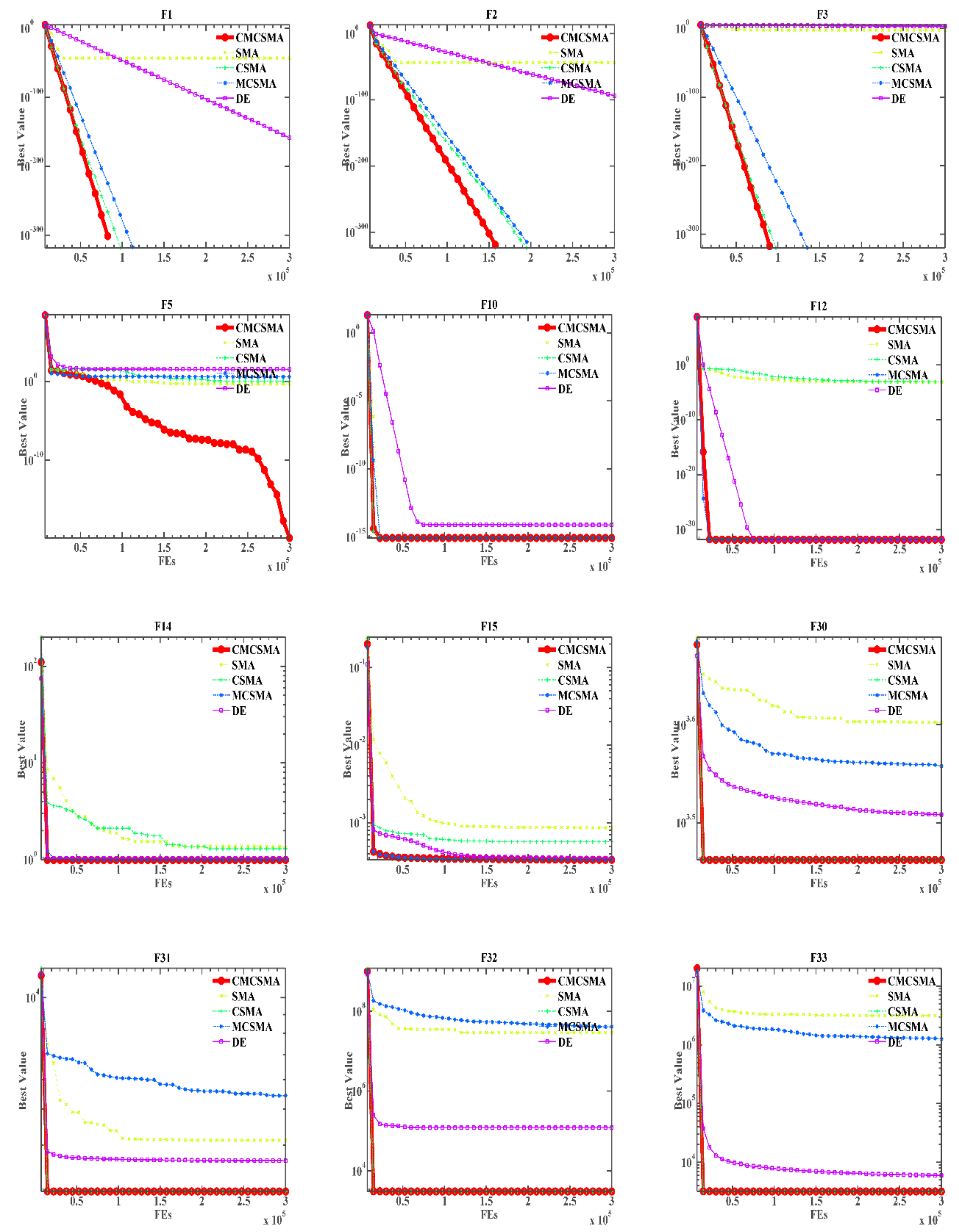

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, F.; Zheng, P.; Heidari, A.A.; Liang, G.; Chen, H.; Karim, F.K.; Elmannai, H.; Lin, H. Mutational Slime Mould Algorithm for Gene Selection. Biomedicines 2022, 10, 2052. https://doi.org/10.3390/biomedicines10082052
Qiu F, Zheng P, Heidari AA, Liang G, Chen H, Karim FK, Elmannai H, Lin H. Mutational Slime Mould Algorithm for Gene Selection. Biomedicines. 2022; 10(8):2052. https://doi.org/10.3390/biomedicines10082052
Chicago/Turabian StyleQiu, Feng, Pan Zheng, Ali Asghar Heidari, Guoxi Liang, Huiling Chen, Faten Khalid Karim, Hela Elmannai, and Haiping Lin. 2022. "Mutational Slime Mould Algorithm for Gene Selection" Biomedicines 10, no. 8: 2052. https://doi.org/10.3390/biomedicines10082052
APA StyleQiu, F., Zheng, P., Heidari, A. A., Liang, G., Chen, H., Karim, F. K., Elmannai, H., & Lin, H. (2022). Mutational Slime Mould Algorithm for Gene Selection. Biomedicines, 10(8), 2052. https://doi.org/10.3390/biomedicines10082052







