MEMS-Based Cantilever Sensor for Simultaneous Measurement of Mass and Magnetic Moment of Magnetic Particles
Abstract
1. Introduction
2. Experimental
2.1. Materials Description and Characterization
2.1.1. Magnetic Particles Samples
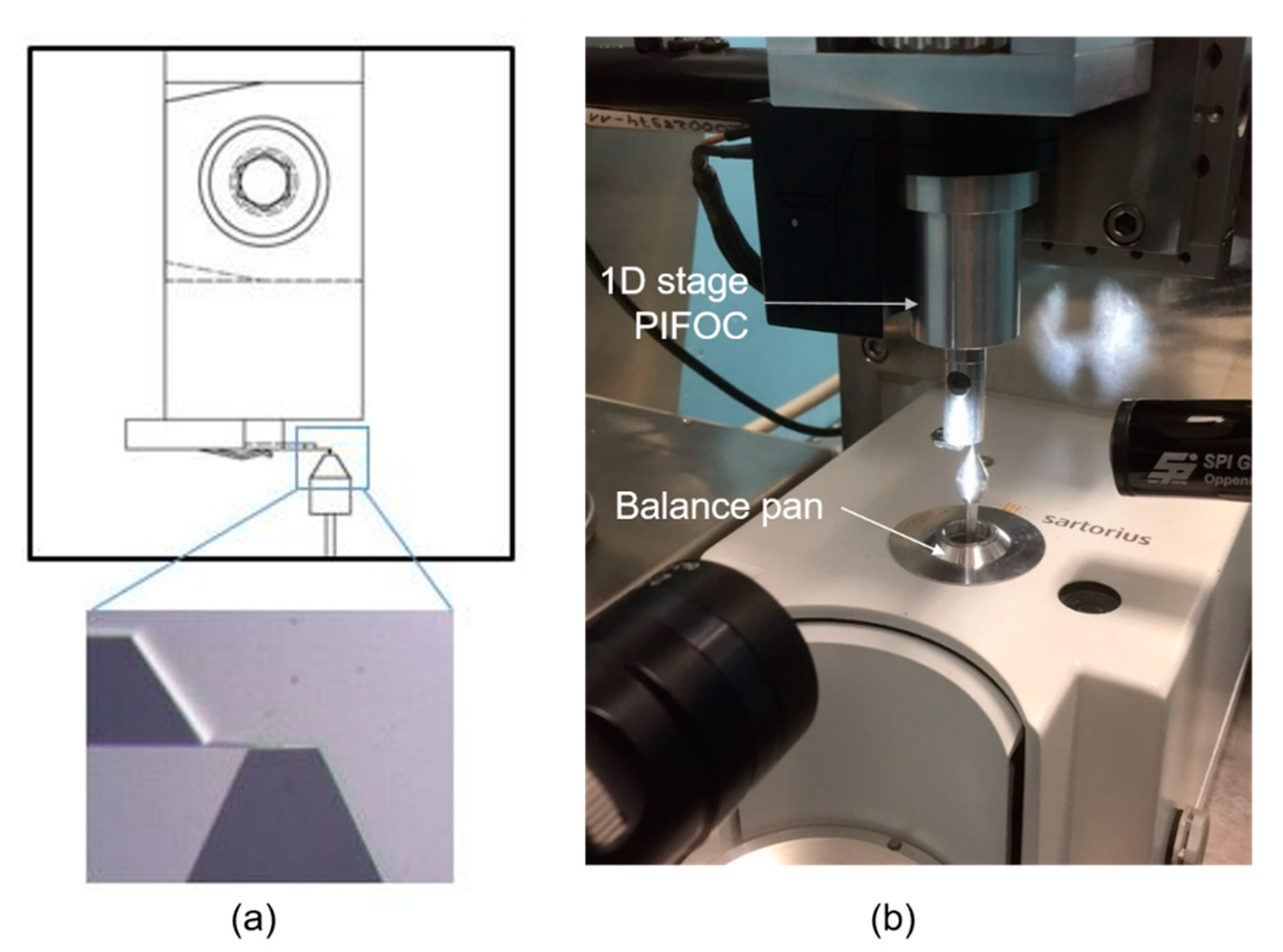
2.1.2. MEMS Cantilevers Sensors
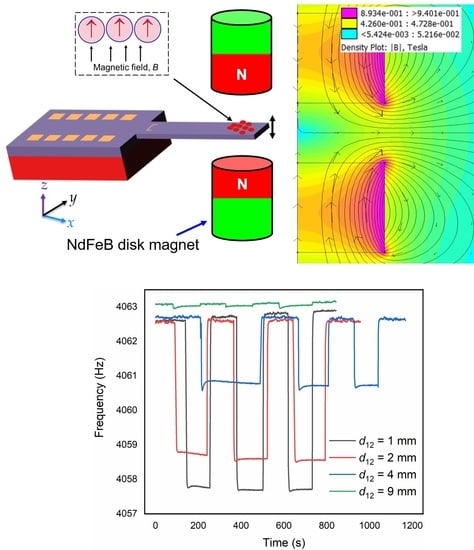
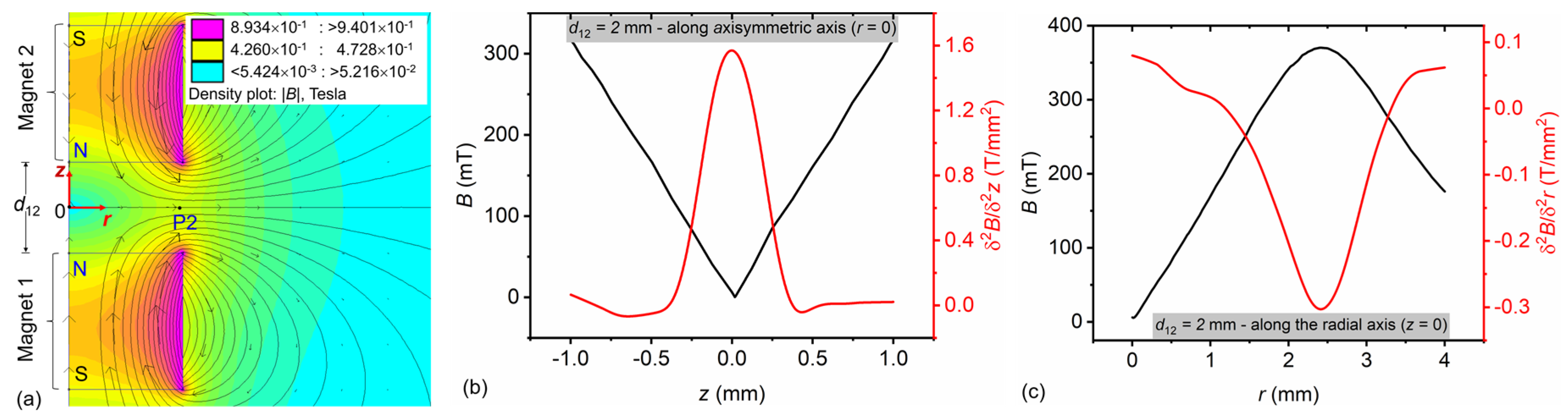
2.1.3. Magnets and Magnet Assembly
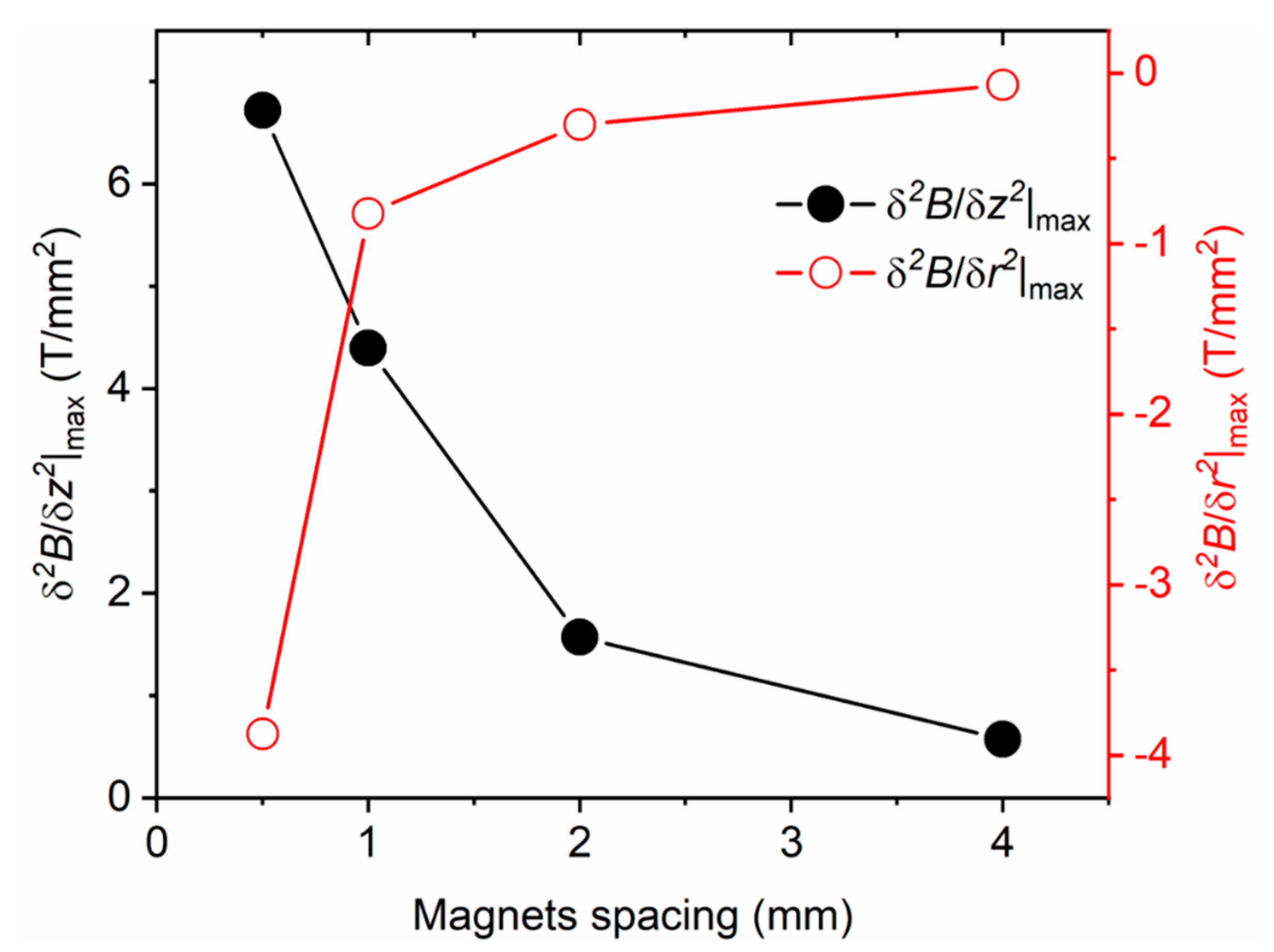
2.2. Finite Element Modeling of Second-Derivative Magnetic Field
3. Results and Discussion
3.1. Magnetic Force Gradient Sensing
3.2. Magnetic Moment Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohammed, L.; Gomaa, H.G.; Ragab, D.; Zhu, J. Magnetic nanoparticles for environmental and biomedical applications: A review. Particuology 2017, 30, 1–14. [Google Scholar] [CrossRef]
- Horák, D.; Babic, M.; Macková, H.; Benes, M.J. Preparation and properties of magnetic nano- and microsized particles for biological and environmental separations. J. Sep. Sci. 2007, 30, 1751–1772. [Google Scholar] [CrossRef]
- Schaller, V.; Kräling, U.; Rusu, C.; Petersson, K.; Wipenmyr, J.; Krozer, A.; Wahnström, G.; Sanz-Velasco, A.; Enoksson, P.; Johansson, C. Motion of nanometer sized magnetic particles in a magnetic field gradient. J. Appl. Phys. 2008, 104, 93918. [Google Scholar] [CrossRef]
- Ruffert, C. Magnetic Bead-Magic Bullet. Micromachines 2016, 7, 21. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Brown, S.I.; Frank, T.G.; Cuschieri, A. Ferromagnetization of target tissues by interstitial injection of ferrofluid: Formulation and evidence of efficacy for magnetic retraction. IEEE Trans. Biomed. Eng. 2009, 56, 2244–2252. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Philippova, O.; Barabanova, A.; Molchanov, V.; Khokhlov, A. Magnetic polymer beads: Recent trends and developments in synthetic design and applications. Eur. Polym. J. 2011, 47, 542–559. [Google Scholar] [CrossRef]
- Yoon, T.-J.; Kim, J.S.; Kim, B.G.; Yu, K.N.; Cho, M.-H.; Lee, J.-K. Multifunctional nanoparticles possessing a “magnetic motor effect” for drug or gene delivery. Angew. Chem. Int. Engl. 2005, 44, 1068–1071. [Google Scholar] [CrossRef] [PubMed]
- Williams, H.M. The application of magnetic nanoparticles in the treatment and monitoring of cancer and infectious diseases. Biosci. Horiz. Int. J. Stud. Res. 2017, 10, 257. [Google Scholar] [CrossRef]
- Alexiou, C.; Diehl, D.; Henninger, P.; Iro, H.; Rockelein, R.; Schmidt, W.; Weber, H. A High Field Gradient Magnet for Magnetic Drug Targeting. IEEE Trans. Appl. Supercond. 2006, 16, 1527–1530. [Google Scholar] [CrossRef]
- Tenório-Neto, E.T.; Jamshaid, T.; Eissa, M.; Kunita, M.H.; Zine, N.; Agusti, G.; Fessi, H.; El-Salhi, A.E.; Elaissari, A. TGA and magnetization measurements for determination of composition and polymer conversion of magnetic hybrid particles. Polym. Adv. Technol. 2015, 26, 1199–1208. [Google Scholar] [CrossRef]
- Liu, C.; Stakenborg, T.; Peeters, S.; Lagae, L. Cell manipulation with magnetic particles toward microfluidic cytometry. J. Appl. Phys. 2009, 105, 102014. [Google Scholar] [CrossRef]
- Aziz, T.; Masum, S.; Qadir, M.; Gafur, A.; Huq, D. Physicochemical Characterization of Iron Oxide Nanoparticle Coated with Chitosan for Biomedical Application. IRJPAC 2016, 11, 1–9. [Google Scholar] [CrossRef]
- Moreland, J.; Nakashima, Y.; Alldredge, J.W.; Zabow, G. Novel methods for in situ characterization of individual micro- and nanoscale magnetic particles. MRS Bull. 2013, 38, 933–937. [Google Scholar] [CrossRef][Green Version]
- Alldredge, J.W.; Moreland, J. Magnetic particle imaging with a cantilever detector. J. Appl. Phys. 2012, 112, 23905. [Google Scholar] [CrossRef]
- Draack, S.; Viereck, T.; Nording, F.; Janssen, K.-J.; Schilling, M.; Ludwig, F. Determination of dominating relaxation mechanisms from temperature-dependent Magnetic Particle Spectroscopy measurements. J. Magn. Magn. Mater. 2019, 474, 570–573. [Google Scholar] [CrossRef]
- Draack, S.; Lucht, N.; Remmer, H.; Martens, M.; Fischer, B.; Schilling, M.; Ludwig, F.; Viereck, T. Multiparametric Magnetic Particle Spectroscopy of CoFe 2 O 4 Nanoparticles in Viscous Media. J. Phys. Chem. C 2019, 123, 6787–6801. [Google Scholar] [CrossRef]
- van de Loosdrecht, M.M.; Draack, S.; Waanders, S.; Schlief, J.G.L.; Krooshoop, H.J.G.; Viereck, T.; Ludwig, F.; Ten Haken, B. A novel characterization technique for superparamagnetic iron oxide nanoparticles: The superparamagnetic quantifier, compared with magnetic particle spectroscopy. Rev. Sci. Instrum. 2019, 90, 24101. [Google Scholar] [CrossRef]
- Viereck, T.; Draack, S.; Schilling, M.; Ludwig, F. Multi-spectral Magnetic Particle Spectroscopy for the investigation of particle mixtures. J. Magn. Magn. Mater. 2019, 475, 647–651. [Google Scholar] [CrossRef]
- Llandro, J.; Palfreyman, J.J.; Ionescu, A.; Barnes, C.H.W. Magnetic biosensor technologies for medical applications: A review. Med. Biol. Eng. Comput. 2010, 48, 977–998. [Google Scholar] [CrossRef]
- Ejsing, L.; Hansen, M.F.; Menon, A.K.; Ferreira, H.A.; Graham, D.L.; Freitas, P.P. Magnetic microbead detection using the planar Hall effect. J. Magn. Magn. Mater. 2005, 293, 677–684. [Google Scholar] [CrossRef]
- Moreland, J. Micromechanical instruments for ferromagnetic measurements. J. Phys. D: Appl. Phys. 2003, 36, R39. [Google Scholar] [CrossRef]
- Micromod GmbH. Magnetic Polystyrene Particles. Available online: https://www.micromod.de/en/produkte-11-magnetic_psm.html (accessed on 29 June 2021).
- Micromod GmbH. Iron Oxide Particles. Available online: https://www.micromod.de/pdf/generate_pdf.php?article_number=45-00-252&tds_en=true (accessed on 29 June 2021).
- Graham, D.L.; Ferreira, H.; Bernardo, J.; Freitas, P.P.; Cabral, J.M.S. Single magnetic microsphere placement and detection on-chip using current line designs with integrated spin valve sensors: Biotechnological applications. J. Appl. Phys. 2002, 91, 7786. [Google Scholar] [CrossRef]
- Cardarelli, F. Materials Handbook; Springer: Cham, Germany, 2018; ISBN 978-3-319-38923-3. [Google Scholar]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young′s Modulus of Silicon? J. Microelectromech. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Stipe, B.C.; Mamin, H.J.; Stowe, T.D.; Kenny, T.W.; Rugar, D. Magnetic dissipation and fluctuations in individual nanomagnets measured by ultrasensitive cantilever magnetometry. Phys. Rev. Lett. 2001, 86, 2874–2877. [Google Scholar] [CrossRef]
- Ono, T.; Esashi, M. Magnetic force and optical force sensing with ultrathin silicon resonator. Appl. Phys. Lett. 2003, 74, 5141–5146. [Google Scholar] [CrossRef]
- Punyabrahma, P.; Jayanth, G.R. A magnetometer for estimating the magnetic moment of magnetic micro-particles. Rev. Sci. Instrum. 2017, 88, 15008. [Google Scholar] [CrossRef]
- Behrens, I.; Doering, L.; Peiner, E. Piezoresistive cantilever as portable micro force calibration standard. J. Micromech. Microeng. 2003, 13, S171–S177. [Google Scholar] [CrossRef]
- Nyang’au, W.O.; Setiono, A.; Schmidt, A.; Bosse, H.; Peiner, E. Sampling and Mass Detection of a Countable Number of Microparticles Using on-Cantilever Imprinting. Sensors 2020, 20, 2508. [Google Scholar] [CrossRef]
- Nyang’au, W.O.; Setiono, A.; Bertke, M.; Bosse, H.; Peiner, E. Cantilever-Droplet-Based Sensing of Magnetic Particle Concentrations in Liquids. Sensors 2019, 19, 4758. [Google Scholar] [CrossRef]
- Webcraft GmbH. Data Sheet Article S-05-03-N. Available online: https://www.supermagnete.de/eng/disc-magnets-neodymium/disc-magnet-5mm-3mm_S-05-03-N (accessed on 30 June 2021).
- Meeker, D. Finite Element Method Magnetics, Version 4.2 (21 April 2019 Build); 2015. Available online: https://www.femm.info/wiki/Files/files.xml?action=download&file=femm42bin_x64_21Apr2019.exe (accessed on 30 June 2021).
- Elrefai, A.L.; Enpuku, K.; Yoshida, T. Effect of easy axis alignment on dynamic magnetization of immobilized and suspended magnetic nanoparticles. J. Appl. Phys. 2021, 129, 93905. [Google Scholar] [CrossRef]
- Schmid, S.; Villanueva, L.G.; Roukes, M.L. Fundamentals of Nanomechanical Resonators; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-28691-4. [Google Scholar]
- Quantum Design GmbH. MPMS3 SQUID Magnetometer. Available online: https://qd-europe.com/de/en/product/mpms3-squid-magnetometer/ (accessed on 14 December 2020).
- Kahmann, T.; Ludwig, F. Magnetic field dependence of the effective magnetic moment of multi-core nanoparticles. J. Appl. Phys. 2020, 127, 233901. [Google Scholar] [CrossRef]
- Friedrich, R.-M.; Zabel, S.; Galka, A.; Lukat, N.; Wagner, J.-M.; Kirchhof, C.; Quandt, E.; McCord, J.; Selhuber-Unkel, C.; Siniatchkin, M.; et al. Magnetic particle mapping using magnetoelectric sensors as an imaging modality. Sci. Rep. 2019, 9, 2086. [Google Scholar] [CrossRef] [PubMed]


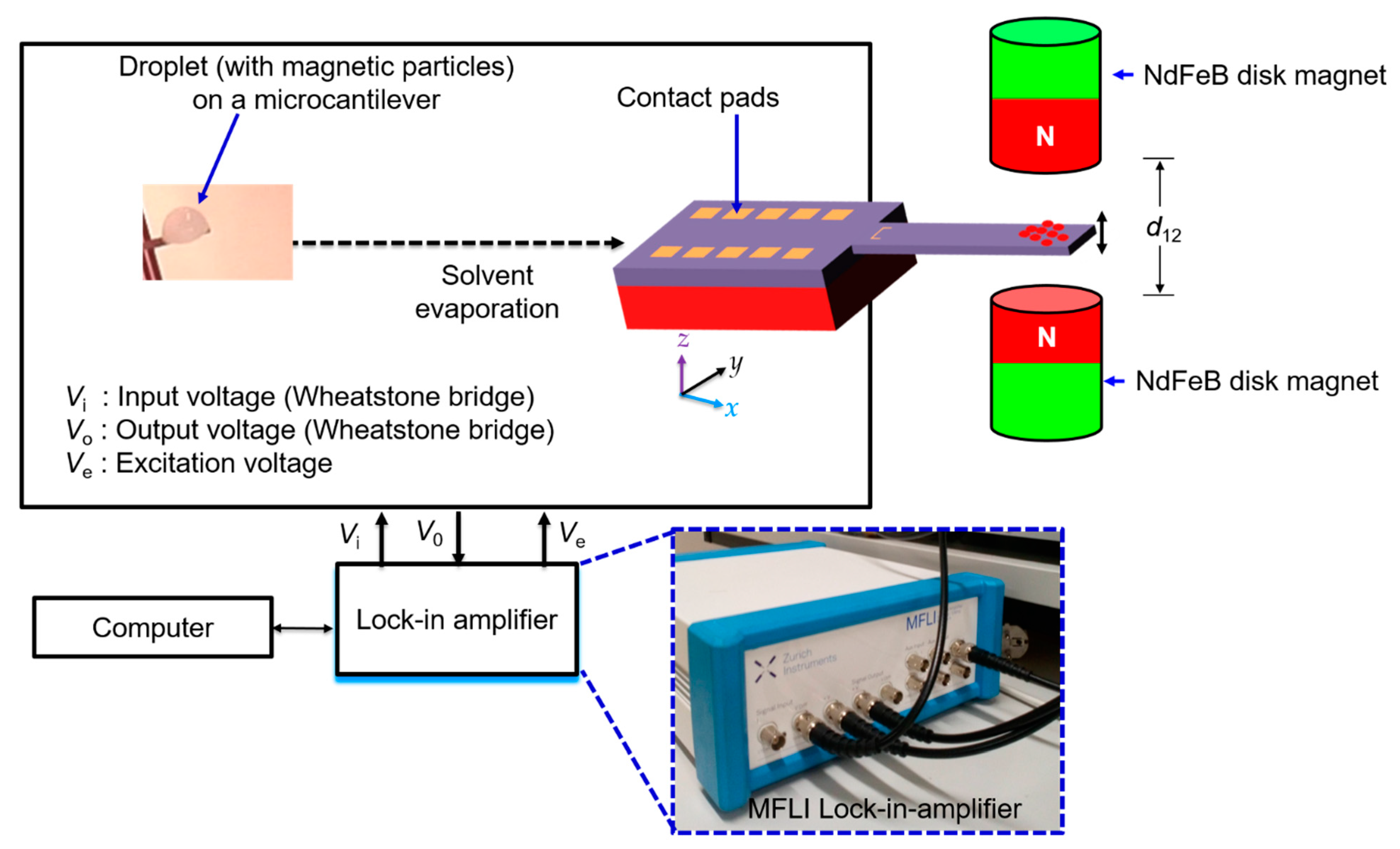
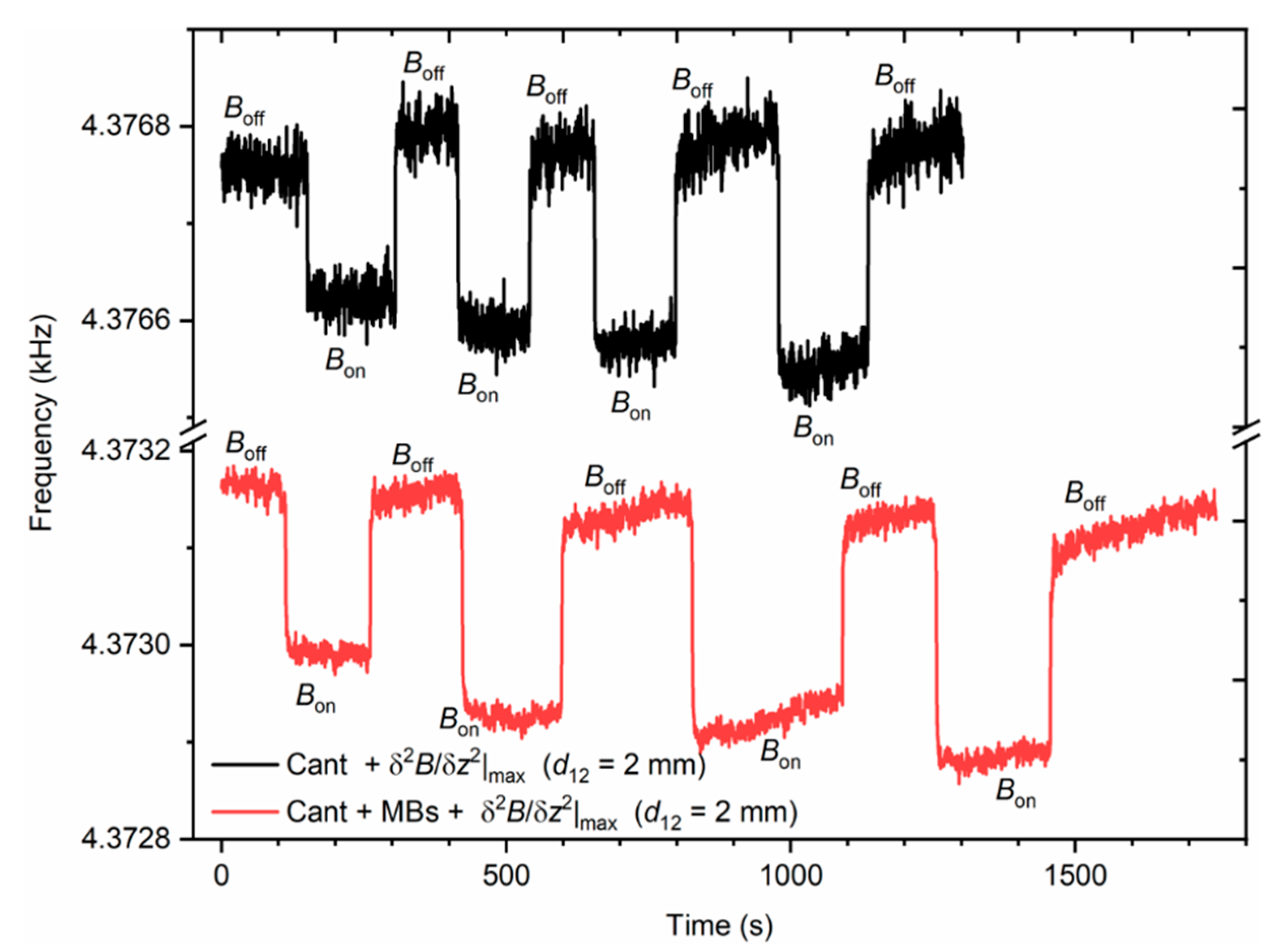

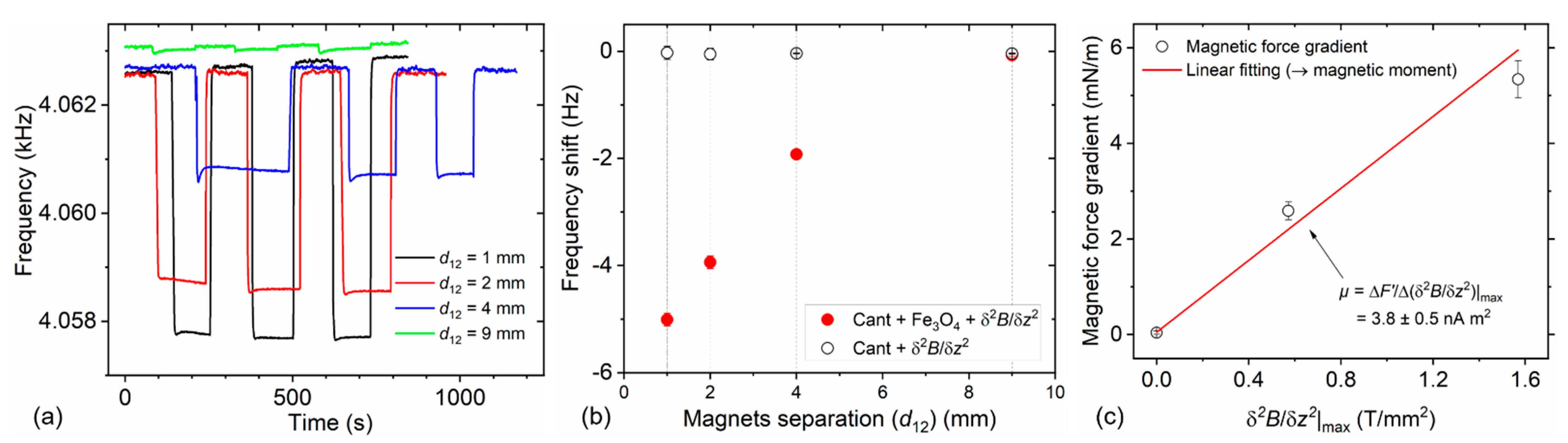
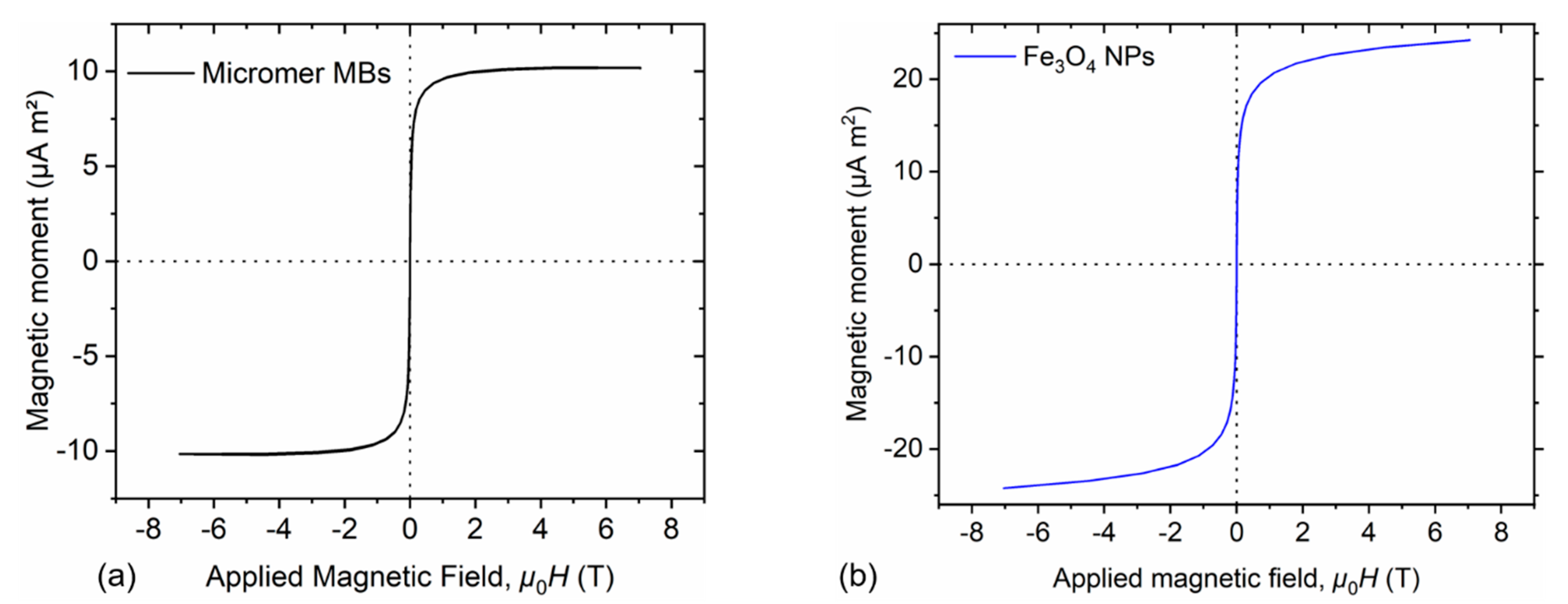
| Property/Parameter | Magnetic Polystyrene Particles | Iron Oxide NPs |
|---|---|---|
| Particle size (nominal diameter), dp | 2 µm | 250 nm |
| Particle volume, Vp (π/6 × dp3) | 4.19 × 10−18 m3 | 8.18 × 10−21 m3 |
| Density of polystyrene, ρPS | 1070 kg/m3 [26] | - |
| Density of magnetic material (magnetite), ρFe3O4 | 5350 kg/m3 | 5350 kg/m3 |
| Effective particle density, ρeff, Equation (3) | 1100 kg/m3 | 5350 g/m3 |
| Volume of magnetite per particle, Vp,Fe3O4 | 1.43 × 10−19 m3 | 8.18 × 10−21 m3 |
| Mass per particle, mp, Equation (2) | 5.1 × 10−15 kg | 4.4 × 10−17 kg |
| Mass of magnetite per particle, mp,Fe3O4 | 7.6 × 10−16 kg | 4.4 × 10−17 kg |
| Particles mass concentration, Cp,m | 2.2 × 1014 MPs per kg | 2.3 × 1016 MPs per kg |
| Saturation mass magnetization, Mm,s (at H = 800 kA/m) | 6.5 A m2/kg | 51 A m2/kg † |
| Magnetic moment per particle, µp (Equation (1), Mm = Mm,s) | 33 fA m2 | 2 fA m2 |
| Parameter | Cantilever Type | ||
|---|---|---|---|
| CAN50-2-5 | CAN30-1-2 | CAN15-3-2 | |
| m0 (µg) | 116.5 ± 2.3 | 17.48 ± 0.07 | 2.62 ± 0.17 |
| f0 (Hz) | 2400.0 ± 0.3 | 4377.0 ± 0.2 | 22,462.4 ± 0.1 |
| k0 (N/m), Equation (4) | 8.5 ± 0.3 | 2.4 ± 0.2 | 10.1 ± 0.8 |
| k0 (N/m), Equation (5) | 6.4 ± 0.1 | 3.2 ± 0.1 | 12.5 ± 0.8 |
| Q | 379 ± 3 | 432 ± 12 | 768 ± 50 |
| σ (ppm) | 20.8 | 1.5 | 4.1 |
| ∆fmin (mHz) | 50 ± 10 | 6.7 ± 1.0 | 93 ± 1 |
| ∆mmin (pg), Equation (8) | 1164 ± 24 | 12.8 ± 0.5 | 5.2 ± 0.4 |
| μmin (pA m2), Equation (9) | 169 ± 34 | 6 ± 1 | 66 ± 4 |
| Cantilever ID/Type (MPs) | f0 (Hz) | Δf0 (Hz) | Δm × 10−9 (g) | k0 (N/m) | Δf0′ (Hz) | F’(z) (mN/m) |
|---|---|---|---|---|---|---|
| S97/CAN30-1-2 (Micromer) | 4667.75 ± 0.02 | −1.87 ± 0.04 | 3.79 ± 0.26 | 3.61 ± 0.24 | −0.01 ± 0.01 | 0.02 ± 0.01 |
| S80/CAN30-1-2 (Micromer) | 4377.08 ± 0.01 | −3.72 ± 0.02 | 8.22 ± 0.54 | 4.46 ± 0.09 † | −0.02 ± 0.01 | 0.04 ± 0.02 |
| 3.17 ± 0.13 | 0.03 ± 0.02 | |||||
| 2.45 ± 0.20 ‡ | 0.02 ± 0.01 | |||||
| S95/CAN30-1-2 (Micromer) | 4611.90 ± 0.05 | −10.51 ± 0.05 | 23.2 ± 1.5 | 3.52 ± 0.23 | −0.11 ± 0.02 | 0.17 ± 0.04 |
| S89/CAN15-3-2 (Fe3O4) | 21,448.63 ± 0.06 | −18.50 ± 0.06 | 1.63 ± 0.11 | 11.43 ± 0.75 | −0.08 ± 0.03 | 0.09 ± 0.03 |
| S88/CAN15-3-2 (Fe3O4) | 22,465.52 ± 0.12 | −131.67 ± 0.13 | 11.06 ± 0.73 | 12.53 ± 0.82 | −4.06 ± 0.20 | 4.53 ± 0.94 |
| S84/CAN30-1-2 (Fe3O4) | 4148.50 ± 0.01 | −84.90 ± 0.01 | 230 ± 20 | 2.85 ± 0.19 | −3.89 ± 0.12 | 5.34 ± 0.39 |
| Cantilever ID/Type (MPs) | F’(z0) (mN/m) | Σµ (pA m2) | Np | µ per MP (fA m2) | ||
| by Cantilever♀ | Nominal | by SQUID | ||||
| S97/CAN30-1-2 (Micromer) | 0.02 ± 0.01 | 10 ± 6 | 945 ± 65 | 11 ± 7 | 33 | 116.6 ± 0.5 † 120.8 ± 0.4 ‡ |
| S80/CAN30-1-2 (Micromer) | 0.04 ± 0.02 | 28 ± 15 | 2050 ± 135 | 14 ± 8 | ||
| S95/CAN30-1-2 (Micromer) | 0.17 ± 0.04 | 110 ± 21 | 5792 ± 382 | 19 ± 4 | ||
| S88/CAN15-3-2 (Fe3O4) | 4.53 ± 0.94 | 2887 ± 602 | (254 ± 21) × 103 | 11 ± 3 | 2 | 2.379 ± 0.001 † 2.571 ± 0.013 ‡ |
| S89/CAN15-3-2 (Fe3O4) | 0.09 ± 0.03 | 55 ± 21 | (37 ± 3) × 103 | 1.5 ± 0.8 | ||
| S84/CAN30-1-2 (Fe3O4) | 5.34 ± 0.39 | 3402 ± 247 | (4506 ± 372) × 103 | 0.75 ± 0.08 | ||
| 3761 ± 526 * | 0.83 ± 0.1 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyang’au, W.O.; Kahmann, T.; Viereck, T.; Peiner, E. MEMS-Based Cantilever Sensor for Simultaneous Measurement of Mass and Magnetic Moment of Magnetic Particles. Chemosensors 2021, 9, 207. https://doi.org/10.3390/chemosensors9080207
Nyang’au WO, Kahmann T, Viereck T, Peiner E. MEMS-Based Cantilever Sensor for Simultaneous Measurement of Mass and Magnetic Moment of Magnetic Particles. Chemosensors. 2021; 9(8):207. https://doi.org/10.3390/chemosensors9080207
Chicago/Turabian StyleNyang’au, Wilson Ombati, Tamara Kahmann, Thilo Viereck, and Erwin Peiner. 2021. "MEMS-Based Cantilever Sensor for Simultaneous Measurement of Mass and Magnetic Moment of Magnetic Particles" Chemosensors 9, no. 8: 207. https://doi.org/10.3390/chemosensors9080207
APA StyleNyang’au, W. O., Kahmann, T., Viereck, T., & Peiner, E. (2021). MEMS-Based Cantilever Sensor for Simultaneous Measurement of Mass and Magnetic Moment of Magnetic Particles. Chemosensors, 9(8), 207. https://doi.org/10.3390/chemosensors9080207