Simulation Study of the Effects of Solution Properties on Ion Separation Performance Using Microchip Electrophoresis

Abstract

Microchip electrophoresis (ME) has been recognized as a promising analytical technique in life sciences, disease diagnostics, and environmental monitoring due to advantages such as minimal reagent consumption, rapid analysis, and compact size. While extensive efforts have been made to enhance ion analysis performance, the influence of solution properties—such as zeta potential, diffusion coefficient, ionic charge, and dynamic viscosity—has not been fully explored. In this study, the influence of solution properties on the performance of ion separation via ME was systematically evaluated through numerical simulations. A finite element method (FEM) model was established, in which multiple physical fields were considered. To verify the model, ion analysis experiments were conducted under corresponding conditions. Based on the validated model, a series of simulations were carried out to evaluate the effects of solution properties on separation performance. It was demonstrated that solution properties significantly affect the separation behavior, including ion arrival time, concentration-peak height, and separation resolution. These findings suggest that solution properties should not be overlooked in the design and optimization of ME systems. The simulation approach presented in this work is expected to provide valuable insights into the improvement of ion analysis using ME.

1. Introduction

Ion detection plays a crucial role in environmental monitoring, soil nutrient management, and medical diagnostics [1,2,3]. The development of fast and convenient methods for ion detection has long been a topic of significant research interest [4,5,6]. Among various techniques, ME, an analytical chemistry method, has attracted considerable attention since the 1990s due to its advantages such as rapid separation, high efficiency, low sample consumption, and reduced cost [7,8,9,10]. In ME systems, ions in solution are driven and separated under the influence of both electrophoretic forces and electro-osmotic flow (EOF) when a direct voltage is applied on the two ends of a microchannel [11]. In combination with other detection methods, such as the capacitively coupled contactless conductivity detection (C⁴D) method [12,13,14], ion species and their concentrations can be identified based on their migration times—from injection to detection—and the corresponding signal intensities.

Previous research has primarily focused on improving ME through new microchip fabrication methods, structural optimization, tuning of operating parameters, and expansion of application areas. For instance, Guijt et al. [15] proposed a bottom-up fabrication approach using dry film photoresist on printed circuit boards (PCB), which significantly simplified the process and lowered production costs. Henderson et al. [16] printed polyaniline detection electrodes using laser printing, reducing the fabrication cost by a factor of 20. Liu et al. [17] achieved an ultra-low limit of detection (LOD) using a microchip with a 0.6 μm thick insulating layer. Our team has also developed several types of microchips for ME. For instance, a detachable microchip was fabricated using CNC machining and hot-embossing techniques [18]. Additionally, a Y-shaped microchip capable of simultaneously detecting cations and anions was developed, simplifying the analysis of heterogeneous ions [19].

In parallel with experimental advancements, theoretical studies have also been conducted to model ME processes. Saville et al. [20] developed the first one-dimensional (1D) mathematical model to describe the evolution of ion concentrations under the influence of flow, diffusion, and electric fields, though without considering EOF. Bianchi et al. [21] later extended this to a two-dimensional (2D) model involving T-shaped channels with EOF included. Kovarik et al. [22] successfully used the FEM software COMSOL Multiphysics 5.0a to predict sample transport and electrokinetic injection behavior in ME. Meng et al. [23] presented a numerical simulation method for designing a buffer system in ME equipped with C⁴D. In recent years, Thormann and Mosher have made several significant contributions to the study of electrophoresis through computer simulations [24,25,26]. Notably, they employed simulation techniques to investigate the mobilization process in two-step capillary isoelectric focusing.

However, compared to chip design, fabrication techniques, and operating conditions, the influence of solution properties on separation performance in ME has received relatively little attention. Systematic investigations of how solution properties affect detection performance in ME remain scarce in the literature. This does not imply that these properties are unimportant. Thormann and Mosher have paid attention to solution properties and utilized computer simulation techniques to investigate the underlying mechanisms by which factors such as solution pH influence electrophoretic mobility and separation efficiency [26]. Based on fragmented findings from previous studies, some key relationships can be inferred: zeta potential is known to be a critical factor in EOF velocity [27]; diffusion coefficients influence ion dispersion [28]; ionic charge determines migration behavior [27]; and dynamic viscosity alters fluid resistance [29]. Systematic investigations into how parameters such as zeta potential, ion diffusion coefficient, ionic charge, and dynamic viscosity affect electrophoretic separation remain scarce. This knowledge gap highlights the need for further research to elucidate the role of these factors in governing separation efficiency and reliability.

In this work, a 2D ME model was established in the multi-physics simulation platform COMSOL Multiphysics 5.0a. The model incorporated multiple physical fields and was validated by comparison with experimental results under similar conditions, demonstrating good agreement in predicting ME detection performance. Subsequently, the effects of solution properties—including zeta potential, diffusion coefficient, ionic charge number, and dynamic viscosity—on separation performance were systematically analyzed through simulation, due to limitations in experimental conditions. Nevertheless, the insights obtained are of significant value. The results clearly demonstrate the critical role of solution properties in electrophoretic separation, underscore their importance, and call for further attention to this underexplored yet influential aspect of ME research.

2. Materials and Methods

2.1. Theory

As illustrated in Figure 1, the process of ion separation using ME involves several steps. First, an ion sample is introduced into the sample reservoir. Then, by applying a DC voltage across the injection channel (the vertical channel shown), ions are injected from the sample reservoir into the injection channel. Subsequently, a DC voltage is applied across the separation channel (the horizontal channel shown), allowing different ionic species within the sample to be separated. After separation, various detection methods—such as capacitively coupled contactless conductivity detection (C⁴D)—can be employed to detect the ions.

ME is a complex process involving the coupling of multiple physical fields, including the electric field, flow field, and mass transport field. The governing mathematical equations for these fields are described in this section.

Ions near a solid–liquid interface rearrange to form an electrical double layer (EDL), which consists of two ionic layers [30]. Near the microchannel wall, the first layer—called the attached layer—is fixed and immobile. Beyond this, the second layer, known as the diffuse layer, is free to move under the influence of an electric field. The interface between these two layers is referred to as the shear plane, at which the electric potential is defined as the zeta potential—a key parameter governing EOF. The movement of the diffuse layer under the applied electric field drives the bulk fluid motion along the microchannel. EOF is the most significant electrokinetic phenomenon in microfluidic systems.

The EOF velocity is given by

$$u={\mu }_{eo}{E}_x$$

(1)

where $E_x$ is the local electric field strength, and ${\mu }_{eo}$ is the EOF mobility, expressed as

$${\mu }_{eo}={\displaystyle \frac{{\epsilon }_0{\epsilon }_r\zeta }{\eta }}$$

(2)

Here, ε₀, and ε_r are the vacuum permittivity and relative permittivity, respectively; ζ is the zeta potential; and η is the dynamic viscosity of the fluid.

The fluid flow of an incompressible Newtonian fluid is governed by the Navier–Stokes (NS) and continuity equations:

$$\rho {\displaystyle \frac{\partial u}{\partial t}}+\rho u\cdot \nabla u=-\nabla p+\eta {\nabla }^{2}u$$

(3)

$$\nabla \cdot u=0$$

(4)

where ρ is the fluid density; u is the fluid velocity; p is the pressure; η is the dynamic viscosity.

The Reynolds number is a key dimensionless parameter for characterizing fluid flow regimes and determining whether the flow is laminar or turbulent. It is defined as

$$Re={\displaystyle \frac{\rho uL}{\eta }}$$

(5)

where the characteristic length of the channel (taken as the side length) is L = 1.0 × 10⁻⁴ m; the flow velocity range is approximately u = 1–3 mm/s; the fluid density is ρ = 1000 kg/m³; and the dynamic viscosity is η = 1.0 × 10⁻³ Pa⋅s.

Based on these parameters, the Reynolds number is calculated to be in the range of 0.10–0.30. This value is far below unity and well below the classical laminar–turbulent transition threshold, indicating that the flow is viscosity-dominated and falls within the laminar (creeping) flow regime, where inertial forces can be neglected. Consequently, the flow can be regarded as steady and laminar, which allows the Navier–Stokes equations to be simplified to the Stokes equations.

Furthermore, in the absence of applied pressure gradients and with the presence of electric body forces, the NS Equation reduces to

$$\rho {\displaystyle \frac{\partial u}{\partial t}}=-\nabla p+\eta {\nabla }^{2}u+{\rho }_{e}E$$

(6)

where ρ_e is the local charge density and E is the local electric field strength.

The mass transport process of charged particles in ME is governed by the Nernst-Planck Equation:

$${\displaystyle \frac{\partial c_i}{\partial t}}+\nabla \cdot \left(-D_i\nabla c_i-z_i{u}_{i}F{c}_i\nabla V\right)+u\cdot \nabla c_i=0$$

(7)

where F is the Faraday constant; D_i is the diffusion coefficient of ionic species i; c_i is the concentration; z_i is the charge number; u_i is the mobility; V is the electric potential; u is the fluid velocity.

According to the Nernst-Einstein relation, the mobility u_i is defined as

$$u_i={\displaystyle \frac{D_i}{RT}}$$

(8)

where R is the universal gas constant; T is the absolute temperature.

2.2. Finite Elements Model

The structure and dimensions of the ME chip used in the subsequent simulations and experiments are shown in Figure 2. The total length of the separation microchannel is 53 mm, and the effective separation length—defined as the distance from the intersection of the injection and separation channels to the detection point—is 35 mm. The height and the width of the microchannel are both 100 μm. At the initial condition, the sample concentration near the inlet is defined as a Gaussian pulse, which more closely resembles the actual ion distribution compared to a uniform distribution. A narrow region with a width of 0.8 mm is designated as the detection zone to monitor ion concentration changes. This width corresponds to the distance between the signal-sending and -receiving electrodes in the detection platform [18] used in the subsequent experiments.

Based on the above equations, a 2D model was established and solved using the FEM software COMSOL Multiphysics 5.0a (COMSOL Inc., Stockholm, Sweden). COMSOL Multiphysics 5.0a is a powerful multi-physics simulation tool that has been widely used by researchers to analyze various microfluidic phenomena [31,32]. In this study, the sample injection and the electrophoretic separation of ions within a ME system was modeled and simulated using this software.

In this study, ion migration is defined as the combined effect of electroosmotic flow and electrophoretic force, without accounting for the interactions between cations and anions. Focusing solely on cations simplifies the analysis and minimizes ambiguities related to the sign of ionic mobility. Therefore, three commonly used cations in electrophoresis experiments—potassium (K⁺), sodium (Na⁺), and lithium (Li⁺)—were selected to investigate the influence of solution properties on ion separation performance. Another key reason for selecting these three ions is their low propensity for cross-reactivity during electrophoretic detection. Based on our experience and supported by extensive literature [12,17,18,19], signal overlap among these ions is rare and typically does not compromise detection accuracy. To obtain the time-dependent concentration distributions of these ions within the microchannel, the transient solution of the mass transport equation must be computed. Since both the fluid velocity field and the electric field distribution remain constant during the process, they can be solved under steady-state conditions, while the mass transport equation is calculated under transient conditions. This strategy significantly reduces computational time.

As illustrated in Figure 3, the ME process consists of two stages: the injection stage and the separation stage. During the injection stage, a 1000 V injection voltage is applied between the sample reservoir (hereafter referred to as the S reservoir) and the sample waste reservoir (SW reservoir). Under the influence of EOF, the sample migrates from the S reservoir toward the SW reservoir, gradually filling the entire injection channel (the vertical channel in the figure). In the separation stage, a 2000 V separation voltage is applied between the buffer reservoir and the buffer waste reservoir. A small portion of the sample located at the intersection region is driven by both EOF and electrophoretic forces, causing the three ionic species in the sample to gradually separate.

The simulation parameters used in the simulation model are listed in

Table 1. Parameters used in the simulation for the separation of K⁺ Na⁺, and Li⁺ under a direct voltage.

Symbol	Value	Description
ρ	1000 kg/m3	Density of running buffer
Vi	1000 V	Injection voltage
Vs	2000 V	Separation voltage
εr	78.5	Relative dielectric constant
ε0	8.854 × 10−12 C2/J·m	Vacuum dielectric constant
η	10−3 Pa·s	Viscosity of running buffer
ζ	−50 mV	Zeta potential
DK+	1.957 × 10−9 m2/s	Diffusion coefficient of ion K+
DNa+	1.334 × 10−9 m2/s	Diffusion coefficient of ion Na+
DLi+	1.029 × 10−9 m2/s	Diffusion coefficient of ion Li+
zK+	1	Charge number of ion K+
zNa+	1	Charge number of ion Na+
zLi+	1	Charge number of ion Li+

. Boundary and initial conditions used in simulations are listed in

Table 2. Boundary and initial conditions in the FEM simulations.

	Boundary Conditions
Inlet	p = 0 Vi = 1000 V Vs = 2000 V	c1(t) = c2(t) = c3(t) = 0
Outlet	p = 0 V = 0 V	c1(t), c2(t), c3(t)
Wall	$u={\mu }_{eo}E$, ${\mu }_{eo}={\displaystyle \frac{{\epsilon }_0{\epsilon }_r\zeta }{\eta }}$
Initial Conditions	p = 0, V = 0 V, c1(t) = c2(t) = c3(t) = cin $cin={0.5}^{{-0.5\left({\displaystyle \frac{x-x_m}{sigma}}\right)}^2}\left(y>0\right)$ cin is a concentration Gaussian pulse with peak value 0.5 mM

.

2.3. Experimental Validation of the Finite Element Model

According to Section 2.1 and Section 2.2, an FEM model was established in COMSOL Multiphysics 5.0a, and simulations were performed to obtain the injection and separation results for the three ions. To validate the effectiveness of the model, electrophoresis experiments were conducted in parallel.

Deionized water was used throughout the experiments. 2-(N-morpholino) ethanesulfonic acid (MES) and histidine (His) were purchased from Hefei Baierdi Chemical Technology Co., Ltd., Hefei, China. Potassium chloride, sodium chloride, and lithium chloride were obtained from Sinopharm Chemical Reagent Co., Ltd., Shanghai, China. All reagents were of analytical grade.

The microchip used in the electrophoresis experiments was fabricated using hot embossing and hot bonding processes, as described in our previous work [18]. The dimensions of the chip used in the experiments were identical to those used in the FEM simulations. Ion detection for K⁺, Na⁺, and Li⁺ was performed using an external platform [18] (Figure 4). In this platform, printed circuit board (PCB) electrodes served as the C⁴D electrodes in a three-electrode configuration. The signal transmitting and receiving electrodes were each 1 mm wide, while the ground electrode was 0.3 mm wide. All electrodes had a height of 33 μm and were fabricated using a standard PCB manufacturing process involving copper cladding on a resin substrate followed by etching. The cross length between the transmitting and receiving electrodes was 2 mm. The C⁴D electrodes were positioned to align with the detection area at the downstream end of the microchip’s separation channel, consistent with the simulation layout (see Figure 2). The platform incorporated a custom-designed C⁴D signal processing system, comprising pre-amplification, C⁴D signal computation, post-amplification, and signal filtering modules, with a sampling frequency of 100 Hz.

The electrophoresis experimental procedure was briefly as follows: Prior to the experiment, the microchannels of the microchip were rinsed with deionized water and then with the running buffer 20 mM MES/His for 20 min each. All ion samples, including potassium chloride, sodium chloride, and lithium chloride, were prepared by dissolving the salts in the running buffer. Sample injection was carried out electrokinetically using the standard cross-injection method as described in our previous work [18]. The injection voltage and separation voltage were set to 1000 V and 2000 V, respectively. The C⁴D excitation signal amplitude was set to 10 V_p-p, while the reference signal amplitude was maintained at 5 V_p-p for all measurements. Both the reference and excitation signals operated at a frequency of 800 kHz. All experiments were conducted under laboratory conditions (temperature: 20–25 °C; relative humidity: 40–60%).

2.4. Effects of Solution Properties on Ion Separation Performance

In this study, the effects of four key solution-related parameters—zeta potential, ion diffusion coefficient, ionic charge number, and dynamic viscosity—on ion separation performance in ME were systematically investigated. A univariate approach was adopted for the analysis, in which only the parameter of interest was varied while all other parameters remained constant at their original values (as listed in Table 1).

In commonly used unmodified PMMA microfluidic chips, the zeta potential of the channel walls mainly originates from negatively charged surface groups such as carboxyl and hydroxyl groups. Under neutral pH conditions (pH ≈ 7), the typical zeta potential range is −30 mV to −70 mV [33,34]. To evaluate the influence of zeta potential on detection performance, a series of values (−30 mV, −40 mV, −50 mV, −60 mV, and −70 mV) were examined, while keeping the other parameters unchanged in the simulations.

Regarding the diffusion coefficients, Table 1 summarizes the values for commonly used ions in microfluidic experiments—K⁺, Na⁺, and Li⁺—in aqueous solutions at approximately 25 °C [31]. The diffusion coefficient of an ion is strongly influenced by temperature and ion concentration. However, under typical laboratory conditions, a variation of ±20% is frequently observed and generally considered acceptable [35]. To assess the impact of diffusion coefficient variability, a series of scaling factors—0.8, 0.9, 1.0, 1.1, and 1.2—were applied to the baseline diffusion coefficients. These adjusted values were subsequently employed in simulations to represent different diffusion behaviors.

The movement of anions under an electric field is more complex than that of cations, primarily because the direction of EOF is opposite to that of electrophoretic mobility for anions. Therefore, for simplicity, only cations were considered in the simulations. Moreover, since the charge number of most cations in typical ME applications rarely exceeds 3, only three representative charge numbers—1, 2, and 3—were selected for the analysis.

For dynamic viscosity, aqueous solutions are the most commonly used fluids in microfluidic systems, and their viscosity is highly sensitive to temperature. At 20 °C, the dynamic viscosity of pure water is approximately 1.000 × 10⁻³ Pa·s [31,36]. When buffers or salt-containing solutions are used, the viscosity tends to increase slightly, typically varying within ±10% of the water value. In this study, a broader range of ±20% from the standard value was considered to account for variations under typical experimental conditions. To investigate the impact of viscosity on separation performance, a series of scaling factors (0.8, 0.9, 1.0, 1.1, and 1.2) was applied to the baseline viscosity. These adjusted values were then used in simulations to evaluate how variations in dynamic viscosity affect the separation efficiency.

3. Results and Discussion

3.1. Experimental Verification of the Simulation Model

To verify the validity of the simulation model, a comparative analysis was conducted between the simulated and experimental results for the separation of K⁺, Na⁺, and Li⁺ under a direct voltage. The corresponding results are presented in Figure 5 and Figure 6. Several observations can be made: the three ions were clearly and completely separated in both the simulation and the experiment, following the same migration order—K⁺, Na⁺, and Li⁺. The arrival times of the ions in the experimental data closely matched those in the simulations, indicating strong temporal consistency. Although the peak heights in the two results represent different signal types—voltage signals in the experiment and concentration profiles in the simulation—and thus cannot be directly compared quantitatively, their trends show good agreement. Overall, the consistency between the simulation and experimental results confirms the reliability and accuracy of the proposed simulation model.

3.2. Effects of Solution Properties on the Detection Performance

To compare and evaluate detection performance in an electrophoresis microchip with varying solution properties, three parameters representing separation performance were defined: ionic arrival time T_a, concentration peak height P_c, and ionic separation degree S_d.

Ionic arrival time T_a indicates the detection speed of the microchip and is defined as the time taken for ions to migrate from the injection point to the detection area.

Concentration peak height P_c refers to the peak concentration of ions upon arrival at the detection zone. A higher P_c corresponds to a stronger detected signal and an improved signal-to-noise ratio.

The ionic separation degree S_d(i) quantifies the distinguishability of ion i among multiple ions, accounting for possible overlap of detection signals. It is defined as

$$S_{\mathrm{d}(i)}={\displaystyle \frac{T_{\mathrm{a}(i+1)}-T_{\mathrm{a}(i)}}{T_{\mathrm{total}}}}$$

(9)

where T_a(i) is the arrival time of ion i, and T_total is the total electrophoresis separation time, set to 60 s in both simulations and experiments in this study.

In the following sections, the effects of varying zeta potential, diffusion coefficient, ionic charge number, and dynamic viscosity on detection performance are evaluated based on these three parameters.

To date, few studies have systematically addressed how solution properties affect detection performance in electrophoretic microchips. Nevertheless, we aim to substantiate our simulation results through supporting evidence from prior experiments, relevant theories, and logical deductions.

3.2.1. Effects of Zeta Potential

To investigate the effects of zeta potential on detection performance, a series of values (−30 mV, −40 mV, −50 mV, −60 mV, and −70 mV) were evaluated through simulations, while all other parameters were kept constant.

As shown in Figure 7a, the arrival times of all three ions decrease consistently as the zeta potential becomes more negative. According to EOF theory [11], EOF velocity is directly proportional to the zeta potential. Therefore, a higher (more negative) zeta potential leads to faster EOF and shorter ion migration times, which is consistent with the simulation results. Figure 7b illustrates that the ion concentration peak heights increase as the zeta potential rises from −30 mV to −60 mV, reaching a maximum at −60 mV, and then decrease thereafter. This behavior is governed by two competing factors: increased EOF velocity promotes ion migration but also enhances diffusion, while the reduced separation time limits diffusion. The observed peak height thus reflects the balance between these opposing effects. As depicted in Figure 7c, the separation degree decreases with increasing zeta potential. Given the positive correlation between zeta potential and EOF velocity, higher zeta potentials accelerate the bulk fluid flow, reducing the separation time and thereby diminishing the separation degree.

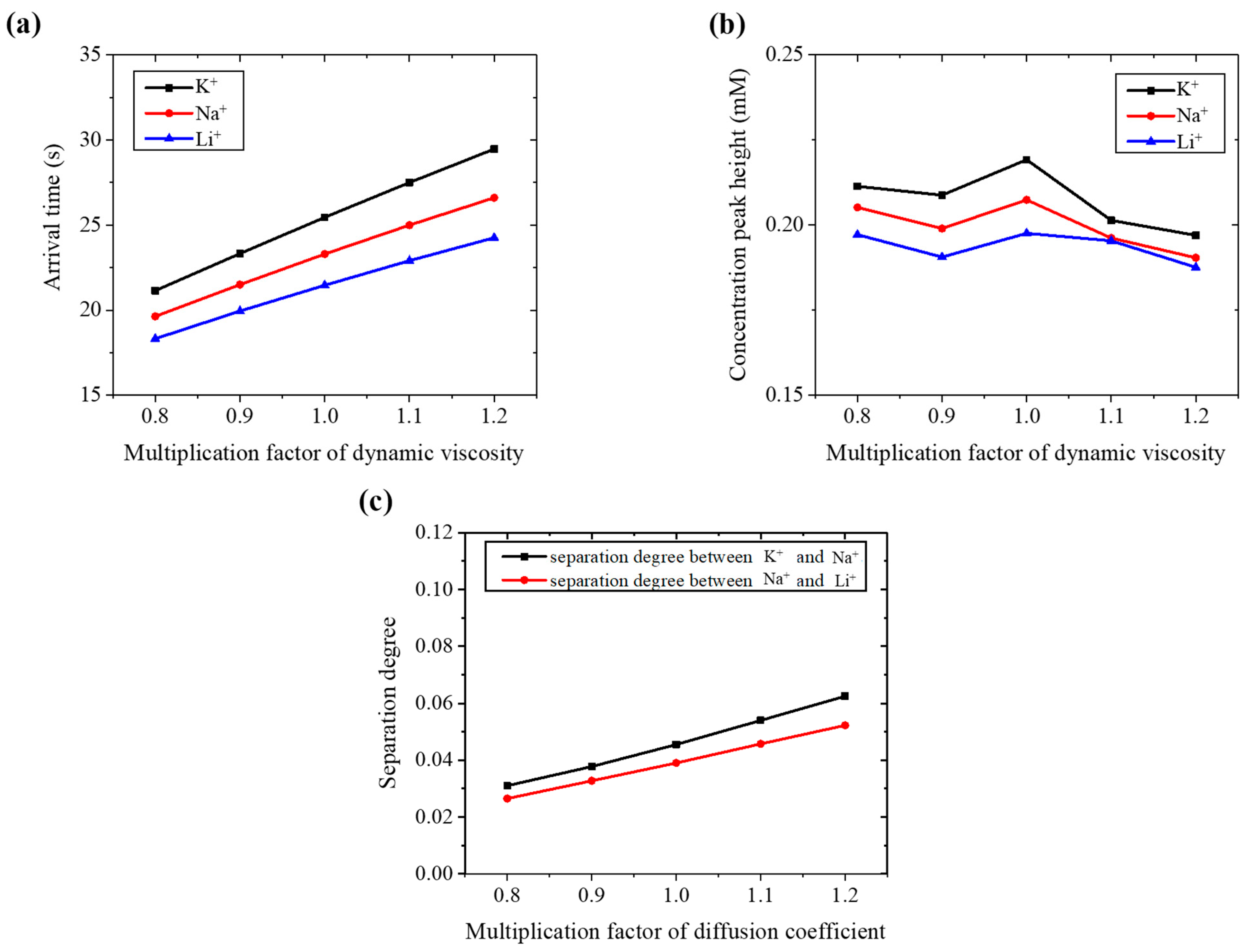
3.2.2. Effects of Diffusion Coefficient

To evaluate the influence of diffusion on ion separation, the original diffusion coefficient was scaled by a series of multiplication factors: 0.8, 0.9, 1.0, 1.1, and 1.2. These scaled values were applied in the simulations while all other parameters were kept constant.

As shown in Figure 8a, the ionic arrival time decreases approximately linearly as the diffusion coefficient increases. A higher diffusion coefficient indicates that ions can move more easily through the solution, leading to faster migration under a direct voltage.

However, as illustrated in Figure 8b, a greater diffusion coefficient also results in lower concentration peak heights due to increased dispersion of the ions during migration. In contrast, the separation degree improves with increasing diffusion coefficient (Figure 8c), likely because enhanced diffusion promotes differences in migration behavior between ions with distinct properties, thereby improving their resolution.

3.2.3. Effects of Ionic Charge Number

The migration behavior of anions under an electric field is more complex than that of cations, as the direction of EOF opposes electrophoretic motion for anions. Therefore, to simplify the analysis, only cations were considered in the simulations. Moreover, cationic charge numbers in typical applications rarely exceed three; thus, charge numbers of 1, 2, and 3 were selected for this study.

According to electrophoresis theory [11], the migration velocity of an ion under an applied electric field is the sum of two components: EOF and electrophoretic mobility. In the simulation, the EOF contribution is identical for all ions, while the electrophoretic velocity is linearly proportional to the ionic charge number. As a result, ions with higher charge numbers exhibit faster migration. The simulation results confirm that the arrival time decreases inversely with increasing charge number, as shown in Figure 9a. A shorter arrival time implies reduced diffusion and consequently a higher concentration peak. However, as the charge number increases, the electrophoretic force becomes stronger, which also intensifies ion diffusion. When the charge number exceeds two, the enhanced diffusion becomes dominant, leading to a reduction in concentration peak height, as seen in Figure 9b. In addition, a greater ionic charge number corresponds to a stronger electrophoretic driving force, which improves the resolution between ions and results in a higher separation degree (Figure 9c).

3.2.4. Effects of the Dynamic Viscosity

To investigate the impact of dynamic viscosity on ionic arrival time, concentration peak height, and separation degree, the original viscosity was scaled by multiplication factors of 0.8, 0.9, 1.0, 1.1, and 1.2 in the simulations, while other parameters remained constant.

As shown in Figure 10a, the arrival time of all three ions increases approximately linearly with increasing viscosity. This is because higher viscosity results in greater fluidic resistance, which reduces flow velocity and prolongs migration time. Figure 10b illustrates the relationship between dynamic viscosity and concentration peak height. A non-monotonic trend is observed, with the highest peak heights occurring when the multiplication factor is 1.0. As viscosity increases, the separation time becomes longer, which generally leads to broader peaks and lower peak heights. However, increased viscosity also suppresses ion diffusion, which can help maintain sharper concentration profiles. The interplay between these two effects results in the observed fluctuation in peak height. Achieving the highest peak height requires an optimal dynamic viscosity value. As indicated in Figure 10b, a dynamic viscosity of 1.0 × 10⁻³ Pa·s yields the maximum peak height and, consequently, the greatest peak discrimination. In most ME experiments, a ±20% variation around this optimal value typically accommodates typical electrophoresis conditions, with fluctuations in peak height remaining acceptable within this range. Figure 10c shows that the separation degree improves with increasing viscosity. This can be attributed to the extended migration times, which allow more spatial separation between ions. Additionally, the reduced diffusion enhances peak definition, contributing to higher separation resolution.

4. Conclusions

In this study, the effects of key solution properties—including zeta potential, diffusion coefficient, ionic charge number, and dynamic viscosity—on ion separation performance in an electrophoresis microchip were systematically investigated using FEM simulations. The results clearly demonstrate that these properties significantly influence key performance indicators such as arrival time, concentration peak height, and separation degree. By understanding how solution properties affect separation behavior, it becomes feasible to predict and optimize microchip performance through simple adjustments to the solution, without the need to alter chip geometry or incur additional fabrication costs. This approach is particularly valuable in systems where structural modifications are limited or expensive. Moreover, the solution properties offer a means to modulate ion sensitivity, detection time, and separation efficiency, thereby enhancing the performance of existing ME sensors. To date, much research in ME has focused on novel chip architectures, materials, and operating methods. However, our findings highlight the critical but often overlooked role of solution properties. Both theoretical and experimental efforts directed toward this area could yield substantial improvements in detection efficiency and system tunability. The simulation work presented here serves as an initial step—a reminder that solution properties are not secondary parameters but essential factors that can substantially enhance or impair performance in ME. It is anticipated that this study will stimulate further investigation and advancement in this area in future research.