Stretching the Limits of Refractometric Sensing in Water Using Whispering-Gallery-Mode Resonators
Abstract
1. Introduction
2. Materials and Methods
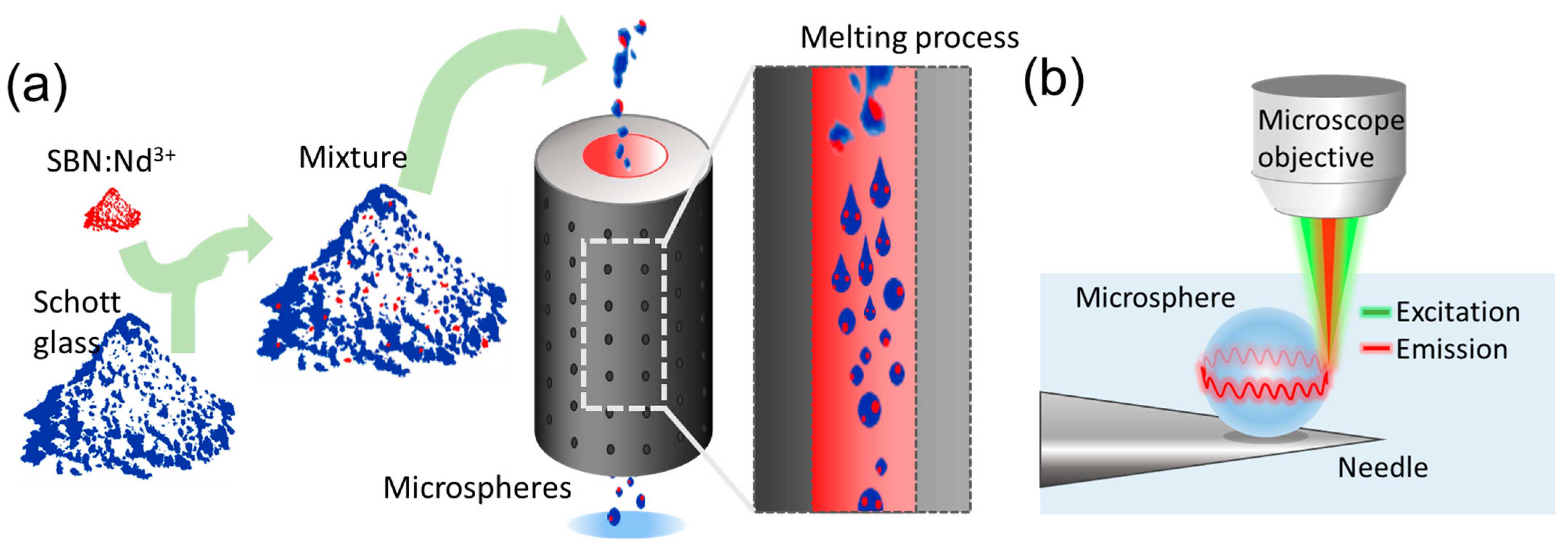
2.1. Materials and Fabrication
2.2. Optical Characterization
3. Results and Discussion
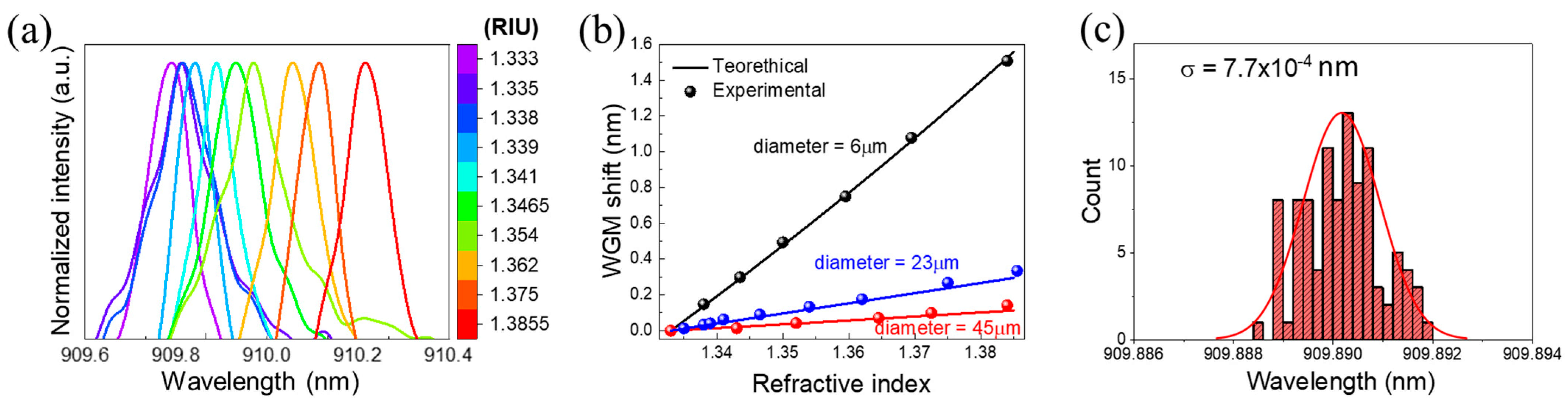
3.1. Nd3+-Doped SBN Microspheres
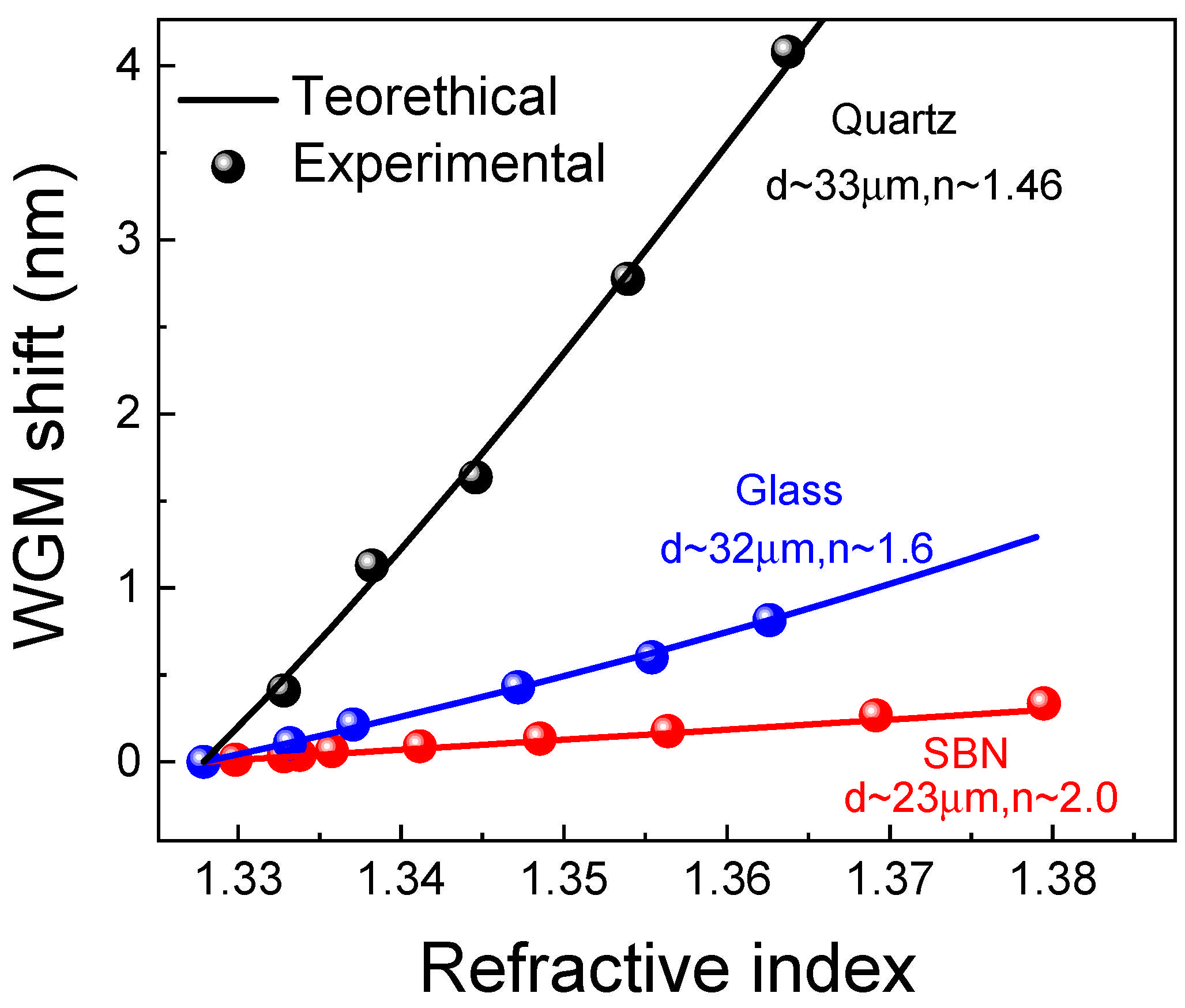
3.2. Nd3+-Doped Blend Microspheres
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Velasco-Muñoz, J.F.; Aznar-Sánchez, J.A.; Belmonte-Ureña, L.J.; Román-Sánchez, I.M. Sustainable Water Use in Agriculture: A Review of Worldwide Research. Sustainability 2018, 10, 1084. [Google Scholar] [CrossRef]
- Oral, H.V.; Carvalho, P.; Gajewska, M.; Ursino, N.; Masi, F.; van Hullebusch, E.D.; Kazak, J.K.; Exposito, A.; Cipolletta, G.; Andersen, T.R.; et al. A review of nature-based solutions for urban water management in European circular cities: A critical assessment based on case studies and literature. Blue-Green Syst. 2020, 2, 112–136. [Google Scholar] [CrossRef]
- Berglund, E.Z.; Pesantez, J.E.; Rasekh, A.; Shafiee, M.E.; Sela, L.; Haxton, T. Review of Modeling Methodologies for Managing Water Distribution Security. J. Water Resour. Plan. Manag. 2020, 146, 1–23. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Yang, S.; Wang, Y.; Sun, H. Advances and Prospects for Whispering Gallery Mode Microcavities. Adv. Opt. Mater. 2015, 3, 1136–1162. [Google Scholar] [CrossRef]
- Wen, K.; Cao, Y.; Gu, L.; Wang, S.; Qian, D.; Wang, J.; Kuang, Z.; Luo, M.; Wang, G.; Guan, S.; et al. Continuous-Wave Lasing in Perovskite LEDs with an Integrated Distributed Feedback Resonator. Adv. Mater. 2023, 35, e2303144. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, G.; Gao, Z.; Liao, Y.; Gong, C.; Kim, M.; Chang, G.-E.; Feng, S.; Xu, T.; Liu, T.; et al. Autonomous Microlasers for Profiling Extracellular Vesicles from Cancer Spheroids. Nano Lett. 2023, 23, 2502–2510. [Google Scholar] [CrossRef]
- Mao, W.; Gao, X.; Li, B.; Zhang, Y.; Wang, P.; Dong, H.; Zhang, L. Randomized whispering-gallery-mode microdisk laser arrays via cavity deformations for anti-counterfeiting labels. Photonics Res. 2023, 11, 1227. [Google Scholar] [CrossRef]
- Jiang, X.; Qavi, A.J.; Huang, S.H.; Yang, L. Whispering Gallery Microsensors: A review. Matter 2020, 3, 371–392. [Google Scholar] [CrossRef]
- Yu, D.; Humar, M.; Meserve, K.; Bailey, R.C.; Nic Chormaic, S.; Vollmer, F. Whispering-gallery-mode sensors for biological and physical sensing. Nat. Rev. Methods Prim. 2021, 1, 83. [Google Scholar] [CrossRef]
- Zhang, C.; Pu, S.; Liu, W.; Hao, Z.; Xu, T.; Duan, S.; Fu, J.; Han, S. Simultaneous measurement of bidirectional magnetic field and temperature with a dual-channel sensor based on the whispering gallery mode. Opt. Express 2024, 32, 19541. [Google Scholar] [CrossRef]
- Zhang, C.; Pu, S.; Hao, Z.; Wang, B.; Yuan, M.; Zhang, Y. Magnetic Field Sensing Based on Whispering Gallery Mode with Nanostructured Magnetic Fluid-Infiltrated Photonic Crystal Fiber. Nanomaterials 2022, 12, 862. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Xu, L.; Zhang, X.Y.; Chen, J.-X. Dual-Band Dual-Mode Dielectric Resonator Filtering Power Divider With Flexible Output Phase Difference and Power Split Ratio. IEEE Trans. Microw. Theory Tech. 2022, 70, 190–199. [Google Scholar] [CrossRef]
- Jin, L.; Di Lauro, L.; Pasquazi, A.; Peccianti, M.; Moss, D.J.; Morandotti, R.; Little, B.E.; Chu, S.T. Optical multi-stability in a nonlinear high-order microring resonator filter. APL Photonics 2020, 5, 056106. [Google Scholar] [CrossRef]
- Gizatulin, A.; Sultanov, A. Application of whispering gallery modes (WGM) in optical communications. In Optical Technologies in Telecommunications 2017; Andreev, V.A., Burdin, V.A., Morozov, O.G., Sultanov, A.H., Bourdine, A.V., Eds.; SPIE: Bellinghan, WA, USA, 2018; p. 22. [Google Scholar]
- Hanumegowda, N.M.; Stica, C.J.; Patel, B.C.; White, I.; Fan, X. Refractometric sensors based on microsphere resonators. Appl. Phys. Lett. 2005, 87, 201107. [Google Scholar] [CrossRef]
- Sedlmeir, F.; Zeltner, R.; Leuchs, G.; Schwefel, H.G. High-Q MgF_2 whispering gallery mode resonators for refractometric sensing in aqueous environment. Opt. Express 2014, 22, 30934. [Google Scholar] [CrossRef]
- Li, H.; Fan, X. Characterization of sensing capability of optofluidic ring resonator biosensors. Appl. Phys. Lett. 2010, 97, 011105. [Google Scholar] [CrossRef]
- Zamora, V.; Díez, A.; Andrés, M.V.; Gimeno, B. Refractometric sensor based on whispering-gallery modes of thin capillarie. Opt. Express 2007, 15, 12011. [Google Scholar] [CrossRef]
- Eryürek, M.; Karadag, Y.; Ghafoor, M.; Bavili, N.; Cicek, K.; Kiraz, A. Liquid refractometric sensors based on optical fiber resonators. Sens. Actuators A Phys. 2017, 265, 161–167. [Google Scholar] [CrossRef]
- Hassan, E.A.; Al-Mfrji, A.A.; Mahmood, A.I. Wavelength Tuning of the Cylindrical Structure Whispering Gallery Mode Micro-Resonator for Sensing Applications. J. Opt. 2024, 1–9. [Google Scholar] [CrossRef]
- Suebka, S.; McLeod, E.; Su, J. Ultra-high-Q free-space coupling to microtoroid resonators. Light. Sci. Appl. 2024, 13, 75. [Google Scholar] [CrossRef]
- Haro-González, P.; Martín, I.R.; Arbelo-Jorge, E.; González-Pérez, S.; Cáceres, J.M.; Núñez, P. Laser irradiation in Nd3+ doped strontium barium niobate glass. J. Appl. Phys. 2008, 104, 013112. [Google Scholar] [CrossRef]
- Elliott, G.R.; Hewak, D.W.; Murugan, G.S.; Wilkinson, J.S. Chalcogenide glass microspheres; their production, characterization and potential. Opt. Express 2007, 15, 17542. [Google Scholar] [CrossRef] [PubMed]
- Aldoğan, K.Y.; İde, C. Experimental Investigation of Refractive Index Measurement of Common Solvents and Aqueous Solutions in the Infrared Wavelengths. Balk. J. Electr. Comput. Eng. 2018, 6, 159–164. [Google Scholar] [CrossRef]
- Ewbank, M.D.; Neurgaonkar, R.R.; Cory, W.K.; Feinberg, J. Photorefractive properties of strontium-barium niobate. J. Appl. Phys. 1987, 62, 374–380. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mishchenko, M.I.; Videen, G.; Yang, P. Extinction by a homogeneous spherical particle in an absorbing medium. Opt. Lett. 2017, 42, 4873–4876. [Google Scholar] [CrossRef]
- Chýlek, P.; Zhan, J. Interference structure of the Mie extinction cross section. J. Opt. Soc. Am. A 1989, 6, 1846–1851. [Google Scholar] [CrossRef]
- Wade, S.A.; Collins, S.F.; Baxter, G.W. Fluorescence intensity ratio technique for optical fiber point temperature sensing. J. Appl. Phys. 2003, 94, 4743–4756. [Google Scholar] [CrossRef]
- Lahoz, F.; de Armas-Rillo, S.; Hernández-Rodríguez, C.; Gil-Rostra, J.; Yubero, F. Optical monitoring of detergent pollutants in greywater. Opt. Express 2023, 31, 15227. [Google Scholar] [CrossRef]
- Al-Jayyousi, O.R. Greywater reuse: Towards sustainable water management. Desalination 2003, 156, 181–192. [Google Scholar] [CrossRef]
- Finley, S.; Barrington, S.; Lyew, D. Reuse of Domestic Greywater for the Irrigation of Food Crops. Water Air Soil Pollut. 2008, 199, 235–245. [Google Scholar] [CrossRef]
- Misra, R.K.; Patel, J.H.; Baxi, V.R. Reuse potential of laundry greywater for irrigation based on growth, water and nutrient use of tomato. J. Hydrol. 2010, 386, 95–102. [Google Scholar] [CrossRef]
- Lado, M.; Ben-Hur, M. Treated domestic sewage irrigation effects on soil hydraulic properties in arid and semiarid zones: A review. Soil Tillage Res. 2009, 106, 152–163. [Google Scholar] [CrossRef]
- Sawadogo, B.; Sou, M.; Hijikata, N. Effect of Detergents from Greywater on Irrigated Plants: Case of Okra (Abelmoschus esculentus) and Lettuce (Lactuca sativa) (Desert Technology 11 International Conference). J. Arid. Land Stud. 2014, 24, 117–120. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soler-Carracedo, K.; Ruiz, A.; Ríos, S.; de Armas-Rillo, S.; Martín, L.L.; Hohmann, M.; Martín, I.R.; Lahoz, F. Stretching the Limits of Refractometric Sensing in Water Using Whispering-Gallery-Mode Resonators. Chemosensors 2025, 13, 33. https://doi.org/10.3390/chemosensors13020033
Soler-Carracedo K, Ruiz A, Ríos S, de Armas-Rillo S, Martín LL, Hohmann M, Martín IR, Lahoz F. Stretching the Limits of Refractometric Sensing in Water Using Whispering-Gallery-Mode Resonators. Chemosensors. 2025; 13(2):33. https://doi.org/10.3390/chemosensors13020033
Chicago/Turabian StyleSoler-Carracedo, Kevin, Antonia Ruiz, Susana Ríos, Sergio de Armas-Rillo, Leopoldo L. Martín, Martin Hohmann, Inocencio R. Martín, and Fernando Lahoz. 2025. "Stretching the Limits of Refractometric Sensing in Water Using Whispering-Gallery-Mode Resonators" Chemosensors 13, no. 2: 33. https://doi.org/10.3390/chemosensors13020033
APA StyleSoler-Carracedo, K., Ruiz, A., Ríos, S., de Armas-Rillo, S., Martín, L. L., Hohmann, M., Martín, I. R., & Lahoz, F. (2025). Stretching the Limits of Refractometric Sensing in Water Using Whispering-Gallery-Mode Resonators. Chemosensors, 13(2), 33. https://doi.org/10.3390/chemosensors13020033





