Detection of Harmful H2S Concentration Range, Health Classification, and Lifespan Prediction of CH4 Sensor Arrays in Marine Environments
Abstract
1. Introduction
- (1)
- To limit the time complexity to O (n logn), we changed the traditional self-attention mechanism to ESS attention. The proposed model used the idea of sorting the product weights of the query and the key value from high to low. Using the original distribution of the training data, we retained the first third and sparse the rest with an explainable mask.
- (2)
- We enhanced the attention of the Ocean X GPT model with a Rotary Position Embedding (RoPE) attention mechanism. This attention not only had RoPE position information but also retained the original information. Applying the idea of a residual network, we added the original data to the query and key, which were mapped by RoPE. Then, we mapped the total return data into the RoPE again. For the question-and-answer task, the model obtained the position information between the question and the answer from the first RoPE operation. Then, we increased the accuracy of the answer according to the second RoPE operating by combining the question and the target answer.
- (3)
- We proposed a real-time interactive health management and life prediction system. The basic framework was the Ocean X GPT model with an ESS transformer model embedded inside. When performing the task, according to the keyword in the question, the program jumped into the ESS transformer model and waited for input data. After we entered random validation data x into the trained toxic gas concentration interval detection model (ESS transformer), the model returned the corresponding concentration information, poisoning grade, and remaining life information as a voice broadcast.
2. Theoretical Fundamentals
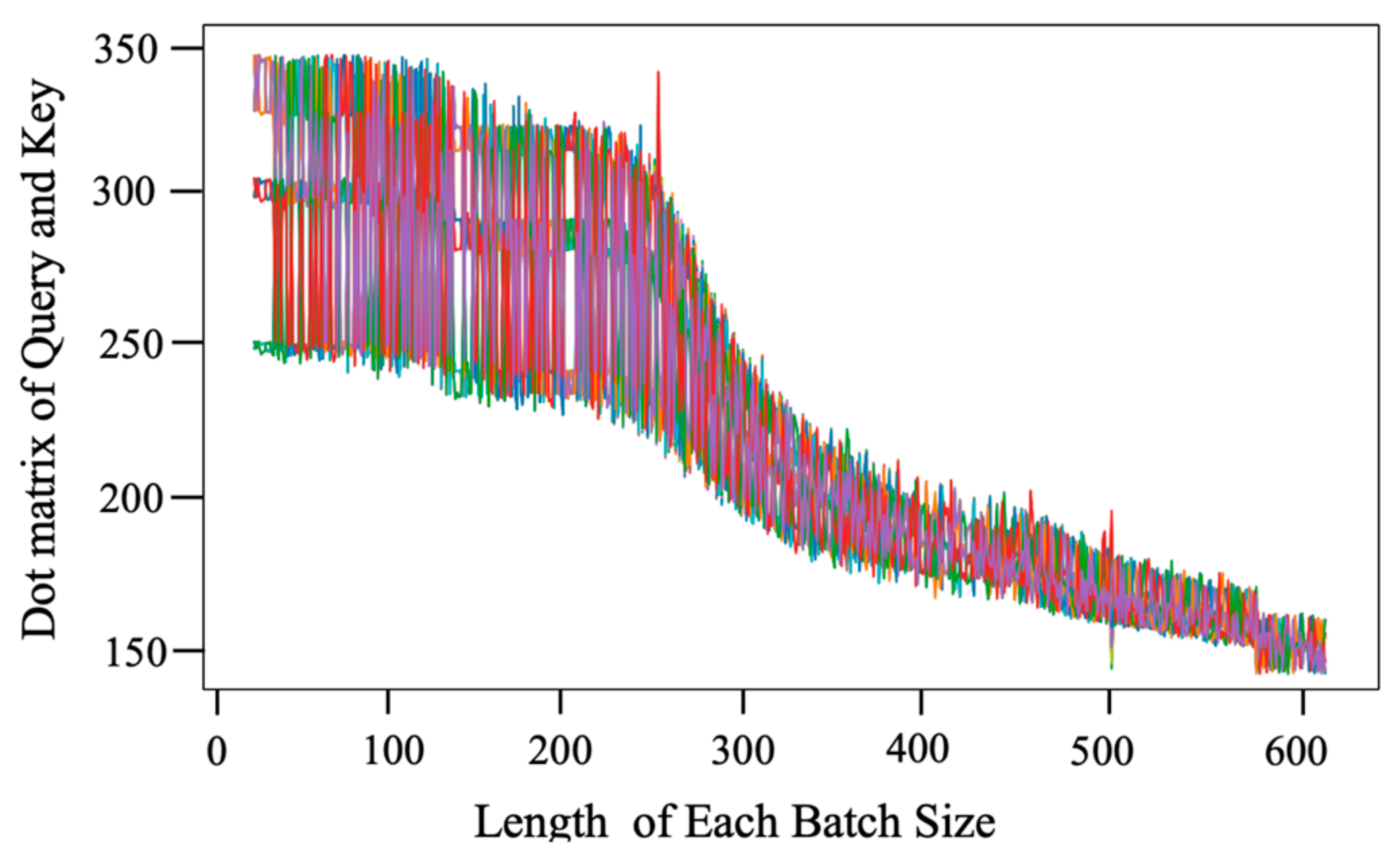
2.1. ESS Mask
2.2. ESS Attention
| Algorithm 1 ESS Attention | |
| Function | ESS Attention (Xinput) |
| | | Q, K ← Xinput |
| | | (Batch, Head, 608, 25) |
| | | K ← Randint (len(X) = 25) |
| | | QK_sample ← Q ∗ K |
| | | M_top ← Sort (QK_sample) |
| | | Visualized (M_top) |
| | | QSortedSparse ← Q ∗ Mask |
| | | Score = QSortedSparse ∗ KT |
| End | |
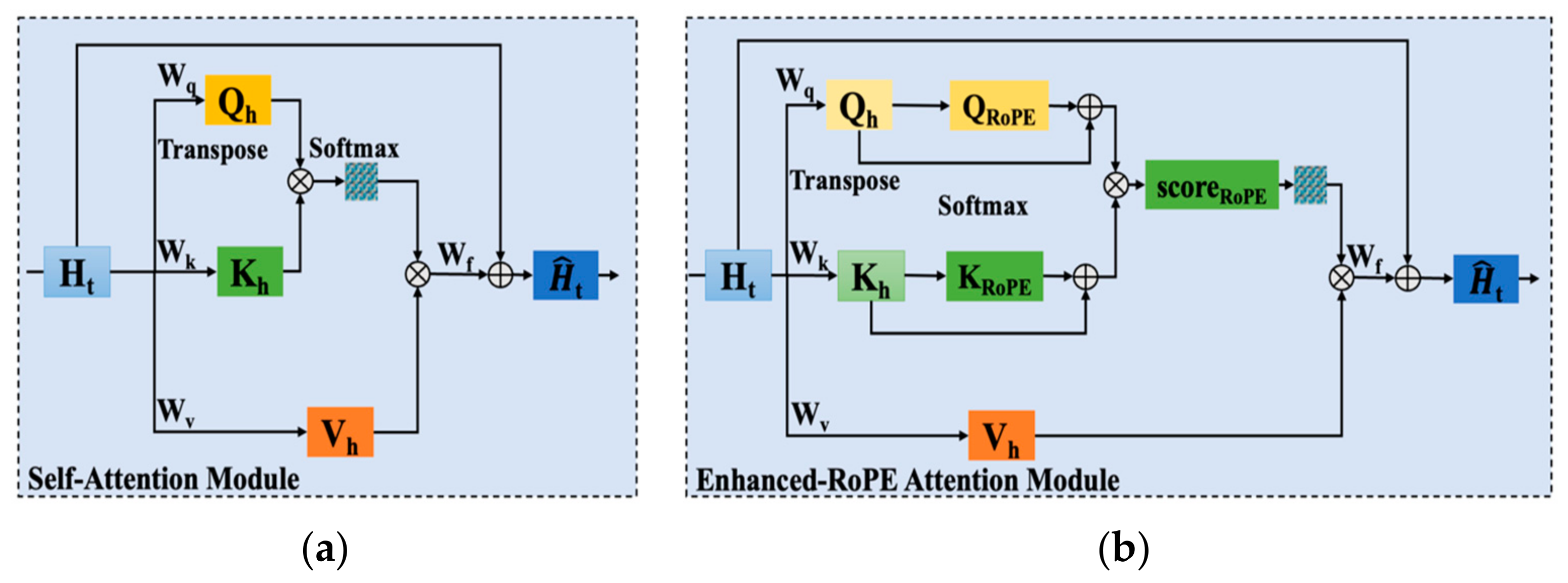
2.3. Enhanced Rotary Positional Embedding Attention
| Algorithm 2 Enhanced-RoPE Attention | |
| Function | Enhanced-RoPE Attention (Xinput) |
| | | Q, K ← Xinput |
| | | QRoPE← · Q, KRoPE← · K |
| | | Score = (QRoPE + Q) ∗ (KRoPE + K) T |
| | | ScoreRoPE ←·Score |
| End | |
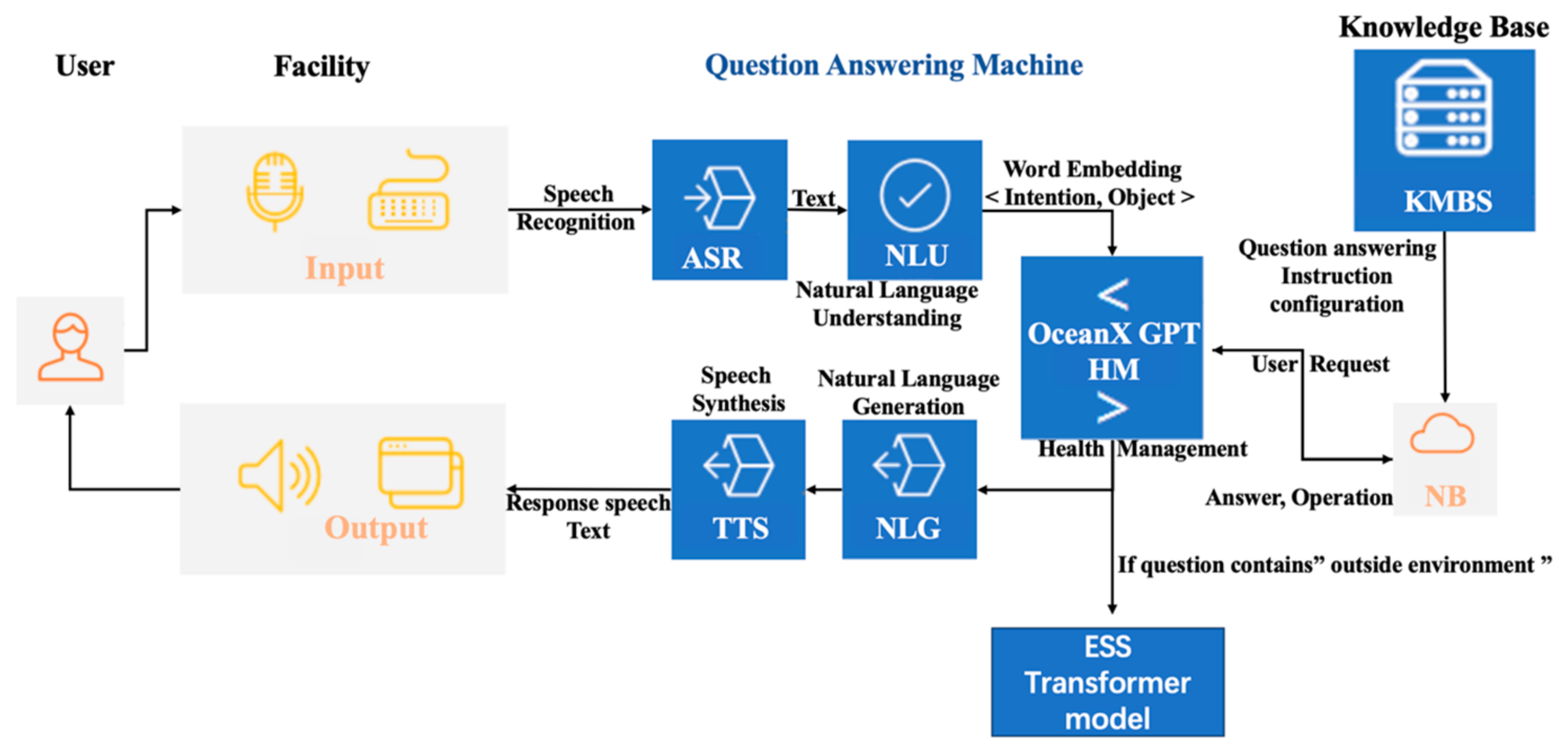
2.4. Ocean X GPT Question-Answering System with Embodied Intelligence
| Algorithm 3 Ocean X GPT Question-and-Answer System with Embodied Intelligence | |
| Question ← “Input:” | |
| While True: | |
| temp_sentence == input (“…”) | |
| Question ← temp_sentence | |
| If Question == “The environment outside” | |
| | b ← model. Predict (XRandom_inside). Argmax (−1) | |
| | If b == 0: | |
| | | a == “answer 0” | |
| | elif b == 1: | |
| | | a == “answer 1” | |
| | elif b == 2: | |
| | | a == “answer 2” | |
| | elif b == 3: | |
| | | a == “answer 3” | |
| else a ← GPT.answer (Question) | |
| Return a | |
2.5. Encoder and Decoder Stacks
3. Experiment, Results and Discussion
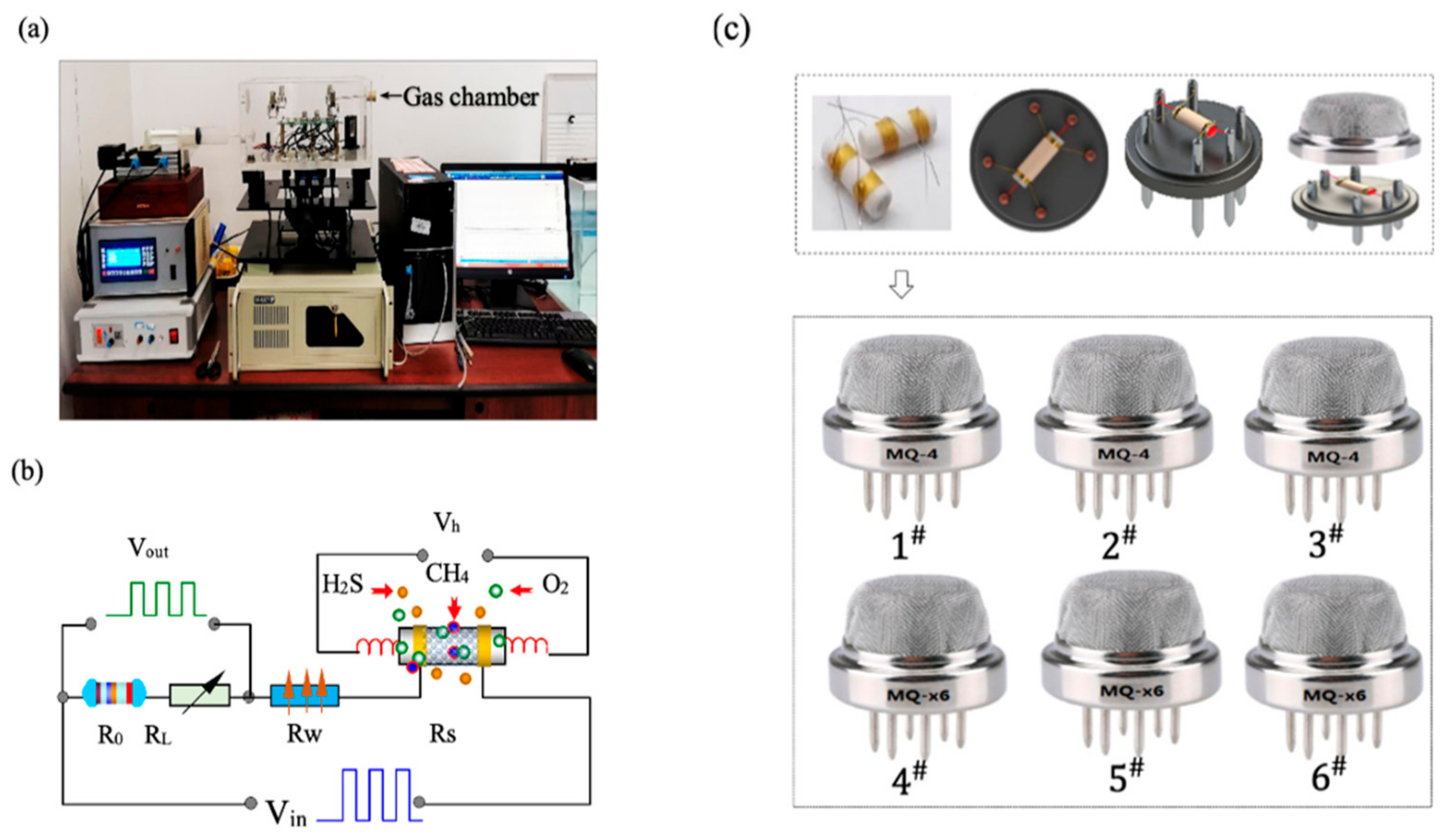
3.1. Setup of Experiment
3.2. Flowchart of Question-and-Answer Health Management Systems with Embodied AI
3.3. Validation of Anomaly Detection Method and Inference
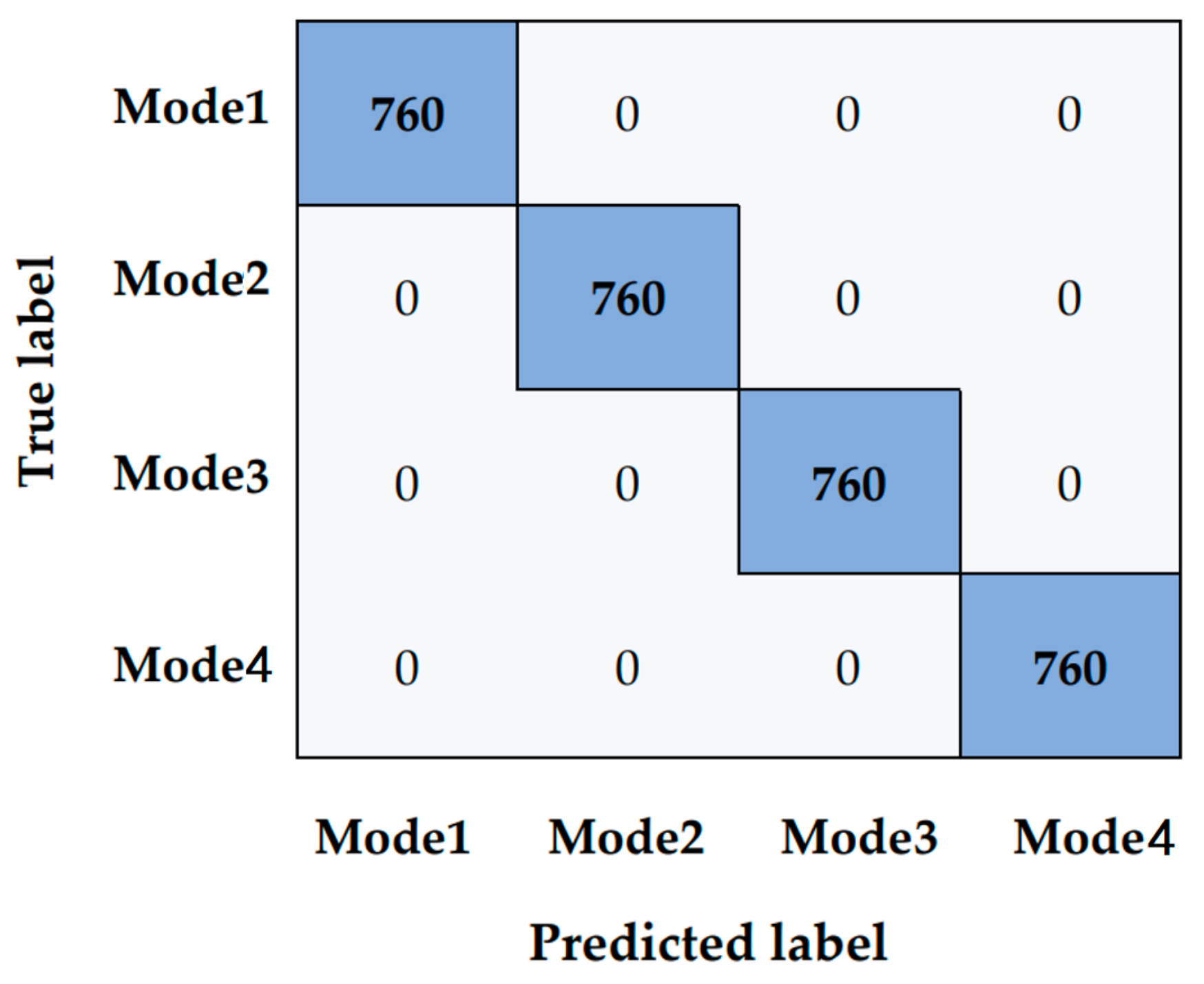
3.3.1. Toxic Gas Concentration Interval Detection Evaluation Metrics
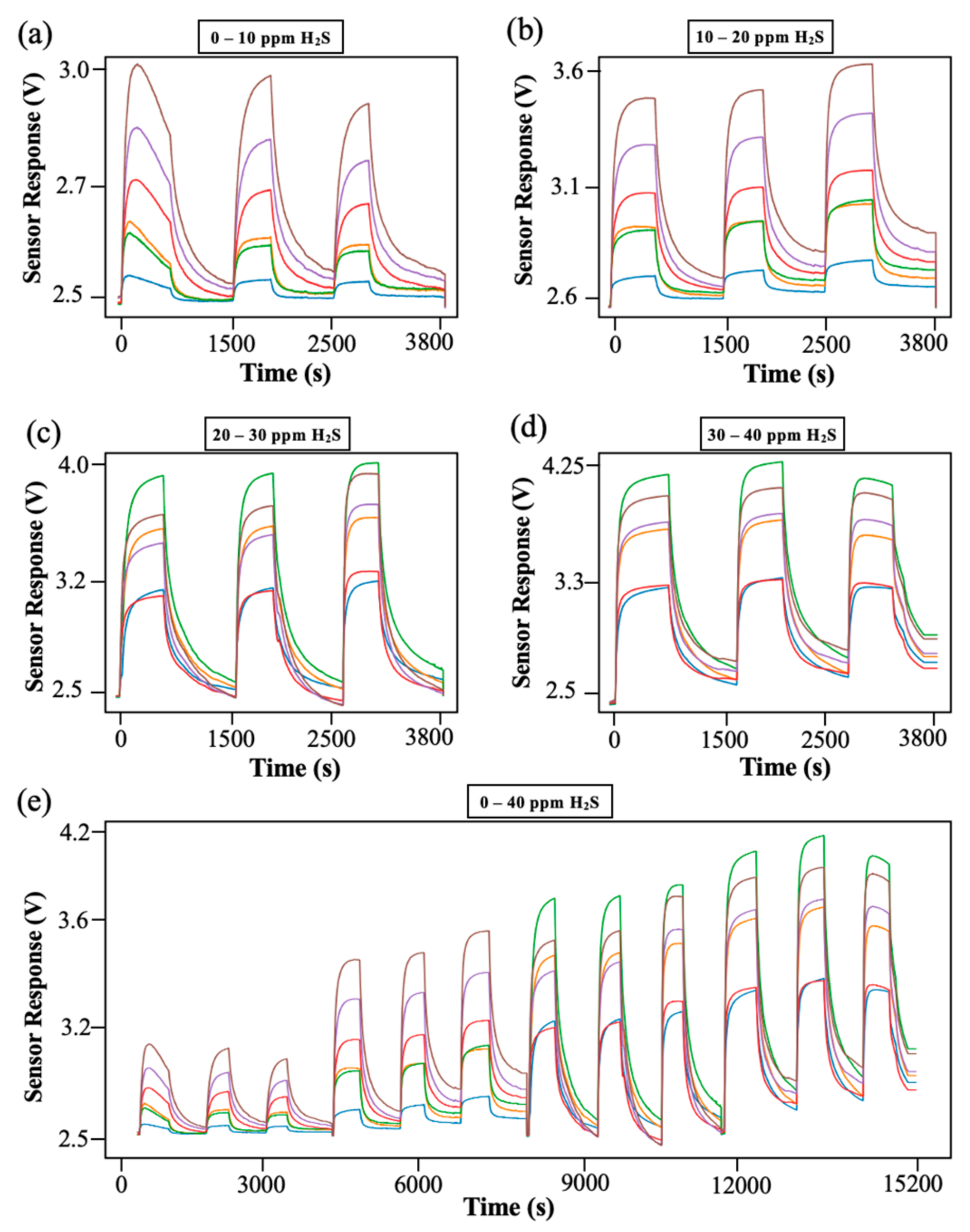
3.3.2. ESS Transformer Toxic Gas Concentration Interval Detection Results and Discussion
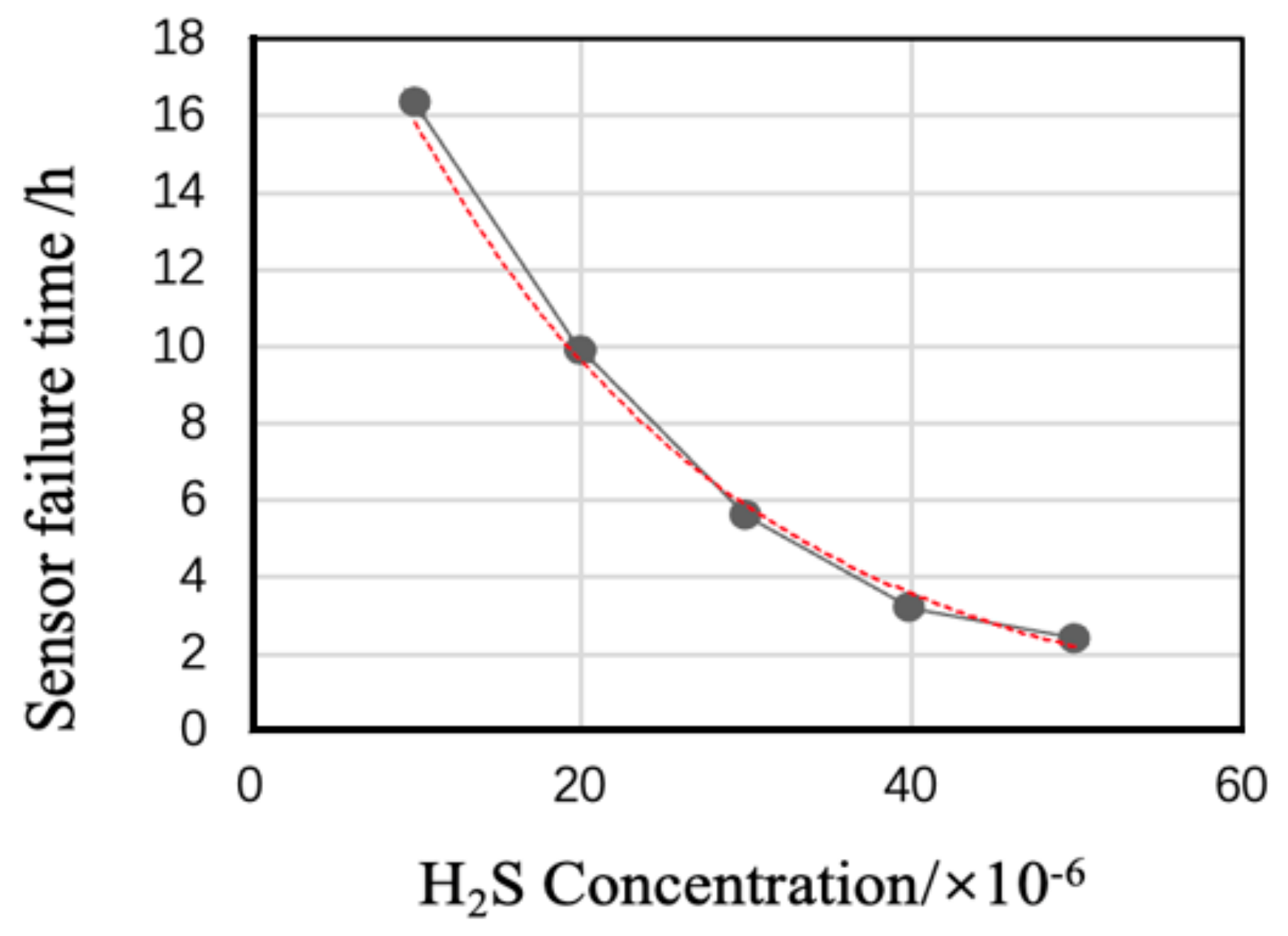
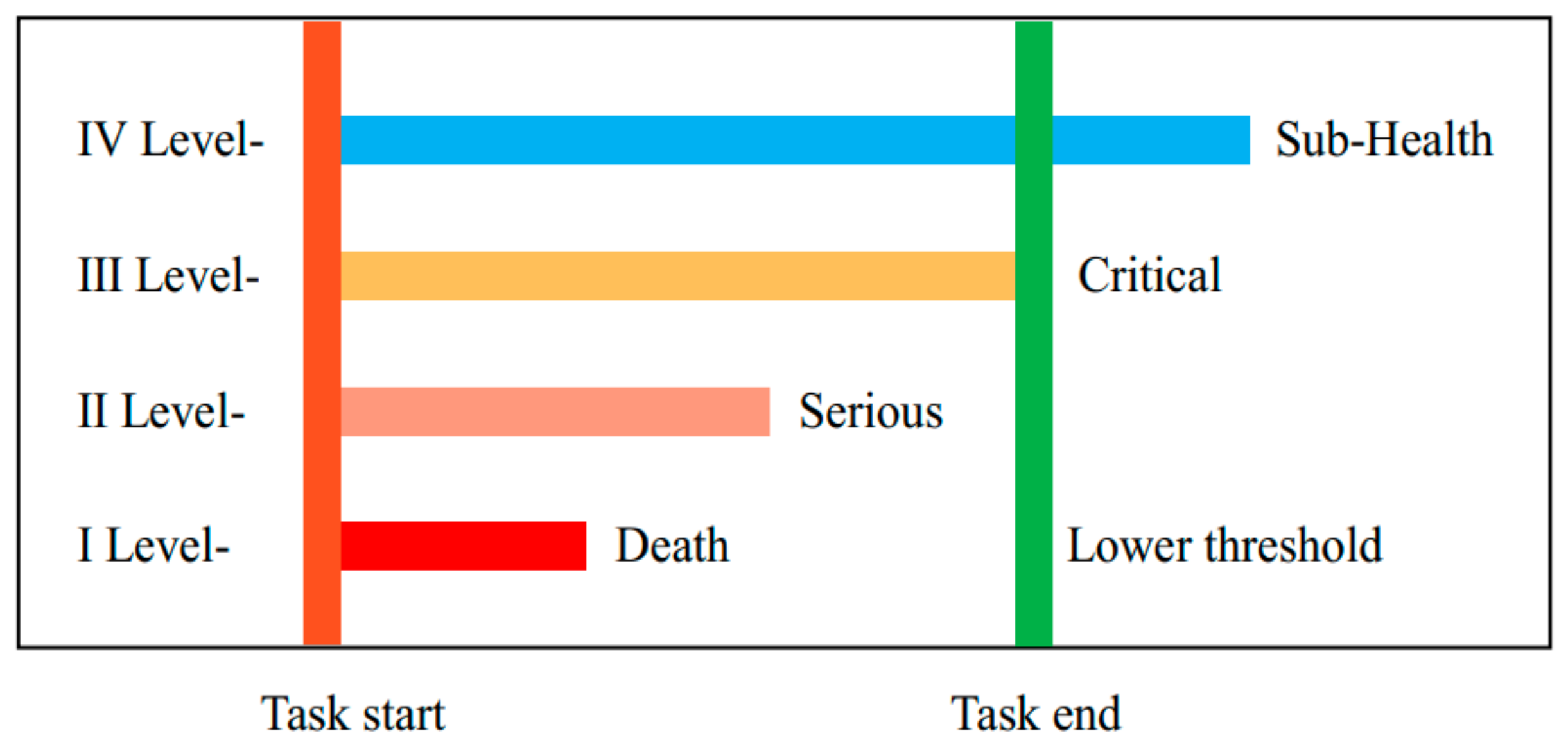
3.3.3. Health Levels and Lifetime Prediction Results and Discussion
3.3.4. Offline Question-and-Answer System Experimental Results and Discussion
3.4. Attention Visualization for Anomaly Detection in the Training Process
3.5. Comparison of Model Memory Cost
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Xue, M.; Cui, X.; Peng, W. A review on the methane emission detection during offshore natural gas hydrate production. Front. Energy Res. 2023, 11, 12607–12617. [Google Scholar]
- Ying, W.; Xu, G.; Hong, Z. Characteristics and emissions of isoprene and other non-methane hydrocarbons in the Northwest Pacific Ocean and responses to atmospheric aerosol deposition. Sci. Total Environ. 2023, 10, 162808. [Google Scholar]
- Irina, T.; Ilya, F.; Aleksandr, S. Mapping onshore CH4 seeps in Western Siberian floodplains using convolutional neural network. Remote Sens. 2022, 14, 2611. [Google Scholar]
- Itziar, I.; Javier, G.; Daniel, Z. Satellites detect a methane ultra-emission event from an Offshore Platform in the Gulf of Mexico. Environ. Sci. Technol. Lett. 2022, 9, 520–525. [Google Scholar]
- Ian, B.; Vassilis, K.; Andrew, R. Simultaneous high-precision, high-frequency measurements of methane and nitrous oxide in surface seawater by cavity ring-down spectroscopy. Front. Mar. Sci. 2023, 10, 186–195. [Google Scholar]
- Xuan, Z.; Miaomiao, Z.; Lingbing, B. Simulation and error analysis of methane detection globally using spaceborne IPDA Lidar. Remote Sens. 2023, 15, 3239. [Google Scholar]
- Wei, K.; Thor, S. A review of gas hydrate nucleation theories and growth models. J. Nat. Gas Sci. Eng. 2019, 61, 169–196. [Google Scholar]
- Abrahamsson, K.; Damm, E.; Björk, G.; Bunse, C.; Sellmaier, S.; Broström, G.; Assmann, V.; Dumitrascu, A.; Maciute, A.; Olofsson, N.; et al. Methane plume detection after the 2022 Nord stream pipeline explosion in the Baltic Sea. Nature 2024, 14, 12848. [Google Scholar] [CrossRef]
- Cooper, L.J.; Dubey, A. Hawkes, Methane detection and quantification in the upstream oil and gas sector: The role of satellites in emissions detection, reconciling and reporting. Environ. Sci. Atmos. 2022, 2, 9–23. [Google Scholar] [CrossRef]
- Xi-lai, L.; Meng-han, W.; Yong, H. Influences of Impurity Gases in Air on Room-Temperature Hydrogen-Sensitive Pt–SnO2 Composite Nanoceramics: A Case Study of H2S. Chemosensors 2023, 11, 31. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, C.; Meng, F. Strategies for improving the sensing performance of semiconductor gas sensors for high-performance formaldehyde detection: A review. Chemosensors 2021, 9, 179. [Google Scholar] [CrossRef]
- Chen, Y.S.; Xu, Y.H. Fault detection, isolation, and diagnosis of status self-validating gas sensor arrays. Rev. Sci. Instrum. 2010, 87, 045001. [Google Scholar] [CrossRef]
- Sana, J.; Young, L.; Jungpil, S. Sensor fault classification based on support vector machine and statistical time-domain features. IEEE Access 2017, 5, 8682–8690. [Google Scholar]
- Yang, J.; Chen, Y. An efficient approach for fault detection, isolation, and data recovery of self-validating multifunctional sensors. IEEE Trans. Instrum. Meas. 2017, 66, 543–558. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar]
- Lu, J.; Huang, J.; Lu, F. Sensor fault diagnosis for aero engine based on online sequential extreme learning machine with memory principle. Energies 2017, 10, 39. [Google Scholar] [CrossRef]
- Tsui, K.L.; Chen, N. Prognostics and health management: A review on data driven approaches. Math. Probl. Eng. 2015, 6, 793161. [Google Scholar] [CrossRef]
- Bai, G.; Wang, P.; Hu, C. A self-cognizant dynamic system approach for prognostics and health management. J. Power Sources 2015, 278, 163–174. [Google Scholar] [CrossRef]
- Coble, J.; Ramuhalli, P.; Bond, L. A review of prognostics and health management applications in nuclear power plants. Int. J. Progn. Health Manag. 2015, 6, 1–22. [Google Scholar]
- Shen, Z.; He, Z. A monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time. Sensors 2012, 12, 10109–10135. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, C.H.A. Hybrid feature model and deep-learning-based bearing fault diagnosis. Sensors 2017, 17, 2876. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, X.; Wang, L. Modeling of BN lifetime prediction of a system based on integrated multi-level information. Sensors 2017, 17, 2123. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, V.; Lybeck, N.J. Development of Asset Fault Signatures for Prognostic and Health Management in the Nuclear Industry; Prognostics and Health Management: Austin, TX, USA, 2015; pp. 1–7. [Google Scholar]
- Kumar, S.; Pecht, M. Modeling approaches for prognostics and health management of electronics. Int. J. Perform. Eng. 2010, 6, 222–229. [Google Scholar]
- Feng, Z.G.; Wang, Q. Research on health evaluation system of liquid-propellant rocket engine ground-testing bed based on fuzzy theory. Acta Astronaut. 2007, 61, 840–853. [Google Scholar] [CrossRef]
- Xia, T.; Xi, L. Dynamic maintenance decision-making for series–parallel manufacturing system based on MAM–MTW methodology. Eur. J. Oper. Res. 2012, 221, 231–240. [Google Scholar] [CrossRef]
- Berges, L.; Galar Gustafson, A. Maintenance decision making based on different types of data fusion. Eksploat. I Niezawodn.-Maint. Reliab. 2012, 14, 135–144. [Google Scholar]
- Cates, G.L.; Skinner, C.H.; Watson, T.S. Instructional effectiveness and instructional efficiency as considerations for data-based decision making: An evaluation of interspersing procedures. Sch. Psychol. Rev. 2003, 32, 601–616. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, S.; Yang, J. Grey bootstrap method for data validation and dynamic uncertainty estimation of self-validating multifunctional sensors. Chemometr. Intell. Lab. Syst. 2015, 146, 63–76. [Google Scholar] [CrossRef]
- Song, K.; Wang, Q. In quantitative measurement of gas component using multi-sensor array and NPSO-based LS-SVR. Instrum. Meas. Technol. Conf. 2013, 80, 1740–1743. [Google Scholar]
- Shen, Z.; Wang, Q. Data-driven health evaluation of multifunctional self-validating sensor using health reliability degree. Inf. Technol. J. 2012, 11, 1597–1604. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q. A novel health evaluation strategy for multifunctional self-validating sensors. Sensors 2013, 13, 587–610. [Google Scholar] [CrossRef] [PubMed]
- Aughenbaugh, J.M.; Herrmann, J.W. Reliability-based decision making: A comparison of statistical approaches. J. Stat. Theory Pract. 2009, 3, 289–303. [Google Scholar] [CrossRef][Green Version]
- Wang, A.; Jiang, J.; Zhang, H. Multi-sensor image decision level fusion detection algorithm based on D-S evidence theory. In Proceedings of the Fourth International Conference on Instrumentation and Measurement, Computer, Communication and Control, Harbin, China, 18–20 September 2014; pp. 620–623. [Google Scholar]
- He, Z.; Zhang, H.; Zhao, J. Classification of power quality disturbances using quantum neural network and DS evidence fusion. Eur. Trans. Electr. Power 2013, 22, 533–547. [Google Scholar] [CrossRef]
- Wang, H.; Lin, D. Research on multi-objective group decision-making in condition-based maintenance for transmission and transformation equipment based on D-S evidence theory. IEEE Trans. Smart Grid 2015, 6, 1035–1045. [Google Scholar] [CrossRef]
- Lin, S.; Li, C. The strategy research on electrical equipment condition-based maintenance based on cloud model and grey D-S evidence theory. Intell. Decis. Technol. 2018, 3, 283–292. [Google Scholar] [CrossRef]
- Mehta, P.; Werner, A. Condition based maintenance-systems integration and intelligence using Bayesian classification and sensor fusion. J. Intell. Manuf. 2015, 26, 331–346. [Google Scholar] [CrossRef]
- Herrle, S.R.; Corbett, E.C. Bayes’ theorem and the physical examination: Probability assessment and diagnostic decision making. Acad. Med. J. Assoc. Am. Med. Coll. 2011, 86, 618. [Google Scholar] [CrossRef]
- Lin, P.C.; Gu, J.C.; Yang, M.T. Intelligent maintenance model for condition assessment of circuit breakers using fuzzy set theory and evidential reasoning. IET Gener. Transm. Distrib. 2014, 8, 1244–1253. [Google Scholar] [CrossRef]
- Yin, K.; Yang, B.; Li, X. Multiple attribute group decision-making methods based on trapezoidal fuzzy two-dimensional linguistic partitioned bonferroni mean aggregation operators. Int. J. Environ. Res. Public Health 2018, 15, 194. [Google Scholar] [CrossRef]
- Chen, S.; Cheng, S.; Chiou, C. Fuzzy multi-attribute group decision making based on intuitionistic fuzzy sets and evidential reasoning methodology. Inf. Fusion 2016, 27, 215–227. [Google Scholar] [CrossRef]
- Efe, B. An integrated fuzzy multi criteria group decision making approach for ERP system selection. Appl. Soft Comput. 2016, 38, 106–117. [Google Scholar] [CrossRef]
- Joshi, D.; Kumar, S. Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. Eur. J. Oper. Res. 2016, 248, 183–191. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 12. [Google Scholar] [CrossRef]
- Su, J.; Ahmed, M.; Lu, Y.; Pan, S.; Bo, W.; Liu, Y. RoFormer: Enhanced transformer with Rotary Position Embedding. Neurocomputing 2024, 568, 127063. [Google Scholar] [CrossRef]
- Dai, Z.; Yang, Z.; Yang, Y.; Carbonell, J.; Le, Q.V.; Salakhutdinov, R. Transformer-XL: Attentive language models beyond a fixed-length context. arXiv 2019, arXiv:1901.02860. [Google Scholar]
- Child, R.; Gray, S.; Radford, A.; Sutskever, I. Generating long sequences with sparse transformers. arXiv 2019, arXiv:1904.10509. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. Int. Conf. Learn. Represent. 2020, 4, 148–156. [Google Scholar]
- Vaswani, A.; Shazeer, N. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 4–9, 5998–6008. [Google Scholar]
- Katharopoulos, A.; Vyas, A.; Pappas, N.; Fleuret, F. Transformers are RNNs: Fast autoregressive transformers with linear attention. Int. Conf. Mach. Learn. 2020, 119, 5156–5165. [Google Scholar]
- Shen, Z.; Zhang, M. Efficient Attention: Attention with Linear Complexities. WACV 2021, 8, 3530–3538. [Google Scholar]



| Model | Training Time (s) | Accuracy (%) | Recall (%) | Testing Time (s) |
|---|---|---|---|---|
| CNN + SVM | 480 | 97.5% | 97% | 0.1 |
| Transformerencoder | 600 | 98.3% | 98% | 0.2 |
| ESS transformer model | 520 | 99.9% | 99% | 0.2 |
| Question | Generated Answer Token | Correct | Accuracy Rate (%) |
|---|---|---|---|
| What are the application areas of CH4 sensors? | 37 | ✓ | 99.7% |
| What are the H2S poisoning phenomena of sensors? | 40 | ✓ | 99.4% |
| What are the hazards of CH4 gas? | 39 | ✓ | 99.9% |
| What is the transformer algorithm? | 46 | ✓ | 99.5% |
| What are the implications of detecting ocean CH4? | 37 | ✓ | 99.2% |
| What are the components of an array sensor? | 40 | ✓ | 99.6% |
| What are the components of the signal collector? What are the gas identification methods? | 41 56 | ✓ ✓ | 99.3% 98.9% |
| What is the mechanism of sensor poisoning caused by H2S? | 52 | ✓ | 98.7% |
| What is the degree of poisoning of the CH4 sensor arrays caused by H2S gas? | 84 | ✓ | 98.9% |
| What is the level of H2S? | 52 | ✓ | 99.1% |
| What is the significance of predicting failure? | 15 | ✓ | 99.9% |
| Model | Mean Accuracy | <40 Tokens | 40–50 Tokens | >50 Tokens | Prompt or Not | I Do Not Know Assignment |
|---|---|---|---|---|---|---|
| LSTM-ecoder | 96.6% | 97.1% | 96.5% | 96.2% | ✓ | No |
| GPTDecoder | 98.1% | 98.3% | 98.1% | 97.9% | ✓ | No |
| Ocean X GPT | 99.4% | 99.7% | 99.5% | 98.9% | ✓ | No |
| Model/Paper | Complexity | Decode | Class |
|---|---|---|---|
| Trans.-XL (Dai et al., 2019) [47] | O(n2) | RC | |
| Sparse Trans. (Child et al., 2019) [48] | ) | FP | |
| Reformer (Kitaev et al., 2020) [49] | O(nlogn) | LP | |
| ESS transformer model | O(nlogn) | FP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Zhang, Y.; Wu, J.; Wang, T.; Jiang, W.; Zeng, M.; Yang, Z. Detection of Harmful H2S Concentration Range, Health Classification, and Lifespan Prediction of CH4 Sensor Arrays in Marine Environments. Chemosensors 2024, 12, 172. https://doi.org/10.3390/chemosensors12090172
Zhang K, Zhang Y, Wu J, Wang T, Jiang W, Zeng M, Yang Z. Detection of Harmful H2S Concentration Range, Health Classification, and Lifespan Prediction of CH4 Sensor Arrays in Marine Environments. Chemosensors. 2024; 12(9):172. https://doi.org/10.3390/chemosensors12090172
Chicago/Turabian StyleZhang, Kai, Yongwei Zhang, Jian Wu, Tao Wang, Wenkai Jiang, Min Zeng, and Zhi Yang. 2024. "Detection of Harmful H2S Concentration Range, Health Classification, and Lifespan Prediction of CH4 Sensor Arrays in Marine Environments" Chemosensors 12, no. 9: 172. https://doi.org/10.3390/chemosensors12090172
APA StyleZhang, K., Zhang, Y., Wu, J., Wang, T., Jiang, W., Zeng, M., & Yang, Z. (2024). Detection of Harmful H2S Concentration Range, Health Classification, and Lifespan Prediction of CH4 Sensor Arrays in Marine Environments. Chemosensors, 12(9), 172. https://doi.org/10.3390/chemosensors12090172







