Rational Design and Optimization of Plasmonic Nanohole Arrays for Sensing Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Ordered Gold Nanoholes Arrays Fabrication
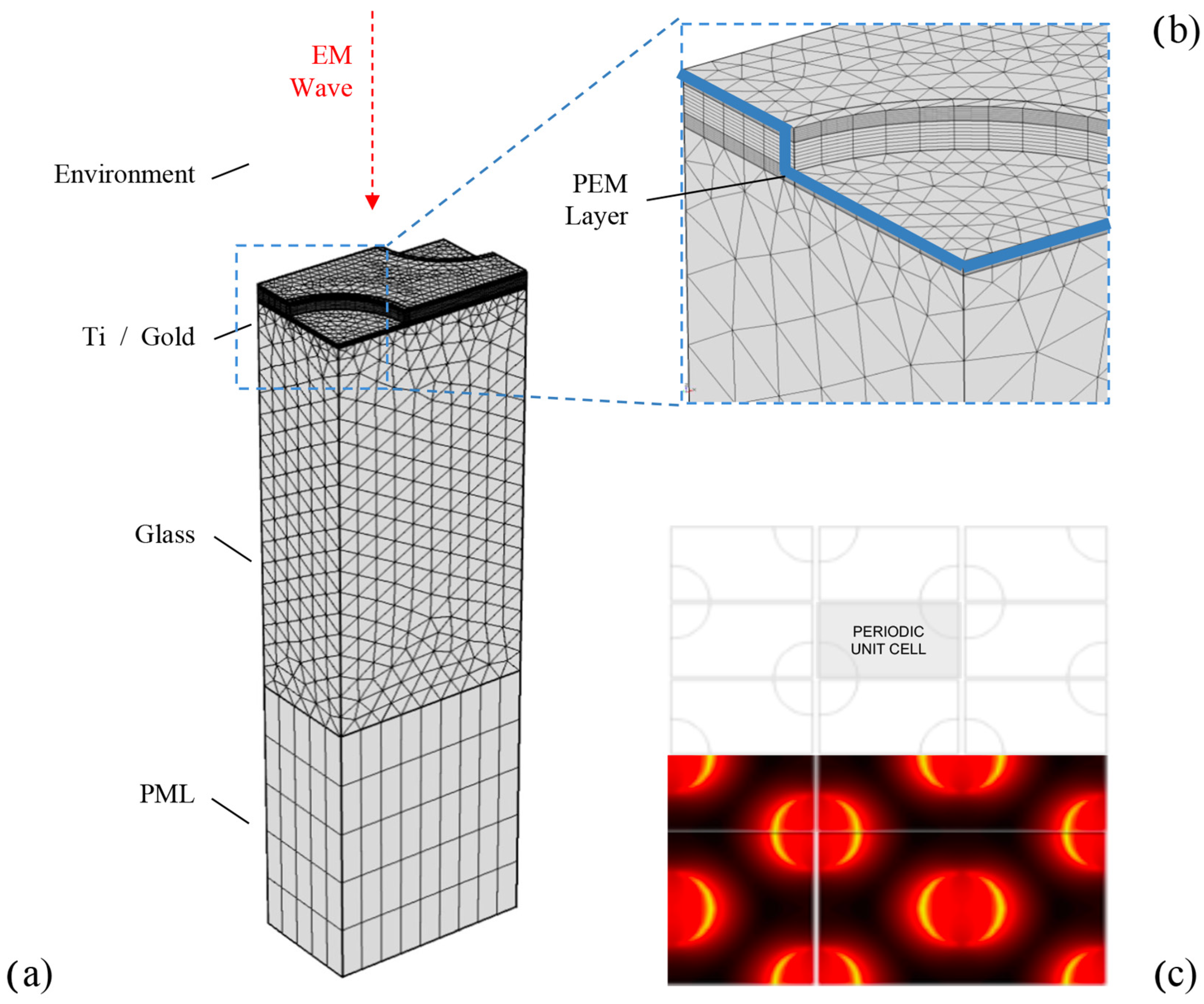
2.2. FEM Simulations
2.3. Morphological and Optical Characterization
2.4. Sensitivity Performance Measurements
3. Results and Discussion
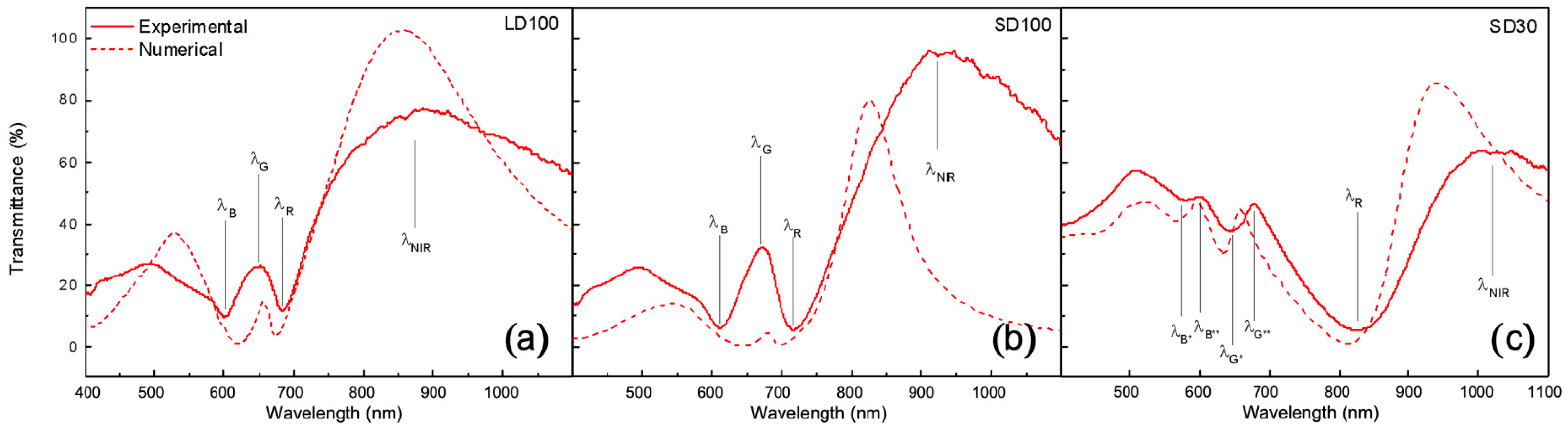
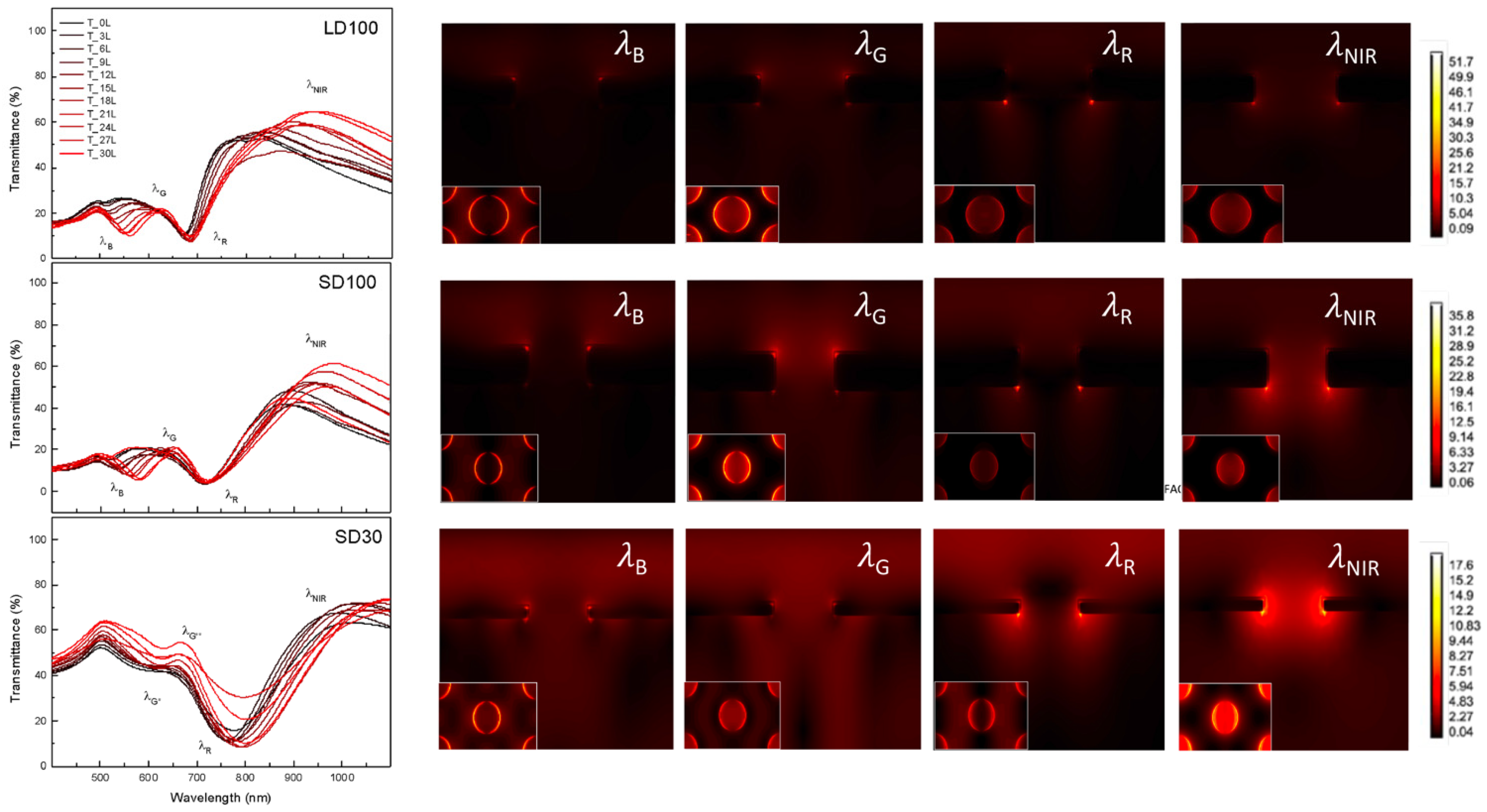
3.1. Optical and Morphological Description
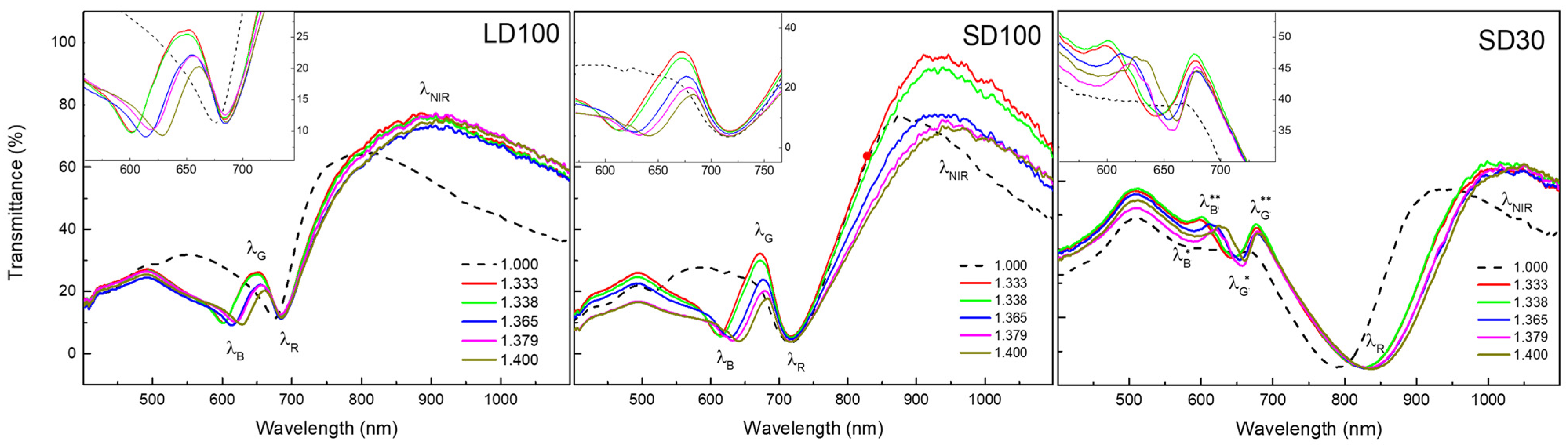
3.2. Sensitivity Performances
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Li, Z.; Ye, S.; Wu, S.; Zhang, J.; Cui, L.; Li, A.; Wang, T.; Li, S.; Yang, B. Elevated Ag Nanohole Arrays for High Performance Plasmonic Sensors Based on Extraordinary Optical Transmission. J. Mater. Chem. 2012, 22, 8903–8910. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for Improved Photovoltaic Devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.B.; Hu, X.L.; Zeng, B.; Wang, L.S.; Yang, S.M.; Tai, R.Z.; Fecht, H.J.; Zhang, D.X.; Jiang, J.Z. Effect of Relative Nanohole Position on Color Purity of Ultrathin Plasmonic Subtractive Colour Filters. Nanotechnology 2015, 26, 305204. [Google Scholar] [CrossRef]
- Mahani, F.F.; Mokhtari, A.; Mehran, M. Dual Mode Operation, Highly Selective Nanohole Array-based Plasmonic Colour Filters. Nanotechnology 2017, 28, 385203. [Google Scholar] [CrossRef] [PubMed]
- Yokogawa, S.; Burgos, S.P.; Atwater, H.A. Plasmonic Color Filters for CMOS Image Sensor Applications. Nano Lett. 2012, 12, 4349–4354. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Xu, S.; Wang, H.; Gu, Y.; Lombardi, J.R.; Xu, W. Active-Tuned Plasmonic Angle Modulator of Light Beams for Potential Application of 3D Display. ACS Photonics 2014, 1, 677–682. [Google Scholar] [CrossRef]
- Sannomiya, T.; Scholder, O.; Jefimovs, K.; Hafner, C.; Dahlin, A.B. Investigation of Plasmon Resonances in Metal Films with Nanohole Arrays for Biosensing Applications. Small 2011, 7, 1653–1663. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Zhang, X.; Chang, L.; Wang, T.; Li, Z.; Zhang, J.; Yang, B. High-Performance Plasmonic Sensors Based on Two-Dimensional Ag Nanowell Crystals. Adv. Opt. Mater. 2014, 2, 779–787. [Google Scholar] [CrossRef]
- Zheng, P.; Cushing, S.K.; Suri, S.; Wu, N. Tailoring Plasmonic Properties of Gold Nanohole Arrays for Surface-Enhanced Raman Scattering. Phys. Chem. Chem. Phys. 2015, 17, 21211–21219. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wong, T.I.; Bauch, M.; Zhang, Q.; Zhang, J.; Liu, X.; Zhou, X.; Bai, P.; Dostalek, J.; et al. Directional Fluorescence Emission co-Enhanced by Localized and Propagating Surface Plasmons for Biosensing. Nanoscale 2016, 8, 8008–8016. [Google Scholar] [CrossRef]
- Im, H.; Lesuffleur, A.; Lindquist, N.C.; Oh, S.-H. Plasmonic Nanoholes in a Multichannel Microarray Format for Parallel Kinetic Assays and Differential Sensing. Anal. Chem. 2009, 81, 2854–2859. [Google Scholar] [CrossRef] [PubMed]
- Pang, L.; Hwang, G.M.; Slutsky, B.; Fainman, Y. Spectral Sensitivity of Two-Dimensional Nanohole Array Surface Plasmon Polariton Resonance Sensor. Appl. Phys. Lett. 2007, 91, 123112. [Google Scholar] [CrossRef]
- Stark, P.R.H.; Halleck, A.E.; Larson, D.N. Short Order Nanohole Arrays in Metals for Highly Sensitive Probing of Local Indices of Refraction as the Basis for a Highly Multiplexed Biosensor Technology. Methods 2005, 37, 37–47. [Google Scholar] [CrossRef] [PubMed]
- Rindzevicius, T.; Alaverdyan, Y.; Käll, M.; Murray, W.A.; Barnes, W.L. Long-Range Refractive Index Sensing Using Plasmonic Nanostructures. J. Phys. Chem. C 2007, 111, 11806–11810. [Google Scholar] [CrossRef]
- Correia-Ledo, D.; Gibson, K.F.; Dhawan, A.; Couture, M.; Vo-Dinh, T.; Graham, D.; Masson, J.F. Assessing the Location of Surface Plasmons Over Nanotriangle and Nanohole Arrays of Different Size and Periodicity. J. Phys. Chem. C 2012, 116, 6884–6892. [Google Scholar] [CrossRef] [PubMed]
- Gibson, K.F.; Correia-Ledo, D.; Couture, M.; Grahama, D.; Masson, J.-F. Correlated AFM and SERS Imaging of the Transition from Nanotriangle to Nanohole Arrays. Chem. Commun. 2011, 47, 3404–3406. [Google Scholar] [CrossRef] [PubMed]
- Murray-Méthot, M.P.; Mathieu Ratel, M.; Masson, J.-F. Optical Properties of Au, Ag, and Bimetallic Au on Ag Nanohole Arrays. J. Phys. Chem. C 2010, 114, 8268–8275. [Google Scholar] [CrossRef]
- Murray-Methot, M.-P.; Menegazzo, N.; Masson, J.-F. Analytical and Physical Optimization of Nanohole-Array Sensors Prepared by Modified Nanosphere Lithography. Analyst 2008, 133, 1714–1721. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, J.C.; Mitchell, J.C.; Lin, L.; Sedoglavich, N.; Blaikie, R.J. Gold Nanohole Array Substrates as Immunobiosensors. Anal. Chem. 2008, 80, 2244–2249. [Google Scholar] [CrossRef]
- Zhu, X.; Cao, N.; Thibeault, B.J.; Pinsky, B.; Yanik, A.A. Mechanisms of Fano-Resonant Biosensing: Mechanical Loading of Plasmonic Oscillators. Opt. Commun. 2020, 469, 125780. [Google Scholar] [CrossRef]
- Schwind, M.; Kasemo, B.; Zorić, I. Localized and Propagating Plasmons in Metal Films with Nanoholes. Nano Lett. 2013, 13, 1743–1750. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, T.M.; Frederiksen, M.; Bochenkov, V.; Sutherland, D.S. Exploring Plasmonic Coupling in Hole-Cap Arrays. Beilstein J. Nanotechnol. 2015, 6, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bochenkov, V.E.; Frederiksen, M.; Sutherland, D.S. Enhanced Refractive Index Sensitivity of Elevated Shortrange Ordered Nanohole Arrays in Optically thin Plasmonic Au Films. Opt. Express 2013, 21, 14763–14770. [Google Scholar] [CrossRef] [PubMed]
- Junesch, J.; Emilsson, G.; Xiong, K.; Kumar, S.; Sannomiya, T.; Pace, H.; Vörös, J.; Oh, S.H.; Bally, M.; Dahlin, A.B. Location-Specific Nanoplasmonic Sensing of Biomolecular Binding to Lipid Membranes with Negative Curvature. Nanoscale 2015, 7, 15080–15085. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, S.G.; Martín-Moreno, L.; Nikitin, A.Y.; Kats, A.V.; Spevak, I.S.; García-Vidal, F.J. Extraordinary Optical Transmission Through Hole Arrays in Optically Thin Metal Films. Opt. Lett. 2009, 34, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Braun, J.; Gompf, B.; Kobiela, G.; Dressel, M. How Holes Can Obscure the View: Suppressed Transmission through an Ultrathin Metal Film by a Subwavelength Hole Array. Phys. Rev. Lett. 2009, 103, 203901. [Google Scholar] [CrossRef] [PubMed]
- Spevak, I.S.; Nikitin, A.Y.; Bezuglyi, E.V.; Levchenko, A.; Kats, A.V. Resonantly Suppressed Transmission and Anomalously Enhanced Light Absorption in Periodically Modulated Ultrathin Metal Films. Phys. Rev. B 2009, 79, 161406. [Google Scholar] [CrossRef]
- Yoon, J.W.; Jung, M.J.; Song, S.H.; Magnusson, R. Analytic Theory of the Resonance Properties of Metallic Nanoslit Arrays. IEEE J. Quantum Electron. 2012, 48, 852–861. [Google Scholar] [CrossRef]
- Yoon, J.W.; Magnusson, R. Fano Resonance Formula for Lossy Two-Port Systems. Opt. Express 2013, 21, 17751–17759. [Google Scholar] [CrossRef]
- Liu, M.; Song, Y.; Zhang, Y.; Wang, X.; Jin, C. Mode Evolution and Transmission Suppression in a Perforated Ultrathin Metallic Film with a Triangular Array of Holes. Plasmonics 2012, 7, 397–410. [Google Scholar] [CrossRef]
- Valsecchi, C.; Gomez Armas, L.E.; Weber de Menezes, J. Large Area Nanohole Arrays for Sensing Fabricated by Interference Lithography. Sensors 2019, 19, 2182. [Google Scholar] [CrossRef]
- Larson, S.; Carlson, D.; Ai, B.; Zhao, Y. The Extraordinary Optical Transmission and Sensing Properties of Ag/Ti Composite Nanohole Arrays. Phys. Chem. Chem. Phys. 2019, 21, 3771–3780. [Google Scholar] [CrossRef]
- Martin-Moreno, L.; Garcia-Vidal, F.J.; Lezec, H.J.; Pellerin, K.M.; Thio, T.; Pendry, J.B.; Ebbesen, T.W. Theory of Extraordinary Optical Transmission through Subwavelength Hole Arrays. Phys. Rev. Lett. 2001, 86, 1114–1117. [Google Scholar] [CrossRef] [PubMed]
- Cesaria, M.; Colombelli, A.; Lospinoso, D.; Taurino, A.; Melissano, E.; Rella, R.; Manera, M.G. Long-and Short-Range Ordered Gold Nanoholes as Large-Area Optical Transducers in Sensing Applications. Chemosensors 2019, 7, 13. [Google Scholar] [CrossRef]
- Colombelli, A.; Lospinoso, D.; Rella, R.; Manera, M.G. Shape Modulation of Plasmonic Nanostructures by Unconventional Lithographic Technique. Nanomaterials 2022, 12, 547. [Google Scholar] [CrossRef]
- Decher, G.; Hong, J.-D.; Schmitt, J. Buildup of Ultrathin Multilayer Films by a Self-Assembly Process: III. Consecutively Alternating Adsorption of Anionic and Cationic Polyelectrolytes on Charged Surfaces. Thin Solid Films 1992, 210–211, 831–835. [Google Scholar] [CrossRef]
- Kedem, O.; Tesler, A.B.; Vaskevich, A.; Rubinstein, I. Sensitivity and Optimization of Localized Surface Plasmon Resonance Transducers. ACS Nano 2011, 5, 748–760. [Google Scholar] [CrossRef]
- Gandra, N.; Portz, C.; Tian, L.; Tang, R.; Xu, B.; Achilefu, S.; Singamaneni, S. Probing Distance-Dependent Plasmon-Enhanced Near-Infrared Fluorescence Using Polyelectrolyte Multilayers as Dielectric Spacers. Angew. Chem. Int. Ed. 2014, 53, 866–870. [Google Scholar] [CrossRef]
- Larson, S.; Zhao, Y. Localized Surface Plasmonic Resonance and Sensing Properties of Ag–MgF2 Composite Nanotriangles. J. Phys. Chem. C 2018, 122, 7374–7381. [Google Scholar] [CrossRef]
- Couture, M.; Liang, Y.; Poirier Richard, H.-P.; Faid, R.; Peng, W.; Masson, J.-F. Tuning the 3D Plasmon Field of Nanohole Arrays. Nanoscale 2013, 5, 12399. [Google Scholar] [CrossRef]
- Lospinoso, D.; Colombelli, A.; Lomascolo, M.; Rella, R.; Manera, M.G. Self-Assembled Metal Nanohole Arrays with Tunable Plasmonic Properties for SERS Single-Molecule Detection. Nanomaterials 2022, 12, 380. [Google Scholar] [CrossRef] [PubMed]
- Nishida, M.; Hatakenaka, N.; Kadoya, Y. Multipole Surface Plasmons in Metallic Nanohole Arrays. Phys. Rev. B 2005, 91, 235406. [Google Scholar] [CrossRef]
- Jonsson, M.P.; Dahlin, A.B. Nanoplasmonic Biosensing with Focus on Short-range Ordered Nanoholes in Thin Metal Films. Biointerphases 2008, 3, FD30–FD40. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, S.G.; de León-Pérez, F.; Martín-Moreno, L. Extraordinary Optical Transmission: Fundamentals and Applications. Proc. IEEE 2016, 104, 2288–2306. [Google Scholar] [CrossRef]
- Malinsky, M.D.; Kelly, K.L.; Schatz, G.C.; Van Duyne, R.P. Chain Length Dependence and Sensing Capabilities of the Localized Surface Plasmon Resonance of Silver Nanoparticles Chemically Modified with Alkanethiol Self-Assembled Monolayers. J. Am. Chem. Soc. 2001, 123, 1471–1482. [Google Scholar] [CrossRef]
- Jung, L.S.; Campbell, C.T.; Chinowsky, T.M.; Mar, M.N.; Yee, S.S. Quantitative Interpretation of the Response of Surface Plasmon Resonance Sensors to Adsorbed Films. Langmuir 1998, 14, 5636–5648. [Google Scholar] [CrossRef]
- Haes, A.J.; Van Duyne, R.P. A Nanoscale Optical Biosensor: Sensitivity and Selectivity of an Approach Based on the Localized Surface Plasmon Resonance Spectroscopy of Triangular Silver Nanoparticles. J. Am. Chem. Soc. 2002, 124, 10596–10604. [Google Scholar] [CrossRef]
- Kang, E.S.H.; Ekinge, H.; Jonsson, M.P. Plasmonic Fanoholes: On the Gradual Transition from Suppressed to Enhanced Optical Transmission through Nanohole Arrays in Metal Films of Increasing Film Thickness. Opt. Mater. Express 2019, 9, 1404–1415. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, F.; Gao, R.; Jao, C.-Y.; Ma, C.; Li, J.; Li, X.; Guan, B.-O.; Cetin, A.E.; Chen, K. Rayleigh Anomaly-Enabled Mode Hybridization in Gold Nanohole Arrays by Scalable Colloidal Lithography for Highly-Sensitive Biosensing. Nanophotonics 2022, 11, 507–517. [Google Scholar] [CrossRef]
- Haes, A.J.; Zou, S.; Schatz, G.C.; Van Duyne, R.P. A Nanoscale Optical Biosensor: The Long Range Distance Dependence of the Localized Surface Plasmon Resonance of Noble Metal Nanoparticles. J. Phys. Chem. B 2004, 108, 109–116. [Google Scholar] [CrossRef]
- Michieli, N.; Kalinic, B.; Scian, C.; Cesca, T.; Mattei, G. Optimal Geometric Parameters of Ordered Arrays of Nanoprisms for Enhanced Sensitivity in Localized Plasmon Based Sensors. Biosens. Bioelectron. 2015, 65, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Vala, M.; Ertsgaard, C.T.; Wittenberg, N.J.; Oh, S.H. Plasmonic sensing on symmetric nanohole arrays supporting high-Q hybrid modes and reflection geometry. ACS Sens. 2019, 4, 3265–3274. [Google Scholar] [CrossRef] [PubMed]
- Tobing, L.Y.; Soehartono, A.M.; Mueller, A.D.; Yong, K.T.; Fan, W.; Zhang, D.H. Hybridized surface lattice modes in intercalated 3-disk plasmonic crystals for high figure-of-merit plasmonic sensing. Nanoscale 2021, 13, 4092–4102. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.K.; Suchitta, A.; Dhawan, A. Nanostructured plasmonic chips employing nanopillar and nanoring hole arrays for enhanced sensitivity of SPR-based biosensing. RSC Adv. 2022, 12, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Genet, C.; van Exter, M.P.; Woerdman, J.P. Fano-Type Interpretation of Red Shifts and Red Tails in Hole Array Transmission Spectra. Opt. Commun. 2003, 225, 331–336. [Google Scholar] [CrossRef]
- Lindquist, N.C.; Turner, M.A.; Heppner, B.P. Template Fabricated Plasmonic Nanoholes on Analyte-Sensitive Substrates for Real-Time Vapor Sensing. RSC Adv. 2014, 4, 15115. [Google Scholar] [CrossRef]
- Kee, J.S.; Lim, S.Y.; Perera, A.P.; Zhang, Y.; Park, M.K. Plasmonic Nanohole Arrays for Monitoring Growth of Bacteria and Antibiotic Susceptibility Test. Sens. Actuators B 2013, 182, 576–583. [Google Scholar] [CrossRef]
- Cruz, J.G.; Nair, S.; Manjarrez-Hernandez, A.; Gavilanes-Parra, S.; Ascanio, G.; Escobedo, C. Cost-Effective Flow-through Nanohole Array-based Biosensing Platform for the Label-Free Detection of Uropathogenic E. coli in Real Time. Biosens. Bioelectron. 2018, 106, 105–110. [Google Scholar] [CrossRef]
- Jackman, J.A.; Linardy, E.; Yoo, D.; Seo, J.; Ng, W.B.; Klemme, D.J.; Wittenberg, N.J.; Oh, S.-H.; Cho, N.-J. Plasmonic Nanohole Sensor for Capturing Single Virus-Like Particles toward Virucidal Drug Evaluation. Small 2016, 12, 1159–1166. [Google Scholar] [CrossRef]
- Belushkin, A.; Yesilkoy, F.; Altug, H. Nanoparticle-Enhanced Plasmonic Biosensor for Digital Biomarker Detection in a Microarray. ACS Nano 2018, 12, 4453–4461. [Google Scholar] [CrossRef]
- Carcelen, M.; Vidal, V.; Franco, A.; Gomez, M.; Moreno, F.; Fernandez-Luna, J.L. Plasmonic Biosensing for Label-Free Detection of Two Hallmarks of Cancer Cells: Cell-Matrix Interaction and Cell Division. Biosensors 2022, 12, 674. [Google Scholar] [CrossRef] [PubMed]
- So, T.; Lee, D.; Lee, C.; Moon, G.; Eun Ha, G.; Lee, H.; Kwak, H.; Cheong, E.; Kim, D. Superlocalized Three-Dimensional Live Imaging of Mitochondrial Dynamics in Neurons Using Plasmonic Nanohole Arrays. ACS Nano 2019, 13, 3063–3074. [Google Scholar]
- Li, X.; Soler, M.; Szydzik, C.; Khoshmanesh, K.; Schmidt, J.; Coukos, G.; Mitchell, A.; Altug, H. Label-Free Optofluidic Nanobiosensor Enables Real-Time Analysis of Single-Cell Cytokine Secretion. Small 2018, 14, 1800698. [Google Scholar] [CrossRef]
- Li, X.; Soler, M.; Özdemir, C.I.; Belushkin, A.; Yesilköy, F.; Altug, H. Plasmonic Nanohole Array Biosensor for Label-Free and Real-Time Analysis of Live Cell Secretion. Lab Chip 2017, 17, 2208–2217. [Google Scholar] [CrossRef] [PubMed]
- Soler, M.; Belushkin, A.; Cavallini, A.; Kebbi-Beghdadi, C.; Greub, G.; Altug, H. Multiplexed Nanoplasmonic Biosensor for One-Step Simultaneous Detection of Chlamydia Trachomatis and Neisseria Gonorrhoeae in Urine. Biosens. Bioelectron. 2017, 94, 560–567. [Google Scholar] [CrossRef] [PubMed]
- del Castillo, G.F.-D.; Emilsson, G.; Dahlin, A. Quantitative Analysis of Thickness and pH Actuation of Weak Polyelectrolyte Brushes. J. Phys. Chem. C 2018, 122, 27516–27527. [Google Scholar] [CrossRef]
- Luo, X.; Xing, Y.; Galvan, D.D.; Zheng, E.; Wu, P.; Cai, C.; Yu, Q. Plasmonic Gold Nanohole Array for Surface-Enhanced Raman Scattering Detection of DNA Methylation. ACS Sens. 2019, 4, 1534–1542. [Google Scholar] [CrossRef]
- Lenyk, B.; Figueroa-Miranda, G.; Pavlushko, I.; Lo, Y.; Tanner, J.A.; Offenhäusser, A.; Mayer, D. Dual-Transducer Malaria Aptasensor Combining Electrochemical Impedance and Surface Plasmon Polariton Detection on Gold Nanohole Arrays. ChemElectroChem 2020, 7, 4594–4600. [Google Scholar] [CrossRef]
- Saboktakin, M.; Ye, X.; Chettiar, U.K.; Engheta, N.; Murray, C.B.; Kagan, C.R. Plasmonic Enhancement of Nanophosphor Upconversion Luminescence in Au Nanohole Arrays. ACS Nano 2013, 7, 7186–7192. [Google Scholar] [CrossRef]

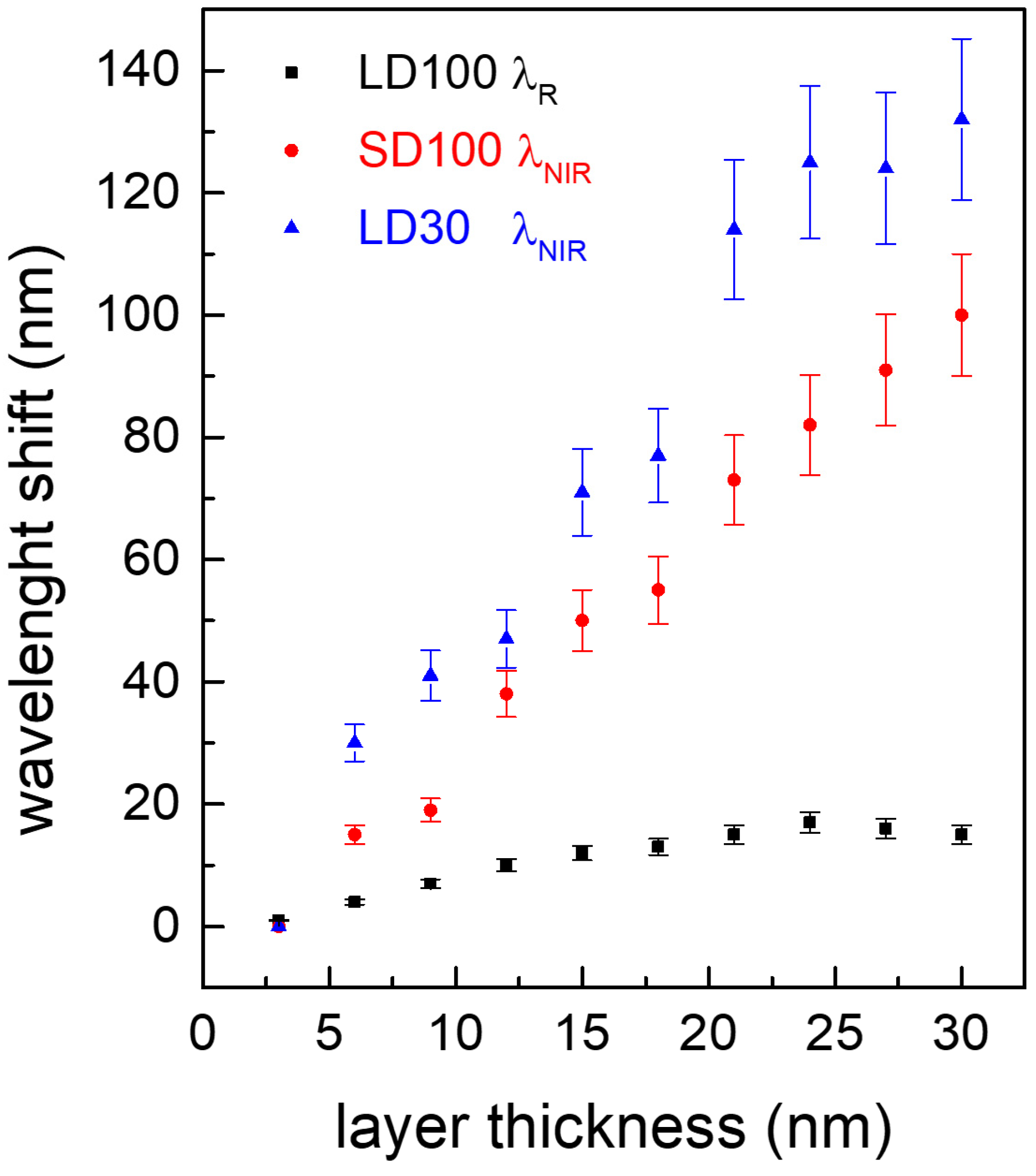
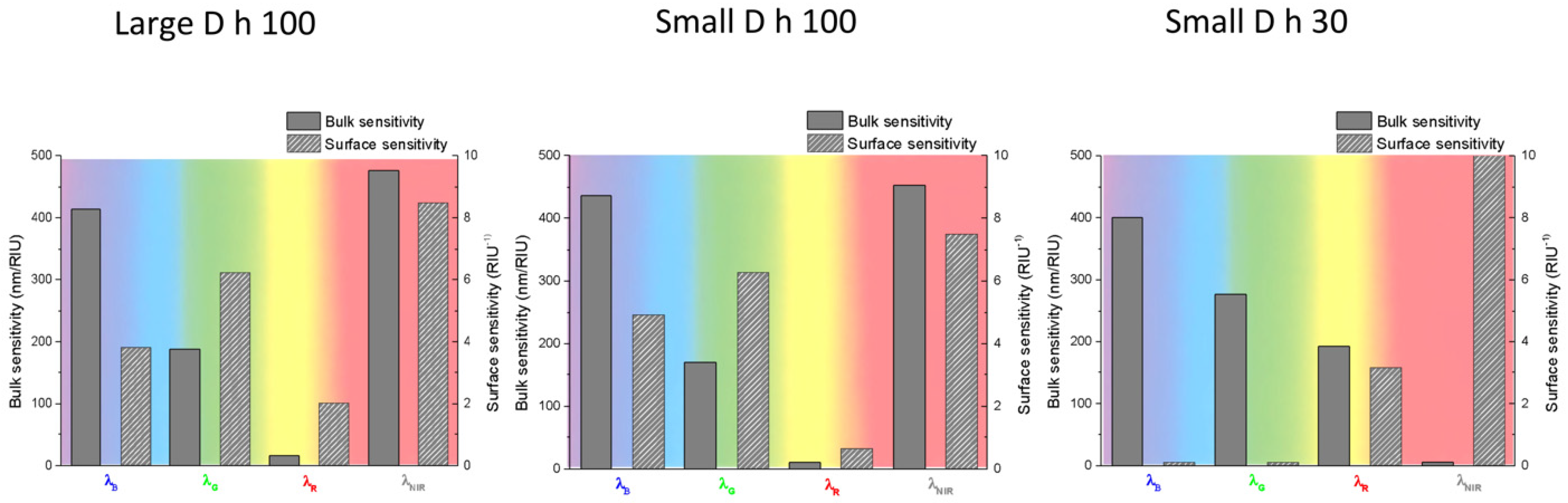
| LARGE D h 100 | λB | λG | λR | λNIR |
| Bulk sens. (nm RIU−1) | 410 ± 60 | 190 ± 30 | 16 ± 3 | 480 ± 70 |
| Surf. sens. (RIU−1) | 3.81 ± 0.17 | 6.25 ± 0.24 | 2.03 ±0.01 | 8.48 ± 0.47 |
| SMALL D h 100 | λB | λG | λR | λNIR |
| Bulk sens. (nm RIU−1) | 440 ± 65 | 170 ± 25 | - | 450 ± 70 |
| Surf. sens. (RIU−1) | 4.92 ± 0.24 | 6.27 ± 0.40 | 0.64 ± 0.52 | 7.50 ± 0.24 |
| SMALL D h 30 | λB | λG | λR | λNIR |
| Bulk sens. (nm RIU−1) | 280 ± 40 * | 240 ± 40 * | 190 ± 30 | - |
| 420 ± 60 ** | - ** | |||
| Surf. sens. (RIU−1) | - | 1.36 ± 0.11 | 3.15 ± 0.19 | 10.0 ± 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lospinoso, D.; Colombelli, A.; Rella, R.; Manera, M.G. Rational Design and Optimization of Plasmonic Nanohole Arrays for Sensing Applications. Chemosensors 2024, 12, 157. https://doi.org/10.3390/chemosensors12080157
Lospinoso D, Colombelli A, Rella R, Manera MG. Rational Design and Optimization of Plasmonic Nanohole Arrays for Sensing Applications. Chemosensors. 2024; 12(8):157. https://doi.org/10.3390/chemosensors12080157
Chicago/Turabian StyleLospinoso, Daniela, Adriano Colombelli, Roberto Rella, and Maria Grazia Manera. 2024. "Rational Design and Optimization of Plasmonic Nanohole Arrays for Sensing Applications" Chemosensors 12, no. 8: 157. https://doi.org/10.3390/chemosensors12080157
APA StyleLospinoso, D., Colombelli, A., Rella, R., & Manera, M. G. (2024). Rational Design and Optimization of Plasmonic Nanohole Arrays for Sensing Applications. Chemosensors, 12(8), 157. https://doi.org/10.3390/chemosensors12080157







