Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy
Abstract
:1. Introduction
2. Experiment
2.1. Sample Preparation
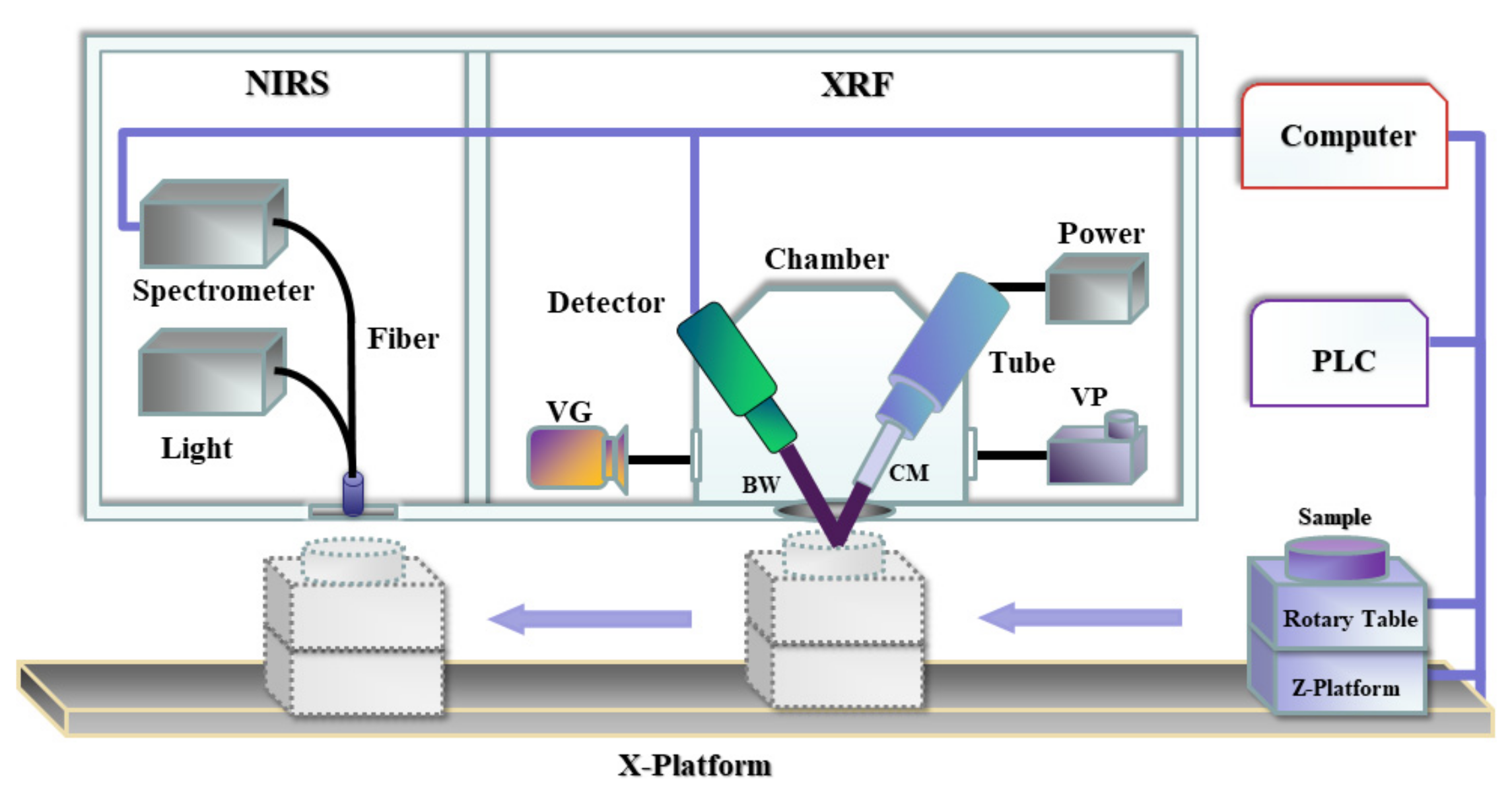
2.2. Experimental Setup and Measurement
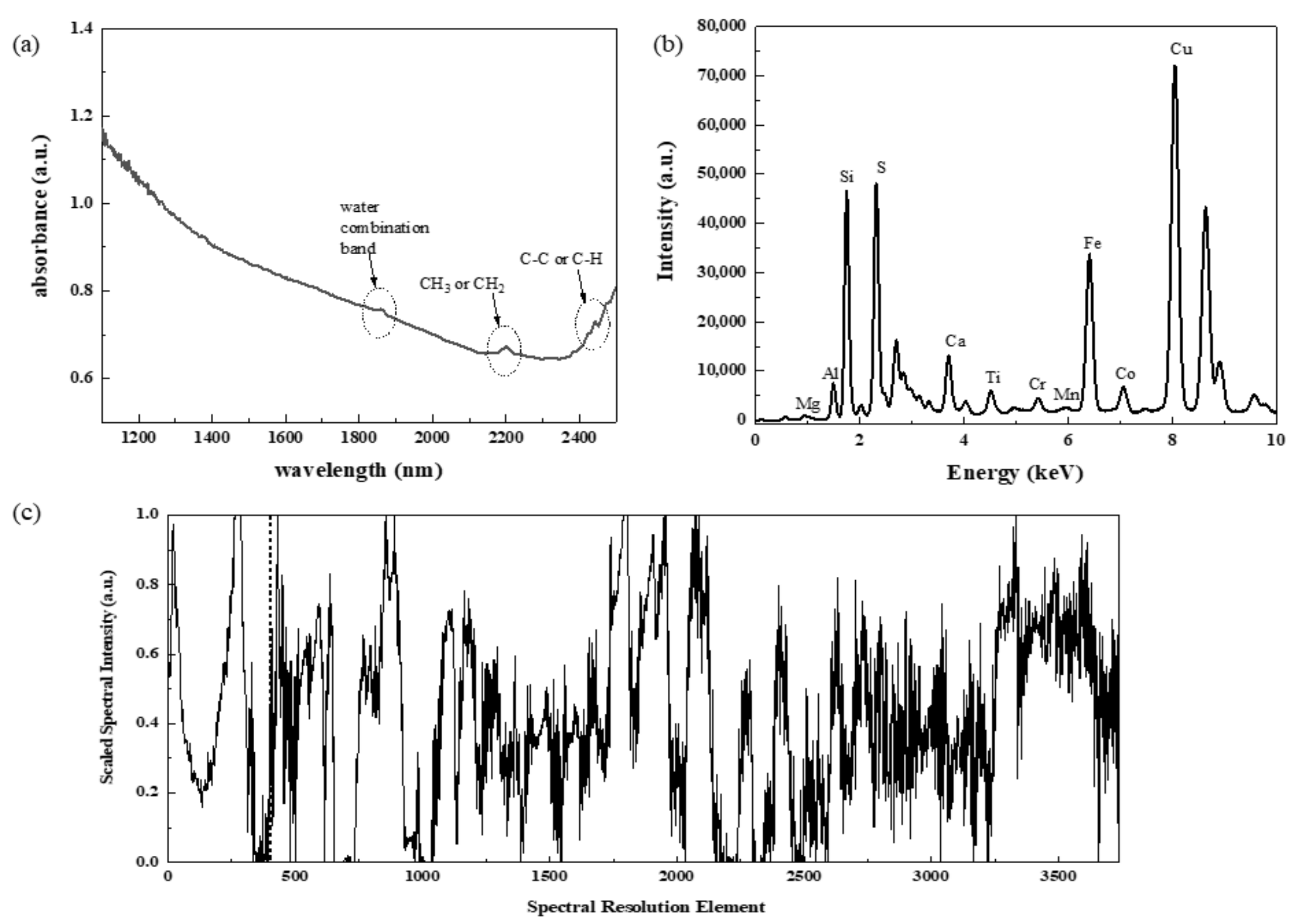
2.3. Spectral Pre-Processing Methods
2.4. Prediction Model
2.5. Evaluation Indexes
3. Results and Discussion
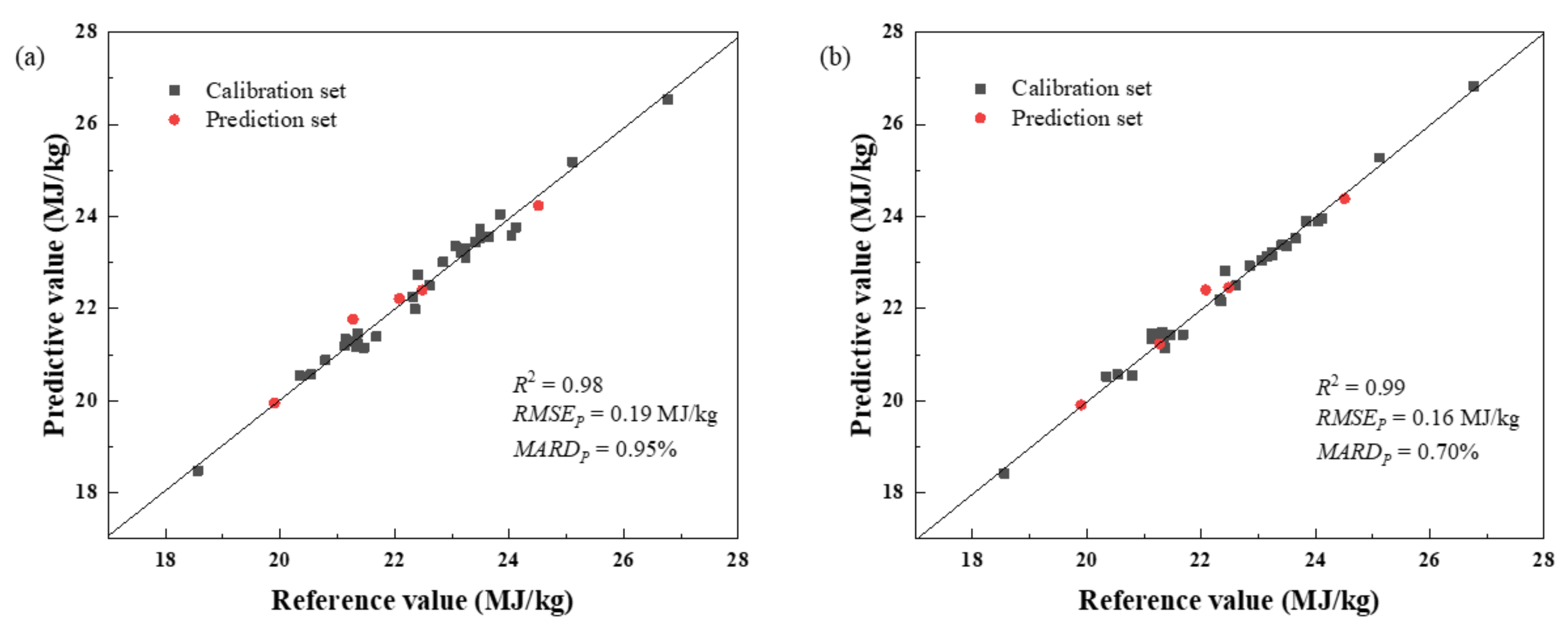
3.1. Analysis of Coal Calorific Value via Low-Level Fusion Model
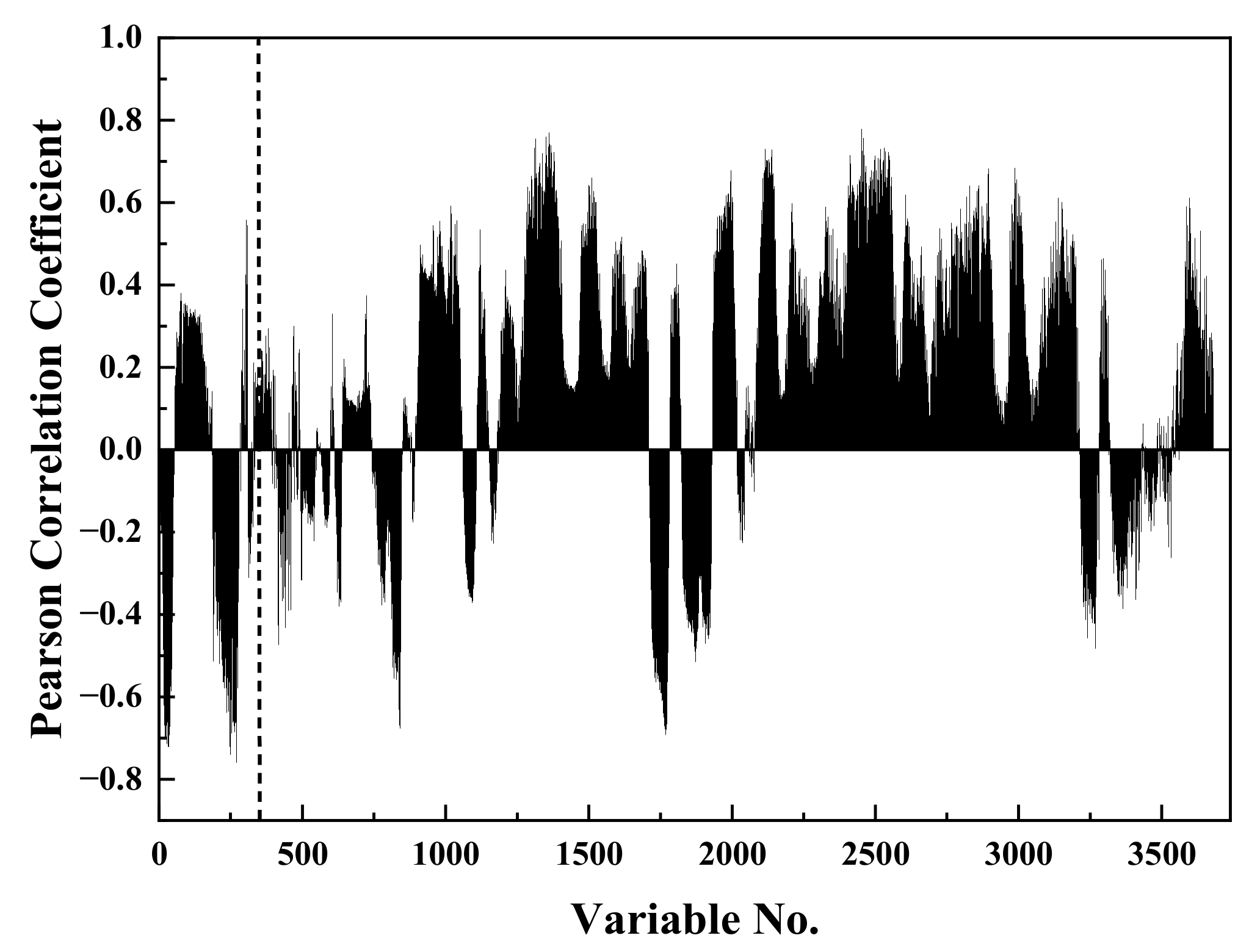
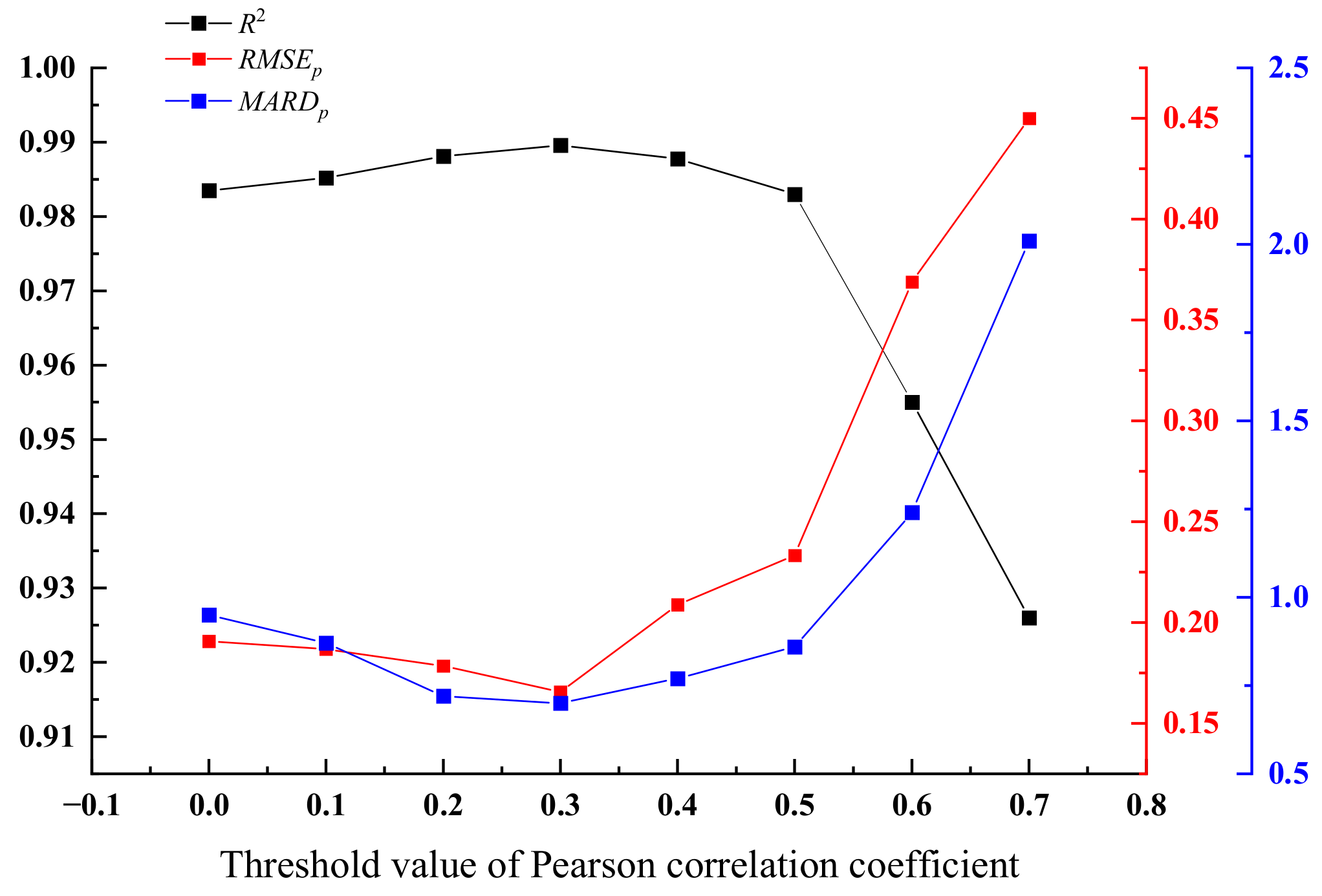
3.2. Analysis of Coal Calorific Value via Mid-Level Fusion Model
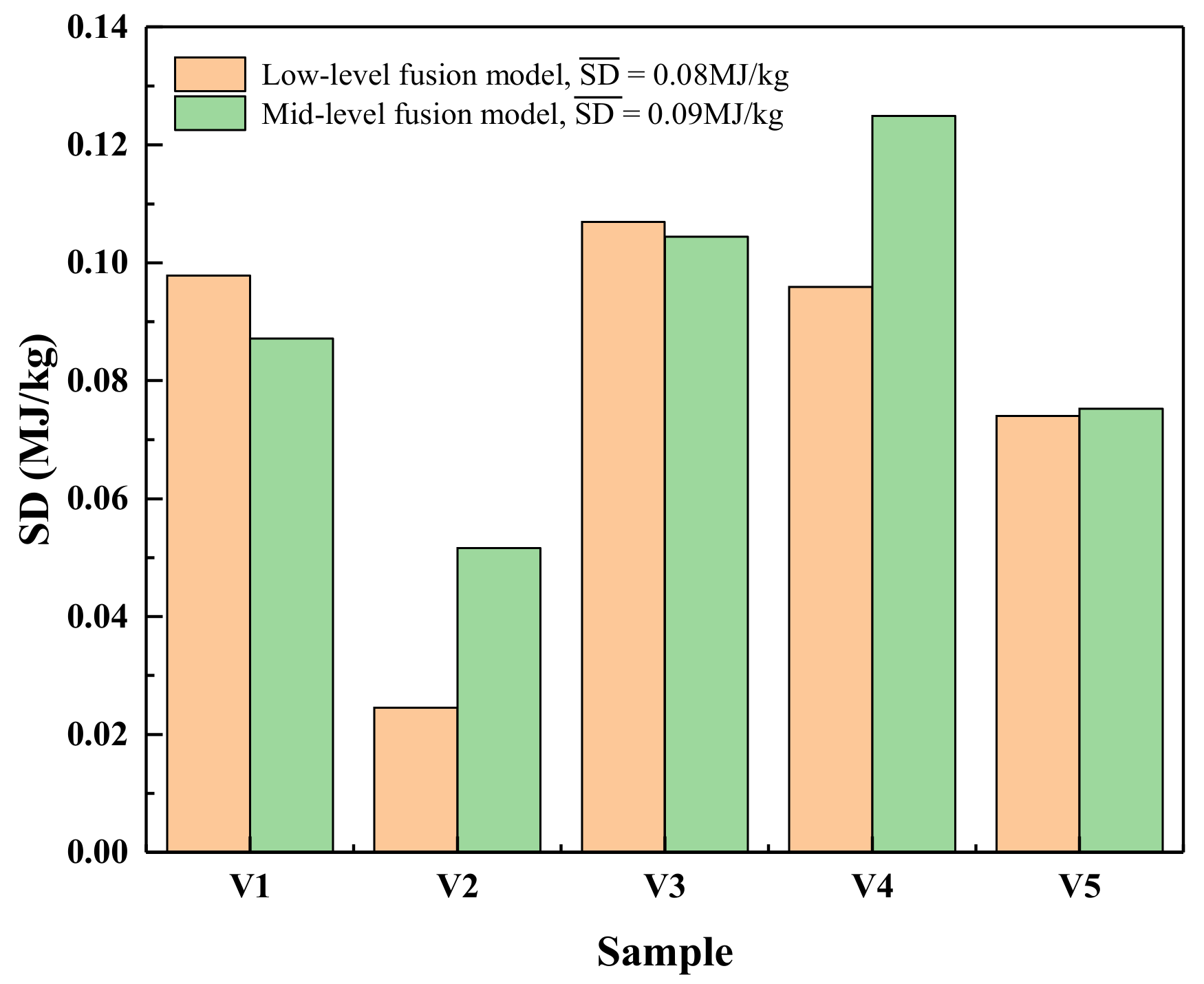
3.3. Repeatability Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Q.; Zhang, L.; Zou, S.; Zhang, J. Intertemporal optimization of the coal production capacity in China in terms of uncertain demand, economy, environment, and energy security. Energy Policy 2020, 139, 111360. [Google Scholar] [CrossRef]
- Liu, K.; He, C.; Zhu, C.; Chen, J.; Zhan, K.; Li, X. A review of laser-induced breakdown spectroscopy for coal analysis. TrAC Trends Anal. Chem. 2021, 143, 116357. [Google Scholar] [CrossRef]
- Mason, D.M.; Gandhi, K.N. Formulas for calculating the calorific value of coal and coal chars: Development, tests, and uses. Fuel Process. Technol. 1983, 7, 11–22. [Google Scholar] [CrossRef]
- Sheta, S.; Afgan, M.S.; Hou, Z.; Yao, S.-C.; Zhang, L.; Li, Z.; Wang, Z. Coal analysis by laser-induced breakdown spectroscopy: A tutorial review. J. Anal. At. Spectrom. 2019, 34, 1047–1082. [Google Scholar] [CrossRef]
- Ikävalko, E.; Laitinen, T.; Revitzer, H. Optimised method of coal digestion for trace metal determination by atomic absorption spectroscopy. Fresenius J. Anal. Chem. 1999, 363, 314–316. [Google Scholar] [CrossRef]
- Baysal, A.; Akman, S. A practical method for the determination of sulphur in coal samples by high-resolution continuum source flame atomic absorption spectrometry. Talanta 2011, 85, 2662–2665. [Google Scholar] [CrossRef]
- Caroli, S.; Mazzeo, A.F.; Laurenzi, A.; Senofonte, O.; Violante, N. Determination of sulphur in coal products by inductively coupled plasma atomic emission spectrometry. J. Anal. At. Spectrom. 1988, 3, 245–248. [Google Scholar] [CrossRef]
- Iwashita, A.; Nakajima, T.; Takanashi, H.; Ohki, A.; Fujita, Y.; Yamashita, T. Effect of pretreatment conditions on the determination of major and trace elements in coal fly ash using ICP-AES. Fuel 2006, 85, 257–263. [Google Scholar] [CrossRef]
- Jia, W.-B.; Hei, D.-Q.; Xu, A.-G.; Chen, X.-W.; Li, A.-M. Influence of sample weight in coal composition online analysis by PGNAA. At. Energy Sci. Technol. 2011, 45, 1011. [Google Scholar]
- CLim, S.; Abernethy, D.A. On-line coal analysis using fast neutron-induced gamma-rays. Appl. Radiat. Isot. 2005, 63, 697–704. [Google Scholar]
- Yao, S.; Mo, J.; Zhao, J.; Li, Y.; Zhang, X.; Lu, W.; Lu, Z. Development of a Rapid Coal Analyzer Using Laser-Induced Breakdown Spectroscopy (LIBS). Appl. Spectrosc. 2018, 72, 1225–1233. [Google Scholar] [CrossRef]
- Li, W.; Dong, M.; Lu, S.; Li, S.; Wei, L.; Huang, J.; Lu, J. Improved measurement of the calorific value of pulverized coal particle flow by laser-induced breakdown spectroscopy (LIBS). Anal. Methods 2019, 11, 4471–4480. [Google Scholar] [CrossRef]
- Haider, A.F.M.Y.; Rony, M.A.; Lubna, R.S.; Abedin, K.M. Detection of multiple elements in coal samples from Bangladesh by laser-induced breakdown spectroscopy. Opt. Laser Technol. 2011, 43, 1405–1410. [Google Scholar] [CrossRef]
- Yao, S.; Qin, H.; Wang, Q.; Lu, Z.; Yao, X.; Yu, Z.; Chen, X.; Zhang, L.; Lu, J. Optimizing analysis of coal property using laser-induced breakdown and near-infrared reflectance spectroscopies. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 239, 118492. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.-T.; Gu, W.-L.; Hou, Z.-Y.; Muhammed, S.A.; Li, T.-Q.; Wang, Y.; Wang, Z. Mechanism of signal uncertainty generation for laser-induced breakdown spectroscopy. Front. Phys. 2020, 16, 22502. [Google Scholar] [CrossRef]
- Lestander, T.A.; Samuelsson, R. Prediction of Resin and Fatty Acid Content of Biorefinery Feedstock by On-line Near-Infrared (NIR) Spectroscopy. Energy Fuels 2010, 24, 5148–5152. [Google Scholar] [CrossRef]
- Tripathi, M.M.; Hassan, E.B.M.; Yueh, F.-Y.; Singh, J.P.; Steele, P.H.; Ingram, L.L. Reflection–absorption-based near infrared spectroscopy for predicting water content in bio-oil. Sens. Actuators B Chem. 2009, 136, 20–25. [Google Scholar] [CrossRef]
- Bona, M.; Andrés, J. Coal analysis by diffuse reflectance near-infrared spectroscopy: Hierarchical cluster and linear discriminant analysis. Talanta 2007, 72, 1423–1431. [Google Scholar] [CrossRef]
- Andrés, J.; Bona, M. Analysis of coal by diffuse reflectance near-infrared spectroscopy. Anal. Chim. Acta 2005, 535, 123–132. [Google Scholar] [CrossRef]
- Andrés, J.; Bona, M. ASTM clustering for improving coal analysis by near-infrared spectroscopy. Talanta 2006, 70, 711–719. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Wei, G.; Hu, R.; Luo, Z.; Li, G. Improved PLS regression based on SVM classification for rapid analysis of coal properties by near-infrared reflectance spectroscopy. Sens. Actuators B Chem. 2014, 193, 723–729. [Google Scholar] [CrossRef]
- Wang, S.-H.; Zhao, Y.; Hu, R.; Zhang, Y.-Y.; Han, X.-H. Analysis of Near-Infrared Spectra of Coal Using Deep Synergy Adaptive Moving Window Partial Least Square Method Based on Genetic Algorithm. Chin. J. Anal. Chem. 2019, 47, e19034–e19044. [Google Scholar] [CrossRef]
- Begum, N.; Chakravarty, D.; Das, B.S. Estimation of Gross Calorific Value of Bituminous Coal using various Coal Properties and Reflectance Spectra. Int. J. Coal Prep. Util. 2019, 42, 979–985. [Google Scholar] [CrossRef]
- Shirazi, A.R.; Börtin, O.; Eklund, L.; Lindqvist, O. The impact of mineral matter in coal on its combustion, and a new approach to the determination of the calorific value of coal. Fuel 1995, 74, 247–251. [Google Scholar] [CrossRef]
- West, M.; Ellis, A.T.; Potts, P.J.; Streli, C.; Vanhoof, C.; Wobrauschek, P. 2015 Atomic Spectrometry Update—A review of advances in X-ray fluorescence spectrometry and their applications. J. Anal. At. Spectrom. 2015, 30, 1839–1889. [Google Scholar] [CrossRef]
- Ward, C.R.; Kelloway, S.J.; Vohra, J.; French, D.; Cohen, D.R.; Marjo, C.E.; Wainwright, I.E. In-situ inorganic analysis of coal seams using a hand-held field-portable XRF Analyser. Int. J. Coal Geol. 2018, 191, 172–188. [Google Scholar] [CrossRef]
- Vincze, L.; Somogyi, A.; Osán, J.; Vekemans, B.; Török, S.; Janssens, K.; Adams, F. Quantitative Trace Element Analysis of Individual Fly Ash Particles by Means of X-ray Microfluorescence. Anal. Chem. 2002, 74, 1128–1135. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; XinLei, Z.; WenBao, J.; Qing, S.; YongSheng, L.; DaQian, H.; Da, C. Online X-ray Fluorescence (XRF) Analysis of Heavy Metals in Pulverized Coal on a Conveyor Belt. Appl. Spectrosc. 2016, 70, 272–278. [Google Scholar] [CrossRef] [PubMed]
- Redoglio, D.; Golinelli, E.; Musazzi, S.; Perini, U.; Barberis, F. A large depth of field LIBS measuring system for elemental analysis of moving samples of raw coal. Spectrochim. Acta Part B At. Spectrosc. 2016, 116, 46–50. [Google Scholar] [CrossRef]
- Borràs, E.; Ferré, J.; Boqué, R.; Mestres, M.; Aceña, L.; Busto, O. Data fusion methodologies for food and beverage authentication and quality assessment—A review. Anal. Chim. Acta 2015, 891, 1–14. [Google Scholar] [CrossRef]
- Moros, J.; Javier Laserna, J. Unveiling the identity of distant targets through advanced Raman-laser-induced breakdown spectroscopy data fusion strategies. Talanta 2015, 134, 627–639. [Google Scholar] [CrossRef] [PubMed]
| No. | Calorific Value (MJ/kg) | No. | Calorific Value (MJ/kg) | No. | Calorific Value (MJ/kg) |
|---|---|---|---|---|---|
| C1 | 24.11 ± 0.03 | C2 | 23.15 ± 0.05 | C3 | 21.14 ± 0.05 |
| C4 | 23.65 ± 0.02 | C5 | 25.11 ± 0.05 | C6 | 23.41 ± 0.04 |
| C7 | 21.32 ± 0.07 | C8 | 21.46 ± 0.04 | C9 | 23.06 ± 0.01 |
| C10 | 21.13 ± 0.04 | C11 | 20.79 ± 0.06 | C12 | 20.34 ± 0.08 |
| C13 | 20.54 ± 0.05 | C14 | 23.84 ± 0.09 | C15 | 22.41 ± 0.04 |
| C16 | 21.31 ± 0.04 | C17 | 21.35 ± 0.07 | C18 | 18.56 ± 0.07 |
| C19 | 23.24 ± 0.08 | C20 | 23.49 ± 0.08 | C21 | 23.23 ± 0.03 |
| C22 | 21.68 ± 0.03 | C23 | 22.32 ± 0.01 | C24 | 23.49 ± 0.01 |
| C25 | 21.36 ± 0.04 | C26 | 22.35 ± 0.04 | C27 | 22.85 ± 0.04 |
| C28 | 24.04 ± 0.07 | C29 | 26.77 ± 0.03 | C30 | 22.61 ± 0.09 |
| P1 | 22.48 ± 0.04 | P2 | 24.51 ± 0.02 | P3 | 21.27 ± 0.07 |
| P4 | 22.08 ± 0.06 | P5 | 19.90 ± 0.03 |
| Method | R2 | RMSEP (MJ/kg) | MARDP (%) |
|---|---|---|---|
| NIRS | 0.95 | 0.33 | 1.21 |
| XRF | 0.94 | 0.39 | 1.60 |
| NIRS-XRF | 0.98 | 0.19 | 0.95 |
| t | Number of Variables | Calculation Time (s) | t | Number of Variables | Calculation Time (s) |
|---|---|---|---|---|---|
| 0.0 | 3739 | 0.309 | 0.4 | 1406 | 0.106 |
| 0.1 | 3188 | 0.267 | 0.5 | 763 | 0.074 |
| 0.2 | 2673 | 0.175 | 0.6 | 298 | 0.052 |
| 0.3 | 2302 | 0.151 | 0.7 | 75 | 0.041 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Gao, R.; Zhang, Y.; Wang, S.; Zhang, L.; Yin, W.; Jia, S. Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy. Chemosensors 2023, 11, 363. https://doi.org/10.3390/chemosensors11070363
Li J, Gao R, Zhang Y, Wang S, Zhang L, Yin W, Jia S. Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy. Chemosensors. 2023; 11(7):363. https://doi.org/10.3390/chemosensors11070363
Chicago/Turabian StyleLi, Jiaxuan, Rui Gao, Yan Zhang, Shuqing Wang, Lei Zhang, Wangbao Yin, and Suotang Jia. 2023. "Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy" Chemosensors 11, no. 7: 363. https://doi.org/10.3390/chemosensors11070363
APA StyleLi, J., Gao, R., Zhang, Y., Wang, S., Zhang, L., Yin, W., & Jia, S. (2023). Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy. Chemosensors, 11(7), 363. https://doi.org/10.3390/chemosensors11070363






