Multifunctional Superhydrophobic Platform for Control of Water Microdroplets by Non-Uniform Electrostatic Field

Abstract

At the moment, manipulation of liquid microdroplets is required in various microfluidic and lab-on-a-chip devices, as well as advanced sensors. The platforms used for these purposes should provide the possibility of controlled selective movement and coalescence of droplets, and the manipulation speed should be sufficiently high (more than 10 mm/s). In addition, to facilitate their practical application, such platforms should have a simple planar geometry and low manufacturing cost. We report here a new method for microdroplet manipulation based on the use of non-uniform electrostatic fields. Our platform uses an electrode array embedded in a dielectric planar superhydrophobic substrate (50 × 50 mm). When a voltage is applied to a certain sequence of electrodes, a non-uniform electrostatic field is produced, which acts to attract a droplet on the substrate to the electrodes. This achieves a stepwise movement of the droplet. We realized non-contact, selective and high speed (up to 80 mm/s) movement of the individual droplets along specified trajectories (like a chess game) and their selective coalescence. It allowed us to demonstrate several controllable chemical reactions including an analytical one. In our opinion, this approach has a huge potential for chemical technology applications, especially in advanced sensors.

1. Introduction

Platforms for manipulating liquid microdroplets (PMD) are required in microfluidic systems [1,2,3,4], in particular in laboratories on a chip, as well as advanced sensors and other devices [2,5,6,7]. The implementation of a sequence of controlled biochemical, biological and analytical reactions on such platforms is achieved by controlled selective movement and coalescence of droplets or their groups on the working surface of PMD [8,9]. Moreover, the manipulation speed must be sufficiently high, up to ~100 mm/s, to meet modern requirements for device performance [10,11,12,13]. For ease of use, PMD should, if possible, dispense with external (in relation to the platform) movers for droplets and also have a planar geometry [9]. In addition, it is necessary to ensure the stability of PMD with respect to external influences (impact and vibrations) in order to avoid accidental movement of droplets under their influence. Finally, one of the most important requirements is the low cost of manufacture and operation.

At present, PMDs using the effects of electrowetting on a dielectric (EWOD) are widely used [13,14,15,16,17,18]. They do not use external movers and, depending on the design of the control electrodes, can provide either high-speed movement of droplets along predetermined trajectories or coalescence of selected droplets. However, simultaneously providing both functions for such platforms is not a trivial task [13]. In addition, a complex multi-stage manufacturing procedure leads to a high cost of such PMD.

Another approach to the creation of PMD is the use of various photothermal and pyroelectric effects [12,19,20]. This versatile approach enables movement of droplets along complex trajectories, their coalescing and separation within a single platform. However, the implementation of this approach requires the use of auxiliary equipment to set the droplets in motion (laser, lenses, and other elements external to the PMD). Because of this, the resulting devices can hardly be called planar. It is also important to take into account that the manufacturing process of such platforms is multi-stage and, accordingly, expensive.

Recently, an approach has been demonstrated that uses droplet electrostatic tweezer (DEST) to manipulate droplets [11]. Due to the non-uniform electrostatic field (NEF) created near the metal rod, a droplet moves following the tweezers, repeating their trajectory. This effect makes it possible to set different trajectories of movement of one or several droplets and to coalesce them at a sufficiently high speed. However, as in the previous case, the geometry of the platform is hardly planar, since it involves the use of an external mover—tweezers and drives that control its movement.

In this paper, we report a new approach to the control of liquid microdroplets based on non-uniform electrostatic fields. This field, created near the selected droplet, leads to its polarization. That is, the droplet acquires a pronounced dipole moment. Since the field is non-uniform, the force of its action on the pole of the induced dipole, placed in the point of greater electric field strength, exceeds the counter-directional force of action on the other. As a result, the droplet begins to accelerate in the direction of the field gradient. We emphasize that the possible modulation of the contact angle due to the polarization of the droplet is not the cause of its motion in our case.

Note also in contrast to the mentioned DEST approach [11] that, in our platform, we use an electrode array embedded in a planar dielectric substrate to create a non-uniform field. The electrodes are located at a certain depth below the substrate surface so as to avoid their direct contact with the electrically neutral droplet. When a voltage is applied to any of the electrodes, a non-uniform electrostatic field is created near it, by which the droplet is attracted to the switched-on electrode. Due to this, the movement of the droplet to the selected position is achieved. At the same time, acceptable thresholds of control voltages and a high speed of droplet control are achieved by imparting superhydrophobic properties to the substrate surface. As will be shown below, the proposed approach allows contactless and selective movement of individual droplets of various sizes or their groups along specified trajectories, as well as their selective coalescence, controlled analytical and other chemical reactions. In addition, the stability of the position of droplets and the possibility of controlling their movement when the PMD is tilted will be demonstrated.

2. Methodology

The superhydrophobic platform for control of water micro-droplets (PMD) is fabricated on polytetrafluoroethylene (PTFE) substrate. This material, being a fluoropolymer, has a high degree of chemical inertness, which makes it possible to use PMD for chemical reactions with alkalis and acids without fear of the substrate material affecting the results of chemical analysis. In addition, it is hydrophobic by itself without additional coatings and is easily amenable to laser processing.

The working area used directly for manipulating droplets is located on the upper surface of the substrate. An array of micropillars with multimodal roughness is created on it by laser structuring [21,22,23]. This makes it possible to achieve superhydrophobic properties of working area with a contact angle θ~155° [24,25]. On the reverse side of the substrate, an array of cylindrical copper electrodes (CE) is installed in pre-prepared holes so that a PTFE layer of ~0.3 mm remains between their upper side and the working area. Since PTFE is an excellent insulator, such a gap turns out to be quite enough to prevent electrical breakdown even at a voltage of several kV on CE. On the side face of the substrate, there is a common electrode, isolated from the working area by a glass plate (Figure 1).

The electric field gradients on the working surface of the PMD which we use to manipulate the droplets appear due to a significant difference in the area of the common electrode (25 cm²) and control electrode tip (0.25 mm²). It should be noted that the value of the field gradient does not depend on the polarity of the electrodes. Therefore, the force acting on the droplet will always be directed towards the CE. However, in this work, for definiteness, a negative potential was applied to the control electrodes, and a positive potential was applied to the common electrode (Figure 1a). At the same time, it is possible to selectively apply voltage from a high-voltage source to each of the control electrodes or simultaneously to a selected group of CEs.

As a rule, water droplets with a V_d volume of no more than 40 µL (diameter ≲ 4 mm) are used in microfluidic systems. Therefore, in order to avoid accidental coalescence of droplets, the distance between the control electrodes in the PMD is chosen to be slightly larger than that and equal to h = 5 mm. This distance also corresponds to the movement of the droplet from some selected electrode to the nearest neighboring one, which will be called below a “step”.

Preliminary experiments have shown that application of voltages U ≥ U_crt~10 kV to the CE leads to undesirable spontaneous displacements of droplets on the working area. This effect may be due to the charging of the droplet and the PMD surface caused by an excessively high voltage. Indeed, at U ≈ U_crt, the average electric field strength in the gap between the common and control electrodes is ~10⁶ V/M, i.e., it reaches the threshold value at which the air acquires electrical conductivity [26,27]; this explains the above phenomena. This undesirable effect completely disappears when the voltage applied to the CE is reduced to 7 kV, at which the air can be considered as a good insulator. This makes it possible to neglect the processes of charge inflow, at least during the manipulation of microdroplets. Therefore, in further experiments, the voltages applied to the electrodes did not exceed this value.

3. Results and Discussion

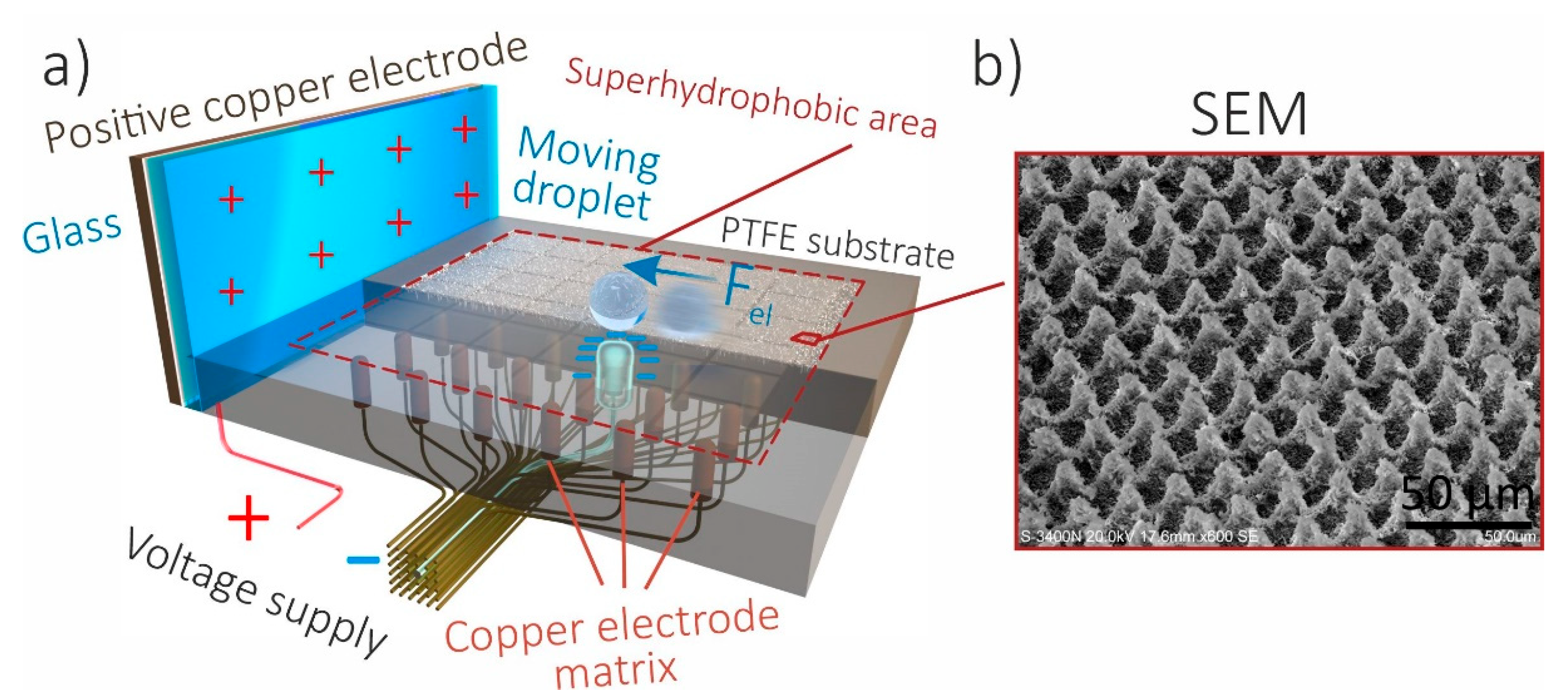
3.1. Controllable Movements of Droplets

Below, the threshold voltage U_th will be understood as the minimum voltage at the electrode at which the droplet starts moving towards it. As experiments have shown, for a droplet located at a distance of one step from the control electrode, the value of U_th depends only on the volume of the droplet wherein U_th does not depend on the polar angle at which the droplet is located with respect to the CE. In other words, the CE-created force field is practically axisymmetric in the local vicinity of the electrode. The experimental dependence of U_th on the volume of a deionized water droplet located at one step distance from the control electrode is illustrated by curve 1 in Figure 2.

It can be seen that, with an increase in volume from 0.5 to 7 μL, an approximately twofold increase in threshold voltages is observed. With further increase in volume, however, this trend is reversed so that at V_d = 35 µL, the threshold voltages again decrease to the level U_thr for V_d = 0.5 µL.

It also follows from Figure 2 that the necessary and sufficient condition for the movement of droplets of all considered volumes (0.5 ÷ 35 μL) by one step is the application of voltage U_w ≈ 3.5 kV to the CE. We shall, therefore, hereinafter call this voltage the working voltage (WV).

It is important to emphasize that relatively high values of the control voltages are not a significant problem. Indeed, technically it can be easy realized. In addition, a very large internal resistance can be choosen for the voltage sources (in our case, 10⁹ Ω). This implies that currents are so small that in the event of short circuits they do not pose a serious threat to equipment or personnel.

The nature of the dependences presented in Figure 2 is discussed within the framework of the following model. We will assume that the absolute value of the electric field strength E near the control electrode is proportional to the charge acquired by this electrode q = CU, where C is the capacitance of the CE. Let us assume that a function f(r) describes a certain law of decrease in the field strength with change in distance r from the end of the electrode, taking into account the distribution of the charge density on the electrode and the contribution of the PMD polarization. In other words, E = CUf(r).

The force acting on a spherical droplet in the non-uniform field of CE can be written as ${\mathit{F}}_{\mathit{e}\mathit{l}}=\frac{1}{2}{\epsilon }_{env}\alpha \nabla {\mathit{E}}^2$, where $\alpha =\pi \frac{a^3}{4}{\epsilon }_0\frac{{\epsilon }_{water}-{\epsilon }_{env}}{{\epsilon }_{water}+{\epsilon }_{env}}$—is the polarizability of a spherical drop; a—is its diameter; ${\epsilon }_{water}$—is the permittivity of water; ${\epsilon }_{env}$—is the permittivity of the environment; $\nabla$—is the gradient operator. Taking into account that ${\epsilon }_{water}\gg {\epsilon }_{env}$, this force can be written as ${\mathit{F}}_{\mathit{e}\mathit{l}}=\frac{3}{2}{\epsilon }_0{\epsilon }_{env}{V}_d{C}^2{U}^2\left(\nabla f^2{|}_{r_0}\right)$, where $r_0=\sqrt{{\left(a/2\right)}^2+h^2}$.

Due to their mobility, excess like charges are not distributed uniformly in an extended conductor but are concentrated at the greatest possible distance from each other. In accordance with this statement, the highest excess charge density will be observed near the upper end of the CE. Accordingly, in this region, the highest field strength gradients will be achieved and, as a result, the force ${\mathit{F}}_{\mathit{e}\mathit{l}}$ acting on the droplet will be directed towards it. Therefore, the horizontal component of this force will be equal to

$$F_{e{l}_r}\left(U\right)=\mathsf{\chi }{V}_d{U}^2$$

(1)

where $\mathsf{\chi }=\frac{3}{2}{\epsilon }_0{\epsilon }_{env}{C}^2\left(\nabla f^2{|}_{r_0}\right)\cos \left(\theta \right)$, $\theta$ is the angle at which the center of the droplet is visible from the top of the CE. When the threshold voltage U_th on the CE is reached, this component exceeds the pinning force, which, based on [28], can be represented as:

$$F_p=\mathsf{\eta }V{ }_d^{1/3}$$

(2)

where the coefficient $\mathsf{\eta }$ depends on the value of the contact angle, its hysteresis and other vapor-liquid surface tension parameters, while $V{ }_d^{1/3}$ specifies the contact zone perimeter up to a constant coefficient. Based on this, the value of the threshold voltage can be found as:

$$U_{th}={\left(\frac{\mathsf{\eta }}{\mathsf{\chi }}\right)}^{1/2}V{ }_d^{-1/3}$$

(3)

Strictly speaking, $\cos \left(\theta \right)$ and, consequently, the value of $\mathsf{\chi }$ depend on the volume of the drop. However, for a droplet located a step away from the CE, ${(\frac{2h}{a})}^2>>1$ and $\cos \left(\theta \right)=h/\sqrt{{\left(a/2\right)}^2+h^2}\approx 1$. Therefore, the value of $\mathsf{\chi }$ can be considered a constant. If, in addition, the coefficient $\mathsf{\eta }$ is also assumed to be constant, then, as can be seen from Expression (1), the threshold voltage should decrease monotonically with an increase in the droplet volume, which is experimentally observed only at V_d > 7 μL.

Due to the complexity of calculating the exact value of the coefficient $\mathsf{\chi }$, the ratio $\frac{\mathsf{\eta }}{\mathsf{\chi }}$ in Expression (1) can be viewed as a fitting parameter. It is chosen in such a way that the calculated dependence $U_{th}\left(V_d\right)$, illustrated by curve 2 in Figure 2, agrees with the experimental curve 1 for droplets of the largest volume. As can be seen, a significant discrepancy between the experimental and calculated curves is already observed at V_d < 15 µL. This discrepancy can be explained by the fact that, in the presence of voltage on the CE, the coefficient $\mathsf{\eta }$ in Expression (2) becomes a function of the volume V_d.

It was noted above that we exclude the possibility of direct leakage of excess charge onto the droplet. Therefore, the phenomena caused by the NEF on the PMD should be associated with the polarization of the droplet in an electric field. This effect leads to the appearance of polarization charges in the zone of its contact with the dielectric surface. As a result, conditions for a phenomenon known as electrowetting on a dielectric (EWOD) are realized at the solid/liquid interface [29,30].

In contrast to the classical case of EWOD [30,31], in our case there is no direct electrical contact between the voltage source and the droplet. In addition, the electrode located below the droplet is not flat but rod-shaped, with the diameter of no more than 500 μm. Therefore, the electric field created by it is highly non-uniform even on the scale of the smaller droplets with a diameter of ~1 mm. This leads to the appearance of higher-order multipole charges on the droplet. This process leads to a strong non-uniformity of the surface charge density in the region of its contact with the dielectric. These features significantly complicate the mathematical description of the features of electrowetting in our case, in comparison with the classical EWOD. Such a description is possible only on the basis of additional studies, which, in our opinion, are beyond the scope of this work.

However, some correction of the analytical curve 2 in Figure 2 can be performed using the results of the following experiment.

Droplets of various volumes are deposited from a capillary onto an inclined PMD at a point located above the selected CE. A short-term voltage pulse (~1 s) with an amplitude of 4 kV is applied to it, which initiates the deposition process and the initial retention of the droplet on the PMD. In the case when the angle of inclination of the PMD exceeds the roll-off angle modified by the electric field, the droplet begins to move immediately after the end of the pulse. Otherwise, the droplet remains “fixed” for another ~1000 ms. We interpret this delay as the time required for the transition from electrowetting to normal conditions.

The obtained results of measuring the angle ${\mathsf{\theta }}_{roll}^{EWOD}$ modified as a result of the EWOD phenomenon (V_d) are shown by points 1 in Figure 3a. For comparison, the same Figure 2 shows curve 2, which illustrates the dependence of the roll-off angle ${\mathsf{\theta }}_{roll}\left(V_d\right)$ in the absence of voltage. Let us assume that ${\mathsf{\theta }}_{roll}^{EWOD}$ depends on the volume of the droplet according to the power law $\propto V_d^{-p}$, as is the case for the “usual” roll-off angle ${\mathsf{\theta }}_{roll}$ [32,33,34]. It can be seen from Figure 3 that, with an increase in the droplet volume, the angle ${\mathsf{\theta }}_{roll}^{EWOD}$ decreases more slowly than does ${\mathsf{\theta }}_{roll}$. Therefore, the exponent p in $V_d^{-p}$ will be somewhat smaller for ${\mathsf{\theta }}_{roll}^{EWOD}$ than for ${\mathsf{\theta }}_{roll}$. The best fit of the experimental data for ${\mathsf{\theta }}_{roll}^{EWOD}$ is achieved with p = 1/2 (curve 2 in Figure 3).

The droplet starts rolling at the moment when the force of gravity ${\mathsf{\rho }}_{aqua}{V}_{d}sin{\mathsf{\theta }}_{roll}$ acting on it (where ${\mathsf{\rho }}_{aqua}$ is the density of water) becomes equal to the modified pinning force $F_p^{EWOD}$. Based on this statement, it is easy to recalculate the data in Figure 3a to obtain the dependence of the modified pinning force on the droplet volume. The corresponding results of processing the experimental data (points) are shown in Figure 3b along with the approximating dependence, which, in this case, is given by the expression

$$F_p^{EWOD}=const\ast V{ }_d^{1-p}\approx const\ast V{ }_d^{1/2}$$

(4)

This character of the increase in the pinning force, in the presence of NEF, in turn requires the modification of Expressions (2) and (3), so that the coefficient $\mathsf{\eta }$ in them becomes dependent on the volume of the droplet according to the law $const\ast V{ }_d^{\frac{2}{3}-p}\approx const\ast V{ }_d^{\frac{1}{6}}$. This leads to the correction of the dependence $U_{th}(V_d$), which is illustrated by curve 3 in Figure 2. As can be seen, the corrected analytical dependence correlates somewhat better with the experimental curve 1, although, as before, it does not explain its behavior at V_d ≲ 7 µL. Apparently, this is because the model being used becomes inaccurate for such volumes of the droplet.

In the experiments on the movement of droplets on the PMD, the movement by one step distance takes time $t_{trans}$, after which the droplet performs damped oscillations for the time $t_{vibr}$ near the CE that attracts it. Microscopic observations show that, in the course of oscillations, the droplet slides back and forth about the equilibrium position as a whole without visible shape deformations. This process is illustrated in the high-speed footage in the Supplementary Materials (Video S1). It increases the total time to complete one step, which becomes equal to $t_{pass}=t_{trans}+t_{vibr}$. This, accordingly, reduces the average speed of movement by one step to the value $v_{pass}=\frac{h}{t_{pass}}$, approximately three times less than the translational speed $v_{trans}=\frac{h}{t_{trans}}$.

The dependences of the times $t_{trans}$, $t_{vibr}$ and $t_{pass}$ on the droplet volume in the case when U_w = 3.5 kV are shown in Figure 4, curves 1, 2, and 3, respectively. It is also seen that the total time of one step t_pass for droplets in the volume range of 3–15 μL, which is the most interesting from a practical point of view, does not exceed ~300 ms. This sets the lower limit of the average droplet velocity $v_{avr}=\frac{h}{t_{pass}}$ for this range of volumes to ~17 mm/s. The upper limit of the average velocity is reached for droplets of the smallest volume of 3 µL, and is 50 mm/s. In addition, the maximum droplet movement velocity $v_{max}=\frac{h}{t_{trans}}$ reaches 150 mm/s.

We also studied the possibility of controlling droplets whose volumes exceed those considered above by more than an order of magnitude. As it turned out, the possibilities of fail-safe control are exhausted when the volume V_d exceeds 200 μm. In this case, a too massive droplet does not always stop above the selected CE, and, while continuing to move, it can roll out of the working area of the PMD or coalesce uncontrollably with another droplet. The Video S2 demonstrates the process of controlled movement of a 200-µL droplet. It can be seen that, for this droplet, it is still possible to implement a complex broken trajectory of travel, with the average velocity reduced to 10 mm/s.

Usually, the damping of the pendulum oscillations, which, in our case, is a droplet of water near the CE, is considered a result of viscous friction. In this case, there is a gradual damping of the oscillation amplitude according to an exponential law. Moreover, weak oscillations of the system can be detected for a prolonged period of time, much longer than the characteristic decay time. In our case, however, the droplet oscillation amplitude decays almost linearly down to a complete stop. This damping process is typical for oscillations occurring with a constant friction force, for which the pinning force $F_p^{EWOD}$ given by Expression (4) can be taken as an estimate. This expression can also be recast as $F_p^{EWOD}=\mu m_{d}g$, where m_d is the mass of the droplet, g is the free fall acceleration, and the coefficient of sliding friction μ depends on the volume, according to the law $const\ast V{ }_d^{-p}\approx const\ast V{ }_d^{-1/2}$ As follows from the solution of the problem of free oscillations of a spring pendulum weighing m_d, the time until it stops completely under the action of a constant friction force turns out to be inversely proportional to the product $\mu m_d^{1/2}$. For the law of change of the coefficient μ obtained above, this product turns out to be equal to $const\ast V{ }_d^{\frac{1}{2}-p}\approx const$. As a result, the deceleration time ta should be almost independent of the droplet volume. Such (or similar) character of the t_vibr(V_d) dependence is observed only for droplets larger than 7 μL (curve 2 in Figure 4). A different character of this dependence for droplets of smaller volumes is obviously due to the poor accuracy of the model being used at V_d ≲ 7 µL as discussed above.

Sequential application of the control voltage U_w to a series of electrodes makes it possible to achieve a step-by-step movement of a selected droplet along predetermined, including non-rectilinear trajectories (Video S3). To exclude accidental movement of all other droplets, a holding voltage equal to U_fix = 2 kV is applied to the electrodes located under them (Video S4). In this case, this technique allows one to selectively move selected droplets along straight, broken, zigzag, including closed trajectories, similar to how pieces move in a chess game. In addition, due to the combination of holding and control voltages on the CE, it is possible to implement parallel control of the movements of several droplets at once (Video S5).

Generally speaking, the time of complete movement of the droplet by several steps N_pass grows as t_passN, where N is the number of steps. However, in the case where it is required to move the droplet along a straight line, this time can be significantly reduced by simultaneously switching on a series of CEs along this straight line at once. With such a movement, the droplet “flies” over the next control electrode due to its inertia, enters the field of the next one and then moves under its influence (Video S6). In this case, the damped vibration of the droplet occurs only at the last of the switched-on CEs. As a result, the average velocity of the droplet in this mode v_Npass increases significantly compared to the velocity of movement by one step. In Figure 4b the dependence of v_Npass on the distance traveled by a 4 μL droplet is shown. As might be expected, the average speed v_Npass increases with the number of steps. For 4 steps, it reaches 75 mm/s, at V_d = 4 µL.

3.2. Controllable Coalescence and Microliter Reactions

In the proposed PMD, the coalescence of two or more liquid droplets can be realized. It is carried out in the following ways. The first of them (Figure 5a,b, Video S7) consists of applying a control voltage (3.5 kV) to the CE located in the gap between two or more droplets at a distance of about a step from each of them. Under the action of the NEF, all droplets move towards this CE, above which the droplets merge. The second method is suitable only for manipulations with two droplets (Figure 5c,d). It consists in applying a voltage to the CE located under one of them, and the second one is located at a distance of no more than one step h. In this case, successful coalescence requires higher values of the CE voltage (6 kV), since the fixed droplet is reducing the field gradient in the region of the moving droplet. For the coalescence of three droplets in this way, higher voltages on the CE are needed, which, as mentioned above, leads to negative consequences.

Actually, in both approaches, the droplets can be located at a greater distance than h, but this also requires increasing voltages beyond acceptable levels. This implies the need to set certain starting positions of the droplets before coalescence, which can have been achieved by the preliminary selective movement of the droplets.

Using the proposed PMD, various chemical reactions can be implemented in microliter volumes, which obviously requires much smaller quantities of reagents than in the usual case of reactions “in test tubes”. In the Video S8, an example of the implementation of a chemical reaction is demonstrated when droplets of solutions of copper sulfate and sodium hydroxide merge. The formation of a blue precipitate of copper hydroxide is visible.

Figure 5c,d and Video S9 illustrate an example of the implementation of an analytical reaction for the detection of a hydroxyl radical. In this case, droplets of sodium hydroxide and methyl orange solutions merge. As can be seen, immediately after coalescence, the less dense methyl orange is concentrated in the upper part of the merged droplet, while sodium hydroxide is in the lower part. Further, during the diffusion of hydroxide, a gradual change in the color of the upper half of the droplet to yellow is observed, which demonstrates the detection of the desired radicals.

It is known that an important problem of superhydrophobic surfaces is the initial deposition of droplets at a given point. Due to the low adhesion of such surfaces, even slight vibrations of the capillary can lead to uncontrolled movement of the drop or even its rolling off. In our platform, this problem is completely solved by applying a holding voltage (2.5 kV is enough) to the CE located at the surface point chosen for deposition. Even with an inaccurate location of the capillary or an accidental jump of a droplet during the deposition process, the latter will still be deposited in the selected position.

Another problem with superhydrophobic surfaces is the capillary deposition of droplets with a volume of less than 1 μL. In this case, the total action of gravity and pinning forces on the droplet from the superhydrophobic surface is insufficient to overcome the pinning forces from the capillary, which prevents its deposition on the substrate. This problem can also be solved by applying voltage to the CE at the selected point of the PMD. In our case, it was possible to deposit droplets with a volume down to 0.1 µL in this way.

The use of holding voltages makes it possible not only to solve the problems of uncontrolled movement and rolling of droplets under random vibrations and inclinations of superhydrophobic substrates but also to realize controlled movement and even coalescence of droplets on an inclined PMD, at an inclination angle ${\mathsf{\alpha }}_{\mathrm{tlt} }$ of up to 20° (Figure 6a,b. In the case where ${\mathsf{\alpha }}_{\mathrm{tlt} }$ > 5°, moving the droplets by several steps at once by simultaneous activation of several CEs is no longer possible. Apparently, this is due to the fact that, when moving up the slope after moving to a nearby CE, the inertia of the droplet is not enough to get into the area of action of the next electrode. When moving down, a droplet gets accelerated too much and rolls off the working area. Therefore, in this case, the movement of the droplet can only be step-by-step.

On an inclined PMD, the mode of droplet coalescence can also be achieved, which is illustrated in Figure 6 and Video S10. Merging of droplets in this case is realized only in the second way, when both droplets are initially held on the PMD by the application of holding voltages U_fix = 2.5 kV. Then there is a pulsed increase in voltage to 6 kV under the selected motionless droplet, as a result of which the second droplet is attracted to it.

Based on experiments with inclined PMDs, it is possible to estimate the maximum allowed accelerations a_imp caused by lateral displacements of the horizontal platform, its vibrations and mechanical impacts. Based on the value of the maximum allowable slope angle ${\mathsf{\alpha }}_{\mathrm{tlt} }=20°$, we obtain that ${\mathrm{a}}_{\mathrm{imp}}=gsin{\mathsf{\alpha }}_{\mathrm{tlt} }\approx 3 \mathrm{m}/{\mathrm{s}}^2$.

4. Conclusions

Thus, the demonstrated superhydrophobic platform for manipulating liquid microdroplets makes it possible to deposit and move droplets along predefined trajectories in the volume range from 0.2 μL to 200 μL. In the most demanded from a practical point of view range of volumes 3 ÷ 15 µL, the speed of movement is 17 ÷ 75 mm/s. The proposed platform also provides the possibility of controlled coalescence of droplets, which makes it possible to carry out controlled chemical reactions, including analytical ones. The platform supports all described manipulations with superhydrophobic surface slopes up to 20°, as well as shocks and vibrations with maximum accelerations of up to 3 m/s².

We believe that the presented liquid droplet micromanipulation platform has great potential in chemical and biological analysis and can become a useful tool for various microfluidics applications.