Dynamic Potentiometry with an Ion-Selective Electrode: A Tool for Qualitative and Quantitative Analysis of Inorganic and Organic Cations
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents and Solutions
2.2. Apparatus and Electrodes
2.3. Membrane Preparation
2.4. Measurement Procedure
2.5. Selectivity Coefficients
2.6. Data Processing
3. Results and Discussion
3.1. Transient Potential Signals for Different Ions
3.2. Principal Components Analysis of the Transient Signals
3.3. Reconstruction of the Signals from PCAs
3.4. Transient Signals for Mixture of Ions: Detection of Interference
3.5. Application of the Transient Signals to Quantitative Analysis
3.6. Comparison with Other Quantitative Analytical Methods Based on Potential Transient Signals
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Serjeant, E.P. Potentiometry and Potentiometric Titrations; Chemical Analysis; Wiley: New York, NY, USA, 1984; ISBN 978-0-471-07745-9. [Google Scholar]
- Cuartero, M.; Crespo, G.; Cherubini, T.; Pankratova, N.; Confalonieri, F.; Massa, F.; Tercier-Waeber, M.-L.; Abdou, M.; Schäfer, J.; Bakker, E. In Situ Detection of Macronutrients and Chloride in Seawater by Submersible Electrochemical Sensors. Anal. Chem. 2018, 90, 4702–4710. [Google Scholar] [CrossRef] [PubMed]
- Ortuño, J.; Sánchez-Pedreño, C.; Fernández De Bobadilla, R. Transient Signals with an Antimony(V) Ion-Selective Electrode: The Relative Signal Return Rate as a Selectivity Parameter. Talanta 1994, 41, 627–630. [Google Scholar] [CrossRef]
- Ortuño, J.A.; Sánchez-Pedreño, C.; Martinez, D. Nonmonotonic Transient Potential Signals with an 18-Crown-6 Based Ion-Selective Electrode in a Flow-Injection System. Electroanalysis 2003, 15, 1536–1540. [Google Scholar] [CrossRef]
- Cuartero, M.; Ruiz, A.; Oliva, D.J.; Ortuño, J.A. Multianalyte Detection Using Potentiometric Ionophore-Based Ion-Selective Electrodes. Sens. Actuators B Chem. 2017, 243, 144–151. [Google Scholar] [CrossRef]
- Calvo, D.; Durán, A.; del Valle, M. Use of Pulse Transient Response as Input Information for an Automated SIA Electronic Tongue. Sens. Actuators B Chem. 2008, 131, 77–84. [Google Scholar] [CrossRef]
- Lindner, E.; Tóth, K.; Pungor, E. Dynamic Characteristics of Ion-Selective Electrodes; CRC Press: Boca Ratón, FL, USA, 2018; p. 136. ISBN 978-1-351-07153-6. [Google Scholar]
- Morf, W.E. The Principles of Ion-Selective Electrodes and of Membrane Transport; Studies in Analytical, Chemistry; Akadémiai Kiadó: Budapest, Hungary; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands, 1981; ISBN 978-963-05-2511-4. [Google Scholar]
- Mikhelson, K.N. Ion-Selective Electrodes; Lecture Notes in Chemistry; Springer: Berlin/Heidelberg, Germany, 2013; Volume 81, ISBN 978-3-642-36885-1. [Google Scholar]
- Bakker, E. The Phase-Boundary Potential Model. Talanta 2004, 63, 3–20. [Google Scholar] [CrossRef] [PubMed]
- Morf, W.E.; Pretsch, E.; de Rooij, N.F. Theory and Computer Simulation of the Time-Dependent Selectivity Behavior of Polymeric Membrane Ion-Selective Electrodes. J. Electroanal. Chem. 2008, 614, 15–23. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Morf, W.E.; Pretsch, E.; de Rooij, N.F. Memory Effects of Ion-Selective Electrodes: Theory and Computer Simulation of the Time-Dependent Potential Response to Multiple Sample Changes. J. Electroanal. Chem. 2009, 633, 137–145. [Google Scholar] [CrossRef][Green Version]
- Egorov, V.V.; Novakovskii, A.D.; Zdrachek, E.A. Modeling of the Effect of Diffusion Processes on the Response of Ion-Selective Electrodes by the Finite Difference Technique: Comparison of Theory with Experiment and Critical Evaluation. J. Anal. Chem. 2017, 72, 793–802. [Google Scholar] [CrossRef]
- Egorov, V.V.; Novakovskii, A.D.; Zdrachek, E.A. An Interface Equilibria-Triggered Time-Dependent Diffusion Model of the Boundary Potential and Its Application for the Numerical Simulation of the Ion-Selective Electrode Response in Real Systems. Anal. Chem. 2018, 90, 1309–1316. [Google Scholar] [CrossRef] [PubMed]
- Hambly, B.; Guzinski, M.; Pendley, B.; Lindner, E. Kinetic Description of the Membrane–Solution Interface for Ion-Selective Electrodes. ACS Sens. 2020, 5, 2146–2154. [Google Scholar] [CrossRef]
- Sokalski, T.; Lingenfelter, P.; Lewenstam, A. Numerical Solution of the Coupled Nernst−Planck and Poisson Equations for Liquid Junction and Ion Selective Membrane Potentials. J. Phys. Chem. B 2003, 107, 2443–2452. [Google Scholar] [CrossRef]
- Sokalski, T.; Lewenstam, A. Application of Nernst–Planck and Poisson Equations for Interpretation of Liquid-Junction and Membrane Potentials in Real-Time and Space Domains. Electrochem. Commun. 2001, 3, 107–112. [Google Scholar] [CrossRef]
- Umezawa, Y.; Bühlmann, P.; Umezawa, K.; Tohda, K.; Amemiya, S. Potentiometric Selectivity Coefficients of Ion-Selective Electrodes. Part I. Inorganic cations (technical report). IUPAC Pure Appl. Chem. 2000, 72, 1851–2082. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Karlberg, B. The Transient Characteristics of the Two-Ion Response of Hydrogen Selective Glass Electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1973, 42, 115–126. [Google Scholar] [CrossRef]
- Gratzl, M.; Lindner, E.; Pungor, E. Theoretical Interpretation of Transient Signals Obtained with Precipitate-Based Ion-Selective Electrodes in the Presence of Interfering Ions. Anal. Chem. 1985, 57, 1506–1511. [Google Scholar] [CrossRef]
- Cuartero, M.; Carretero, A.; García, M.S.; Ortuño, J.A. New Potentiometric Electronic Tongue for Analysing Teas and Infusions. Electroanalysis 2015, 27, 782–788. [Google Scholar] [CrossRef]
- Shishkanova, T.V.; Pospíšilová, E.; Prokopec, V. Screening of Synthetic Cathinones by Potentiometric Sensor Array and Chemometrics. Electroanalysis 2022, 34, 1–9. [Google Scholar] [CrossRef]
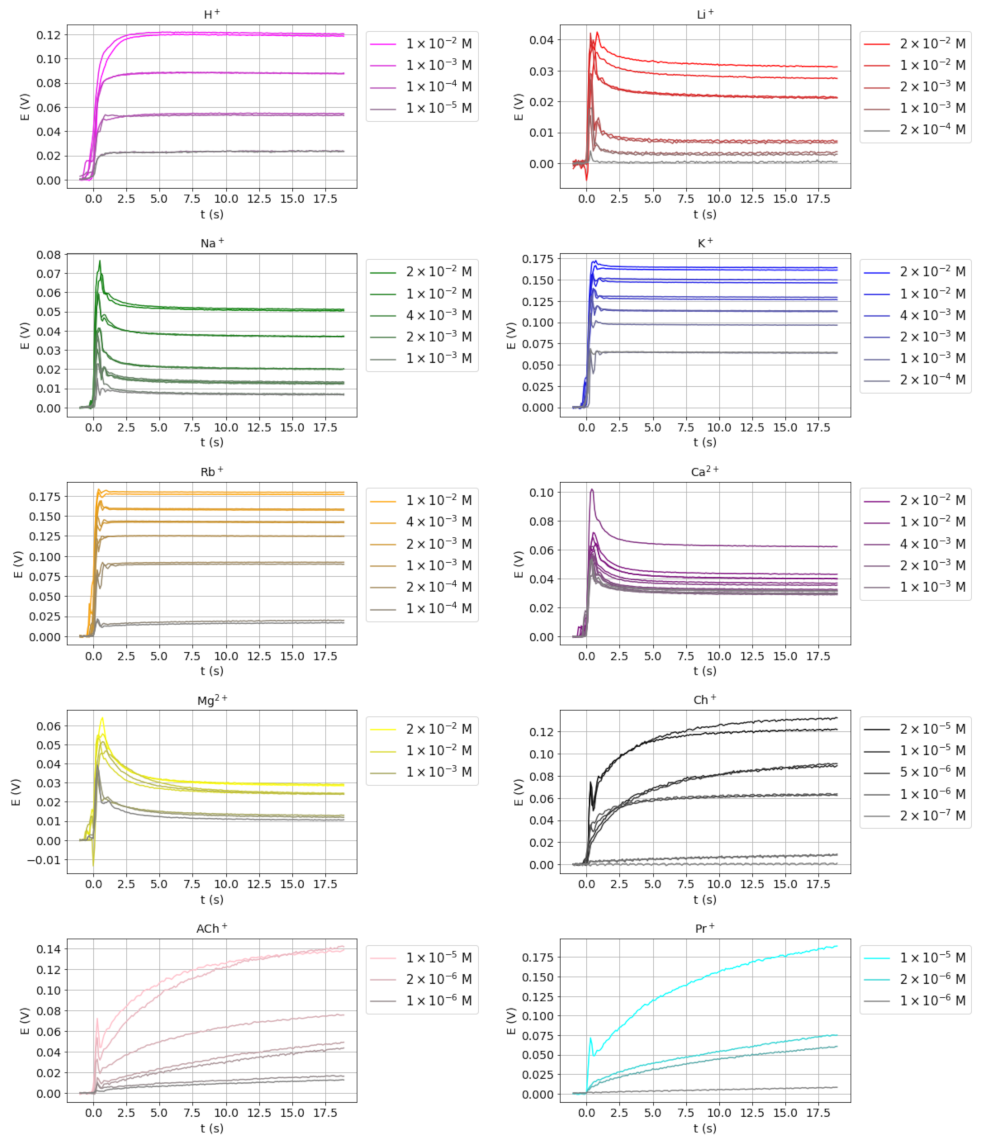
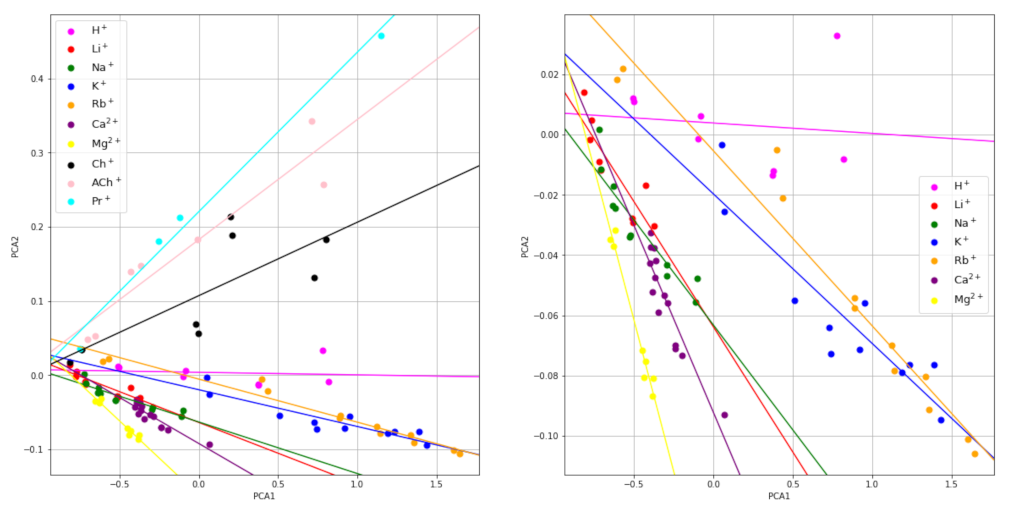
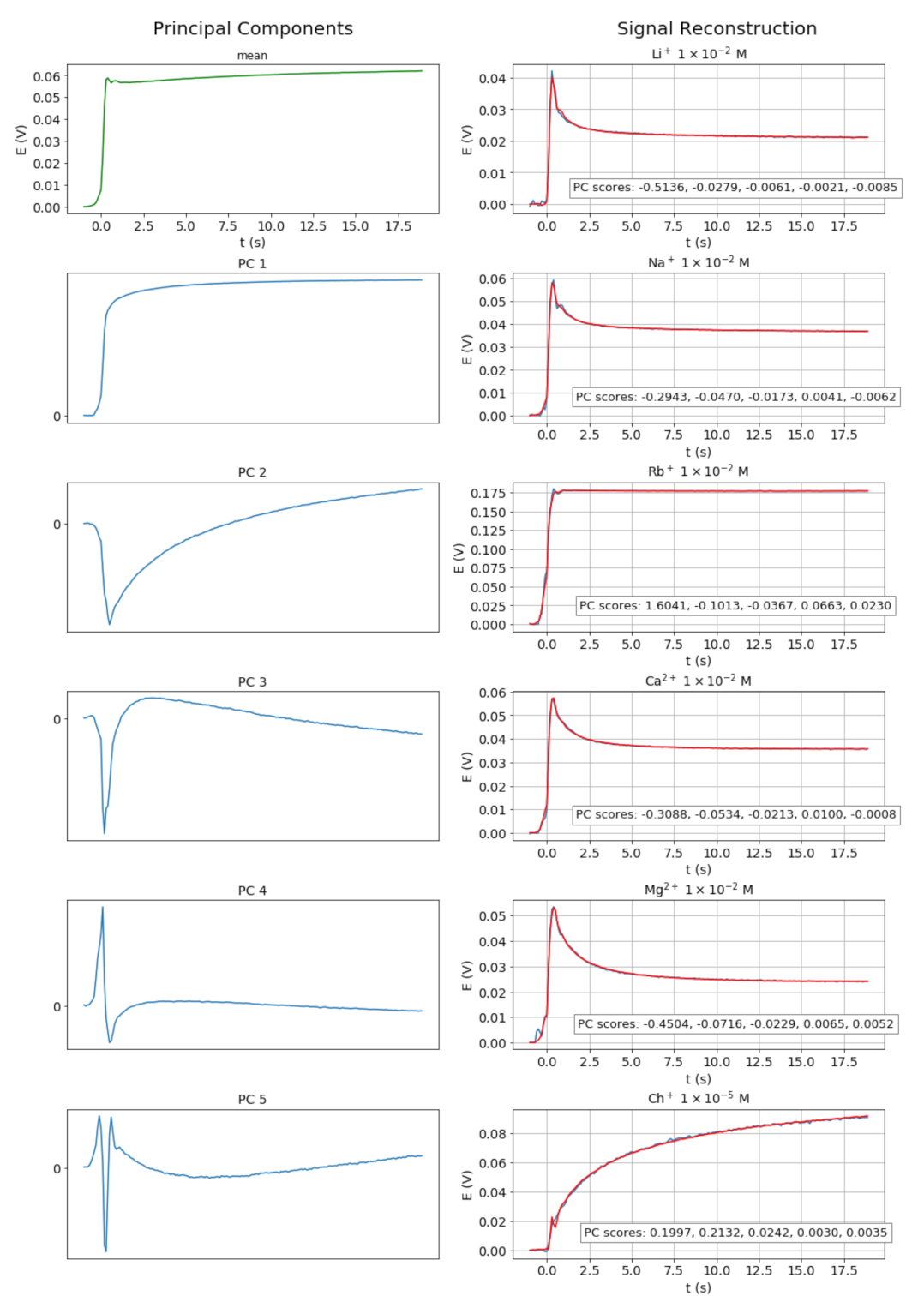
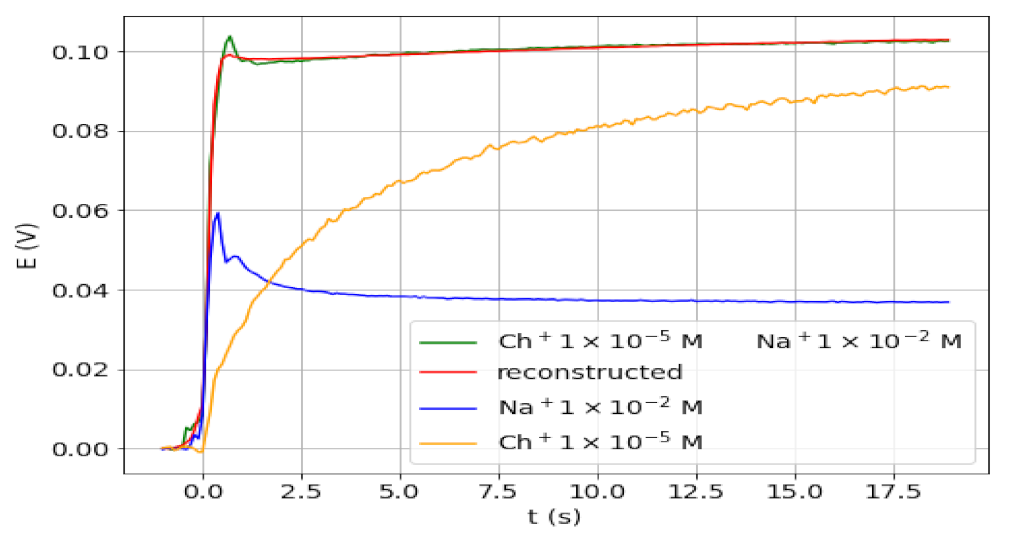
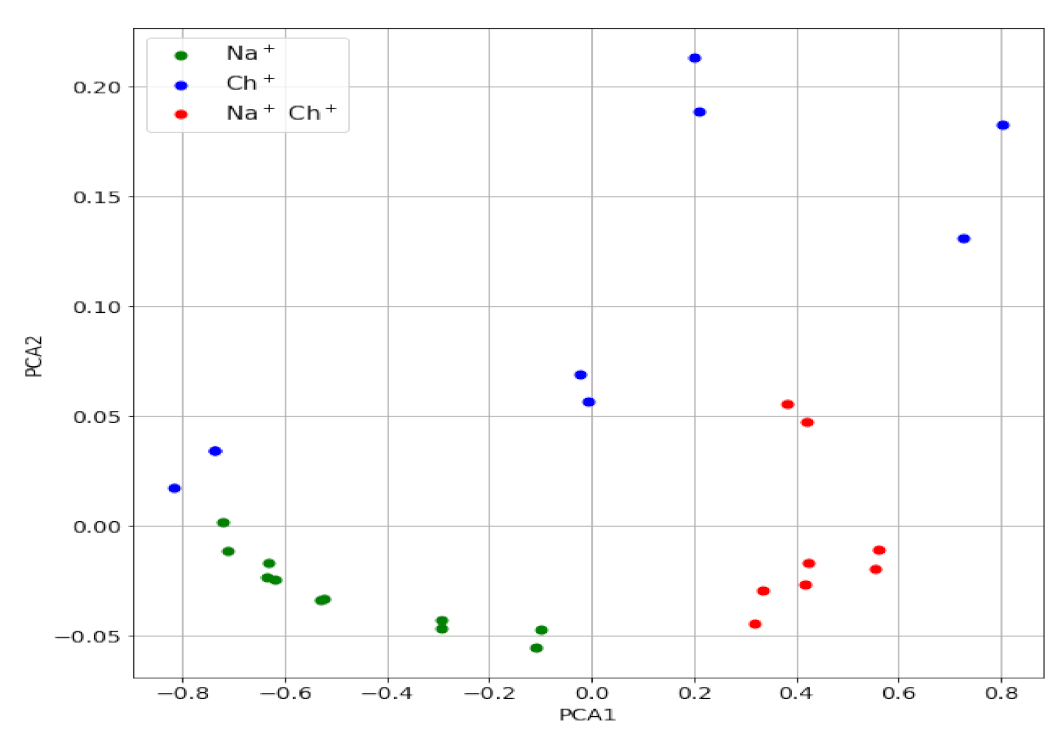
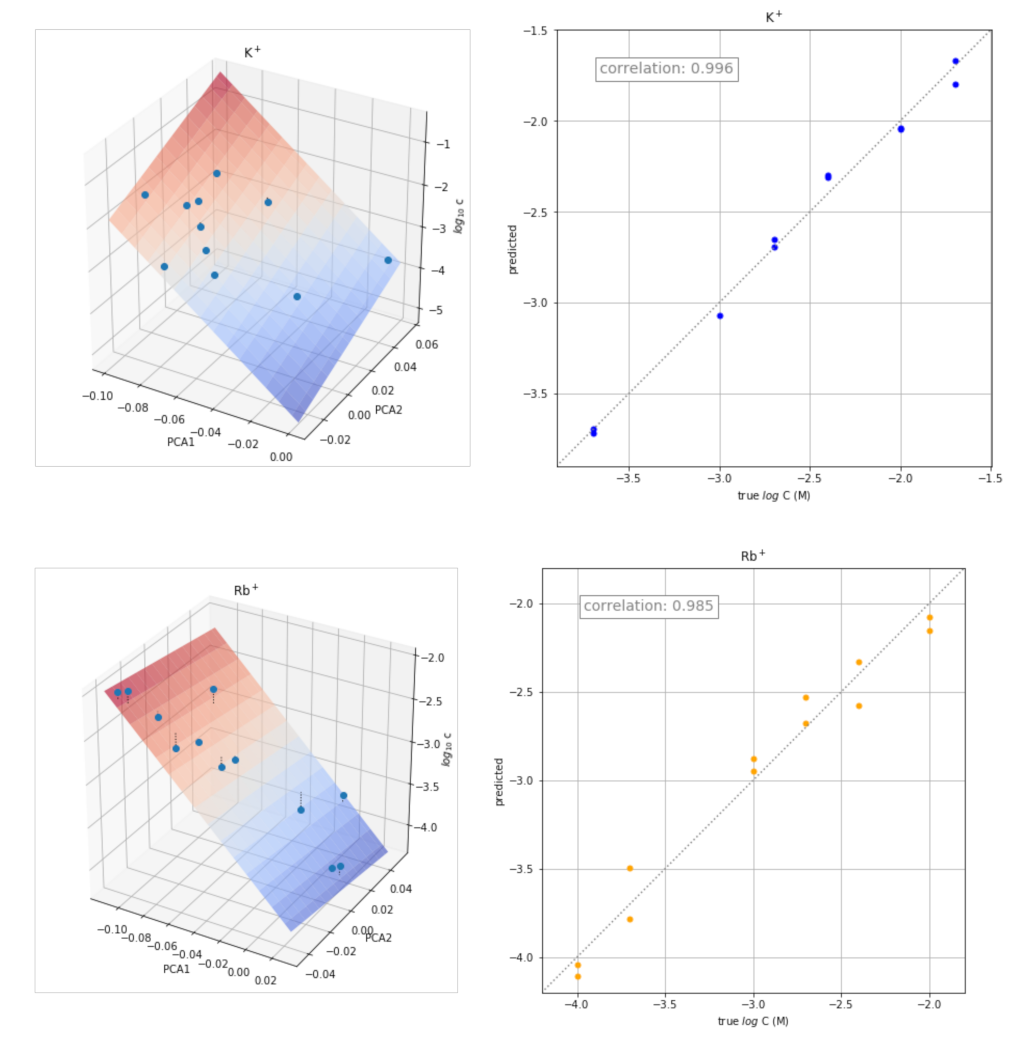
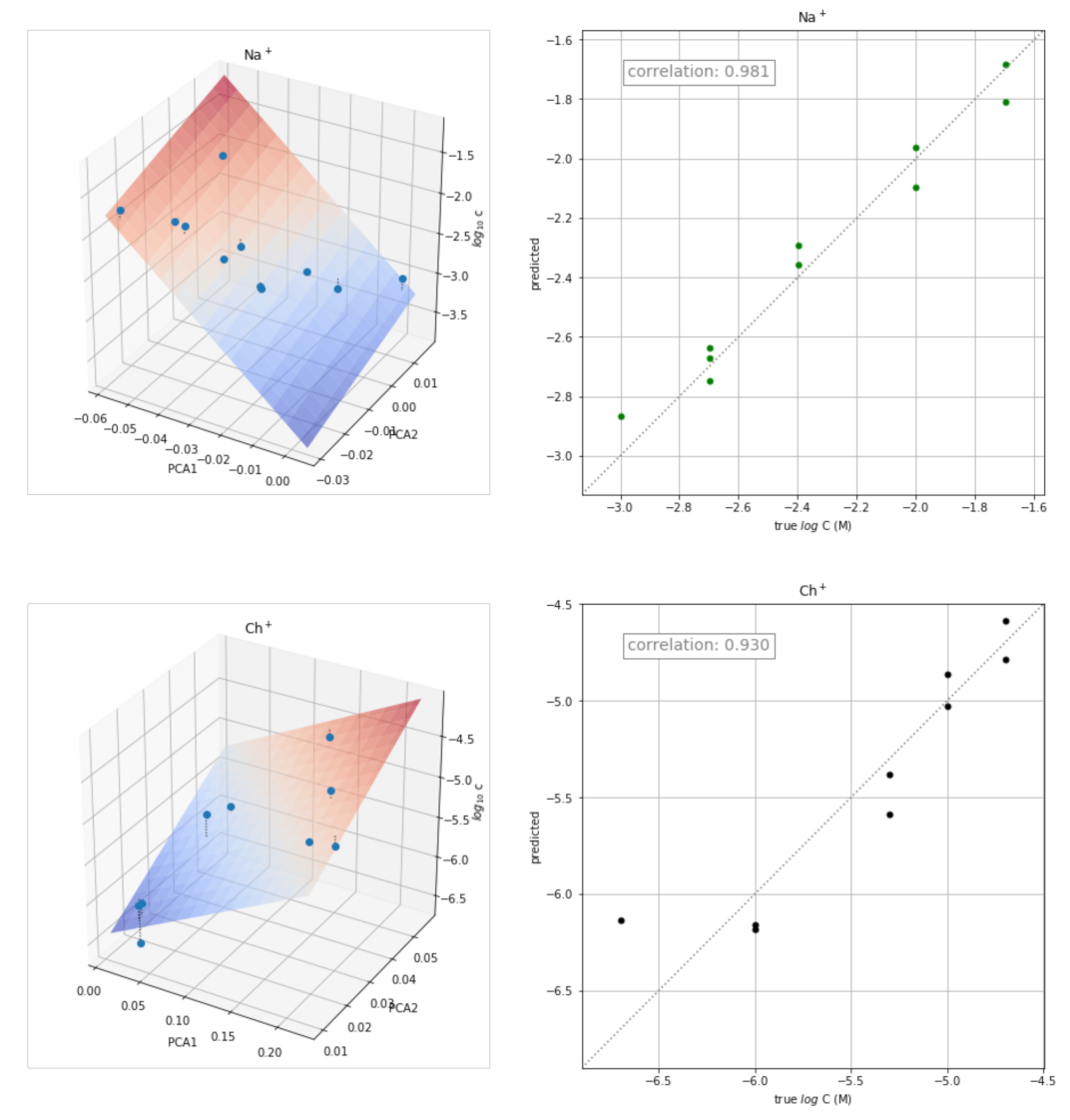
| H+ | Li+ | Na+ | K+ | Rb+ | Mg2+ | Ca2+ | Ch+ | AcCh+ | Pr+ |
|---|---|---|---|---|---|---|---|---|---|
| −0.65 ± 0.01 | −2.62 ± 0.01 | −2.24 ± 0.01 | 0 | 0.59 ± 0.01 | −3.56 ± 0.01 | −3.35 ± 0.01 | 1.62 ± 0.01 | 2.14 ± 0.04 | 2.63 ± 0.11 |
| C | a | b | c | r | R2 |
|---|---|---|---|---|---|
| H+ | −60.215 | 60.939 | −5.469 | 0.971 | 0.942 |
| Li+ | −43.493 | 18.149 | −3.081 | 0.978 | 0.956 |
| Na+ | −33.190 | 13.167 | −3.296 | 0.981 | 0.962 |
| K+ | −33.877 | 17.088 | −4.724 | 0.996 | 0.992 |
| Rb+ | −14.998 | −2.282 | −3.754 | 0.985 | 0.970 |
| Ca2+ | −34.589 | 21.681 | −3.828 | 0.879 | 0.773 |
| Mg2+ | −24.877 | −2.469 | −3.865 | 0.991 | 0.982 |
| Ch+ | 5.664 | 24.544 | −6.665 | 0.930 | 0.865 |
| AcCh+ | 4.944 | 10.496 | −6.301 | 0.982 | 0.964 |
| Pr+ | −0.223 | −12.133 | −5.899 | 0.993 | 0.986 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Franco, J.A.; Ruiz, A.; Ortuño, J.Á. Dynamic Potentiometry with an Ion-Selective Electrode: A Tool for Qualitative and Quantitative Analysis of Inorganic and Organic Cations. Chemosensors 2022, 10, 116. https://doi.org/10.3390/chemosensors10030116
González-Franco JA, Ruiz A, Ortuño JÁ. Dynamic Potentiometry with an Ion-Selective Electrode: A Tool for Qualitative and Quantitative Analysis of Inorganic and Organic Cations. Chemosensors. 2022; 10(3):116. https://doi.org/10.3390/chemosensors10030116
Chicago/Turabian StyleGonzález-Franco, José Antonio, Alberto Ruiz, and Joaquín Ángel Ortuño. 2022. "Dynamic Potentiometry with an Ion-Selective Electrode: A Tool for Qualitative and Quantitative Analysis of Inorganic and Organic Cations" Chemosensors 10, no. 3: 116. https://doi.org/10.3390/chemosensors10030116
APA StyleGonzález-Franco, J. A., Ruiz, A., & Ortuño, J. Á. (2022). Dynamic Potentiometry with an Ion-Selective Electrode: A Tool for Qualitative and Quantitative Analysis of Inorganic and Organic Cations. Chemosensors, 10(3), 116. https://doi.org/10.3390/chemosensors10030116







