Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method
Abstract
1. Introduction
2. Double Spectral Correction Method
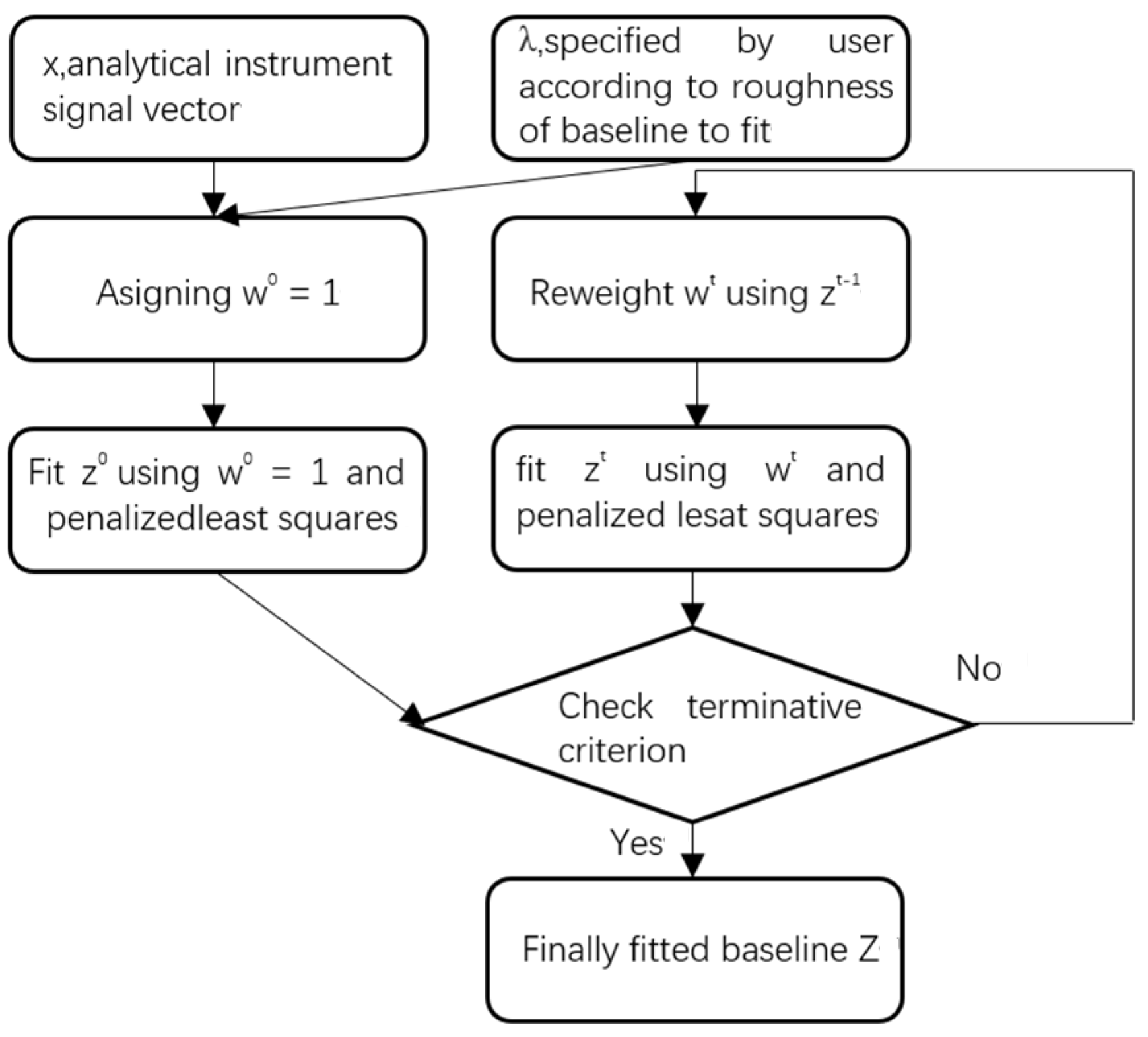
2.1. Baseline Correction
2.2. Plasma Temperature Compensation and Spectral Normalization
3. Experiment
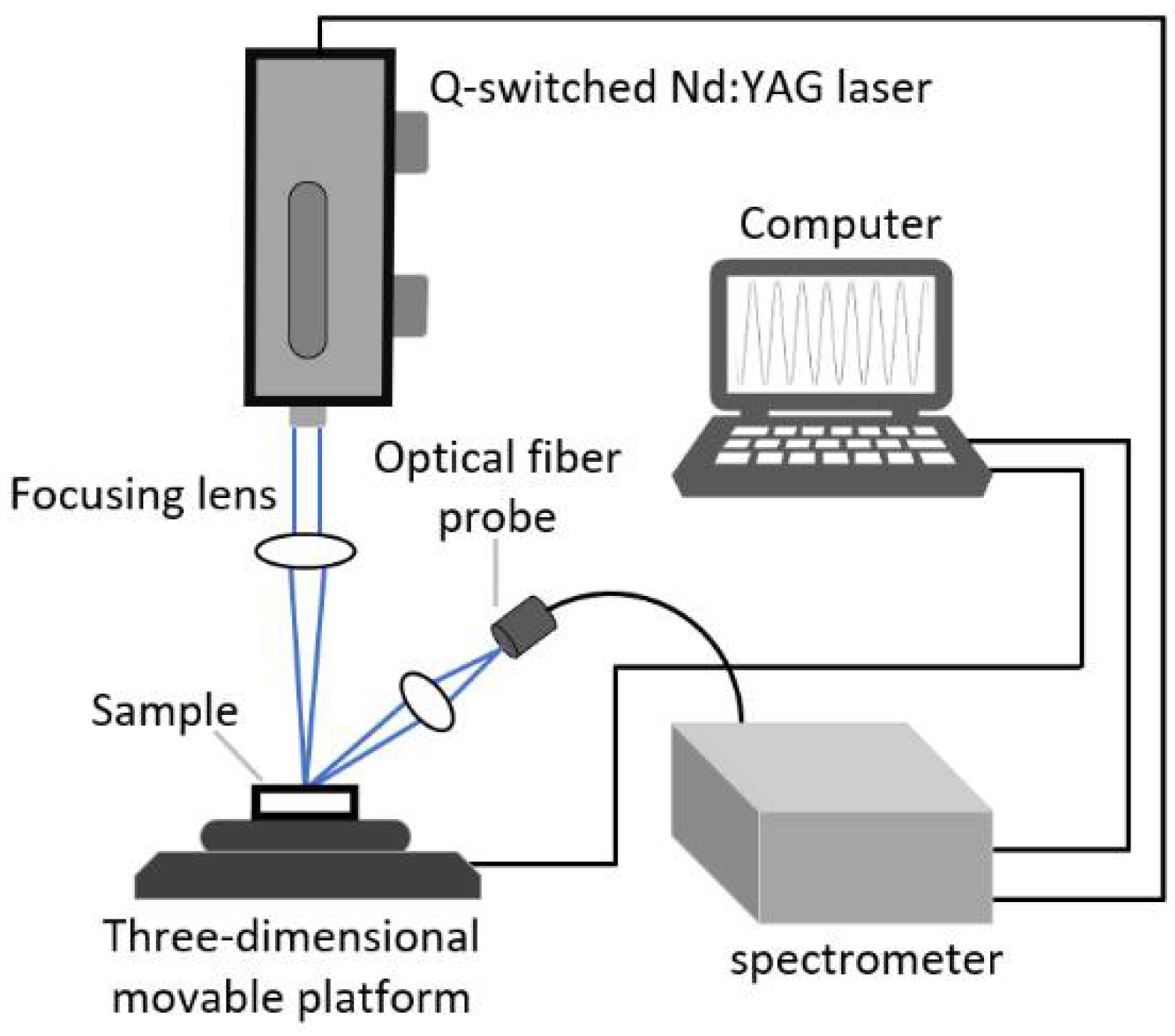
3.1. Experimental Setup
3.2. Sample Setup
4. Results and Discussion
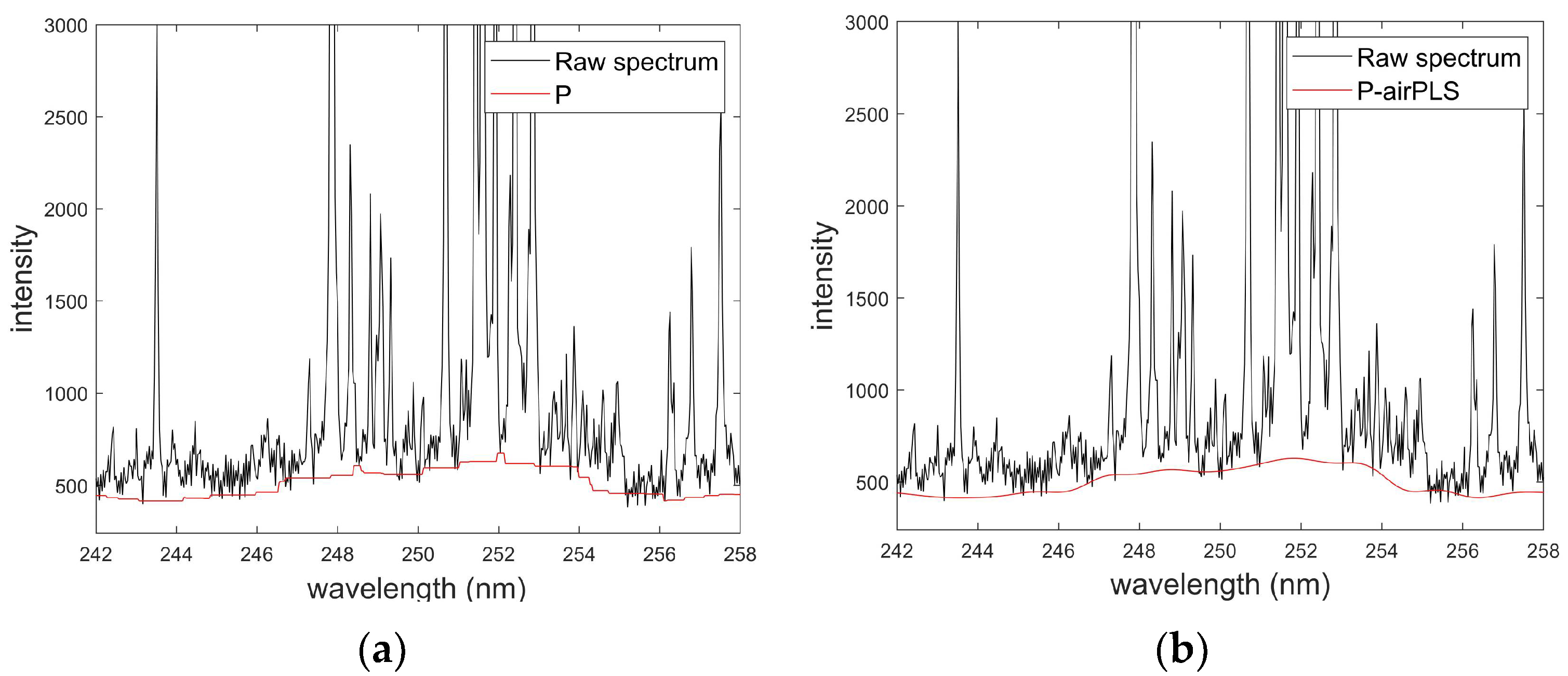
4.1. Spectral Correction
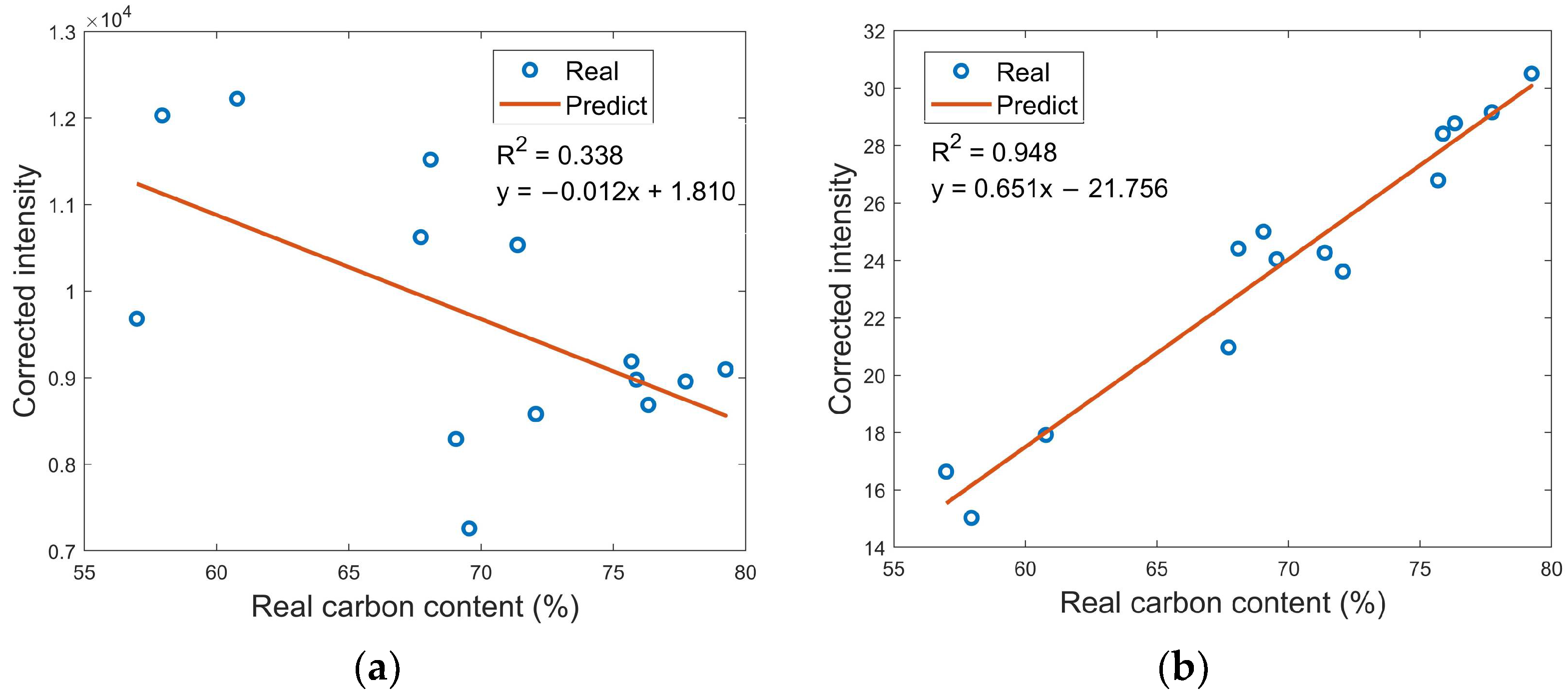
4.2. Predictive Effect of the Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.M.; Chen, X.; Wang, L.; Bei, K.; Wang, J.L.; Chou, L.M.; Pan, Z.Y. Progress of Raman spectroscopic investigations on the structure and properties of coal. J. Raman. Spectrosc. 2020, 51, 1874–1884. [Google Scholar] [CrossRef]
- Sheta, S.; Afgan, M.X.; Hou, Z.Y.; Yao, S.C.; Zhang, L.; Li, Z.; Wang, Z. Coal analysis by laser-induced breakdown spectroscopy: A tutorial review. J. Anal. Atom. Spectrom. 2019, 34, 1047–1082. [Google Scholar] [CrossRef]
- Oliveira, C.; Salgado, J. Elemental composition of coal by using prompt gamma-neutron activation analysis. J. Radioanal. Nucl. Chem. 1993, 167, 153. [Google Scholar] [CrossRef]
- Yao, S.C.; Mo, J.H.; Zhao, J.B.; Li, Y.S.; Zhang, X.; Lu, W.Y.; Lu, Z.M. Development of a Rapid Coal Analyzer Using Laser-Induced Breakdown Spectroscopy (LIBS). Appl. Spectrosc. 2018, 72, 1225–1233. [Google Scholar] [CrossRef] [PubMed]
- Cremers, D.A.; Radziemski, L.J. Handbook of Laser-Induced Breakdown Spectroscopy, 2nd ed.; John Wiley & Sons, Ltd.: New York, NY, USA, 2013. [Google Scholar]
- Ray Bauer, A.J.; Buckley, S.G. Novel Applications of Laser-Induced Breakdown Spectroscopy. Appl. Spectrosc. 2017, 71, 553–566. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Q.Q.; Yang, R.Z.; Cui, X.T. Quantitative determination of hydrogen isotope in titanium using LIBS. In Proceedings of the Applied Optics and Photonics China (AOPC2019), Beijing, China, 7–9 July 2019; SPIE: Beijing, China, 2019; Volume 11337, p. 1133712. [Google Scholar]
- Yao, S.C.; Zhao, J.B.; Wang, Z.Z.; Deguchi, Y.; Lu, Z.M.; Lu, J.D. Analysis of spectral properties for coal with different volatile contents by laser-induced breakdown spectroscopy. Spectrochim. Acta B 2018, 149, 249–255. [Google Scholar] [CrossRef]
- Liu, K.; He, C.; Zhu, C.W.; Chen, J.; Zhan, K.P.; Li, X.Y. A review of laser-induced breakdown spectroscopy for coal analysis. Trac-Trend. Anal. Chem. 2021, 143, 116357. [Google Scholar] [CrossRef]
- Hai, R.; Tong, W.N.; He, Z.L.; Sattar, H.; Li, C.; Ding, H.B. Quantitative analysis of titanium alloys using one-point calibration laser-induced breakdown spectroscopy. Appl. Phys B 2021, 127, 37. [Google Scholar] [CrossRef]
- Mo, Y.J.; Chen, Y.Q.; Li, R.H.; Zhou, Q.; Lou, Y. Microanalysis of silver jewellery by laser-ablation laser-induced breakdown spectroscopy with enhanced sensitivity and minimal sample ablation. Chin. Opt. Lett. 2014, 12, 083001. [Google Scholar]
- Chatterjee, S.; Singh, M.; Biswal, B.P.; Sinha, U.K.; Patbhaje, S.; Sarkar, A. Application of laser-induced breakdown spectroscopy (LIBS) coupled with PCA for rapid classification of soil samples in geothermal areas. Anal. Bioanal. Chem. 2019, 411, 2855–2866. [Google Scholar] [CrossRef]
- Bol, A.A.; Pandey, S.J.; Mao, X.L.; Liu, C.Y. Analysis of liquid petroleum using a laser-induced breakdown spectroscopy instrument. Spectrochim. Acta B 2021, 179, 106094. [Google Scholar]
- Han, W.W.; Su, M.G.; Sun, D.X.; Ying, Y.P.; Wang, Y.P.; Gao, C.L.; Yang, F.C.; Fu, Y.B. Analysis of metallic elements dissolution in the Astragalus at different decocting time by using LIBS technique. Plasma. Sci. Technol. 2020, 22, 156. [Google Scholar] [CrossRef]
- Lu, P.; Zhuo, Z.; Zhang, W.H.; Tang, J.; Xing, T.; Wang, Y.; Sun, T.F.; Lu, J.Q. Determination of calorific value in coal by LIBS coupled with acoustic normalization. Appl. Phys B 2021, 127, 82. [Google Scholar] [CrossRef]
- Yan, C.H.; Zhang, T.L.; Sun, Y.Q.; Tang, H.S.; Li, H. A hybrid variable selection method based on wavelet transform and mean impact value for calorific value determination of coal using laser-induced breakdown spectroscopy and kernel extreme learning machine. Spectrochim. Acta B 2019, 154, 75–81. [Google Scholar] [CrossRef]
- Stefano, L.; Beatrice, C.; Stefano, P.; Francesco, P.; Vincenzo, P. Determination of Ash Content of coal by Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta B 2019, 155, 123–126. [Google Scholar]
- Peng, H.B.; Chen, G.H.; Chen, X.X.; Lu, Z.M.; Yao, S.C. Hybrid classification of coal and biomass by laser-induced breakdown spectroscopy combined with K-means and SVM. Plasma. Sci. Technol. 2019, 21, 034008. [Google Scholar] [CrossRef]
- Song, W.R.; Hou, Z.Y.; Afgan, M.S.; Gu, W.L.; Wang, H.; Cui, J.C.; Wang, Z.; Wang, Y. Validated ensemble variable selection of laser-induced breakdown spectroscopy data for coal property analysis. J. Anal. Atom. Spectrom. 2021, 36, 111–119. [Google Scholar] [CrossRef]
- Zheng, J.P.; Lu, J.D.; Zhang, B.; Dong, M.R.; Yao, S.C.; Lu, W.Y.; Dong, X. Experimental Study of Laser-Induced Breakdown Spectroscopy (LIBS) for Direct Analysis of Coal Particle Flow. Appl. Spectrosc. 2014, 68, 672–679. [Google Scholar] [CrossRef]
- Li, X.W.; Yang, Y.; Li, G.D.; Chen, B.W.; Hu, W.S. Accuracy improvement of quantitative analysis of calorific value of coal by combining support vector machine and partial least square methods in laser-induced breakdown spectroscopy. Plasma. Sci. Technol. 2020, 22, 122. [Google Scholar] [CrossRef]
- Yao, S.C.; Xu, J.L.; Bai, K.J.; Lu, J.D. Improved Measurement Performance of Inorganic Elements in Coal by Laser-Induced Breakdown Spectroscopy Coupled with Internal Standardization. Plasma. Sci. Technol. 2015, 17, 938. [Google Scholar] [CrossRef]
- Zhao, N.; Li, J.M.; Ma, Q.X.; Guo, L.; Zhang, Q.M. Periphery excitation of laser-induced CN fluorescence in plasma using laser-induced breakdown spectroscopy for carbon detection. Chin. Opt. Lett. 2020, 18, 083001. [Google Scholar] [CrossRef]
- Li, X.W. Matrix Effect in Measurements of Carbon Content in Coal by Laser Induced Breakdown Spectroscopy and Its Correction Methods. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Chen, Y.L.; Dai, L.K. An Automated Baseline Correction Method Based on Iterative Morphological Operations. Appl. Spectrosc. 2018, 72, 731–739. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Chen, S.; Liang, Y.Z. Baseline correction using adaptive iteratively reweighted penalized least squares. Analyst 2010, 135, 1138–1146. [Google Scholar] [CrossRef]
- Najarian, M.L.; Chinni, R.C. Temperature and electron density determination on Laser-Induced Breakdown Spectroscopy(LIBS) plasmas: A physical chemistry experiment. J. Chem. Educ. 2013, 90, 244–247. [Google Scholar] [CrossRef]
- Lin, J.Y.; Yang, J.F.; Huang, Y.T.; Lin, X.M. A study of the temperature variation effect in a steel sample for rapid analysis using LIBS. Opt. Laser. Technol. 2020, 147, 107707. [Google Scholar] [CrossRef]
- Determination of Carbon and Hydrogen in Coal, National Standards of People’s Republic of China. Available online: https://www.chinesestandard.net/PDF/English.aspx/GBT476-2008 (accessed on 1 November 2022).
- Gabrielli, M.; LanconVerdier, V.; Picouet, P.; Maury, C. Hyperspectral Imaging to Characterize Table Grapes. Chemosensors 2021, 9, 71. [Google Scholar] [CrossRef]
- Ribeiro, M.C.S.; Senesi, G.S.; Cabral, K.S.; Cena, C.; Marangoni, B.S.; Kiefer, C.; Nicolodelli, G. Evaluation of rice varieties using LIBS and FTIR techniques associated with PCA and machine learning algorithms. Appl. Optics. 2020, 59, 10043–10048. [Google Scholar] [CrossRef]




| No. | Sample Number | Carbon Content (%) | Content Fluctuation (%) |
|---|---|---|---|
| 1 | GBW11110-q | 56.99 | 0.47 |
| 2 | GBW11110-u | 57.95 | 0.47 |
| 3 | GBW11110-t | 60.78 | 0.53 |
| 4 | GBW11102-d | 67.72 | 0.42 |
| 5 | GBW11111-w | 68.09 | 0.61 |
| 6 | GBW11108-u | 69.05 | 0.48 |
| 7 | GBW11108-t | 69.55 | 0.34 |
| 8 | GBW11111-t | 71.38 | 0.34 |
| 9 | GBW11111-u | 72.07 | 0.49 |
| 10 | GBW11102-b | 75.68 | 0.33 |
| 11 | GBW11107-k | 75.87 | 0.44 |
| 12 | GBW11107-i | 76.32 | 0.37 |
| 13 | GBW11101-o | 77.73 | 0.49 |
| 14 | GBW11101-l | 79.24 | 0.46 |
| Wavelength (nm) | Degeneracy | Transition Probability (108 s−1) | Energy Value (eV) |
|---|---|---|---|
| Ca315.919 | 4 | 3.10 | 7.04717 |
| Ca317.948 | 6 | 3.60 | 7.04955 |
| Ca393.341 | 4 | 1.47 | 3.15098 |
| Ca396.829 | 2 | 1.40 | 3.12335 |
| No. | Sample Number | Plasma Temperature (K) |
|---|---|---|
| 1 | GBW11110-q | 10,088.25 |
| 2 | GBW11110-u | 10,886.04 |
| 3 | GBW11110-t | 10,649.28 |
| 4 | GBW11102-d | 10,066.38 |
| 5 | GBW11111-w | 10,089.13 |
| 6 | GBW11108-u | 10,294.08 |
| 7 | GBW11108-t | 10,174.94 |
| 8 | GBW11111-t | 10,119.93 |
| 9 | GBW11111-u | 10,003.03 |
| 10 | GBW11102-b | 10,483.80 |
| 11 | GBW11107-k | 10,020.31 |
| 12 | GBW11107-i | 10,063.76 |
| 13 | GBW11101-o | 10,461.12 |
| 14 | GBW11101-l | 10,122.57 |
| Standard deviation | \ | 258.86 |
| Sample | Content (%) | Uncertainty of the Concentrations (%) | PLS | DSC-PLS | ||
|---|---|---|---|---|---|---|
| Predict (%) | Error (%) | Predict (%) | Error (%) | |||
| GBW 11107-i | 76.32 | 0.37 | 74.361 | 2.57 | 76.748 | 0.56 |
| GBW 11101-o | 77.73 | 0.49 | 76.563 | 4.68 | 77.974 | 0.31 |
| GBW 11102-b | 75.68 | 0.33 | 72.902 | 0.75 | 75.309 | 0.49 |
| GBW 11102-d | 67.72 | 0.42 | 68.367 | 0.96 | 67.428 | 0.43 |
| GBW 11110-t | 60.78 | 0.53 | 52.185 | 14.14 | 60.751 | 0.05 |
| GBW 11110-u | 57.95 | 0.47 | 60.762 | 4.85 | 58.298 | 0.60 |
| Average | \ | 0.435 | \ | 4.658 | \ | 0.406 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, C.; Wu, T.; Chen, J.; Li, M. Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method. Chemosensors 2022, 10, 490. https://doi.org/10.3390/chemosensors10110490
Guan C, Wu T, Chen J, Li M. Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method. Chemosensors. 2022; 10(11):490. https://doi.org/10.3390/chemosensors10110490
Chicago/Turabian StyleGuan, Congrong, Tianyu Wu, Jiwen Chen, and Ming Li. 2022. "Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method" Chemosensors 10, no. 11: 490. https://doi.org/10.3390/chemosensors10110490
APA StyleGuan, C., Wu, T., Chen, J., & Li, M. (2022). Detection of Carbon Content from Pulverized Coal Using LIBS Coupled with DSC-PLS Method. Chemosensors, 10(11), 490. https://doi.org/10.3390/chemosensors10110490








