1. Introduction
Presently, concurrent software systems are widely used in our daily life. In particular, they are successfully applied in so many safety-critical scenarios, e.g., health-care, intelligent traffic, and stock exchange. Thus, how to guarantee the correctness of concurrent systems has become a bone of contention for people’s lives and properties. In reality, the correctness of concurrent systems is closely related with control-flows and data-flows. However, the most existing studies mainly focus on the error detections of control-flows such as deadlocks, livelocks and compatibility [
1,
2,
3]. In fact, concurrent systems are vulnerable to data-flow errors, e.g., missing data, lost data and data inconsistency [
4,
5,
6]. Although the testing-based methods can detect these errors, they need to design a series of test cases to cover as many execution paths as possible. Due to the difficulty in the completeness of test cases, it is hard for these methods to guarantee a concurrent system error-free.
The Petri net-based model-checking is a prominent method/technique for analyzing data-flows of concurrent software systems. This is because Petri nets [
7,
8,
9,
10] have a great capability of explicitly specifying parallelism, concurrency and synchronization [
11,
12]. Thus, many different kinds of Petri nets are used to check data-flow errors, such as algebraic Petri net (or extended concurrent algebraic nets, ECANets), predicate/transitions net (PrTNet), and colored Petri nets (CPN), etc. Kheldoun et al. [
13] transformed BPMN (Business Process Model and Notation) models of complex business processes into to Recursive ECATNets (RECATNets), which combine the expressive power of abstract data types with recursive Petri nets. Furthermore, they used rewriting logics to check proper terminations and LTL properties. Buchs et al. [
14] proposed Concurrent Object-Oriented Petri Nets (CO-OPN/2) to ensure the specifications of control/data-flows in a large distributed system. Barkaoui et al. [
15] provided an approach for detecting data consistency with respect to a multilevel security policy based on ECATNets. He et al. [
16] modeled smart contracts by predicate/transition nets, and then checked their correctness of pre/post-conditions. Wu et al. [
17] developed a model-based method for quantitative safety analysis of safety-critical systems by Timed Colored Petri Nets (TCPNs). Yu et al. [
18] proposed an E-commerce Business Process Net (EBPN) to verify the rationality and transaction consistency between trading parties. All these methods place emphasis on the formalizations of data structures and abstract data types. Thus, they are suitable to check data-flow errors caused by these aspects.
By comparison, some checking methods based on Petri nets focus on the modeling of conceptual data operations, e.g.,
read,
write and
delete. Dual Flow Nets (DFNs) [
19] were proposed to model control- and data-flows of embedded systems. Awad et al. [
20] mapped BPMN models into Petri nets, and then detected and repaired errors based on the work in [
21]. Contextual net (C-net) [
22,
23] was proposed to model a concurrent read operation. Furthermore, its unfolding technique was developed to generate a minimal test suite for multi-threaded programs [
24]. Referring to contextual nets, Petri Net with Data Operations (PN-DO) [
5] was given to detect data-flow errors of concurrent software systems. However, these explicit formalizations of read/write arcs and data places easily increase the scales and complexity of Petri net models. Fortunately,
WFD-net (WorkFlow net with Data) [
4,
25,
26], as a high-level Petri net [
8], is extended with conceptual labeling data operations and guards. Thus, on the one hand, a WFD-net can greatly model control-flows and data-flows of concurrent systems. On the other hand, the model scales of WFD-nets are much smaller than other Petri nets with data-flow arcs (e.g., read arcs, write arcs and delete arcs), such as C-net and PN-DO. Furthermore, WFD-net has been widely used to do model-checking, e.g., soundness [
25], completion requirements [
27] and data consistencies [
28], although it is an easy way to model software systems. In general, these verification/analysis methods are based on the classical reachability graphs (CRG) [
25] of WFD-nets. However, they easily suffer from the problems of state–space explosion and illegal states (or pseudo-states). This is because a state may have an exponential number of successor states since they are produced based on the possible values of all guards. Moreover, the exclusive logical relations (e.g., multiple choice conditions) between guards easily lead to pseudo-states. In order to alleviate these problems, we proposed a guard-driven reachability graph (GRG) of WFD-nets in our previous work [
29].
Although a GRG of WFD-nets can describe all running information of concurrent systems and save their state–space compared with CRG, it still likely suffers from the state–space explosion problem. As shown in
Figure 1, it easily leads to a rapid increase of state–space with the increase of concurrent operations of WFD-nets. This is because the interleaving semantics of GRG is based on the partial orders of fired transitions, and it describes the behaviors of concurrent systems only by global states. Thus, a GRG-based analysis method needs to find out all precedence relations between activities, and generates their successor states. Compared with the interleaving-semantics-based methods, some studies are conducted on a concurrency analysis of Petri nets [
30,
31]. In particular, the unfolding technique [
32] can both alleviate the state space explosion problem and characterize the concurrency relations due to its true concurrency semantics [
33]. Currently, this technique has been successfully applied in different kinds of model-checking, e.g., fault diagnosis [
34], concurrent planning [
35], test case generations [
36], deadlock detection [
37], and verifying soundness [
38], reachability and coverability [
39]. Thus, in view of these advantages, we proposed an unfolding-based method [
5] to check errors of data inconsistency. Specifically, we use an acyclic net to represent all behaviors of a Petri net with data (PD-net [
5]). On the one hand, all concurrent operations can be directly recorded in this acyclic net. On the other hand, this formal model can store all states and save much more space especially when a system has so many concurrent activities.
To support and improve the above previous work [
5,
29], we develop a new model checker DICER 2.0. Currently, there are many Petri net tools [
40,
41,
42] such as PIPE, Snoopy, CPN Tools, Protos, and ProM. These tools can support different kinds of Petri net modeling, e.g., Place/Transition nets [
7], Timed Petri nets [
9], Stochastic Petri nets [
10] and High-level Petri net [
8]. Furthermore, they can be used to do structural analysis, generate condensed state spaces, construct reachability graphs, and analyze place/transition invariants. However, most of these tools fail in unfolding a Petri net. Although Mole, ERVunfold and Punf can do this work and conduct some model-checking (e.g., deadlocks, reachability and coverability), they cannot support the modeling and checking of data-flows that have been considered in some abstracted models, such as WFD-net [
43] and PD-net [
5]. Therefore, the most existing Petri net tools are not suitable to analyze data-flow errors of concurrent systems especially based on the unfolding techniques. The specified comparisons between some Petri net tools are summarized as
Table 1.
In this paper, we develop DICER 2.0 to analyze data-flows of concurrent systems. Specifically, we can use this tool to model concurrent systems by general Petri nets, WFD-nets and PD-nets. Meanwhile, we can draw, edit, import and export these models in DICER 2.0. Moreover, the errors of data inconsistency can be detected based on the unfolding technique of PD-nets, and some GRG-based model-checking can be done in our tool.
This paper is organized as follows.
Section 2 presents some basic notations.
Section 3 introduces our model checker DICER 2.0.
Section 4 gives two case studies on concurrent systems.
Section 5 conducts a group of experiments to show the advantages of our tool. The last section concludes this paper.
2. Basic Notations
A
net is a triple
, where
P and
T are two finite and disjoint sets, and they are called
place and
transition, respectively.
denotes a
flow relation. A
marking of a net is a mapping function
m:
, where
is a set of non-negative integers. In details, we use a multi-set to represent a marking. A net
N with an initial marking
is called a
Petri net [
7], i.e.,
. Given a node
x∈
P∪
T, its
preset and
postset are respectively denoted by
and
, where
=
|
∈
and
=
|
) ∈
.
As a particular class of Petri net, workflow net (WF-net) is widely used to model control-flows of concurrent systems.
Definition 1. A net is a WF-net (workflow net) [43,44] if (1) there exists only one source place i and one sink place o satisfying and ; and
(2) each node is on a path from i to o.
Besides modeling control-flows of concurrent systems, we can use a net with some data information to formalize data-flows.
Definition 2. A 7-tuple N =, T, F, D, , , is a net with data (D-net) [5], if (1) is a net;
(2) D is a finite set of data elements;
(3) : is a labeling function of reading data;
(4) : is a labeling function of writing data; and
(5) : is a labeling function of deleting data.
Given two nodes x, y∈P∪T in an acyclic D-net N =, T, F, D, , , ,
(1) x and y are in causality relation if the net N contains a path from x to y, which is denoted by x⪯y. In particular, if ;
(2) x and y are in conflict relation if ∃: ⪯x, ⪯y and ∩≠∅, which is denoted by ;
(3) x and y are in backward-conflict relation if ∩≠∅, which is denoted by ; or
(4) x and y are in concurrency relation if , which is denoted by xy, i.e., x and y are neither in causality relation nor in conflict relation.
OD-net (Occurrence Net with Data) is a simple acyclic net, which can be used in the unfolding technique of PD-nets [
5].
Definition 3. A D-net , T, F, D, , , is an OD-net (Occurrence net with Data) [5] if (1) : ;
(2) : ; and
(3) no transition is in self-conflict relation, i.e., :.
In an OD-net, places and transitions are called conditions and events, respectively. In general, we use , E, G, D, , , to denote an occurrence net with data for convenience. With respect to this formalization, B, E and G are conditions, events and arcs, respectively. , and are labeling functions of data operations (read, write and delete), respectively.
3. DICER 2.0
DICER 2.0 is developed to model and analyze the control-/data-flows of concurrent systems. It is the derivative version of our model checker for detecting data inconsistency [
45]. Currently, we can use it to do many more model checking.
3.1. The Modeling of Concurrent Systems Based on the Petri Net with Data Information
As is well known, we usually use read/write arcs, data places, labeling functions of data operations and guards to formalize data-flows of concurrent systems [
4,
19,
46]. In these formalizations, Petri nets such as DFN [
19], PN-DO [
47] and Awad method [
20] mainly use data places and flow relations to model data operations, e.g., read, write and delete. Although these methods are suitable to accurately model the control structures of data-flows, it lacks formal semantic descriptions about shared reading and overwriting. Contextual net [
46] can describe the concurrent (shared) reading operation by read arcs, but it needs extra data places and flow relations to formalize data-flows, and thus may be much more complex [
48].
Compared with the above modeling methods, WFD-net [
4,
49] has a prominent advantage. It combines the traditional workflow nets with conceptual data operations, and uses labeling functions and guards to describe data operations and routing conditions, respectively. Thus, it is not only greatly suitable to model the control-flows and data-flows of a concurrent system but also much smaller than other Petri nets with data-operation arcs (e.g., contextual net and PN-DO) in the scales of nodes and arcs [
48]. Now, this modeling method has been widely applied to various model-checking, e.g., detecting data-flow errors [
4] and data inconsistency in the migrations of service cases [
28], checking data inaccuracy [
50] and completed requirements [
27], and verifying may/must soundness of workflow systems [
25].
Definition 4. A workflow net with data (WFD-net) is a 9-tuple N =, T, F, D, , , , , [25], if (1) is a WF-net;
(2) D is a finite set of data elements;
(3) : is a labeling function of reading data;
(4) : is a labeling function of writing data;
(5) : is a labeling function of deleting data;
(6) is a finite set of guards that are related with data elements in D; and
(7) : is a labeling function of assigning guards to transitions.
Referring to the labeling functions of data operations in WFD-nets, a
Petri net with data (PD-net) [
5] is proposed, i.e., a PD-net
is a D-net
N with an initial marking
, i.e.,
. Although this modeling method neglects the formalization of guards, it is much suitable for generating the unfolding of Peri nets with data information due to its simple structural semantics. For example,
is a WFD-net in
Figure 2a, while
is a PD-net in
Figure 2c,d is its unfolding.
DICER 2.0 supports the modeling of WFD-nets and PD-nets. By this tool, we can formalize the control-/data-flows of concurrent systems. Furthermore, it provides a series of model-checking based on the guard-driven methods and unfolding techniques.
3.2. The Model-Checking Based on the GRG of WFD-Nets
The classical reachability graph [
25] is a fundamental method for analyzing a WFD-net. However, this method easily suffers from the problems of state–space explosion and pseudo-states (or illegal states) due to its guard evaluations and their exclusive relations. Hence, we proposed a
Guard-driven Reachability Graph (GRG) in our previous work [
29], and now achieve this function in DICER 2.0.
To construct a GRG of WFD-nets, we define a state as a weak configuration in DICER 2.0, which includes a marking and some evaluations of data and guards.
Definition 5. (Weak configuration) Given a WFD-net N = , T, F, D, , , , , , is a weak configuration, if
(1) is a WF-net, and m is its marking;
(2) a mapping function assigns a defined value or an undefined value to each data element; and
(3) a mapping function assigns the values of TRUE, FALSE, ⊥ or ⊤ to each guard.
In DICER 2.0, we also define the basic enabling/firing rules of WFD-nets based on weak configurations.
Definition 6. (Enabling/firing rules) Given a WFD-net N = , T, F, D, , , , , and its weak configuration , a transition t is enabled at c and denoted by , if
(1) ;
(2) ; and
(3) : ∧, where the function is to obtain all variables in a guard.
After firing a transition t at the weak configuration c, a new weak configuration can be generated, i.e., , where
(1) ;
(2) ;
(3) ;
(4) ;
(5) ; and
(6) .
Let and be two weak configurations of a WFD-net. is may-reachable from , denoted as , if there exist some weak configurations such that . Furthermore, a set of may-reachable weak configurations from is denoted by . Based on may-reachable sets and enabling/firing rules, we can formalize a GRG in DICER 2.0 as follows.
Definition 7. Given a WFD-net N = , T, F, D, , , , , and its initial weak configuration , is a guard-driven reachability graph (GRG), where
(1) , =|, , and
(2) : → such that ∧∧ .
For example,
Figure 2b shows a guard-driven reachability graph of
Figure 2a, where
and
are two exclusive guards,
and
are two weak configurations such that
.
Since a GRG of a WFD-net contains all execution information of a concurrent system, we can traverse its reachable weak configurations by DICER 2.0 to do some model-checking such as deadlocks [
51] and proper completeness [
27], i.e., given a WFD-net
N and its guard-driven reachability graph
,
o is its sink place and
is a weak configuration such that
.
If
and no transition is enabled at the weak configuration
c, then
c is a
deadlock. Thus, we can check deadlocks in
N according to this formal specification. For example, the WFD-net in
Figure 2a have a deadlock at the weak configuration
because
cannot read the data
and no transition is enabled at this time.
If
, then
N is
properly completed. For example, the WFD-net in
Figure 2a is not properly completed since the final weak configuration is not reachable from the initial weak configuration and the sink place
o has no token at this time.
3.3. The Model-Checking Based on the Unfolding Techniques of PD-Nets
Besides the model-checking based on GRGs of WFD-nets, DICER 2.0 can be used to detect errors of data inconsistency based on the unfolding techniques of PD-nets. We first define branching processes in DICER 2.0.
Definition 8. Given a PD-net , T, F, , D, , , and an OD-net , E, G, D, , , , the mapping is a homomorphism between Σ and O. is a branching process if satisfying:
(1) and ;
(2)for each event e belonging to E, the restriction of h onto (resp., ) is a bijection between and (resp., between and );
(3)the restriction of h onto is a bijection between and ;
(4): ) ∧ (; and
(5) = ∧ = ∧ = .
Given two branching processes
=
,
,
,
D,
,
,
,
and
,
is a prefix of
if
. All branching processes of a PD-net
forms a partial order set
w.r.t the binary relation of
prefix, and its greatest element is
Unfolding [
46], which is denoted by
. Please note that the unfolding of a PD-net is also an occurrence net with data. Although the unfolding of a PD-net records its running information, it may be infinite if there exists an infinite execution path. Therefore, it needs to be truncated so as to get a
finite complete prefix (FCP) [
52]. In DICER 2.0, we refer to the ERV method [
52] to cut off the unfolding of PD-nets, and then generate its FCP.
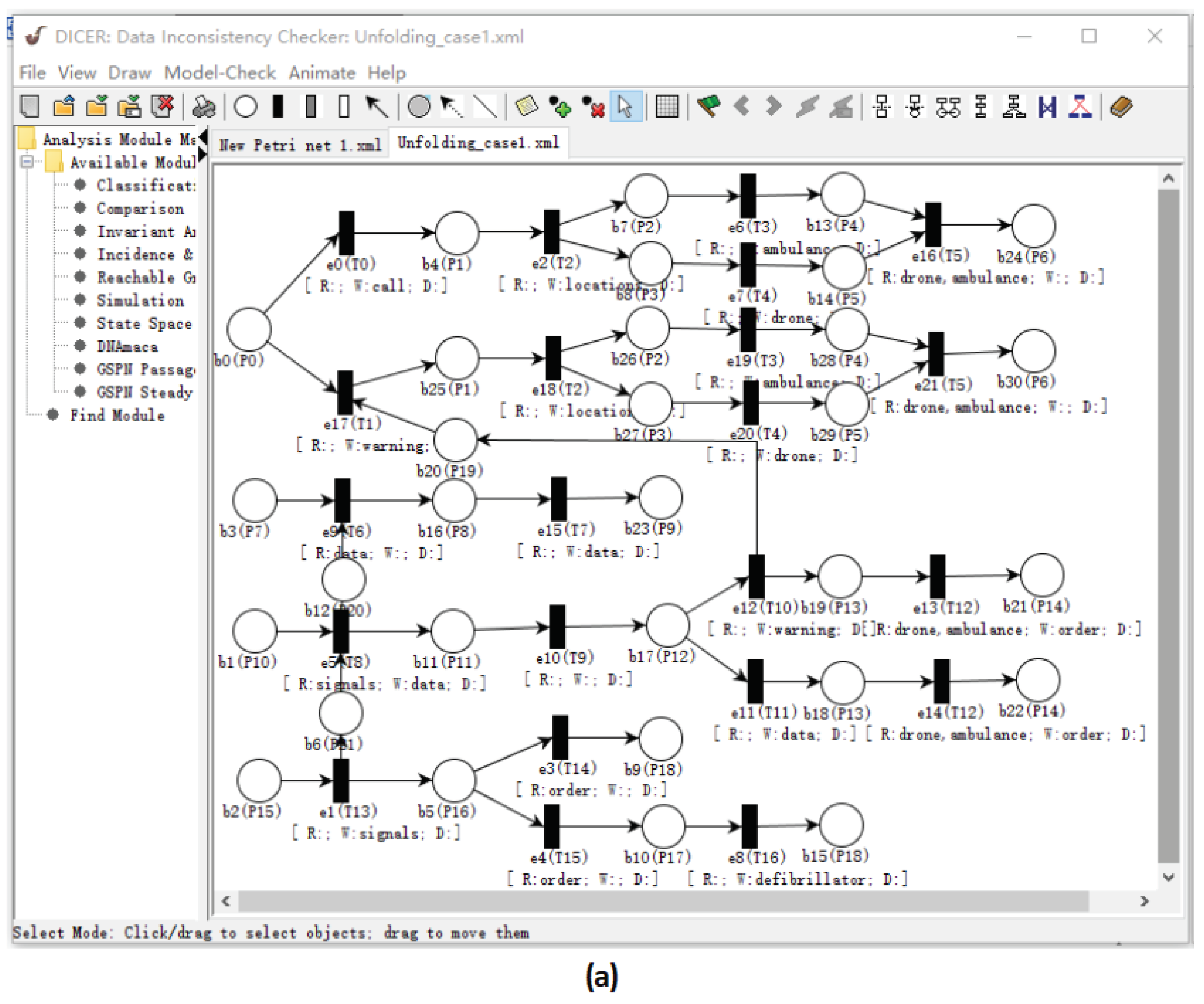
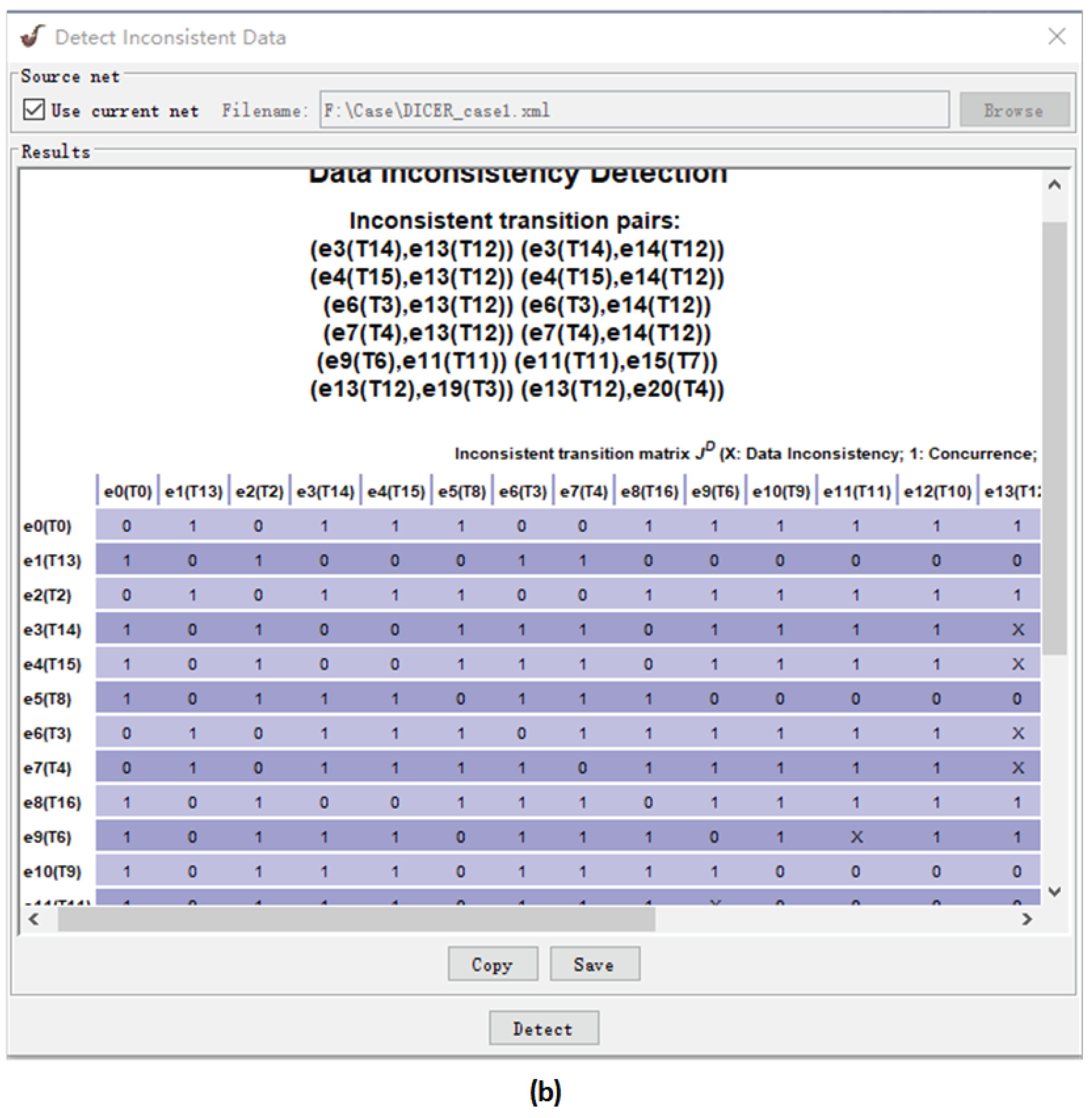
As a matter of fact, ERV method does not consider the Petri net modeling with data information. Moreover, it does not specify a highly efficient calculations on configurations, cuts and cut-off events. This is mainly caused by the following two facts. On the one hand, the most computing methods of configurations and cuts need a lot of repetitive calculations. On the other hand, once some new events are added into a given finite prefix, these methods usually match up them with all existing events and determine whether they are cut-off events or not. In order to solve these problems, DICER 2.0 uses recursion formulas and contextual information of events to compute configurations, concurrent conditions and cuts. Meanwhile, it uses backward conflicts to guide the calculations of cut-off events.
After generating an FCP of a PD-net
in DCIER 2.0, we can use its matrix manipulations to detect data inconsistencies since it contains the same behavioral information as the reachability graph of
(i.e., the completeness property [
5] of FCP). In details, we first get an incidence matrix of this FCP, and then use Warshell algorithm to calculate its causality matrix
. Afterwards, we obtain a conflict matrix
according to the mathematical definition of conflicts. Then, a concurrency matrix
is calculated by
and
,
i.e., two events are in concurrency relation if they are neither in causality relation nor in conflict relation, i.e.,
,
and
, where
,
(
), and
Based on the concurrency matrix
, we can check the errors of data inconsistency in
, i.e., there exists an error of data inconsistency if two concurrent events
and
have some data operations on a share data element,
i.e.,
For example,
Figure 2d is an FCP of the PD-net in
Figure 2c. Its related matrix calculations are conducted as shown in
Figure 3. From this concurrency matrix, we can find that
,
and
are three concurrent events. Furthermore, they suffer from the errors of data inconsistency because
∩
∩
.
3.4. The Implementations of DICER 2.0
Corresponding to the specified modeling and checking methods, we now introduce the basic framework and implementations of DICER 2.0.
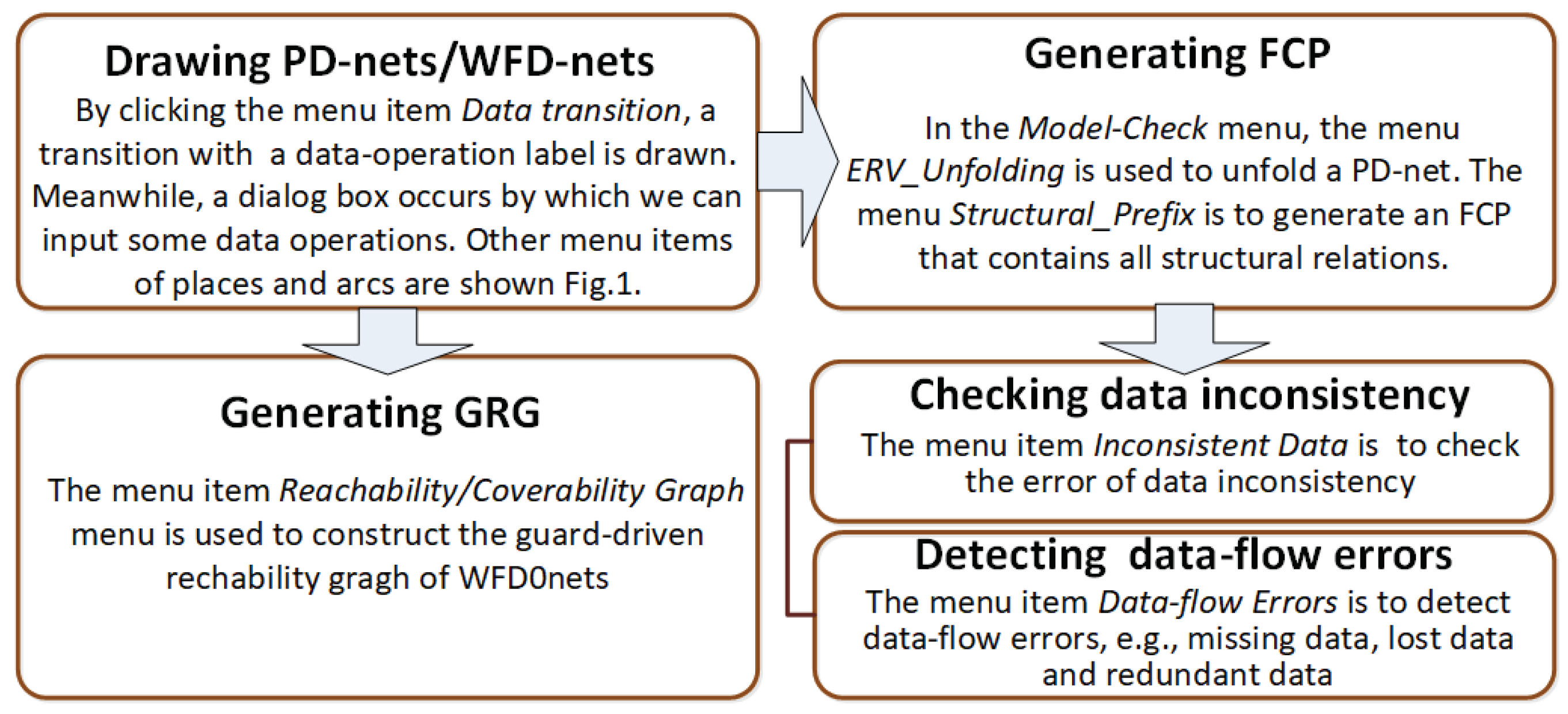
Figure 4 and
Figure 5 show the user interface (UI) and basic functions of DICER 2.0, respectively. Its framework is made up of two modules: graphical user interface (GUI) and model checker (MC), as shown in
Figure 6. These two modules respectively correspond to the menus of drawing and model-checking in
Figure 4.
In the module of graphical user interface, Place/Transition nets, WFD-nets and PD-nets can be imported, exported, drawn and edited. The labeling functions of data operations (e.g., read, write and delete) can be added, deleted and modified in DICER 2.0. Moreover, different kinds of Petri nets are imported and exported in the format of an extended Petri Net Markup Language [
53] (ePNML). In fact, ePNML provides a common interchange format for all types of Petri nets based on XML, and defines specifications of data operations and guard functions. As shown in
Figure 7, the label
formalizes data-flows of concurrent systems, including labeling functions of
read,
write,
delete and
guards. Since ePNML is an XML-based document, we can create or parse these Petri nets according to some configuration files, e.g.,
GenerateObjectList.xsl and
GeneratePNML.xsl.
In the module of model checker, Place/Transition nets and PD-nets can be unfolded, and then we can get their FCPs. As for the FCPs of PD-nets, we can use their matrix calculations (e.g., causality matrix, conflict matrix and concurrency matrix) to find out all concurrent events and then check errors of data inconsistency. Additionally, both classical reachability graphs and guard-driven reachability graphs of WFD-nets can be constructed in DICER 2.0. Furthermore, they are used to analyze some data-flow properties of concurrent systems, e.g., deadlocks, data inconsistency and soundness [
29].
DICER 2.0 is developed-based on Platform Independent Petri Net Editor (PIPE) [
40], which is an open source and graphical tool for drawing and analyzing Petri nets. In details, it is made up of a series of Java classes.
Figure 8 shows the main hierarchy of these classes, which includes some flow information, inheritance relations, interfaces and methods.
The class DataLayer acts on the Petri net modeling of concurrent systems. It can be used to create, edit (e.g., add, move, or modify), import and export a PD-net or a WFD-net. In this class, the method getNewData() is to obtain some information about the Petri net components of FCPs such as events, conditions and arcs.
The class Unfolding is developed to unfold a PD-net or a Place/Transition net. Their FCPs can be generated by the method of unfolding_PDNet(visual, “ERV”, null). In this Java method, the parameter visual indicates whether an FCP needs to be displayed in the software interface, and the parameter ERV means a selected unfolding method, such as ERV, merged process, and directed unfolding.
The class ReachabilityGraphGenerator is used to construct a guard-driven reachability graph of WFD-nets, and the methods generateGraph() and run(DataLayer) correspond to this function.
The class InconsistentData is developed to check errors of data inconsistencies based on the unfolding of PD-nets, and the method detectISData() achieves this work in details.
The classes GuiView and GuiFrame are used to create the front end, and display the software interface of DICER 2.0.
A homomorphism from conditions to places (or from events to transitions) is represented by a hashmap. Its keys and values are in the form of , or , , where Place and Transition are Java classes of Petri net components. Additionally, in order to improve the unfolding efficiency of PD-nets, we use some linked hash tables to store the contextual information of events and concurrent conditions, e.g., local configurations, pre/post-sets and cuts.
6. Conclusions
Data-flow analysis plays an important role in the correctness verification of concurrent software systems. Petri net-based model checkings are a prominent method/technique for analyzing these data-flows. Currently, many different kinds of Petri nets have been used to do this work such as algebraic Petri net, predicate/transitions net, and colored Petri nets. WFD-net, as a high-level Petri net, is extended with conceptual labeling data operations. Thus, it can greatly model control/data- flows of concurrent systems. Moreover, its model scale is much smaller than other Petri nets with data-flow arcs such as C-net and PN-DO. Furthermore, WFD-net has been widely used to do model checkings. However, concurrent data operations and guard functions easily lead to the problems of state–space explosion and pseudo-states. In order to alleviate these problems, we proposed some efficient methods to detect data-flow errors and verify some properties. In this paper, we develop a new model checker DICER 2.0. By this tool, we can do a series of model checkings, e.g., detecting data inconsistencies based on the unfolding technique of PD-nets, and checking deadlocks via the GRG of WFD-nets.
In the future work, we plan to do the following studies:
(1) The unfolding methods of WFD-nets are studied to check many more data-flow errors and concurrency bugs [
64,
65] of concurrent systems;
(2) DICER 2.0 is further improved to support many more efficient model checkings; and
(3) Timed concurrent systems are modeled and checked by the unfolding techniques of Petri nets.