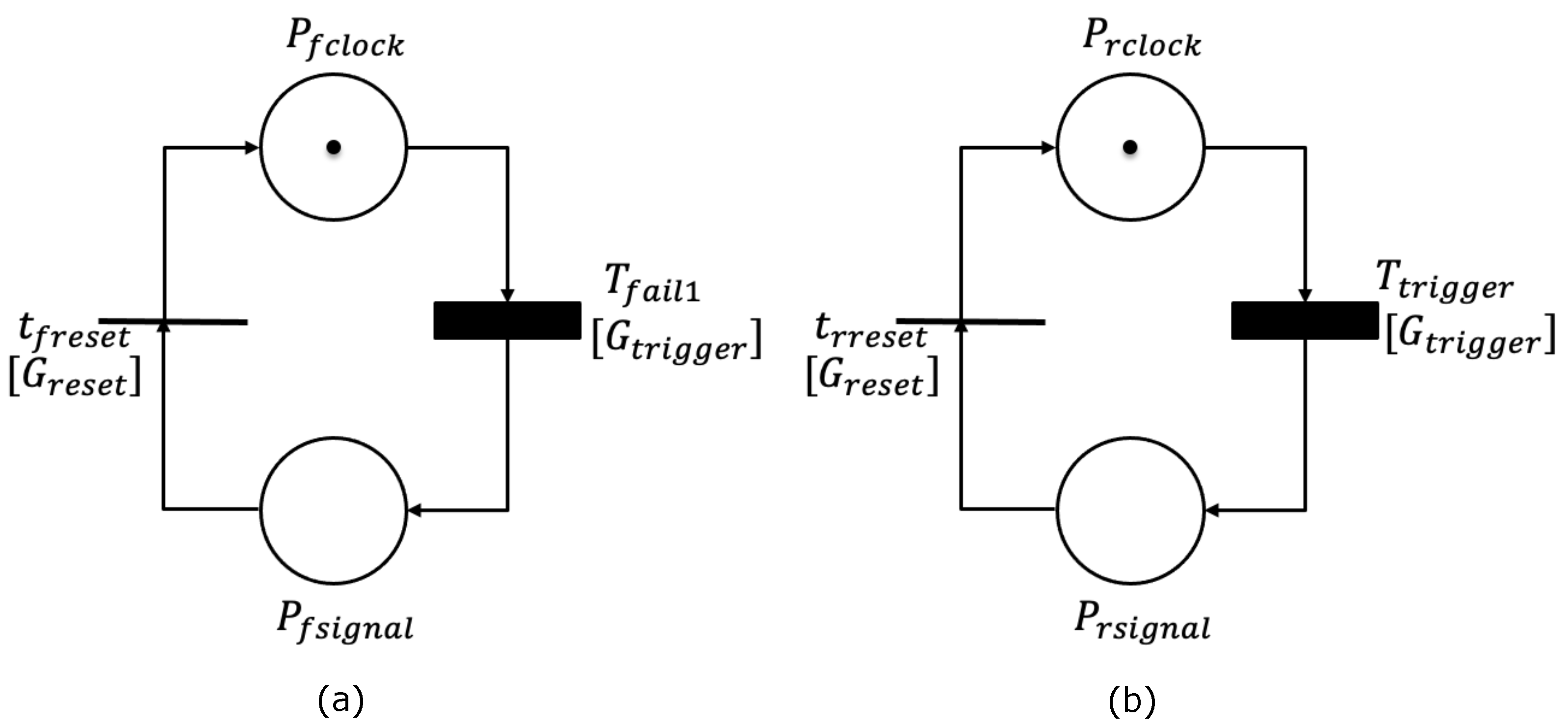
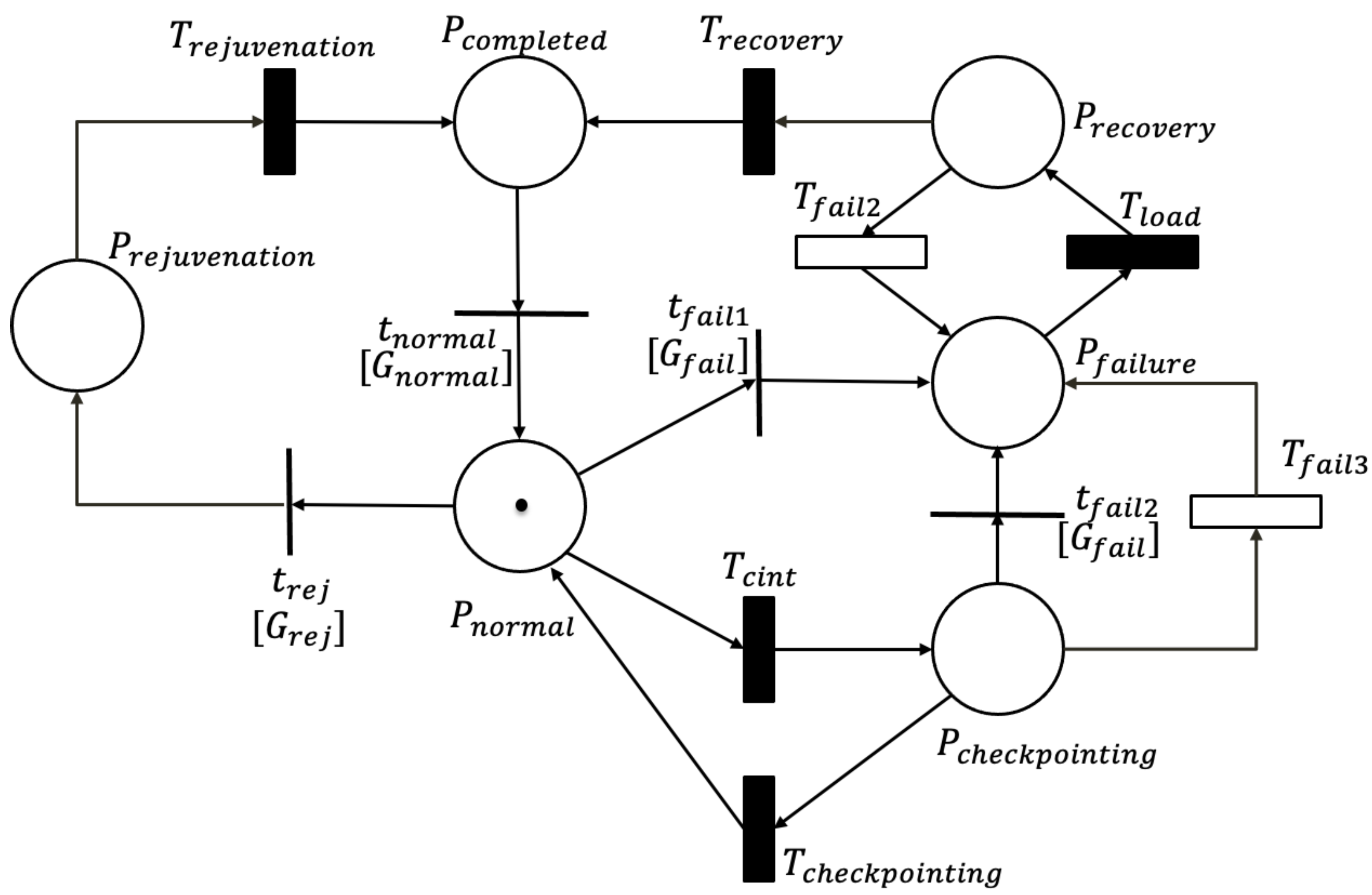
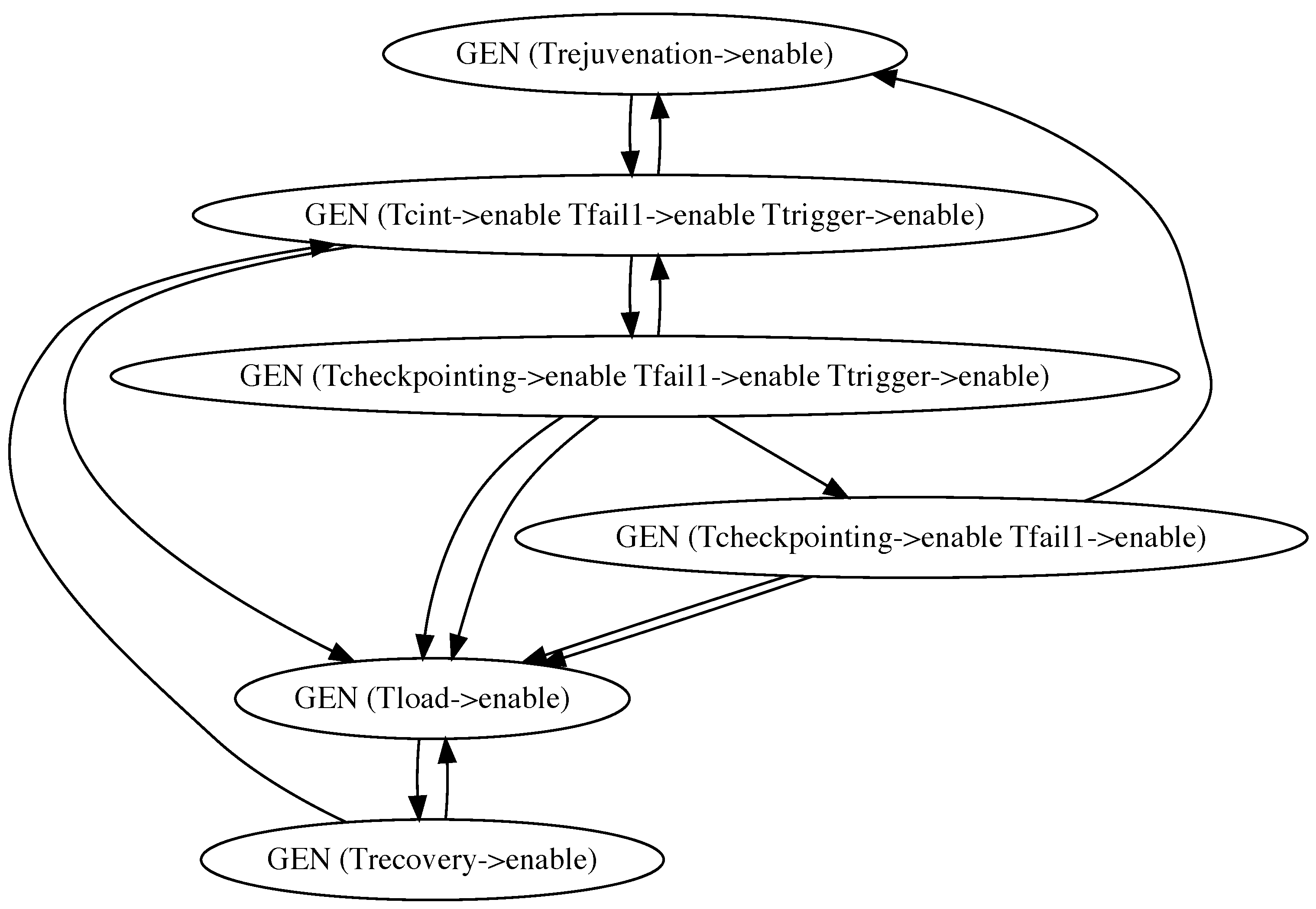
1. Introduction
In software reliability engineering, various software fault-tolerance techniques such as software rejuvenation and checkpointing are widely used for enhancing system reliability and strengthening data protection. Software rejuvenation is a countermeasure against software aging, which refers to the phenomenon that the performance or dependability of software systems degrades with time, caused by aging-related bugs [
1,
2], eventually resulting in system failures. In 1995, Huang et al. [
3] first reported the aging phenomenon in real telecommunication billing applications where the application experienced a crash or a hang failure over time. The software-aging phenomenon exists in the real world and is inevitable, but can nevertheless be controlled or even reversed [
1,
2,
4]. Software rejuvenation plays a central role in counteracting aging issues by refreshing the system’s internal states. However, as pointed out by Alonso et al. [
5], the software rejuvenation can address aging issues well, but typically involves an overhead since the system becomes unavailable during rejuvenation. That is to say, it is necessary and important to determine an optimal rejuvenation schedule for achieving the best trade-off between target performance or dependability and the associated overhead. To date, there are a number of works devoted to solving such optimization problems [
6,
7,
8,
9,
10]. For example, Vaidyanathan and Trivedi [
6] presented a semi-Markov reward model for a UNIX operating system, and used this model to derive optimal software-rejuvenation schedules in terms of system availability or downtime cost. Dohi et al. [
9] considered two basic software-rejuvenation models described by Markov regenerative processes (MRGPs), and provided transient solutions using Laplace–Stieltjes transform (LST) and their numerical inversion. In [
9], an optimal software-rejuvenation policy that maximized interval system reliability was numerically determined. Wang and Liu [
10] recently offered a real-time decision method for optimal software-rejuvenation timing through simulating and modeling the state-transition process of software aging and constructing the rejuvenation decision function using an analytic hierarchy process.
In the context of data protection, a typical technique is checkpointing, which is an efficient method for saving re-execution time in the presence of faults [
11] through saving current data in the main memory to secondary storage. Checkpointing is easy to conduct and has been widely studied for decades [
12,
13,
14,
15,
16]. For example, Fukumoto et al. [
12], and Dohi et al. [
13] introduced different checkpointing schemes for database systems, and Ranganathan and Upadhyaya [
14] considered the temporal behavior related to database system states from a macroscopic viewpoint. Some of the literature also considered software rejuvenation and checkpointing together [
17,
18,
19,
20]. Okamura and Dohi [
17] focused on two kinds of maintenance policies for a software system, and adopted a dynamic programming approach to comprehensively evaluate aperiodic checkpointing and rejuvenation schemes in the system. In [
19], the authors introduced a stochastic reward Petri net (SRN) [
21] to model a software system of which the state moves to the execution process immediately after a rollback recovery. In particular, according to SRN analysis, a non-Markovian state-transition diagram was derived. More recently, a similar to but somewhat different system from [
19] was considered in [
20], in which the system executes checkpointing immediately after a rollback recovery in order to update the starting point of the recovery operation from the past to the current time. In these previous works, the systems underwent both aperiodic checkpointing and software rejuvenation, and their transition diagrams are not one of the trivial stochastic models such as semi-Markov process (SMP) and MRGP. That means that common approaches such as the LST and embedded Markov chain techniques cannot be directly applied. To solve these complex non-Markovian transition diagrams, the phase (PH) expansion approach [
22,
23], which is an approximation technique by using phase-type (PH) distribution, was utilized and worked well in different contents. Moreover, in [
19,
20], it was assumed that system failures are caused by only aging problems, but in fact, human error is inescapable [
24], and the system operator’s misoperations during checkpointing cannot be ignored [
25].
In this paper, we consider the different software systems from [
19,
20], where both aperiodic checkpointing and software rejuvenation were executed, and system failure occurred due to both software aging and human errors in checkpointing. A stochastic framework composed of a composite SRN and its resulting non-Markovian availability model is presented to capture the dynamics of the system from a macroscopic point of view. More specifically, the non-Markovian availability model was derived from the reachability graph of the composite SRN model. On the basis of the non-Markovian availability model, which is also a nontrivial model including multiple competitive events as in [
19,
20], we formulated the steady-state availability of the system by means of PH expansion, and then determined the optimal software-rejuvenation schedule that maximized steady-state system availability. The effects of human-error factors on both steady-state system availability and optimal software-rejuvenation schedule are investigated. The main differences between this work and previous ones [
19,
20] are that we (i) consider both aging-related and human-error-related system failures, of which the latter was overlooked in previous works; and (ii) investigate the effect of human-error factors on system availability and software rejuvenation. For brevity, the main contributions of this paper are summarized as twofold:
stochastic modeling of software systems that undergo both software rejuvenation and checkpointing, and may fail due to both the aging problem and human errors in checkpointing;
investigation of the effects of human-error factors on both steady-state system availability and optimal software-rejuvenation trigger timing by the comparison of cases where human-error-related system failures are considered or not.
The remainder of this paper is organized as follows. In
Section 2, a stochastic framework composed of a composite SRN and its corresponding non-Markovian state-transition diagram for an operational software system with software rejuvenation and checkpointing are introduced. In particular, a reachability graph was generated from the composite SRN, and on its basis, a non-Markovian state-transition diagram was obtained.
Section 3 first defines continuous PH distribution and presents an approach to formulate the steady-state system availability of the non-Markovian model by using the underlying approximate CTMC of the non-Markovian model, which was derived by replacing all general distributions with their corresponding PH distributions. In
Section 4, we describe conducted numerical experiments that evaluated system availability, determined the optimal software-rejuvenation trigger timing, and quantified the effects of human-error factors. Lastly, in
Section 5, we conclude this paper with some remarks.
3. System Availability Analysis
This section first introduces the well-known continuous PH distribution [
22] and then derives the underlying approximate CTMC for the non-Markovian state-transition diagram in
Figure 4 via PH expansion approach, of which the essential idea is to replace general distribution with its corresponding PH distribution at a high accuracy level. Lastly, the stationary solution for the model in
Figure 4 through CTMC analysis is presented. The measure of interest is steady-state system availability, which is defined as the probability that the system is operational in the steady state.
3.1. Continuous PH Distribution
Continuous PH distribution is defined as the probability distribution of absorbing time in a finite CTMC with absorbing states, and it is widely applied in various fields, such as reliability assessment [
26], queueing systems [
27], and random telegraph noise analysis [
28]. Without loss of generality, we define
as an infinitesimal generator matrix of a CTMC that has
m transient states and one absorbing state, and then partition
into four parts as below:
In the above,
and
represent transition rates among transient states and exit rates from transient states to the absorbing state, respectively. Defining
as an initial probability vector over the transient states, we have the CDF and probability density function (PDF) for the continuous PH distribution:
where
is a column vector of ones. Exit vector
is given by
. Transient states are called phases in general.
Continuous PH distribution can be categorized into several subclasses according to the structure of
[
29]. When phase transition is acyclic, the corresponding PH distribution is called acyclic PH distribution (APH). The APH is the widest class among mathematically tractable PH distributions, and it can be converted into the canonical form (CF), which is the minimal representation of APH with the smallest number of free parameters [
30]. The APH and its CF are important from the viewpoint of practical applications because it covers some well-known probability distributions, such as exponential distribution, Erlang distribution, and their mixtures. In particular, canonical form 1 (CF1) is usually considered and defined by
where
,
and
for
m phases.
In this paper, continuous PH distribution was applied to approximate all general distributions in the non-Markovian state-transition diagram, that is, to determine PH distribution with parameters
, which can fit the target distribution well by means of maximum likelihood estimation (MLE) approach [
22].
3.2. PH-Expanded CTMC
According to the definition of PH distribution in
Section 3.1, we define the general distributions in
Table 4 by PH distributions with appropriate phases as follows:
Here, PH parameters
,
,
,
,
,
,
,
were estimated on the basis of MLE using an expectation–maximization (EM) algorithm [
22,
31]. Using the above-estimated PH distributions to replace general distributions, the non-Markovian transition diagram was expanded into an approximate CTMC, alternatively called PH-expanded CTMC, of which the infinitesimal generator matrix is given by
The infinitesimal generator matrix is derived on the basis of the Kronecker representation [
23], and the order of states is {
Normal, Checkpointing, Checkpointing’, Rejuvenation, Failure1, Recovery, Failure2}. In Equation (
13), ⊕ and ⊗ are the Kronecker product and sum [
32],
is an identity matrix, and
and
are the mean values of EXP distributions
and
, say the mean times to failure during rollback recovery and checkpointing, respectively.
Entry shows that the clock of the rejuvenation trigger is not reset and continuously accumulates, even when the system executes the checkpointing. Since the checkpointing operation just saves the current data and does not refresh system aging, entry indicates that only the clock of checkpointing trigger is reset. When a rejuvenation point is reached while the system is under checkpointing, rejuvenation waits until checkpointing is completed; in such a case, the system transits from to with entry . Entries , , and indicate aging-related failures in both normal and checkpointing states, while entries and represent human-error-related failures during checkpointing. In addition, the system is regarded to be as good as new after either rollback recovery or rejuvenation, so the corresponding transitions are represented by entries , and , where implies that the clocks of checkpointing trigger, system aging, and rejuvenation trigger are refreshed at the same time.
3.3. Steady-State System Availability
Steady-state system availability gives the probability that the system is operational in the steady state, so that it provides a significant insight into the long-term performance of a repairable system. Let
define the steady-state system availability. Then, we can obtain it by
where
is the steady-state probability vector of the PH-expanded CTMC,
, and can be computed by solving the following linear equation [
33]:
and
is the reward (column) vector of the PH-expanded CTMC and given by
It is clear that the system is only available in the normal execution process state. In this paper, one problem of interest is to determine optimal software-rejuvenation timing that maximizes steady-state system availability.
5. Conclusions
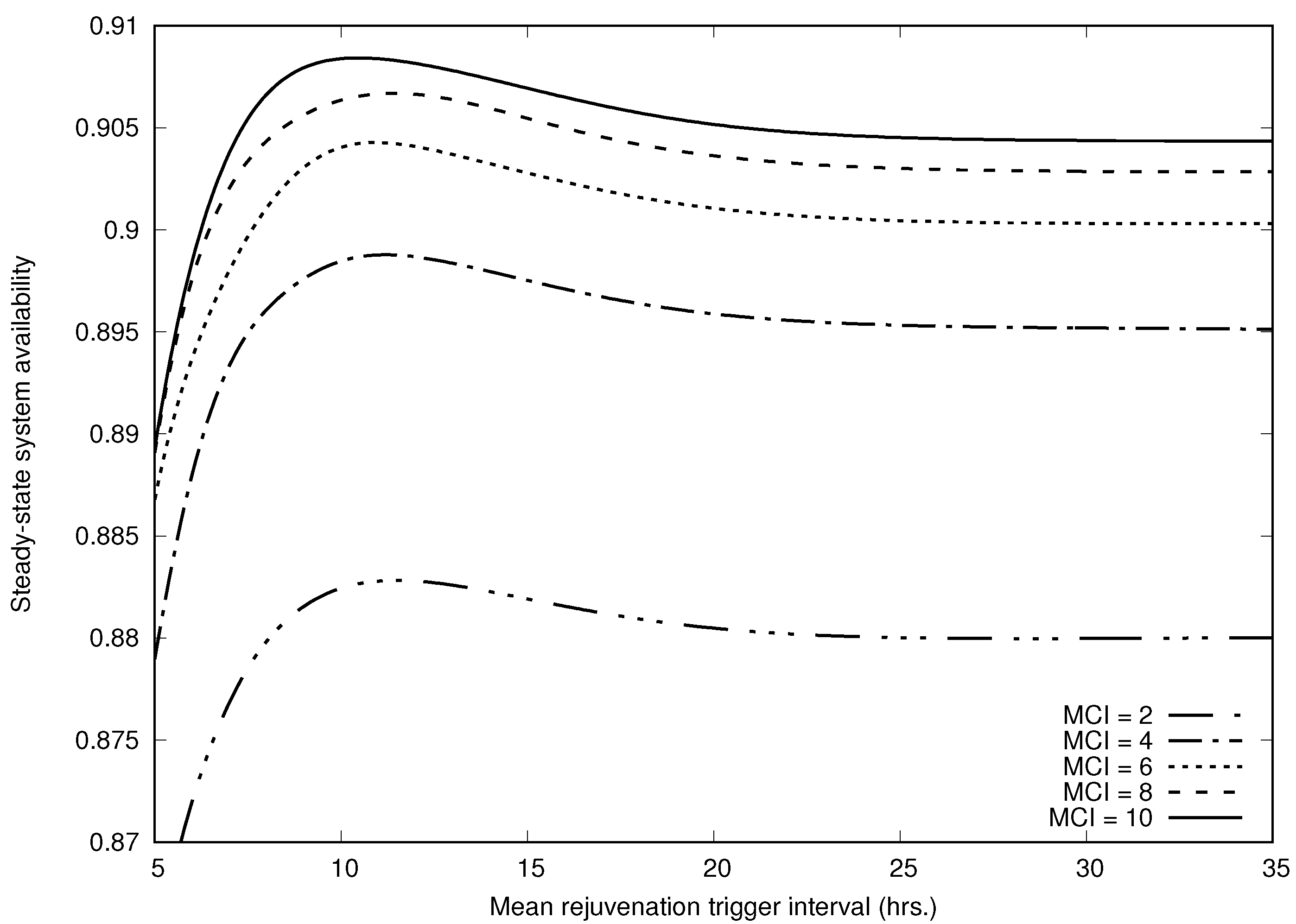
In this paper, we presented a composite stochastic Petri reward net and its resulting non-Markovian availability model for operational software systems where both checkpointing and software rejuvenation are adopted to protect data and to enhance the system availability, and the system may fail due to both the aging problem and human errors during checkpointing. More specifically, the non-Markovian availability model was derived on the basis of a reachability graph that was generated from the original SRNs. In particular, the PH expansion approach was applied to solve the stationary solution of the non-Markovian availability model since the model was not one of the trivial stochastic models such as SMP and MRGP, so that common approaches such as LST and embedded Markov chain techniques do not work. Numerical results showed that human-error factors both decreased steady-state system availability and brought a significant effect on optimal rejuvenation-trigger timing, which means that human-error factors during system modeling should not be overlooked.
The model presented in this paper was based on a macroscopic view, providing a fundamental idea of how to model such a software system that undergoes both checkpointing and software rejuvenation, and in which the system behaves with multiple competitive events. The system’s actual behavior is very complex, and more possible events need to be considered, for example, software environment upgrades and time-scope limitations of used versions of libraries. Although this improvement may vastly increase difficulty in numerical analysis, it is significant to take a microscopic look at system behavior, which will be one of our future directions. This paper only considered both aperiodic checkpointing and software rejuvenation, but to the best of our knowledge, there exist various kinds of checkpointing [
35] and rejuvenation techniques [
8]. In the future, we aim to extend this work to solve more complicated software systems considering different rejuvenation and checkpointing schemes.