Analytical Modelling of LACFCST Stub Columns Subjected to Axial Compression
Abstract
:1. Introduction
2. Finite Element Modelling of LACFCST Stub Columns
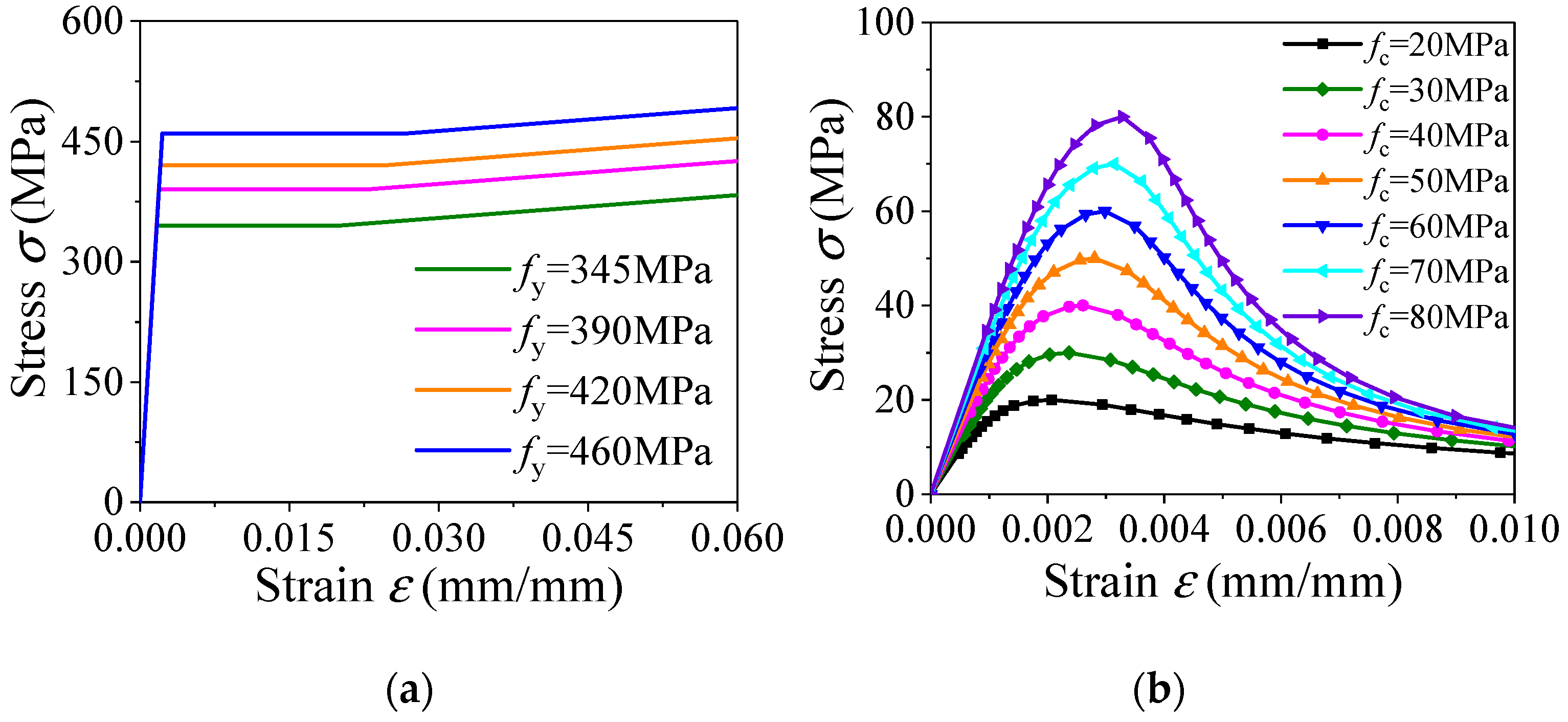
2.1. Constitutive Relation of the Steel Tube
2.2. Constitutive Relation of Lightweight Aggregate Concrete
2.3. Element Type and Mesh Size
2.4. Contact Interaction, Boundary Conditions and Loading
2.5. Constitutive Model Parameter Settings
2.6. Geometric Imperfection and Residual Stresses
3. Finite Element Analysis
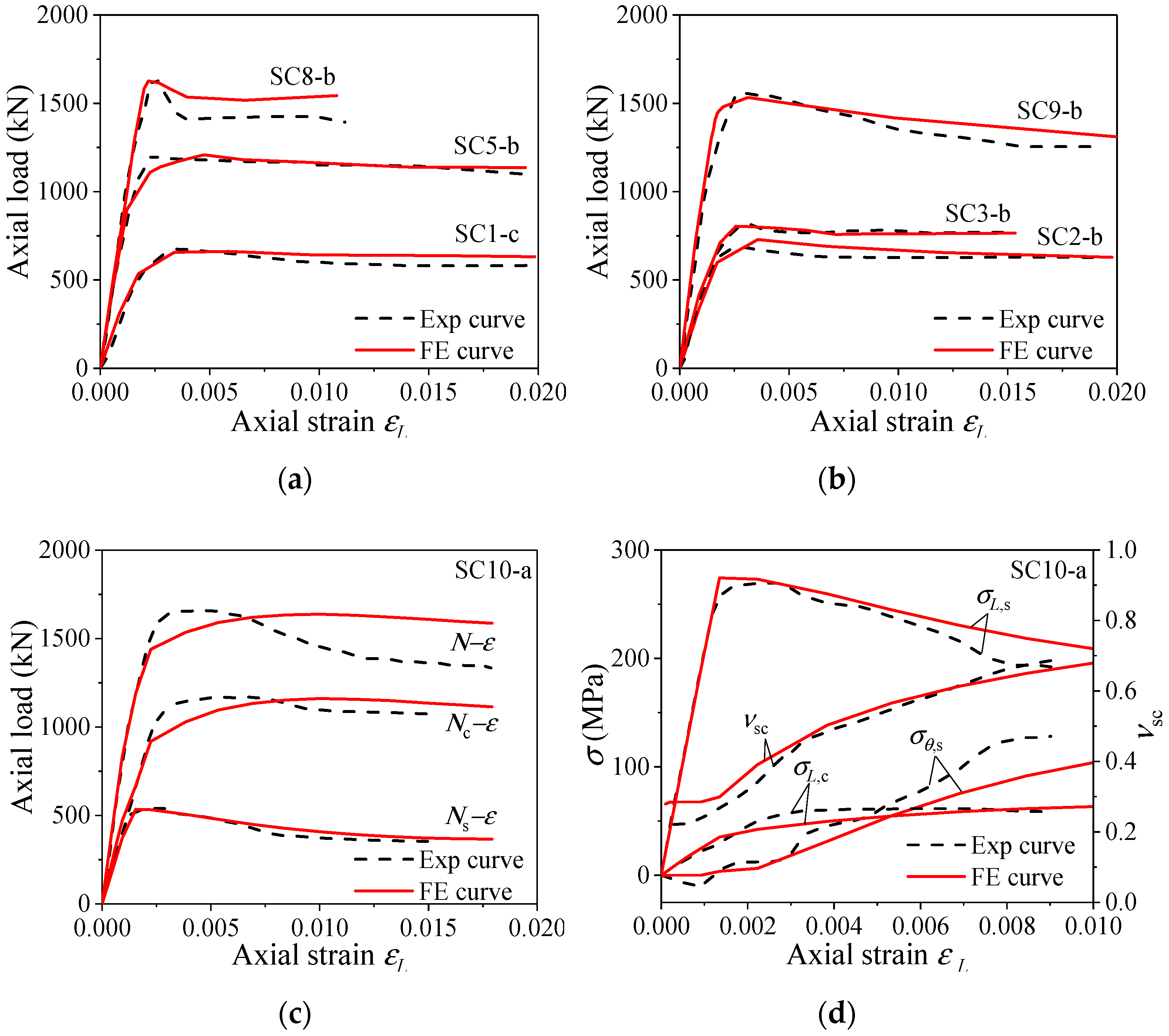
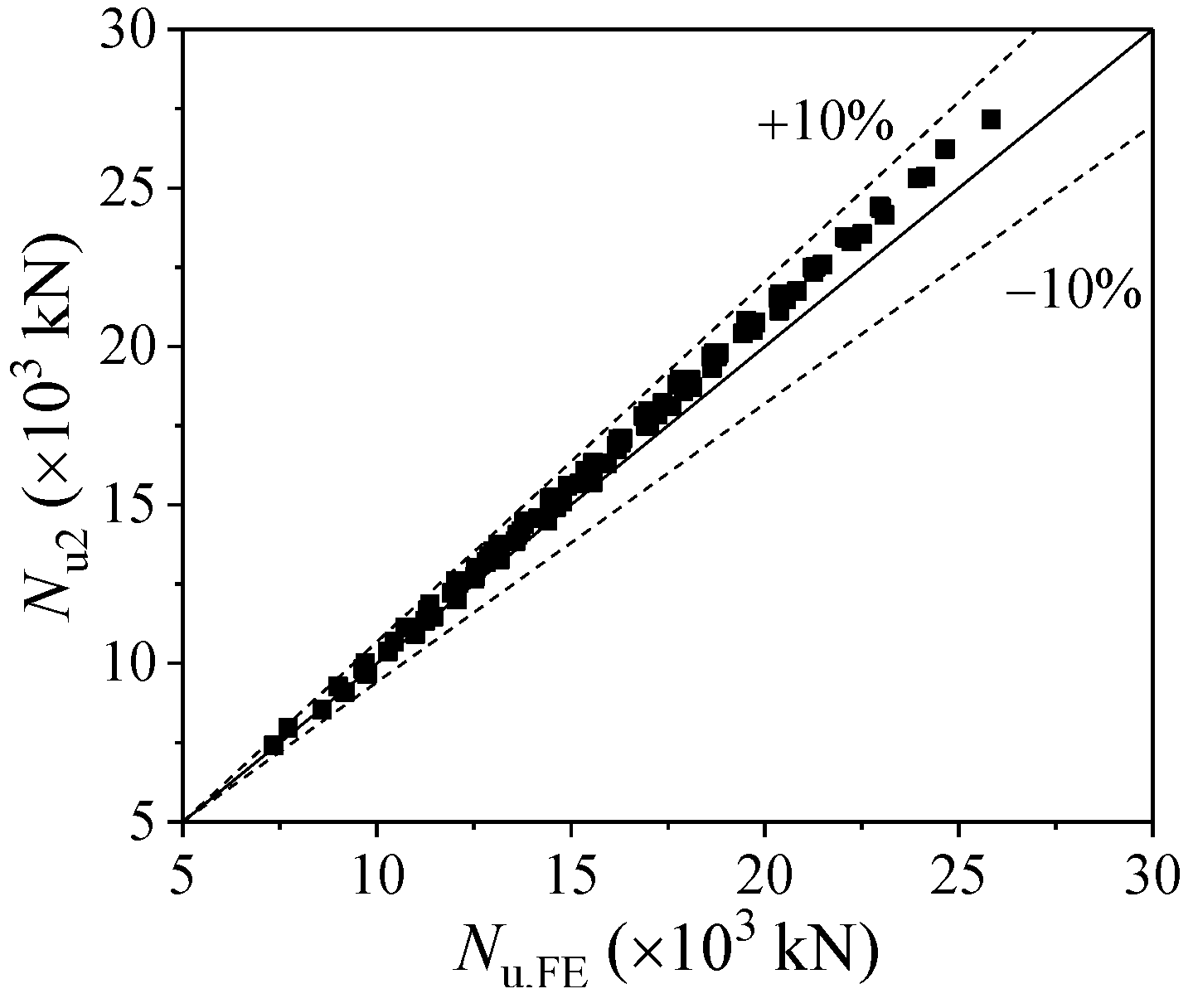
3.1. Model Validation
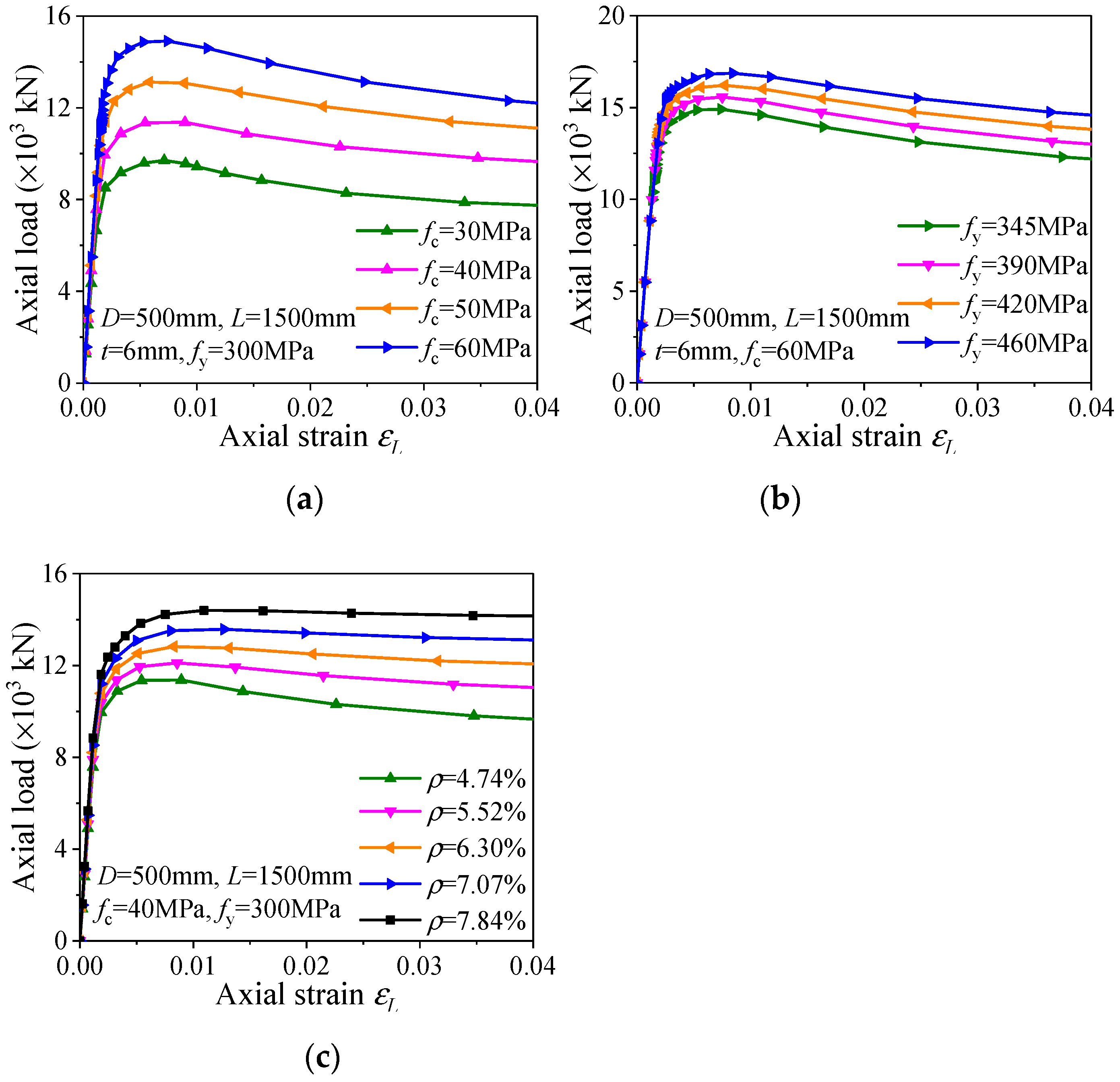
3.2. Parametric Study
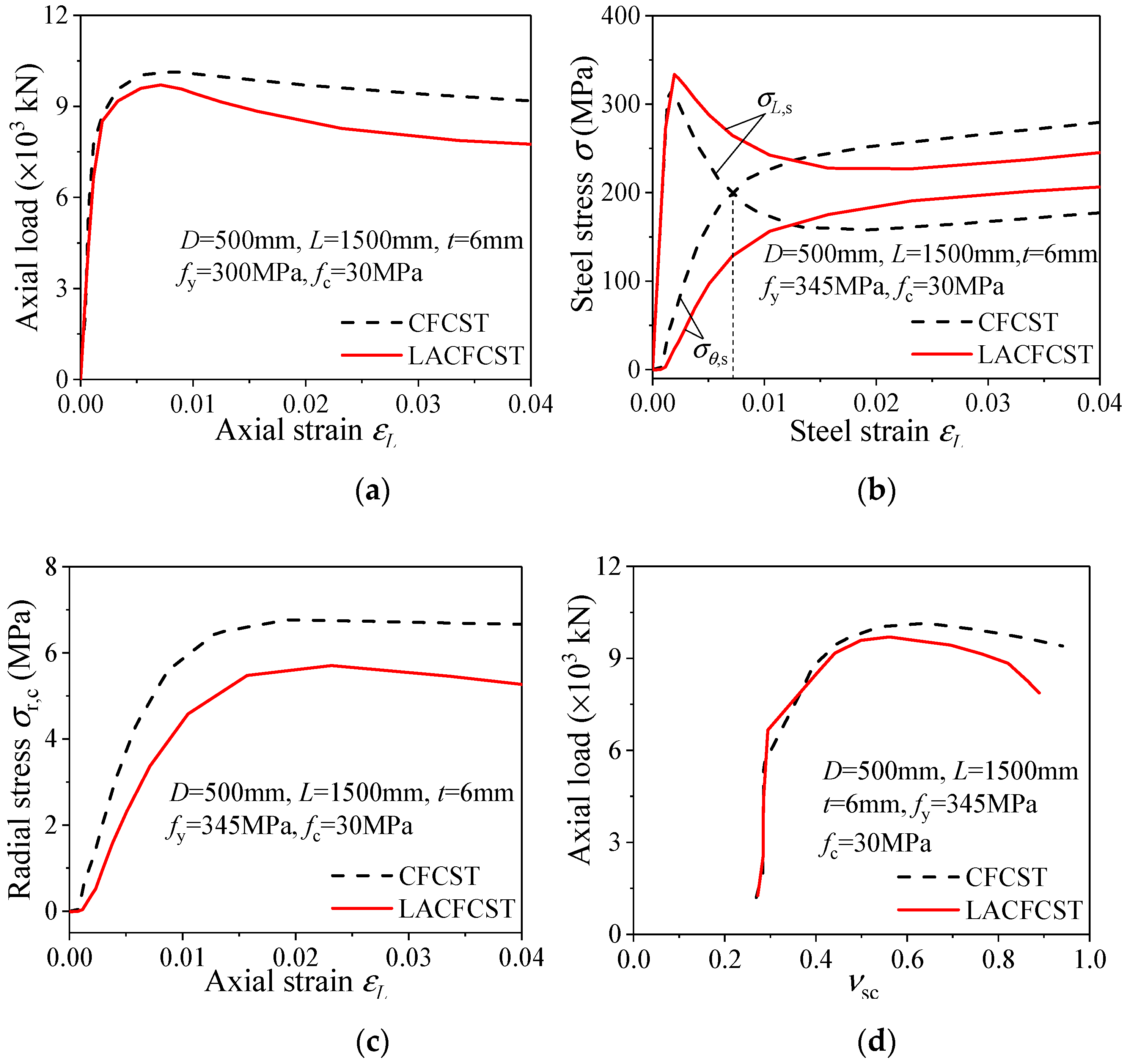
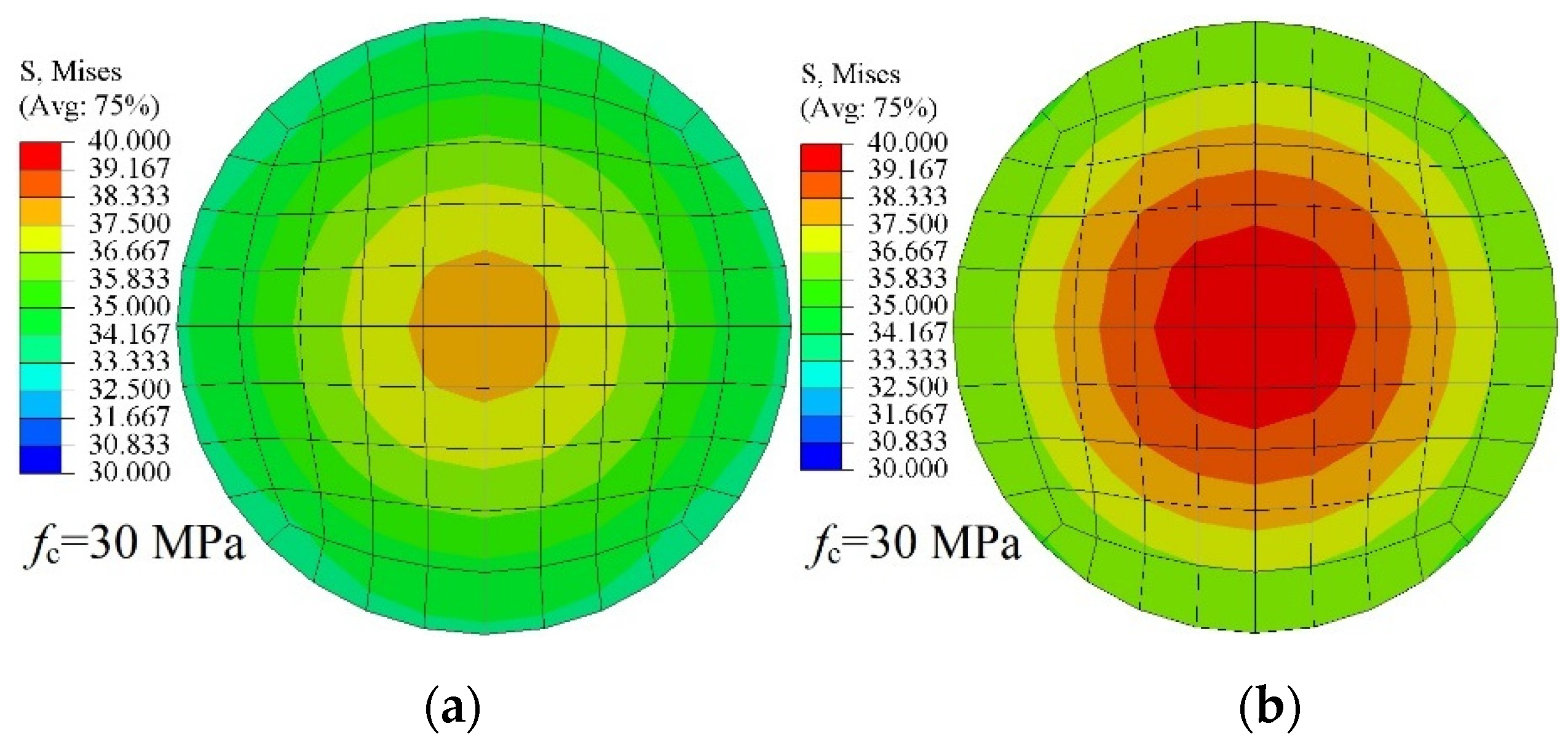
3.3. Comparison of CFCST and LACFCST Columns
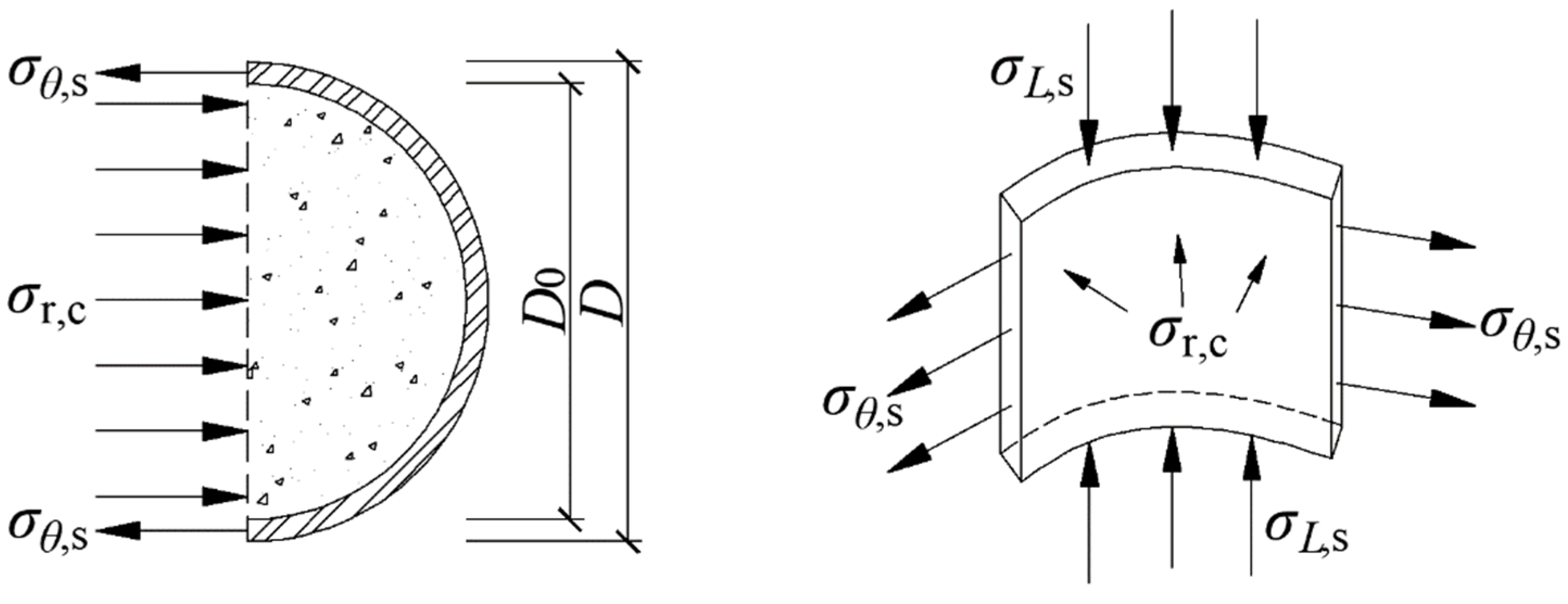
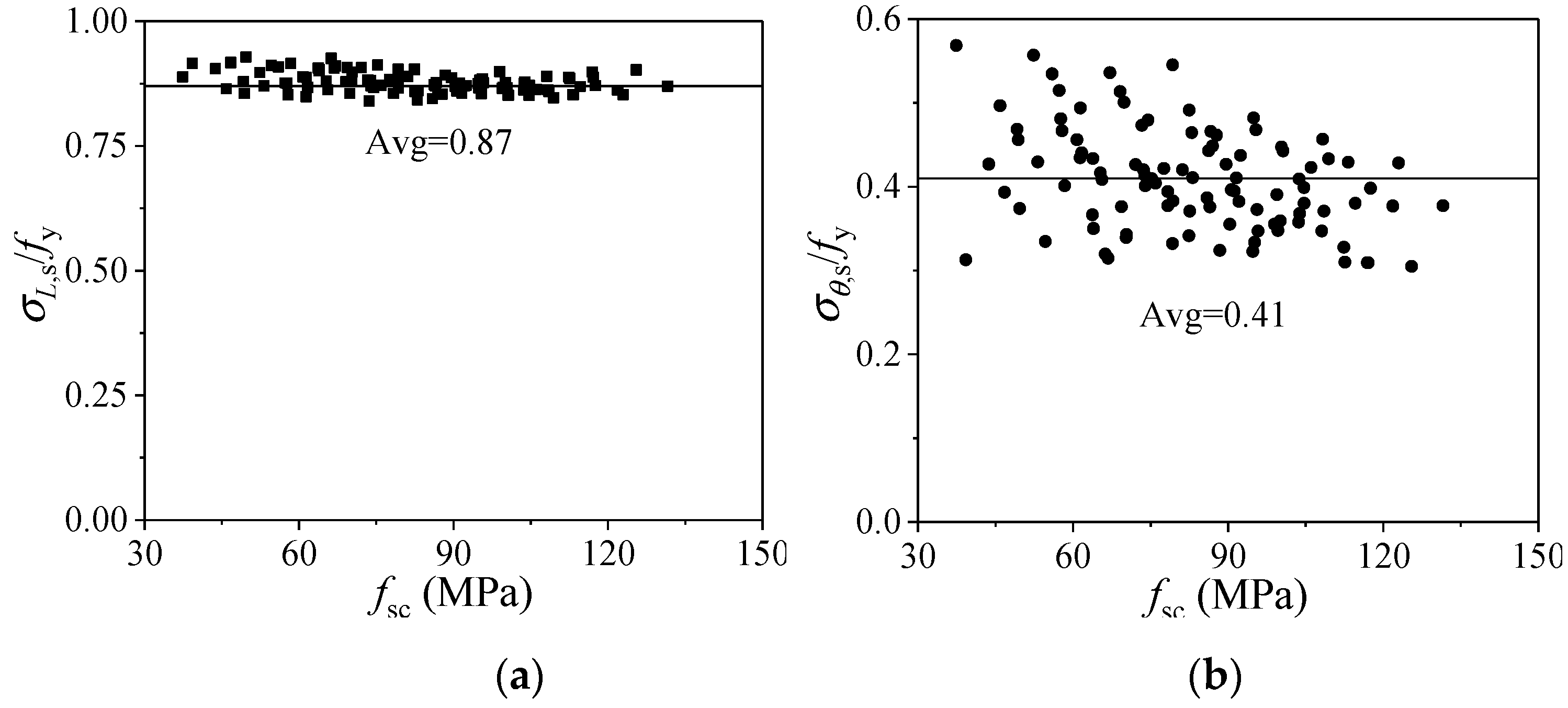
3.4. Composite Action Model of LACFCST Stub Columns
4. Practical Design Formula for the Load-Bearing Capacity of LACFCST Stub Columns
4.1. Model Simplification
4.2. Formulation
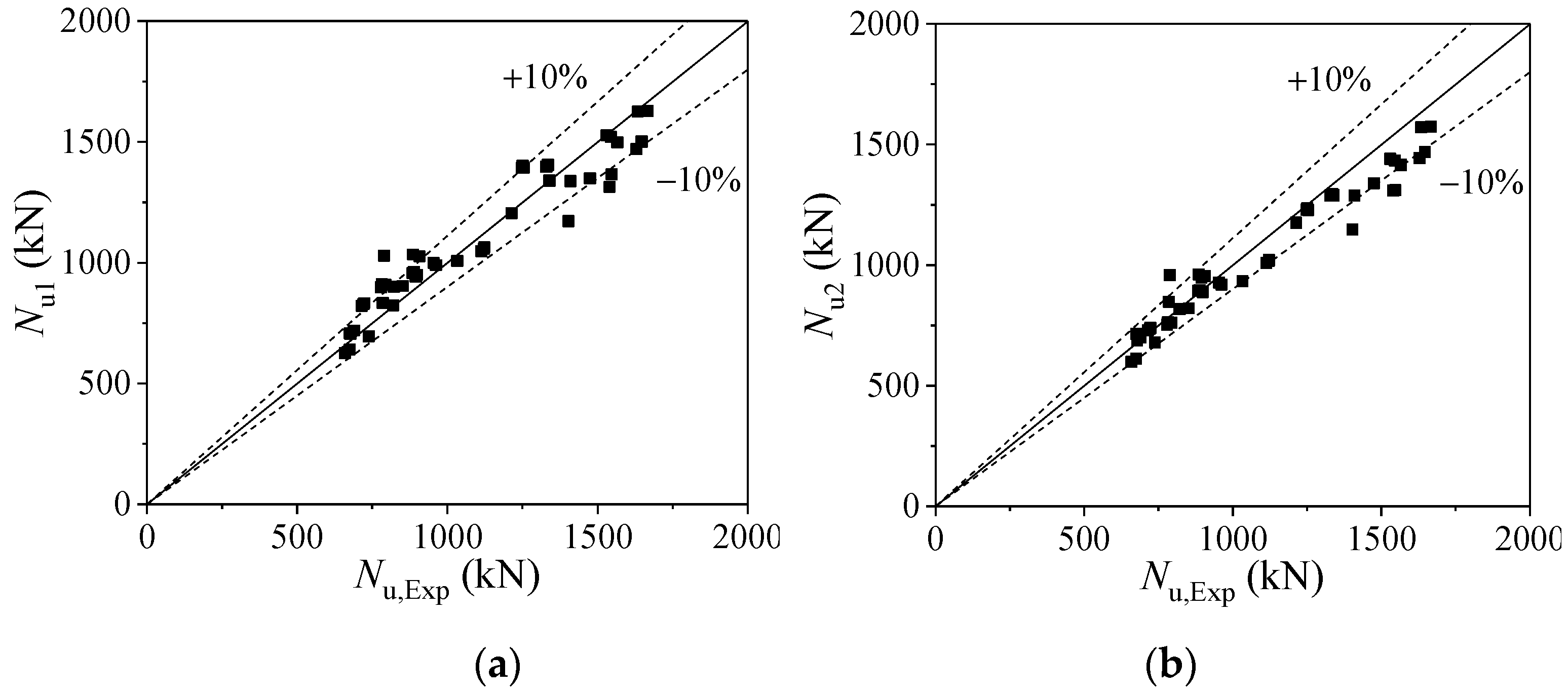
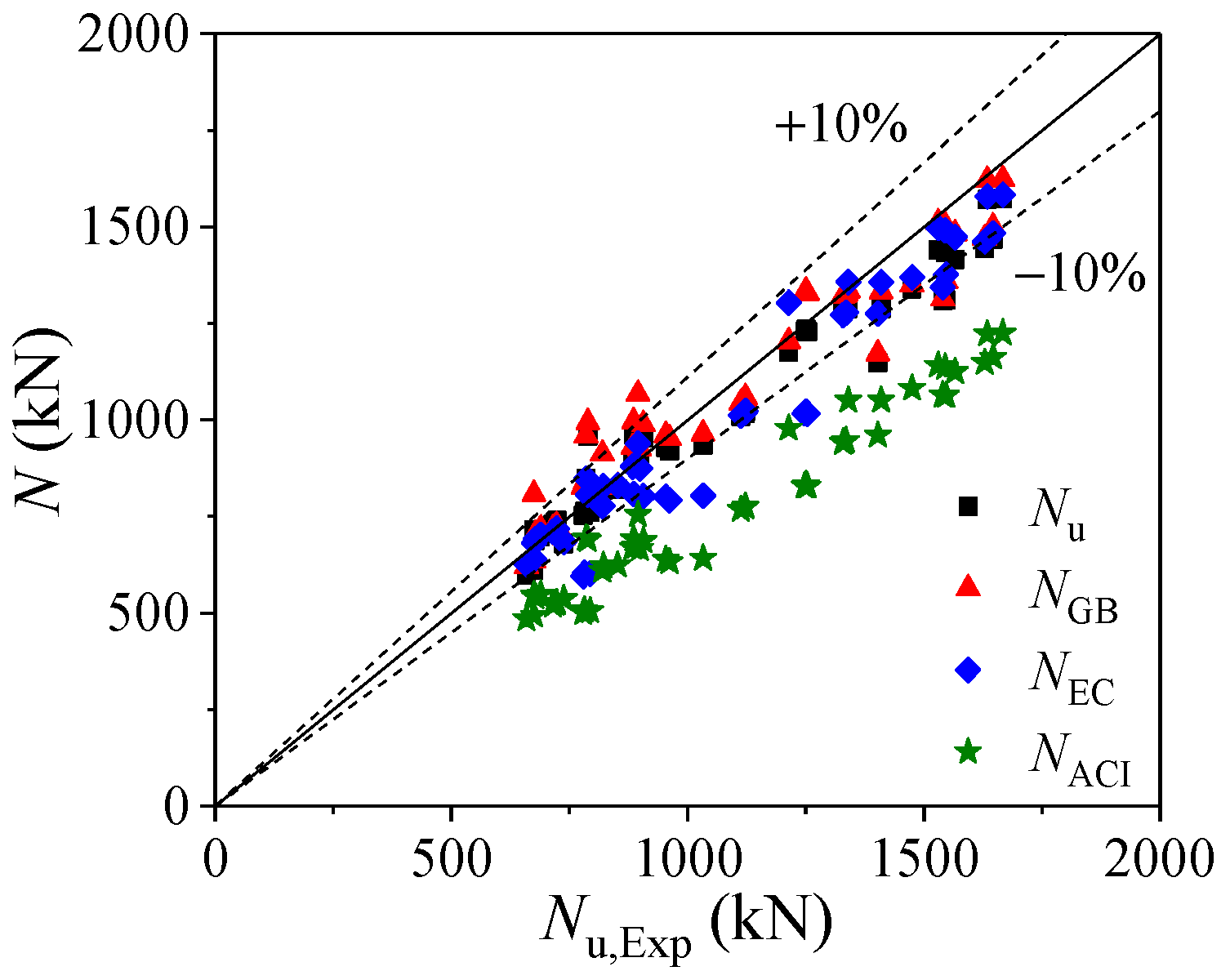
4.3. Formulas Validation
5. Conclusions
- Using a plastic-damage constitutive model of LAC and an elastoplastic model with isotropic strain hardening of the steel tube, a fine-meshed finite 3D solid element model of the LACFCST stub column was established in ABAQUS. The validity of the established FEM was verified against the test results of the ultimate bearing capacity and strain responses of the steel tube, and the load-shortening curves.
- A total of 95 full-scale FEMs, using the abovementioned FE modeling method, were established for the parametric study. The analytical results revealed that the composite action in LACFCST stub columns is weaker than that in CFST stub columns.
- Regression models of the axial and transverse stress of the outer steel tube at the ultimate state of the columns were proposed, respectively. This model considered the three-dimensional stress state of the outer tube and is a more authentic expression when the column reaches its ultimate state.
- A design formula of ultimate bearing capacity of LACFCST stub columns under axial loading was derived based on the proposed composite action model. A simplified formula using an enhancement factor was proposed as well. The derived enhancement factor of LACFCST stub columns is 1.57, which is slightly smaller than 1.62 of CFCST stub columns. The proposed formula was verified as more accurate and concise than current design methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ac | Cross-sectional area of infilled concrete |
| As | Cross-sectional area of steel tube |
| Asc | Cross-sectional area of LACFCST column |
| D | Outer diameter of steel tube |
| D0 | Inner diameter of steel tube |
| Es | Elastic modulus of steel tube |
| fc | Uniaxial compressive strength of LAC |
| fcu | Compressive cubic strength of LAC |
| fsc | Nominal average axial stress |
| fu | Ultimate strength of steel tube |
| fy | Yield strength of steel tube |
| K | Enhancement factor |
| L | Length of column specimen |
| NACI | Ultimate bearing capacity calculated by ACI-318 |
| NEC | Ultimate bearing capacity calculated by EC 4 |
| NGB | Ultimate bearing capacity calculated by GB 50936 |
| Nu | Ultimate bearing capacity of stub columns |
| Nu,Exp | Ultimate bearing capacity obtained from test |
| Nu,FE | Ultimate bearing capacity obtained from FEMs |
| t | Wall-thickness of steel tube |
| ξ | Confinement factor |
| ρ | Steel ratio of LACFCST column |
| εc | Strain at the peak compressive stress |
| εL | Longitudinal strain of steel tube |
| εst | Hardening strain of steel tube |
| εu | Ultimate strain of steel tube |
| εy | Yield strain of steel tube |
| σL,c | Axial compressive stress of infilled concrete |
| σL,s | Axial compressive stress of steel tube |
| σr,c | Radial stress of infilled concrete |
| σθ,s | Transverse tensile stress of steel tube |
| νsc | Transverse deformation coefficient |
References
- Ghazijahani, T.G.; Jiao, H.; Holloway, D. Rectangular steel tubes with timber infill and CFRP confinement under compression: Experiments. J. Constr. Steel Res. 2015, 114, 196–203. [Google Scholar] [CrossRef]
- Assi, I.M.; Qudeimat, E.M.; Hunaiti, Y.M. Ultimate moment capacity of foamed and lightweight aggregate concrete-filled steel tubes. Steel Compos. Struct. 2003, 3, 199–212. [Google Scholar] [CrossRef]
- Mouli, M.; Khelafi, H. Strength of short composite rectangular hollow section columns filled with lightweight aggregate concrete. Eng. Struct. 2007, 29, 1791–1797. [Google Scholar] [CrossRef]
- Cui, H.; Lo, T.Y.; Memon, S.A.; Xu, W. Effect of lightweight aggregates on the mechanical properties and brittleness of lightweight aggregate concrete. Constr. Build. Mater. 2012, 35, 149–158. [Google Scholar] [CrossRef]
- Elremaily, A.; Azizinamini, A. Behavior and strength of circular concrete-filled tube columns. J. Constr. Steel Res. 2002, 58, 1567–1591. [Google Scholar] [CrossRef]
- Ding, F.; Wang, W.; Liu, X.; Wang, L.; Sun, Y. Mechanical behavior of outer square inner circular concrete-filled dual steel tubular stub columns. Steel Compos. Struct. 2021, 38, 305–317. [Google Scholar] [CrossRef]
- Gupta, P.K.; Ahuja, A.K.; Khaudhair, Z.A. Modelling, verification and investigation of behaviour of circular CFST columns. Struct. Concr. 2014, 15, 340–349. [Google Scholar] [CrossRef]
- Ghannam, S.; Jawad, Y.A.; Hunaiti, Y. Failure of lightweight aggregate concrete-filled steel tubular columns. Steel Compos. Struct. 2004, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Abhilash, M.; Jhanjhari, S.; Parthiban, P.; Karthikeyan, J. Axial behaviour of semi-lightweight aggregate concrete-filled steel tube columns—A DOE approach. J. Constr. Steel Res. 2019, 162, 105614. [Google Scholar] [CrossRef]
- Salgar, P.B.; Patil, P.S. Experimental Investigation on Behavior of High-Strength Light weight Concrete-Filled Steel Tube Strut Under Axial Compression. INAE Lett. 2019, 4, 207–214. [Google Scholar] [CrossRef]
- European Committee for Standardization. EUROCODE 4. Design of Steel Composite Steel and Concrete Structures; Part 1-1, General Rules and Rules for Building, BS EN 1994-1-1; British Standards Institution: London, UK, 2004. [Google Scholar]
- American Concrete Institute. ACI-318-11. Building Code Requirements for Structural Concrete and Commentary ACI Committee 318; American Concrete Institute: Detroit, MI, USA, 2011. [Google Scholar]
- Zhang, X.; Kuang, X.; Yang, J.; Fan, Y. Bearing Capacity of Stone-Lightweight Aggregate Concrete-Filled Steel Tubular Stub Column Subjected to Axial Compression. KSCE J. Civ. Eng. 2019, 23, 3122–3134. [Google Scholar] [CrossRef]
- Fu, Z.; Ji, B.; Zhou, Y.; Wang, X. An experimental behavior of lightweight aggregate concrete filled steel tubular stub under axial compression. Geotech. Spec. Publ. ASCE 2011, 219, 24–32. [Google Scholar] [CrossRef]
- Yang, M. Research on the Behavior of Core Lightweight Aggregate Concrete under the Confinement of Steel Tube. Master’s Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar] [CrossRef]
- Fu, Z.Q.; Ji, B.H.; Ge, H.B.; Yang, M. Combined strength of lightweight aggregate concrete-filled steel tube. Mater. Res. Innov. 2015, 19, 5–898. [Google Scholar] [CrossRef]
- Fu, Z.; Ge, H.; Ji, B.; Chen, J. Interface bond behaviour between circular steel tube and lightweight aggregate concrete. Adv. Steel Constr. 2018, 14, 424–437. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.Y.; Li, B. Experimental Research on Seismic Behavior for Lightweight Aggregate Concrete-Filled Steel Tubular Frame. Adv. Mater. Res. 2010, 163–167, 2194–2198. [Google Scholar] [CrossRef]
- Ding, F.-X.; Yin, Y.-X.; Mao, J.-F.; Wang, L.-P.; Yu, Y.-J.; Luo, L.; Yu, Z.-W. Analytical behaviors of concrete-filled circular stainless steel tubular (CFCSST) stub columns under axial loading. Structures 2019, 19, 277–285. [Google Scholar] [CrossRef]
- Ding, F.; Yin, Y.; Wang, L.; Yu, Y.; Luo, L.; Yu, Z. Confinement coefficient of concrete-filled square stainless steel tubular stub columns. Steel Compos. Struct. 2019, 30, 337–350. [Google Scholar] [CrossRef]
- Ding, F.; Ying, X.; Zhou, L.; Yu, Z. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete. Front. Arch. Civ. Eng. China 2011, 5, 381–393. [Google Scholar] [CrossRef]
- Ding, F.; Ying, X.; Yu, Z. Unified calculation method of uniaxial mechanical properties of lightweight aggregate concrete. J. Cent. South. Univ. 2010, 41, 1973–1979. Available online: https://www.researchgate.net/publication/291828442_Unified_calculation_method_of_uniaxial_mechanical_properties_of_lightweight_aggregate_concrete (accessed on 22 April 2021). (In Chinese).
- ABAQUS. ABAQUS Standard User’s Manual, Version 6.14; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2014. [Google Scholar]
- ABAQUS. ABAQUS Analysis User’s Manual, Volume IV: Elements; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2014. [Google Scholar]
- Zhang, T.; Ding, F.; Wang, L.; Liu, X.; Jiang, G. Behavior of polygonal concrete-filled steel tubular stub columns under axial loading. Steel Compos. Struct. 2018, 28, 573–588. [Google Scholar] [CrossRef]
- Wosatko, A.; Winnicki, A.; Polak, M.A.; Pamin, J. Role of dilatancy angle in plasticity-based models of concrete. Arch. Civ. Mech. Eng. 2019, 19, 1268–1283. [Google Scholar] [CrossRef]
- Zhu, Z. Research on Behaviour of Lightweight Aggregate Concrete-Filled Thin-Walled Steel Tube Columns under Compression. Master’s Thesis, Guangxi University, Nanning, China, 2019. [Google Scholar]
- Ashraf, M.; Gardner, L.; Nethercot, D.A. Finite element modelling of structural stainless steel cross-sections. Thin Walled Struct. 2006, 44, 1048–1062. [Google Scholar] [CrossRef]
- Gardner, L.; Nethercot, D.A. Numerical Modeling of Stainless Steel Structural Components—A Consistent Approach. J. Struct. Eng. 2004, 130, 1586–1601. [Google Scholar] [CrossRef]
- Tao, Z.; Uy, B.; Liao, F.-Y.; Han, L.-H. Nonlinear analysis of concrete-filled square stainless steel stub columns under axial compression. J. Constr. Steel Res. 2011, 67, 1719–1732. [Google Scholar] [CrossRef]
- Ellobody, E.; Young, B. Structural performance of cold-formed high strength stainless steel columns. J. Constr. Steel Res. 2005, 61, 1631–1649. [Google Scholar] [CrossRef]
- Zhao, T. Study on Uniaxial Compressive Behavior of High Strength Lightweight Aggregate Concrete. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Ding, F.-X.; Yu, Z.-W.; Bai, Y.; Gong, Y.-Z. Elasto-plastic analysis of circular concrete-filled steel tube stub columns. J. Constr. Steel Res. 2011, 67, 1567–1577. [Google Scholar] [CrossRef]
- Yu, F.; Fang, Y.; Zhang, Y.; Xu, L.; Bai, R. Mechanical behavior of self-stressing steel slag aggregate concrete filled steel tubular stub columns. Struct. Concr. 2020, 21, 1597–1611. [Google Scholar] [CrossRef]
- Sakino, K.; Nakahara, H.; Morino, S.; Nishiyama, I. Behavior of Centrally Loaded Concrete-Filled Steel-Tube Short Columns. J. Struct. Eng. 2004, 130, 180–188. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D. Numerical model for the behavior and capacity of circular CFT columns, Part II: Verification and extension. Eng. Struct. 2008, 30, 1579–1589. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, S.; Zhang, X.; Guo, L. Behavior and strength of circular tube confined reinforced-concrete (CTRC) columns. J. Constr. Steel Res. 2009, 65, 1447–1458. [Google Scholar] [CrossRef]
- Shirakawa, M.A.; John, V.M.; Gaylarde, C.C.; Gaylarde, P.; Gambale, W. Mould and phototroph growth on masonry façades after repainting. Mater. Struct. 2004, 37, 472–479. [Google Scholar] [CrossRef]
- Taha, M.M.R.; El-Dieb, A.S.; Shrive, N.G. Sorptivity: A reliable measurement for surface absorption of masonry brick units. Mater. Struct. 2001, 34, 438–445. [Google Scholar] [CrossRef]
- Lu, D.-R.; Wang, W.-J.; Ding, F.-X.; Liu, X.-M.; Fang, C.-J. The impact of stirrups on the composite action of concrete-filled steel tubular stub columns under axial loading. Structures 2021, 30, 786–802. [Google Scholar] [CrossRef]
- Wei, Y.; Jiang, C.; Wu, Y.-F. Confinement effectiveness of circular concrete-filled steel tubular columns under axial compression. J. Constr. Steel Res. 2019, 158, 15–27. [Google Scholar] [CrossRef]
- GB 50936-2014. Technical Code for Concrete-Filled Steel Tubular Structures; China Architecture & Building Press: Beijing, China, 2014.


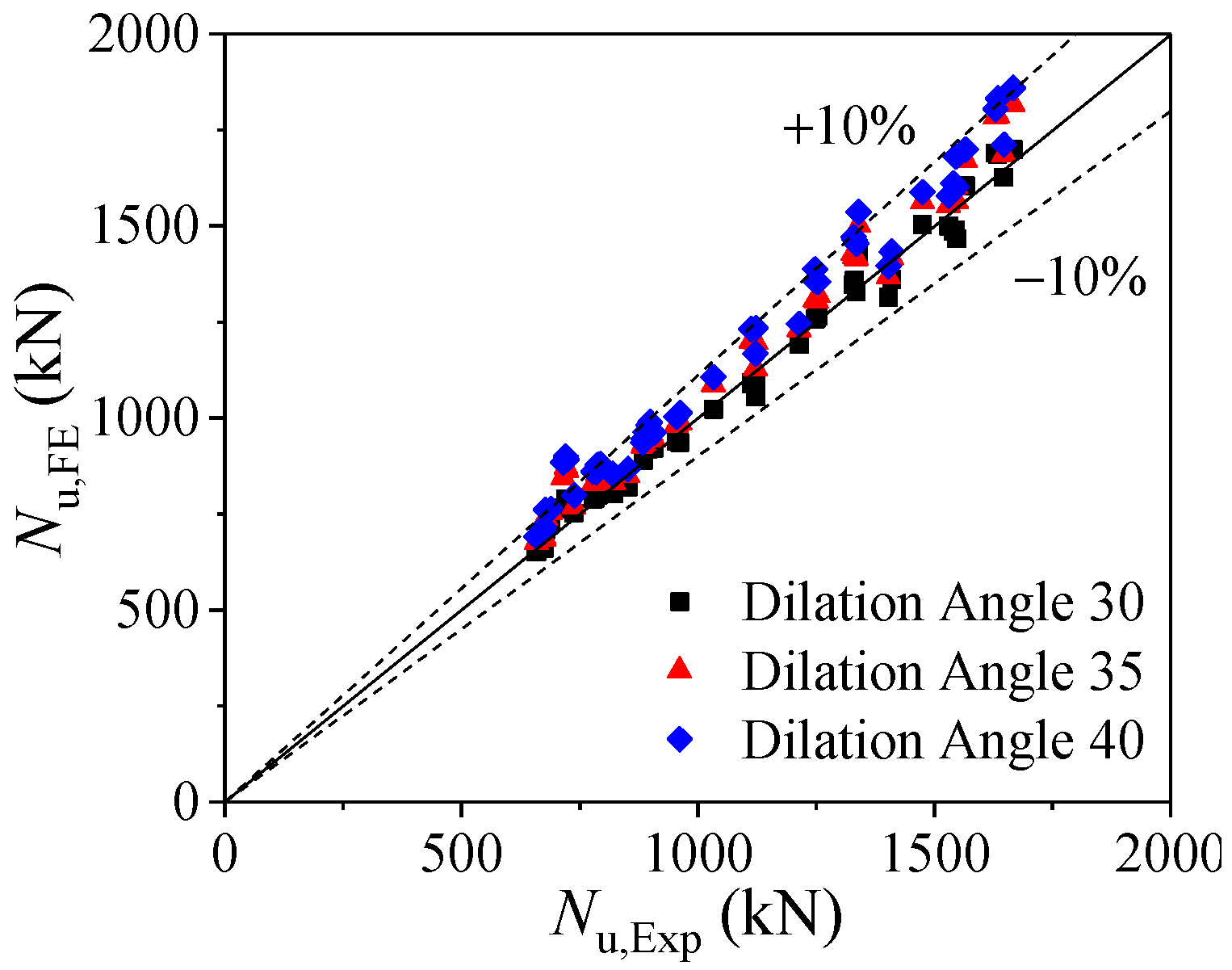


| Dilation Angle | 30° | 35° | 40° |
|---|---|---|---|
| Average ratio (Nu,Exp/Nu,FE) | 0.997 | 0.947 | 0.923 |
| C.V. | 0.034 | 0.042 | 0.045 |
| Specimens | Ref. | D × t × L (mm) | Ec (MPa) | fc (MPa) | fy (MPa) | Nu,Exp (kN) | Nu,FE (kN) | Nu,Exp/Nu,FE |
|---|---|---|---|---|---|---|---|---|
| SC1-a | [14] | 111.2 × 2.04 × 342 | 23,840 | 29.21 | 305.6 | 659 | 651 | 1.013 |
| SC1-c | 111.5 × 2.11 × 342 | 23,840 | 29.21 | 305.6 | 675 | 661 | 1.021 | |
| SC2-a | 111.4 × 2.06 × 342 | 24,830 | 37.66 | 305.6 | 738 | 752 | 0.982 | |
| SC2-b | 111.4 × 2.19 × 342 | 24,830 | 37.66 | 305.6 | 689 | 729 | 0.945 | |
| SC2-c | 111.3 × 2.12 × 342 | 24,830 | 37.66 | 305.6 | 678 | 708 | 0.957 | |
| SC3-a | 113.5 × 3.79 × 342 | 23,840 | 29.21 | 274.7 | 852 | 821 | 1.038 | |
| SC3-b | 113.4 × 3.78 × 342 | 23,840 | 29.21 | 274.7 | 822 | 804 | 1.023 | |
| SC4-a | 113.3 × 3.79 × 342 | 24,830 | 37.66 | 274.7 | 884 | 909 | 0.972 | |
| SC4-b | 113.4 × 3.81 × 342 | 24,830 | 37.66 | 274.7 | 889 | 920 | 0.966 | |
| SC4-c | 113.3 × 3.75 × 342 | 24,830 | 37.66 | 274.7 | 899 | 942 | 0.954 | |
| SC5-b | 164.5 × 2.64 × 495 | 23,840 | 29.21 | 281.7 | 1214 | 1192 | 1.018 | |
| SC5-c | 164.4 × 2.51 × 495 | 23,840 | 29.21 | 281.7 | 1403 | 1315 | 1.067 | |
| SC6-a | 164.3 × 2.63 × 495 | 24,830 | 37.66 | 281.7 | 1475 | 1503 | 0.981 | |
| SC6-c | 164.8 × 2.45 × 495 | 24,830 | 37.66 | 281.7 | 1540 | 1486 | 1.036 | |
| SC7-a | 165.5 × 2.99 × 495 | 23,840 | 29.21 | 293.9 | 1410 | 1360 | 1.037 | |
| SC7-b | 165.2 × 3.01 × 495 | 23,840 | 29.21 | 293.9 | 1340 | 1421 | 0.943 | |
| SC7-c | 165.2 × 3.11 × 495 | 23,840 | 29.21 | 293.9 | 1547 | 1466 | 1.055 | |
| SC8-b | 164.5 × 3.11 × 495 | 24,830 | 37.66 | 293.9 | 1647 | 1626 | 1.013 | |
| SC8-c | 165.0 × 2.96 × 495 | 24,830 | 37.66 | 293.9 | 1629 | 1689 | 0.964 | |
| SC9-a | 165.2 × 3.98 × 495 | 23,840 | 29.21 | 275.8 | 1530 | 1499 | 1.021 | |
| SC9-b | 164.8 × 3.88 × 495 | 23,840 | 29.21 | 275.8 | 1566 | 1603 | 0.977 | |
| SC9-c | 165.0 × 3.96 × 495 | 23,840 | 29.21 | 275.8 | 1545 | 1489 | 1.038 | |
| SC10-a | 164.7 × 3.86 × 495 | 24,830 | 37.66 | 275.8 | 1667 | 1699 | 0.981 | |
| SC10-b | 164.5 × 3.86 × 495 | 24,830 | 37.66 | 275.8 | 1634 | 1685 | 0.970 | |
| SC11-a | 163.9 × 2.47 × 495 | 19,500 | 22.9 | 281.7 | 1113 | 1090 | 1.021 | |
| SC11-b | 163.9 × 2.53 × 495 | 19,500 | 22.9 | 281.7 | 1123 | 1101 | 1.020 | |
| SC11-c | 164.4 × 2.49 × 495 | 19,500 | 22.9 | 281.7 | 1122 | 1055 | 1.064 | |
| SC12-a | 113.3 × 3.59 × 342 | 19,500 | 22.9 | 274.7 | 721 | 790 | 0.913 | |
| SC12-b | 113.5 × 3.60 × 342 | 19,500 | 22.9 | 274.7 | 723 | 762 | 0.949 | |
| SC12-c | 113.1 × 3.56 × 342 | 19,500 | 22.9 | 274.7 | 715 | 766 | 0.933 | |
| SC13-a | 164.5 × 3.90 × 495 | 19,500 | 22.9 | 275.8 | 1335 | 1329 | 1.005 | |
| SC13-b | 164.3 × 3.88 × 495 | 19,500 | 22.9 | 275.8 | 1329 | 1347 | 0.986 | |
| SC13-c | 164.6 × 3.87 × 495 | 19,500 | 22.9 | 275.8 | 1331 | 1357 | 0.981 | |
| SC1-A | [15] | 163.9 × 2.47 × 495 | 18,500 | 16.7 | 299.0 | 962 | 936 | 1.028 |
| SC1-B | 164.0 × 2.53 × 495 | 18,500 | 16.7 | 299.0 | 1033 | 1022 | 1.011 | |
| SC1-C | 164.4 × 2.49 × 495 | 18,500 | 16.7 | 299.0 | 954 | 939 | 1.016 | |
| SC2-A | 113.4 × 3.57 × 342 | 24,800 | 39.3 | 315.0 | 789 | 799 | 0.987 | |
| SC2-B | 113.3 × 3.60 × 342 | 24,800 | 39.3 | 315.0 | 886 | 890 | 0.996 | |
| SC2-C | 113.0 × 3.58 × 342 | 24,800 | 39.3 | 315.0 | 907 | 920 | 0.986 | |
| SC3-A | 113.5 × 3.60 × 342 | 18,500 | 16.7 | 315.0 | 782 | 791 | 0.989 | |
| SC3-B | 113.1 × 3.56 × 342 | 18,500 | 16.7 | 315.0 | 779 | 789 | 0.987 | |
| SC3-C | 113.3 × 3.60 × 342 | 18,500 | 16.7 | 315.0 | 794 | 805 | 0.986 | |
| SC4-A | 164.5 × 3.90 × 495 | 18,500 | 16.7 | 295.2 | 1251 | 1262 | 0.991 | |
| SC4-B | 164.3 × 3.88 × 495 | 18,500 | 16.7 | 295.2 | 1254 | 1265 | 0.991 | |
| SC4-C | 164.6 × 3.87 × 495 | 18,500 | 16.7 | 295.2 | 1248 | 1258 | 0.992 | |
| SC1-1-1a | [27] | 165.0 × 1.32 × 578 | 19,600 | 22.9 | 226.7 | 675 | 665 | 1.015 |
| SC1-1-2a | 165.0 × 2.05 × 578 | 19,600 | 22.9 | 214.1 | 820 | 806 | 1.017 | |
| SC1-2-1a | 165.0 × 1.32 × 577 | 23,400 | 29.3 | 226.7 | 785 | 801 | 0.980 | |
| SC1-2-2a | 165.0 × 2.05 × 577 | 23,400 | 29.3 | 214.1 | 895 | 918 | 0.975 | |
| Mean | - | - | - | - | - | - | - | 0.997 |
| C.V. | - | - | - | - | - | - | - | 0.034 |
| D (mm) | L (mm) | Es (MPa) | t (mm) | fy (MPa) | fc (MPa) |
|---|---|---|---|---|---|
| 500 | 1500 | 20, 600, 0 | 6, 7, 8, 9, 10 | 235 | 20, 30, 40, 50 |
| 345 | 30, 40, 50, 60 | ||||
| 390 | 40, 50, 60, 70 | ||||
| 420 | 50, 60, 70, 80 | ||||
| 460 | 60, 70, 80 |
| References | Formulas | Addition |
|---|---|---|
| GB 50936 (2014) [42] | When , ; When , | If fcu ≤ 50 MPa, α = 2.0 If 50 MPa ≤ fcu ≤ 80 MPa, α = 1.8 |
| EC 4 (2004) [11] | , | |
| ACI-318 (2011) [12] |
| Specimens | Ref. | Nu2 (kN) | NGB (kN) | NEC (kN) | NACI (kN) | Nu,Exp (kN) | Nu2/ Nu,Exp | NGB/ Nu,Exp | NEC/ Nu,Exp | NACI/ Nu,Exp |
|---|---|---|---|---|---|---|---|---|---|---|
| SC1-a | [14] | 599 | 622 | 627 | 485 | 659 | 0.909 | 0.943 | 0.951 | 0.737 |
| SC1-c | 612 | 637 | 639 | 494 | 675 | 0.907 | 0.943 | 0.947 | 0.732 | |
| SC2-a | 680 | 696 | 685 | 537 | 738 | 0.921 | 0.943 | 0.928 | 0.728 | |
| SC2-b | 699 | 718 | 702 | 549 | 689 | 1.015 | 1.042 | 1.019 | 0.797 | |
| SC2-c | 688 | 705 | 692 | 542 | 678 | 1.015 | 1.040 | 1.020 | 0.799 | |
| SC3-a | 821 | 828 | 830 | 624 | 852 | 0.963 | 0.972 | 0.975 | 0.733 | |
| SC3-b | 818 | 826 | 828 | 623 | 822 | 0.996 | 1.005 | 1.007 | 0.758 | |
| SC4-a | 893 | 930 | 879 | 670 | 884 | 1.010 | 1.052 | 0.994 | 0.758 | |
| SC4-b | 897 | 933 | 883 | 672 | 889 | 1.009 | 1.049 | 0.993 | 0.756 | |
| SC4-c | 888 | 925 | 874 | 667 | 899 | 0.987 | 1.029 | 0.973 | 0.742 | |
| SC5-b | 1175 | 1204 | 1304 | 978 | 1214 | 0.968 | 0.992 | 1.074 | 0.806 | |
| SC5-c | 1147 | 1172 | 1276 | 961 | 1403 | 0.818 | 0.835 | 0.909 | 0.685 | |
| SC6-a | 1339 | 1351 | 1370 | 1082 | 1475 | 0.908 | 0.916 | 0.929 | 0.733 | |
| SC6-c | 1309 | 1314 | 1344 | 1065 | 1540 | 0.850 | 0.853 | 0.873 | 0.692 | |
| SC7-a | 1288 | 1333 | 1357 | 1051 | 1410 | 0.914 | 0.945 | 0.962 | 0.745 | |
| SC7-b | 1289 | 1335 | 1357 | 1050 | 1340 | 0.962 | 0.996 | 1.013 | 0.784 | |
| SC7-c | 1311 | 1360 | 1377 | 1064 | 1547 | 0.847 | 0.879 | 0.890 | 0.688 | |
| SC8-b | 1469 | 1501 | 1483 | 1162 | 1647 | 0.892 | 0.911 | 0.900 | 0.706 | |
| SC8-c | 1444 | 1471 | 1462 | 1149 | 1629 | 0.886 | 0.903 | 0.897 | 0.705 | |
| SC9-a | 1440 | 1511 | 1498 | 1141 | 1530 | 0.941 | 0.988 | 0.979 | 0.746 | |
| SC9-b | 1415 | 1483 | 1474 | 1125 | 1566 | 0.904 | 0.947 | 0.941 | 0.718 | |
| SC9-c | 1434 | 1504 | 1491 | 1137 | 1545 | 0.928 | 0.973 | 0.965 | 0.736 | |
| SC10-a | 1573 | 1624 | 1583 | 1225 | 1667 | 0.944 | 0.974 | 0.949 | 0.735 | |
| SC10-b | 1571 | 1621 | 1579 | 1223 | 1634 | 0.961 | 0.992 | 0.967 | 0.748 | |
| SC11-a | 1008 | 1044 | 1012 | 768 | 1113 | 0.906 | 0.938 | 0.909 | 0.690 | |
| SC11-b | 1021 | 1059 | 1024 | 776 | 1123 | 0.909 | 0.943 | 0.912 | 0.691 | |
| SC11-c | 1017 | 1054 | 1021 | 774 | 1122 | 0.907 | 0.939 | 0.910 | 0.690 | |
| SC12-a | 736 | 724 | 716 | 525 | 721 | 1.021 | 1.005 | 0.993 | 0.728 | |
| SC12-b | 739 | 727 | 719 | 527 | 723 | 1.023 | 1.006 | 0.994 | 0.729 | |
| SC12-c | 730 | 719 | 710 | 521 | 715 | 1.021 | 1.006 | 0.993 | 0.729 | |
| SC13-a | 1294 | 1327 | 1278 | 946 | 1335 | 0.969 | 0.994 | 0.957 | 0.709 | |
| SC13-b | 1287 | 1321 | 1271 | 942 | 1329 | 0.969 | 0.994 | 0.957 | 0.709 | |
| SC13-c | 1289 | 1323 | 1273 | 943 | 1331 | 0.968 | 0.994 | 0.957 | 0.709 | |
| SC1-A | [15] | 919 | 952 | 793 | 633 | 962 | 0.956 | 0.990 | 0.824 | 0.658 |
| SC1-B | 934 | 964 | 804 | 642 | 1033 | 0.904 | 0.934 | 0.778 | 0.622 | |
| SC1-C | 928 | 961 | 800 | 639 | 954 | 0.973 | 1.007 | 0.839 | 0.670 | |
| SC2-A | 958 | 994 | 807 | 690 | 789 | 1.214 | 1.260 | 1.022 | 0.875 | |
| SC2-B | 961 | 996 | 808 | 692 | 886 | 1.085 | 1.124 | 0.912 | 0.781 | |
| SC2-C | 954 | 990 | 803 | 687 | 907 | 1.052 | 1.091 | 0.885 | 0.758 | |
| SC3-A | 763 | 838 | 604 | 507 | 782 | 0.976 | 1.072 | 0.772 | 0.649 | |
| SC3-B | 753 | 827 | 596 | 501 | 779 | 0.967 | 1.062 | 0.766 | 0.643 | |
| SC3-C | 761 | 836 | 602 | 506 | 794 | 0.959 | 1.053 | 0.759 | 0.637 | |
| SC4-A | 1234 | 1335 | 1021 | 832 | 1251 | 0.986 | 1.067 | 0.816 | 0.665 | |
| SC4-B | 1228 | 1328 | 1016 | 828 | 1254 | 0.979 | 1.059 | 0.810 | 0.660 | |
| SC4-C | 1228 | 1329 | 1017 | 829 | 1248 | 0.984 | 1.065 | 0.815 | 0.664 | |
| SC1-1-1a | [27] | 716 | 808 | 681 | 547 | 675 | 1.060 | 1.197 | 1.009 | 0.810 |
| SC1-1-2a | 818 | 912 | 777 | 610 | 820 | 0.998 | 1.113 | 0.947 | 0.744 | |
| SC1-2-1a | 848 | 959 | 848 | 693 | 785 | 1.081 | 1.222 | 1.081 | 0.883 | |
| SC1-2-2a | 949 | 1068 | 939 | 754 | 895 | 1.060 | 1.193 | 1.050 | 0.843 | |
| Mean | - | - | - | - | - | - | 0.967 | 1.009 | 0.933 | 0.729 |
| C.V. | - | - | - | - | - | - | 0.072 | 0.088 | 0.086 | 0.079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Lyu, F.; Ding, F.; Liu, C.; Wang, E. Analytical Modelling of LACFCST Stub Columns Subjected to Axial Compression. Mathematics 2021, 9, 948. https://doi.org/10.3390/math9090948
Xu Y, Lyu F, Ding F, Liu C, Wang E. Analytical Modelling of LACFCST Stub Columns Subjected to Axial Compression. Mathematics. 2021; 9(9):948. https://doi.org/10.3390/math9090948
Chicago/Turabian StyleXu, Yunlong, Fei Lyu, Faxing Ding, Chenglu Liu, and En Wang. 2021. "Analytical Modelling of LACFCST Stub Columns Subjected to Axial Compression" Mathematics 9, no. 9: 948. https://doi.org/10.3390/math9090948
APA StyleXu, Y., Lyu, F., Ding, F., Liu, C., & Wang, E. (2021). Analytical Modelling of LACFCST Stub Columns Subjected to Axial Compression. Mathematics, 9(9), 948. https://doi.org/10.3390/math9090948







