Equity Cost Induced Dichotomy for Optimal Dividends with Capital Injections in the Cramér-Lundberg Model
Abstract
:1. Introduction
- x is the initial surplus;
- q is a discount factor;
- are the cumulative dividends;
- are the cumulative forced capital injections each time the process attempts to cross into , and is a proportional cost for injecting capital;
- is the process modified by capital injections and dividends, and .
- ; the optimal policy is (RP), i.e., pay dividends at an upper barrier and always inject capital at 0, implying that bankruptcy never occurs;
- ; the optimal policy is (AP), i.e., pay dividends in order to reflect the surplus process at some upper barrier , and never inject capital.
- we prove the optimality of policies such as those described at the very beginning for which, in general, (i.e., de Finetti and Shreve, Lehoczky and Gaver policies fail to be optimal);
- the resulting value function is not of class at 0 (in the sense that its derivative does not exist at and, more, the right-hand derivative at 0 is not k as assumed, for Brownian claims, in [14], 5.2). This can be found in Remark 14 and it implies, in particular, that the verification Theorem 4 has to be given for absolutely-continuous functions. Working with super-solutions also explains the particular form of the Equation (8) on .
- the optimal parameters and are completely characterized by non-trivial equations and so is the alternative-inducing cost .
- Guess a family of policies which yields the optimum for all possible values of the parameters, and compute its expected net present value (EPV) in terms of the scale functions.
- 2.
- Identify the optimal arguments with respect to the parameters of our policies. This step forced us to restrict to the case of exponential jumps, where the independence of ruin and ruin overshoots leads to simplifying factorizations related to the memoryless property of this distribution.
- 3.
- In the final step, confirm the optimality of the selected candidate optimal policy via a verification theorem (sufficient condition for optimality). If the conjectured value function were sufficiently smooth (this means in our problem), this would require only verifying that it satisfies an associated HJB equation (system of variational inequalities).
2. Optimizing Dividends and Capital Injections with Proportional Costs
2.1. The Framework
- given a couple : describing dividends and capital injection, the modified surplus process is defined (under the ) by setting
- the cumulative dividend strategy L is adapted, non-decreasing and càdlàg (right-continuous, left-limits), ;
- the cumulative capital injection process I is adapted, non-decreasing and càdlàg, ;
- the triplet satisfying the previous conditions is referred to as (general) strategy and the family of all such strategies is denoted by .
- (prior to ruin) for every , the dividends should satisfy
- (after the ruin time ), we set (The reader is invited to note that in this case one of the jumping times for N such that remain adapted, non-decreasing and càdlàg).
- the satisfying the dividends restriction is called an admissible strategy and the family of all such strategies is denoted by .
- for an admissible strategy ,
- (a)
- we consider the ruin time (if a “very large” claim occurs, bankruptcy is declared; as we will see in the main result, it is never optimal to take and modify the equity I accordingly).
- (b)
- the associated cost is
- (c)
- Every strategy can be replaced with by modifying if such that and improving the associated cost . From now on, whenever a policy is considered, we identify it with and reason accordingly.
- (d)
- In connection to this type of policies and the related cost, we set
2.2. The Value Function
- First, we focus on the regularity properties of the value function (lower and upper-bound and Lipschitz-continuity) in Proposition 2.
- Second, we prove the connection between this value function and the associated partial-integral differential system (of HJB-type) in Proposition 3.
- Third, we show in Theorem 4 that the value function is the lowest absolutely-continuous super-solution of the associated equation and, as a verification result, give the optimality condition for candidate policies.
2.3. Some Elementary Properties of the Value Function
- For every , the set of admissible strategies is non-empty. If , then and, for every , .
- For every and every , one has .
- If , then, for every and every policy , one has .
- For every and every , .
2.4. The HJB System
2.5. The Value Function as Smallest Super-Solution
- The value function is non-negative, for and .
- Every non-negative -regular of growth viscosity super-solution of (8), where α is introduced in Proposition 15, is greater than or equal to on .
- If is a family of admissible strategies such that the associated costs is an super-solution for (8), then is optimal and .
3. The Value Function for the Cramér-Lundberg Model
3.1. The Guess Step: Severity-Constrained Double Barrier Policies, for the Cramér-Lundberg Process with Exponential Jumps
- the inverse Laplace transform of , where is the Laplace exponent, and
- .
- ;
- ;
- ;
- , for all ;
- The cost function satisfies, for ,In particular, if we setthen
- Moreover, the cost can be explicitly written asand
- The first step of the previous proposition applies also to the perturbed Cramér-Lundberg process obtained by adding a Brownian term to (3). The second and third however use specific features available only if (in particular that ).
- Note thatwhere the last identity as well as the notation appear in [15]. Our formula interpolates between the de Finetti and Shreve, Lehoczky and Gaver cases:(Again, for details, the reader is guided to [15] and references therein).
- The Equation (20) may also be expressed asand making shows that the expected discounted dividends are . It follows that the expected capital injections when are .
- a term depending on b, which is multiplied by the scale function , and
- a term independent of b, , which has been called sometimes “smooth Gerber-Shiu function”—see for example [35], and also “smooth harmonic extension of , see [2]. It is striking that the scale function and the Gerber-Shiu function are the same for these three problems. This begs for a formula for the Gerber-Shiu function which does not depend on the problem, and such a candidate is offered by the “LRZ harmonic extension” obtained in [36,37]. However, this has only been rigorously proved in particular examples – see for example [12].
4. The Optimal for the Cramér-Lundberg Model with Exponential Claims
4.1. Preliminary Remarks
- As a consequence, picking can never be optimal.
- For fixed and , there exists a unique critical point satisfying
4.2. Determining the Candidate Maximal Arguments
- either , in which case (27) implies that satisfies
- or satisfiesand
5. From Guess to Optimality
- A.
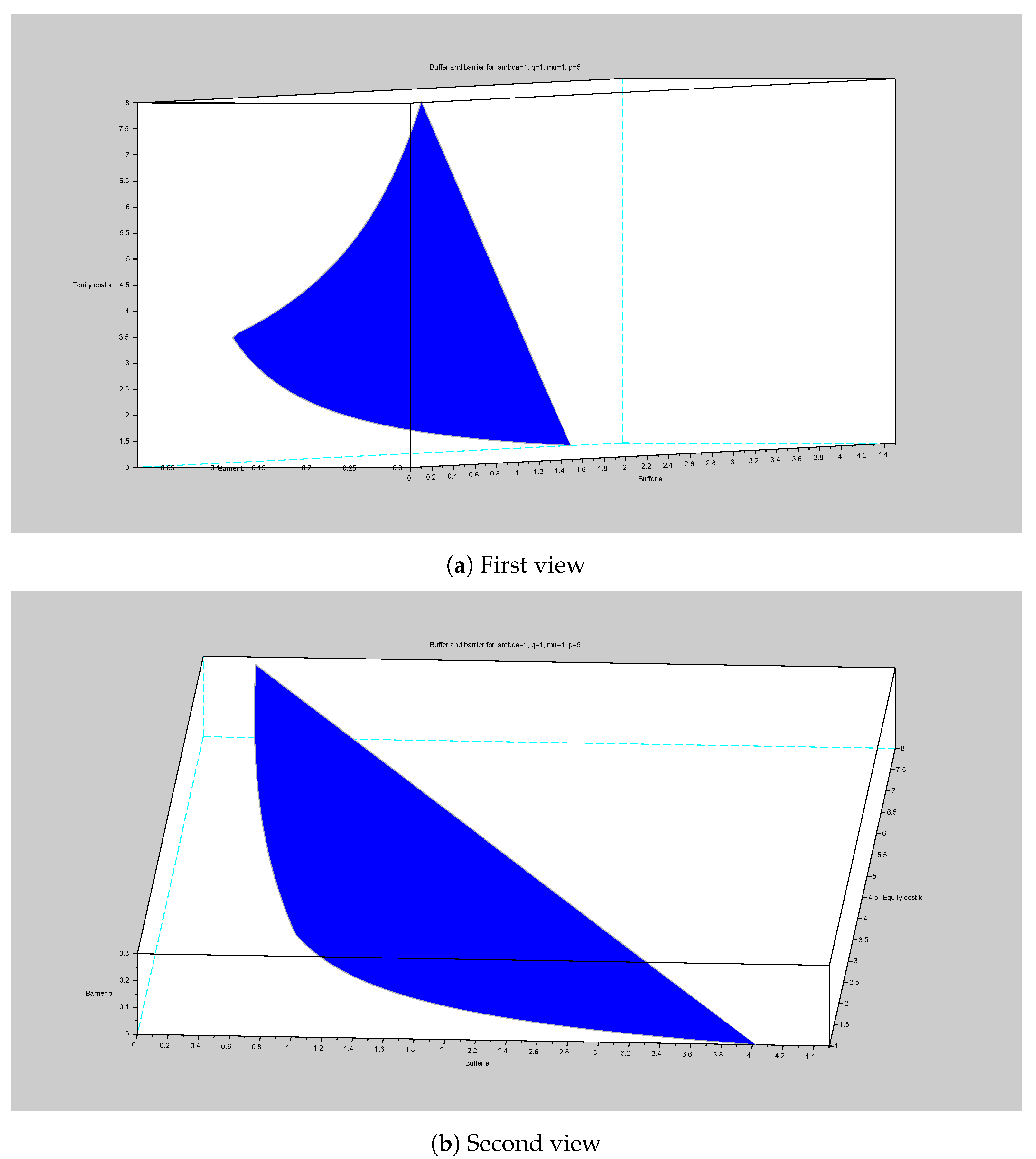
- If , then, we have the following dichotomy.
- A1.
- The “cheap” equity regime, with , holds for , where is the unique solution ofHere the strategy consists in injecting capital to take reserve to 0 (for levels above satisfying (28)) and paying dividends with the barrier 0 (i.e., “take the money and run”) is optimal, and the optimal value function is
- A2.
- For “expensive” equity i.e., ,
- B.
- In the remaining case , independently of , and the value function is got as in A1:with given by the Equation (28).
- A careful look at the upper-bound in 2.2.2 (in the proof) shows that . As a consequence:
- the heuristic intuition in ([14], 5.2) no longer holds true for our case ( and fails to hold true);
- is only absolutely continuous (but not ) such that the comparison in Theorem 4 must be given among absolutely continuous super-solutions.
- The equality in (50) gives a way to characterize when is known.
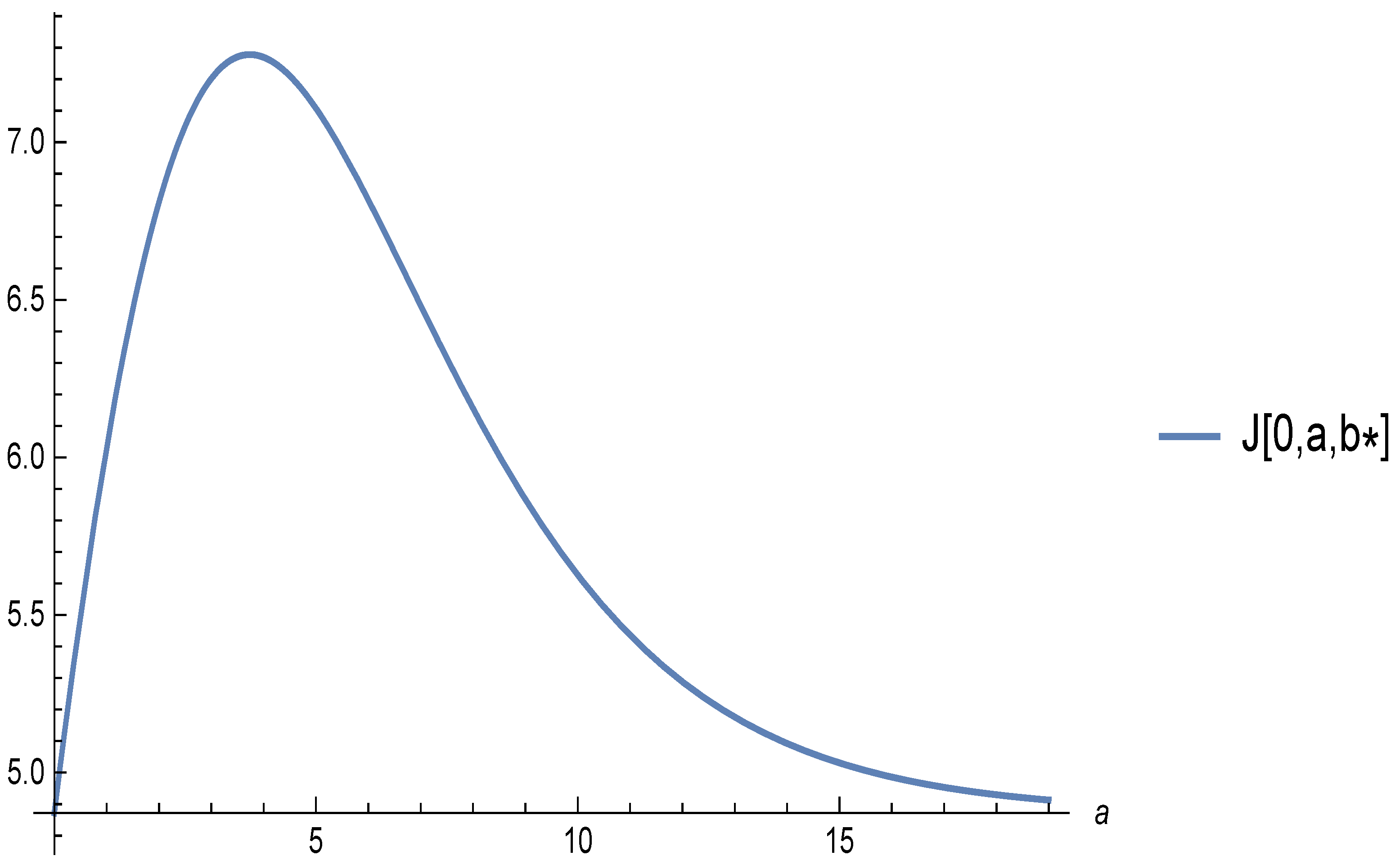
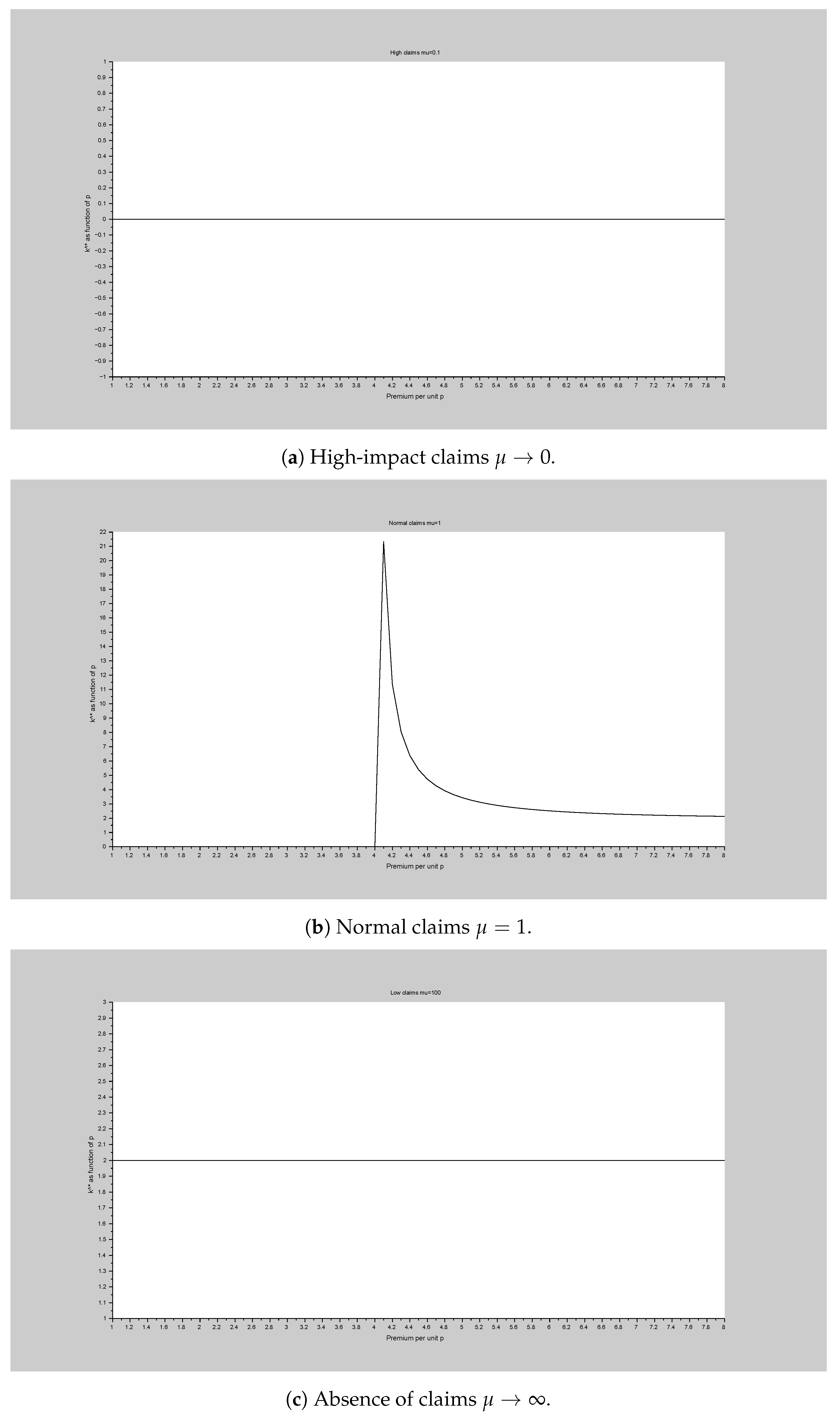
- As , the claims approach ∞ average. In a highly impacted market, the notion of equity expensiveness vanishes and it is not optimal to wait for any amount of time (Figure 2a).
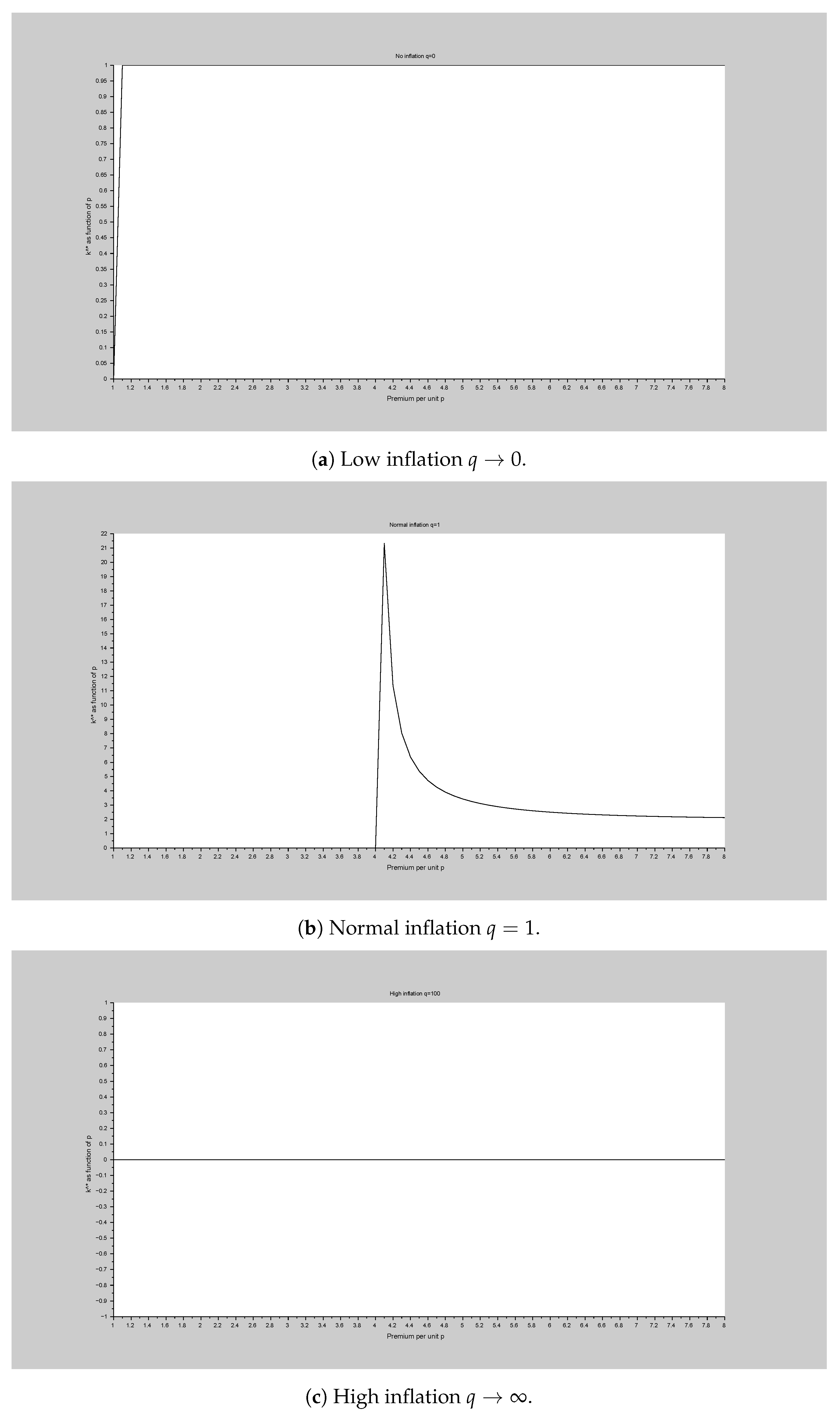
- On the other hand (Figure 3a), as the discount parameter , for all p that may give a dichotomy (cf. A), such that the Equation (31) leads to . In other words, absence of inflation makes every equity expensive. Conversely (Figure 3c), high inflation (large q) makes the notion of equity expensiveness vanish.
6. Proofs of the Results
6.1. Proofs for the Value Function: Estimates, Dynamic Programming, Solution
- The classical (no dividend, no injection) policy is an admissible strategy. The second result is a mere consequence of the definition of .
- For , we consider the strategy consisting in no capital injection (), then paying and (continuously) the premium and declare bankruptcy at the first (positive) claim. For this admissible strategy , the ruin time (the first jumping time except on the 0-probability event ). We have
- One merely notes that, for every ,on . Then,
- 4.
- The first inequality follows by modifying an arbitrary strategy into on to get . For the last inequality, one modifies (on ) an admissible strategy into .
- on ;
- on ;
- (pointwise a.e. on ).
6.2. Proofs for the Guess Step
6.3. Proofs for the Optimal Couple
6.4. Proof of the Main Theorem
- if and only if ;
- , for all .
- The continuous function satisfies and . We let denote the first solution of .
- We consider . One notes that . Moreover, such that , for all . In particular, . Owing to the monotonicity of , one deduces that .
Author Contributions
Funding
Conflicts of Interest
References
- Schmidli, H. Stochastic Control in Insurance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Avram, F.; Grahovac, D.; Vardar-Acar, C. The W,Z scale functions kit for first passage problems of spectrally negative Lévy processes, and applications to the optimization of dividends. arXiv 2019, arXiv:1706.06841. [Google Scholar]
- Albrecher, H.; Asmussen, S. Ruin Probabilities; World Scientific: Singapore, 2010; Volume 14. [Google Scholar]
- De Finetti, B. Su un’impostazione alternativa della teoria collettiva del rischio. In Transactions of the XVth International Congress of Actuaries; International Congress of Actuaries: New York, NY, USA, 1957; Volume 2, pp. 433–443. [Google Scholar]
- Shreve, S.E.; Lehoczky, J.P.; Gaver, D.P. Optimal consumption for general diffusions with absorbing and reflecting barriers. SIAM J. Control Optim. 1984, 22, 55–75. [Google Scholar] [CrossRef]
- Avram, F.; Palmowski, Z.; Pistorius, M.R. On the optimal dividend problem for a spectrally negative Lévy process. Ann. Appl. Probab. 2007, 17, 156–180. [Google Scholar] [CrossRef]
- Kulenko, N.; Schmidli, H. Optimal dividend strategies in a Cramér–Lundberg model with capital injections. Insur. Math. Econ. 2008, 43, 270–278. [Google Scholar] [CrossRef]
- Eisenberg, J.; Schmidli, H. Minimising expected discounted capital injections by reinsurance in a classical risk model. Scand. Actuar. J. 2011, 2011, 155–176. [Google Scholar] [CrossRef]
- Eisenberg, J.; Schmidli, H. Optimal control of capital injections by reinsurance with a constant rate of interest. J. Appl. Probab. 2011, 48, 733–748. [Google Scholar] [CrossRef] [Green Version]
- Pérez, J.L.; Yamazaki, K.; Yu, X. On the bail-out optimal dividend problem. J. Optim. Theory Appl. 2018, 179, 553–568. [Google Scholar] [CrossRef] [Green Version]
- Noba, K.; Pérez, J.L.; Yu, X. On the Bailout Dividend Problem for Spectrally Negative Markov Additive Models. SIAM J. Control Optim. 2020, 58, 1049–1076. [Google Scholar] [CrossRef] [Green Version]
- Avram, F.; Pérez, J.L.; Yamazaki, K. Spectrally negative Lévy processes with Parisian reflection below and classical reflection above. Stoch. Process. Appl. 2018, 128, 255–290. [Google Scholar] [CrossRef] [Green Version]
- Junca, M.; Moreno-Franco, H.A.; Pérez, J.L. Optimal Bail-Out Dividend Problem with Transaction Cost and Capital Injection Constraint. Risks 2019, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Løkka, A.; Zervos, M. Optimal dividend and issuance of equity policies in the presence of proportional costs. Insur. Math. Econ. 2008, 42, 954–961. [Google Scholar] [CrossRef]
- Avram, F.; Goreac, D.; Renaud, J.F. The Løkka–Zervos Alternative for a Cramér–Lundberg Process with Exponential Jumps. Risks 2019, 7, 120. [Google Scholar] [CrossRef] [Green Version]
- Azcue, P.; Muler, N. Stochastic Optimization in Insurance: A Dynamic Programming Approach; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Li, Y.; Liu, G. Optimal dividend and capital injection strategies in the Cramér-Lundberg risk model. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Strini, J.A.; Thonhauser, S. On a dividend problem with random funding. Eur. Actuar. J. 2019, 9, 607–633. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Woo, J.K. Optimal dividend and capital injection strategy with a penalty payment at ruin: Restricted dividend payments. Insur. Math. Econ. 2020, 92, 1–16. [Google Scholar] [CrossRef]
- Gajek, L.; Kuciński, L. Complete discounted cash flow valuation. Insur. Math. Econ. 2017, 73, 1–19. [Google Scholar] [CrossRef]
- Avram, F.; Goreac, D.; Adenane, R.; Solon, U., Jr. Optimizing dividends and capital injections limited by bankruptcy, and practical approximations for the Cram∖’er-Lundberg process. arXiv 2021, arXiv:2102.10107. [Google Scholar]
- Avram, F.; Perez-Garmendia, J.L. A Review of First-Passage Theory for the Segerdahl-Tichy Risk Process and Open Problems. Risks 2019, 7, 117. [Google Scholar] [CrossRef] [Green Version]
- Avanzi, B.; Shen, J.; Wong, B. Optimal dividends and capital injections in the dual model with diffusion. ASTIN Bull. J. IAA 2011, 41, 611–644. [Google Scholar] [CrossRef] [Green Version]
- Bayraktar, E.; Kyprianou, A.E.; Yamazaki, K. On optimal dividends in the dual model. ASTIN Bull. J. IAA 2013, 43, 359–372. [Google Scholar] [CrossRef] [Green Version]
- Yin, C.; Wen, Y. Optimal dividend problem with a terminal value for spectrally positive Lévy processes. Insur. Math. Econ. 2013, 53, 769–773. [Google Scholar] [CrossRef] [Green Version]
- Bayraktar, E.; Kyprianou, A.E.; Yamazaki, K. Optimal dividends in the dual model under transaction costs. Insur. Math. Econ. 2014, 54, 133–143. [Google Scholar] [CrossRef] [Green Version]
- Yao, D.; Yang, H.; Wang, R. Optimal risk and dividend control problem with fixed costs and salvage value: Variance premium principle. Econ. Model. 2014, 37, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Yao, D.; Yang, H.; Wang, R. Optimal dividend and reinsurance strategies with financing and liquidation value. ASTIN Bull. J. IAA 2016, 46, 365–399. [Google Scholar] [CrossRef] [Green Version]
- Yao, D.; Wang, R.; Xu, L. Optimal dividend, capital injection and excess-of-loss reinsurance strategies for insurer with a terminal value of the bankruptcy. Sci. Sin. Math. 2017, 47, 969–994. [Google Scholar]
- Suprun, V. Problem of destruction and resolvent of a terminating process with independent increments. Ukr. Math. J. 1976, 28, 39–51. [Google Scholar] [CrossRef]
- Bertoin, J. Lévy Processes; Cambridge University Press: Cambridge, UK, 1998; Volume 121. [Google Scholar]
- Avram, F.; Kyprianou, A.; Pistorius, M. Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Ann. Appl. Probab. 2004, 14, 215–238. [Google Scholar] [CrossRef]
- Kyprianou, A. Fluctuations of Lévy Processes with Applications: Introductory Lectures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kuznetsov, A.; Kyprianou, A.E.; Rivero, V. The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II; Springer: Berlin/Heidelberg, Germany, 2013; pp. 97–186. [Google Scholar]
- Avram, F.; Palmowski, Z.; Pistorius, M.R. On Gerber–Shiu functions and optimal dividend distribution for a Lévy risk process in the presence of a penalty function. Ann. Appl. Probab. 2015, 25, 1868–1935. [Google Scholar] [CrossRef]
- Loeffen, R.L.; Renaud, J.F.; Zhou, X. Occupation times of intervals until first passage times for spectrally negative Lévy processes. Stoch. Process. Their Appl. 2014, 124, 1408–1435. [Google Scholar] [CrossRef] [Green Version]
- Loeffen, R. On obtaining simple identities for overshoots of spectrally negative L∖’evy processes. arXiv 2014, arXiv:1410.5341. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avram, F.; Goreac, D.; Li, J.; Wu, X. Equity Cost Induced Dichotomy for Optimal Dividends with Capital Injections in the Cramér-Lundberg Model. Mathematics 2021, 9, 931. https://doi.org/10.3390/math9090931
Avram F, Goreac D, Li J, Wu X. Equity Cost Induced Dichotomy for Optimal Dividends with Capital Injections in the Cramér-Lundberg Model. Mathematics. 2021; 9(9):931. https://doi.org/10.3390/math9090931
Chicago/Turabian StyleAvram, Florin, Dan Goreac, Juan Li, and Xiaochi Wu. 2021. "Equity Cost Induced Dichotomy for Optimal Dividends with Capital Injections in the Cramér-Lundberg Model" Mathematics 9, no. 9: 931. https://doi.org/10.3390/math9090931
APA StyleAvram, F., Goreac, D., Li, J., & Wu, X. (2021). Equity Cost Induced Dichotomy for Optimal Dividends with Capital Injections in the Cramér-Lundberg Model. Mathematics, 9(9), 931. https://doi.org/10.3390/math9090931





