F-Operators for the Construction of Closed Form Solutions to Linear Homogenous PDEs with Variable Coefficients
Abstract
:1. Introduction
2. Preliminaries
2.1. Generalized Gaussian Functions
2.2. The Fourier Transform—Classical Formulas
3. Main Results
3.1. The Fourier Transform of the Generalized Gaussian Function
3.2. Differentiation of the Fourier Transform
4. Construction of Solutions to Homogenous Linear Partial Differential Equations with Variable Coefficients
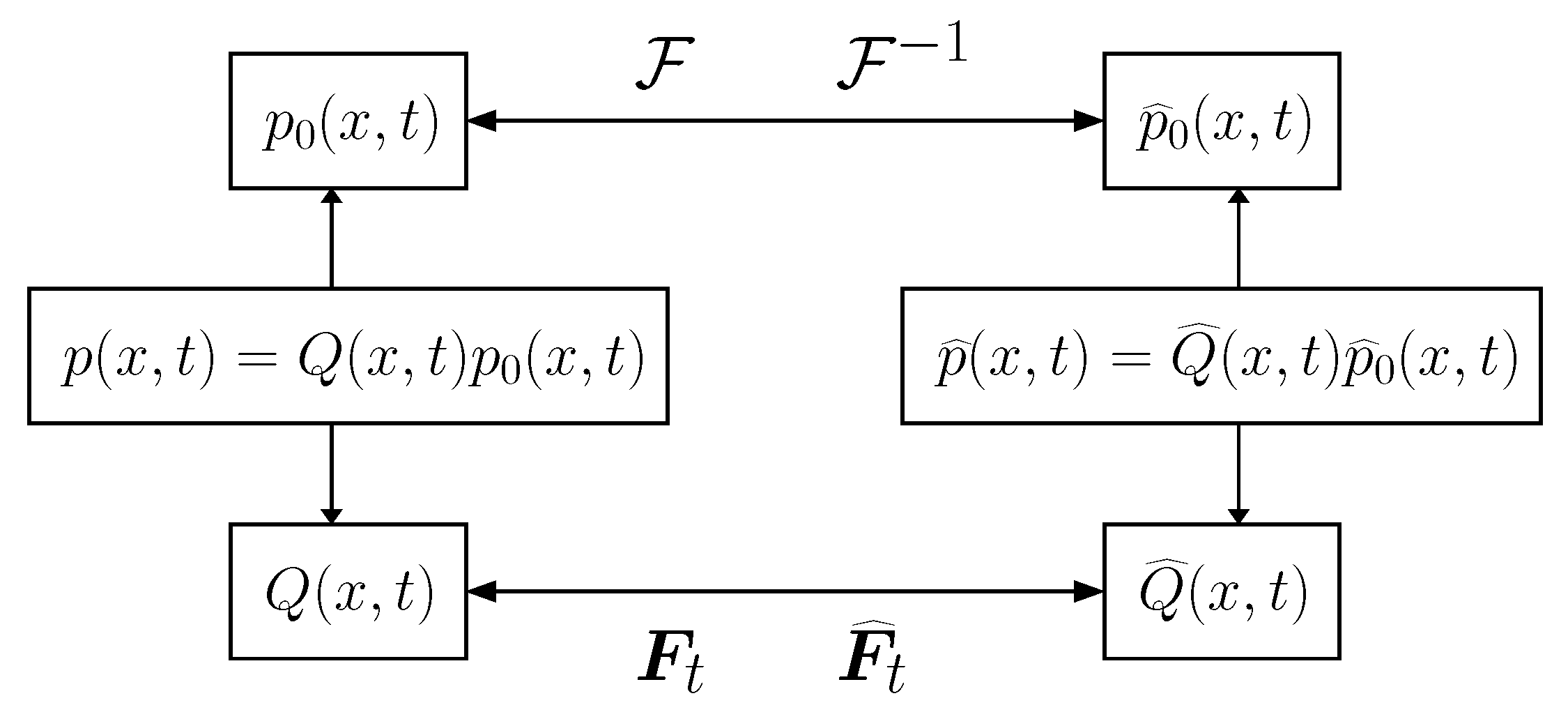
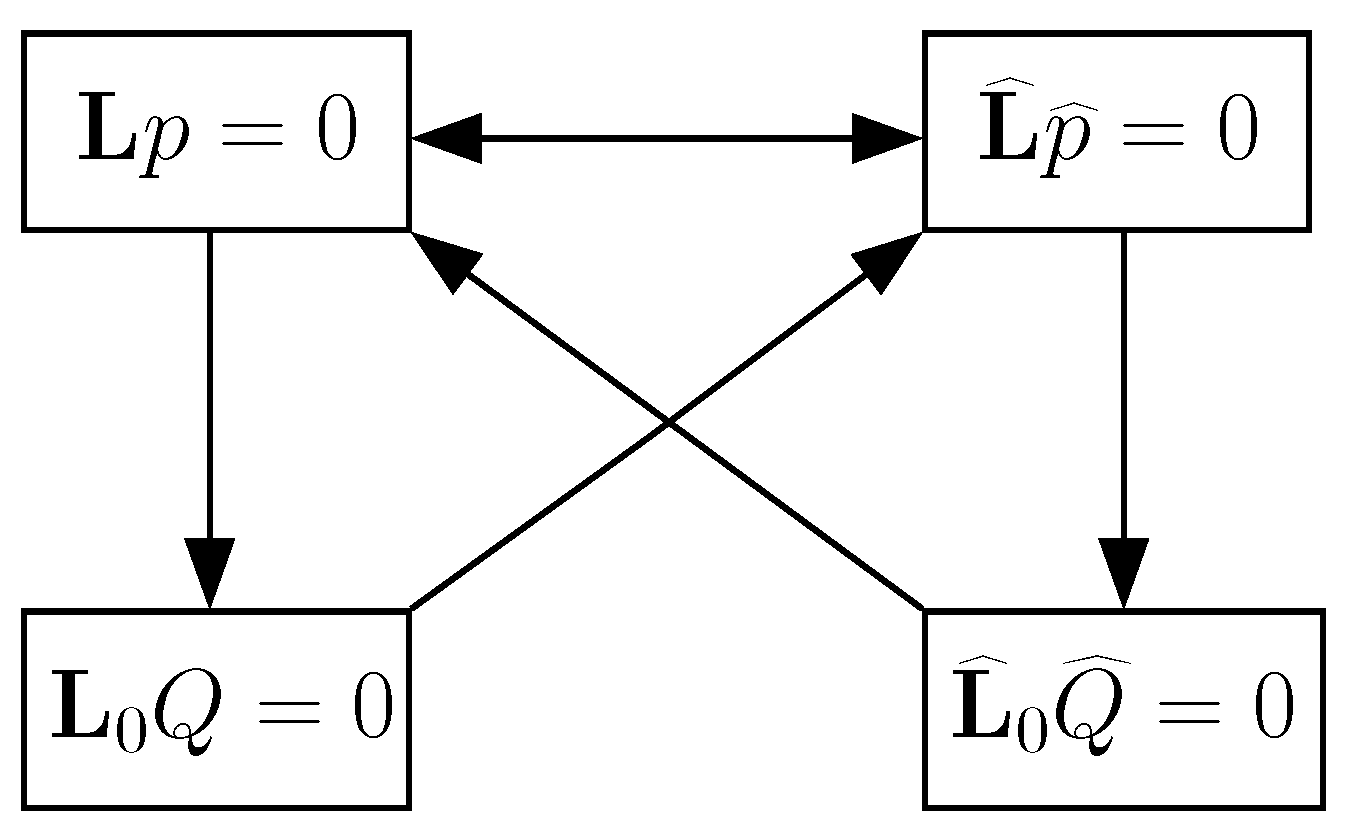
4.1. Mappings of Partial Differential Equations
4.1.1. Mapping between and
4.1.2. Mapping between and
4.1.3. Mapping between and ; and
4.2. Formulation of Cauchy Initial Conditions
5. Several Examples
5.1. Solving Cauchy Problem Given the PDE
5.2. Mappings between PDEs
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stein, D.B.; Guy, R.D.; Thomases, B. Immersed boundary smooth extension: A high-order method for solving PDE on arbitrary smooth domains using Fourier spectral methods. J. Comput. Phys. 2016, 304, 252–274. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, UK, 2016. [Google Scholar]
- Bakhos, T.; Saibaba, A.K.; Kitanidis, P.K. A fast algorithm for parabolic PDE-based inverse problems based on Laplace transforms and flexible Krylov solvers. J. Comput. Phys. 2015, 299, 940–954. [Google Scholar] [CrossRef] [Green Version]
- Sokhal, S.; Verma, S.R. A Fourier wavelet series solution of partial differential equation through the separation of variables method. Appl. Math. Comput. 2020, 388, 125480. [Google Scholar]
- Pindza, E.; Owolabi, K.M. Fourier spectral method for higher order space fractional reaction–diffusion equations. Commun. Nonlinear Sci. Numer. Simul. 2016, 40, 112–128. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Cai, J.; Wang, Y. Some new structure-preserving algorithms for general multi-symplectic formulations of Hamiltonian PDEs. J. Comput. Phys. 2014, 279, 80–102. [Google Scholar] [CrossRef]
- Nazari-Golshan, A.; Nourazar, S.S.; Ghafoori-Fard, H.; Yildirim, A.; Campo, A. A modified homotopy perturbation method coupled with the Fourier transform for nonlinear and singular Lane-Emden equations. Appl. Math. Lett. 2013, 26, 1018–1025. [Google Scholar] [CrossRef]
- Mahor, T.C.; Mishra, R.; Jain, R. Analytical solutions of linear fractional partial differential equations using fractional Fourier transform. J. Comput. Appl. Math. 2021, 385, 113202. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Xiao, A. Fourier Pseudospectral Method for Fractional Stationary Schrödinger Equation. Appl. Numer. Math. 2021, 165, 137–151. [Google Scholar] [CrossRef]
- Saridakis, Y.G.; Sifalakis, A.G.; Papadopoulou, E. Efficient numerical solution of the generalized Dirichlet-Neumann map for linear elliptic PDEs in regular polygon domains. J. Comput. Appl. Math. 2012, 236, 2515–2528. [Google Scholar] [CrossRef] [Green Version]
- Vermeersch, B.; Mey, G.D. A shortcut to inverse Fourier transforms: Approximate reconstruction of transient heating curves from sparse frequency domain data. Int. J. Therm. Sci. 2010, 49, 1319–1332. [Google Scholar] [CrossRef]
- Wang, J.; Dai, H.; Hui, Y. Conservative Fourier spectral scheme for higher order Klein-Gordon-Schrödinger equations. Appl. Numer. Math. 2020, 156, 446–466. [Google Scholar] [CrossRef]
- Ji, B.; Zhang, L.; Sun, Q. A dissipative finite difference Fourier pseudo-spectral method for the symmetric regularized long wave equation with damping mechanism. Appl. Numer. Math. 2020, 154, 90–103. [Google Scholar] [CrossRef]
- Huijskens, T.P.; Ruijter, M.J.; Oosterlee, C.W. Efficient numerical Fourier methods for coupled forward–backward SDEs. J. Comput. Appl. Math. 2016, 296, 593–612. [Google Scholar] [CrossRef]
- Larsson, E.; Ahlander, K.; Hall, A. Multi-dimensional option pricing using radial basis functions and the generalized Fourier transform. J. Comput. Appl. Math. 2008, 222, 175–192. [Google Scholar] [CrossRef] [Green Version]
- Temme, N. Special Functions: An Introduction to the Classical Functions of Mathematical Physics; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Feinsilver, P.; Schott, R. Algebraic Structures and Operator Calculus, Vol. I: Representations and Probability Theory; Kluwer Academic Publishers: Dordrecht, Germany, 1993. [Google Scholar]
- Navickas, Z. Constructive solution of the Cauchy problem for a special class of partial differential equations with constant coefficients. Lith. Math. J. 1994, 34, 404–414. [Google Scholar] [CrossRef]
- Navickas, Z.; Bikulciene, L.; Rahula, M.; Ragulskis, M. Algebraic operator method for the construction of solitary solutions to nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1374–1389. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navickas, Z.; Telksnys, T.; Marcinkevicius, R.; Cao, M.; Ragulskis, M. F-Operators for the Construction of Closed Form Solutions to Linear Homogenous PDEs with Variable Coefficients. Mathematics 2021, 9, 918. https://doi.org/10.3390/math9090918
Navickas Z, Telksnys T, Marcinkevicius R, Cao M, Ragulskis M. F-Operators for the Construction of Closed Form Solutions to Linear Homogenous PDEs with Variable Coefficients. Mathematics. 2021; 9(9):918. https://doi.org/10.3390/math9090918
Chicago/Turabian StyleNavickas, Zenonas, Tadas Telksnys, Romas Marcinkevicius, Maosen Cao, and Minvydas Ragulskis. 2021. "F-Operators for the Construction of Closed Form Solutions to Linear Homogenous PDEs with Variable Coefficients" Mathematics 9, no. 9: 918. https://doi.org/10.3390/math9090918
APA StyleNavickas, Z., Telksnys, T., Marcinkevicius, R., Cao, M., & Ragulskis, M. (2021). F-Operators for the Construction of Closed Form Solutions to Linear Homogenous PDEs with Variable Coefficients. Mathematics, 9(9), 918. https://doi.org/10.3390/math9090918







