1. Introduction
To obtain optimal designs, it is common to assume a homoscedastic normal distribution of the response variable and under this assumption there is vast literature focused mainly on nonlinear models. However, there are also papers that use probability distributions different from a normal distribution [
1,
2,
3,
4,
5,
6,
7]. At this point, it is important to remember that the probability distribution of the response variable is assumed, on many occasions, from the nature of the experiment to be performed. However, there are usually no prior observations to allow this assumption to be checked.
There are very few available references that set out a general framework for optimal experimental design for any probability distribution of the response variable. Ref. [
8] present a method to compute the D-optimal designs for Generalized Linear Models with a binary response allowing uncertainty in the link function, ref. [
9] study the Generalized Linear Model from the perspective of optimal experimental design, ref. [
10] present the “elemental information matrix” for different probability distributions, and [
11] compute optimal designs based on the maximum quasi-likelihood estimator to avoid the misspecification in the probability distribution of the response. The aim of this paper is to analyze the effect of misspecification in the probability distribution in optimal design. In other words, it allows those cases to be identified in which it is important to pay special attention to the assumed probability distribution. In this study, apart from theoretical results, real applications involving the linear quadratic model and a dose-response model are considered. For the latter, we focus on the well-known Hill model, widely used to describe dependence between the concentration of a substance and a variety of responses in biochemistry, physiology or pharmacology. From the point of view of optimal experimental design, this model is studied in many papers [
12,
13,
14,
15]. Specifically, ref. [
13] study the effect of some drugs which inhibit the growth of tumor cells providing D-optimal designs under the assumption of the response variable follows a heteroscedastic normal distribution with a given structure for the variance.
The article is organized as follows.
Section 2 introduces the model used and the theory of optimal experimental design.
Section 3 presents the structure of the variance of the heteroscedastic normal distribution and proves a general theoretical result.
Section 4 focuses on the linear quadratic model and provides some theoretical results for gamma or Poisson distributions. This section also shows applications of these results to real examples found in the literature. Finally, the 4-parameter Hill model is studied in
Section 5. Assuming the heteroscedastic normal distribution, as in [
13], an efficiency analysis is performed, considering the Poisson, or gamma, as the true probability distribution. A sensitivity analysis with respect to a parameter of the variance structure is also performed. The paper concludes with a summary and conclusions section.
2. Model and Optimal Experimental Design
The model of interest to the practitioner is expressed in a general way as
where
y is the response variable, following a probability distribution with pdf
, where
is the vector of parameters of the assumed distribution,
is the regression function (linear or nonlinear in the parameters),
is the vector of controllable variables and
the vector of unknown parameters that must be estimated. Lastly,
g is the link function relating the regression function to the mathematical expectation of the response. Ref. [
16] carry out an in-depth study of the link function and Generalized Linear Models. In line with these authors, this paper considers the canonical link function for the probability distributions involved in the study, as it guarantees that the maximum likelihood estimators of the model parameters,
, are sufficient.
An exact design of size
n is defined as a set of values of the explanatory variables,
, in which some may be repeated. These values belong to a compact set called design space
, which is usually a subset of
. However, the real applications, examples and results in this study consider the one-dimensional case. Assuming that only
q of these values are distinct, we may consider the set
and associate with it a probability measure defined by
, where each
represents the proportion of experiments carried out under the condition
. This suggests a more general definition of approximate design as a probability measure
over the design space
:
where
and
represents the set of all approximate designs.
The scenario studied in this work is the estimation of a single parameter of the probability distribution of the response, with the rest being fixed. Thus, the elemental information matrix (EIM), introduced by [
10], is scalar and is defined as
which contains information about the probability distribution of the response variable
y, given by the pdf
. The relationship between the parameters to estimate,
, of the probability distribution and the regression function
is established by the link function,
g, shown in (
1).
Table 1 sets out the canonical link function, the mathematical expectation of the response variable as a function of
and the EIM for the probability distributions used in this paper, some of which are derived in
Section 3.
The single-point information matrix in
is given by
where
is the EIM defined in (
2) and
Finally, the Fisher information matrix (FIM) is defined for the approximate design with probability measure
as
The FIM establishes a connection between optimal experimental design and the Generalized Regression Model. The standard form of FIM under the normality hypothesis can be generalized to any probability distribution by including the EIM. By definition, the inverse of the FIM is asymptotically proportional to the variance and covariance matrix of estimators of
, the parameters of the model. This matrix may depend on these parameters, so nominal values for them are necessary and therefore locally optimal designs can be obtained. By Carathéodory’s theorem, it is known that for any design there is always another with the same information matrix of at most
different points, where
m is the number of unknown parameters to be estimated for the model
[
17]. Therefore, it is sufficient to seek designs with finite support.
Optimization criteria express functions of the FIM that allow this matrix to be optimized in different ways. Consider the criterion function
as a real convex bounded function defined over the space of the information matrix
. A design
will then be
-optimal if
. A number of studies, for example Chapter 10 of [
18], give the criteria most commonly used in the literature. This paper uses the D-optimality criterion, whose goal is to minimize the volume of the confidence ellipsoid of
, the estimators of
. This criterion may be expressed by
In practice this criterion is equivalent to maximizing the determinant of the information matrix. The General Equivalence Theorem (see [
19]) is a tool that allows optimality of a given design under a specific criterion to be checked. The sensitivity function
is defined as a directional derivative
where
is an arbitrary design centered on a point
x. Given an optimal design,
, we find that
, and the equality is found in the support points of the optimal design. The sensitivity function for the D-optimization criterion is given by
The efficiency allows any design
to be compared to the
-optimal design
,
Also, if
is positively homogeneous, the value of the efficiency can be interpreted practically. If the efficiency value is 0.7, this means that the
-optimal design can be used to obtain the same information, or equivalently, the same statistical inference of the estimators of the model parameters, with a saving of 30% of the observations. For D-optimization criterion, which is positively homogeneous, D-efficiency is calculated as follows:
This expression will be termed “efficiency” from here on, as there is no possible confusion.
3. Variance Structure and EIM for a Heteroscedastic Normal Distribution
In most applications in the context of optimal experimental design, the homoscedastic normal distribution is used. However, when the response follows the gamma or the Poisson distribution the variance depends on the explanatory variable. To compare in a fair way with these distributions it is considered the heteroscedastic normal distribution with a variance structure given by
where
and
are constants and
. Thus, taking
, for a value of
the variance structure for the heteroscedastic normal distribution is similar to that of the Poisson distribution (
). On the other hand, with
and
, the structure of the variance for the heteroscedastic normal distribution is
, similar to the variance of the gamma distribution,
, when parameter
is constant. Finally, the case
corresponds to the homoscedastic normal distribution.
Then, using (
2), the EIM for the heteroscedastic normal distribution with variance given by (
5) is
Theorem 1. Let be the function of some regression model, for any optimization criterion Φ
based on the FIM, then the Φ
-optimal designs for the heteroscedastic normal distribution with in the variance defined in (
5)
and for the gamma distribution with constant α coincide. Also, the Φ
-optimal design obtained is independent of α and k. Proof. Taking
in the variance given by (
5), the EIM for the heteroscedastic normal distribution is
, while the EIM for the gamma distribution is
, and so
Therefore the -optimal design calculated with any of the matrices will agree. Also, the parameters k and are constants, multiplied in each expression of the FIM, and so do not affect -optimal design. □
The form of the EIMs of heteroscedastic normal () and Poisson distribution are hardly proportional. Therefore, in this case, there is no possible similar result to Theorem 1.
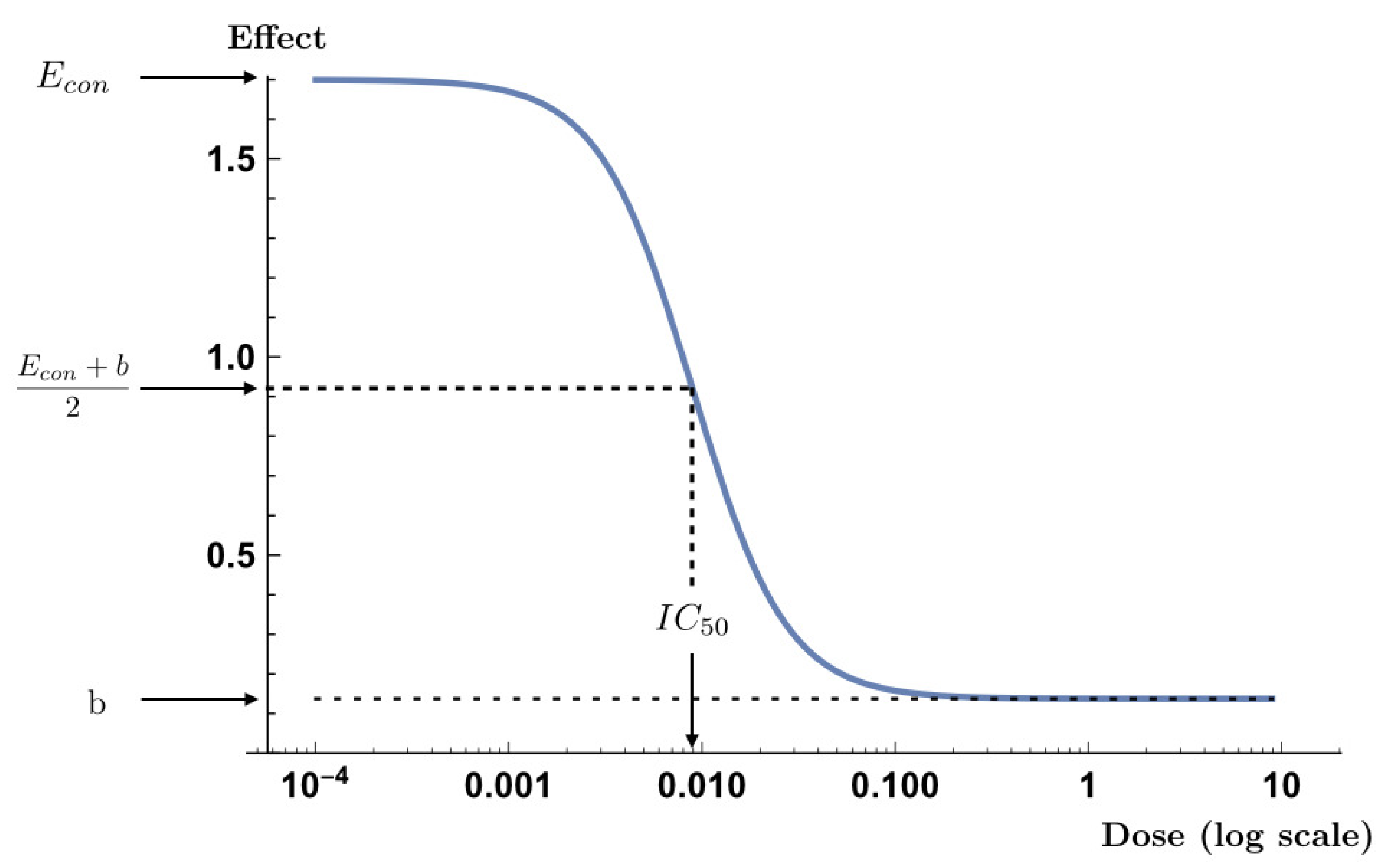
5. Extended Hill Model
The Hill model is a dose-response model commonly used in practice to describe the relationship between the concentration of a drug and its effect. Several papers [
12,
14,
15] have addressed this issue from the point of view of optimal experimental design. This model may explain both discrete and continuous responses, such as counting cells [
25] or the effect of a drug on cell growth [
13], among many others. Here we focus on the 4-parameter Hill model.
If we consider
x to be the dose of an administered drug, the function of the regression model which explains the effect can be expressed as
where
are the parameters to be estimated. The parameter
is the effect on the control, i.e., where there is no dose. The parameter
b corresponds to the asymptotic value of the response when the concentration of the drug tends to infinity and
corresponds to the dose at which a response would be found equal to the middle of the effect range,
. Finally, the parameter
s is a form parameter: if
,
will be strictly increasing, and if
, strictly decreasing. Thus, when the parameter
and
the drug has an inhibitory effect where
b implies that the whole cell population is not destroyed, as shown in
Figure 1. This is the case considered in this paper. Here it is studied from two perspectives simultaneously, where the gamma, or Poisson, is the true distribution of the response variable and the practitioner assumes a heteroscedastic normal distribution with the variance structure given by (
5).
Ref. [
13] bring together different maximum likelihood estimations of the parameters of (
12) for different types of drugs.
Table 4 shows these nominal values and the 4-point D-optimal designs obtained for different probability distributions of the response variable:
(gamma distribution with constant
),
(heteroscedastic normal distribution with variance structure given by (
5)) and
(Poisson distribution). By Theorem 1, when
in (
5)
and
coincide. However, the designs
and
with
are distinct, even though both comparisons show a similar relationship between the mean and the variance.
Table 4 shows only the inner points (intermediate doses) of the D-optimal designs, as the extremes of the design space
are included in all the cases studied. The maximum dosage
was given by the value
, except for the drug AG2009, since the authors considered this dosage to be impractical. It can be seen that the D-optimal design leads to experimenting with three very low doses, and at the maximum dose (
), except for drug AG2009, where the doses are more spread out.
The last column of
Table 4 shows that the efficiency computed by (
11) of the D-optimal designs when a heteroscedastic normal distribution with
is assumed with respect to the Poisson distribution, is around 73%, except for the drug AG2009, whose efficiency is higher. Again, in this practical case there is a considerable loss of efficiency in estimating the model parameters, with regard to misspecification in the probability distribution. All D-optimal designs in this section have been computed using the Wynn-Fedorov’s algorithm [
26].
Sensitivity Analysis
The main aim of this section is to study the effect of the relationship between
and
, characterized by the parameter
r in (
5), on the efficiency. So, a sensitivity analysis of this parameter is done. Ref. [
11] studies the influence of misspecification in the structure of the variance in an analysis carried out for the gamma distribution and the heteroscedastic normal distribution separately. Here, a similar study was carried out with a point of view in which a practitioner considers a heteroscedastic normal response, but the true distribution of the response is gamma, or Poisson. For both distributions, efficiencies, using (
11), are computed by comparing D-optimal designs for heteroscedastic normal distribution with the D-optimal design for the true probability distribution, as a function of the values of
r.
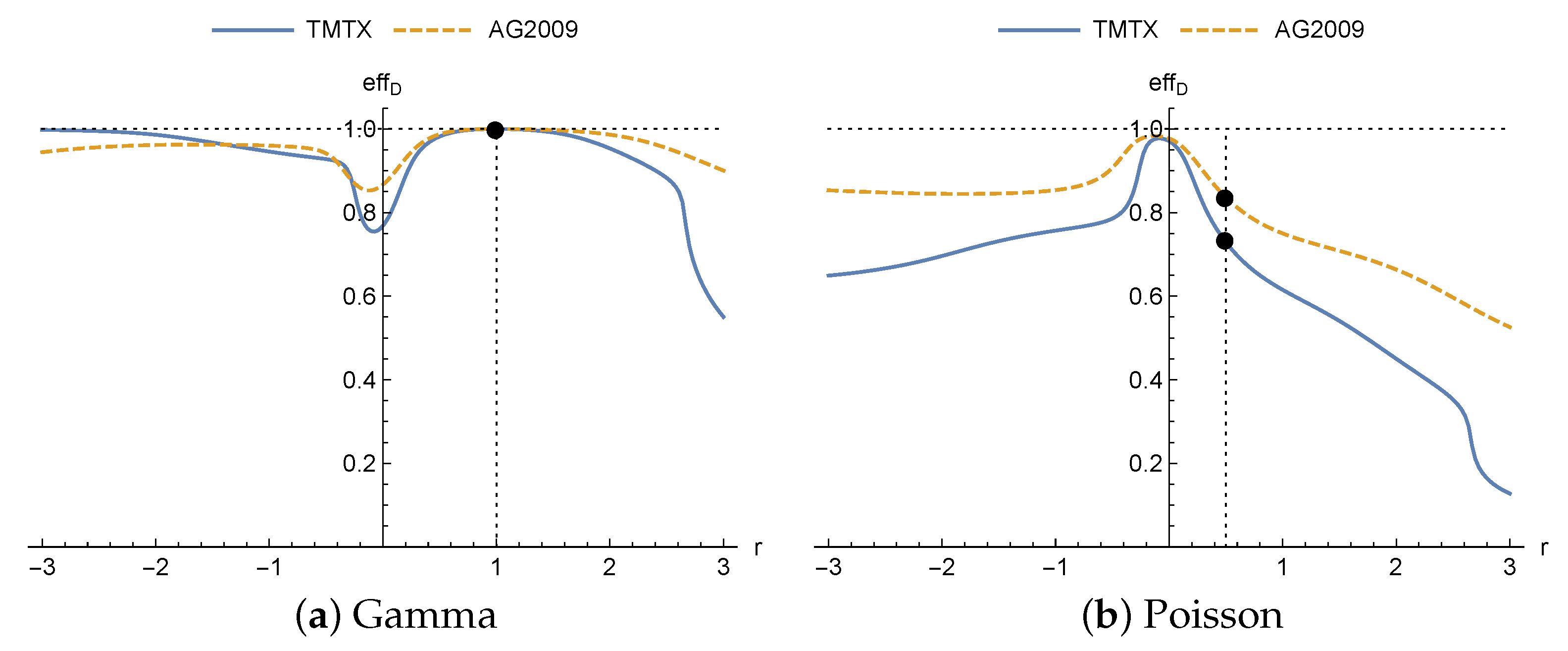
The efficiencies achieved for different drugs are shown in
Figure 2. It can be seen how, when the true distribution is gamma (
Figure 2a), the efficiency is 1 for
(dot), since in this case the designs coincide as proven in Theorem 1. However, when the true distribution is the Poisson (
Figure 2b), maximum efficiency is not obtained for
(dots), as might be expected. It is achieved in this case for negative values of
r, close to
, and so it would have been better, in terms of efficiency, for the practitioner to have assumed the homoscedastic normal distribution rather than heteroscedastic normal with
. Furthermore, it does not reach the value 1 for any value of
r. Finally, for this model in the neighborhood of
(homoscedastic normal distribution) opposite effects are produced on the efficiency for each of the distributions: greater efficiencies when the true distribution is the Poisson, and lower in the case of the gamma. It is important to highlight that there is no analytic explanation for this effect, and it is motivated by the model and nominal values.
For that, the effect of
r on the trend of the efficiency is studied depending on the values taken by
. Again, in this analysis, it is assumed that
y follows a heteroscedastic normal distribution with variance structure given by (
5) when the distribution of
y is the Poisson or the gamma and a misspecification takes place.
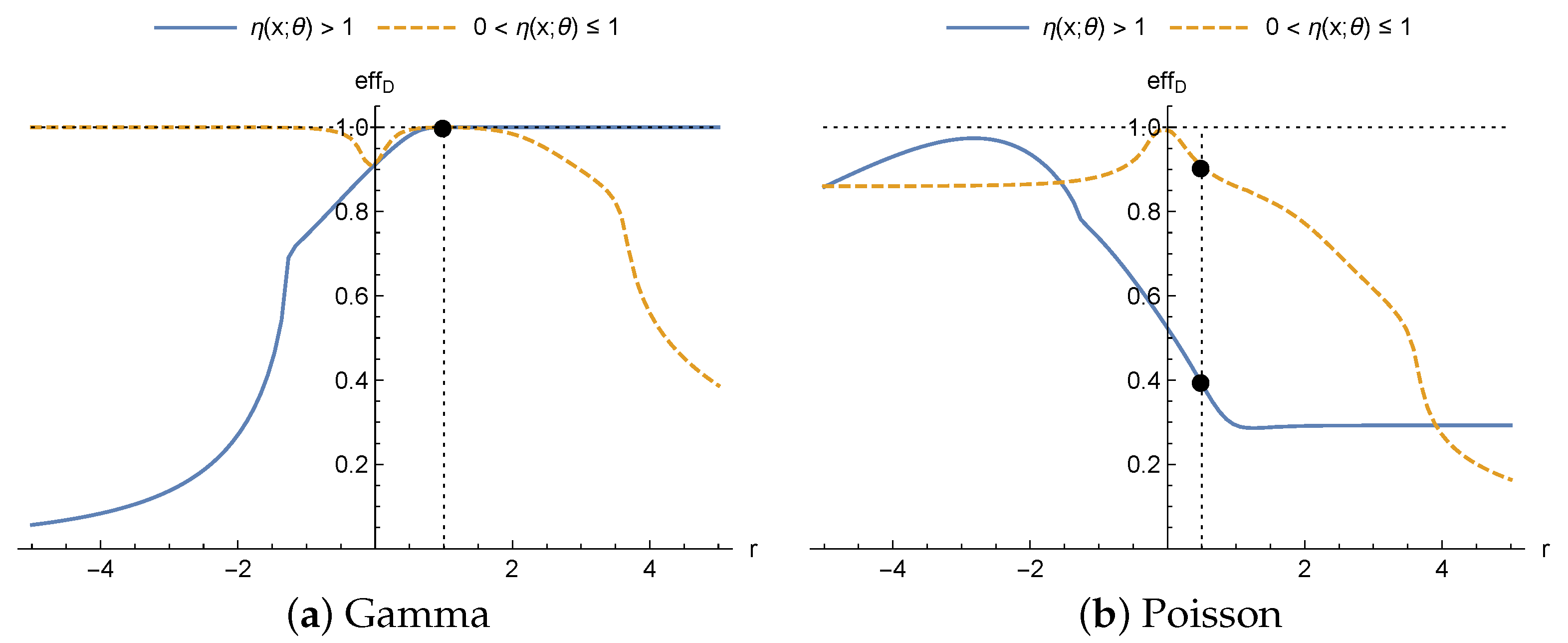
First, for sufficiently large values of
r and
,
, given that
, we have
Thus, when the true probability distribution is a gamma distribution,
Figure 3a (solid line) shows how, on increasing the value of
r the efficiency tends to 1. On the other hand, the lower the value of
r, the greater the difference between
and
, therefore the efficiency tends to 0 as can be seen in
Figure 3a. However, if
(dashed line),
, the effect of
r on the trend of the efficiencies of the designs obtained for the heteroscedastic normal distribution when the true distribution is a gamma distribution is the opposite. As it is shown in
Figure 3a, if
r increases, the efficiency tends to 0, and if
r decreases, the efficiency tends to 1.
When the true distribution is a Poisson distribution there is no direct comparison between its EIM and the EIM of a heteroscedastic normal distribution. However, it can be seen in
Figure 3b how the efficiency reaches a maximum for a particular value of
r and loses efficiency for values away from that value. This is because the study looks at values of
, and so
and
are monotonic. Therefore, the maximum efficiency is at the value of
r where the distance between
and
is minimal (independently of whether
or
). Although the 4-parameter Hill model is taken as an example and the graphs in
Figure 3 are obtained based on that model, the whole study on the trend of
r on the efficiency is general for any regression function satisfying the inequalities.
Finally, it is interesting to point out differences between the graphs in
Figure 2 and
Figure 3. First, the trends in the efficiencies as a function of
r do not coincide. This is because, for the drugs in the study for the 4-parameter Hill model, the inequalities
or
are not satisfied on the design spaces considered in the examples. Secondly, when the true distribution is the Poisson distribution, maximum efficiency in
Figure 3b is obtained for a value close to
when
, as also it takes place in
Figure 2b, while for the case with
maximum efficiency is obtained close to
, i.e., for the same model, the nominal values defined by the context of the problem affect the loss of efficiency.
6. Summary and Conclusions
This study has been carried out to analyze the effect of misspecification in the probability distribution of the response variable. We measure that effect by calculating the efficiency of the optimal design obtained with an assumed or working distribution compared to that obtained with the true probability distribution. The typical case is when a researcher assumes a normal distribution, even a heteroscedastic one, for the response variable of his or her problem, but at a greater depth, another distribution is more appropriate, for example a gamma (or Poisson) distribution. When there is misspecification in the probability distribution, there is a loss of efficiency which depends both on the assumed probability distribution and on the regression function .
We provide some theoretical results, as well as practical ones. The first is quite general, valid for any regression function and any criterion based on FIM which guarantees that there is no loss of efficiency when the response variable follows a gamma distribution, and there is assumed to be a heteroscedastic normal distribution with in the variance structure given by (5). For the linear quadratic model, analytical results are obtained on computing the optimal design for Poisson and gamma distributions. These theoretical results have been used in real applications from the literature, providing designs useful for practitioners.
Finally, the 4-parameter Hill model was used to illustrate and quantify the loss of efficiency. Assuming a heteroscedastic normal distribution, taking values close to
in (
5), between about 18% and 25% efficiency is lost for all the drugs looked at in the study when the true distribution is a gamma distribution. Thus, in this case, the usual assumption of normality and homoscedasticity (
) of the response variable is not a good option. However, when the true distribution is the Poisson, the loss of efficiency is less severe, reaching maximum values of efficiency for values close to
for all the drugs. This is a striking case, as one might expect maximum efficiency to be achieved at the value
, which leads to the same relationship between the mean and the variance for the heteroscedastic normal and the Poisson distributions.
It is worth finishing this paper by mentioning that the EIM is an essential tool, as it collects information both about the regression function and the probability distribution of the response variable. As already mentioned, to assume the homoscedastic normal distribution when obtaining optimal designs may lead to a great loss of efficiency. Nonetheless, the examples given show that this will depend on the true distribution of the response variable and on the model function chosen. The existence of uncertainty about the probability distribution of the response variable will therefore lead to the future goal of obtaining robust designs to reduce this uncertainty.