2.2. Classical Formulation of the Problem
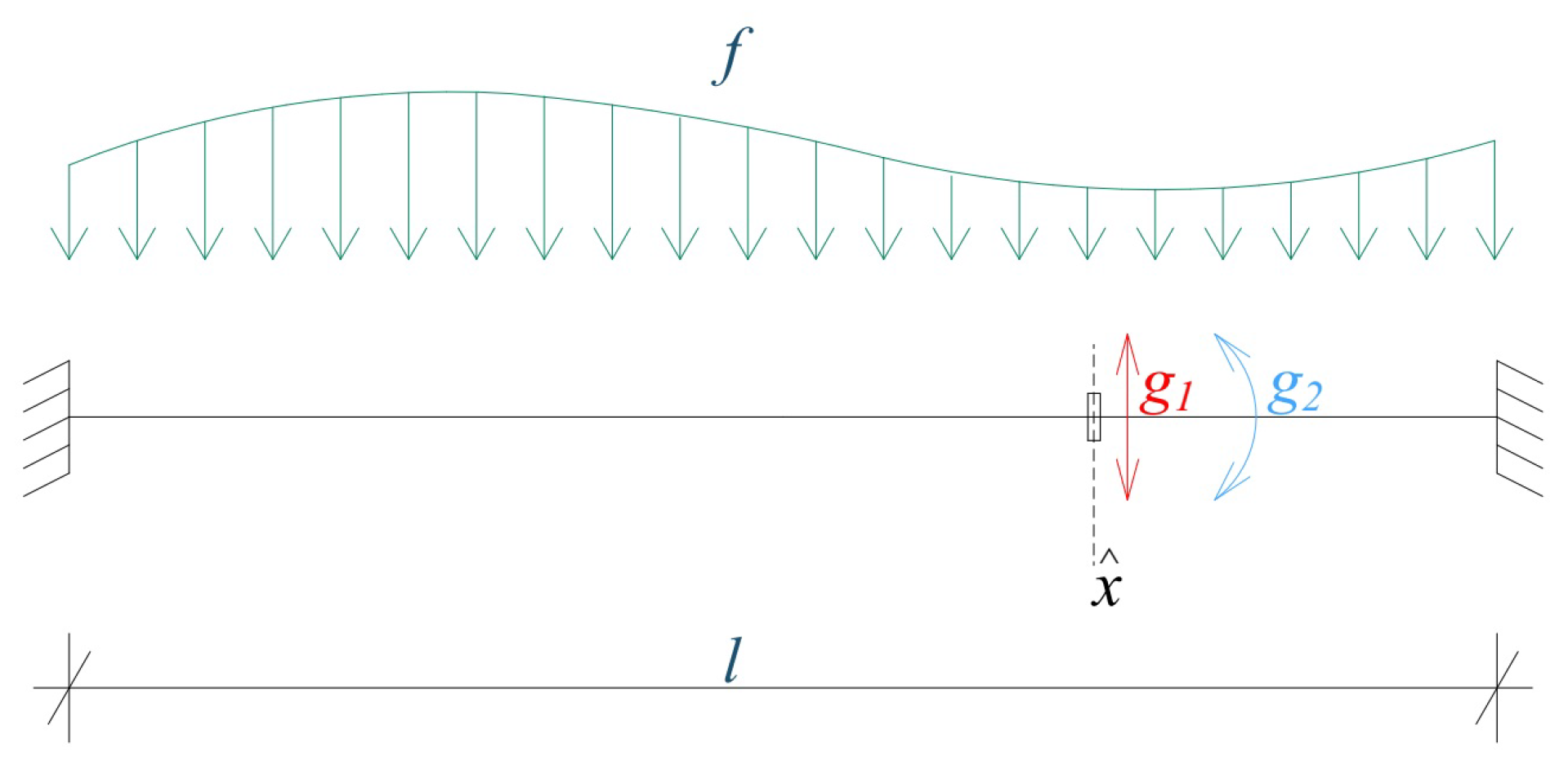
To introduce the continuous classical formulation, we assume a beam of length
, load function
,
, and internal point obstacle
, given sliding friction
and given swivel friction
. We consider the following problem: find a function
u, such that
Function u, corresponding to the problem , will be called a classical solution of the considered problem.
The differential equation (
1) is a mathematical model of the bending of the Euler–Bernoulli beam. The boundary conditions (
2) define the clamping of the beam at both ends, relations (
3) and (
4) represent the conditions of given sliding friction, and relations (
5) and (
6) are the conditions of the given swivel friction.
2.3. Weak and Variational Formulation
As the classical formulation of the problem is too strong and therefore not suitable for direct numerical solution, we formulate the considered problem as a variational one.
Let
,
, and
. We define the space
V of test functions, corresponding to the boundary conditions, as a Sobolev space (see, e.g., in [
11,
13]) as follows:
Next, we introduce the functional
, corresponding to given swivel and sliding frictions, in the form
Let
u be a solution of the problem
and
. By scalar multiplication of Equation (
1) by the function
and integration (using Green’s theorem—see, e.g., [
14]) on the interval
, we obtain
From (
4) and (
6), we have
Using (
12), (
13) and (
3), (
5), it follows from (
11) that
Afterwards, we can define a weak formulation of the problem
as a problem of finding a function
u such that
where
The sought function u is a weak solution of the problem .
Remark 1. The weak formulation of the problem is formulated as an elliptical variational inequality of the second type with non-differentiable functional q (see, e.g., in [8]). Let form
and functional
be given by relations (
15) and (
16) and
,
such that
Obviously, the form
a is bilinear and symmetric. To prove its continuity we use Hölder’s inequality (see, e.g., in [
7])
where
. From the assumptions (
17) and (
18) of functions
E,
J and from
, we have
Here, we apply Friedrichs’s inequality (see, e.g., [
7]) to obtain the
V-ellipticity of the form
a
where
and
k is the positive constant from Friedrichs’s inequality. It is also clear that the functional
F is linear. Using Cauchy–Schwarz inequality (see, e.g., in [
7]), we can prove its continuity, i.e.,
.
Let
. Then, for functional
q given by (
10), it holds that
which means that
q is convex. Immediately from the definition of
q, we can see that
. Moreover, for zero function
, it holds
, i.e.,
and thus
q is proper on
V. It is clear that the functional
q is continuous. The convexity and continuity of
q imply its semi-continuity from below. Therefore, the existence and uniqueness of the solution of problem
are guaranteed by the following Theorem 1, the assumptions of which are thus fulfilled.
Theorem 1. Let be bounded, V-elliptical bilinear form, and let functional be convex, semi-continuous from below and proper on V. Then, there exists an unique solution of For more detail, see, e.g., in [8,15]. As
a is bounded; the
V-elliptical is bilinear and of symmetric form; functional
q is convex, semi-continuous from below, and proper on
V; and the problem
is equivalent to the variational problem of minimizing quadratic energy functional, i.e.,
where
2.4. Approximation
Let
and
satisfy relations (
17) and (
18), respectively. Let the form
and the functional
be given by (
15) and (
16), respectively. We consider a system of partitions
,
of the interval
into subintervals
such that points
are nodal points, i.e.,
where
is the number of nodal points of
and
h is the maximum length of intervals
. Moreover, the point obstacle
for any
h. We define the following finite-dimensional subspace
:
Therefore, spaces
satisfy classical boundary conditions and additionally
and
We approximate the functional
q for each
h by functional
by
Functional
is convex, semi-continuous from below and proper in the space
. We can approximate problem
by the sequence of problems of finding
such that
The existence and uniqueness of the solution of is guaranteed by the Theorem 1.
As the form
a is symmetric, the problem
is equivalent to the problem of finding
such that
where
To approximate the function
, we use the Hermitian cubic spline function for each
such that
Remark 2. For the given function , the Hermitian cubic spline function is given by 2.5. Convergence Analysis
To prove the convergence of the approximated solutions to the weak solution u of the considered problem, we use the following theorem.
Theorem 2. Let be bounded, V-elliptical bilinear form on V. Let there exist operator such thatwhere such that . Let the system of functionals meet the following two conditions: For more details, see, e.g., in [16]. As the functional
is convex and semi-continuous from below on
, it is also weakly semi-continuous from below. In our case, operators
are operators of the appropriate Hermitian interpolation. From the (
28), it follows that
This means that assumptions of Theorem 2 are satisfied, i.e., the sequence of solution approximations of the problem converges to the solution u of the problem in the V-space norm.
2.6. The Algebraic Formulation
Let the form
a and the functional
F be defined by (
15) and (
16), respectively. We choose a finite-dimensional space
,
with
. Let
be a basis of
chosen by FEM, i.e.,
To obtain a shape of basis functions, we apply the Hermite’s cubic splines. We have
For an example of geometric representation, please see
Figure 2.
Any function
can be uniquely written in the form of linear combination of basis functions, i.e.,
where
are the corresponding coordinates of
in the basis. It is clear that
,
depend on
h. If we substitute
from (
33) into the functional
given by (
27), we obtain
where
is a stiffness matrix with elements ,
is a vector of right-hand sides with elements ,
is a vector of unknown coefficients of linear combination (
33),
is vector of base functions .
Functional
is expressed as a quadratic function of variables
. Let us define an isomorphism
by relation
Then, the problem
can be rewritten in the equivalent form where it is required to find
such that
where
is inverse of
, and
is index of the nodal point
.
Problem is the algebraic form of problem .
2.7. Numerical Realization
In this section, we examine two different approaches for the practical numerical solution of the problem. For simplicity, we consider an equidistant grid
where
is a number of nodal points and
is a size of intervals. Following the Ritz–Galerkin method, we approximate
V by finite-dimensional space
Additionally, we assume that there exists
such that
, i.e., the point with defined conditions (
3)–(
6) is one of the used nodal points.
Remark 3. Note that because the solution in boundary points is given by conditions (2). The optimization problem
can be written in the form
with
symmetric positive definite (SPD) matrix
, and vector
.
The solution
of (
38) represents the coordinates (
33) of unknown discretized deflection
in the considered basis.
Although the problem (
38) has a simple structure, we are still dealing with a nonlinear optimization problem with a non-differentiable objective function. In our case, we are dealing with absolute values in
(
39). The optimization problems with absolute values in objective functions arise in various applications, and they are already well examined. For example, when one uses L1-regularization (i.e., so-called least absolute shrinkage and selection operator-LASSO [
17]) for regularization of linear regression, the problem has a similar form to (
38).
Generally, there exist two types of numerical methods to solve the problem-approximation of a non-differentiable term in objective function or dualization of the problem.
2.7.1. Method of Regularization
The idea is to replace (approximate) the non-differentiable term in objective function with a more suitable differentiable one. In our case, we decided to use the piecewise quadratic approximation, i.e., we approximate absolute value
by
where
is a sufficiently small regularization parameter. The example of this approximation is presented in
Figure 3. The derivative is given by
Using this approximation, the non-differentiable function
(
39) can be written in form
AS we use piecewise quadratic approximation (
40), the derivative is piecewise linear function (
41). Additionally, the gradient of quadratic function
(
39) is linear, and consequently the necessary optimality condition for unconstrained optimization problem (
38) is given by the system of linear equations
The components of gradient
are equal to zero except for the components corresponding to partial derivatives of
and
. These values depend on conditions from definition of (
40) with respect to values
and
. The values are presented in
Table 1.
The final system of linear equations can be written in form
where
is a matrix
with diagonal elements modified by coefficients of linear terms in
and
is a vector
b with additional constant terms from
.
It is necessary to solve the problem for all possible cases with respect to
. The solution of the problem
(
38) is the vector
, for which the corresponding condition on
with respect to
is satisfied.
2.7.2. Dual Problem
The idea of this approach is based on simple observation of the following equivalent form of absolute value:
Using this identity, we can rewrite the function
(
39) into
where we denoted
Using the separability of variables and the saddle-point property [
12], we can write optimization problem (
38) in equivalent form
Function
can be considered as a Lagrange function. From the first Karush–Kuhn–Tucker optimality condition [
18], we can derive (note that
is SPD, i.e., non-singular)
and substitute into objective function
L to get (for more details see in [
19])
As the original problem (
47) is a maximization problem, we can change the sign of the objective function to obtain
Please, notice that the dual problem (
49) is a minimization of a strictly convex quadratic function on a feasible set defined by box constraints. Such a problem always has a unique solution [
12]. The dimension of the problem is 2, which is much more lower number then the dimension of original primal problem (
38). Moreover, the problem belongs to the most basic nonlinear optimization problems and it is solvable by several types of methods, for example, Interior Point, Active set, or Projected Gradient methods [
18].
2.8. Numerical Experiments
As a demonstration of the presented theory and methods of solution, we consider three numerical benchmarks: with analytical solution (Benchmark 1), with non-trivial load function (Benchmark 2), and with more internal points with given sliding and swivel friction (Benchmark 3).
Benchmark 1
We consider a most simple case: we suppose problem
(
1)–(
6), i.e., optimization problem
(
38), with constant
. It can be easily shown that this problem has an analytical solution. In this paper, the solution is used for measuring the absolute error of proposed numerical algorithms. The form of solution is given by
with
and unknown
and
. These unknown constants can be computed from the conditions (
3), (
5), (
4), and (
6). We derived and simplified the corresponding derivatives and form the system of nonlinear equation and inequalities:
with
and
We solve the system (
51) by solving only the equations (which consist of the elimination of absolute values, dividing by the
and
to obtain systems of linear equations), and afterwards we choose the solution which satisfies all the equations and inequalities (
51).
To use the numerical algorithms, we will need to prepare objects in optimization problem
(
38). It can be easily shown that in the case of constant
, matrix
is a block tridiagonal Toeplitz matrix and together with vector
, it can be written in a form
with
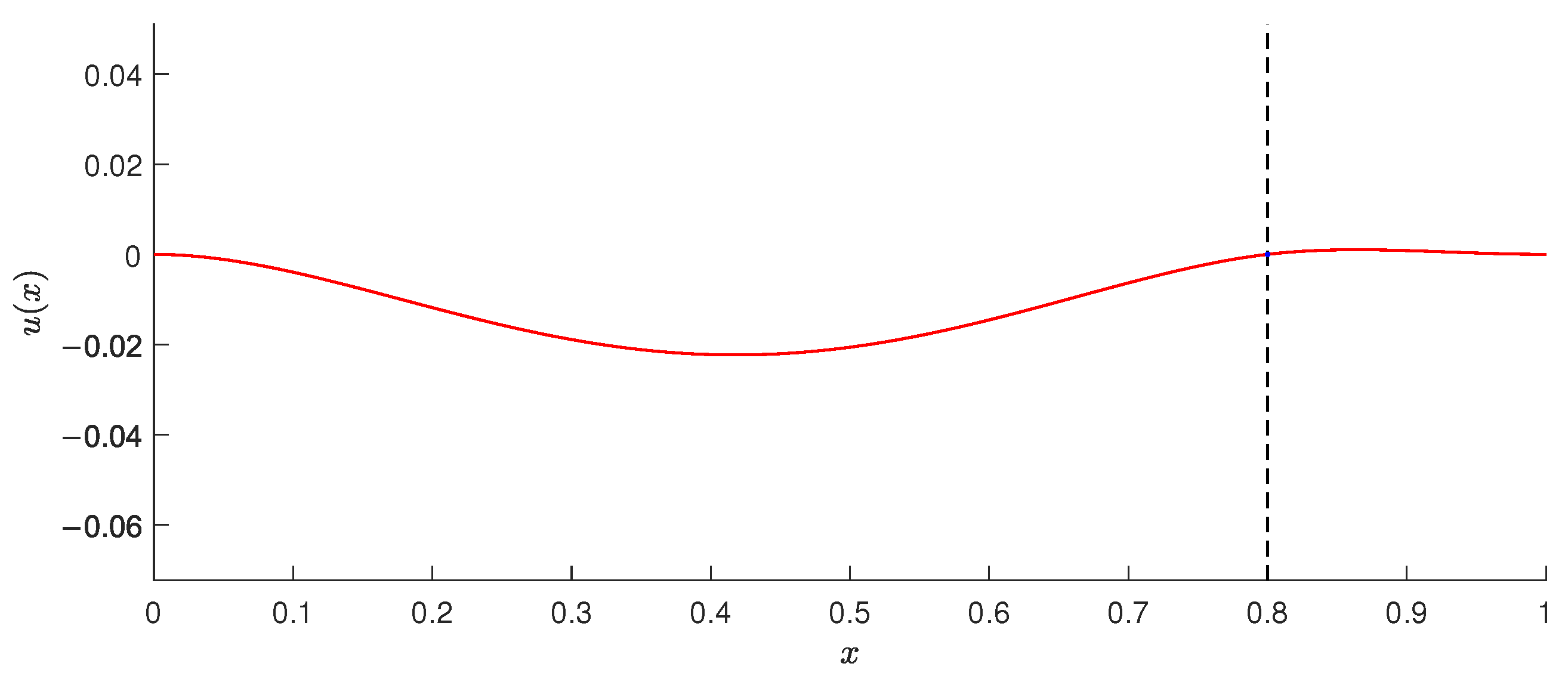
To provide a specific set of data for benchmark, we examine algorithms on the example of a steel beam (
E = 2.15 × 10
Nm
) of the length
m. The point obstacle with given friction is given by
m with friction values
N and
N. We suppose the load function
f = 50,000 N. The beam has a rectangular cross section of height
m and width
m. The analytical solution of this problem is presented in
Figure 4.
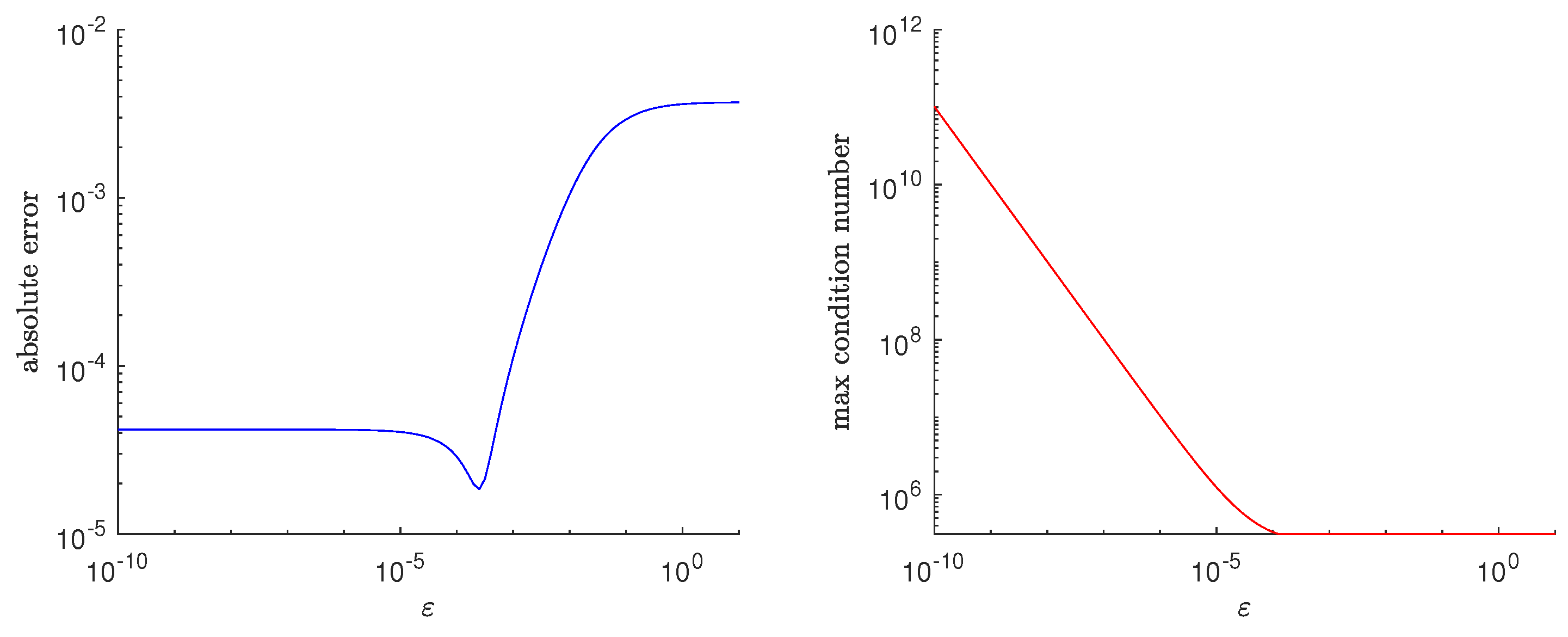
We start our examination with number of used elements as
and analyze the influence of regularization parameter on absolute error of the solution of regularized problem. We introduce the error measure by
where
is analytical solution and
is numerical solution computed by solving (
43) with regularization parameter
. This formula measures the relative difference between the solutions in used nodal points. The results are presented in
Figure 5.
In the case of the dual problem, the absolute error decreases naturally with the increase of the discretization density, see
Figure 6. The main bottleneck of this approach is the computation of the inverse.
Benchmark 2
In this benchmark, we consider the same problem parameters as in the case of Benchmark 1 except for a shape of cross section and a load function. We consider a solid circular cross section of radius
m and a load function
with given parameters
. Obviously,
f is a linear function with
and
.
Computing the corresponding integrals, it is easy to derive the components of a vector of right–hand sides
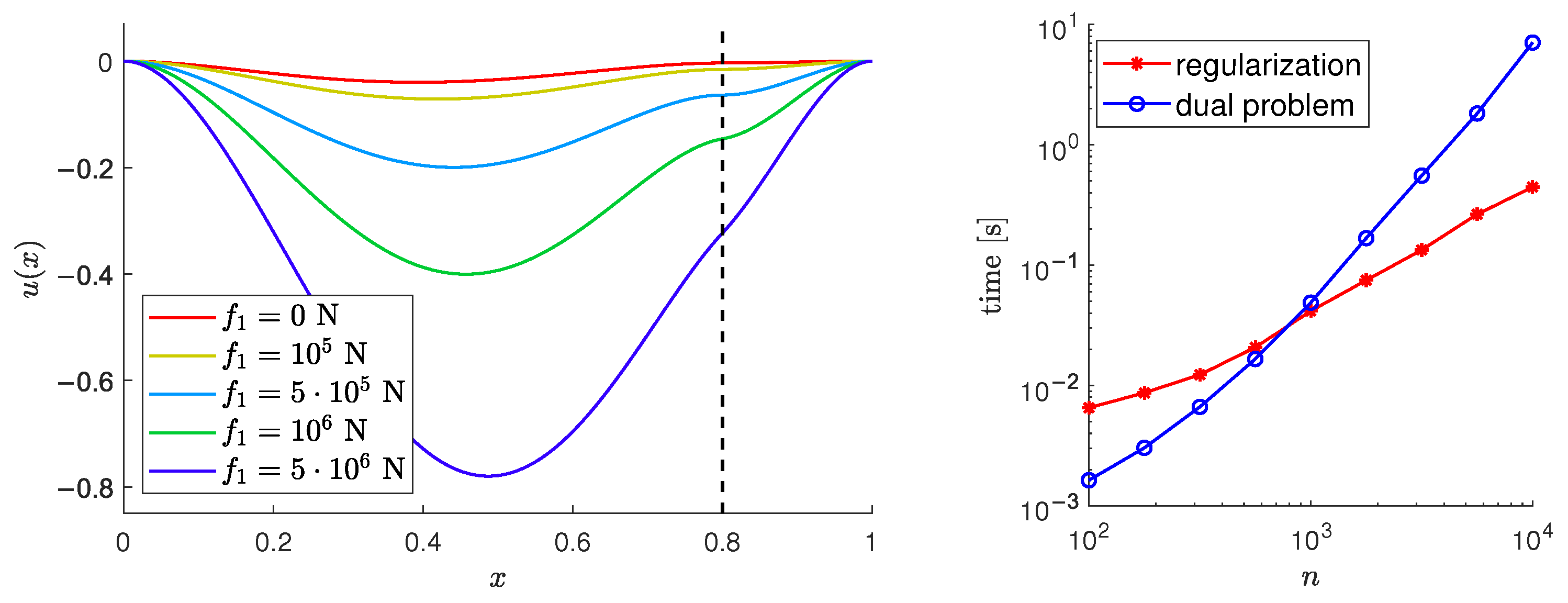
We set
N and solve the problem for various choice of
, see
Figure 7 (left). To compare the regularization method and the dual problem method, we solve the problem with
N for increasing the problem dimension
n. The computational time is demonstrated in
Figure 7 (right). To decrease the small oscillations of the results (especially in the case of short time), we compute all problems 100 times and present the average computational time.
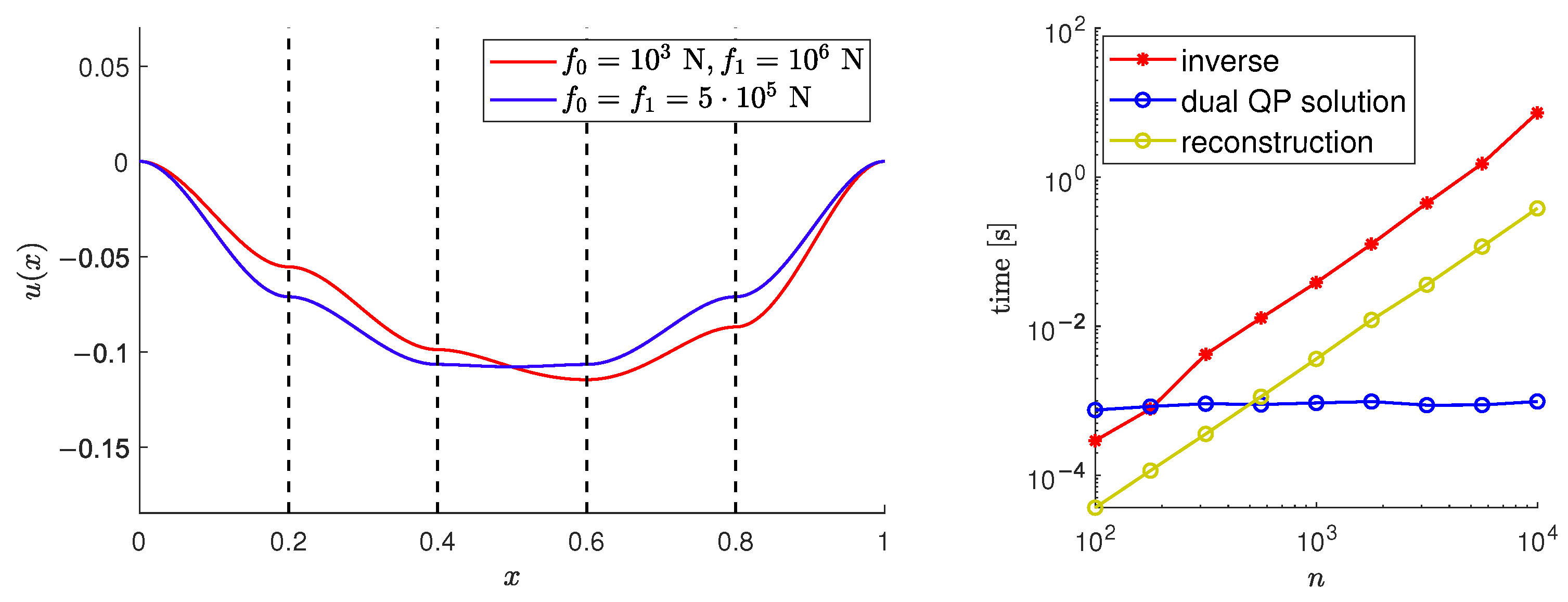
Benchmark 3
In our last benchmark, we increase the number of internal point obstacles with given friction coefficients to 4 equidistantly distributed on
. We consider the coefficients of given sliding and swivel friction the same for all points
N and
N. We consider material constants defined in Benchmark 1 and the solid circular cross section and load function defined in Benchmark 2. The solution provided by the dual problem approach is presented in
Figure 8 (left). In the case of 4 obstacle points, the number of corresponding Lagrange multipliers
is 8,
and matrix
(
45) has 8 rows. The dimension of dual problem (
49) is 8; however, the most time-consuming operation remains the inverse of the Hessian matrix, see
Figure 8 (right).