Sensitivity of the Solution to Nonsymmetric Differential Matrix Riccati Equation

Abstract

Nonsymmetric differential matrix Riccati equations arise in many problems related to science and engineering. This work is focusing on the sensitivity of the solution to perturbations in the matrix coefficients and the initial condition. Two approaches of nonlocal perturbation analysis of the symmetric differential Riccati equation are extended to the nonsymmetric case. Applying the techniques of Fréchet derivatives, Lyapunov majorants and fixed-point principle, two perturbation bounds are derived: the first one is based on the integral form of the solution and the second one considers the equivalent solution to the initial value problem of the associated differential system. The first bound is derived for the nonsymmetric differential Riccati equation in its general form. The perturbation bound based on the sensitivity analysis of the associated linear differential system is formulated for the low-dimensional approximate solution to the large-scale nonsymmetric differential Riccati equation. The two bounds exploit the existing sensitivity estimates for the matrix exponential and are alternative.

1. Introduction and Notations

In the present paper, we consider the nonsymmetric differential matrix Riccati equation /NDRE/

$$\begin{array}{ccc}\hfill \dot{X}\left(t\right)& =& -AX\left(t\right)-X\left(t\right)D+X\left(t\right)SX\left(t\right)+Q,\hfill \\ \hfill X\left(0\right)& =& X_0.\hfill \end{array}$$

(1)

where the solution $X\left(t\right)$ is a $n\times p$ real matrix and $A\in {\mathbb{R}}^{n\times n}$, $D\in {\mathbb{R}}^{p\times p}$, $Q\in {\mathbb{R}}^{n\times p}$ and $S\in {\mathbb{R}}^{p\times n}$ are the coefficient matrices and $X_0\in {\mathbb{R}}^{n\times p}$ is a given initial value.

We assume that the matrix

$$\begin{array}{c}\hfill \mathcal{H}=\left[\begin{array}{cc}\hfill D& \hfill -S\\ \hfill -Q& \hfill A\end{array}\right]\in {\mathbb{R}}^{p+n\times p+n}\end{array}$$

is a nonsingular M-matrix, or an irreducible singular M-matrix. (Recall that a real square matrix A is said M-matrix if $A=sI-B$ with $B\ge 0$ and $s\ge r\left(B\right)$, where $r(.)$ denotes the spectral radius. If $s>r\left(B\right)$, the M-matrix A is nonsingular.) As a consequence, [1], A and D are both nonsingular M-matrices and can be decomposed as $A=A_1-A_2$ and $D=D_1-D_2$, where $A_2$, $D_2$ are positive and $A_1$, $D_1$ are nonsingular M-matrices. The NDRE (1) can then be formulated as

$$\begin{array}{ccc}\hfill \dot{X}\left(t\right)+X\left(t\right)D_1+A_{1}X\left(t\right)& =& A_{2}X\left(t\right)+X\left(t\right)D_2+X\left(t\right)SX\left(t\right)+Q\hfill \\ \hfill X\left(0\right)& =& X_0.\hfill \end{array}$$

The solution of NDRE (1) is given by the implicit formula [2]

$$\begin{array}{ccc}\hfill X\left(t\right)& =& e^{-t{A}_1}{X}_0{e}^{-t{D}_1}+{\int }_0^t{e}^{-(t-\tau )A_1}Q{e}^{-(t-\tau )D_1}d\tau \hfill \\ & & +{\int }_0^t{e}^{-(t-\tau )A_1}\left(X\left(\tau \right)SX\left(\tau \right)+A_{2}X\left(\tau \right)+X\left(\tau \right)D_2\right)e^{-(t-\tau )D_1}d\tau .\hfill \end{array}$$

(2)

Let us now consider a nonsingular solution $X^{*}$ to the nonsymmetric algebraic Riccati equation

$$\begin{array}{c}\hfill -AX-XD+XSX+Q=0.\end{array}$$

In [1], it is proved that if $\mathcal{H}$ is assumed to be a nonsingular M-matrix, then the NDRE (1) has a global solution $X\left(t\right)$, provided that the initial value $X_0$ satisfies the condition $0\le X_0\le X^{*}$, where for every matrices A, $B\in {\mathbb{R}}^{m\times n}$, we write $A\le B$ if $a_{ij}\le b_{ij}$ for all $i\in \{1,\cdots ,m\}$ and $j\in \{1,\cdots ,n\}$.

Nonsymmetric differential Riccati equations are related to linear boundary value problems arising in game and control theory, oscillation criterion problems for second order differential systems, variational calculus and theory of transport processes [3]. NDRE are an intermediate step in problems from singular perturbations and control theory when linear transformations are applied to reduce high-order systems to lower order or to partially decomposed systems. The properties of nonsymmetric differential Riccati equations determine the existence of the optimal open-loop strategies in Nash and Stackelberg control in game theory [4]. NDRE are induced via invariant embedding and interpretation formula from an “angularly shifted” transport model in the slab geometry [2]. Of mathematical interest, nonsymmetric differential Riccati equation describes the local coordinates of the restriction to a subset of the Lagrangian Grassmannian manifold. The most important results for NDRE are generalized in [5]. Fital and Guo, in [1], prove that for a suitable initial value $X_0$, the initial value problem (1) has a nonnegative solution $X\left(t\right)$, which converges to the stable equilibrium of (1). A closed formula, in terms of exponential of data matrices, for the general solution of (1), when S is invertible, is proposed in [6]. An analytical review of existing numerical methods to find the minimal nonnegative solution to low-dimensional NDRE (1) is given in [7], where the approximate low-dimensional solution to the large-scale case with low-dimensional right hand side is obtained after projecting (1) to low-dimensional differential equation by applying the extended block Arnoldi process.

The numerically computed solution contains errors, as a result of truncation of infinite series, round-off errors due to the finite precision machine arithmetic, error of stopping iteration procedures, etc. The computed perturbed solution can be represented as the exact solution of a slightly perturbed problem, simulating the effect of the errors mentioned above by equivalent perturbations in the data matrices. To estimate the actual error in the computed solution, it is important to find a bound of the error in the computed solution in terms of the perturbations in the data. Perturbation analysis of the nonsymmetric algebraic Riccati equation is given in [8], normwise, mixed and componentwise condition numbers, as well as residual bounds are proposed in [9,10,11]. To the best of our knowledge, the sensitivity and the conditioning of the NDRE are not yet analyzed.This work has two goals. First, we study the sensitivity of the solution $X\left(t\right)$ to (1) to perturbations in the matrix coefficients A, D, Q, S, $X_0$. It is done by adapting the bounds established for the symmetric differential Riccati equation, obtained by [12,13] to the nonsymmetric Riccati equation, which show good upper sensitivity. The perturbation bounds are very important for interpreting a numerically computed solution. The second objective is to apply the derived nonlocal perturbation bound to estimate the error of approximation in the solution when solving large-scale nonsymmetric differential Riccati equations by Krylov-type methods.

The paper is organized as follows: In Section 2, nonlocal sensitivity analysis of the nonsymmetric differential matrix Riccati Equation (1) is presented. An effective perturbation bound is proposed. In Section 3, an alternative perturbation bound based on the sensitivity analysis of the associated differential system is derived and then applied for estimating the error of approximation of the low-dimensional approximate solution. The bounds exploit existing sensitivity estimates of the matrix exponential. Numerical examples are presented in Section 4 to illustrate the theoretical results established in this work.

Throughout the paper, the following notations are used: ${\mathbb{R}}^{m\times n}$ denotes the space on $m\times n$ real matrices, $\parallel .\parallel$ is the spectral norm $\parallel M\parallel ={\left[{\lambda }_{max}\left(M^{\top }M\right)\right]}^{1/2}$, where ${\lambda }_{max}\left(N\right)$ is the maximum eigenvalue of the symmetric matrix N, ${\parallel .\parallel }_{\mathrm{F}}$ is the Frobenius norm, $A^{\top }$ is the transpose of the matrix $A\in {\mathbb{R}}^{m\times n}$, $I_n$ is the $n\times n$ unit matrix, and the symbol $:=$ stands for “equal by definition”.

2. Nonlocal Perturbation Bound of NDRE

In this section, we will extend the approach proposed in [12] to the nonsymmetric differential Riccati Equation (1).

Let us denote by $\mathcal{Z}:=(A,D,Q,S,X_0)$ the collection of matrix coefficients and by $\mathsf{\Delta }\mathcal{Z}:=(\mathsf{\Delta }Z,\mathsf{\Delta }D,\mathsf{\Delta }Q,\mathsf{\Delta }S,\mathsf{\Delta }{X}_0)$ the collection of equivalent perturbations in the data. The perturbation $\mathsf{\Delta }Z$$\in \mathsf{\Delta }\mathcal{Z}$ is continuous with $\parallel \mathsf{\Delta }Z\parallel$$\approx \mathtt{macheps}\varphi \left(n\right)\parallel Z\parallel$, where $\varphi \left(n\right)$ is a low-order polynomial in n and $\mathtt{macheps}$ is the round-off unit of the machine arithmetic. If some of the matrix coefficients are not perturbed, then the corresponding perturbations are assumed to be zero. The perturbed nonsymmetric differential matrix Riccati equation, obtained from (1) by replacing the nominal values $Z\in \mathcal{Z}$ by $Z+\mathsf{\Delta }Z$, ($\mathsf{\Delta }Z\in \mathsf{\Delta }\mathcal{Z}$) is given by

$$\begin{array}{ccc}\hfill {(X\left(t\right)+\mathsf{\Delta }X\left(t\right))}^{\prime }& =& -(A+\mathsf{\Delta }A)\left(X\right(t)+\mathsf{\Delta }X(t\left)\right)\hfill \\ & & -\left(X\right(t)+\mathsf{\Delta }X(t\left)\right)(D+\mathsf{\Delta }D)\hfill \\ & & +\left(X\right(t)+\mathsf{\Delta }X(t\left)\right)(S+\mathsf{\Delta }S)\left(X\right(t)+\mathsf{\Delta }X(t\left)\right)+Q+\mathsf{\Delta }Q,\hfill \\ \hfill X\left(0\right)+\mathsf{\Delta }X\left(0\right)& =& X_0+\mathsf{\Delta }{X}_0,\hfill \end{array}$$

(3)

where $X\left(t\right)+\mathsf{\Delta }X\left(t\right)$ is the solution to the perturbed nonsymmetric differential matrix Riccati Equation (3). For sufficiently small perturbations $\mathsf{\Delta }Z\in \mathsf{\Delta }\mathcal{Z}$ in the data $Z\in \mathcal{Z}$, the solution $X\left(t\right)+\mathsf{\Delta }X\left(t\right)$ to the perturbed Equation (3) exists and depends continuously on the elements of the perturbations $\mathsf{\Delta }Z$ in the data Z. Let $\delta :=[{\delta }_A$; ${\delta }_D$; ${\delta }_Q$; ${\delta }_S$; ${\delta }_{X_0}]\in {\mathbb{R}}_{+}^5$ be the perturbation vector, where ${\delta }_Z:=\parallel \mathsf{\Delta }Z\parallel$ for $\mathsf{\Delta }Z\in \mathsf{\Delta }\mathcal{Z}$.

Our aims in this section, are to extend the results obtained in [12] for the symmetric differential matrix Riccati equation to the nonsymmetric case (1) and to give a bound for the perturbations in the solution $\parallel \mathsf{\Delta }X\left(t\right)\parallel \le f(\delta ,t)$ as a function of the perturbation vector $\delta$.

From (3), taking into account (1), we can write the perturbation of the solution as

$$\begin{array}{ccc}\hfill \mathsf{\Delta }\dot{X}\left(t\right)& =& -A_c\left(t\right)\mathsf{\Delta }X\left(t\right)-\mathsf{\Delta }X\left(t\right)D_c\left(t\right)+\mathcal{M}(t,\mathsf{\Delta }X\left(t\right)),\hfill \\ \hfill \mathsf{\Delta }X\left(0\right)& =& \mathsf{\Delta }{X}_0,\hfill \end{array}$$

(4)

where $A_c\left(t\right):=A-X\left(t\right)S$, $D_c\left(t\right):=D-SX\left(t\right)$ are the closed-loop matrices and $\mathcal{M}(t,P)$ is the operator

$$\begin{array}{ccc}\hfill \mathcal{M}(t,P)& :=& {\mathcal{M}}_1(t,P)+{\mathcal{M}}_2(t,P),\hfill \end{array}$$

(5)

defined for some matrix $P\in {\mathbb{R}}^{n\times p}$, with

$$\begin{array}{ccc}\hfill {\mathcal{M}}_1(t,P)& :=& X\left(t\right)\mathsf{\Delta }SX\left(t\right)-\mathsf{\Delta }AX\left(t\right)-X\left(t\right)\mathsf{\Delta }D+\mathsf{\Delta }Q,\hfill \\ \hfill {\mathcal{M}}_2(t,P)& :=& -(\mathsf{\Delta }A-X(t\left)\mathsf{\Delta }S\right)P-P(\mathsf{\Delta }D-\mathsf{\Delta }SX(t\left)\right)+P(S+\mathsf{\Delta }S)P\hfill \end{array}$$

(6)

and spectral norm

$$\begin{array}{ccc}\hfill \parallel \mathcal{M}(t,P)\parallel & \le & {\parallel X\left(t\right)\parallel }^2{\delta }_S+\parallel X\left(t\right)\parallel ({\delta }_A+{\delta }_D)+{\delta }_Q\hfill \\ & & +\parallel P\parallel ({\delta }_A+2\parallel X\left(t\right)\parallel {\delta }_S+{\delta }_D{)+\parallel P\parallel }^2(\parallel S\parallel +{\delta }_S).\hfill \end{array}$$

(7)

From (4), we can state the following nonlocal perturbation bound:

Theorem 1.

Let $\mathsf{\Delta }X\left(t\right)$ be the perturbation in a solution $X\left(t\right)$ to Equation (1), solved by a numerically stable algorithm in finite precision arithmetic according to the perturbation vector $\delta :=({\delta }_A$, ${\delta }_D$, ${\delta }_Q$, ${\delta }_S$, ${\delta }_{X_0})$. Let us define the set ${\Omega }_t$

$$\begin{array}{c}\hfill {\Omega }_t:=\{\delta \ge 0,a_1\left(\delta \right)+2\sqrt{a_0\left(\delta \right)a_2\left(\delta \right)}\le 1\}\in {\mathbb{R}}_{+}^5,\end{array}$$

(8)

where

$$\begin{array}{ccc}\hfill a_0\left(\delta \right)& :=& \nu (\parallel S\parallel +{\delta }_S),\hfill \\ \hfill a_1\left(\delta \right)& :=& \nu ({\delta }_A+2\parallel X\left(t\right)\parallel {\delta }_S+{\delta }_D),\hfill \\ \hfill a_2\left(\delta \right)& :=& \nu {\delta }_Q+\nu \parallel X\left(t\right)\parallel ({\delta }_A+{\delta }_D)+\nu {\parallel X\left(t\right)\parallel }^2{\delta }_S+\beta {\delta }_{X_0},\hfill \end{array}$$

(9)

with

$$\begin{array}{ccc}\hfill \beta & =& max\left\{\parallel {\Phi }_{A_c}(0,t)\parallel \parallel {\Phi }_{D_c}(0,t)\parallel :t\in T\right\},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \nu & =& max\left\{{\int }_0^t\parallel {\Phi }_{A_c}(\tau ,t)\parallel \parallel {\Phi }_{D_c}(\tau ,t)\parallel d\tau :t\in T\right\},\hfill \end{array}$$

(11)

and ${\Phi }_P(t,t_0)=e^{(t-t_0)P}$ is the fundamental matrix of equation $\dot{\eta }\left(t\right)=P\eta \left(t\right)$ for some real matrix P.

If δ satisfies the inclusion

$$\begin{array}{ccc}\hfill & & \delta \in {\Omega }_t,\hfill \end{array}$$

(12)

for ${\Omega }_t$ given in (8), then the norm of the perturbation $\mathsf{\Delta }X\left(t\right)$ is bounded by the nonlocal perturbation bound

$$\begin{array}{ccc}\hfill & & \parallel \mathsf{\Delta }X\left(t\right)\parallel \le f(\delta ,t):=\frac{2a_2\left(\delta \right)}{1-a_1\left(\delta \right)+\sqrt{{(1-a_1\left(\delta \right))}^2-4a_0\left(\delta \right)a_2\left(\delta \right)}}.\hfill \end{array}$$

(13)

Proof. 

Premultiplying and postmultiplying the differential Equation (4) by the factors $e^{-(t-\tau )A_c\left(\tau \right)}$ and $e^{-(t-\tau )D_c\left(\tau \right)}$ respectively, and integrating with respect to $\tau$ from 0 to t, we obtain the equivalent integral form of the initial value problem (4) [2]:

$$\begin{array}{ccc}\hfill \mathsf{\Delta }X\left(t\right)& =& e^{-t{A}_c\left(t\right)}\mathsf{\Delta }{X}_0{e}^{-t{D}_c\left(t\right)}\hfill \\ & & +{\int }_0^t{e}^{-(t-\tau )A_c\left(\tau \right)}\mathcal{M}(\tau ,\mathsf{\Delta }X\left(\tau \right))e^{-(t-\tau )D_c\left(\tau \right)}\delta \tau .\hfill \end{array}$$

(14)

According to its definition, ${\Phi }_P(t,t_0)$ satisfies

$$\begin{array}{c}\hfill {\dot{\Phi }}_P\left(t\right)={\Phi }_P\left(t\right)P\left(t\right),{\Phi }_P(t,t)=\Phi (t-t)=\Phi \left(0\right)=I,fort\in T.\end{array}$$

(15)

Equation (14) can be stated as

$$\begin{array}{ccc}\hfill \mathsf{\Delta }X\left(t\right)& =& \Pi \left(\mathsf{\Delta }X\right)\left(t\right),\hfill \end{array}$$

(16)

where the operator $\Pi$ is defined as

$$\Pi \left(\mathsf{\Delta }X\right)\left(t\right):={\Phi }_{A_c}(0,t)\mathsf{\Delta }{X}_0{\Phi }_{D_c}(0,t)+{\int }_0^t{\Phi }_{A_c}(\tau ,t)\mathcal{M}(\tau ,\mathsf{\Delta }X\left(\tau \right)){\Phi }_{D_c}(\tau ,t)d\tau .$$

The spectral norm of the operator $\Pi \left(P\right)\left(t\right)$ in terms of (7), (9)–(11) is

$$\begin{array}{c}\hfill \parallel \Pi \left(P\right)\left(t\right)\le \beta {\delta }_{X_0}+\nu \parallel \mathcal{M}(t,P)\parallel ,\end{array}$$

(17)

and the second order polynomial

$$\begin{array}{c}\hfill h(\parallel \mathsf{\Delta }X\left(t\right)\parallel ,\delta ):=a_0{\left(\delta \right)\parallel \mathsf{\Delta }X\left(t\right)\parallel }^2+a_1\left(\delta \right)\parallel \mathsf{\Delta }X\left(t\right)\parallel +a_2\left(\delta \right),\end{array}$$

(18)

with $a_i\left(\delta \right)$, $i=0,1,2,$ defined in (9) via (10), (11) is a Lyapunov majorant for the operator $\Pi (.)$ such that

$$\begin{array}{c}\hfill \parallel \Pi \left(\mathsf{\Delta }X\right)\left(t\right)\parallel \le h(\parallel \mathsf{\Delta }X(t)\parallel ,\delta ).\end{array}$$

(19)

In a similar way, for two arbitrary matrices $V\left(t\right)$, $W\left(t\right)\in {\mathbb{R}}^{n\times p}$ with $\parallel V\left(t\right)\parallel ,\parallel W\left(t\right)\parallel \le \parallel \mathsf{\Delta }X\left(t\right)\parallel$, we get

$$\begin{array}{ccc}\hfill \parallel \Pi \left(V\right)\left(t\right)-\Pi \left(W\right)\left(t\right)\parallel & \le & \frac{\partial h(\theta ,\delta )}{\partial \theta }\parallel V\left(t\right)-W\left(t\right)\parallel \hfill \\ & =& (a_1\left(\delta \right)+2a_0\left(\delta \right)\theta )\parallel V\left(t\right)-W\left(t\right)\parallel ,\hfill \end{array}$$

(20)

where $\theta :=max\{\parallel V(t)\parallel ,\parallel W(t)\parallel \}$. If inequalities (17) and (20) hold and for any positive number $\rho$ such as

$$\begin{array}{c}\hfill h(\rho ,\delta )\le \rho ,h^{\prime }(\rho ,\delta )=\frac{\partial h(\rho ,\delta )}{\partial \rho }<1,\end{array}$$

(21)

then the operator $\Pi (.)$ is a contraction on the ball $M_{\rho }:=\{\parallel V\left(t\right)\parallel \in {\mathbb{R}}^{n\times p}:\parallel V\left(t\right)\parallel \le \rho \}.$ According to the fixed-point principle [14], the operator Equation (16) admits a solution $\mathsf{\Delta }X\left(t\right)\in M_{\rho }$ such that for

$$\begin{array}{ccc}& & \delta \in {\Omega }_t:=\{\delta \in {\mathbb{R}}_{+}^5,a_1\left(\delta \right)+2\sqrt{a_0\left(\delta \right)a_2\left(\delta \right)}\le 1\}\in {\mathbb{R}}_{+}^5,\hfill \end{array}$$

we have

$$\begin{array}{ccc}& & \parallel \mathsf{\Delta }X\left(t\right)\parallel \le \frac{2a_2\left(\delta \right)}{1-a_1\left(\delta \right)+\sqrt{{(1-a_1\left(\delta \right))}^2-4a_0\left(\delta \right)a_2\left(\delta \right)}},\hfill \end{array}$$

which concludes the proof.  □

The perturbation bound formulated in Theorem 1 is a nonlocal sensitivity bound. The inclusion (12), (8) guarantees that there exists a solution $X\left(t\right)+\mathsf{\Delta }X\left(t\right)$ of the perturbed Equation (3) for which the bound (13) holds.

Let $\alpha =max\{{\delta }_A,{\delta }_D,{\delta }_Q,{\delta }_S,{\delta }_{X_0}\}$. Then (9) and (8) yield

$$\begin{array}{ccc}\hfill a_0\left(\alpha \right)& =& \nu (\parallel S\parallel +\alpha ),a_1\left(\alpha \right)=2\alpha \nu \sigma ,a_2\left(\alpha \right)=\alpha (\nu {\sigma }^2+\beta ),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\Omega }_t& =& \{\alpha <(-\kappa +\sqrt{{\kappa }^2+\beta /\nu })/2\beta \},\hfill \end{array}$$

with $\sigma :=1+\parallel X\left(t\right)\parallel$ and $\kappa :=\sigma +\parallel S\parallel (\beta +\nu {\sigma }^2)$. The estimate (13) becomes

$$\begin{array}{c}\hfill \parallel \mathsf{\Delta }X\left(t\right)\parallel \le \frac{1-2\alpha \nu \sigma -\sqrt{1-4\alpha \nu (\kappa +\alpha \beta )}}{2\nu (\parallel S\parallel +\alpha )}.\end{array}$$

The assumption for $\mathcal{H}$ to be a nonsingular M-matrix implies that the closed loop-matrices $A_c\left(t\right)=A-X\left(t\right)S$ and $D_c\left(t\right)=D-SX\left(t\right)$ are nonsingular M-matrices too [15]. This allows us, to facilitate the computation of the terms $\nu$ and $\beta$, to derive computable bounds for the spectral norm of the fundamental matrices ${\Phi }_{A_c}(0,t)$ and ${\Phi }_{D_c}(0,t)$

$$\begin{array}{ccc}\hfill \parallel {\Phi }_{A_c}(0,t)\parallel & \le & e^{-{\int }_0^t\lambda \left(\tau \right)d\tau };\hfill \\ \hfill \parallel {\Phi }_{D_c}(0,t)\parallel & \le & e^{-{\int }_0^t\xi \left(\tau \right)d\tau },\hfill \end{array}$$

(22)

based on the logarithmic norms

$$\begin{array}{ccc}\hfill \lambda \left(t\right)& =& 0,5{\lambda }_{max}\left[A_c\left(t\right)+A_c{\left(t\right)}^{\top }\right];\xi \left(t\right)=0,5{\xi }_{max}\left[D_c\left(t\right)+D_c{\left(t\right)}^{\top }\right]\hfill \end{array}$$

of the closed-loop matrices $A_c\left(t\right)=A-X\left(t\right)S$ and $D_c\left(t\right)=D-SX\left(t\right)$, respectively.

3. Sensitivity of Low-Dimensional Approximate Solutions to Large-Scale NDRE

For large NDRE with low-rank matrix Q, decomposed as $Q=F{G}^{\top }$ with $F\in {\mathbb{R}}^{n\times s}$, $G\in {\mathbb{R}}^{p\times s}$ and $s<<n$, we proposed in [7] to project the problem (1) onto extended Krylov subspace ${\mathbb{K}}_m(A,F)$ and ${\mathbb{K}}_m(D,G)$ applying the Extended block Arnoldi algorithm and to obtain the approximate solution

$$\begin{array}{c}\hfill X_m\left(t\right)={\mathcal{V}}_m{Y}_m\left(t\right){\mathcal{W}}_m^{\top }\in {\mathbb{R}}^{n\times p},\end{array}$$

(23)

where $Y_m$ solves the projected low-dimensional NDRE

$$\begin{array}{ccc}\hfill {\dot{Y}}_m\left(t\right)& =& -{\mathcal{T}}_m^A{Y}_m\left(t\right)-Y_m\left(t\right){\mathcal{T}}_m^D+Y_m\left(t\right)S_m{Y}_m\left(t\right)+F_m{G}_m^{\top },\hfill \\ \hfill Y_m\left(0\right)& =& Y_0={\mathcal{V}}_m^{\top }{X}_0{\mathcal{W}}_m\in {\mathbb{R}}^{2ms\times 2ms},\hfill \end{array}$$

(24)

instead of the exact solution to (1). Here $S_m={\mathcal{W}}_m^{\top }S{\mathcal{V}}_m\in {\mathbb{R}}^{2ms\times 2ms}$, $F_m={\mathcal{V}}_m^{\top }F\in {\mathbb{R}}^{2ms\times s}$, $G_m={\mathcal{W}}_m^{\top }G\in {\mathbb{R}}^{2ms\times s}$ and the block Hessenberg matrices ${\mathcal{T}}_m^A={\mathcal{V}}_m^{\top }A{\mathcal{V}}_m^{\top }\in {\mathbb{R}}^{2ms\times 2ms}$ and ${\mathcal{T}}_m^D={\mathcal{W}}_m^{\top }D{\mathcal{W}}_m\in {\mathbb{R}}^{2ms\times 2ms}$ are obtained after transformation by the orthonormal matrices ${\mathcal{V}}_m=\left[\begin{array}{ccc}{V}_1,& \cdots ,& V_m\end{array}\right]\in {\mathbb{R}}^{n\times 2ms}$ and ${\mathcal{W}}_m=\left[\begin{array}{ccc}{W}_1,& \cdots ,& W_m\end{array}\right]\in {\mathbb{R}}^{p\times 2ms}$ composed of the orthonormal bases $\{V_1,\cdots ,V_m\},$$(V_i\in {\mathbb{R}}^{n\times 2s},i=1,\cdots .m)$ and $\{W_1,\cdots ,W_m\}$, $(W_i\in {\mathbb{R}}^{p\times 2s},i=1,\cdots .m)$. The orthonormal bases are generated after applying the Extended block Arnoldi algorithm to the pairs $(A,F)$ and $(D,G)$; see [7] for more details.

The classical theory of Radon (see, e.g., [5]) states that any solution $Y_m\left(t\right)$ of the low-dimensional NDRE (24) is locally equivalent to a solution of the initial value problem

$$\begin{array}{ccc}\hfill \dot{\Psi }\left(t\right)& =& {\mathcal{H}}_m\left(t\right)\Psi \left(t\right),\Psi \left(0\right):=\left[\begin{array}{c}I\\ Y_0\end{array}\right]\in {\mathbb{R}}^{4ms\times 2ms},\hfill \end{array}$$

(25)

where ${\mathcal{H}}_m={\mathcal{U}}_m^{\top }\mathcal{H}{\mathcal{U}}_m:=\left[\begin{array}{cc}{\mathcal{T}}_m^D& -S_m\\ F_m{G}_m^{\top }& -{\mathcal{T}}_m^A\end{array}\right]\in {\mathbb{R}}^{4ms\times 4ms}$, with $\mathcal{H}:=\left[\begin{array}{cc}D& -S\\ F{G}^{\top }& -A\end{array}\right]$ and ${\mathcal{U}}_m:=\left[\begin{array}{cc}{\mathcal{W}}_m& 0\\ 0& {\mathcal{V}}_m\end{array}\right]$, ${\mathcal{U}}_m^{\top }{\mathcal{U}}_m=I$.

The solution of (25) is

$$\begin{array}{ccc}\hfill \Psi \left(t\right)& :=& \left[\begin{array}{c}{Y}_{1,m}\left(t\right)\\ Y_{2,m}\left(t\right)\end{array}\right]=e^{t{\mathcal{H}}_m}\Psi \left(0\right):=\left[\begin{array}{cc}{\Psi }_{11}\left(t\right)& {\Psi }_{12}\left(t\right),\\ {\Psi }_{21}\left(t\right)& {\Psi }_{22}\left(t\right)\end{array}\right]\Psi \left(0\right),\hfill \\ & =& \left[\begin{array}{c}{\Psi }_{11}\left(t\right)+{\Psi }_{12}\left(t\right)Y_0\\ {\Psi }_{21}\left(t\right)+{\Psi }_{22}\left(t\right)Y_0\end{array}\right].\hfill \end{array}$$

(26)

If the matrix $Y_{1,m}\left(t\right)$ is nonsingular, the solution $Y_m\left(t\right)$ of the projected low-order nonsymmetric differential Riccati Equation (24) is represented as [16]

$$\begin{array}{ccc}\hfill Y_m\left(t\right)& =& Y_{2,m}\left(t\right)Y_{1,m}^{-1}\left(t\right)=\left({\Psi }_{21}\left(t\right)+{\Psi }_{22}\left(t\right)Y_0\right){\left({\Psi }_{11}\left(t\right)+{\Psi }_{12}\left(t\right)Y_0\right)}^{-1}.\hfill \end{array}$$

(27)

To estimate the sensitivity of the problem (24), we consider the strategies proposed in [13]. We represent the calculated perturbed solution to (24) with collection of data coefficients ${\mathcal{Z}}_m$=$\left({\mathcal{T}}_m^A,\right.$${\mathcal{T}}_m^D,$$S_m,$$F_m,$$G_m,$$\left.Y_0\right)$ as the exact solution to a slightly perturbed problem with collection of data coefficients ${\mathcal{Z}}_m+\mathsf{\Delta }{\mathcal{Z}}_m$. The data perturbation $\mathsf{\Delta }{Z}_m$∈$\mathsf{\Delta }{\mathcal{Z}}_m$$:=$$\left(\mathsf{\Delta }{\mathcal{T}}_m^A,\right.$$\mathsf{\Delta }{\mathcal{T}}_m^D,$$\mathsf{\Delta }{S}_m,$$\mathsf{\Delta }{F}_m,$$\mathsf{\Delta }{G}_m,$$\left.\mathsf{\Delta }{Y}_0\right)$ with $\parallel \mathsf{\Delta }Z\parallel \le {\delta }_Z$, ${\delta }_Z\approx \mathtt{macheps}\varphi \left(n\right)\parallel Z\parallel$, reflects the effect of round-off errors and approximation errors in the computed solution to (24).

The perturbed projected low-dimensional NDRE is

$$\begin{array}{ccc}\hfill {(Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right))}^{\prime }& =& -({\mathcal{T}}_m^A+\mathsf{\Delta }{\mathcal{T}}_m^A)(Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right))\hfill \\ & & -(Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right))({\mathcal{T}}_m^D+\mathsf{\Delta }{\mathcal{T}}_m^D)\hfill \\ & & +(Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right))(S_m+\mathsf{\Delta }{S}_m)(Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right))\hfill \\ & & +(F_m+\mathsf{\Delta }{F}_m){(G_m+\mathsf{\Delta }{G}_m)}^{\top },\hfill \\ \hfill Y_m\left(0\right)+\mathsf{\Delta }{Y}_m\left(0\right)& =& Y_0+\mathsf{\Delta }{Y}_0.\hfill \end{array}$$

(28)

The equivalent to (28) initial value problem is

$$\begin{array}{ccc}\hfill {(\Psi \left(t\right)+\mathsf{\Delta }\Psi \left(t\right))}^{\prime }& :=& ({\mathcal{H}}_m\left(t\right)+\mathsf{\Delta }{\mathcal{H}}_m\left(t\right))(\Psi \left(t\right)+\mathsf{\Delta }\Psi \left(t\right)),\hfill \\ \hfill \Psi \left(0\right)+\mathsf{\Delta }\Psi \left(0\right)& :=& \left[\begin{array}{c}{Y}_{1,m}\left(0\right)\\ Y_{2,m}\left(0\right)\end{array}\right]+\left[\begin{array}{c}\mathsf{\Delta }{Y}_{1,m}\left(0\right)\\ \mathsf{\Delta }{Y}_{2,m}\left(0\right)\end{array}\right],\hfill \end{array}$$

(29)

where

$$\begin{array}{ccc}\hfill \mathsf{\Delta }{\mathcal{H}}_m& :=& \left[\begin{array}{cc}\hfill \mathsf{\Delta }{\mathcal{T}}_m^D& -\mathsf{\Delta }{S}_m\\ \hfill \mathsf{\Delta }{F}_m{G}_m^{\top }+F_m\mathsf{\Delta }{G}_m^{\top }+\mathsf{\Delta }{F}_m\mathsf{\Delta }{G}_m^{\top }& -\mathsf{\Delta }{\mathcal{T}}_m^A\end{array}\right]\hfill \\ \hfill and\mathsf{\Delta }\Psi \left(t\right)& =& \left[\begin{array}{c}\mathsf{\Delta }{Y}_{1,m}\left(t\right)\\ \mathsf{\Delta }{Y}_{2,m}\left(t\right)\end{array}\right]:=\left[\begin{array}{cc}\hfill \mathsf{\Delta }{\Psi }_{11}\left(t\right)& \hfill \mathsf{\Delta }{\Psi }_{12}\left(t\right)\\ \hfill \mathsf{\Delta }{\Psi }_{21}\left(t\right)& \hfill \mathsf{\Delta }{\Psi }_{22}\left(t\right)\end{array}\right].\hfill \end{array}$$

The perturbations $\mathsf{\Delta }{\Psi }_{11}\left(t\right)$, $\mathsf{\Delta }{\Psi }_{12}\left(t\right)$, $\mathsf{\Delta }{\Psi }_{21}\left(t\right)$, $\mathsf{\Delta }{\Psi }_{22}\left(t\right)$ are analytical functions of the data perturbations $\mathsf{\Delta }{Z}_m\in \mathsf{\Delta }{\mathcal{Z}}_m$ and reflect the errors in the solution $\Psi \left(t\right)$ + $\mathsf{\Delta }\Psi \left(t\right)$ to the perturbed linear differential system

$$\begin{array}{ccc}\hfill \Psi \left(t\right)+& & \mathsf{\Delta }\Psi \left(t\right)=e^{t({\mathcal{H}}_m+\mathsf{\Delta }{\mathcal{H}}_m)}(\Psi \left(0\right)+\mathsf{\Delta }\Psi \left(0\right)),\hfill \\ & & =\left[\begin{array}{c}{Y}_{1,m}\left(t\right)\\ Y_{2,m}\left(t\right)\end{array}\right]+\left[\begin{array}{c}\mathsf{\Delta }{Y}_{1,m}\left(t\right)\\ \mathsf{\Delta }{Y}_{2,m}\left(t\right)\end{array}\right],\hfill \\ & & :=\left[\begin{array}{cc}{\Psi }_{11}\left(t\right)+\mathsf{\Delta }{\Psi }_{11}\left(t\right)& {\Psi }_{12}\left(t\right)+\mathsf{\Delta }{\Psi }_{12}\left(t\right),\\ {\Psi }_{21}\left(t\right)+\mathsf{\Delta }{\Psi }_{21}\left(t\right)& {\Psi }_{22}\left(t\right)+\mathsf{\Delta }{\Psi }_{22}\left(t\right)\end{array}\right](\Psi \left(0\right)+\mathsf{\Delta }\Psi \left(0\right)).\hfill \end{array}$$

(30)

According to (26) and (30), the perturbation $\mathsf{\Delta }\Psi \left(t\right)$ is

$$\begin{array}{ccc}\hfill \mathsf{\Delta }\Psi \left(t\right)& =& e^{t\left({\mathcal{H}}_m+\mathsf{\Delta }{\mathcal{H}}_m\right)}(\Psi \left(0\right)+\mathsf{\Delta }\Psi \left(0\right))-e^{t{\mathcal{H}}_m}\Psi \left(0\right)\hfill \\ & =& \left[\begin{array}{c}\mathsf{\Delta }{Y}_{1,m}\left(t\right)\\ \mathsf{\Delta }{Y}_{2,m}\left(t\right)\end{array}\right]=\left[\begin{array}{c}\mathsf{\Delta }{\Psi }_{11}\left(t\right)+\mathsf{\Delta }{\Psi }_{12}\left(t\right)Y_0+({\Psi }_{12}\left(t\right)+\mathsf{\Delta }{\Psi }_{12}\left(t\right))\mathsf{\Delta }{Y}_0,\\ \mathsf{\Delta }{\Psi }_{21}\left(t\right)+\mathsf{\Delta }{\Psi }_{21}\left(t\right)Y_0+({\Psi }_{22}\left(t\right)+\mathsf{\Delta }{\Psi }_{22}\left(t\right))\mathsf{\Delta }{Y}_0\end{array}\right].\hfill \end{array}$$

(31)

If the matrix

$$\begin{array}{c}\hfill Y_{1,m}\left(t\right)+\mathsf{\Delta }{Y}_{1,m}\left(t\right):={\Psi }_{11}\left(t\right)+\mathsf{\Delta }{\Psi }_{11}\left(t\right)+({\Psi }_{12}\left(t\right)+\mathsf{\Delta }{\Psi }_{12}\left(t\right))(Y_0+\mathsf{\Delta }{Y}_0)\end{array}$$

is invertible, then the solution

$$\begin{array}{c}\hfill Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right)=\left(Y_{2,m}\left(t\right)+\mathsf{\Delta }{Y}_{2,m}\left(t\right)\right){\left(Y_{1,m}\left(t\right)+\mathsf{\Delta }{Y}_{1,m}\left(t\right)\right)}^{-1},\end{array}$$

(32)

with $\mathsf{\Delta }{Y}_{1,m}\left(t\right)$ and $\mathsf{\Delta }{Y}_{2,m}\left(t\right)$ given in (31) to the perturbed projected low-dimensional Equation (28) exists.

The perturbation bound of the solution $Y_m\left(t\right)$ to the NDRE (24) consists of finding an interval $T:[0,t^{*})$ such that for each $t\in T$, the matrix $Y_{1,m}\left(t\right)+\mathsf{\Delta }{Y}_{1,m}\left(t\right)$ is invertible and then the perturbed solution $Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right)$ given by (32) exists, as well as to derive a normwise bound in terms of spectral norm for the error $\mathsf{\Delta }{Y}_m\left(t\right)$ in the solution $Y_m\left(t\right)+\mathsf{\Delta }{Y}_m\left(t\right)$ (32) as a function of the equivalent perturbations $\mathsf{\Delta }{Z}_m$ in the data coefficients $Z_m$.

We formulate the following perturbation bound of the solution to the projected low-dimensional NDRE (24).

Theorem 2.

Let us denote

$$\begin{array}{ccc}\hfill {\omega }_1(t,{\delta }_m)& :=& \parallel {\Psi }_{12}\left(t\right)\parallel {\delta }_{Y_0}+\sqrt{\mathrm{rank}(\mathsf{\Delta }\Psi (t\left)\right)}(1+\parallel Y_0\parallel +{\delta }_{Y_0})\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel ,\hfill \\ \hfill {\omega }_2(t,{\delta }_m)& :=& \sqrt{\mathrm{rank}(\mathsf{\Delta }\Psi (t\left)\right)}(1+\parallel Y_0\parallel +{\delta }_{Y_0})\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel +\parallel {\Psi }_{22}\left(t\right)\parallel {\delta }_{Y_0},\hfill \end{array}$$

(33)

for $Y_0$, ${\Psi }_{1,i}\left(t\right),i=1,2$, ${\Psi }_{22}\left(t\right)$ and $\mathsf{\Delta }\Psi \left(t\right)$ as defined in (25), (26) and (29) respectively.

For $t\in [0,t^{*})$, where

$$\begin{array}{c}\hfill t^{*}=sup\left\{t\in T:{\omega }_1(t,{\delta }_m)\parallel Y_{1,m}{\left(t\right)}^{-1}\parallel <1\right\},\end{array}$$

(34)

$Y_{1,m}\left(t\right)$ as stated in (26) and ${\delta }_m:={\left[\begin{array}{cccccc}{\delta }_{{\mathcal{T}}_m^A}& {\delta }_{{\mathcal{T}}_m^D}& {\delta }_{F_m}& {\delta }_{G_m}& {\delta }_{Sm}& {\delta }_{Y_0}\end{array}\right]}^{\top }$, the spectral norm of the perturbation $\mathsf{\Delta }{Y}_m\left(t\right)$ in the calculated solution $Y_m\left(t\right)$ to (24) satisfies the inequality

$$\begin{array}{c}\hfill \parallel \mathsf{\Delta }{Y}_m\left(t\right)\parallel \le f_m(t,{\delta }_m):=\frac{({\omega }_2(t,{\delta }_m)+{\omega }_1(t,{\delta }_m)\parallel Y_m\left(t\right)\parallel )\parallel Y_{1,m}^{-1}\left(t\right)\parallel }{1-{\omega }_1(t,{\delta }_m)\parallel Y_{1,m}^{-1}\left(t\right)\parallel }.\end{array}$$

(35)

Proof. 

The initial value of problem (25) is $\Psi \left(0\right)=\left[\begin{array}{c}I\\ Y_0\end{array}\right]$. Then, according to (26) ${\Psi }_{11}\left(0\right)=I_n$, ${\Psi }_{12}\left(0\right)=0$. The matrix $Y_{1,m}\left(0\right)={\Psi }_{11}\left(0\right)+{\Psi }_{12}\left(0\right)Y_0=I_n$ is invertible and its inverse is $Y_{1,m}{\left(0\right)}^{-1}={\left({\Psi }_{11}\left(0\right)+{\Psi }_{12}\left(0\right)Y_0\right)}^{-1}=I_n$. Denote by ${\sigma }_1\left(t\right)\ge {\sigma }_2\left(t\right)\ge \cdots \ge {\sigma }_n\left(t\right)\ge 0$ the singular values of the matrix ${\Psi }_{11}\left(t\right)$. Then the interval $T=\left[0,t^{*}\right)$ can be chosen from

$$\begin{array}{ccc}\hfill t^{*}& :=& sup\left\{t:\parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel +\parallel {\Psi }_{12}\left(t\right)\parallel \parallel Y_0\parallel <{\sigma }_n\left(t\right)\right\}.\hfill \end{array}$$

(36)

From (32) and taking into account (27), the perturbation $\mathsf{\Delta }{Y}_m\left(t\right)$ in the solution to the projected low-dimensional NDRE satisfies

$$\begin{array}{ccc}\hfill \mathsf{\Delta }{Y}_m\left(t\right)& =& \left(Y_{2,m}+\mathsf{\Delta }{Y}_{2,m}\left(t\right)\right){\left(Y_{1,m}\left(t\right)+\mathsf{\Delta }{Y}_{1,m}\left(t\right)\right)}^{-1}-Y_{2,m}\left(t\right)Y_{1,m}^{-1}\left(t\right)\hfill \\ & =& \left(\mathsf{\Delta }{Y}_{2,m}\left(t\right)-Y_m\left(t\right)\mathsf{\Delta }{Y}_{1,m}\left(t\right)\right){\left(Y_{1,m}\left(t\right)+\mathsf{\Delta }{Y}_{1,m}\left(t\right)\right)}^{-1}.\hfill \end{array}$$

(37)

Applying the property $\parallel {\left(I_n+X^{-1}Y\right)}^{-1}\parallel \le \frac{1}{1-\parallel X^{-1}\parallel \parallel Y\parallel }$, which is valid for any matrices $X,Y\in {\mathbb{R}}^{n\times n}$, with existing inverse $X^{-1}$ and $\parallel X^{-1}\parallel \parallel Y\parallel \le 1$ [17], from (37), we obtain

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Delta }{Y}_m\left(t\right)\parallel & \le & \left(\parallel \mathsf{\Delta }{Y}_{2,m}\left(t\right)\parallel +\parallel Y_m\left(t\right)\parallel \parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel \right)\times \hfill \\ & & \times \frac{\parallel Y_{1,m}^{-1}\left(t\right)\parallel }{1-\parallel Y_{1,m}^{-1}\left(t\right)\parallel \parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel }\hfill \end{array}$$

(38)

provided that

$$\begin{array}{c}\hfill \parallel Y_{1,m}^{-1}\left(t\right)\parallel \parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel <1.\end{array}$$

Using the fact that for any matrix $M=\left[M_{ij}\right]\in {\mathbb{R}}^{2ms\times 2ms}$, we have

$$\parallel M_{ij}{\parallel }_{\mathrm{F}}{<\parallel M\parallel }_{\mathrm{F}}<\sqrt{\mathrm{rank}\left(M\right)}{\parallel M\parallel }_2,$$

the norms of the perturbations $\mathsf{\Delta }{Y}_{1,m}\left(t\right)$ and $\mathsf{\Delta }{Y}_{2,m}\left(t\right)$ can be estimated by

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel & \le & \parallel \mathsf{\Delta }{\Psi }_{11}{\left(t\right)\parallel }_{\mathrm{F}}+\parallel {\Psi }_{12}\left(t\right)\parallel {\delta }_{Y_0}+\parallel \mathsf{\Delta }{\Psi }_{12}{\left(t\right)\parallel }_{\mathrm{F}}(\parallel Y_0\parallel +{\delta }_{Y_0}\hfill \\ & \le & \parallel \parallel {\Psi }_{12}\left(t\right)\parallel {\delta }_{Y_0}+(1+\parallel Y_0\parallel +{\delta }_{Y_0}{)\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel }_{\mathrm{F}}\hfill \\ & \le & \parallel {\Psi }_{12}\left(t\right)\parallel {\delta }_{Y_0}+\sqrt{\mathrm{rank}(\mathsf{\Delta }\Psi (t\left)\right)}(1+\parallel Y_0\parallel +{\delta }_{Y_0})\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel \hfill \\ & \le & {\omega }_1(t,{\delta }_m),\hfill \end{array}$$

(39)

and

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Delta }{Y}_{2,m}\left(t\right)\parallel & \le & \sqrt{\mathrm{rank}(\mathsf{\Delta }\Psi (t\left)\right)}(1+\parallel Y_0\parallel +{\delta }_{Y_0})\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel +\parallel {\Psi }_{22}\left(t\right)\parallel {\delta }_{Y_0}\hfill \\ & \le & {\omega }_2(t,{\delta }_m).\hfill \end{array}$$

(40)

Replacing $\parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel$ and $\parallel \mathsf{\Delta }{Y}_{2,m}\left(t\right)\parallel$ in (38) by ${\omega }_1(t,{\delta }_m)$ and ${\omega }_2(t,{\delta }_m)$ from (39), (40), we prove the non-local bound $\parallel \mathsf{\Delta }{Y}_m\left(t\right)\parallel \le f_m(t,{\delta }_m)$ as stated in (35).

Finally, the expression $\parallel \mathsf{\Delta }{Y}_{1,m}\left(t\right)\parallel +\parallel {\Psi }_{12}\left(t\right)\parallel \parallel Y_0\parallel <{\sigma }_n\left(t\right)$ from (36) in view of (39), becomes ${\omega }_1(t,{\delta }_m)<\parallel Y_{1,m}\left(t\right)\parallel$. Then, since $Y_{1,m}\left(0\right)=I_n$ and ${\omega }_1(t,0)=0$, the interval

$$\begin{array}{c}\hfill t^{*}=sup\left\{t\in T:{\omega }_1(t,{\delta }_m)\parallel Y_{1,m}{\left(t\right)}^{-1}\parallel <1\right\}\end{array}$$

from (34) is correctly defined, which achieves the proof.  □

In order to represent the norm $\parallel \mathsf{\Delta }\Psi \left(t\right)\parallel$ of the perturbation $\mathsf{\Delta }\Psi \left(t\right)$ in terms of ${\omega }_1$ and ${\omega }_2$ by the norms of the perturbations in the data matrices ${\mathcal{T}}_m^A,{\mathcal{T}}_m^D,F_m,G_m,S_m$ and $Y_0$, we consider the perturbed differential Equation (29). We have

$$\begin{array}{ccc}\hfill \mathsf{\Delta }\Psi \left(t\right)& =& {\int }_0^t{e}^{{\mathcal{H}}_m(t-\tau )}\mathsf{\Delta }{\mathcal{H}}_m{e}^{({\mathcal{H}}_m+\mathsf{\Delta }{\mathcal{H}}_m)\tau }d\tau .\hfill \end{array}$$

Then, taking the spectral norm, we have

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Delta }\Psi \left(t\right)\parallel & \le & {\delta }_{{\mathcal{H}}_m}{\int }_0^t\parallel e^{{\mathcal{H}}_m(t-\tau )}\parallel \parallel e^{({\mathcal{H}}_m+\mathsf{\Delta }{\mathcal{H}}_m)\tau }\parallel d\tau \hfill \\ & \le & {\delta }_{{\mathcal{H}}_m}{\int }_0^{t}g(t-\tau )\left(\parallel \mathsf{\Delta }\Psi \left(\tau \right)\parallel +g\left(\tau \right)\right)d\tau ,\hfill \end{array}$$

where ${\delta }_{{\mathcal{H}}_m}:=\parallel \mathsf{\Delta }{\mathcal{H}}_m\parallel <{\delta }_m$ and $g\left(t\right)$ is an upper bound for $\parallel e^{{\mathcal{H}}_m\left(t\right)}\parallel$, i.e., $\parallel e^{{\mathcal{H}}_m\left(t\right)}\parallel \le g\left(t\right)$.

Some bounds for the matrix exponential $e^{{\mathcal{H}}_m\left(t\right)}$ based on Jordan and Schur matrix decompositions, logarithmic norm and power series are summarized in [18]:

$$\begin{array}{c}\hfill g\left(t\right)=c_0{e}^{\varrho t}\sum _{k=0}^{p-1}{\left(\varpi t\right)}^k/k!,\end{array}$$

(41)

with constants $c_0$, $\varrho$, $\varpi$ and p, listed in Table 1.

Table 1. Values of the constants in the matrix exponential bounds.

	$\mathbf{Jordan}\left(1\right)$	$\mathbf{Jordan}\left(2\right)$	$\mathbf{Schur}$	$\mathbf{Log}\mathbf{Norm}$	$\mathbf{Power}\mathbf{Series}$
$c_0$	$cond\left(Y\right)$	$cond\left(Y\right)$	1	1	1
$\varrho$	$\alpha \left({\mathcal{H}}_m\left(t\right)\right)$	$\alpha \left({\mathcal{H}}_m\left(t\right)\right)+d_{\varsigma }$	$\alpha \left({\mathcal{H}}_m\left(t\right)\right)$	$\mu \left({\mathcal{H}}_m\left(t\right)\right)$	$\parallel {\mathcal{H}}_m\left(t\right)\parallel$
$\varpi$	1	0	$\varpi$	0	0
p	m	-	l	-	-

Here $\mu \left({\mathcal{H}}_m\left(t\right)\right)={\lambda }_{max}\left({\mathcal{H}}_m\left(t\right)+{\mathcal{H}}_m{\left(t\right)}^{\top })/2\right)$; $\varsigma \ge 1$ is the dimension of the maximum block in the Jordan canonical form $J=Y^{-1}{\mathcal{H}}_m\left(t\right)Y$ of ${\mathcal{H}}_m\left(t\right),$ where the matrix Y is chosen so as the condition number $cond\left(Y\right)=\parallel Y\parallel \parallel Y^{-1}\parallel$ to be minimized; $d_{\varsigma }=cos\left(\frac{\pi }{\varsigma +1}\right)$; $\alpha \left({\mathcal{H}}_m\left(t\right)\right)$ is the spectral abscissa of ${\mathcal{H}}_m\left(t\right)$, i.e., the maximum real part of the eigenvalues of ${\mathcal{H}}_m\left(t\right)$; $T=U^H{\mathcal{H}}_m\left(t\right)U=\Lambda +\mathcal{N}$ is the Schur decomposition of ${\mathcal{H}}_m\left(t\right)$ with unitary matrix U, chosen so as $\varpi =\parallel \mathcal{N}\parallel$ to be minimized, diagonal matrix $\Lambda$ and $\mathcal{N}$ - strictly upper triangular matrix with index of nilpotency $l=min\{s:{\mathcal{N}}^s=0\}.$

The results stated in Theorem 2 can be used to formulate a perturbation bound for the solution $X\left(t\right)$ to the large-scale NDRE (1).

Theorem 3.

Let a large-scale NDRE (1) for which the constant matrix coefficient Q is low-rank and can decomposed as $Q=F{G}^{\top }$ with $F\in {\mathbb{R}}^{n\times s}$, $G\in {\mathbb{R}}^{p\times s}$, ($s<<n$) be projected onto a pair of extended Krylov subspaces ${\mathbb{K}}_m(A,F)$ and ${\mathbb{K}}_m(D,G)$. Let $X_m\left(t\right)={\mathcal{V}}_m{Y}_m\left(t\right){\mathcal{W}}_m^{\top }\in {\mathbb{R}}^{n\times p}$ be its approximate solution as stated in (23), obtained by applying the Extended block Arnoldi algorithm to the projected low-dimensional NDRE

$$\begin{array}{ccc}\hfill {\dot{Y}}_m\left(t\right)& =& -{\mathcal{T}}_m^A{Y}_m\left(t\right)-Y_m\left(t\right){\mathcal{T}}_m^D+Y_m\left(t\right)S_m{Y}_m\left(t\right)+F_m{G}_m^{\top },\hfill \\ \hfill Y_m\left(0\right)& =& Y_0={\mathcal{V}}_m^{\top }{X}_0{\mathcal{W}}_m\in {\mathbb{R}}^{2ms\times 2ms}.\hfill \end{array}$$

with solution $Y_m\left(t\right)$ and perturbation bound $\parallel \mathsf{\Delta }{Y}_m\left(t\right)\parallel \le f_m(t,{\delta }_m)$ (35) as defined in Theorem 2. A perturbation bound in terms of spectral norm for the approximate solution $X\left(t\right)$ to (1) is given by

$$\begin{array}{c}\hfill \parallel \mathsf{\Delta }X\left(t\right)\parallel \le f_m(t,{\delta }_m):=\frac{({\omega }_2(t,{\delta }_m)+{\omega }_1(t,{\delta }_m)\parallel Y_m\left(t\right)\parallel )\parallel Y_{1,m}^{-1}\left(t\right)\parallel }{1-{\omega }_1(t,{\delta }_m)\parallel Y_{1,m}^{-1}\left(t\right)\parallel },\end{array}$$

(42)

for $t\in [0,t^{*})$, with $t^{*}$ as defined in (34) and $Y_{1,m}\left(t\right)$ stated in (26), ${\omega }_1(t,{\delta }_m)$, $\omega (t,{\delta }_m)$ stated in (33), ${\delta }_m:={\left[\begin{array}{cccccc}{\delta }_{{\mathcal{T}}_m^A}& {\delta }_{{\mathcal{T}}_m^D}& {\delta }_{F_m}& {\delta }_{G_m}& {\delta }_{Sm}& {\delta }_{Y_0}\end{array}\right]}^{\top }$.

Proof. 

The proof follows directly from the definition (23) of the approximate solution $Y_m\left(t\right)$ and the preservation of the spectral norm by unitary matrices.  □

Next, we apply the preceding results to estimate the approximation error ${\mathcal{E}}_m=X\left(t\right)-X_m\left(t\right)$ of the approximate solution $X_m\left(t\right)$ to the projected low-dimensional NDRE versus the exact solution to (1) from Theorem (4), which was already established by the authors in [19].

Theorem 4.

[Theorem 4. form [19] Let $X_m$ be the approximate solution given by (23). Then we have

$$\begin{array}{ccc}\hfill {\displaystyle {\dot{X}}_m\left(t\right)}& =& -(A-{\mathsf{\Delta }}_m^A)X_m\left(t\right)-X_m\left(t\right)(D-{\mathsf{\Delta }}_m^D)+X_m\left(t\right)S{X}_m\left(t\right)+F{G}^T,\hfill \\ \hfill R_m\left(t\right)& =& {\mathsf{\Delta }}_m^A{X}_m\left(t\right)+X_m\left(t\right){\mathsf{\Delta }}_m^D,and\hfill \\ \hfill {\dot{\mathcal{E}}}_m\left(t\right)& =& -(A-X_m\left(t\right)S){\mathcal{E}}_m\left(t\right)-{\mathcal{E}}_m\left(t\right)(D-S{X}_m\left(t\right))+{\mathcal{E}}_m\left(t\right)S{\mathcal{E}}_m\left(t\right)\hfill \\ & & -{\mathsf{\Delta }}_m^A{X}_m\left(t\right)-X_m\left(t\right){\mathsf{\Delta }}_m^D.\hfill \end{array}$$

where ${\mathsf{\Delta }}_m^A=V_{m+1}{T}_{m+1,m}^A{V}_m^T$, ${\mathsf{\Delta }}_m^D=W_m{T}_{m+1,m}^D{W}_m^T$, ${\mathcal{E}}_m\left(t\right)=X\left(t\right)-X_m\left(t\right)$ and $X\left(t\right)$ is an exact solution $X\left(t\right)$ of (1).

Let us rewrite the NDRE associated with the error ${\mathcal{E}}_m\left(t\right)$

$$\begin{array}{ccc}\hfill {\dot{\mathcal{E}}}_m\left(t\right)& =& -(A-X_m\left(t\right)S){\mathcal{E}}_m\left(t\right)-{\mathcal{E}}_m\left(t\right)(D-S{X}_m\left(t\right))+{\mathcal{E}}_m\left(t\right)S{\mathcal{E}}_m\left(t\right)\hfill \\ & & -{\mathsf{\Delta }}_m^A{X}_m\left(t\right)-X_m\left(t\right){\mathsf{\Delta }}_m^D\hfill \end{array}$$

(43)

in the equivalent form

$$\begin{array}{c}\hfill {\dot{\mathcal{E}}}_m\left(t\right)=-A_{c,m}\left(t\right){\mathcal{E}}_m\left(t\right)-{\mathcal{E}}_m\left(t\right)D_{c,m}\left(t\right)+{\mathcal{M}}_m(t,{\mathcal{E}}_m\left(t\right)),\end{array}$$

(44)

where $A_{c,m}\left(t\right)=A-X_m\left(t\right)S$, $D_{c,m}\left(t\right)=D-S{X}_m\left(t\right)$, $\mathcal{M}(t,{\mathcal{E}}_m):={\mathcal{M}}_{1,m}(t,{\mathcal{E}}_m)+$${\mathcal{M}}_{2,m}(t,{\mathcal{E}}_m)$ with

$$\begin{array}{ccc}\hfill {\mathcal{M}}_{1,m}(t,{\mathcal{E}}_m\left(t\right))& :=& -{\mathsf{\Delta }}_m^A{\mathcal{E}}_m\left(t\right)-{\mathcal{E}}_m\left(t\right){\mathsf{\Delta }}_m^D;{\mathcal{M}}_{2,m}(t,{\mathcal{E}}_m\left(t\right)):={\mathcal{E}}_m\left(t\right)S{\mathcal{E}}_m\left(t\right).\hfill \end{array}$$

(45)

Here ${\mathsf{\Delta }}_m^A=V_{m+1}{T}_{m+1,n}^A{V}_{,}^{\top }$, ${\mathsf{\Delta }}_m^D=W_m{T}_{m+1,n}^D{W}_{m+1}^{\top }$. As the unitary matrices $V_m$ and $W_m$ have unit spectral norm, we have $\parallel {\mathsf{\Delta }}_m^A\parallel =\parallel T_{m+1,n}^A\parallel$ and $\parallel {\mathsf{\Delta }}_m^D\parallel =\parallel T_{m+1,n}^D\parallel$. We notice that the fact that the term $T_{m+1,n}$ tends normwisely to 0 as m increases implies that the spectral norm of ${\mathsf{\Delta }}_m^A$, ${\mathsf{\Delta }}_m^D$ decreases towards 0. This allows us to consider ${\mathsf{\Delta }}_m^A$, ${\mathsf{\Delta }}_m^D$ as equivalent data perturbations, and Equation (43) as an equation of the perturbation in the solution. Equation (43) is equivalent to the NDRE (4) of the perturbation $\mathsf{\Delta }X\left(t\right)$ in the perturbed NDRE (2). This allows us to apply the technique of the nonlocal perturbation analysis of the NDRE, based on the integral solution to the NDRE and the statements of Theorem 1 to formulate a bound for the error ${\mathcal{E}}_m\left(t\right)$.

Theorem 5.

For ${\mathsf{\Delta }}_m^D$, ${\mathsf{\Delta }}_m^D$, satisfying $\delta :={\left[\begin{array}{cc}\parallel {\mathsf{\Delta }}_m^A\parallel & \parallel {\mathsf{\Delta }}_m^D\parallel \end{array}\right]}^{\top }\in {\Omega }_{t,m}:=\{a_0\left(\delta \right)a_2\left(\delta \right)\le 0.25\}$, the spectral norm of the error ${\mathcal{E}}_m\left(t\right)$, solution to the NDRE (43), is bounded by

$$\begin{array}{c}\hfill \parallel {\mathcal{E}}_m\left(t\right)\parallel \le f(\delta ,t)=\frac{2a_2\left(\delta \right)}{1+\sqrt{1-4a_0\left(\delta \right)a_2\left(\delta \right)}},\end{array}$$

(46)

where

$$\begin{array}{c}\hfill a_0\left(\delta \right)=\nu \parallel S\parallel ;a_2=\nu \parallel X_m\left(t\right)\parallel \left(\parallel {\mathsf{\Delta }}_m^A\parallel +\parallel {\mathsf{\Delta }}_m^D\parallel \right)+\beta \parallel {\mathcal{E}}_m\left(0\right)\parallel ,\end{array}$$

for $\nu =max\left\{{\int }_0^t\parallel {\Phi }_{A_{c,m}}(\tau ,t)\parallel \parallel {\Phi }_{D_{c,m}}(\tau ,t)\parallel d\tau ,t\in T\right\}$, $\beta =max\left\{\parallel {\Phi }_{A_{c,m}}(0,t)\parallel \parallel {\Phi }_{D_{c,m}}(0,t)\parallel \right\}$ and ${\Phi }_Z(t,t_0)=e^{(t-t_0)Z}$ being the fundamental matrix of equation $\dot{\eta }\left(t\right)=Z\eta \left(t\right)$.

Proof. 

Comparing ${\mathcal{M}}_{1,m}(t,{\mathcal{E}}_m\left(t\right))$, ${\mathcal{M}}_{2,m}(t,{\mathcal{E}}_m\left(t\right))$ (45) to ${\mathcal{M}}_1(t,P)$, ${\mathcal{M}}_2(t,P)$ (6), for the coefficients $a_i\left(\delta \right)$ (9) we obtain

$$\begin{array}{c}\hfill a_0\left(\delta \right)=\nu \parallel S\parallel ;a_1\left(\delta \right)=0;a_2\left(\delta \right)=\nu \parallel X_m\left(t\right)\parallel (\parallel {\mathsf{\Delta }}_m^A\parallel +\parallel {\mathsf{\Delta }}_m^D\parallel )+\beta \parallel {\mathcal{E}}_m\left(0\right)\parallel .\end{array}$$

Replacing the coefficients $a_i\left(\delta \right)$, $i=0,1,2$ in the inequality of the set ${\Omega }_{t,m}$ (8) and the bound $f(\delta ,t)$ (13) we obtain

$$\begin{array}{c}\hfill 2\sqrt{a_0\left(\delta \right)a_2\left(\delta \right)}\le 1,or{a}_1\left(\delta \right)a_2\left(\delta \right)\le 0.25.\end{array}$$

Then the existence condition of the bound becomes

$$\begin{array}{c}\hfill \delta :={\left[\begin{array}{cc}\parallel {\mathsf{\Delta }}_m^A\parallel & \parallel {\mathsf{\Delta }}_m^D\parallel \end{array}\right]}^{\top }\in {\Omega }_{t,m}:=\{a_0\left(\delta \right)a_2\left(\delta \right)\le 0.25\},\end{array}$$

and we obtain the bound

$$\begin{array}{c}\hfill f(\delta ,t)=\frac{2a_2\left(\delta \right)}{1+\sqrt{1-4a_0\left(\delta \right)a_2\left(\delta \right)}}.\end{array}$$

□

4. Numerical Examples

To illustrate the effectiveness of the bounds proposed in Theorems 1 and 2, we consider nonsymmetric differential matrix Riccati equations of type (1) on a time interval $T=[0,1]$, for different matrix coefficients and for several sizes. The experimental tests are performed with Matlab R2020a on an Intel processor laptop equipped with 16GB of RAM. The reference solutions $X\left(t\right)$ to the NDRE (1) and $X\left(t\right)+\mathsf{\Delta }X\left(t\right)$ to the perturbed NDRE (3) are computed by the backward differential formula - BDF1-Newton method, see [19] for more details.

Example 1.

Consider the NDRE (1), constructed according to the rules given in [15]. This scheme is used in [10] to analyze the effectiveness of mixed and componentwise condition numbers, and in [11], to illustrate the validity of a condition number and backward errors of nonsymmetric algebraic Riccati equation.

The matrix coefficients of the NDRE (1) are:

$$\begin{array}{ccc}\hfill A& =& W(n+1:2n,n+1:2n)+\alpha I;D=W(1:n,1:n)+\alpha I,\hfill \\ \hfill S& =& -W(1:n,n+1:2n);Q=-W(n+1:2n,1:n),\hfill \end{array}$$

where W is a singular M-matrix with nonzero elements: $W=\mathrm{diag}\left(Re\right)-R$, with $R-a2n\times 2n$ nonzero random matrix and $e=$${\left[\begin{array}{cccc}1,& 1,& \cdots ,& 1\end{array}\right]}^{\top }$$\in {\mathbb{R}}^{2n}$. The time interval $T=\left[\begin{array}{cc}0,& 1\end{array}\right]$ is chosen. For $\alpha \ge 0$ the existence of a positive definite solution to (1) is guaranteed.

Experiment 1.

In [10], an equation of size$n=3$is considered and the perturbations are chosen as:

$$\begin{array}{ccc}\hfill \mathsf{\Delta }A& =& \left[\begin{array}{ccc}\hfill -0.3& \hfill 0.2& \hfill 0.1\\ \hfill 0.1& \hfill -0.2& \hfill 0.3\\ \hfill 0.1& \hfill 0.1& \hfill -0.3\end{array}\right]\ast {10}^{-j};\mathsf{\Delta }D=\left[\begin{array}{ccc}\hfill 0.1& \hfill -0.2& \hfill 0.3\\ \hfill 0& \hfill 0.1& \hfill 0.2\\ \hfill -0.2& \hfill 0.3& \hfill 0.1\end{array}\right]\ast {10}^{-j}\hfill \\ \hfill \mathsf{\Delta }S& =& \left[\begin{array}{ccc}\hfill 0.2& \hfill -0.1& \hfill 0.3\\ \hfill -0.1& \hfill 0.2& \hfill 0.3\\ \hfill -0.1& \hfill 0.1& \hfill -0.3\end{array}\right]\ast {10}^{-j};\mathsf{\Delta }Q=\left[\begin{array}{ccc}\hfill -0.2& \hfill -0.3& \hfill 0.1\\ \hfill 0.1& \hfill -0.1& \hfill 0.1\\ \hfill -0.1& \hfill 0.1& \hfill 0.2\end{array}\right]\ast {10}^{-j},\hfill \\ & & forj=12,11,10,9,8,7,\cdots ,2.\hfill \end{array}$$

The results, obtained for the estimated value - the relative perturbation${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$and the estimate—the relative bound${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$, with$f\left(t\right)=f(\delta ,t)$given by (8)–(13) for$j=12,10,8,6,4,2$and$\alpha =0$are listed in Table 2.

Table 2. Relative perturbation ${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$ and bound ${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$.

$\mathit{\alpha }=0$
	$\mathit{t}=0.2$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$	$\mathit{t}=1$
${\rho }_1\left(t\right)$	$2.57\times {10}^{-13}$	$2.46\times {10}^{-13}$	$2.40\times {10}^{-13}$	$2.37\times {10}^{-13}$	$2.36\times {10}^{-13}$
${\rho }_2\left(t\right)$	$2.97\times {10}^{-12}$	$1.75\times {10}^{-12}$	$1.36\times {10}^{-12}$	$1.16\times {10}^{-12}$	$1.05\times {10}^{-12}$
$j=10$
${\rho }_1\left(t\right)$	$2.58\times {10}^{-11}$	$2.46\times {10}^{-11}$	$2.40\times {10}^{-11}$	$2.37\times {10}^{-11}$	$2.36\times {10}^{-11}$
${\rho }_2\left(t\right)$	$2.97\times {10}^{-10}$	$1.75\times {10}^{-10}$	$1.36\times {10}^{-10}$	$1.16\times {10}^{-10}$	$1.05\times {10}^{-10}$
$j=8$
${\rho }_1\left(t\right)$	$2.58\times {10}^{-09}$	$2.46\times {10}^{-09}$	$2.40\times {10}^{-09}$	$2.37\times {10}^{-09}$	$2.36\times {10}^{-09}$
${\rho }_2\left(t\right)$	$2.97\times {10}^{-08}$	$1.75\times {10}^{-08}$	$1.36\times {10}^{-08}$	$1.16\times {10}^{-08}$	$1.05\times {10}^{-08}$
$j=6$
${\rho }_1\left(t\right)$	$2.58\times {10}^{-07}$	$2.46\times {10}^{-07}$	$2.40\times {10}^{-07}$	$2.37\times {10}^{-07}$	$2.36\times {10}^{-07}$
${\rho }_2\left(t\right)$	$2.97\times {10}^{-06}$	$1.75\times {10}^{-06}$	$1.36\times {10}^{-06}$	$1.16\times {10}^{-06}$	$1.05\times {10}^{-06}$
$j=4$
${\rho }_1\left(t\right)$	$2.58\times {10}^{-05}$	$2.46\times {10}^{-05}$	$2.40\times {10}^{-05}$	$2.37\times {10}^{-05}$	$2.36\times {10}^{-05}$
${\rho }_2\left(t\right)$	$2.97\times {10}^{-04}$	$1.75\times {10}^{-04}$	$1.36\times {10}^{-04}$	$1.16\times {10}^{-04}$	$1.05\times {10}^{-04}$
$j=2$
${\rho }_1\left(t\right)$	$2.58\times {10}^{-03}$	$2.46\times {10}^{-03}$	$2.40\times {10}^{-03}$	$2.37\times {10}^{-03}$	$2.36\times {10}^{-03}$
${\rho }_2\left(t\right)$	$3.01\times {10}^{-02}$	$1.77\times {10}^{-02}$	$1.38\times {10}^{-02}$	$1.18\times {10}^{-02}$	$1.06\times {10}^{-02}$

Example 1: Experiment 1, bound f(t)= f(δ, t), (8)–(13), Theorem 1, α = 0, j = 12, 10, 8, 6, 4, 2, t = 0.2 to 1.

Table 3 reports on the obtained results for the bound (8)–(13) from Theorem (1) for the case$\alpha =5$.

Table 3. Relative perturbation ${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$ and bound ${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$.

$\mathit{\alpha }=5$
	$\mathit{t}=0.2$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$	$\mathit{t}=1$
$j=12$
${\rho }_1\left(t\right)$	$1.74\times {10}^{-13}$	$1.60\times {10}^{-13}$	$1.56\times {10}^{-13}$	$1.58\times {10}^{-13}$	$1.64\times {10}^{-13}$
${\rho }_2\left(t\right)$	$2.37\times {10}^{-12}$	$1.48\times {10}^{-12}$	$1.19\times {10}^{-12}$	$1.05\times {10}^{-12}$	$9.63\times {10}^{-13}$
$j=10$
${\rho }_1\left(t\right)$	$1.72\times {10}^{-11}$	$1.60\times {10}^{-11}$	$1.56\times {10}^{-11}$	$1.58\times {10}^{-11}$	$1.63\times {10}^{-11}$
${\rho }_2\left(t\right)$	$2.37\times {10}^{-10}$	$1.48\times {10}^{-10}$	$1.19\times {10}^{-10}$	$1.05\times {10}^{-10}$	$9.63\times {10}^{-11}$
$j=8$
${\rho }_1\left(t\right)$	$1.73\times {10}^{-09}$	$1.60\times {10}^{-09}$	$1.56\times {10}^{-09}$	$1.58\times {10}^{-09}$	$1.64\times {10}^{-09}$
${\rho }_2\left(t\right)$	$2.37\times {10}^{-08}$	$1.48\times {10}^{-08}$	$1.19\times {10}^{-08}$	$1.05\times {10}^{-08}$	$9.65\times {10}^{-09}$
$j=6$
${\rho }_1\left(t\right)$	$1.73\times {10}^{-07}$	$1.59\times {10}^{-07}$	$1.56\times {10}^{-07}$	$1.58\times {10}^{-07}$	$1.64\times {10}^{-07}$
${\rho }_2\left(t\right)$	$2.37\times {10}^{-06}$	$1.48\times {10}^{-06}$	$1.19\times {10}^{-06}$	$1.05\times {10}^{-06}$	$9.63\times {10}^{-07}$
$j=4$
${\rho }_1\left(t\right)$	$1.73\times {10}^{-05}$	$1.59\times {10}^{-05}$	$1.56\times {10}^{-05}$	$2.1.58\times {10}^{-05}$	$1.63\times {10}^{-05}$
${\rho }_2\left(t\right)$	$2.37\times {10}^{-04}$	$1.48\times {10}^{-04}$	$1.19\times {10}^{-04}$	$1.05\times {10}^{-04}$	$9.63\times {10}^{-05}$
$j=2$
${\rho }_1\left(t\right)$	$1.74\times {10}^{-03}$	$1.59\times {10}^{-03}$	$1.56\times {10}^{-03}$	$1.58\times {10}^{-03}$	$1.64\times {10}^{-03}$
${\rho }_2\left(t\right)$	$2.40\times {10}^{-02}$	$1.50\times {10}^{-02}$	$1.21\times {10}^{-02}$	$1.06\times {10}^{-02}$	$9.77\times {10}^{-03}$

Example 1: Experiment 1, bound f(t)= f(δ, t), (8)–(13), Theorem 1, α = 5, j = 12, 10, 8, 6, 4, 2, t = 0.2 to 1.

As it is seen, the estimate based on the perturbation bound$f(\delta ,t)$from (8)–(13) is quite sharp.

The same experimental statement is used to test the accuracy of the estimate (34) and (35) from Theorem 2. The results obtained for$j=12,10,8,6,4,2$are listed in Table 4 for$\alpha =0$and in Table 5 for$\alpha =5$. Comparing the results for the bound (34) and (35) to these for the bound (8)–(13) given in Table 2 and Table 3, it is seen that the two bounds are of the same size of the domain of validity. The bound (8)–(13) from Theorem 1 is superior to the bound (34) and (35) from Theorem 2 with respect of closeness to the estimated quantity. However, the bound (34) and (35) from Theorem 2 has the advantage that it is not related with the solution of the NDRE and hence with problems of divergence of the numerical procedure.

Table 4. Relative perturbation ${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$ and bound ${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$.

$\mathit{\alpha }=0$
	$\mathit{t}=0.2$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$	$\mathit{t}=1$
$j=12$
${\rho }_1\left(t\right)$	$2.17\times {10}^{-13}$	$2.11\times {10}^{-13}$	$2.09\times {10}^{-13}$	$2.11\times {10}^{-13}$	$2.16\times {10}^{-13}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-12}$	$1.82\times {10}^{-12}$	$3.23\times {10}^{-12}$	$5.63\times {10}^{-12}$	$9.80\times {10}^{-12}$
$j=10$
${\rho }_1\left(t\right)$	$2.17\times {10}^{-11}$	$2.11\times {10}^{-11}$	$2.10\times {10}^{-11}$	$2.12\times {10}^{-11}$	$2.17\times {10}^{-11}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-10}$	$1.82\times {10}^{-10}$	$3.22\times {10}^{-10}$	$5.63\times {10}^{-10}$	$9.80\times {10}^{-10}$
$j=8$
${\rho }_1\left(t\right)$	$2.17\times {10}^{-09}$	$2.11\times {10}^{-09}$	$2.11\times {10}^{-09}$	$2.12\times {10}^{-09}$	$2.16\times {10}^{-09}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-08}$	$1.82\times {10}^{-08}$	$3.22\times {10}^{-08}$	$5.63\times {10}^{-08}$	$9.80\times {10}^{-08}$
$j=6$
${\rho }_1\left(t\right)$	$2.17\times {10}^{-07}$	$2.11\times {10}^{-07}$	$2.11\times {10}^{-07}$	$2.12\times {10}^{-07}$	$2.16\times {10}^{-07}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-06}$	$1.82\times {10}^{-06}$	$3.22\times {10}^{-06}$	$5.63\times {10}^{-06}$	$9.80\times {10}^{-06}$
$j=4$
${\rho }_1\left(t\right)$	$2.17-05$	$2.52\times {10}^{-05}$	$2.42\times {10}^{-05}$	$2.36\times {10}^{-05}$	$2.31\times {10}^{-05}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-04}$	$1.82\times {10}^{-04}$	$3.22\times {10}^{-04}$	$5.64\times {10}^{-04}$	$9.80\times {10}^{-04}$
$j=2$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-03}$	$2.52\times {10}^{-03}$	$2.43\times {10}^{-03}$	$2.36\times {10}^{-03}$	$2.32\times {10}^{-03}$
${\rho }_2\left(t\right)$	$1.01\times {10}^{-02}$	$1.83\times {10}^{-02}$	$3.26\times {10}^{-02}$	$5.75\times {10}^{-02}$	$1.02\times {10}^{-01}$

Example 1: Experiment 1, bound f(t)= f_m(t, δ_m) from (34) and (35), Theorem 2, α = 0, j = 12, 10, 8, 6, 4, 2, t = 0.2 to 1.

Table 5. Relative perturbation ${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$ and bound ${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$.

$\mathit{\alpha }=5$
	$\mathit{t}=0.2$	$\mathit{t}=0.4$	$\mathit{t}=0.6$	$\mathit{t}=0.8$	$\mathit{t}=1$
$j=12$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-13}$	$2.53\times {10}^{-13}$	$2.43\times {10}^{-13}$	$2.36\times {10}^{-13}$	$2.31\times {10}^{-13}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-12}$	$2.07\times {10}^{-12}$	$3.49\times {10}^{-12}$	$5.84\times {10}^{-12}$	$9.76\times {10}^{-12}$
$j=10$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-11}$	$2.52\times {10}^{-11}$	$2.42\times {10}^{-11}$	$2.36\times {10}^{-11}$	$2.31\times {10}^{-11}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-10}$	$2.07\times {10}^{-10}$	$3.49\times {10}^{-10}$	$5.85\times {10}^{-10}$	$9.74\times {10}^{-10}$
$j=8$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-09}$	$2.52\times {10}^{-09}$	$2.42\times {10}^{-09}$	$2.36\times {10}^{-09}$	$2.31\times {10}^{-09}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-08}$	$2.07\times {10}^{-08}$	$3.49\times {10}^{-08}$	$5.85\times {10}^{-08}$	$9.74\times {10}^{-08}$
$j=6$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-07}$	$2.52\times {10}^{-07}$	$2.43\times {10}^{-07}$	$2.36\times {10}^{-07}$	$2.31\times {10}^{-07}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-06}$	$2.07\times {10}^{-06}$	$3.49\times {10}^{-06}$	$5.85\times {10}^{-06}$	$9.74\times {10}^{-06}$
$j=4$
${\rho }_1\left(t\right)$	$2.68-05$	$2.52\times {10}^{-05}$	$2.42\times {10}^{-05}$	$2.36\times {10}^{-05}$	$2.31\times {10}^{-05}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-04}$	$2.07\times {10}^{-04}$	$3.49\times {10}^{-04}$	$5.85\times {10}^{-04}$	$9.75\times {10}^{-04}$
$j=2$
${\rho }_1\left(t\right)$	$2.68\times {10}^{-03}$	$2.52\times {10}^{-03}$	$2.43\times {10}^{-03}$	$2.36\times {10}^{-03}$	$2.32\times {10}^{-03}$
${\rho }_2\left(t\right)$	$1.21\times {10}^{-02}$	$2.08\times {10}^{-02}$	$3.53\times {10}^{-02}$	$5.96\times {10}^{-02}$	$1.01\times {10}^{-01}$

Example 1: Experiment 1, bound f(t)= f_m(t, δ_m), (34) and (35), Theorem 2, α = 5, j = 12, 10, 8, 6, 4, 2, t = 0.2 to 1.

Experiment 2.

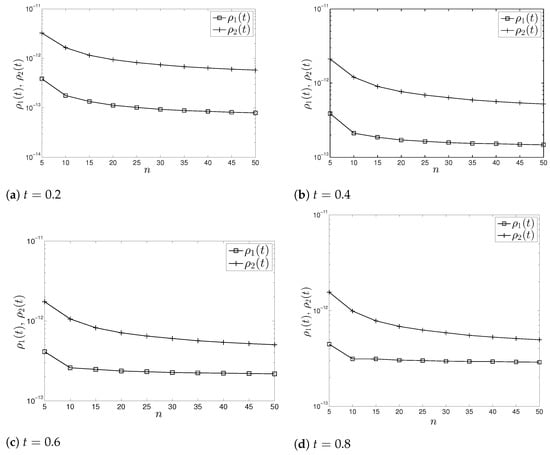
The size n of the matrices$A,D,S,Q\in {\mathbb{R}}^{n\times n}$varies from 5 to 50. The perturbations are randomly generated following the scheme$\mathsf{\Delta }Z=(rand\left(size\left(Z\right)\right)/\parallel Z\parallel )\ast {10}^{-j}$for$Z=A,D,S,Q$and$j=12$. The average values over 30 trials for the relative perturbation${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$and the bound${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$,$f\left(t\right)=f(\delta ,t)$from (8)–(13), for$t=0.2$,$0.4$,$0.6$and$0.8$are displayed in Figure 1 for$\alpha =0$.

Figure 1. Example 2, experiment 2, bound f (t)= f(δ, t), (8)–(13) from Theorem 1, α = 0, j = 12, t = 0.2 to 0.8 and n from 5 to 50.

It appears in Figure 1 that for$\alpha =0$and j from 10 to 4, the bound${\rho }_2\left(t\right)$remains of the order of the estimated value${\rho }_1\left(t\right)$.

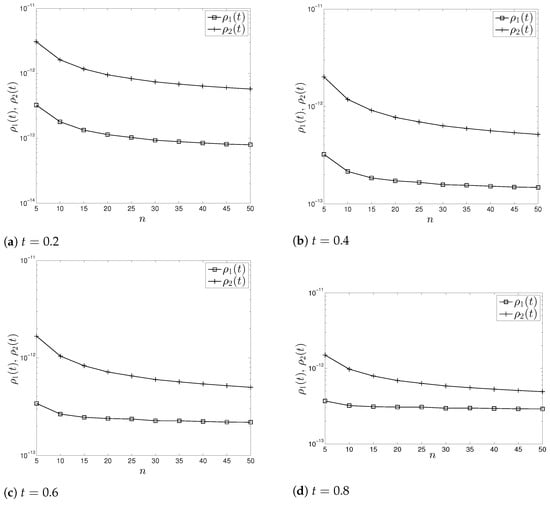
The average values over 30 trials for the relative perturbation${\displaystyle {\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X(t\parallel }}$and the bound${\displaystyle {\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$,$f\left(t\right)=f(\delta ,t)$from (8)–(13) for$t=0.2$,$0.4$,$0.6$and$0.8$are displayed in Figure 2 for$\alpha =5$.

Figure 2. Example 2, experiment 2, bound f (t)= f(δ, t), (8)–(13) from Theorem 1, α = 5, j = 12, t = 0.2 to 0.8, n from 5 to 50.

The results for the perturbation bound$f(\delta ,t)$, (8)–(13) from Theorem 1, visualized on Figure 1 and Figure 2 demonstrate that the perturbation bound$f(\delta ,t)$, (8)–(13) is an effective upper perturbation bound of$X\left(t\right)$in a large range of the size n of the NDRE (1) (n varies from 5 to 50). With the increasing of the dimension n of Equation (1), the accuracy of the estimate improves.

Example 2.

This example tests the effectiveness of the bound (9)–(13) in the case of large-scale NDRE. We consider a NDRE of order $n=4000$, arising in neutron transport theory

$$\begin{array}{c}\hfill \dot{X}\left(t\right)=-(\mathsf{\Delta }-e{q}^{\top })X\left(t\right)-X\left(t\right)(\mathsf{\Gamma }-q{e}^{\top })+X\left(t\right)q{q}^{\top }X\left(t\right)+e{e}^{\top },\end{array}$$

on time interval $T=\left[\begin{array}{cc}0,& 2\end{array}\right]$, with matrices

$$\begin{array}{ccc}\hfill \mathsf{\Delta }& =& \mathrm{diag}({\delta }_1,\cdots ,{\delta }_n),{\delta }_i=\frac{1}{c{\omega }_i(1+\alpha )},i=1,\cdots ,n\hfill \\ \hfill \mathsf{\Gamma }& =& \mathrm{diag}({\gamma }_1,\cdots ,{\gamma }_n),{\gamma }_i=\frac{1}{c{\omega }_i(1-\alpha )},i=1,\cdots ,n,\hfill \\ & & c=0.5,\alpha =0.5\hfill \\ & & e={(1,\cdots ,1)}^{\top },q={(q_1,\cdots ,q_n)}^{\top },with q_i=\frac{c_i}{2{\omega }_i},i=1,\cdots ,n,\hfill \end{array}$$

where the sequences $\left(c_i\right)$ and $\left({\omega }_i\right)$, $i=1,\cdots ,n$ are the nodes and weights of the Gaussian-Legendre quadrature on $\left[\begin{array}{cc}0,& 1\end{array}\right]$, respectively:

$$\begin{array}{c}\hfill c_i>0,\sum _i^n{c}_i=1, and0<{\omega }_1<\cdots <{\omega }_n,i=1,\cdots ,n.\end{array}$$

The perturbation is chosen as:

$$\begin{array}{c}\hfill \delta q=\left(rand\left(size\right(q\right))/\parallel q\parallel )\ast {10}^{-j} for j=12.\end{array}$$

The results, obtained for the relative perturbation ${\rho }_1\left(t\right)=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }$ and the nonlocal bound ${\rho }_2\left(t\right)=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel },f\left(t\right)=f(\delta ,t),$ (8)–(13) for $t=0.4,0.8,1.2,1.6$ and 2 are shown in Table 6.

Table 6. Relative perturbations ${\displaystyle {\rho }_1=\frac{\parallel \mathsf{\Delta }X\left(t\right)\parallel }{\parallel X\left(t\right)\parallel }}$ and ${\displaystyle {\rho }_2=\frac{f\left(t\right)}{\parallel X\left(t\right)\parallel }}$.

	$\mathit{t}=0.4$	$\mathit{t}=0.8$	$\mathit{t}=1.2$	$\mathit{t}=1.6$	$\mathit{t}=2$
$\mathit{j}=\mathbf{10}$
${\rho }_1\left(t\right)$	$3.25\times {10}^{-10}$	$4.09\times {10}^{-10}$	$4.26\times {10}^{-10}$	$4.29\times {10}^{-10}$	$4.29\times {10}^{-10}$
${\rho }_2\left(t\right)$	$3.80\times {10}^{-09}$	$4.09\times {10}^{-09}$	$4.12\times {10}^{-09}$	$4.13\times {10}^{-09}$	$4.13\times {10}^{-09}$

Example 3. Results for size n = 4000, j = 12.

As is seen, over all the interval of integration $T\in \left[\begin{array}{cc}0,& 2\end{array}\right]$, the perturbation bound $f(\delta ,t)$ from (8)–(13) is valid, i.e., the condition (8) for existence of the bound $f(\delta ,t)$ is not deteriorated. The bound $f(\delta ,t)$ is a quite sharp upper bound—remains in the order of the estimated value. The perturbation bound $f(\delta ,t)$ formulated in Theorem 1 is effective and could be used to estimate the sensitivity even of a large-scale NDRE.

5. Conclusions

In this paper, a nonlocal sensitivity analysis of the nonsymmetric differential matrix Riccati equation is presented. Two computable perturbation bounds are derived using the techniques of Fréchet derivatives, Lyapunov majorants and fixed-point principles, developed in [14]. The first bound is based on the integral form of the solution. The second one exploits the statement of the classical Radon’s theory of local equivalence of the solution to the differential matrix Riccati equation to the solution of the initial value problem of the associated differential system. It has the advantage of not being related with the solution of the NDRE and hence with problems of divergence of the numerical procedure. Numerical examples show that the estimates proposed are fairly sharp for both low-dimensional and large-scale NDRE. The perturbation bound is a crucial issue of the process of numerical solution of an equation as well as a tool to evaluate the stability of the computation process. The tight perturbation bounds, proposed in the paper, allow estimation of the accuracy of the solution to a numerically solved nonsymmetric differential matrix Riccati equation.