A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition †
Abstract
1. Introduction
2. Definitions and Notations
2.1. Discrete Cosine Transformation
2.2. Definitions and Properties of the Cosine Product
| Algorithm 1 Computing the c-product. |
| Inputs: and |
| Output: |
| 1. Compute and . |
| 2. Compute each frontal slices of by
|
| 3. Compute . |
| Algorithm 2 The Tensor SVD (c-SVD). |
| Input: Output: , and . |
| 1. Compute . |
| 2. Compute each frontal slices of , and from as follows |
| (a) for |
| (b) End for |
| 3. Compute , and . |
3. Tensor Principal Component Analysis for Face Recognition
3.1. The Matrix Case
- If , then the input image is not even a face image and not recognized.
- If and for all i then the input image is a face image but it is an unknown image face.
- If and for all i then the input images are the individual face images associated with the class vector .
4. The Tensor Golub–Kahan Method
4.1. The Tensor C-Global Golub–Kahan Algorithm
| Algorithm 3 The Tensor Global Golub–Kahan algorithm (TGGKA). |
| 1. Choose a tensor such that and set . |
| 2. For |
| (a) , |
| (b) , |
| (c) , |
| (d) , |
| (e) . |
| (f) . |
| End |
4.2. Tensor Tubal Golub–Kahan Bidiagonalisation Algorithm
| Algorithm 4 Normalization algorithm (Normalize). |
| 1. Input. and a tolerance . |
| 2. Output. The tensor and the tube fiber . |
| 3. Set |
| (a) For |
| i |
| ii if , |
| iii else ; |
| ; |
| (b) End |
| 4. , |
| 5. End |
| Algorithm 5 The Tensor Tube Global Golub–Kahan algorithm (TTGGKA). |
| 1. Choose a tensor such that and set . |
| 2. For |
| (a) , |
| (b) . |
| (c) , |
| (d) . |
| End |
5. The Tensor Tubal PCA Method
| Algorithm 6 The Tensor Tubal PCA algorithm (TTPCA). |
| 1. Inputs Training Image tensor (N images), mean image tensor ,Test image , index of truncation r, k=number of iterations of the TTGGKA algorithm (). |
| 2. Output Closest image in the Training database. |
| 3. Run k iterations of the TTGGKA algorithm to obtain tensors and |
| 4. Compute c-SVD |
| 5. Compute the projection tensor , where |
| 6. Compute the projected Training tensor and projected centred test image |
| 7. Find |
6. Numerical Tests
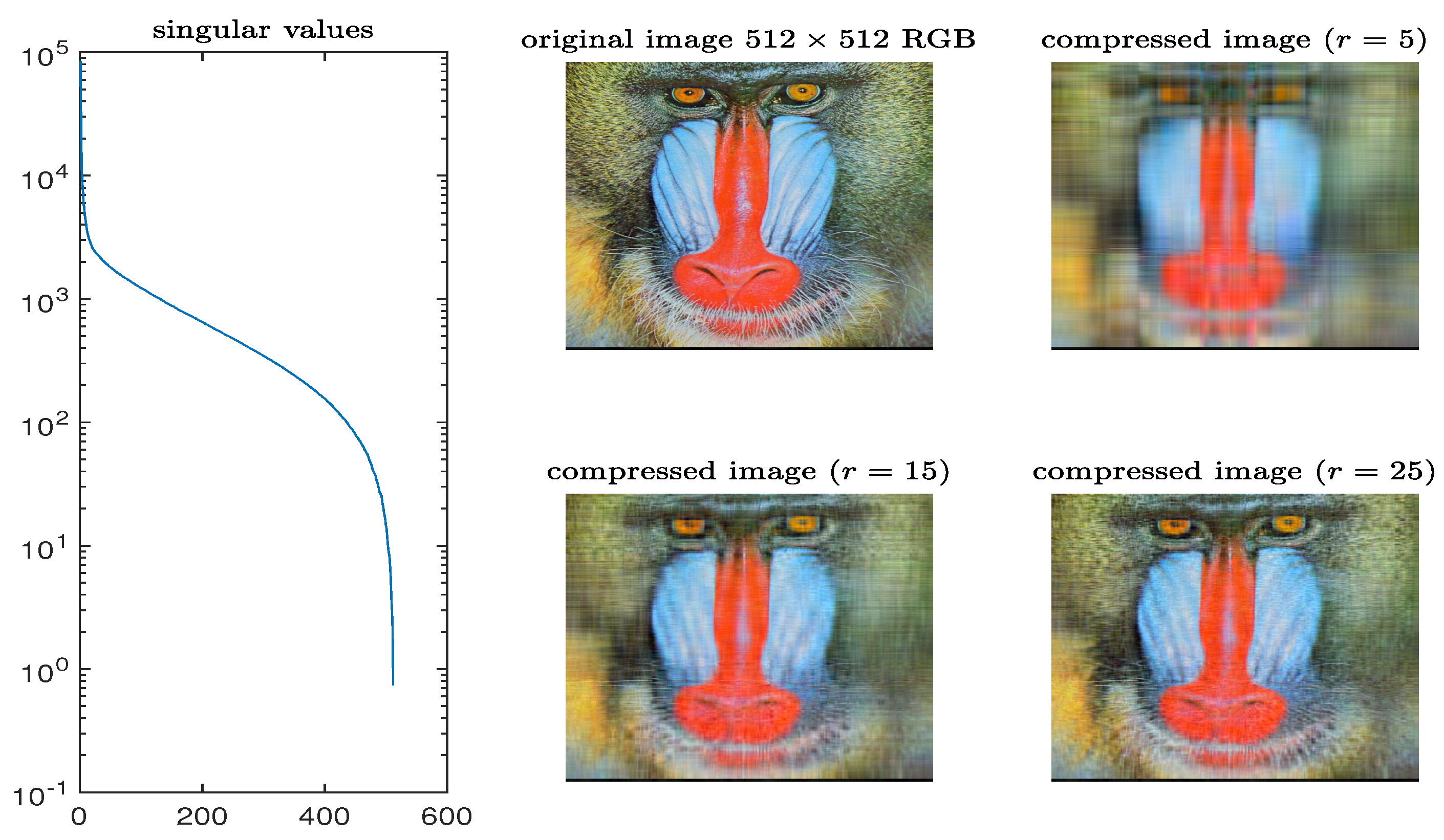
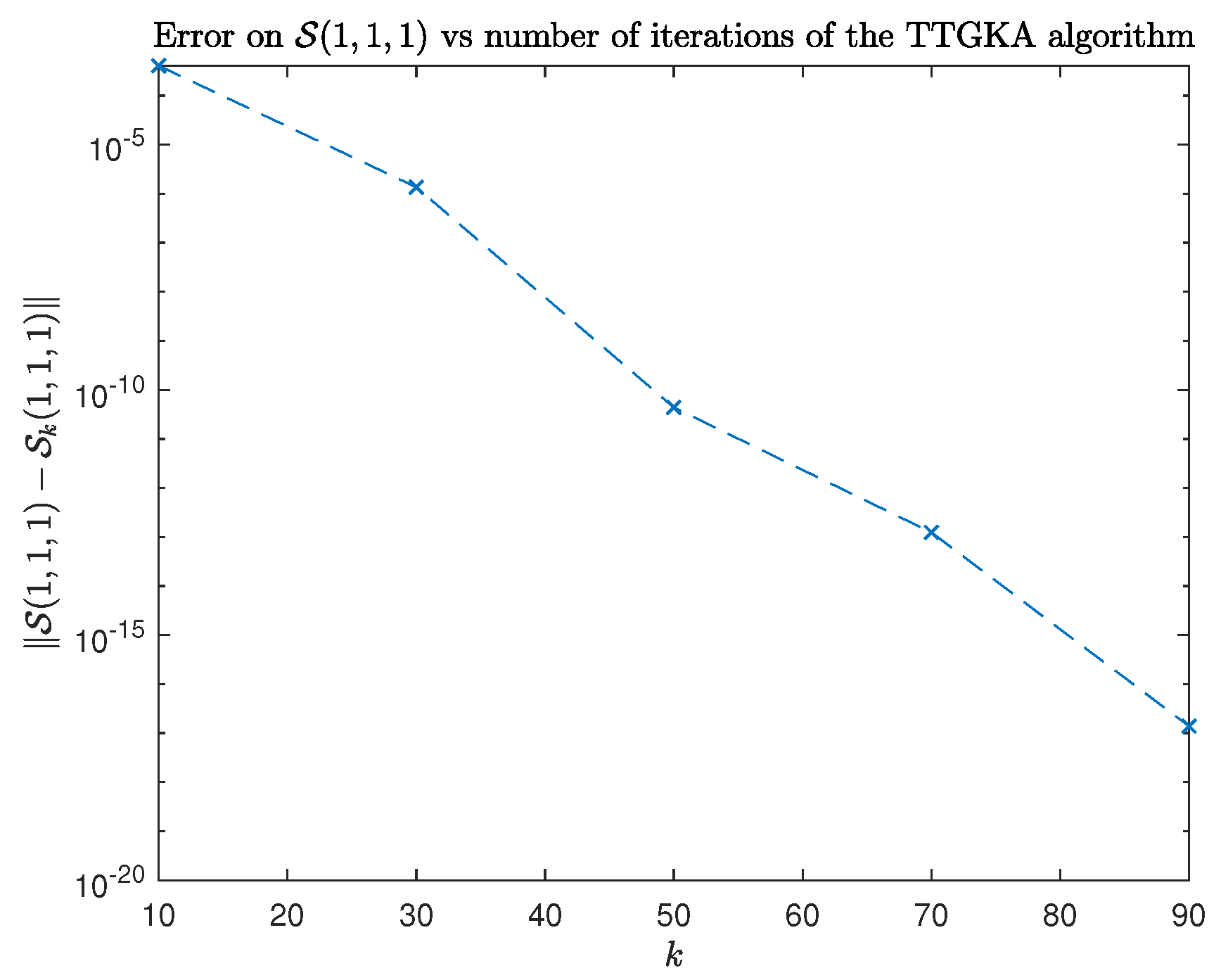
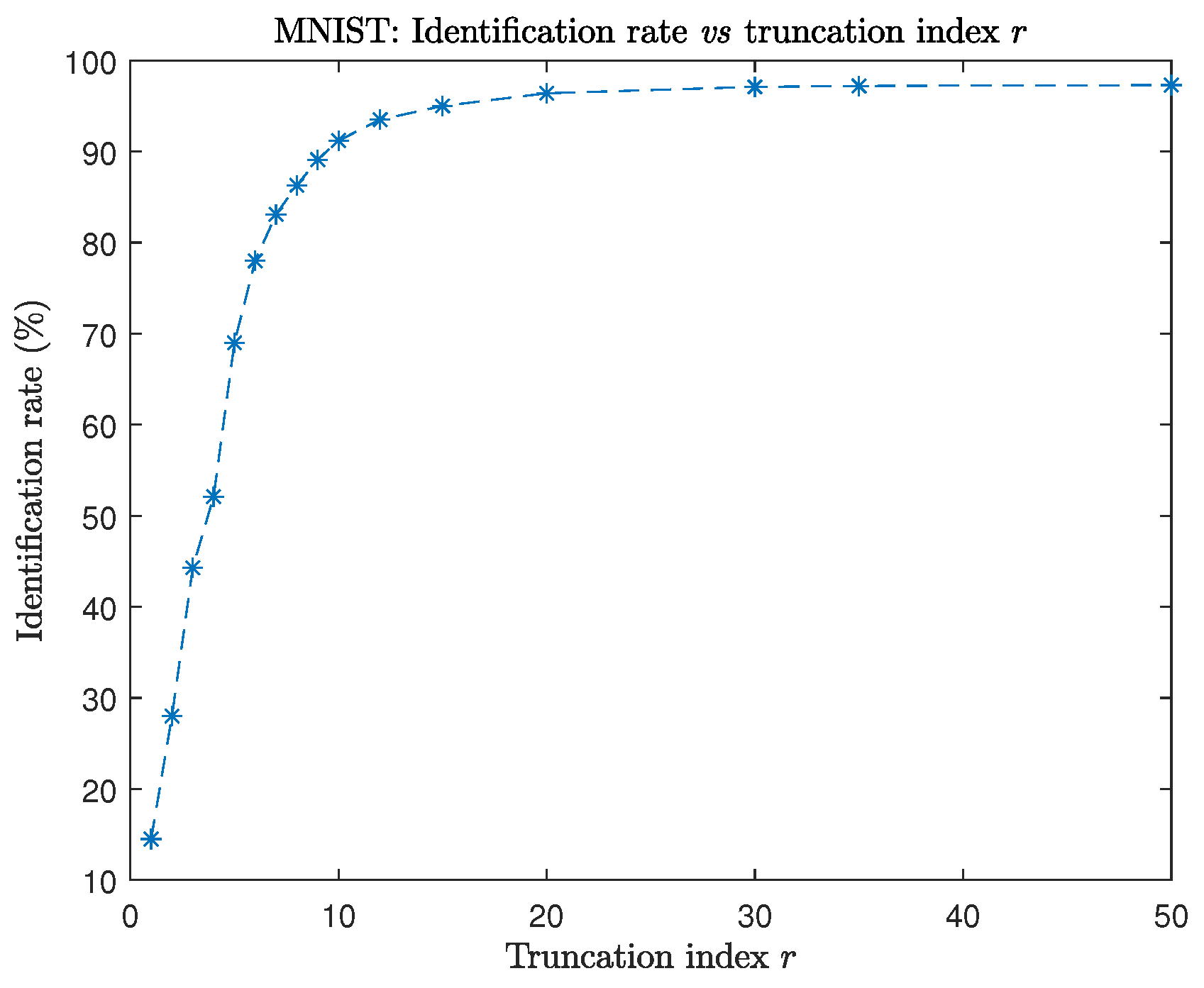
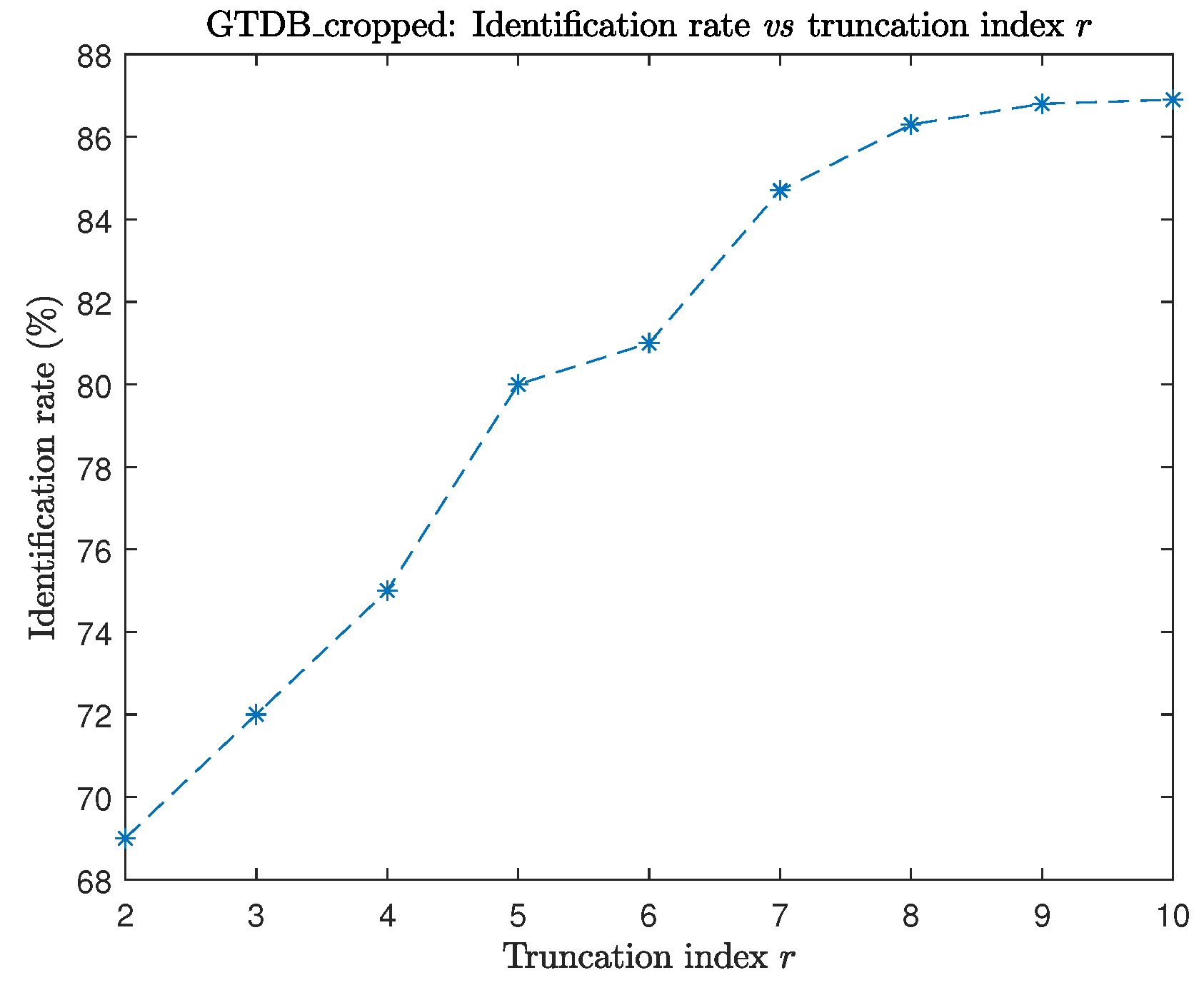
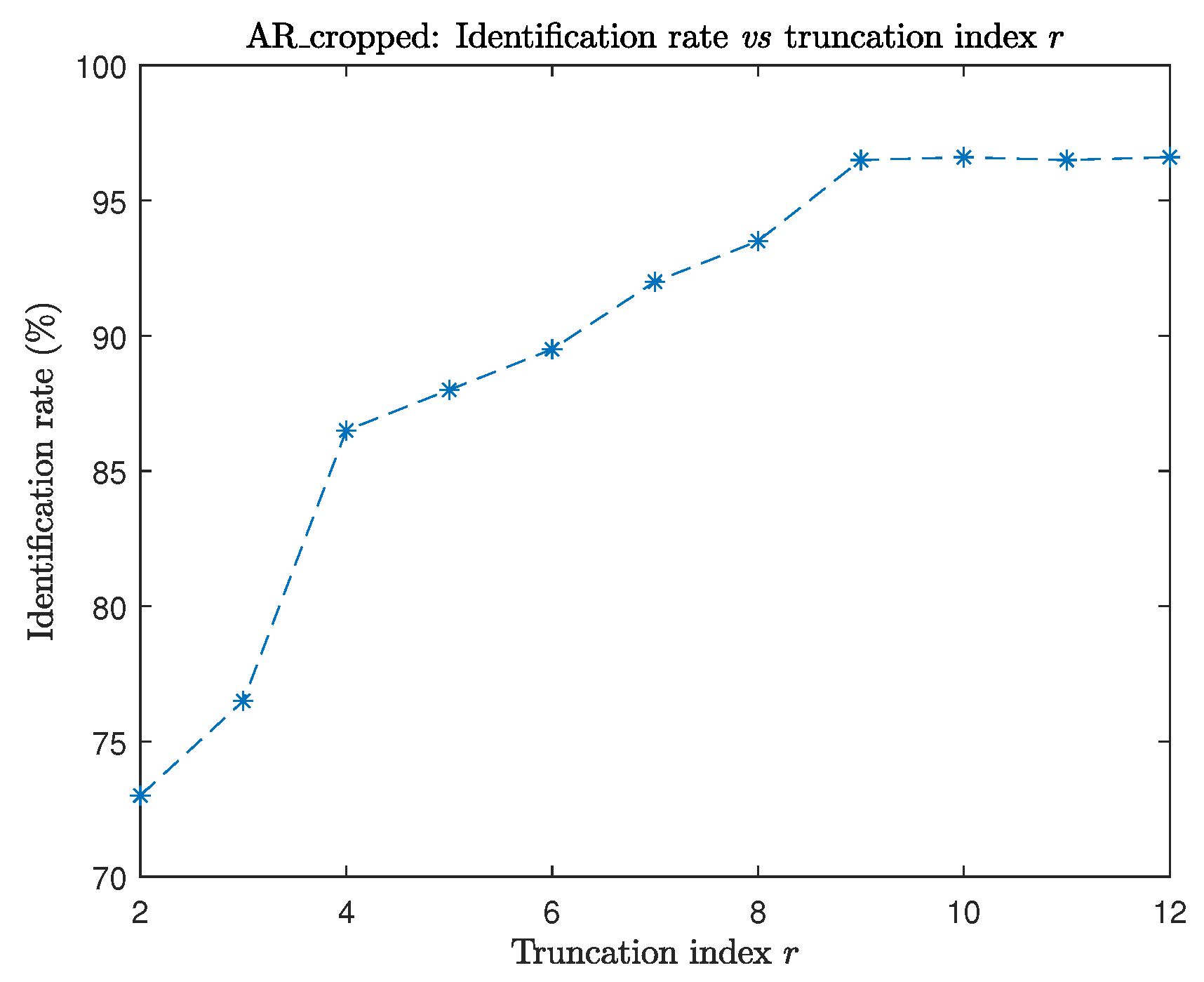
6.1. Example 1
6.2. Example 2
6.3. Example 3
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor Decompositions and Applications. SIAM Rev. 2009, 3, 455–500. [Google Scholar] [CrossRef]
- Zhang, J.; Saibaba, A.K.; Kilmer, M.E.; Aeron, S. A randomized tensor singular value decomposition based on the t-product. Numer Linear Algebra Appl. 2018, 25, e2179. [Google Scholar] [CrossRef]
- Cai, S.; Luo, Q.; Yang, M.; Li, W.; Xiao, M. Tensor robust principal component analysis via non-convex low rank approximation. Appl. Sci. 2019, 9, 1411. [Google Scholar] [CrossRef]
- Kong, H.; Xie, X.; Lin, Z. t-Schatten-p norm for low-rank tensor recovery. IEEE J. Sel. Top. Signal Process. 2018, 12, 1405–1419. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Kang, Z.; Peng, C.; Cheng, Q. Robust PCA via nonconvex rank approximation. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015. [Google Scholar]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis with a New Tensor Nuclear Norm. IEEE Anal. Mach. Intell. 2020, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Martinez, A.M.; Kak, A.C. PCA versus LDA. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 228–233. [Google Scholar] [CrossRef]
- Guide, M.E.; Ichi, A.E.; Jbilou, K.; Sadaka, R. Tensor Krylov subspace methods via the T-product for color image processing. arXiv 2020, arXiv:2006.07133. [Google Scholar]
- Brazell, M.; Navasca, N.L.C.; Tamon, C. Solving Multilinear Systems Via Tensor Inversion. SIAM J. Matrix Anal. Appl. 2013, 34, 542–570. [Google Scholar] [CrossRef]
- Beik, F.P.A.; Jbilou, K.; Najafi-Kalyani, M.; Reichel, L. Golub–Kahan bidiagonalization for ill-conditioned tensor equations with applications. Numer. Algorithms 2020, 84, 1535–1563. [Google Scholar] [CrossRef]
- Ichi, A.E.; Jbilou, K.; Sadaka, R. On some tensor tubal-Krylov subspace methods via the T-product. arXiv 2020, arXiv:2010.14063. [Google Scholar]
- Guide, M.E.; Ichi, A.E.; Jbilou, K. Discrete cosine transform LSQR and GMRES methods for multidimensional ill-posed problems. arXiv 2020, arXiv:2103.11847. [Google Scholar]
- Vasilescu, M.A.O.; Terzopoulos, D. Multilinear image analysis for facial recognition. In Proceedings of the Object Recognition Supported by User Interaction for Service Robots, Quebec City, QC, Canada, 11–15 August 2002; pp. 511–514. [Google Scholar]
- Jain, A. Fundamentals of Digital Image Processing; Prentice–Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Ng, M.K.; Chan, R.H.; Tang, W. A fast algorithm for deblurring models with Neumann boundary conditions. SIAM J. Sci. Comput. 1999, 21, 851–866. [Google Scholar] [CrossRef]
- Kernfeld, E.; Kilmer, M.; Aeron, S. Tensor-tensor products with invertible linear transforms. Linear Algebra Appl. 2015, 485, 545–570. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Savas, B.; Eldén, L. Krylov-type methods for tensor computations I. Linear Algebra Appl. 2013, 438, 891–918. [Google Scholar] [CrossRef]
- Lecun, Y.; Cortes, C.; Curges, C. The MNIST Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 22 February 2021).
- Nefian, A.V. Georgia Tech Face Database. Available online: http://www.anefian.com/research/face_reco.htm (accessed on 22 February 2021).
- Wang, S.; Sun, M.; Chen, Y.; Pang, E.; Zhou, C. STPCA: Sparse tensor Principal Component Analysis for feature extraction. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 2278–2281. [Google Scholar]
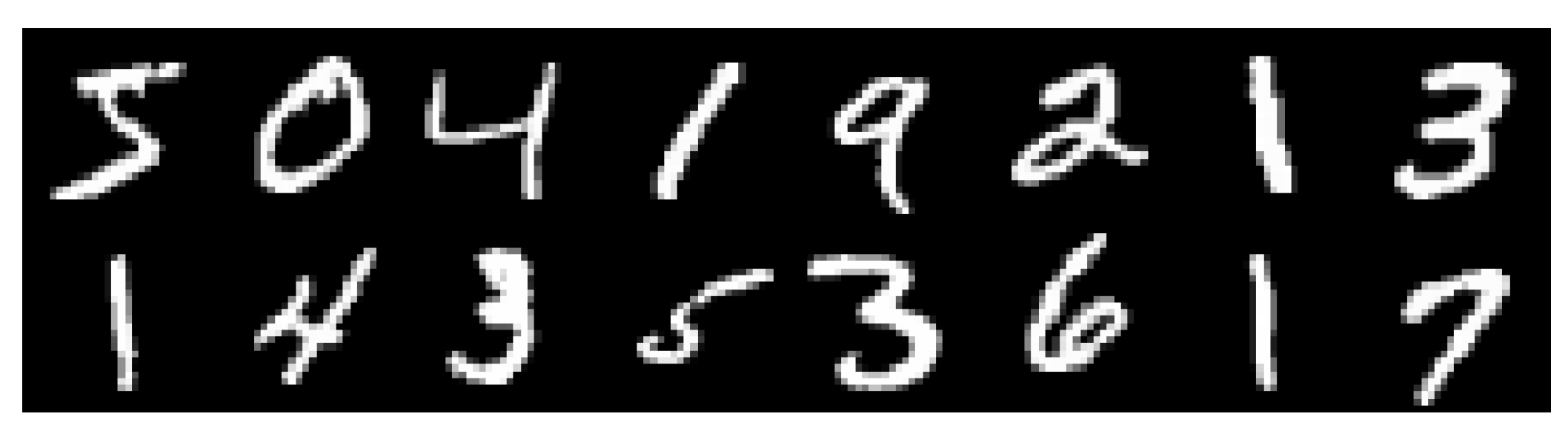



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hached, M.; Jbilou, K.; Koukouvinos, C.; Mitrouli, M. A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition. Mathematics 2021, 9, 1249. https://doi.org/10.3390/math9111249
Hached M, Jbilou K, Koukouvinos C, Mitrouli M. A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition. Mathematics. 2021; 9(11):1249. https://doi.org/10.3390/math9111249
Chicago/Turabian StyleHached, Mustapha, Khalide Jbilou, Christos Koukouvinos, and Marilena Mitrouli. 2021. "A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition" Mathematics 9, no. 11: 1249. https://doi.org/10.3390/math9111249
APA StyleHached, M., Jbilou, K., Koukouvinos, C., & Mitrouli, M. (2021). A Multidimensional Principal Component Analysis via the C-Product Golub–Kahan–SVD for Classification and Face Recognition. Mathematics, 9(11), 1249. https://doi.org/10.3390/math9111249






