Abstract
The InterCriteria Analysis (ICrA) is based on the mathematical formalisms of index matrices and intuitionistic fuzzy sets. It has been elaborated to discern possible similarities in the behavior of criteria pairs when multiple objects are considered, allowing also the accounting of information uncertainty. The focus of this study is to validate the applicability of ICrA over a large set of ECG criteria extracted for arrhythmia analysis and to evaluate its ability to support the pre-selection of criteria that could be further involved in decision making procedures. ICrA is applied over 88 ECG criteria (resulting in 3828 criteria pairs) calculated for 8528 ECGs from PhysioNet/CinC Challenge 2017 database. Three criteria pairs show strong positive consonance, another 26—positive consonance, while another 15 are in negative consonance. ICrA also reveals lack of dependencies in 98 criteria pairs. The correspondence between our observations (high degrees of agreement/disagreement and lack of dependencies) and our expectations based on knowledge of the principles involved in the computation of the ECG criteria validates the application of ICrA for reliable evaluation of the relation between different criteria. This potential of ICrA to highlight useful relations between ECG criteria makes it suitable in the ECG pre-processing stage for criteria pre-selection. Thus, optimization of the feature space could be achieved together with minimization of the computations’ complexity.
1. Introduction
The idea of InterCriteria Analysis (ICrA) was originally developed in the period 2014–2015 by Atanassov et al. [1,2] based on two mathematical formalisms—the theories of Index Matrices (IM) [3,4] and Intuitionistic Fuzzy Sets (IFS) [5,6,7]. ICrA was designed as a method for detecting the levels of pairwise correlations for a set of criteria measured or calculated for a set of objects. This analysis strives to go beyond the nature of the criteria involved in a process of evaluation of multiple objects against multiple criteria, and, thus, to discover some dependencies between the criteria themselves. The ultimate goal of ICrA is to highlight criteria pairs which exhibit high enough correlations, thus selecting a reasonable criteria set that could be involved in a decision-making process and eliminating some of the criteria, when their measurement is time-consuming, comes at a higher cost, or is considered undesirable for any other reason. The selection of such high enough correlations requires either an expert decision or an algorithm for the precise establishment of the thresholds, beyond which the top-correlating criteria are selected in order to yield certain problem-specific conclusions.
Over the years ICrA has attracted an increasing scientific interest both in theoretical plan and for applications in different fields. In the theoretical aspect, some of the most significant improvements are directed towards the additional formulation of rules for defining the ways for estimation of the degrees of agreement and disagreement with respect to the type of data [2,8]. Aiming at easier visual interpretation of the ICrA results, an intuitionistic fuzzy interpretation triangle has been presented [2,8]. Different ways to determine the threshold values for definition of the intercriteria relation are considered in [9]. Four different algorithms for ICrA implementation, namely µ-biased, balanced, ν-biased and unbiased, are demonstrated in [10]. Additionally, the authors of [11,12] present extensions of the theoretical aspect of ICrA, as a prerequisite for improving the applicability of the method in decision-making procedures under uncertainty and in case of missing and incomplete data.
A number of ICrA implementations are directed toward solving real problems in different fields. There are many successful applications of ICrA in various fields, among which economics and transport, ecology and meteorology, artificial intelligence, metaheuristic algorithms, neural networks, biomedicine and quality of life. The problem that has motivated the design of ICrA came from the petrochemical industry, where the approach has been applied to assist the evaluation of bulk and fraction properties of crude oils and thus to select potentially beneficial new crudes for processing in a refinery [13]. In another study, 140 crude oil samples, evaluated by 8 physicochemical criteria, have been submitted to a neural network [14]. This application of ICrA has induced the idea that some of the irrelevant data used during neural network training, i.e., the number of inputs, weights and offsets, can be reduced. This might lead to the design of an optimized smaller neural network with reduced memory requirements for the learning process, shorter conversion time and lower number of iterations.
A numerous of ICrA applications in the field of artificial intelligence are available, among which the assessment of the execution quality of genetic algorithms (GA) as one of the most promising metaheuristic techniques [10,12]. In these applications ICrA allows establishing of relationships and dependencies between some of the basic parameters of GA, namely number of individuals in the population, number of algorithm execution iterations, generation gap, probabilities of crossing and mutation, on the one hand, and algorithm convergence time and accuracy, on the other hand. Following this idea, ICrA has been further applied to assess the performance of other well-known and widely used metaheuristic techniques, such as artificial bee colony, ant colony optimization, bat algorithm, etc. A comparative analysis of different metaheuristic algorithms and their hybrids is presented in [15].
ICrA might be useful in the field of education, i.e., for the purposes of university ratings evaluation in different countries [16], and more specifically in Slovak Republic [17] and India [18]. When the ecology has been in the investigation focus, ICrA has been applied for assessment of the pollution indices of river ecosystems [19] as well as for evaluation of the wastewater treatment (WWT) processes quality in a typical WWT plant [20]. The last study has been applied on real data and has analyzed the interdependencies between various parameters that characterize the quality of the processes in a WWT plant, such as water quantity, pH, petroleum products, mechanical additives, phosphates, nitrates, etc. This application of ICrA has resulted in some new relationships between the considered criteria, especially with regard to seasonal dependencies.
There are also a few applications in the field of biomedicine and quality of life. Using ICrA, the authors of [21] have explored the performance of various scoring functions available in molecular modelling software packages for the purposes of in silico studies of bioactive compounds. In [22] ICrA has been applied for evaluation of indicators associated with the assessment of health-related quality of life (HrQoL). The EQ-5D-3L questionnaire for measuring HrQoL for a representative sample of 1050 records has been used. Dependent and independent indicators, as well as their relationship have been analyzed.
Going toward the focus of this study, i.e., physiological data analysis, the ICrA has been successfully applied to support decision making in different medical investigations. In a dataset of thermo-dynamic parameters derived from blood plasma proteome thermograms of patients with colorectal cancer ICrA has found interdependencies between the parameters that have not been inferred from the calorimetric data so far [23]. Such interdependencies could be important for the clinical application of differential scanning calorimetry. Krumova et al. [24] applied ICrA combined with Pearson’s and Spearman’s correlation analysis over a large dataset of calorimetric and biochemical parameters derived from the serum proteome of patients diagnosed with multiple myeloma. They have identified general dependencies for the various types of multiple myeloma that could be regarded as a characteristic of this largely heterogeneous disease. Another study over a dataset from Behterev’s disease patients applied ICrA to confirm that the health condition depends on the emotional condition and determines the social functioning of the patients under observation [25].
The aim of this study is to validate the application of ICrA in terms of correctness of the derived intercriteria relations over a large set of criteria extracted from electrocardiogram (ECG) signals. Another objective, formulated from the ECG analysis point of view, is to investigate the potential of ICrA to highlight useful relations between ECG criteria that could be applied in the ECG pre-processing stage for criteria pre-selection. Thus, optimization of the feature space could be achieved together with minimization of the computations’ complexity.
2. Materials and Methods
2.1. ECG Criteria
The ECG signals used for derivation of the criteria are from the training part of the PhysioNet/CinC Challenge 2017 database [26], which comprises 8528 ECGs with duration in the range of 9–61 s, annotated in four rhythm categories: 5076 normal sinus rhythms; 758 atrial flutter/fibrillation signals; 2415 other rhythms; 279 noisy ECG signals. The rhythm categories are not in the scope of the current study although they definitely influence the values of the calculated criteria. An illustration that represents the basic designations for ECG signal interpretation are presented in Figure 1.
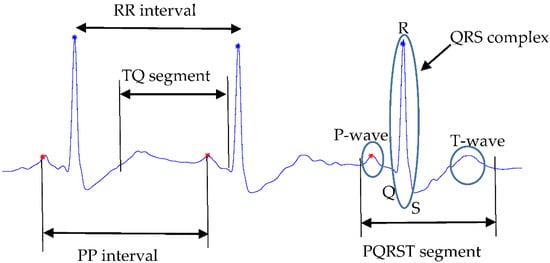
Figure 1.
Basic designations for ECG signals interpretation—P-, Q-, R-, S-, T-waves; PQRST-segment, QRS complex, RR interval, PP interval.
The criteria analyzed in this study could be grouped as follows:
- -
- Group 1: 19 criteria based on heartbeat and rhythm evaluation in the time domain, including:
- Mean, minimal, maximal values and standard deviation of the QRS amplitudes in the analyzed ECG segment. These criteria are calculated once for all beats (MeanAmpVB, MinAmpVB, MaxAmpVB, StdAmpVB—Figure 2, blue asterisks and circles) and a second time only for the normal ventricular beats (MeanAmpN, MinAmpN, MaxAmpN, StdAmpN—Figure 2, only the blue asterisks);
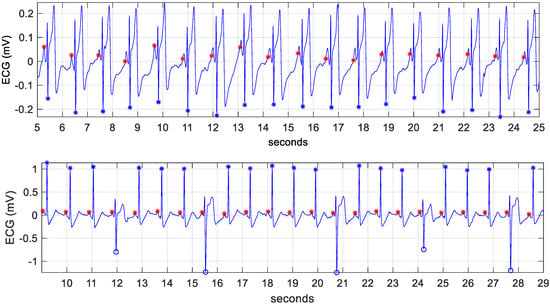 Figure 2. ECG strips with detected normal heartbeats (blue ‘*’), ectopic ventricular beats (blue ‘o’) and P-waves (red ‘*’). The detected heartbeats and P-waves are used for calculation of the time and amplitude criteria in Group 1 and Group 2.
Figure 2. ECG strips with detected normal heartbeats (blue ‘*’), ectopic ventricular beats (blue ‘o’) and P-waves (red ‘*’). The detected heartbeats and P-waves are used for calculation of the time and amplitude criteria in Group 1 and Group 2. - Mean, minimal, maximal values and standard deviation of the RR intervals in the analyzed ECG segment. They are also calculated once for all beats (MeanRRVB, MinRRVB, MaxRRVB, StdRRVB) and a second time only for the normal ventricular beats (MeanRRN, MinRRN, MaxRRN, StdRRN);
- N beats proportion, which is calculated as the ratio between the number of normal heartbeats and the total number of beats detected in the analyzed ECG segment (NBeats(%));
- Probability the rhythm to be atrial fibrillation/flutter based on assessment of the RR irregularity (AF(%));
- ECG segments complexity (C_ECG).
- -
- Group 2: 11 criteria based on evaluation of the P-waves (marked with red asterisks in Figure 2) in the time domain that provide information about the stability of the detected atrial contractions, including:
- Mean, minimal, maximal values and standard deviation of the P-waves amplitudes and the intervals between consecutive P-waves within the analyzed ECG segment (MeanAmpP, MinAmpP, MaxAmpP, StdAmpP, MeanPPint, MinPPint, MaxPPint, StdPPint);
- Mean value and standard deviation of the P-waves number in each RR interval (MeanPcountRRint, StdPcountRRint);
- Percentage of RR intervals with two or more detected P-waves (DoubleP(%)).
- -
- Group 3: 6 Principal Component Analysis (PCA)-based criteria used for assessment of the ECG beat-to-beat irregularity in one ECG signal, including:
- Mean, minimal, maximal values and range of the standard deviation between the samples of all PQRST segments in one ECG recording and the corresponding samples of the PQRST first PCA vector (MeanStdPQRST, MinStdPQRST, MaxStdPQRST, RangeStdPQRST);
- Mean deviation between the samples of all TQ segments in one ECG recording and the corresponding samples of the TQ first PCA vector (MeanStdTQ);
- QRS width measured from the first PCI vector of the PQRST segment (WidthQRS).
- -
- Group 4: 9 criteria describing the TQ segment in the time domain:
- TQ segments complexity (C);
- Mean, minimal, maximal values and standard deviation of the leakage, calculated for individual TQ segments (MeanLeak_TQ, MinLeak_TQ, MaxLeak_TQ, StdLeak_TQ);
- Mean, minimal, maximal values and standard deviation of the period (T), measured for individual TQ segments (MeanT_TQ, MinT_TQ, MaxT_TQ, StdT_TQ).
- -
- Group 5: 44 criteria describing the TQ segment in the frequency domain, including:
- Mean, minimal, maximal values and standard deviation of the dominant frequency in 4s non-overlapping intervals (MeanDF, MinDF, MaxDF, StdDF);
- Mean, minimal, maximal values and standard deviation of the regularity index, which quantifies the sharpness of the dominant peak in the spectra (MeanRI, MinRI, MaxRI, StdRI);
- Mean, minimal, maximal values and standard deviation of the first spectral normalized moment (MeanFSNM, MinFSNM, MaxFSNM, StdFSNM);
- Mean, minimal, maximal values and standard deviation of the spectral width at 4 different levels (0.2, 0.4, 0.6, 0.8) of the maximum power in the range 3 ÷ 15 Hz (MeanSpecWidth_level, MinSpecWidth_level, MaxSpecWidth_level, StdSpecWidth_level);
- Mean, minimal, maximal values and standard deviation of the spectral area between the first and the last cross of 4 different levels (0.2, 0.4, 0.6, 0.8) of the maximum power in the range 3 ÷ 15 Hz (MeanSpecArea_level, MinSpecArea_level, MaxSpecArea_level, StdSpecArea_level);
The criteria in each group are intentionally extracted with redundancy, i.e., part of them or all of them present information that is overlapping. Detailed information about the calculation of the above criteria is presented in [27].
2.2. InterCriteria Analysis
ICrA approach developed by Atanassov et al. [1] in 2014 brings together fundamental concepts of two mathematical apparatuses—the index matrices [3,4] and the intuitionistic fuzzy sets (IFS) [5,6,7]. Here, for completeness, a brief outline of the theoretical background of ICrA is provided.
The intuitionistic fuzzy sets have been introduced by Atanassov [5] as an extension of Zadeh’s fuzzy sets [28], in which the two possible discrete values of a characteristic function (0 for not a member and 1 for a member of a set) are substituted with a value in the interval [0, 1], known as a membership function of an element to a set. Atanassov extended this idea by introducing a degree of non-membership, also in the interval [0, 1], and imposing the constraint that the sum of the membership and non-membership degrees is also in the unit interval. Thus, the intuitionistic fuzzy set A* is defined by:
where E is a universe, , represent the functions that give the degrees of membership and non-membership for each element to a fixed subset A of E, respectively, such that .
Over the years, the intuitionistic fuzzy sets have attracted worldwide interest in both theoretical and application aspects. One of the main areas of fuzzy and intuitionistic fuzzy methods application concerns the decision making under uncertainty [29,30]. A continuation in this direction is the attempt to enrich the respective theories with analogues of classical methods by extending certain concepts, especially concerning probability theory [31] and analogues of classical mathematical analysis [32].
An intuitionistic fuzzy pair (IFP) is an object in the form of an ordered pair , where and [33]. IFPs are basic elements of the intuitionistic fuzzy sets and logics [5,6,7] and ICrA [34]. IFP could be used for the evaluation of objects or processes and its components μ and ν might be interpreted as degrees of membership (validity, agreement, etc.) and non-membership (non-validity, disagreement, etc.), respectively.
An index matrix (IM) is usually denoted as [O, C, ]. In terms of ICrA, the set of rows O = {O1, …, Om} is related with the evaluated objects, while the set of columns C = {C1, …, Cn} stands for the evaluation criteria applied to a considered object. The elements of the index matrix (for every i, k, where 1 ≤ i ≤ m, 1 ≤ k ≤ n) are the evaluations of the ith object against the kth criterion and might be real numbers of a certain type, ordered pairs of real numbers, or some other objects that are comparable according to relation R with all the rest elements of the index matrix. For most of the studies, all the values assigned to the objects by the criteria are assumed to be known and usually to be real numbers. A two-dimensional IM is an object of the following form:
| C1 | … | Ck | … | Cn | |
| O1 | … | … | |||
| … | … | … | … | … | … |
| Oi | … | … | |||
| … | … | … | … | … | … |
| Om | … | … |
ICrA starts with a table of dimensions m and n and produces a table of dimensions n and n, which elements are intuitionistic fuzzy pairs of intercriteria correlations. The main idea of ICrA is to perform a pairwise comparison between every two different criteria along all evaluated objects, as shown in Figure 3.
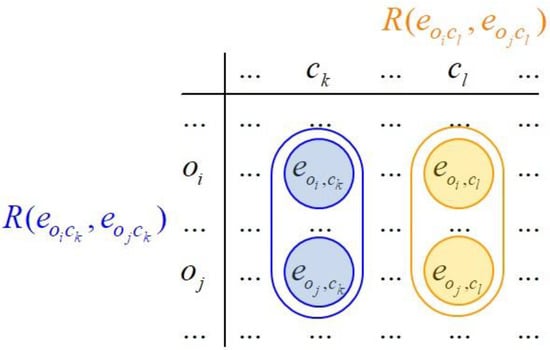
Figure 3.
Intercriteria correlations.
The relation has a dual relation , which is true in the cases when relation R is false, and vice versa (all mathematical justifications of ICrA might be found in details in [1]). Two intuitionistic fuzzy counters and are formed and incremented, based on the following rules:
- -
- is the number of cases, in which the relations and (or the relations and ) are simultaneously satisfied.
- -
- is the number of cases, in which the relation and (or the relations and ) are simultaneously satisfied.
As the total number of pairwise comparisons between the objects is m(m − 1)/2, it is obvious that . For every k, l (1 ≤ k ≤ l ≤ m and m ≥ 2), two values are defined by normalizing the above sums and as follows:
- which, in terms of ICrA, is known as degree of agreement, and
- , known as degree of disagreement.
In fact, degrees of agreement/disagreement between two criteria should be calculated just once, considering that and .
Obviously, both and are numbers in the interval [0, 1], and their sum is a number in this interval as well. The number that complements the sum ( + ) to 1 is called , which corresponds to the degree of uncertainty. In practice, considering that + + = 1, two of these three values are enough to describe the degrees of agreement, disagreement and uncertainty observed between two criteria.
Finally, the collected IFP , which play the role of IF evaluation of the relations between any two criteria Ck and Cl, form the ICrA index matrix:
| C1 | … | Ck | … | Cn | |
| C1 | … | … | |||
| … | … | … | … | … | … |
| Ck | … | … | |||
| … | … | … | … | … | … |
| Cn | … | … |
From a practical point of view, it is more flexible to work with two index matrices IMμ and IMν, rather than with the index matrix of IF pairs shown above.
The result of ICrA algorithm is a kind of classification of the intercriteria relations, based on the thresholds of and , which are a user’s choice. Let α, β ∈ [0, 1] be the threshold values, against which a comparison of the values of and takes place. Then, criteria Ck and Cl are in:
- positive consonance, if > α and < β;
- negative consonance, if < β and > α;
- dissonance, otherwise.
For illustrative purposes, an intuitionistic fuzzy interpretation triangle (Figure 4) has been introduced giving in one representation the thresholds α and β, as well as the zones for positive consonance, negative consonance and dissonance.
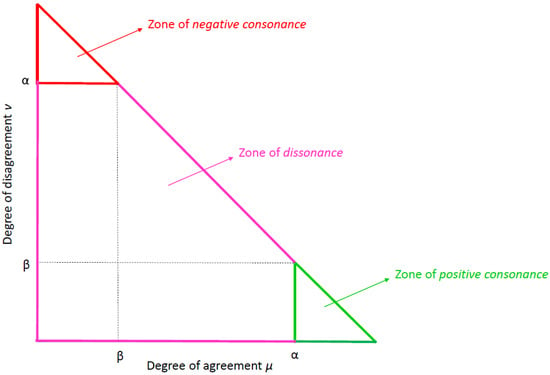
Figure 4.
Intuitionistic fuzzy triangle with zones of positive consonance, negative consonance and dissonance.
A more precise scale for determining consonance or dissonance between criteria pairs, as well as results interpretation according to the degrees of agreement, disagreement and uncertainty, especially focused on the equalities interpretation, are presented in [2]. Later on in [10], all rules defined in [2] are formulated and presented as different algorithms for intercriteria relations calculation, named μ-biased, balanced, ν-biased and unbiased, presented also with their pseudo-code.
In the present study, ICrA is applied for examination of the ECG criteria described in Section 2.1. The analysis is performed via ICrAData v.2.3 implementation (http://intercriteria.net/software/, accessed on 16 August 2020), which is described in detail in [35]. The great number of considered criteria has provoked the necessity of a number of ICrAData improvements. The validation of ICrA for this specific application is going to be performed by analysis of the observed positive and negative consonances and dissonance and their correspondence to the principles implemented in the respective criteria calculations. On the other hand, the derived intercriteria relations will be considered in the light of their application for reduction of the ECG feature space size. Criteria related with complex processing procedures could be avoided if they appear to bring equal information as other criteria, which are easier for calculation. Features that participate in more criteria couples with strong consonance would be preferred for inclusion in a feature set, thus making possible the exclusion of the remaining criteria that participate in these couples and decreasing the feature space. Additionally, criteria that are in dissonance are valuable, since they bring non-overlapping information.
3. Results
In this study, ICrA is applied over the 88 ECG criteria described in Section 2.1. For illustrative purposes only, Figure 5 presents a screenshot of the implementation of ICrAData v.2.3 for such a large number of criteria.
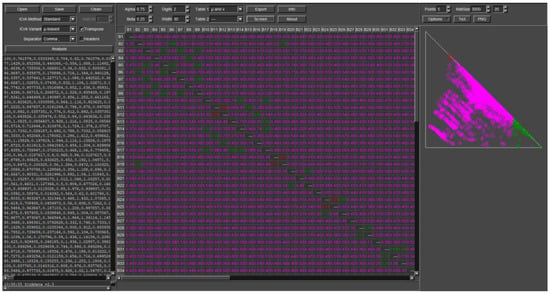
Figure 5.
Result of the application of ICrAData v.2.3 over the 88 ECG criteria described in Section 2.1.
As could be seen from Figure 5, the left panel presents a part view of the input data. The middle panel represents only the intercriteria relations between the first 35 criteria, shown for illustrative purposes only. The right panel demonstrates the intuitionistic fuzzy triangle for visual representation of the results. The presented analysis was performed at the default values of the thresholds of α = 0.75 and β = 0.25 and when the standard μ-biased method for the intercriteria calculation of the degrees of agreement and disagreement is used.
In the case of the 88 ECG criteria considered in this study, 88 × 87/2 = 3828 pairs of criteria are formed, which is a huge amount of data for detailed investigation. After the thorough preliminary analysis, including exploration of various values of thresholds of α and β, as well as implementation of different method for the intercriteria calculation of the degrees of agreement and disagreement, we have focused our attention on the data falling in the following four intervals for µ and/or ν values:
- µ ≥ 0.95—showing an extremely high degree of agreement between two criteria, presenting them as criteria of strong positive consonance [2];
- µ ≥ 0.85—showing a high degree of agreement between two criteria, presenting them as criteria of positive consonance [2];
- ν ≥ 0.70—showing a high degree of disagreement between two criteria, presenting them as criteria of weak dissonance to negative consonance [2];
- 0.49 ≤ µ ≤ 0.51; 0.49 ≤ ν ≤ 0.51; µ + ν ≥ 0.98—showing almost equal values of degrees of agreement and disagreement, presenting such pairs as criteria of dissonance.
3.1. ECG Criteria Showing Extremely High Degree of Agreement
As seen from Figure 5, there is a relatively large number of pairs with degree of agreement µ higher than 0.75 (green circles in the lower right corner of the intuitionistic fuzzy triangle). Thus, we consider as more appropriate to apply ICrA with the thresholds of α = 0.85 and β = 0.15. In such case, three ECG criteria pairs present extremely high degree of agreement µ ≥ 0.95 as follows:
- <MinSpecWidth_08, MinSpecArea_08>, µ = 0.987
- <MinSpecWidth_06, MinSpecArea_06>, µ = 0.972
- <MeanAmpVB, MeanAmpN>, µ = 0.968
These high values of the degree of agreement µ are expected considering the fact that increasing the spectral width on a certain level inevitably leads to increasing the spectral area on the same level (1st and 2nd pair), as well as the mean amplitude of the ventricular beats is strongly related to the mean amplitude of the normal beats (3rd pair), which are usually a predominant part in the analyzed ECG segment. Based on these observed relations one could decide to exclude from the ECG feature set the spectral area criteria MinSpecArea_08 and MinSpecArea_06, as well as MeanAmpN, which is related with supplementary analysis of the heartbeat types.
3.2. ECG Criteria Showing High Degree of Agreement
In addition to the above mentioned 3 criteria pairs, 26 other ECG criteria pairs present high degree of agreement µ > 0.85 (green circles in Figure 6).
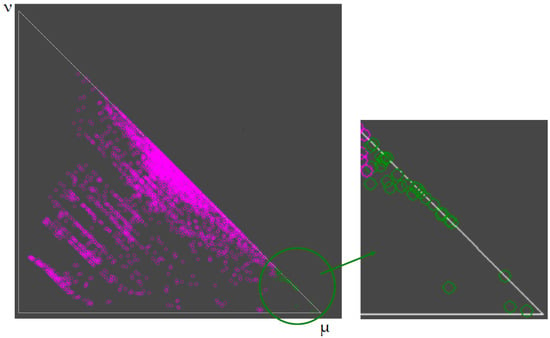
Figure 6.
Twenty-nine criteria pairs that show high degree of agreement µ > 0.85, illustrated with green circles.
The additional 26 other ECG criteria pairs could be grouped as follows:
- Dependencies between criteria that describe the TQ segment in the frequency domain, i.e., <MinSpecWidth_04, MinSpecArea_04>, <StdSpecArea_02, StdSpecArea_04>, <MaxSpecArea_02, MaxSpecArea_04>, <MeanSpecArea_02, MeanSpecArea_04>, <StdSpecArea_04, StdSpecArea_06>, <StdSpecWidth_08, StdSpecArea_08>, <StdSpecWidth_06, StdSpecArea_06>, <MeanSpecWidth_08, MeanSpecArea_08>, <StdSpecWidth_04, StdSpecArea_04>, <StdSpecArea_02, StdSpecArea_06>, <MaxSpecArea_04, MaxSpecArea_06>, <MeanSpecWidth_06, MeanSpecArea_06>, <MeanSpecArea_04, MeanSpecArea_06>, <MaxSpecArea_08 StdSpecArea_08>, with degree of agreement µ in the range from 0.920 to 0.851. All these dependencies are expected and are suggested by the way of calculation of the paired criteria. The observed relations suggest that part of the spectral features, preferably the ones related to calculation of area and standard deviations, could be excluded from the ECG criteria set.
- Dependencies between criteria that describe the TQ segment in the time domain, i.e., <MeanT_TQ, MaxT_TQ>, <MeanT_TQ, MinT_TQ>, <MeanLeak_TQ, MinLeak_TQ>, with degree of agreement µ in the range from 0.878 to 0.854. Again the high degree of agreement is predisposed by the principles followed in the process computation process (i.e., the mean value of the period T measured in the TQ intervals is in coincidence with the minimal and maximal values of the period T, as well as the change in the mean leakage normally follows the change in the minimal leakage). The presence of MeanT_TQ in two criteria couples implies for possible decrease of the feature set by exclusion of MaxT_TQ and MinT_TQ.
- Dependencies between criteria that describe the amplitudes of the ventricular beats within the analyzed ECG segment, i.e., <MaxAmpVB, MaxAmpN>, <StdAmpVB, StdAmpN>, <MinAmpVB, MinAmpN>, with degree of agreement µ in the range from 0.925 to 0.900. In particular, the observed high degree of agreement corresponds to the fact that these criteria represent the minimal, maximal value and standard deviation of the amplitudes of all ventricular beats and the respective amplitude criteria calculated only for the normal beats, which are predominant in considerable part of the analyzed ECGs. The strong consonance within these criteria pairs suggests once again that the features that describe the normal beats could be replaced by the corresponding features calculated for all heartbeats. Thus, the supplementary analysis for initial heartbeat classification could be avoided.
- Dependencies between criteria that describe the RR intervals between the ventricular beats within the analyzed ECG segment such as <MeanRRVB, MeanRRN> and <StdRRN, MaxRRN>, with degree of agreement µ in the range from 0.893 to 0.864. Expectedly, the mean RR interval between the ventricular beats is greatly influenced by the RR intervals between the normal beats and respectively by MeanRRN. On the other hand, increase/decrease of MaxRRN normally leads to increase/decrease of RR intervals range and consecutively to increase/decrease of StdRRN. If analyzed independently, these two pairs of criteria suggest possible exclusion of MeanRRN and StdRRN from the ECG criteria set. It is a subject of deeper investigation if MaxRRN could be substituted with another feature that does not require heartbeat classification.
- Dependence between two criteria that are related to the statistical distribution of the P-wave amplitudes, i.e., <StdAmpP, MaxAmpP> with degree of agreement µ = 0.866. Here again the increase/decrease of MaxAmpP normally leads to increase/decrease of P-wave amplitude range and consecutively to increase/decrease of StdAmpP. Based on these observations, the calculation of StdAmpP, which is obtained by more complicated processing procedures compared to MaxAmpP, could be avoided.
- Dependence between the statistical criteria describing the deviation between the samples of all PQRST segments in one ECG recording and the corresponding samples of the PQRST first PCA vector, i.e., <MeanStdPQRST, MinStdPQRST>, <MeanStdPQRST, MaxStdPQRST>, <MaxStdPQRST, RangeStdPQRST>, with degree of agreement µ in the range from 0.920 to 0.866. Expectedly, the changes in the minimal, maximal values of the assessed standard deviation, which define also its range, are in agreement with the change of the mean value of this standard deviation. It is a user’s choice to exclude MinStdPQRST and MaxStdPQRST or MinStdPQRST and RangeStdPQRST from the ECG criteria set, taking into consideration all other observed relations.
3.3. ECG Criteria Showing a High Degree of Disagreement
As seen from Figure 5, there is a relatively small number of pairs with degree of disagreement ν greater than 0.75 (red circles in the upper left corner of the intuitionistic fuzzy triangle). Thus, we consider as more appropriate to apply ICrA with the thresholds of α = 0.70 and β = 0.30. In such case, fifteen ECG criteria pairs present a high degree of disagreement ν (red circles in Figure 7).

Figure 7.
Fifteen criteria pairs that show a high degree of disagreement ν > 0.7, illustrated with red circles.
These 15 ECG criteria pairs could be grouped as follows:
- Inverse relation between the regularity index, which quantifies the sharpness of the dominant peak in the spectra of the TQ segment on one hand, and the spectral width or area at certain levels, on the other, which lead to a high degree of disagreement ν in the range from 0.790 to 0.702, and degree of agreement µ respectively between 0.197 and 0.292 for the pairs: <MeanSpecWidth_02, MeanRI>, <MeanSpecArea_02, MeanRI>, <MeanSpecWidth_04, MeanRI>, <MaxSpecArea_02, MinRI>, <MaxSpecArea_04, MinRI>, <MaxSpecWidth_02, MinRI>, <MaxSpecWidth_04, MinRI>, <MeanSpecArea_04, MeanRI>, <MaxSpecArea_06, MinRI>. This observation is logical considering that the sharper the dominant peak is, the narrower is the spectrum and the lower is its area. On the other hand, the above listed dependencies provide evidence for possible reduction of the feature space by keeping only MinRI and MeanRI that appear in all criteria pairs.
- Inverse relation between the minimal amplitude of the ventricular beats and in particular the normal beats, and the standard deviation of these amplitudes, i.e., <StdAmpVB, MinAmpVB>, <StdAmpVB, MinAmpN>, <StdAmpN, MinAmpVB>, <StdAmpN, MinAmpN>, with degree of disagreement ν in the range from 0.777 to 0.716 and degree of agreement µ between 0.222 and 0.284. This is again a logical relation considering that in case of constant maximal amplitude the decrease of the minimal amplitude increases the standard deviation of the observed amplitudes. It is an object of deeper analysis whether to keep the criteria related to the amplitudes of the normal beats at the cost of preliminary heartbeat classification, or to relay on criteria based on the computation of standard deviation.
- Inverse relation between the minimal amplitude of the P-waves and the standard deviation of these amplitudes, i.e., <StdAmpP, MinAmpP>, with degree of disagreement ν = 0.767 and degree of agreement µ = 0.232. The explanation is the same as the one provided above concerning the amplitudes of the ventricular beats. The observed strong negative consonance within this criteria pair suggests the exclusion of StdAmpP from the ECG criteria set.
- Inverse relation between the minimal amplitude of the ventricular beats and the range of the deviation between the samples of all PQRST segments in one ECG recording and the corresponding samples of the PQRST first PCA vector, i.e., <MinAmpVB, RangeStdPQRST>, with degree of disagreement ν = 0.711 and degree of agreement µ = 0.289. Although logical, the inverse relation between these two criteria is not obvious at first glance. Revealing such not evident relations could be extremely useful, since it could give a hint for the reduction of criteria related to the application of complex signal processing procedures, which is the case of RangeStdPQRST.
An interesting and very useful observation is the existence of a relatively high degree of disagreement between the criteria related to TQ segment complexity (C) and the mean period measured for individual TQ segments (MeanT_TQ). The dissonance (ν = 0.682, µ = 0.297) for the criteria pair <C, MeanT_TQ > is very close to the strong dissonance, which suggests that C related to ECG signal transformation and consequent complicated computations, could be excluded from the feature set without considerable loss of information. This result also suggests that a criterion analogical to MeanT_TQ but calculated for the RR intervals in the ECG (such criterion is not present in the current feature set) could be an alternative of C_ECG, which is also difficult to calculate.
3.4. ECG Criteria Showing Almost Equal Values of Degrees of Agreement and Disagreement
A total of 953 pairs show values of the degree of agreement µ and degree of disagreement ν in the range from 0.45 to 0.55, presenting the criteria as pairs of dissonance in terms of ICrA. Extremely close to 0.5 degrees of agreement/disagreement with values between 0.49 and 0.51 are observed for 98 of these criteria pairs (Figure 8).
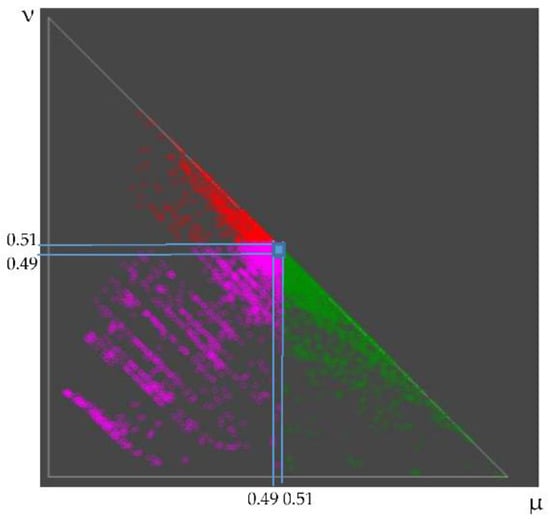
Figure 8.
Ninety-eight criteria pairs that show almost equal values of degrees of agreement and disagreement—illustrated with the blue square.
These 98 criteria pairs could be grouped as follows:
- Forty-six pairs which include criteria related to the QRS and P-waves amplitudes vs. criteria describing the TQ segment in the frequency domain. The dissonance of these criteria is expected, considering that they represent amplitude and spectral ECG characteristics.
- Eight pairs which include criteria reflecting the RR and PP intervals vs. criteria describing the TQ segment in the frequency domain. Neither agreement nor disagreement is expected between these criteria.
- Nine pairs which include amplitudes vs. intervals within the analyzed ECG. No dependencies between these criteria are expected.
- Twelve pairs which include time domain TQ parameters vs. predominantly QRS amplitudes and intervals (11 pairs) and P-wave amplitudes (1 pair). The QRS complex is out of the TQ interval, therefore, the lack of relation between the features that describe them is normal. Considering the fact that the P-waves appear within the TQ interval, the dissonance of these criteria is not so obvious.
- Thirteen pairs which include criteria describing the TQ segment in the time and frequency domains vs. criteria for assessment of PQRST beat-to-beat irregularity. Considering the negligible overlap between the TQ and the PQRST segments, no dependencies between the criteria measured for each of them are expected.
- Three pairs, which include statistical measures over the RR interval vs. criteria describing the PQRST beat-to-beat irregularity. Neither agreement nor disagreement within these pairs is expected.
- Three pairs, which include frequency vs. time domain descriptors of the TQ segment. The lack of agreement between these criteria is expected.
- A pair <MeanAmpN, MaxAmpP>, which shows no dependence between the mean amplitude of the normal QRS complexes within the analyzed ECG interval and the maximal amplitude of the P-waves. A relation between these two criteria is not expected.
- A pair <MaxSpecArea_06, MaxRI>, which shows no dependence between the maximal spectral area on 0.6 level and the maximal regularity index that quantifies the sharpness of the dominant peak. Considering that these are statistical values that normally are not calculated for one and the same TQ segment (for more details see the explanations related to the features calculations in [27]) the observation of such lack of dependence is normal.
- Two pairs <MinAmpVB, MaxAmpVB> and <MeanAmpP, MinAmpP> that show lack of dependence between minimal and maximal amplitudes of the ventricular beats, as well as mean and minimal P-wave amplitude. The observations within these two criteria pairs are not so obvious.
In all presented so far analyses directed towards intercriteria relations, no special attention has been paid on the degree of uncertainty. As can be seen from Figure 5, Figure 6, Figure 7 and Figure 8, it is obvious that there is a great number of criteria pairs with lower (closer to the hypotenuse of the intuitionistic fuzzy triangle) or with higher (closer to the right angle of the intuitionistic fuzzy triangle) degree of uncertainty. There is a logical explanation of this fact, namely that among the huge amount of considered here 3828 pairs of criteria, there are a lot with equal evaluations, which appear as points in the interior of the triangle. It is possible for the user to choose other than µ-biased algorithm for rendering the results with equal evaluations.
4. Discussion
Developed as a tool to assist in decision-making, ICrA has found applications in various fields, including petrochemical industries [13], ecology [19,20], artificial intelligence [10,12,14,15], education [16,17,18], biomedicine and quality of life [21,22,23,24,25], etc. All these studies, however, are conducted over as few as 4 to 36 criteria calculated for limited number of cases (up to 1050 in [22]).
This study presents a novel ICrA application for assessment of the dependencies within a set of ECG criteria measured over more than 8500 ECG signal strips. It answers the following questions:
Is ICrA applicable for derivation of reliable intercriteria relations over a large set of ECG criteria calculated for large population?
The high degree of agreement µ observed for 29 criteria pairs (Section 3.1 and Section 3.2) is suggested by the way of their calculation. They appear for criteria from one and the same group, i.e., descriptors of the TQ-segment in the time domain (Group 4), as well as in the frequency domain (Group 5); amplitudes of the ventricular beats (subgroup in Group 1), as well as RR intervals between the ventricular beats within the analyzed ECG segment (another subgroup in Group 1); descriptors of the P-wave amplitudes statistical distribution (subgroup in Group 2); criteria describing the deviation between the samples of all PQRST segments in one ECG recording and the corresponding samples of the PQRST first PCA vector (subgroup of Group 3). The observed high degree of agreement within these groups and subgroups is expected and confirms the correctness of the positive consonance derived via ICrA.
Among the 15 criteria pairs for which high degree of disagreement ν is observed (Section 3.3), 14 pairs include criteria from one and the same group that are inversely proportional by their way of calculation, i.e., regularity index vs. spectral width or area (Group 5); minimal amplitude vs. standard deviation calculated for the ventricular beats (Group 1) and P-waves (Group 2). The observed high degree of disagreement for these 14 criteria pairs is expected and confirms the correctness of the negative consonance derived via ICrA.
An almost equal values of degrees of agreement µ and disagreement ν are observed for 98 criteria pairs, for 95 of which neither agreement nor disagreement is expected. The criteria involved in these 95 pairs are from different groups, i.e., QRS and P-waves amplitudes, as well as RR and PP intervals (all these from Group 1 and Group 2) vs. criteria describing the TQ-segment in the frequency domain (Group 5); the subgroup of amplitudes in Groups 1 and 2 vs. the subgroup of intervals in the same groups; criteria describing the TQ-segment in the time and frequency domains (Group 4 and Group 5), as well as statistical measures over the RR interval (subgroup in Group 1) vs. criteria for assessment of PQRST beat-to-beat irregularity (PQRST subgroup in Group 3); frequency (Group 5) vs. time domain (Group 4) descriptors of the TQ segment; QRS amplitudes (Group 1) vs. P-wave amplitudes (Group 2). The observed lack of dependencies for these 95 criteria pairs is expected and confirms the ability of ICrA to highlight such criteria.
The observed agreement between the highlighted by ICrA criteria pairs with high degrees of agreement/disagreement and our expectations based on the knowledge for the principles involved in the computation of the estimated ECG criteria validates the application of ICrA for reliable evaluation of the dependencies between different criteria.
Is ICrA able to reveal dependencies or lack of dependencies between criteria that are not obvious and could be applied for arrhythmia detection purposes?
Although logical, the inverse relation (negative consonance in terms of ICrA) between the minimal amplitude of the ventricular beats and the range of the PQRST segments deviation from the first PQRST PCA vector is not obvious at first glance. The application of ICrA has highlighted the high degree of disagreement between these two criteria, thus giving a hint that the QRS amplitude significantly influences the range of the PQRST segments deviation and in a low resources computational system the criteria related with calculation of the first PRQST PCA vector could be skipped, since they seem to be more influenced by the QRS amplitude than by the arrhythmia type.
ICrA also has highlighted the not obvious lack of dependencies within 3 out of 98 criteria pairs—i.e., neither agreement, nor disagreement has been observed between P-wave amplitudes vs. time domain TQ parameters; minimal vs. maximal amplitudes of the ventricular beats, as well as mean vs. minimal P-wave amplitude. This reveals the usefulness of each one of these criteria for arrhythmia detection and prevents the discarding of some of them in criteria set dedicated to arrhythmia recognition purposes.
Obviously, ICrA is able to reveal not obvious dependencies or lack of dependencies between criteria, thus facilitating the process of criteria pre-selection before the training of an arrhythmia classifier.
5. Conclusions
This study presents the application of ICrA over a large set of ECG criteria extracted for arrhythmia classification over a large population. The ICrA application has been validated in terms of correctness of the observed intercriteria relations, as well as hints at its potential use for derivation of useful relations between ECG criteria that could be applied in the ECG pre-processing stage for criteria pre-selection. The obtained results suggest that the intercriteria analysis could facilitate for optimization of the feature space together with minimization of the computations’ complexity related to criteria calculations.
As a future step, we plan to apply the intercriteria analysis within a homogenous arrhythmia groups and to analyze the observed consonances and dissonances. The idea is to search for criteria pairs that show different behavior for the different arrhythmia groups and thus could be valuable for arrhythmia classification. At this stage of our knowledge, we could only speculate that such differences are more expectable for the criteria pairs that show strong consonance, which could not be explained by the principles involved in their computation. The derivation of more detailed conclusions based on comparative analysis between groups, as well as on the results of the current study, could appear to be useful for ECG analysis in terms of arrhythmia classification.
Author Contributions
Conceptualization, I.J. and T.P.; methodology, I.J., P.V., T.P. and T.S.; software, I.J., P.V., and T.S.; validation, I.J. and T.P.; formal analysis, I.J. and T.P.; investigation, I.J., P.V. and T.P.; resources, I.J., P.V., T.P. and T.S.; data curation, I.J. and T.S.; writing—original draft preparation, I.J., P.V. and T.P.; writing—review and editing, I.J., P.V., T.P. and T.S.; visualization, I.J. and T.P.; supervision, T.P.; project administration, I.J. and T.P.; funding acquisition, I.J. and T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bulgarian National Science Fund, grant numbers DN 17/06 “A New Approach, Based on an Intercriteria Data Analysis, to Support Decision Making in in silico Studies of Complex Biomolecular Systems” and KП-06-H42/3 “Computer aided diagnosis of cardiac arrhythmias based on machine learning and deep neural networks”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The ECG signals from the training part of the PhysioNet/CinC Challenge 2017 database are available at: https://archive.physionet.org/physiobank/database/challenge/2017/training/ (accessed on 5 March 2021). The Matlab code for criteria calculation is available at: https://physionet.org/content/challenge-2017/1.0.0/sources/irena-jekova-204.zip (accessed on 5 March 2021).
Acknowledgments
The authors express their thanks to Nikolay Ikonomov, for the necessary improvements made in ICrAData software (v.2.3) in order to meet the specificity of the subject of this investigation, namely the great number of considered criteria.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atanassov, K.; Mavrov, D.; Atanassova, V. Intercriteria Decision making: A new approach for multicriteria decision making, based on index matrices and intuitionistic fuzzy sets. Issues IFSs GNs 2014, 11, 1–8. [Google Scholar]
- Atanassov, K.; Atanassova, V.; Gluhchev, G. Intercriteria analysis: Ideas and problems. Notes Intuit. Fuzzy Sets 2015, 21, 81–88. [Google Scholar]
- Atanassov, K. Generalized index matrices. Compt. Rend. Acad. Bulg. Sci. 1987, 40, 15–18. [Google Scholar]
- Atanassov, K. Index Matrices: Towards an Augmented Matrix Calculus; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Int. J. Bioautom. 2016, 20, S1–S6. [Google Scholar]
- Atanassov, K. On Intuitionistic Fuzzy Sets Theory; Springer: Cham, Switzerland, 2012. [Google Scholar]
- Atanassov, K. Intuitionistic Fuzzy Logics; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Atanassova, V. Interpretation in the intuitionistic fuzzy triangle of the results, obtained by the intercriteria analysis. In Proceedings of the 2015 Conference of the International Fuzzy Systems Association and the European Society for Fuzzy Logic and Technology (IFSA-EUSFLAT-15), Gijón, Spain, 30 June 2015; Atlantis Press: Paris, France, 2015; pp. 1369–1374. [Google Scholar]
- Doukovska, L.; Atanassova, V.; Sotirova, E.; Vardeva, I.; Radeva, I. Defining consonance thresholds in intercriteria analysis: An overview. Stud. Comput. Intell. 2019, 757, 161–179. [Google Scholar]
- Pencheva, T.; Roeva, O.; Angelova, M. Investigation of genetic algorithm performance based on different algorithms for intercriteria relations calculation. Lect. Notes Comput. Sci. 2018, 10665, 390–398. [Google Scholar]
- Vassilev, P.; Ribagin, S.; Todorova, L. On an aggregation of expert value assignments using index matrices. Notes Intuit. Fuzzy Sets 2017, 23, 75–78. [Google Scholar]
- Roeva, O.; Pencheva, T.; Angelova, M.; Vassilev, P. Intercriteria analysis by pairs and triples of genetic algorithms application for models identification. Stud. Comput. Intell. 2016, 655, 193–218. [Google Scholar]
- Stratiev, D.; Sotirov, S.; Shishkova, I.; Nedelchev, A.; Sharafutdinov, I.; Vely, A.; Mitkova, M.; Yordanov, D.; Sotirova, E.; Atanassova, V.; et al. Investigation of relationships between bulk properties and fraction properties of crude oils by application of the intercriteria analysis. Pet. Sci. Technol. 2016, 34, 1113–1120. [Google Scholar] [CrossRef]
- Sotirov, S.; Atanassova, V.; Sotirova, E.; Doukovska, L.; Bureva, V.; Mavrov, D.; Tomov, J. Application of the intuitionistic fuzzy intercriteria analysis method with triples to a neural network preprocessing procedure. Comput. Intell. Neurosci. 2017, 2017, 2157852. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S. Comparison of different metaheuristic algorithms based on intercriteria analysis. J. Comput. Appl. Math. 2018, 340, 615–628. [Google Scholar] [CrossRef]
- Krawczak, M.; Bureva, V.; Sotirova, E.; Szmidt, E. Application of the intercriteria decision making method to universities ranking. Adv. Intell. Syst. Comput. 2016, 401, 365–372. [Google Scholar]
- Bureva, V.; Michalíková, A.; Sotirova, E.; Popov, S.; Riečan, B.; Roeva, O. Application of the intercriteria analysis to the universities rankings system in the Slovak Republic. Notes Intuit. Fuzzy Sets 2017, 23, 128–140. [Google Scholar]
- Parvathi, R.; Atanassova, V.; Doukovska, L.; Yuvapriya, C.; Indhurekha, K. Inter-criteria analysis of rankings of Indian universities. Notes Intuit. Fuzzy Sets 2018, 24, 99–109. [Google Scholar] [CrossRef]
- Ilkova, T.; Petrov, M. Application of intercriteria analysis to the Mesta river pollution modelling. Notes Intuit. Fuzzy Sets 2015, 21, 118–125. [Google Scholar]
- Georgieva, V.; Angelova, N.; Roeva, O.; Pencheva, T. Intercriteria analysis of wastewater treatment quality. J. Int. Sci. Publ. Ecol. Saf. 2016, 10, 365–376. [Google Scholar]
- Tsakovska, I.; Alov, P.; Ikonomov, N.; Atanassova, V.; Vassilev, P.; Roeva, O.; Jereva, D.; Atanassov, K.; Pajeva, I.; Pencheva, T. Intercriteria analysis implementation for exploration of the performance of various docking scoring functions. Stud. Comput. Intell. 2021, 902, 88–98. [Google Scholar]
- Vankova, D.; Sotirova, E.; Bureva, V. An application of the intercriteria analysis approach to health-related quality of life. Notes Intuit. Fuzzy Sets 2015, 21, 40–48. [Google Scholar]
- Todinova, S.; Mavrov, D.; Krumova, S.; Marinov, P.; Atanassova, V.; Atanassov, K.; Taneva, S.G. Blood plasma thermograms dataset analysis by means of intercriteria and correlation analyses for the case of colorectal cancer. Int. J. Bioautom. 2016, 20, 115–124. [Google Scholar]
- Krumova, S.; Todinova, S.; Mavrov, D.; Marinov, P.; Atanassova, V.; Atanassov, K.; Taneva, S. Intercriteria analysis of calorimetric data of blood serum proteome. Biochim. Et Biophys. Acta Gen. Subj. 2017, 1861, 409–417. [Google Scholar] [CrossRef]
- Zaharieva, B.; Doukovska, L.; Ribagin, S.; Radeva, I. Intercriteria analysis of data obtained from patients with Behterev’s disease. Int. J. Bioautom. 2020, 24, 5–14. [Google Scholar] [CrossRef]
- Clifford, G.; Liu, C.; Moody, B.; Lehman, L.W.; Silva, I.; Li, Q.; Johnson, A.E.; Mark, R.G. AF Classification from a short single lead ECG recording: The Physionet Computing in Cardiology Challenge 2017. Comput. Cardiol. 2017, 44. [Google Scholar] [CrossRef]
- Jekova, I.; Bortolan, G.; Stoyanov, T.; Dotsinsky, I. Multi-type arrhythmia classification: Assessment of the potential of time and frequency domain features and different classifiers. Int. J. Bioautom. 2020, 24, 153–172. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Hošková-Mayerová, S.; Maturo, A. Decision-making process using hyperstructures and fuzzy structures in social sciences. Stud. Fuzziness Soft Comput. 2018, 357, 103–111. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. An application of intuitionistic fuzzy set similarity measures to a multi-criteria decision making problem. Lect. Notes Comput. Sci. 2006, 4029, 314–323. [Google Scholar] [CrossRef]
- Michalíková, A.; Riečan, B. On invariant measures on intuitionistic fuzzy sets. Adv. Fuzzy Log. Technol. 2017, 529–534. [Google Scholar] [CrossRef]
- Michalíková, A. The differential calculus on IF sets. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1393–1395. [Google Scholar]
- Atanassov, K.; Szmidt, E.; Kacprzyk, J. On intuitionistic fuzzy pairs. Notes Intuit. Fuzzy Sets 2013, 19, 1–13. [Google Scholar]
- Angelova, N.; Atanassov, K.; Riečan, B. Intercriteria analysis of the intuitionistic fuzzy implication properties. Notes Intuit. Fuzzy Sets 2015, 21, 20–23. [Google Scholar]
- Ikonomov, N.; Vassilev, P.; Roeva, O. ICrAData—software for intercriteria analysis. Int. J. Bioautom. 2018, 22, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).