Abstract
In the study presented here, fuzzy logic was used to analyze the behavior of a model of economic dynamics that assumes income to be in equilibrium when it is composed of consumption and investment, that is, when savings and investment are equal. The study considered that consumption and savings depend on the income of the previous period through uncertain factors, and, at the same time, that investment is an uncertain magnitude across various periods, represented as a fuzzy number with a known membership function. Under these conditions, the model determines the factor of income growth and investments required to maintain equilibrium, as well as the uncertain values of income for the different periods, expressed through fuzzy numbers. The study also analyzes the conditions for their convergence and the fuzzy value that income represents in equilibrium.
1. Introduction
A theoretical mathematical model provides us with certain hypotheses about the causal interrelationship between different magnitudes and the sequence in which they react [1]. At least three questions should always be taken into consideration when creating a model. First, given the complexity of reality, a decision must always be made regarding the choice of variables, either by reasoning why they are considered essential to the model [2,3] or through statistical studies, using a data set to look for variables that can be deleted [4]. Second, there is the decision of what kind of relationship the model should represent between the variables [5,6,7]. The choice of relationships is made while waiting for the model to be able to predict behaviors or quantify aspects of the system in question. Finally, the third decision that must be made when working with a model is to determine the degree of uncertainty to work with [8,9,10]. It should be borne in mind that determining the values of most of the parameters involved in the model always represents a problem since the values are not actually known with any precision. Generally, when models are used to estimate values and make future predictions, the parameters are assigned accurate values usually obtained from estimates based on past data. Thus, in an economic model, for example, if the marginal propensity to consume is estimated to be between 0.7 and 0.8, a mean can be taken as an intermediate value to perform the calculations and predict future trends. However, this means taking an uncertain magnitude as definite in the models, resulting in a loss of information due to all possible cases not being processed. Thanks to the theory of possibility [11], fuzzy sets theory [12] offers a new way of preserving the inaccuracy of economic phenomena [13,14,15]. By assigning a possibility distribution to a magnitude that is not known with certainty, it is possible to obtain a better adaptation to economic reality [16,17,18] since the obtained prediction contemplates and provides more information, given that it will take all information into account when applying the model to ultimately provide possible values for the resulting variables, with a degree of possibility for each. In short, the process consists of considering known possibility distributions for the values of the uncertain magnitudes and determining the corresponding distribution for the variables to be predicted.
This paper presents a dynamic model of income growth in which the parameters linking the variables are considered to be uncertain values, expressed using fuzzy numbers. The aim is to demonstrate a way of incorporating uncertainty into the analysis of the model and show how the prediction process is affected when behavior is studied globally for all the possible values of the uncertain parameters to be taken into account, each with their own degree of possibility. To this end, after this introduction, which comprises Section 1 of the article, we have divided the main body of the work into several distinct sections. Section 2 presents a summary of the need to model economic phenomena by establishing relationships among variables and of the proposed advantages of incorporating uncertainty using fuzzy logic. In Section 3, we discuss some relevant concepts about fuzzy equalities and fuzzy equations, with the inputs used to create the proposed new model. The dynamic model for determining income using fuzzy parameters is presented in Section 4, and Section 5 provides a numerical example of the model’s application. Finally, in Section 6, the study is completed with conclusions and references. This section also includes some limitations of the study and possible areas for further analysis.
2. Fuzzy Modeling in Economic Theory
Economic theory studies how the economic system works as a whole and tries to explain the relationships among an economy’s components, taking into account all the economic facts. Taking this into consideration, we can say that one of the main objectives of economic theory is to analyze past situations to explain their causes. Studying it, therefore, helps establish possible models that partially explain economic reality. A second main objective of economic theory is to make predictions, usually in the short and medium terms, about the evolution of certain economic variables such as national income, investment, and consumption, etc.
The fuzzy logic methodology does not appear to be a suitable tool for achieving the first of these objectives. However, for the second objective, that of making predictions, considering uncertain parameters in order to establish a better fit with reality in chosen models may be useful. It is not a question of creating inaccuracy but of taking into account the variability of the models’ parameters to obtain information, and, as a consequence, more accuracy in future predictions.
Thus, the use of fuzzy logic [12] and, more particularly, fuzzy arithmetic [19], should allow scholars of economic theory to approach growth models from this perspective, using classical calculations and the results of the arithmetic of fuzzy numbers [20,21,22], together with the various methods of solving fuzzy equations discussed in Section 3. In this vein, some early studies [23,24,25] laid the foundations for incorporating fuzzy logic into the formulation of economic models, emphasizing the fact that uncertainty is inherent in economic reality. Knowing the precise values of macroeconomic magnitudes is almost impossible, and if these are to be used to make predictions, it is important to perform calculations that take into account all of their ambiguity. For this reason, in Section 4, we will analyze a simplified dynamic model—which therefore has limitations that distance it from economic reality—in order to illustrate how we can apply the operational techniques of fuzzy logic to the model, determining the membership function of each fuzzy variable and thus ascribing a possibility distribution to the various feasible values of the variable. Using this methodology, we pave the way for future applications in more complex models.
To analyze this further, we decided to study the behavior of a dynamic model of economic theory in which we considered the parameters linking the variables to be uncertain values, expressed through fuzzy numbers. The model has a simple formulation, and we analyzed it with the primary goal of showing how fuzzy logic can be incorporated into the analysis of this model. The originality of the approach lies in it being able to observe how the prediction process is affected when studying the behavior of income for all possible values of the uncertain parameters being taken into account, each with its corresponding degree of possibility. In short, the process is based on considering some possibility distributions for the values of uncertain magnitudes and determining the corresponding possibility distribution for equilibrium income.
By assigning a possibility distribution to a magnitude that is not precisely known, we achieve a better fit to economic reality [8]. Predictions made in this way will also be more accurate because all the information is taken into account in the application of the model. Traditionally, in the practical application of economic models, the values of many of the parameters involved are not known with any precision. To resolve this, when using economic models to make future predictions, parameters are assigned an exact value obtained from estimates based on past data. Indefinite values become definite, and information is lost. In contrast with this, our approach contemplates keeping all the information and incorporating it into the model. We achieve this by representing uncertain magnitudes through fuzzy numbers, which, in reality, will have to be estimated with their uncertainty load via expert systems. To this end, we incorporate uncertainty into the model and use fuzzy arithmetic techniques, thereby keeping the possible imprecision of the estimated variables within the model and not losing information when we apply the model to make predictions. Thus, with a unified treatment that does not unduly complicate the calculations, we manage to take into account the consequences of both optimistic and pessimistic estimates, allowing us to obtain, in one operation, all the possible values of income for the equilibrium, each with their respective degree of possibility. In this way, all the information that can be extracted is incorporated in the same formulation, thus achieving a very complete treatment of the model. At the same time, an analysis of the sensitivity of the model is performed in the same operation, because the variations of the parameters are taken into account.
The aim of the proposed fuzzy model of income formation is therefore to observe and interpret the strength of the use of fuzzy logic within the framework of economic theory applied to a dynamic case of income growth. This has been performed previously in static cases and will also have to be carried out in the future with complex models that take into account a greater number of variables and relationships influencing income formation. However, with the approach proposed in this paper, we introduce a way of thinking and of drawing conclusions that employs fuzzy logic to accommodate estimates about the future, based on expert opinion, that are not foreseen by past data but can be contemplated from economic conjectures and expectations anticipated by expert systems.
Contrary to more traditional approaches, many models are based on a theoretical scheme that represents the functioning of the economic system based on a set of relationships among variables linked by parameters with values obtained from past estimates. If we use this approach exclusively, models become a purely deterministic historical construction that cannot be applied to economic (social) science since they reflect the way of thinking at the time of their construction. This way of making estimates from probability distributions constructed exclusively from past data is often contradicted by economic reality, which is always changing due to factors that are very often not taken into consideration. This is why we propose the model presented in Section 4, which includes all the uncertainty load that variables may have, dictated by past behavior and by present actions and future forecasts that change reality.
3. Fuzzy Equalities and Fuzzy Equations
The following definitions, notes, and properties are provided in an attempt to clarify the concept of fuzzy equalities and fuzzy equations while establishing the terminology used in the present work.
We take as given the reader’s familiarity with the theory of fuzzy subsets, the concept of fuzzy number, the theorem of representation through α-cuts, the main operations that can be performed with them (sum, pseudo-opposed, difference, product, pseudo-inverse, quotient, product of a scalar number, minimum and maximum), the extension principle of operations or composition laws, initially introduced by Zadeh [26] and subsequently modified by other authors [27,28,29,30], and the main theorems that allow the compatibility of operations through the employment of corresponding α-cuts [31,32,33]. Study [3] can be consulted as a practical summary of arithmetic with fuzzy numbers. We will use these operations and the following definitions, where we will apply fuzzy logic to the economic model analyzed.
Definition 1.
A fuzzy equation is an equation in which there are coefficients or variables that are expressed through fuzzy numbers and, more generally, through fuzzy subsets of R. In general, we will write a fuzzy equation as follows:
whereandare fuzzy numbers or, more generally, fuzzy subsets of R (which we usually call fuzzy coefficients) andare the unknowns, which we call fuzzy variables. F(a1,a2,...,an,x1,x2,...,xn) is an implicit function of several variables associated with the fuzzy equation.
Note 1: Without loss of generality, but in order to facilitate notation, we will consider fuzzy equations with a single unknown in the following form:
which has associated as a crisp equation,
We must consider that the parameters a and b from Equation (3) are values of uncertain quantification that can take several possible values expressed through respective possibility distributions, in turn, expressed from the fuzzy numbers (or more rarely of normal fuzzy subsets) and ().
Equation (2) can be understood in several ways. Depending on our interpretation of Equation (2), alternative solutions emerge.
First, we can consider that the equality of (2) expresses equality between fuzzy subsets. With this interpretation of a fuzzy equation, due to the opposite or inverse not existing in fuzzy number algebra, it makes no sense to transpose terms and apply the usual arithmetic. For example, the equation is not equivalent to the equation . While the former equation may have a solution with the interpretation we are considering, the latter does not, since the first member is a fuzzy number, whereas the second is crisp.
Following this interpretation, we know that in order for the fuzzy subsets of the two members of Equation (2) to be equal for each α level, the α-cuts of the two members must match.
Remember that if the function F is continuous with respect to a and x, by virtue of Buckley’s theorem [32], which is a consequence of the extension principle being compatible with α-cuts, then the α-cuts of the first member of Equation (2), which we will denote with Fα, are given by
and Fα = Bα ∀ α ∈ [0,1] therefore needs to be verified.
Therefore, the solution of the equation must be that fuzzy number , such that its α-cuts verify the equality Fα = Bα.
If the function F, in addition to being continuous with respect to each variable, satisfies the hypotheses of Moore’s theorem [33], we can calculate the α-cuts by directly applying the arithmetic of the confidence intervals, that is, by substituting the intervals and in the expression of the function and using the arithmetic of the intervals to determine .
Applying this system, Sánchez [34] showed that it is very common for there to be no fuzzy number as the solution of the equation, and that the conditions are very restrictive for the linear and quadratic equations to admit a solution using this interpretation.
Note 2: To overcome the difficulties presented in Note 1, Buckley and Qu [35] proposed a new interpretation of the fuzzy Equation (2) that was fully consistent with the possibility theory.
Let us consider Equation (2) .
All of the following is equally feasible for the general case of the fuzzy Equation (1), as long as the function F satisfies the assumptions of the implicit function theorem.
Buckley and Qu’s idea was to interpret Equation (2) as a family of true equations
where we assume that a takes all possible values given by the fuzzy number , and b takes all the possible values given by the fuzzy number . It is a question of finding the different values of x, each with its degree of possibility, that verify some of the Equation (4).
To do this, we observe that if we assume F to verify the hypotheses of the implicit function theorem, then we can isolate x from F(a,x) = b to obtain
thus generating the new fuzzy equation
whose solution expresses the solution in the sense interpreted by Buckley and Qu.
This allows us to understand as a binary operation between two magnitudes of uncertain quantities, which results in another uncertain quantity represented by . Thus, it is a question of studying the possibility that this magnitude takes a concrete value x while thinking that there will be several combinations of possible values of a and b such that f(a,b) = x. Each of these possible values of x satisfies one of the equations in the family (4).
Note 3: Let us now see how the solution to Equation (6) is determined in practice.
Under the hypothesis that function f is a continuous function, and by virtue of the principle of extension being compatible with the α-cuts, the α-cuts of are given by
If we consider f to be continuous and and are fuzzy numbers, then the domain of f, , is a compact of R2, and therefore, by virtue of the Weierstrass theorem, the existence of maximum and minimum of f is ensured; this results in
with
Therefore, is, in this case, a closed interval and therefore convex. Thus, is convex. Furthermore, is obviously normal since and are. In fact, since and are normal, a* and b* exist with and . Thus, the value satisfies . Therefore, the solution is a fuzzy number. Furthermore, the membership function of is expressed by applying the extension principle as follows:
It should be noted that when we apply the compatibility of the extension principle with the α-cuts, it is assumed that the uncertain magnitudes represented by and do not interact, meaning that the value taken by one of them does not condition the value taken by the other. However, it is not generally possible to calculate by directly applying the arithmetic of the intervals and substituting and in the expression for the function. In other words, if we have the binary operation and directly calculate the α-cuts by applying the arithmetic of the intervals, thus
then we do not generally verify that , although if f is monotonous with respect to the inclusion of intervals, then . Therefore, if we directly apply the arithmetic of the intervals to calculate the α-cuts of , then we will generally have wider intervals containing the solution. If the calculation of is complicated due to the behavior of the function f, we can admit as an approximation of the true result.
However, we will now highlight two common cases in which the α-cuts can be calculated easily.
(1) When is a rational function in which each variable appears once at most and is raised to the first power, then we encounter the hypotheses in Moore’s theorem [33], and therefore, . Thus, in this case, is determined from the direct calculation using the arithmetic of the confidence intervals.
(2) When is a monotonic function with respect to each of the variables, then the lower and upper limits and will obviously be reached at some of the ends of the α-cuts and , as Table 1 shows.

Table 1.
α-cuts for a monotonic function.
Note 4: We will use the Buckley and Qu [35] resolution method in our study on the behavior of the income growth model in a context of uncertainty since it has been shown to coincide with our interpretation of the values obtained for income in a fuzzy environment.
4. Fuzzy Dynamic Model for Stationary Growth
A dynamic model based on fuzzy logic that is closely related to the classic static model [3] establishes consumption as a linear function of income, although in this case, we will consider income from the previous period. This lends a dynamic character to the model since it allows us to establish a timeline for national income.
Thus, three conditions are imposed in this model for a given period t, expressed through the following three equations:
(a) A Keynesian-type consumption equation with a delay period
where Ct represents consumption in period t, and Yt−1 represents income in period t−1, and c represents the marginal propensity to consume.
(b) An equation for investment, in which we assume that this remains constant
where represents the investment in period t.
(c) Finally, the equilibrium condition imposed by savings and investment being equal, meaning that income is composed of both consumption and investment, by means of which we establish the equation
From these three conditions, we obtain the following:
establishing an equation in linear finite differences of first order, which has the following solution:
being
where indicates the initial income value.
Indeed. Starting from an initial value of income at the present time, we have
where A and B are the values in (15).
With these hypotheses, since 0 ≤ c ≤ 1, we see that a convergent trajectory of income is always obtained. However, to obtain an increasing trajectory of the income, it is necessary that , since, otherwise, the trajectory would be decreasing, which is contrary to the real situations for modeling.
If we consider that the values of the marginal propensity to consume and invest are each of a similar, but uncertain, amount in the various periods, then we can consider them as fuzzy numbers and , respectively, and consider them the same for each period, that is, as having the same membership function for each value of t, which we will represent for and , respectively.
Under these conditions, we can determine the value of income in a period t from the fuzzy equation
determining the fuzzy numbers and from the equations
Given the application of the principle of extension, we can obtain the membership functions from the expression
while
Thus, if we make , then we have
with which, after applying the extension principle again, we obtain the following result:
However, depending on the form of the functions and , the expression (20) for may not be operative, and for this reason, we then determine the expression for through its α-cuts.
If we denote the α-cuts of and for
then the α-cuts of and are
To lend the model a practical sense, in the fact of obtaining a growing trajectory for income, we impose the restriction
which allows us to ensure an increasing trajectory for income.
It should be noted that the function defining in the fuzzy Equation (16) does not verify the hypotheses of Moore’s theorem [33], in this case, meaning that if we directly apply the arithmetic of the intervals to determine the α-cuts of in a given period, we would obtain an undesired result in the sense that the interval thus obtained by a given level of presumption turns out to be wider than the true α-cut of for this level. In fact, using the arithmetic of the intervals it would be
On the other hand, if we consider that , it turns out that for a large enough value of t, regardless of the initial value of income , the partial derivatives of the function
are both positive.
Therefore, function (25) is increasing with respect to c and with respect to I. For this reason, applying Buckley and Qu’s method of solving equations, the α-cuts of are determined from the expression
It, therefore, turns out that, as the studies by Buckley and Qu [32] showed, the inclusion Ytα ⊆ Yt (α) is verified.
Let us recall that several methods exist for comparing fuzzy variables and fuzzy numbers, as analyzed by Bortolan and Degani [36], Nakamura [37], Delgado, Verdegay and Vila [38], Yuan [39], Chang and Lee [40], and Gil Aluja [41]. However, some of those based on establishing fuzzy preference relationships using the idea of possibility lead to counterintuitive results. In this case, we will use the method based on comparing the confidence intervals defined by the α-cuts from the relation
[a1,b1] ≤ [a2,b2] ⇔ a1 ≤ a2 i b1 ≤ b2.
Using this partial order relation, and due to the constraint imposed by (23) and that , then
t ≤ t’ ⇒ Ytα ≤ Yt’α.
Thus, if we define the order relation between fuzzy numbers
then income follows an increasing trajectory with respect to this order, which approximates the fuzzy number that it has for α-cuts
This would coincide with the solution obtained using the classic static version of the model [3].
We observe that by using the fuzzy treatment of the model, an increasing trajectory for income is obtained according to the order defined in (28), which approaches the fuzzy number . We can interpret this as the fuzzy number or value for equilibrium income, which is understood as the fuzzy subset that contains the possible equilibrium values for income, each with its respective degree of possibility.
Finally, note that the expressions corresponding to the particular case in which and are the triangular fuzzy number (TFN) can be obtained immediately, while the specific membership function of is also obtained, in addition to the concrete expression of its α-cuts, the latter being obtained directly if we substitute the specific expressions for the triangular fuzzy numbers in the result of expression (29), which is obtained by applying the general methodology.
5. Examples of Application
We will now use a numerical example to analyze how income increases, and how it is the expression of equilibrium income in the classical model and the new model studied.
5.1. Example 1—Crisp Case
We consider the classic model presented from conditions (11)–(13), assuming that we have the following values of the parameters:
- marginal propensity to consume c = 0.85;
- investment in each period I = 380;
- initial value to the income .
In this certain case, using (15), we have the next trajectory for the income
Obtaining these values for the trajectory of the income in the first seven periods, we achieve the following results:
Moreover, its trajectory converges as time progresses toward its equilibrium value, which is .
5.2. Example 2—Uncertain Case
Let us consider the marginal propensity to consume to be estimated via the TFN = (0.8,0.85,0.87) and the investment volume via the TFN = (350,380,400).
Although trapezoidal fuzzy numbers could be used to better approximate economic reality, we have chosen to model the uncertain values of parameters using triangular fuzzy numbers since the simple structure of triangular fuzzy numbers makes them very convenient in calculations because their membership functions are made up of linear sections, and for this reason, they are widely used to model vague predicates and uncertain magnitudes. Note that, in practice, the actual conceptualization of triangular fuzzy numbers allows them to be readily adapted to different real situations, and particularly, to estimates of economic variables made by expert systems. Thus, experts can determine the values of the two extremes, corresponding to the minimum and maximum estimates, and an intermediate value that is taken as the most likely value. In addition to a TFN’s great adaptability to the structure of human thought, it is also important to consider, as noted earlier, its great ease of use due to the simplicity of its membership function.
Furthermore, we take the initial value for income to be Y0 = 1000. In this case, the respective α-cuts of and are
Note that restriction (23) is verified with the data in the example, since
As we have seen, this constraint ensures an increasing trajectory for all possible values of income; as time increases, it approaches an equilibrium value, which we determine through a fuzzy number.
For a specific value of time t, we obtain the α-cuts of by applying (26), with which we obtain the expression
where
Thus, for example, for cases t = 1 and t = 5, we obtain Table 2 (substituting in the previous expression the value of t = 1 and t = 5, respectively, and α for the corresponding values on an hendecadarian scale of 0 to 1, resulting in the confidence intervals shown in Table 2), which gives the α-cuts of and on the hendecadarian scale.

Table 2.
α-cuts of income in the periods t = 1 and t = 5.
The value of the fuzzy number maintains a triangular structure, but it is not the case for the uncertain values of successive periods (because when t > 1 the linear structure for the extremes of the α-cuts is broken). However, if we take the triangular approximation of using the triangular fuzzy number ()T = (1504.24, 1852.98, 2041.74), then the α-cuts of the triangular approximation are as follows:
[1504.24 + 348.74 · α, 2041.74 − 188.76 · α].
If we use the hendecadarian scale, the confidence intervals for each level of the scale are the values obtained in Table 3, substituting the corresponding values of α in the previous interval that represents the cut at level α (α-cut) for the uncertain value of income in the period t = 5, as shown in the example.

Table 3.
Triangular approximation of income in the period t = 5.
By using the approximation, we obtain the following deviations:
with the result, applying the error dimensioning criterion proposed by Jiménez and Rivas [42], that
and we can therefore consider the triangular approximation ()T as very suitable since, on a hendecadarian scale, any value for the support of ()T with a certain degree of possibility on the scale has the same degree of possibility as .
Similarly, let us determine the fuzzy value of the balanced income , which, in this case, has for α-cuts
which gives rise to the following membership function:
thus completely determining all possible equilibrium values with their respective degrees of possibility.
The triangular approximations for the trajectory of the uncertain income values during the first seven periods are
Figure 1 shows the triangular approximations of the fuzzy values of income for the first seven periods, and the fuzzy value for equilibrium income, which is the fuzzy number where the values of are approximate. We also note that uncertainty increases as time t progresses, as expected, and that the values of income’s time trajectory converge towards the uncertain value of the equilibrium income, as shown through the approximation of TFN = (1750, 2533, 3076).
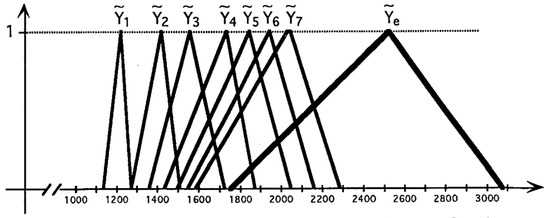
Figure 1.
Fuzzy values for income in the first seven periods.
5.3. Comparison between Fuzzy Case versus Crisp Case
If we make a comparison between the fuzzy case versus the crisp case, we observe that if we compare the result obtained with the approach of example 2 to the classic case of application in the field of certainty of example 1, the classical application becomes a particular case of the new application presented.
On the other hand, in the field of uncertainty, when the period increases, then the entropy or degree of uncertainty of the solution also increases. However, the advantage of this new approach is that we can find, from the initial distributions of possibility, the degree of possibility of each of the possible values of income, both for a given period and for each specific value for all possible income equilibrium values.
6. Conclusions
In this study, we have analyzed the behavior of the dynamic version of a classic model of economic theory by considering the factors that relate the variables of the model as uncertain and expressed via fuzzy numbers. In this way, we have obtained the expression of income and equilibrium income via a fuzzy number, which allows us to obtain, in addition to the possible equilibrium values, their respective degree of possibility. At the same time, a fuzzy expression for the multiplier is obtained by the model, that is, the multiplier becomes a fuzzy subset (in this case, a fuzzy number) with a membership function defined perfectly through the membership function of .
Analyzing the dynamic model of income formation studied here from the point of view of fuzzy logic provides for more realistic predicted results. Thus, the methodology of fuzzy subsets paves the way for the analysis of this dynamic model to have a greater degree of fit to a specific economic reality. This represents a generalization of the classic treatment since, if the parameters we have taken as fuzzy numbers take a certain value, the results obtained coincide with those obtained with the classic application.
In the dynamic model of income determination studied from the point of view of fuzzy logic, the arithmetic of the intervals is not adequate for calculating the α-cuts of income for a given period. However, if t is large enough, α-cuts can be obtained due to the monotony of the function that determines income in period t, depending on the marginal propensity to consume and investment. The membership function for the fuzzy expression of income is obtained by applying the extension principle, although the obtained expression may not be operative depending on the expression of and . In these cases, approximations of the fuzzy expression of income in a given period must be determined by means of numerical methods.
As a relevant conclusion of this study, we would state that with the constraint imposed, we have obtained an increasing time trajectory for the income , stationary in time at equilibrium, which is represented in this case by a fuzzy number , for which we have determined the membership function and expression of its α-cuts based on knowledge of the fuzzy numbers and .
Furthermore, we would add that, by simply increasing the number of fuzzy variables, the situation studied here can be used to determine the multiplier and the corresponding value for income if we incorporate the public sector and the foreign sector within the proposed model. A similar study in this regard and for the case of an explosive trajectory has been conducted by Mansur [24]. It should be noted that, in the field of uncertainty, the proposed model generalizes the classic model of dynamic income growth when the parameters involved are well-established precise numbers since the results obtained with the application of the new approach coincide with the equilibrium values that would be obtained with the classical application. In this sense, the proposed approach is an improvement because it generalizes the classical approach, and the formulation contains an analysis of the sensitivity of the model’s parameters.
Finally, as a limitation of the study, we would point out that the model we have analyzed using fuzzy logic has a simple formulation that explains how the model works but is a long way from being real. As we have stated, the aim of the example applied here was to show the operability of the model’s behavior and analyze it, and to determine the trajectory’s convergence toward a blurred value for equilibrium when the parameters that link variables are fuzzy numbers and fuzzy arithmetic is used. Future research should analyze which hypotheses are required for the stability of this model to be generally applied to new models of income behavior, and to the establishment of specific models based on uncertainty relations among variables. It may also be interesting to study the behavior of the model using approximations of nontriangular fuzzy numbers, such as trapezoidal fuzzy numbers, of the general L–R type or those based on the Agnesi or the Gaussian curves.
Author Contributions
Conceptualization and methodology, J.C.F.-C.; validation, D.C.-C. and S.L.-M.; writing, all authors; funding acquisition, J.C.F.-C. and S.L.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science, Innovation, and Universities and FEDER, grant number RTI2018-095518-B-C21.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We are very grateful for the valuable comments received by reviewers, which have allowed us to improve the quality of the article in many ways.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaldor, N. Capital accumulation and economic growth. In The Theory of Capital; Lutz, F.A., Hague, D.C., Eds.; Palgrave Macmillan: London, UK, 1961. [Google Scholar]
- Ferrer-Comalat, J.C.; Linares-Mustarós, S.; Corominas-Coll, D. A model for optimal investment project choice using fuzzy probability. Econ. Comput. Econ. Cybern. Stud. Res. 2016, 50, 187–203. [Google Scholar]
- Ferrer-Comalat, J.C.; Linares-Mustarós, S.; Corominas-Coll, D. Fuzzy logic in economic models. J. Intell. Fuzzy Syst. 2020, 38, 5333–5342. [Google Scholar] [CrossRef]
- Hair, J.F.; Anderson, R.E.; Tatham, R.; Black, W.C. Multivariate Data Analysis; Macmillan Publishing: New York, NY, USA, 1984. [Google Scholar]
- Linares-Mustarós, S.; Ferrer-Comalat, J.C.; Cassú-Serra, E. The assessment of cash flow forecasting. Kybernetes 2013, 42, 720–735. [Google Scholar] [CrossRef]
- Corominas-Coll, D.; Ferrer-Comalat, J.C.; Linares-Mustarós, S.; Bertran, X. A study of the strong Allee effect with fuzzy parameters for its application in economics. Kybernetes 2017, 46, 191–206. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Baleanu, D. On the solution of an imprecisely defined nonlinear time-fractional dynamical model of marriage. Mathematics 2019, 7, 689. [Google Scholar] [CrossRef]
- Ferrer-Comalat, J.C.; Linares-Mustarós, S.; Corominas-Coll, D. A formalization of the theory of expertons. Theoretical foundations, properties and development of software for its calculation. Fuzzy Econ. Rev. 2016, 21, 23–39. [Google Scholar] [CrossRef]
- Ferrer-Comalat, J.C.; Linares-Mustarós, S.; Corominas-Coll, D. A generalization of the theory of expertons. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26 (Suppl. 1), 121–139. [Google Scholar] [CrossRef]
- Vall-Llosera, L.; Linares-Mustarós, S.; Bikfalvi, A.; Coenders, G. A comparative assessment of graphic and 0-10 rating scales used to measure entrepreneurial competences. Axioms 2020, 9, 21. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- López, C.; Linares-Mustarós, S.; Viñas, J. Evolutionary positioning of outsourcing in the local public administration. Intang. Cap. 2019, 15, 157–170. [Google Scholar] [CrossRef]
- Linares-Mustarós, S.; Ferrer-Comalat, J.C.; Corominas-Coll, D.; Merigó, J.M. The ordered weighted average in the theory of expertons. Int. J. Intell. Syst. 2019, 34, 345–365. [Google Scholar] [CrossRef]
- Linares-Mustarós, S.; Ferrer-Comalat, J.C.; Corominas-Coll, D.; Merigó, J.M. The weighted average multiexperton. Inf. Sci. 2021, 557, 355–372. [Google Scholar] [CrossRef]
- Alfaro-Calderón, G.G.; Godinez-Reyes, N.L.; Gómez-Monge, R.; Alfaro-García, V.G.; Gil-Lafuente, A.M. Forgotten effects in the valuation of the social well-being index in Mexico’s sustainable development. Fuzzy Econ. Rev. 2019, 24, 67–81. [Google Scholar] [CrossRef]
- Flores-Romero, B.; González-Santoyo, F. Forgotten effects and their application in the development of the michoacan msmes. Fuzzy Econ. Rev. 2019, 24, 43–64. [Google Scholar] [CrossRef]
- López, C.; Linares-Mustarós, S.; Viñas, J. The use of fuzzy mathematical tools for local public services outsourcing according to typology. J. Intell. Fuzzy Syst. 2020, 38, 1–11. [Google Scholar] [CrossRef]
- Kaufmann, A.; Gupta, M.M. Introduction to Fuzzy Arithmetic: Theory and Applications; Thomson Computer Press: New York, NY, USA, 1991. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its applications to approximate reasoning—Part 1. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its applications to approximate reasoning—Part 2. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Dijkman, J.G.; Van Haeringen, H.; De Lange, S.J. Fuzzy numbers. J. Math. Anal. Appl. 1983, 92, 301–341. [Google Scholar] [CrossRef]
- Ponsard, C. Partial spatial equilibria with fuzzy constraints. J. Reg. Sci. Phila. 1982, 22, 159–175. [Google Scholar] [CrossRef]
- Mansur, Y.M. Fuzzy Sets and Economics; Edward Elgar Publishing: Aldesrshot, UK, 1995. [Google Scholar]
- Billot, A. Economic Theory of Fuzzy Equilibria; Springer: Berlin, Germany, 1992. [Google Scholar]
- Zadeh, L.A. Similarity relations and fuzzy orderings. Inf. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Fu, K.S.; Tanaka, K.; Shimura, M. Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Jain, R. Tolerance analysis using fuzzy sets. Int. J. Syst. Sci. 1976, 7, 1393–1401. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Zimmerman, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Nguyen, H.T. A note on the Extensions Principle for fuzzy sets. J. Math. Anal. Appl. 1978, 2, 369–380. [Google Scholar] [CrossRef]
- Buckley, J.J. On using α-cuts to evaluate fuzzy equations. Fuzzy Sets Syst. 1990, 38, 309–312. [Google Scholar] [CrossRef]
- Moore, R. Methods and Applications of Interval Analysis; Siam: Philadelphia, PA, USA, 1979. [Google Scholar]
- Sánchez, E. Solutions of fuzzy equations with extended operations. Fuzzy Sets Syst. 1984, 12, 237–248. [Google Scholar] [CrossRef]
- Buckley, J.J.; Qu, Y. Solving fuzzy equations: A new solution concept. Fuzzy Sets Syst. 1991, 39, 291–301. [Google Scholar] [CrossRef]
- Bortolan, G.; Degani, R. A review of some methods for ranking fuzzy subsets. Fuzzy Sets Syst. 1985, 15, 1–19. [Google Scholar] [CrossRef]
- Nakamura, K. Preference relations on a set of fuzzy utilities as a basis for decision making. Fuzzy Sets Syst. 1986, 20, 147–162. [Google Scholar] [CrossRef]
- Delgado, M.; Verdegay, J.L.; Vila, M.A. A procedure for ranking fuzzy numbers using fuzzy relations. Fuzzy Sets Syst. 1988, 26, 49–62. [Google Scholar] [CrossRef]
- Yuan, Y. Criteria for evaluating fuzzy ranking methods. Fuzzy Sets Syst. 1991, 44, 139–157. [Google Scholar] [CrossRef]
- Chang, P.T.; Lee, E.S. Fuzzy arithmetics and comparison of fuzzy numbers. In Fuzzy Optimization: Recent Advances; Delgado, M., Kacprzyk, J., Verdegay, J.L., Vila, M.A., Eds.; Physica: Berlin, Germany, 1994; pp. 69–81. [Google Scholar]
- Gil-Aluja, J. Towards a new paradigm of investment selection in uncertainty. Fuzzy Sets Syst. 1996, 84, 187–197. [Google Scholar] [CrossRef]
- Jiménez, M.; Rivas, J.A. Aproximación de números borrosos. In Proceedings of the III SIGEF Congress, Buenos Aires, Argentina, 10–13 November 1996; pp. 2–12. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).