Functional Symmetry and Statistical Depth for the Analysis of Movement Patterns in Alzheimer’s Patients
Abstract
1. Introduction
- (GDS 1)
- no cognitive impairment,
- (GDS 2)
- early cognitive impairment,
- (GDS 3)
- mild cognitive impairment,
- (GDS 4)
- mild dementia,
- (GDS 5)
- moderate dementia,
- (GDS 6)
- moderately severe dementia and
- (GDS 7)
- severe dementia.
- 7 patients in a mild stage of the disease (GDS 2 and 3),
- 18 patients in a moderate stage of the disease (GDS 4 and 5) and
- 10 patients in a severe stage of the disease (GDS 6 and 7).
2. Methodology
2.1. Symmetry
2.1.1. Difficulties with Notions of Functional Symmetry
- (i)
- X and are equal in law,
- (ii)
- for any [0, 1], the distribution of or of its derivative at is symmetric on around zero and
- (iii)
- for any reasonable notion of symmetry in multivariate spaces, any finite linear combination of the random coefficients in the Karhunen-Loève expansion [12] of the process or of its derivative process, is symmetric around the zero element.
2.1.2. Metric -Symmetry
2.2. Statistical Depth
2.2.1. Difficulties with Functional Depth Constructions
2.2.2. Metric Depth
- (i)
- A distance that makes use of the distribution with respect to which the depth is computed. In the space of continuous functions, the distance between two elements of the space can be defined through the probability of the band determined by them.
- (ii)
- A Sobolev distance that takes into account how rough the datum is with respect to the functional center of symmetry.
3. Illustration
4. Application
4.1. Functional Metric Space Construction
4.2. Tests on the Statistical Depth Values
- Compute the value of the statistic on the observed depth values
- Compute the permutations of the depth values between two groups, one with elements and the other with . There is a total ofpermutations.
- Compute the value of the statistic on each of the permutations,
- The resulting p-value for the test is
4.3. Simulation
4.4. The Data
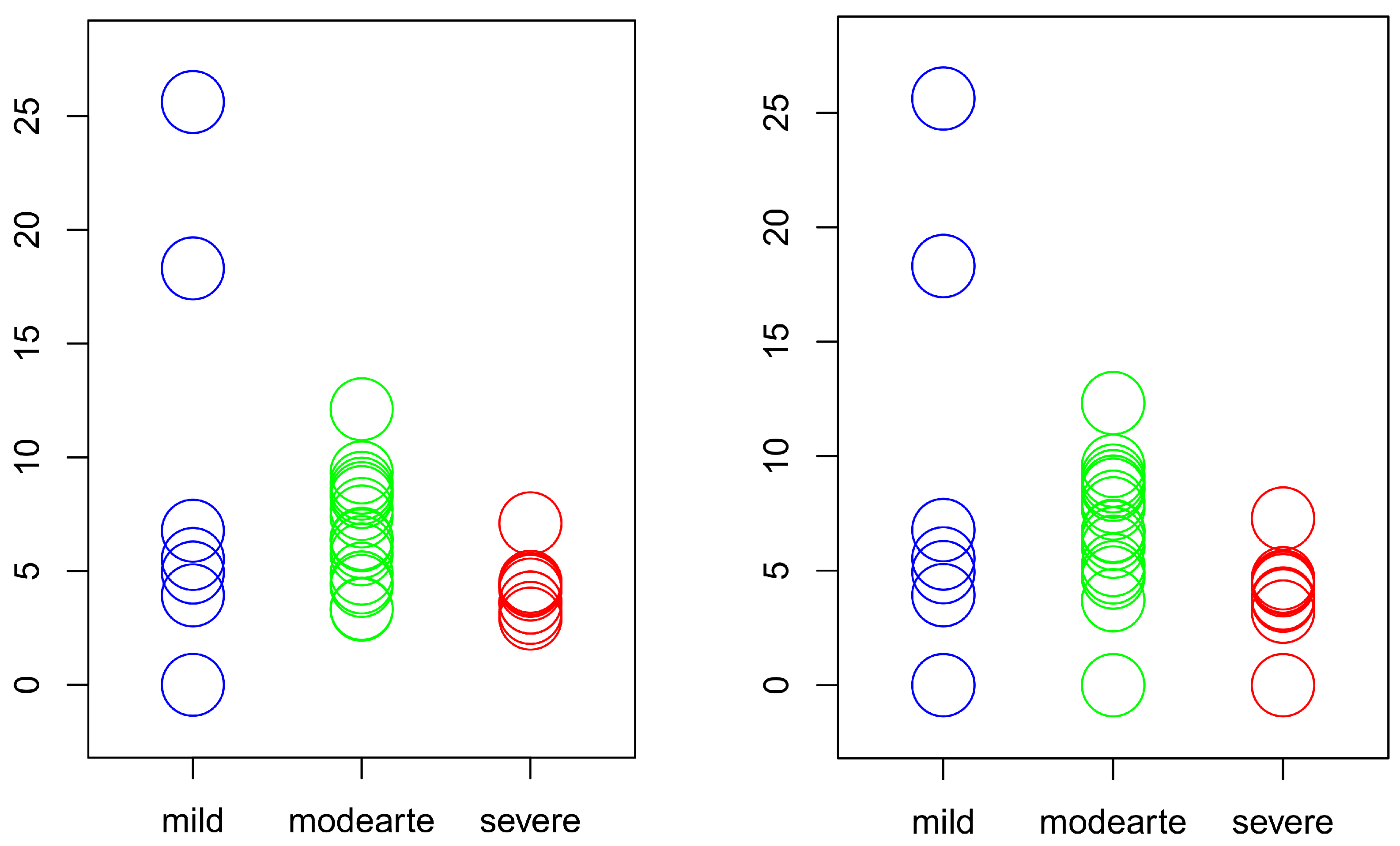
- 7 patients are in the mild stage of the disease with a total of 41 repetitions.
- 18 patients are in the moderate stage of the disease with a total of 100 repetitions.
- 10 patients are in the severe stage of the disease with a total of 46 repetitions.
| Patient | Repetitions | Disease Stage | Maximum Range | Grid Range |
|---|---|---|---|---|
| 1 | 5 | moderate | 3273.8–4149.3 | 457,352–574,918 |
| 2 | 3 | severe | 2721.6–3573.2 | 380,756–493,117 |
| 3 | 3 | mild | 3077.8–3679.8 | 426,027–508,825 |
| 4 | 6 | mild | 3168.5–3847.7 | 447,858–542,706 |
| 5 | 5 | severe | 2786.6–4109.3 | 396,699–583,914 |
| 6 | 3 | severe | 3356.4–3587.0 | 469,298–498,984 |
| 7 | 7 | severe | 2993.3–3878.0 | 426,625–545,839 |
| 8 | 8 | mild | 2610.7–3778.1 | 366,541–531,256 |
| 9 | 3 | severe | 3419.6–3633.7 | 474,456–500,270 |
| 10 | 6 | moderate | 3090.3–3952.5 | 427,229–547,061 |
| 11 | 8 | mild | 2718.5–3870.4 | 267,288–385,509 |
| 12 | 5 | moderate | 3069.8–4112.8 | 257,796–388,149 |
| 13 | 8 | moderate | 2802.8–5003.5 | 245,309–520,520 |
| 14 | 7 | severe | 3365.1–5942.7 | 327,976–560,693 |
| 15 | 7 | mild | 3590.9–4127.8 | 295,551–344,340 |
| 16 | 7 | severe | 3472.2–5452.3 | 327,583–496,692 |
| 17 | 4 | mild | 3405.0–4008.7 | 182,260–295,130 |
| 18 | 6 | moderate | 3168.1–4068.7 | 211,480–389,936 |
| 19 | 5 | mild | 3189.9–3667.0 | 298,743–339,375 |
| 20 | 7 | moderate | 2765.9–4469.5 | 259,898–354,498 |
| 21 | 5 | moderate | 3309.3–5427.6 | 322,132–521,646 |
| 22 | 4 | severe | 3465.3–5303.9 | 301,622–527,696 |
| 23 | 6 | moderate | 3040.7–6346.4 | 246,077–491,322 |
| 24 | 2 | severe | 4666.8–4666.8 | 399,909–399,909 |
| 25 | 7 | moderate | 3305.3–5076.6 | 322,957–484,066 |
| 26 | 4 | moderate | 3203.1–6108.5 | 281,369–590,537 |
| 27 | 7 | moderate | 3535.9–5345.0 | 305,482–481,180 |
| 28 | 3 | moderate | 3147.6–4033.7 | 307,455–376,297 |
| 29 | 7 | moderate | 3502.5–5807.5 | 342,543–558,649 |
| 30 | 4 | moderate | 3605.4–5908.8 | 266,367–537,241 |
| 31 | 5 | moderate | 3043.7–5991.5 | 295,878–469,712 |
| 32 | 6 | moderate | 3326.8–4494.0 | 320,243–419,402 |
| 33 | 3 | moderate | 3078.7–4753.0 | 263,053–462,177 |
| 34 | 6 | moderate | 2329.4–5002.6 | 215,536–529,828 |
| 35 | 5 | severe | 3143.6–4576.0 | 302,221–469,318 |
| Mild | Moderate | Severe | |
|---|---|---|---|
| Number of patients | 7 | 18 | 10 |
| Number of repetitions | 41 | 100 | 46 |
- In the left column panels: the five repetitions of patient 19, who is in a mild stage of the disease.
- In the central column panels: the six repetitions of patient 34, who is in a moderate stage of the disease.
- In the right column panels: the five repetitions of patient 35, who is in a severe stage of the disease.
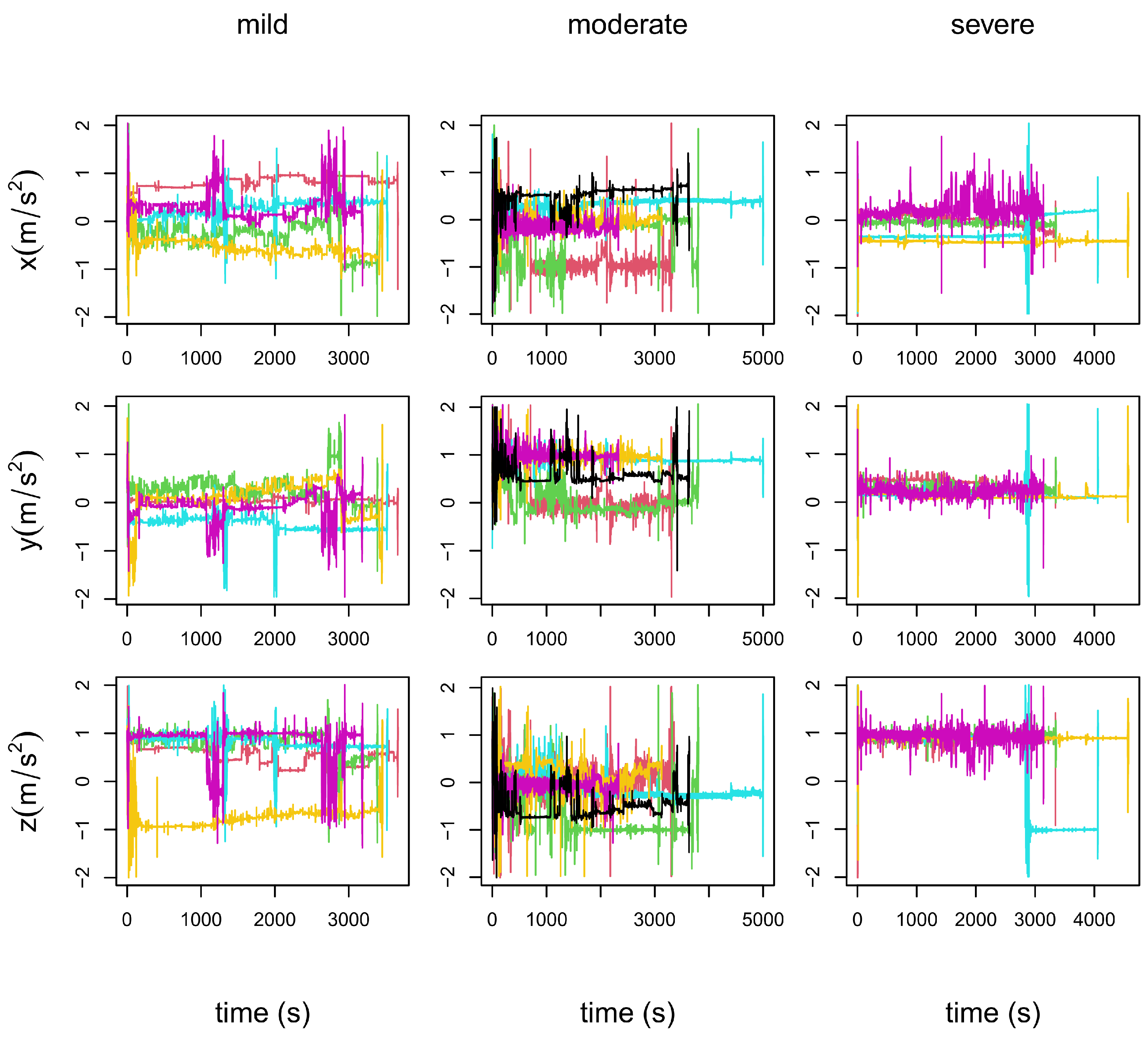
4.5. Results
| Complete Sample | ||
| Distribution | 0.0202 | 0.0027 |
| Median | 0.8090 | 0.0158 |
| Deviance | 0.0339 | 0.0030 |
| Subsamples | ||
| Distribution | 0.6672 | 0.0001 |
| Median | 0.8242 | 0.0140 |
| Deviance | 0.0320 | 0.0332 |
5. Discussion
- There are a different number of recordings for each patient.
- Each recording is over a different time domain.
- Each recording is observed over a different grid.
- The involved center of symmetry is a truly functional center of symmetry.
- It is the only existing instance of depth that satisfies the notion of statistical functional depth.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FDA | Functional Data Analysis |
| GDS | Global Deterioration Scale |
References
- Mayeux, R.; Sano, M. Treatment of Alzheimer’s disease. N. Engl. J. Med. 1999, 341, 1670–1679. [Google Scholar] [CrossRef]
- Reisberg, B.; Ferris, S.H.; de Leon, M.J.; Crook, T. The Global Deterioration Scale for assessment of primary degenerative dementia. Am. J. Psychiatry 1982, 139, 1136–1139. [Google Scholar] [PubMed]
- Bringas, S.; Salomón, S.; Duque, R.; Lage, C.; Montaña, J.L. Alzheimer’s Disease stage identification using deep learning models. J. Biomed. Inform. 2020, 109, 103514. [Google Scholar] [CrossRef] [PubMed]
- Nieto-Reyes, A.; Duque, R.; Montaña, J.L.; Lage, C. Classification of Alzheimer’s patients through ubiquitous computing. Sensors 2017, 17, 1679. [Google Scholar] [CrossRef] [PubMed]
- Park, S.Y.; Staicu, A.M. Longitudinal functional data analysis. STAT Int. Stat. Inst. 2015, 4, 212–226. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis; Springer Series in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis; Springer Series in Statistics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Zuo, Y.; Serfling, R. On the performance of some robust nonparametric location measures relative to a general notion of multivariate symmetry. J. Statist. Plann. Inference 2000, 84, 55–79. [Google Scholar] [CrossRef]
- Zuo, Y.; Serfling, R. General notions of statistical depth function. Ann. Statist. 2000, 28, 461–482. [Google Scholar] [CrossRef]
- Kallenberg, O. Probabilistic Symmetries and Invariance Principles; Probability and Its Applications; Springer: New York, NY, USA, 2005. [Google Scholar]
- Nieto-Reyes, A.; Battey, H. A topologically valid construction of depth for functional data. J. Multivar. Anal. 2021, 184, 104738. [Google Scholar] [CrossRef]
- Fukunaga, K.; Koontz, W.L.G. Application of the Karhunen-Loève Expansion to Feature Selection and Ordering. IEEE Trans. Comput. 1970, 19, 311–318. [Google Scholar] [CrossRef]
- Dudley, R.M. Uniform Central Limit Theorems; Cambridge Studies in Advanced Mathematics, Series Number 63; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hall, P. Two-sided bounds on the rate of convergence to a stable law. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1981, 57, 349–364. [Google Scholar] [CrossRef]
- Nieto-Reyes, A.; Battey, H. A topologically valid definition of depth for functional data. Stat. Sci. 2016, 31, 61–79. [Google Scholar] [CrossRef]
- Chakraborty, A.; Chaudhuri, P. On data depth in infinite dimensional spaces. Ann. Inst. Stat. 2014, 66, 303–324. [Google Scholar] [CrossRef]
- Dutta, S.; Ghosh, A.-K.; Chaudhuri, P. Some intriguing properties of Tukey’s halfspace depth. Bernoulli 2011, 17, 1420–1434. [Google Scholar] [CrossRef]
- Tukey, J. Mathematics and the picturing of data. In Proceedings of the International Congress of Mathematicians, Vancouver, BC, Canada, 21–29 August 1974; Canadian Mathematical Congress: Montreal, QC, Canada, 1975; pp. 523–531. [Google Scholar]
- Liu, R.Y. On a notion of data depth based on random simplices. Ann. Statist. 1990, 18, 405–414. [Google Scholar] [CrossRef]
- López-Pintado, S.; Romo, J. On the concept of depth for functional data. J. Amer. Statist. Assoc. 2009, 104, 718–734. [Google Scholar] [CrossRef]
- López-Pintado, S.; Romo, J. A half-region depth for functional data. Comput. Statist. Data Anal. 2011, 55, 1679–1695. [Google Scholar] [CrossRef]
- Cuevas, A.; Febrero, M.; Fraiman, R. Robust estimation and classification for functional data via projection-based depth notions. Comput. Statist. 2007, 22, 481–496. [Google Scholar] [CrossRef]
- Cuesta-Albertos, J.A.; Nieto-Reyes, A. The random Tukey depth. Comput. Statist. Data Anal. 2008, 52, 4979–4988. [Google Scholar] [CrossRef]
- Cuesta-Albertos, J.A.; Nieto-Reyes, A. Functional Classification and the Random Tukey Depth: Practical Issues. In Combining Soft Computing and Statistical Methods in Data Analysis; Borgelt, C., González-Rodríguez, G., Trutschnig, W., Lubiano, M.A., Gil, M.Á., Grzegorzewski, P., Hryniewicz, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 123–130. [Google Scholar]
- Chakraborty, A.; Chaudhuri, P. The spatial distribution in infinite dimensional spaces and related quantiles and depths. Ann. Statist. 2014, 42, 1203–1231. [Google Scholar] [CrossRef]
- Richter, S.J.; McCann, M.H. Permutation tests of scale using deviances. Commun. Stat. Simul. Comput. 2017, 46, 5553–5565. [Google Scholar] [CrossRef]
- Higgins, J.J. An Introduction to Modern Nonparametric Statistics; Brooks/Cole: Pacific Grove, CA, USA, 2003. [Google Scholar]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. Giorn. Ist. Ital. Attuar. 1933, 4, 83–91. [Google Scholar]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Ijmker, T.; Lamoth, C.J.C. Gait and cognition: The relationship between gait stability and variability with executive function in persons with and without dementia. Gait Posture 2012, 35, 126–130. [Google Scholar] [CrossRef]
- Kirste, T.; Hoffmeyer, A.; Koldrack, P.; Bauer, A.; Schubert, S.; Schroeder, S.; Teipel, S. Detecting the effect of Alzheimer’s disease on everyday motion behavior. J. Alzheimer’s Dis. 2014, 38, 121–132. [Google Scholar] [CrossRef] [PubMed]
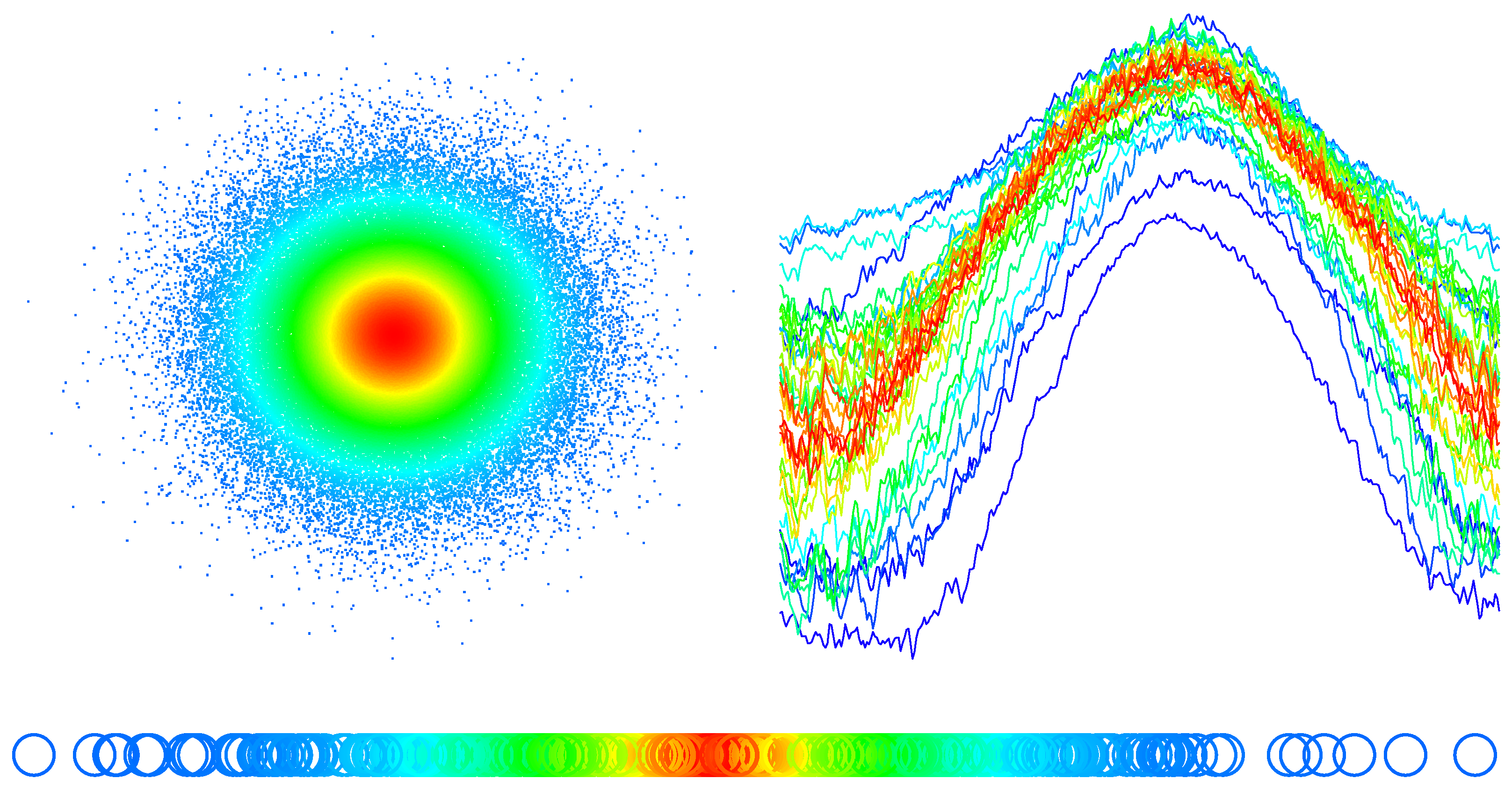
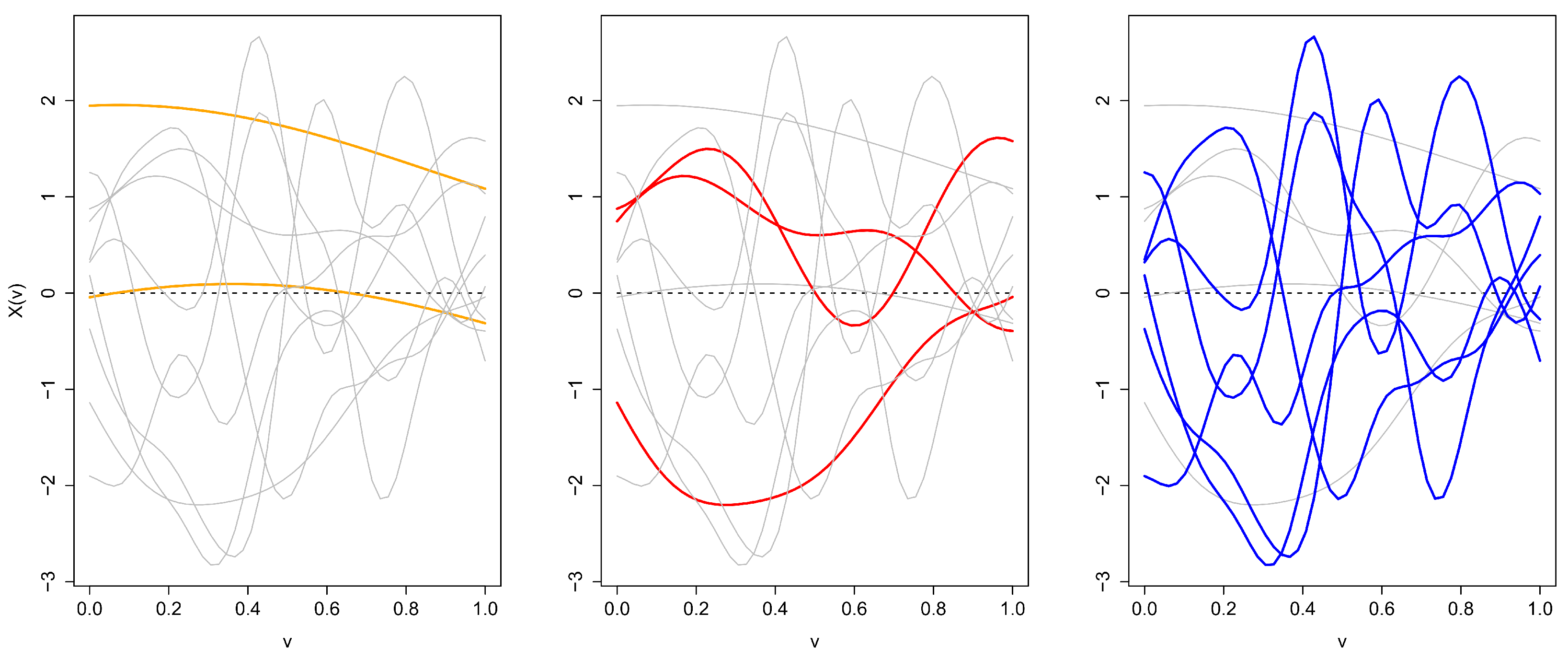
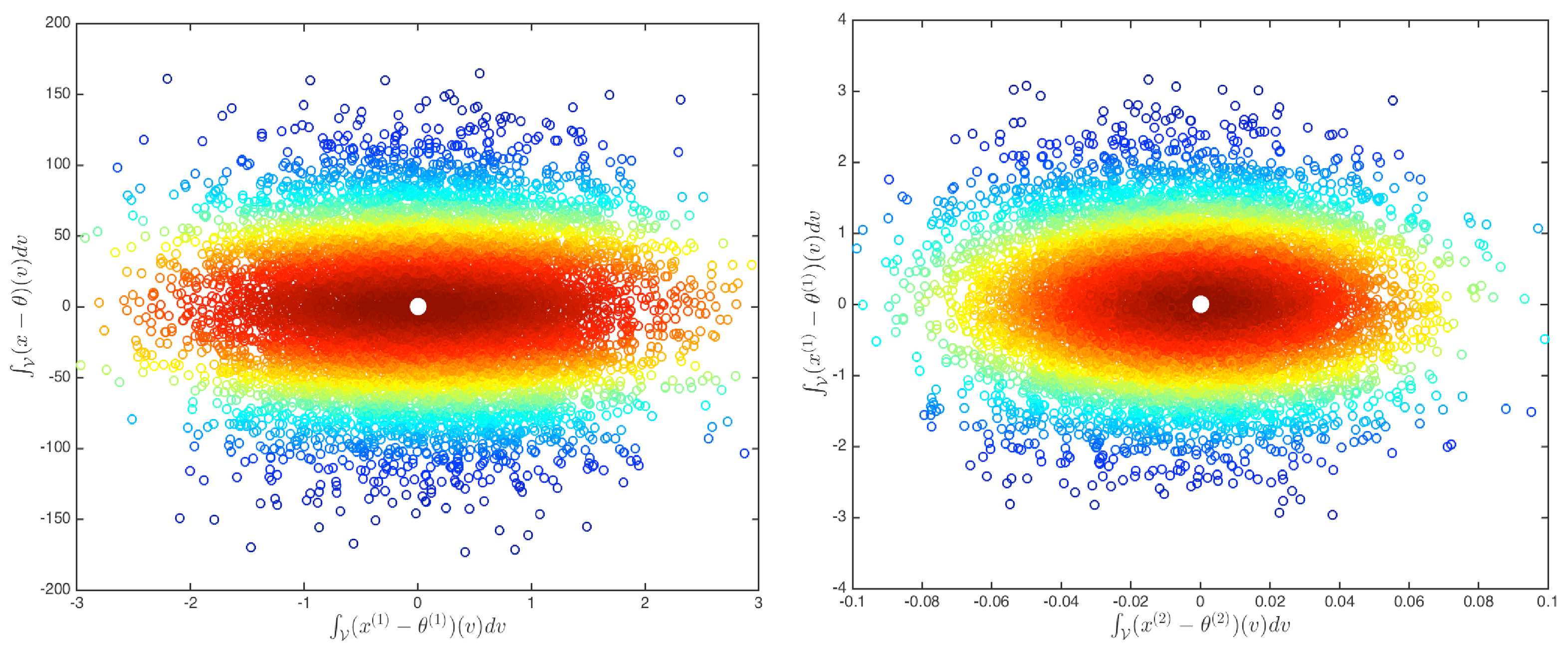
| N(0,1) | U(0,1) | (2,1) | |
|---|---|---|---|
| Distribution | 0.034 | 0.591 | 0.749 |
| Median | 0.053 | 0.795 | 0.891 |
| Deviance | 0.042 | 0.801 | 0.913 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieto-Reyes, A.; Battey, H.; Francisci, G. Functional Symmetry and Statistical Depth for the Analysis of Movement Patterns in Alzheimer’s Patients. Mathematics 2021, 9, 820. https://doi.org/10.3390/math9080820
Nieto-Reyes A, Battey H, Francisci G. Functional Symmetry and Statistical Depth for the Analysis of Movement Patterns in Alzheimer’s Patients. Mathematics. 2021; 9(8):820. https://doi.org/10.3390/math9080820
Chicago/Turabian StyleNieto-Reyes, Alicia, Heather Battey, and Giacomo Francisci. 2021. "Functional Symmetry and Statistical Depth for the Analysis of Movement Patterns in Alzheimer’s Patients" Mathematics 9, no. 8: 820. https://doi.org/10.3390/math9080820
APA StyleNieto-Reyes, A., Battey, H., & Francisci, G. (2021). Functional Symmetry and Statistical Depth for the Analysis of Movement Patterns in Alzheimer’s Patients. Mathematics, 9(8), 820. https://doi.org/10.3390/math9080820






