On the Simulation of a Special Class of Time-Inhomogeneous Diffusion Processes
Abstract
1. Introduction
2. Composition Method for Gauss–Markov Processes
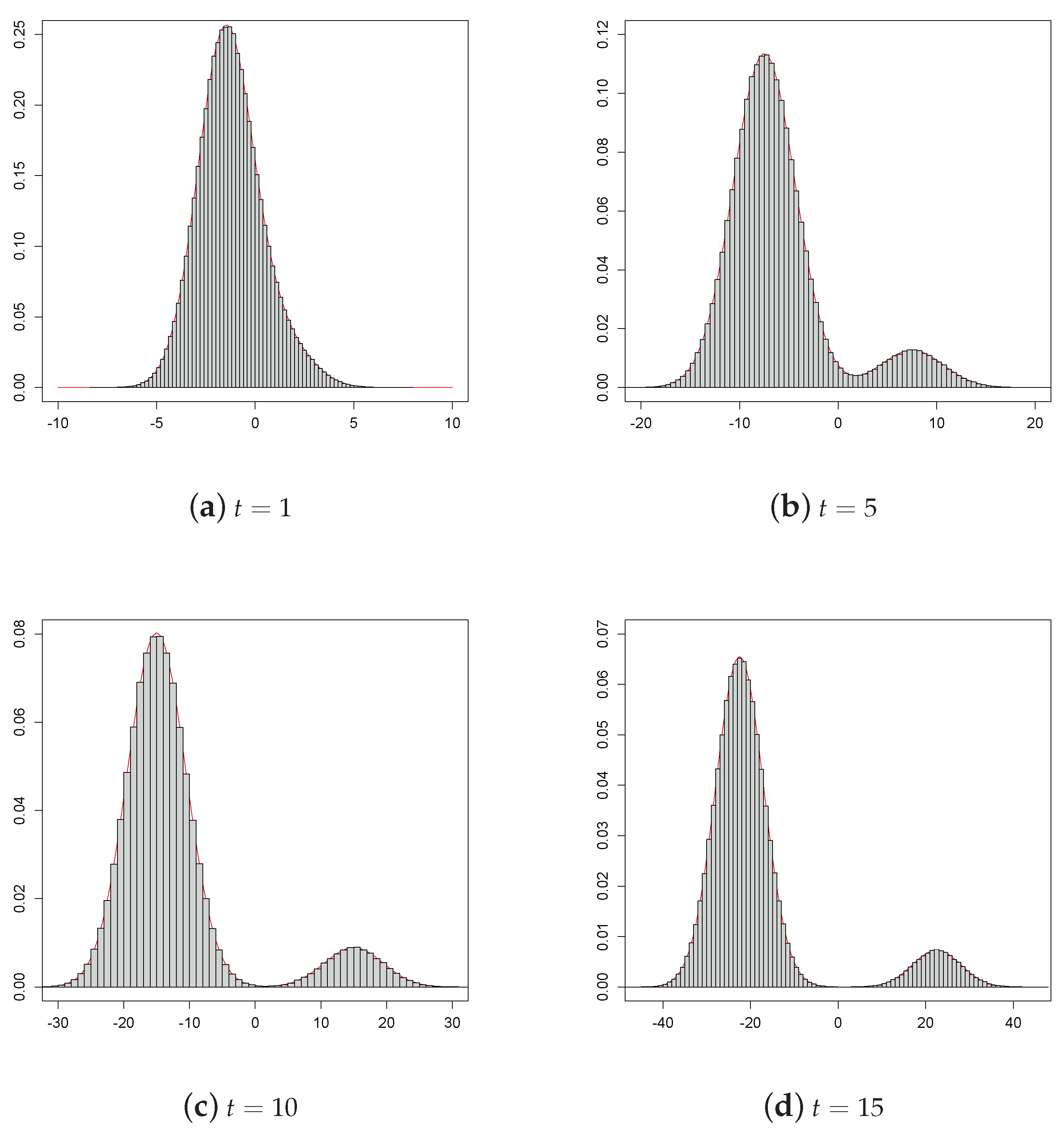
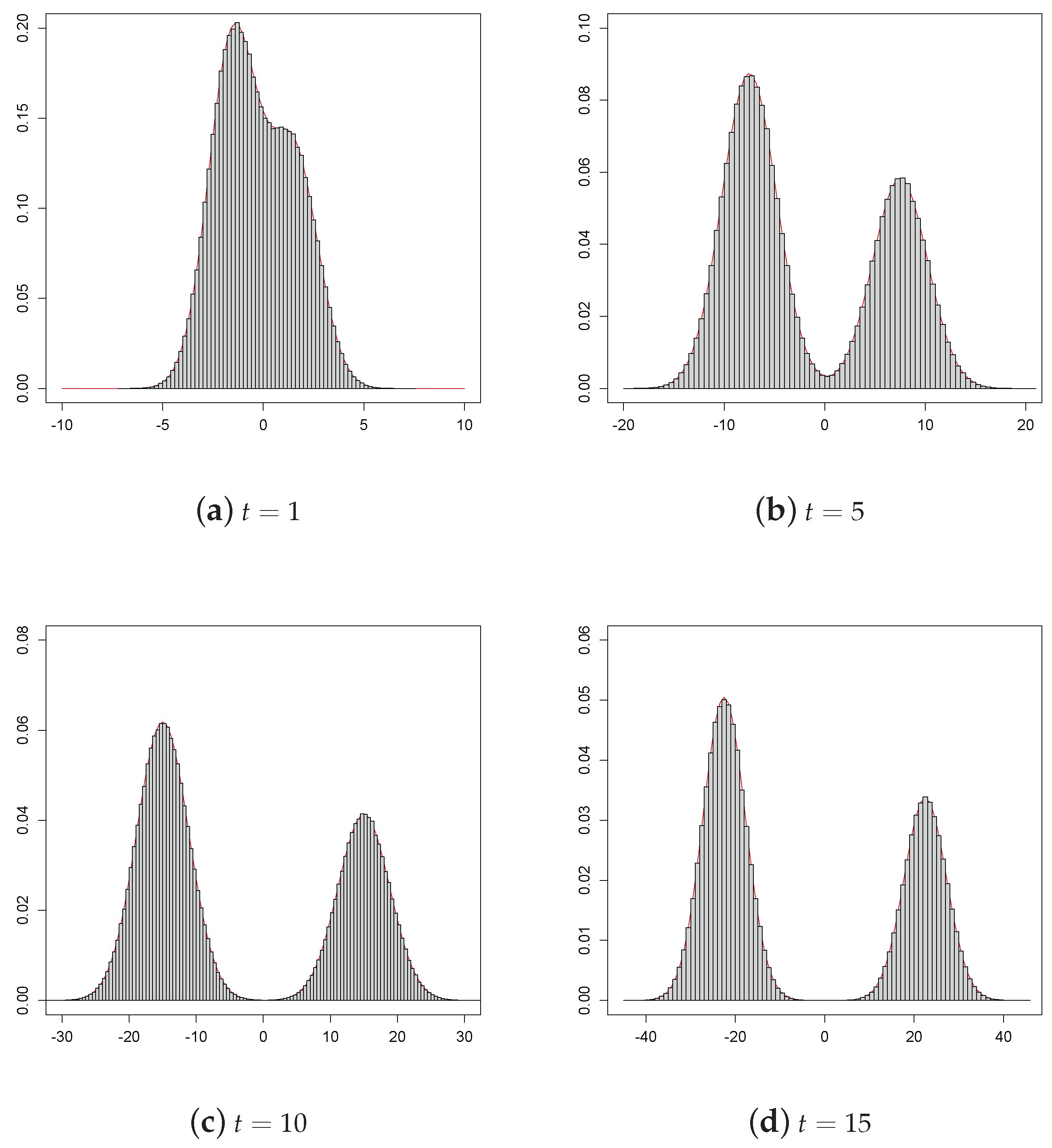
2.1. Simulated Pdf of the Process
| Algorithm 1 |
Let be fixed real constants and be a fixed instant such that . Step 1: Generate and , with and independent random numbers; Step 4: Repeat Steps 1 and 2 for N times, obtaining a random sample of size N from the density (6). The simulated pdf is then depicted by means of a histogram as function of x. The related sample moments can also be obtained. |
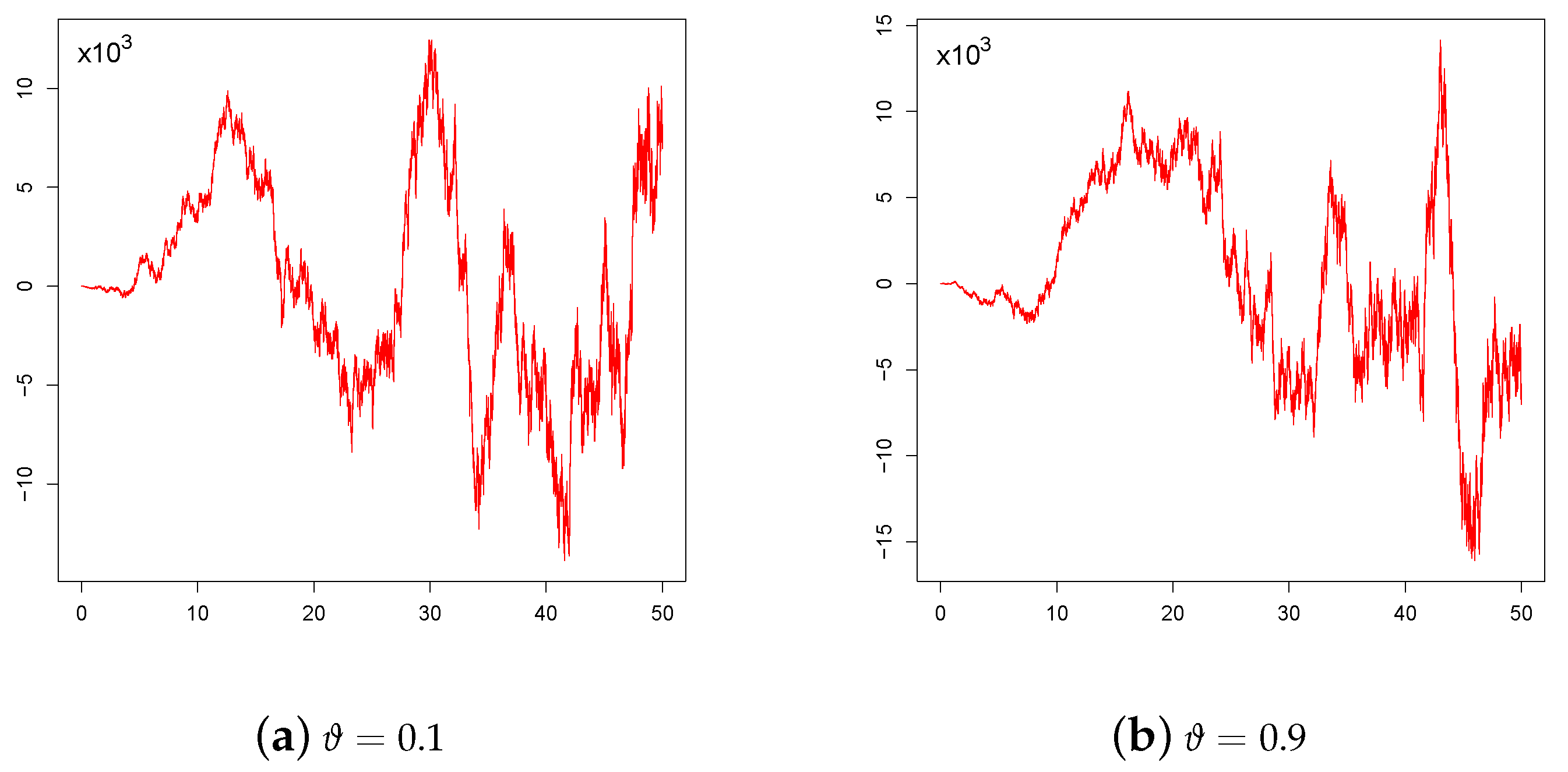
2.2. Simulation of the Sample Paths of
| Algorithm 2 |
Let , with , be the set of equidistant time instants for which the simulation of is required. Step 1: Set and ; Step 2: For set
|
3. Some Time-Inhomogeneous Diffusion Processes
- (a)
- the left endpoint of T is zero, , ;
- (b)
- ,
3.1. Case (a)
3.2. Case (b)
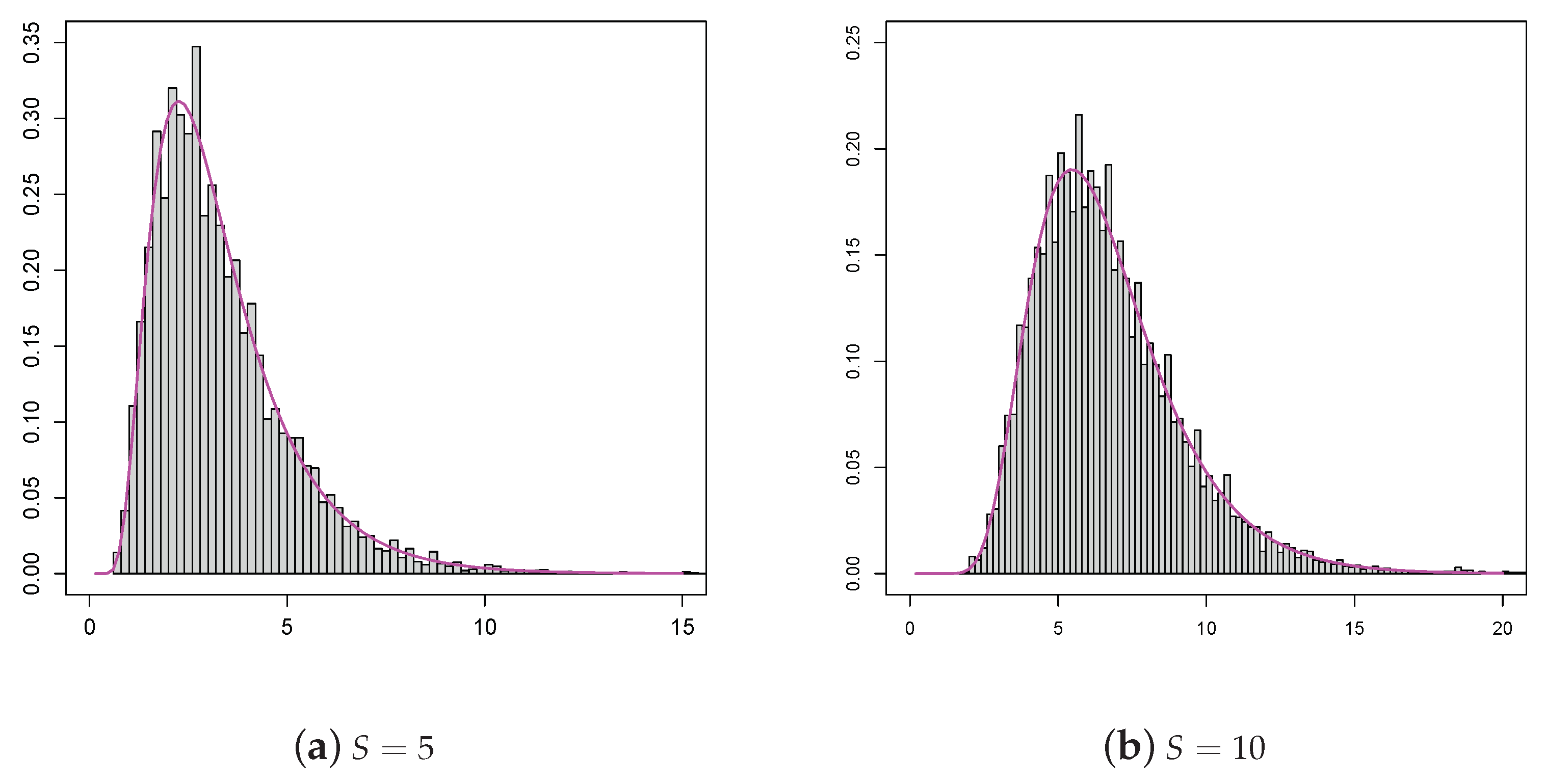
| Algorithm 3 |
Let be the set of distinct time instants for which the simulation of the process is desired. Step 1: Set , , ; Step 2: If compute via
Step 3: If , then collect the first passage time and stop, else and go to Step 2. |
4. Simulation of Processes Generated via the Wiener Process
5. Simulation of Processes Generated via the Ornstein–Uhlenbeck Process
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buonocore, A.; Caputo, L.; Nobile, A.G.; Pirozzi, E. Gauss–Markov processes in the presence of a reflecting boundary and applications in neuronal models. Appl. Math. Comput. 2014, 232, 799–809. [Google Scholar] [CrossRef]
- Buonocore, A.; Caputo, L.; Nobile, A.G.; Pirozzi, E. Restricted Ornstein–Uhlenbeck process and applications in neuronal models with periodic input signals. J. Comput. Appl. Math. 2015, 285, 59–71. [Google Scholar] [CrossRef]
- Albano, G.; Giorno, V. Inference on the effect of non homogeneous inputs in Ornstein–Uhlenbeck neuronal modeling. Math. Biosci. Eng. 2019, 17, 328–348. [Google Scholar] [CrossRef]
- Giorno, V.; Spina, S. On the return process with refractoriness for non-homogeneous Ornstein–Uhlenbeck neuronal model. Math. Biosci. Eng. 2014, 11, 285–302. [Google Scholar] [CrossRef] [PubMed]
- Ricciardi, L.M.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. An outline of theoretical and algorithmic approaches to first passage time problems with applications to biological modeling. Math. Jpn. 1999, 50, 247–322. [Google Scholar]
- Renshaw, E. Stochastic Population Processes: Analysis, Approximations, Simulations; Oxford University Press: Oxford, UK, 2011; pp. 1–672. [Google Scholar]
- Di Crescenzo, A.; Giorno, V.; Krishna Kumar, B.; Nobile, A.G. A time-non-homogeneous double-ended queue with failures and repairs and its continuous approximation. Mathematics 2018, 66, 81. [Google Scholar] [CrossRef]
- Linetsky, V. On the transition densities for reflected diffusions. Adv. Appl. Probab. 2005, 37, 435–460. [Google Scholar] [CrossRef]
- Glasserman, P. Monte Carlo Methods in Financial Engineering, Stochastic Modelling and Applied Probability; Springer: New York, NY, USA, 2003; Volume 53, pp. 1–597. [Google Scholar]
- Di Crescenzo, A.; Giorno, V.; Nobile, A.G. Analysis of reflected diffusions via an exponential time-based transformation. J.Stat. Phys. 2016, 163, 1425–1453. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M. A symmetry-based constructive approach to probability densities for one-dimensional, diffusion processes. J. Appl. Prob. 1989, 27, 707–721. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M. On the construction of densities for time non-homogeneous diffusion processes. Lect. Notes Comput. Sci. 2012, 6927, 80–87. [Google Scholar]
- Abundo, M. On the first-passage times of certain Gaussian processes, and related asymptotics. Stoch. Anal. Appl. 2020. [Google Scholar] [CrossRef]
- Veestraeten, D. On transition and first hitting time densities and moments of the Ornstein–Uhlenbeck process. Stoch. Model. 2014, 30, 143–161. [Google Scholar] [CrossRef]
- Molini, A.; Talkner, P.; Katul, G.G.; Porporato, A. First passage time statistics of Brownian motion with purely time dependent drift and diffusion. Phys. A 2011, 390, 1841–1852. [Google Scholar] [CrossRef]
- Lim, S.C.; Muniandy, S.V. Self-similar Gaussian processes for modeling anomalous diffusion. Phys. Rev. E 2002, 66, 021114. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Chechkin, A.V.; Metzler, R. Scaled Brownian motion: A paradoxical process with a time dependent diffusivity for the description of anomalous diffusion. Phys. Chem. Chem. Phys. 2014, 16, 15811–15817. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, E.; Nobile, A.G.; Pirozzi, E.; Ricciardi, L.M. A computational approach to first-passage-time problems for Gauss–Markov processes. Adv. Appl. Probab. 2001, 33, 453–482. [Google Scholar] [CrossRef]
- Taillefumier, T.; Magnasco, M. A fast algorithm for the first-passage times of Gauss–Markov processes with Hölder continuous boundaries. J. Stat. Phys. 2010, 140, 1130–1156. [Google Scholar] [CrossRef]
- D’Onofrio, G.; Pirozzi, E. Asymptotics of two-boundary first-exit-time densities for Gauss–Markov processes. Methodol. Comput. Appl. Probab. 2019, 21, 735–752. [Google Scholar] [CrossRef]
- Albano, G.; Giorno, V.; Román-Román, P.; Román-Román, S.; Serrano-Pérez, J.J.; Torres-Ruiz, F. Inference on an heteroscedastic Gompertz tumor growth model. Math. Biosci. 2020, 328, 108428. [Google Scholar] [CrossRef]
- Albano, G.; Giorno, V. Inferring time non-homogeneous Ornstein Uhlenbeck type stochastic process. Comp. Stat. Data Anal. 2020, 150, 107008. [Google Scholar] [CrossRef]
- Ramos-Ábalos, E.M.; Gutiérrez-Sánchez, R.; Nafidi, A. Powers of the Stochastic Gompertz and Lognormal diffusion processes, Statistical Inference and Simulation. Mathematics 2020, 8, 588. [Google Scholar] [CrossRef]
- Buonocore, A.; Nobile, A.G.; Pirozzi, E. Simulation of sample paths for Gauss–Markov processes in the presence of a reflecting boundary. Cogent Math. 2017, 4, 1–22. [Google Scholar] [CrossRef]
- Buonocore, A.; Nobile, A.G.; Pirozzi, E. Generating random variates from PDF of Gauss–Markov processes with a reflecting boundary. Comp. Stat. Data Anal. 2018, 118, 40–53. [Google Scholar] [CrossRef]
- Tuerlinckx, F.; Maris, E.; Ratcliff, R.; De Boeck, P. A comparison of four methods for simulating the diffusion process. Behav. Res. Methods Instruments Comput. 2001, 33, 443–456. [Google Scholar] [CrossRef] [PubMed]
- Di Crescenzo, A.; Di Nardo, E.; Ricciardi, L.M. Simulation of first-passage times for alternating Brownian motions. Methodol. Comput. Appl. Probab. 2005, 7, 161–181. [Google Scholar] [CrossRef]
- Giraudo, M.T.; Sacerdote, L.; Zucca, C. A Monte Carlo method for the simulation of first passage times of diffusion processes. Methodol. Comput. Appl. Probab. 2001, 3, 215–231. [Google Scholar] [CrossRef]
- Herrann, S.; Zucca, C. Exact simulation of first exit times for one-dimensional diffusion processes. ESAIM Math. Model. Numer. Anal. 2020, 54, 811–844. [Google Scholar] [CrossRef]
- Headrick, T.C.; Mugdadi, A. On simulating multivariate non-normal distributions from the generalized lambda distribution. Comp. Stat. Data Anal. 2006, 50, 3343–3353. [Google Scholar] [CrossRef]
- Devroye, L. Non-Uniform Random Variate Generation; Springer: New York, NY, USA, 1996; pp. 1–843. [Google Scholar]
- Iacus, S.M. Simulation and Inference for Stochastic Differential Equations with R Examples; Springer Series in Statistics; Springer: New York, NY, USA, 2008; Volume 1, pp. 1–284. [Google Scholar]
- Giorno, V.; Nobile, A.G. On the construction of a special class of time-inhomogeneous diffusion processes. J. Stat. Phys. 2019, 177, 299–323. [Google Scholar] [CrossRef]
- Mehr, C.B.; McFadden, J.A. Certain Properties of Gaussian Processes and their First-Passage Times. J. R. Statist. Soc. B 1965, 27, 505–522. [Google Scholar] [CrossRef]
- Ross, S.M. Simulation; Academic Press: Amsterdam, The Netherlands, 2013; pp. 1–328. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley Series in Probability and Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1–743. [Google Scholar]
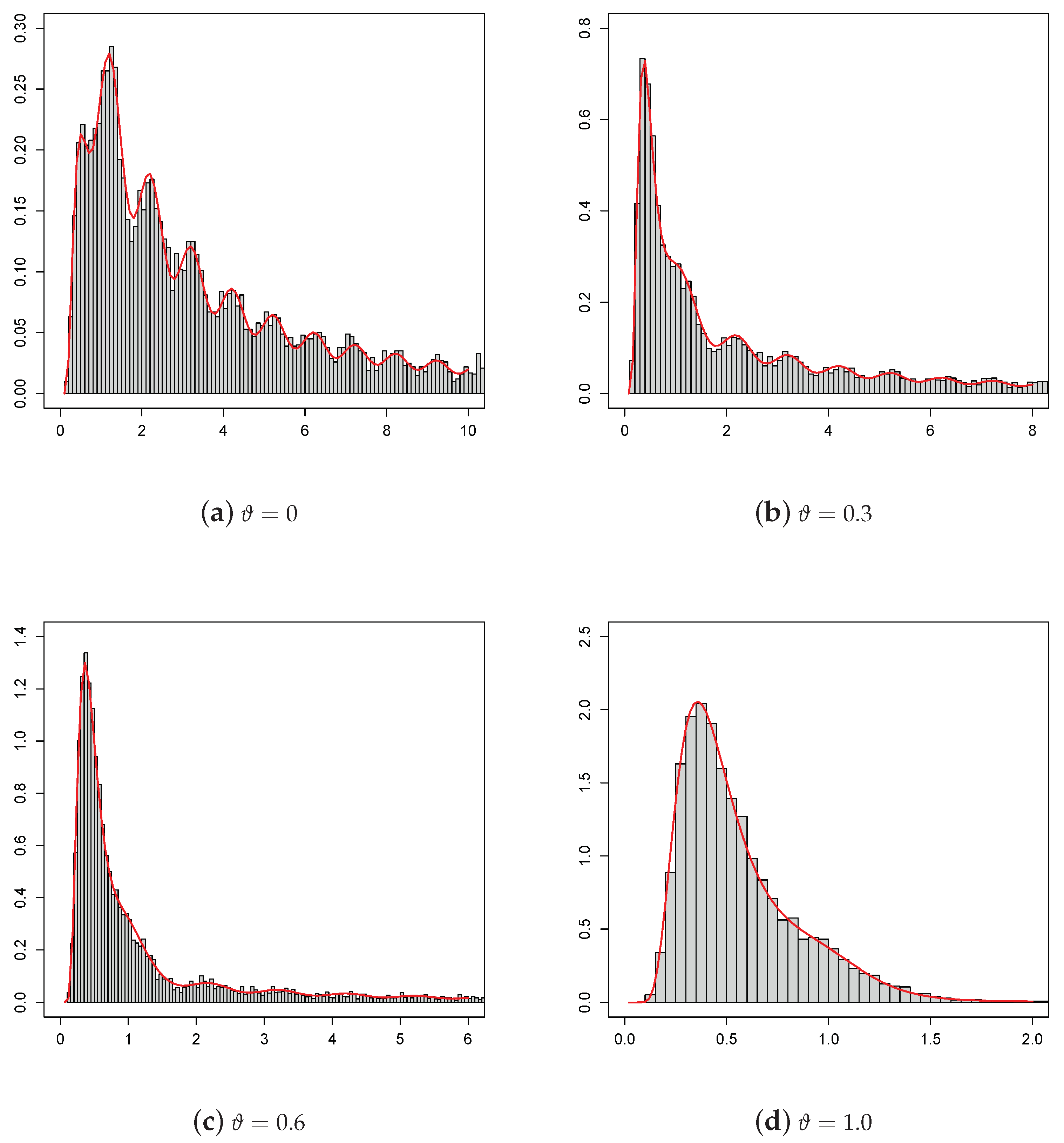
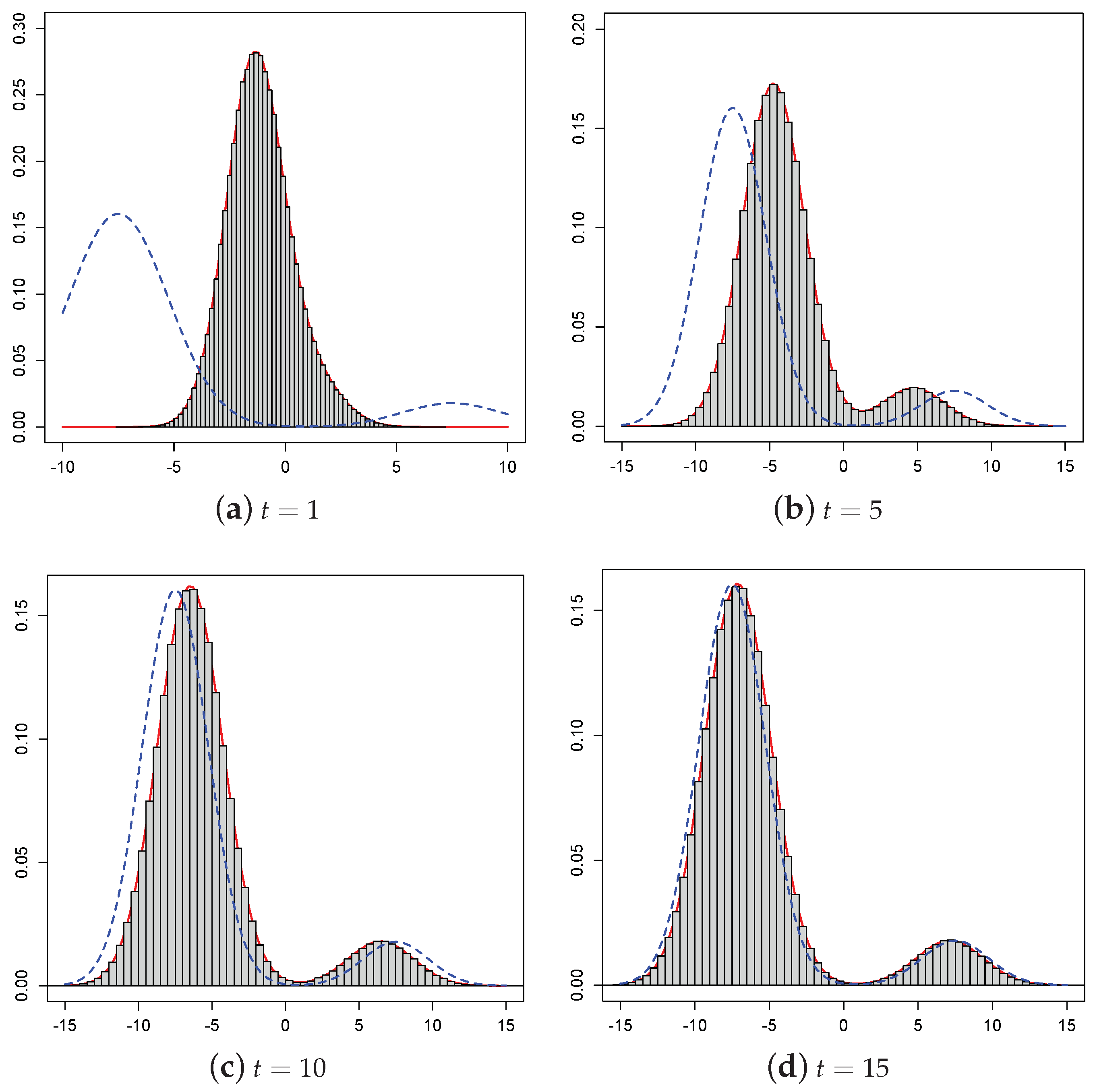
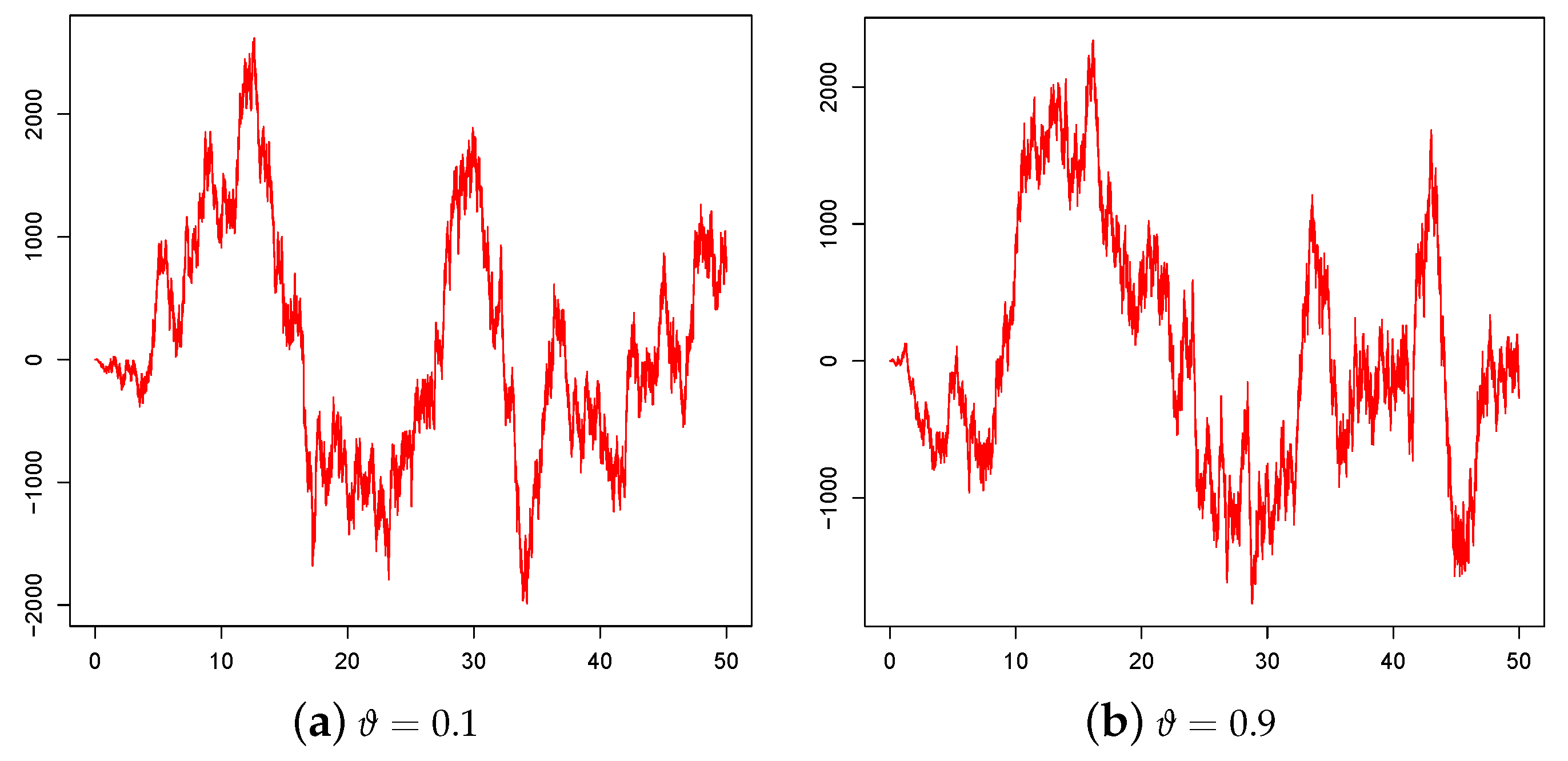
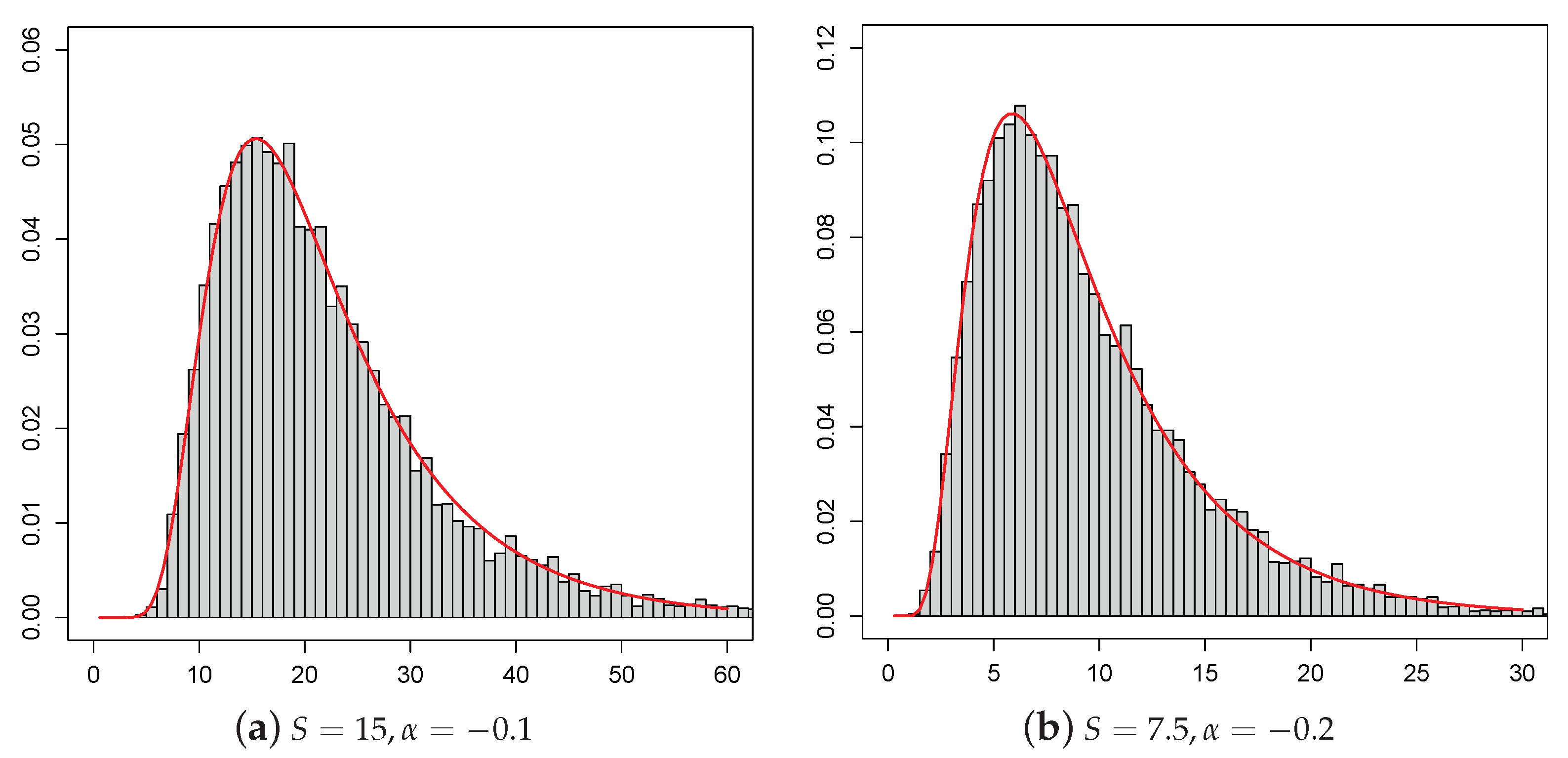
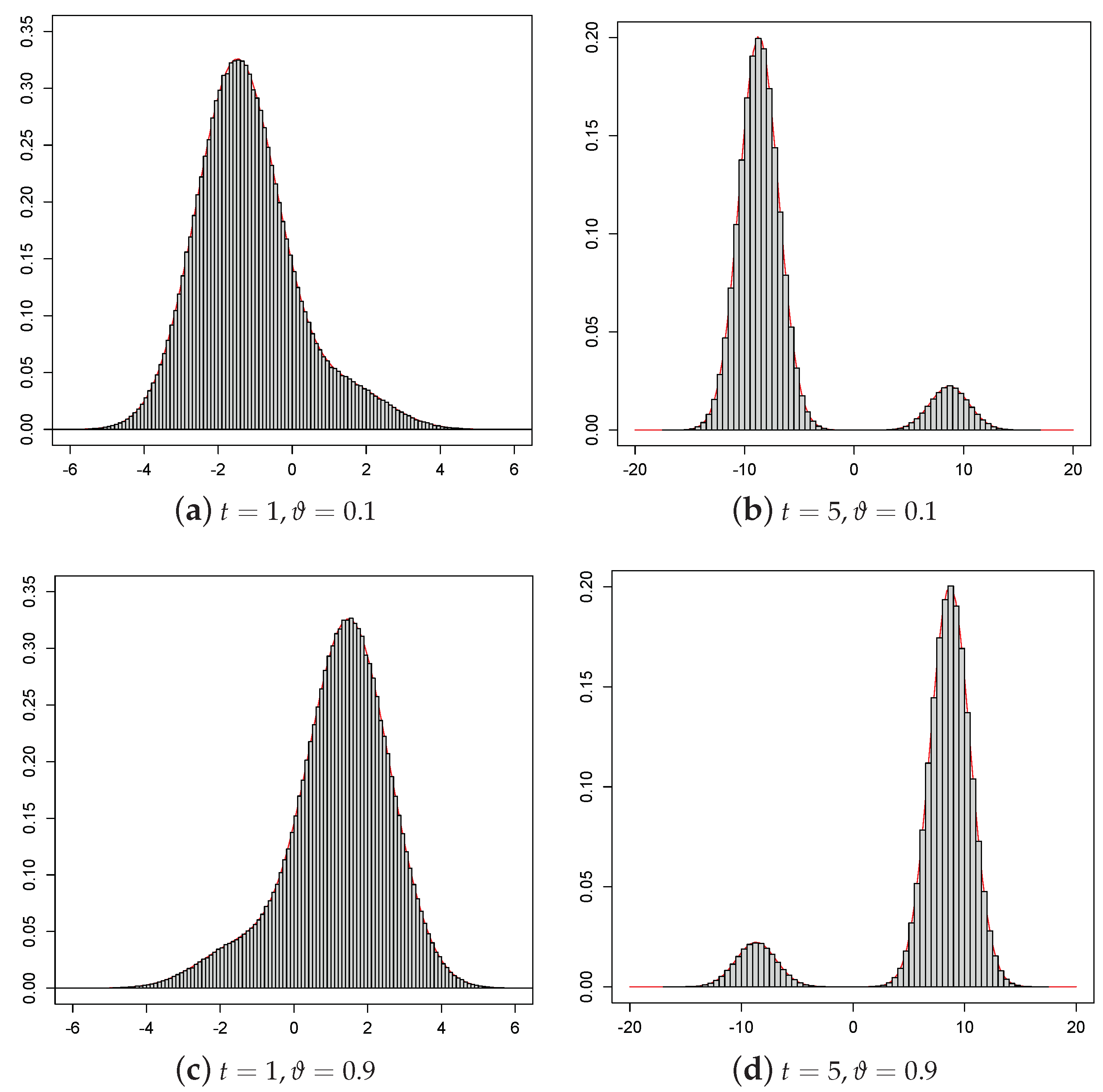
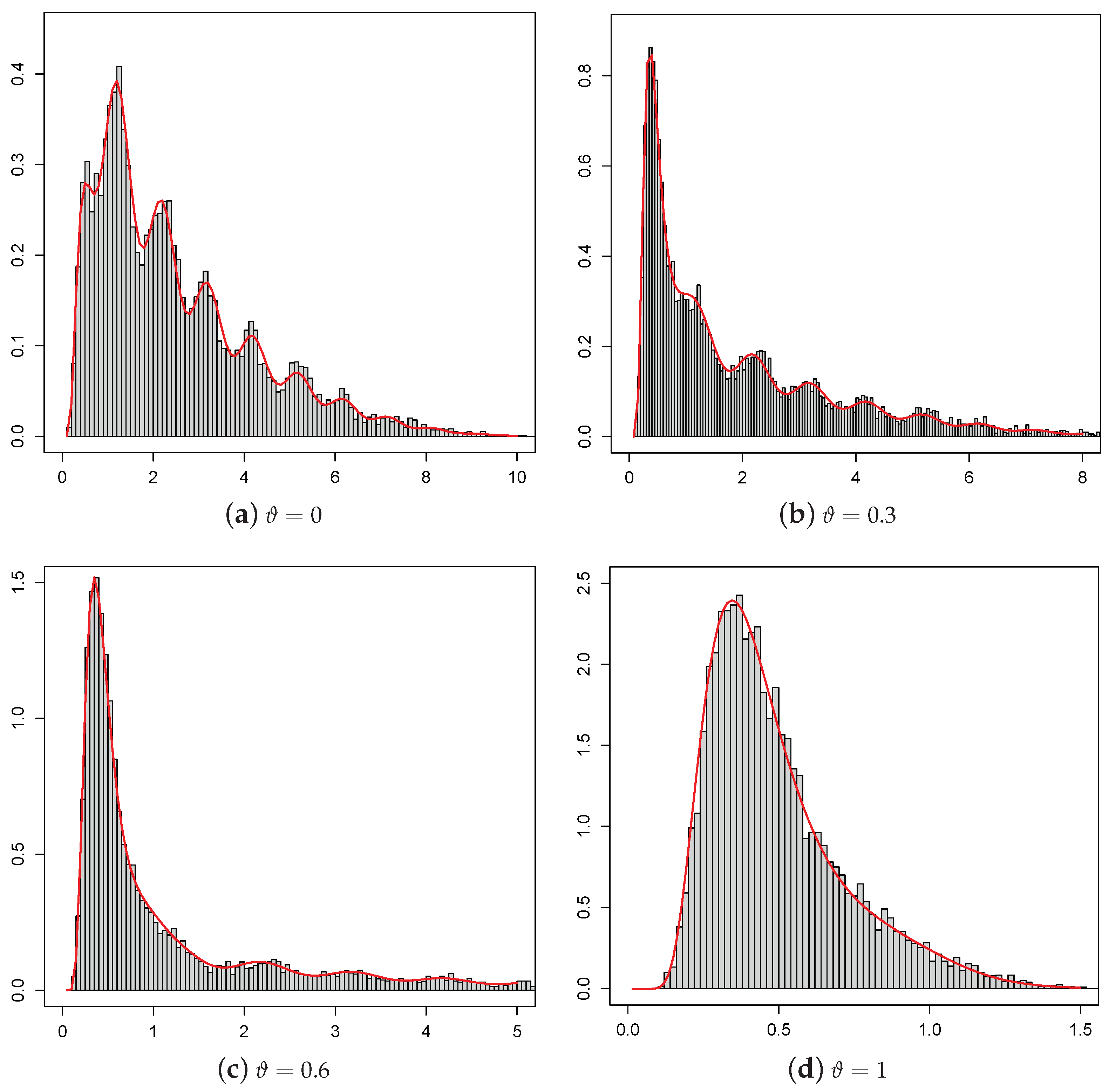
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | −1.200000 | −1.201083 | 2.810000 | 2.81271 | 1.396921 | 1.396334 |
| 5 | −6.0000000 | −6.0033797 | 30.2500000 | 30.2705863 | 0.9166667 | 0.9164623 |
| 10 | −12.0000000 | −12.0057944 | 101.0000000 | 101.0350351 | 0.8374896 | 0.8372306 |
| 15 | −18.0000000 | −18.0080505 | 212.2500000 | 212.2809493 | 0.8093779 | 0.8090751 |
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | −0.300000 | −0.2997934 | 3.660000 | 3.6660900 | 6.377042 | 6.3867430 |
| 5 | −1.500000 | −1.497204 | 61.500000 | 61.576435 | 5.228129 | 5.241146 |
| 10 | −3.000000 | −2.993572 | 231.000000 | 231.231917 | 5.066228 | 5.079654 |
| 15 | −4.500000 | −4.489803 | 508.500000 | 508.947685 | 5.011099 | 5.024690 |
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | −1.087615 | −1.088598 | 2.313785 | 2.316015 | 1.398576 | 1.397987 |
| 5 | −3.7927234 | −3.7949015 | 12.4147457 | 12.4236120 | 0.9290044 | 0.9288026 |
| 10 | −5.1879883 | −5.1906403 | 20.0482345 | 20.0579186 | 0.8630562 | 0.8628236 |
| 15 | −5.7012776 | −5.7040871 | 23.2714247 | 23.2806625 | 0.8461343 | 0.8458854 |
| t | ||||||
|---|---|---|---|---|---|---|
| 1 | −1.191974 | −1.192894 | 2.019084 | 2.021058 | 1.192094 | 1.191757 |
| 5 | −6.9575706 | −6.9605112 | 30.4288148 | 30.4284625 | 0.7928388 | 0.7924993 |
| 10 | −21.4721848 | −21.4793776 | 262.9543652 | 262.8009005 | 0.7552343 | 0.7547302 |
| 15 | −59.3090545 | −59.3271807 | 1982.3207516 | 1980.5425005 | 0.7506992 | 0.7501332 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorno, V.; Nobile, A.G. On the Simulation of a Special Class of Time-Inhomogeneous Diffusion Processes. Mathematics 2021, 9, 818. https://doi.org/10.3390/math9080818
Giorno V, Nobile AG. On the Simulation of a Special Class of Time-Inhomogeneous Diffusion Processes. Mathematics. 2021; 9(8):818. https://doi.org/10.3390/math9080818
Chicago/Turabian StyleGiorno, Virginia, and Amelia G. Nobile. 2021. "On the Simulation of a Special Class of Time-Inhomogeneous Diffusion Processes" Mathematics 9, no. 8: 818. https://doi.org/10.3390/math9080818
APA StyleGiorno, V., & Nobile, A. G. (2021). On the Simulation of a Special Class of Time-Inhomogeneous Diffusion Processes. Mathematics, 9(8), 818. https://doi.org/10.3390/math9080818