Abstract
A characterization of recent Nordic research in didactics of mathematics is presented based on the 32 research reports from the Nordic and Baltic countries in the proceedings from NORMA17 (The eighth Nordic conference on didactics of mathematics). Recent Nordic research in didactics of mathematics is observed from several aspects such as choice of problem, theory, method, result, and target for the message. The analyses of the papers on different levels and from a manifold of perspectives build up an image of what Nordic research in DM (didactics of mathematics) contains and represents currently. The closeness and cooperation between researchers in the Nordic countries is characteristic as well as the breadth and variation in the choice of questions, theories, and methods. Research activity seems to flourish most in Norway. Small-scale studies as well as larger projects are visible. A variety of messages about mathematics teaching and learning for all age groups are directed to students, mathematics teachers, teacher educators, and policymakers. Quantitative and qualitative empirical studies dominate. Conceptual or theoretical investigations are rare. Studies of outcomes of interventions, including teaching approaches and experiments are most common, followed by studies of learning and cognition, including problem-solving. There is a need for surveys and overviews as so many new results are exposed.
1. Introduction
Mathematics is often seen as a difficult school subject, and it has attracted much interest and created discussions in modern societies for many decades now. Thus, it is no wonder that also researchers are involved in investigating the problems around teaching and learning mathematics. In this paper, we will take a closer look at such research in the Nordic and Baltic countries that has taken place recently. The Nordic and Baltic area constitutes an important region in the EU, with about 34 million inhabitants and well-developed national educational systems.
Research in didactics of mathematics (DM) or mathematics education research is a rather young research area in the Nordic countries. Early doctoral theses exist, such as Jonson [1], Nykänen [2], Lahti [3], Werdelin [4], and others, but those studies were often carried out in the academic disciplines of pedagogy or psychology or similar areas.
The first Nordic professorships in DM were created in Finland around 1974, and they were situated at teacher education institutions [5]. Around 1993, professorships in DM were established in Denmark, Iceland, and Norway, and in Sweden a little later, in 2001. This is rather late compared to the international situation [5]. A national graduate school in didactics of mathematics, physics, and chemistry started in Finland in 1995 [6] and ended in 2011. In Sweden, a time-limited graduate school of mathematics with the direction of mathematics didactics was active between 2001 and 2007 [7,8]. The Nordic Graduate School in Mathematics Education (NoGSME) was active during 2004–2010, encompassing 45 institutions from the five Nordic and three Baltic countries and situated at the University of Agder in Norway. It was running alongside a rather impressive graduate program there, which was started in 2002 [9,10,11,12,13,14]. Thus, several Doctors of Philosophy in didactics of mathematics defended their doctoral theses from around 2003 onwards. Several of them have now become professors or university teachers, and there is a steady and continuous production of new doctors. The need for these doctors is deeply rooted in teacher education, and it is a consequence of the demand to make teacher education more research based. Consequently, there is a lively research activity in the Nordic and Baltic countries in DM.
It is of course difficult to give a fair picture of recent Nordic research in DM. Thus, as a relevant reflection of it, the studies presented in the proceedings of the NORMA17 conference will serve as source for this picture. This is the latest Nordic and Baltic conference with long traditions in the area. It is known to all Nordic researchers in DM, and many participate in this event. The first NORMA conference took place in Finland in 1994, and since then, there was in principle one conference every third year circulating among the five Nordic countries. NORMA17 was the eighth conference, and it took place at Stockholm University in Sweden. The next one will be in Oslo in 2021, which was postponed one year because of the pandemic. Using the proceedings as a source of information, the paper will both present objective facts drawn from it and in several ways analyze the research presented in the papers to give a picture of recent research in DM in the Nordic countries. The analyses will be discussed and commented from an insider’s more personal perspective. The review process of NORMA17 is serious, and each paper is evaluated by two to three independent reviewers, who are most often peers in the conference but also outside researchers (sometimes reviewers to the journal Nomad, Nordic Studies in Mathematics Education). Before the publication in the proceedings, there is a second review of the final papers. For NORMA17, the committee decided to group the papers in 10 areas. The scientific committee of NORMA17 represented all Nordic countries, and one representative was from the Baltic countries. There was also a mix of junior and senior researchers.
The theme for the NORMA17 conference was Nordic research in mathematics education, which is highly appropriate for this paper. Nordic and Baltic researchers in mathematics education were given opportunities to introduce their research by regular papers, short communications, working groups, and symposia. Below, when writing in Nordic, also Baltic authors and papers are included all the time.
The author of this paper writes as an insider in Nordic DM, having acted as a mathematics teacher and senior lecturer since 1962 at different levels, as a teacher educator since 1972, as a researcher and professor at several universities in Sweden and Norway, and as a guest professor in Estonia and Denmark.
2. The Aim of This Paper
Recent Nordic research in didactics of mathematics will be characterized in different ways, both in an overarching way and in more detail. For example, by exploring the research study paradigms [15], the studies will be classified in larger groups. By investigating the chosen research question and its justification, the chosen theory, and crucial concepts, and the methods used, a closer view of some of the studies is exposed. Finally, the possible impact of the studies in society will be discussed using the socio-scientific triad of researchers, messages, and targets. The research question posed is: What are the characteristic features of recent Nordic research in didactics of mathematics?
3. Literature Review
Good reasons exist to why it is relevant to explore DM in the Nordic countries. A long tradition of cooperation and collaboration is visible in the Nordic area [10,11,12,16,17]. It started already in the 1960s when the Nordic Committee for Modernizing Mathematics Education (NKMM) was created as a result of the Royaumont seminar in 1959 [18]. The representatives for the Nordic countries present at the seminar decided to cooperate in the work to reform school mathematics. Later, a series of Nordic conferences in DM took place with mathematics teachers, researchers, and teacher educators as participants. For example, from the conference in 1993 in Åbo, the proceedings were published [16], and they contain contributions from Denmark, Finland, Norway, and Sweden, many of them with a Nordic perspective. In 1994, the first NORMA conference took place in Lahti, Finland, initiated by Erkki Pehkonen and Trygve Breiteig. It was called a Nordic conference on mathematics teaching, and the main purpose of the conference was to study the influence of the latest learning theories on the practice of teaching mathematics and to give examples of how to realize these ideas in school practice [19]. In this conference, also, teachers and researchers from the Baltic countries took part. The later NORMA conference proceedings give the state of the art of research in DM at the time when they were published [20,21,22,23,24,25]. In the proceedings from the first conference [19], there are 20 research papers from Nordic and Baltic authors. They are short stories of about 5–7 pages, were not reviewed, and expose constructivism as the dominating learning theory. As will be shown below, the situation in the latest proceedings is different. In 1993, the first issue of the journal Nomad, Nordic Studies in Mathematics Education was published as a cooperative effort between the five Nordic countries [26]. Nomad is now an international journal but has served as an entry to publishing for many Nordic researchers.
A few researchers have tried to characterize Nordic research in DM already. The publication of the proceedings mentioned above from Åbo was entitled Matematikdidaktik i Norden (Didactics of mathematic in the Nordic area), and it is an early example [16]. The Nordic perspective was emphasized with descriptions of the state of the field at the time and outlooks on where Nordic mathematics education was heading. Most chapters are in a Scandinavian language and thus not accessible for non-Nordic readers. In the end of the 1990s, Nordic researchers were invited to contribute to an anthology with recent research reports (in Swedish). The book was called “Didactics of mathematics—A Nordic perspective” [27] and was also translated to Norwegian and published in Norway [28]. Another example that gives an overview is the Nordic presentations at ICME10 (The Tenth International Congress on Mathematics Education) in 2004, as documented in the Proceedings [29].
In 2005, an overview of recent research in the Nordic countries was presented at a conference in Jyväskylä. The paper in the proceedings [30] illustrates what was going on in Nordic DM at the time by using examples from work by doctoral students and larger research groups. The perspectives that are exposed are studies of mathematics textbooks and texts, studies on mathematics teachers and teaching, studies of specific areas of the mathematics curriculum or the development of mathematical concepts, studies of mathematics teaching and learning in the classroom, and studies of the history of mathematics related to learning and teaching. It was pointed out that international overviews often give little insight into what is going on in the Nordic countries. The languages might be a problem, but there is anyhow an unbalance in the presentations. The report was concluded with the words, “Maybe we need another five to ten years’ perspective to really be able to discern from all this, what is important, influential and viable.” Today, 15 years later, it is still not easy to find specific and important features or topics that could be characterizing the Nordic studies, as will be shown.
In the First sourcebook on Nordic research in mathematics education [31], there are five sections, one for each of the Nordic countries, and they expose a rather unbalanced situation, as there are only four chapters from Finland and 17 from Norway. That might not be a reasonable reflection of the research production in the two countries in 2010, even if it is clear that DM greatly expanded in Norway after 2002. Although there are some national summaries in the book, the main editor does not try to summarize or indicate features or brands specific to the Nordic research.
Another book with a collection of papers on Nordic research studies is Nordic research in didactics of mathematics: Past, Present, and Future [32]. In the summary, several general aspects of mathematics learning are discussed, such as the use of ICT (information and communication technology), textbooks, mathematical reasoning, use of language and communication, feedback, and students’ attitudes and beliefs and vocational mathematics. The concepts of inquiry and doctoral supervision are also addressed.
Additionally, overviews of certain aspects of Nordic research in DM were treated in the book “Mathematics textbooks, their content, use and influences; Research in Nordic and Baltic countries” [33] and in the chapter “Mathematical Learning and Its Difficulties: The Case of Nordic Countries.” edited by Räsänen et al. [34] in the book “International Handbook of Mathematical Learning Difficulties”. They reflect the outcomes and interests among the Nordic networks of researchers of textbook studies and of studying students with learning difficulties. These two areas are visible also in the earlier overviews.
Thus, with this paper, a more recent overview of Nordic research in DM is given, attempting to add to and expand the earlier documentations. The research activity in DM in the Nordic area has been impressive during the latest decades, and consequently, there are many new aspects to investigate.
The latest Nordic conference in DM was NORMA17, and the editors of the proceedings summarize the content of the proceedings in this way: “Although teaching and learning of mathematics is the common interest for all participants, the papers make visible a great diversity in how this is considered. They include a variety of mathematical topics as well as a currency from preschool to university mathematics. Furthermore, various methodologies and theoretical perspectives are used in the research presented. This variation shows that the Nordic research in mathematics education is a broad field and that the field was well represented at the conference.” [35] (p. ii). This paper will expose more of the varied content and of the diversity of the papers. That will certainly confirm the summary of the editors.
4. Theoretical Approach
For this selection of Nordic research papers, a first overarching classification will be presented based on the categories of research study paradigms and of predominant choice of methods presented by Niss [15]. Niss defines a research study paradigm as a constellation of overarching characteristic features with respect to five components in what he calls a research study vector: purposes and interest, research questions, design, findings, and reporting format. He underlines that the notion of a research study paradigm is not the same as a research paradigm. The latter is according to him a general view of, approach to, and way of doing research at large. Niss identifies ten different research study paradigms, and we will use six of them. The others are not needed for or relevant to the papers in NORMA17. These are the paradigms used in this paper:
- 1
- Studies of learning and cognition, including problem-solving strategies.
- 2
- Studies of outcomes of interventions, including teaching approaches and experiments.
- 3
- Suggesting and implementing theoretical/analytic constructs or frameworks.
- 4
- Uncovering beliefs, attitudes, affects, or identities with teachers and students.
- 5
- Textbook studies, mostly of comparative nature.
- 7
- Meta studies—surveys of previous research on a given topic.
The following paradigms from Niss [15] will not be necessary in this analysis:
- 6
- Classroom and discourse studies;
- 8
- Analytic essays;
- 9
- Design of instruments for investigation;
- 10
- Studies of mathematics in vocations and professions.
The choices of methods Niss is presenting are:
- 1
- Conceptual or theoretical investigation.
- 2
- Qualitative empirical investigations.
- 3
- Quantitative empirical investigations.
Using these categories will help us see the great picture of the papers in NORMA17, but there is also need for some more fine-grained analyses.
The papers will be further analyzed in several ways. Building on the main points that are evaluated in the review process for NORMA conferences, we will use three critical issues, namely statement of problem/issue and discussion of its significance, theoretical framework, and methodology. For the readers to be able to follow the arguments, the start is a short overview of the papers concerning these issues. In addition to that, analyses follow of the possible societal impact of the studies using the socio-scientific triad, researchers, messages, and targets.
To illuminate some relations between the research and society, I use the socio-scientific triad (see Figure 1), where the corners in the triangle are researchers, messages, and targets. The link between the researchers and the messages are inquiry and questions to answer, the link between the message and the target is the dissemination of research results, and the third link can be represented by the impact of the research in society. Doing research and disseminating the results are two of the tasks that all university teachers have in common. It is well known that the dissemination work is not always as easy as the doing of the research itself. This exploration may give some indications of the impact of the research in society.
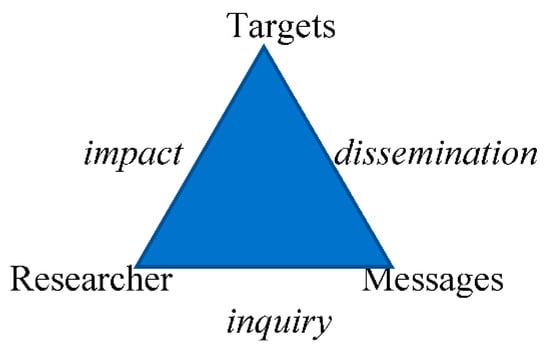
Figure 1.
Socio-scientific triad.
5. Research Design, Method, and Methodology
The study takes an interpretivist approach and is designed as an explanatory case study of the Nordic and Baltic papers in the proceedings of NORMA17. An explanatory design uses the researcher’s ideas and thoughts on a subject to further explore the phenomena. The research explains unexplored aspects of a subject and details about what, how, and why of the research question. Content analysis of a multitude of aspects of the papers is carried out. Mixed methods are used, and data are both quantitative and qualitative. An overarching picture of the papers concerning research study paradigms and choice of methods is created by using the categorisations from Niss [15]. A closer view is given by investigating the aspects of papers that are guided by the emphases in the review process of NORMA17. Those are the criteria for the papers to be accepted. The societal interplay of the papers is studied with the help of the socio-scientific triad (Figure 1), consisting of researchers, messages, and targets.
After the selection of papers and before the analyses of the papers, I read and reread them several times to be able to create understanding in a hermeneutic process [36].
This is the plan for the analyses, which are carried out in the study:
The analyses start with an exploration of some facts about the papers, the authors, and their national belonging. This is reported in Section 6.1.
The categories of research study paradigm and choice of methods are presented in Section 6.2.
The problems or issues presented in the papers and the significance of them, according to the authors, are reported in Section 6.3.1.
The theoretical frameworks and the crucial concepts used, as presented by the authors of the papers, are listed in Section 6.3.2.
The data used, methods, and analysis outcome are listed in Section 6.3.3.
The literature review of the papers is presented in Section 6.4.
The researchers, the messages in the papers, and the targets of the messages are investigated as indicated in the socio-scientific triad. These results are presented in Section 6.5.
A short overview of the results in this investigation is presented in Section 6.6.
The limitations of the study are presented and discussed in Section 6.7.
5.1. Methods
The first task was to select the papers that were going to be the basis for the study. Rather than making a personal selection of an appropriate set of papers in DM, I preferred to take the proceedings from NORMA17 as my object of study. The two papers by Audrey Cooke [37] and Eva Müller-Hill and Annika M. Wille [38] are excluded as the authors do not represent Nordic or Baltic universities. The paper by Joana Villalonga Pons and Paul Andrews [39] could be questioned, as neither of them are Nordic by birth, but as Andrews works at Stockholm University, he represents Sweden. Thus, the paper is included for Sweden. Then, there are 32 Nordic papers in the proceedings [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]. The full list of the selected papers (with titles indicating their content) for NORMA17 is given in Appendix A. For papers with authors from more than one country, the lead author’s affiliation has decided what country it represents. The authors were listed with the national affiliation, and so were the papers. The number of authors of each paper was noted as well as if there were mixed national affiliations for a paper. Then, the categories of research study paradigms were applied by deciding which category is most relevant for the paper if more than one is appropriate. As Niss [15] (p. 402) writes, this is not a straightforward task. There are cases where multiple or alternative classifications could be made. In such cases, the suggestion by Niss was followed, and one possible paradigm was chosen to be the primary one.
After that, the statement of problem/issue and discussion of its significance, theoretical framework, and methods for each of the 20 first papers are identified and listed. To use 20 of the 32 papers for this part is sufficient for the purpose here, which among other things is to show the breadth and variation. The writers’ own way to describe theoretical frameworks and methods in the papers have been respected, and the author of this paper has not reinterpreted the actual use of frameworks and methods. Finally, the three corners of the socio-scientific triad are focused on and determined for each paper.
5.2. Some Methodological Issues
Selection of papers: The task to select appropriate papers for an overview of the kind wanted here is delicate. In whatever way it is done, it can be criticized for being biased. Thus, it seems proper to take a naturally existing selection, namely all the Nordic papers in the latest and most important Nordic research conference, NORMA17 [35]. Then, the selection is made by the researchers themselves by showing activity, participating, and publishing in the proceedings. There can of course be some irregularities in such a choice, but it seems less dependent on personal preferences than if specific papers are chosen.
Analyses of papers: There were 44 paper presentations during the NORMA17 conference. Thus, 10 presenters have not published in the proceedings. Some papers were published later in scientific journals, some papers were presented by teachers in school who had no intention to publish. Among those papers could be some of the categories that are missing in the investigation. Another issue is the short descriptions given of research questions, theoretical frameworks, and methods. They are my interpretations of what the authors intended to say in the papers. There could be misinterpretations, and the short character of the descriptions might not do justice to what is written in the paper. The categorization in research study paradigms is also open to discussion. When there are multiple options, the choice of which is the primary one can be questioned.
The fact that the content analysis is a case study makes it difficult to generalize results. The story can be told of what this specific case can expose to us. However, in this case, much is known from earlier reports on Nordic research in DM, and the local findings in the case of NORMA17 can be related to that knowledge. This is supported in the conclusions, and it is appropriate to use a case study.
The justification for the use of the socio-scientific triad is the fact that society has expectations and demands on the outcomes from DM. Research in DM deals with all kinds of issues and questions about teaching and learning mathematics at all levels in the educational system. Normally, such research is financed by society, as the benefits of the research are directed to the educational system and rarely concern industry or business. Thus, society has some expectations for results that in some sense will improve the educational system.
The case study carried out here can be replicated by any researcher as the data, the proceedings of NORMA17, are available on the internet, and the methods are openly described.
6. Results
6.1. Facts about Papers and Authors
The results section starts with some facts about the papers, authors, and national affiliations. This will give the readers a background for the following presentation.
The Nordic researchers seem to prefer to work collaboratively in writing. Most of the papers (13) have 3 or more authors, 12 papers have 2 authors, and only 7 papers have a single author. How the countries are represented with papers can be seen from the Table 1 here.

Table 1.
Number of papers from each country at the conference.
Papers from Norway dominate in the proceedings, with Finland and Sweden following as second and third with equal numbers. From Estonia, there is no paper (but Estonians contribute to two papers), from Iceland, there is one, and from Denmark, there are three papers. Table 2 shows the number of authors from each of the participating countries.

Table 2.
Number of authors in the proceedings from each country.
Most authors are affiliated in Norway (34), followed by 15 from Finland and 14 from Sweden. It is somewhat surprising that the Norwegian participation is strongly dominant, as Sweden has a population almost twice that in Finland, Norway, and Denmark, respectively. However, this Norwegian overweight confirms the expansion of DM in Norway that has taken place since 2002. Many of the researchers are experienced in the area, but there are also a few doctoral students represented, often writing together with their supervisors. A few of the papers are reporting parts of larger studies, but many of the papers are small-scale case studies.
6.2. Findings of Categories of Research Study Paradigms in the Papers in NORMA17
As said above in Section 4, there are six categories from Niss’ classification that are applicable here. Table 3 lists the research study paradigms according to Niss. This is how the NORMA17 papers are distributed among the categories:

Table 3.
Categorisation in research study paradigms of the papers in NORMA17.
Categories 1, 2, and 3 are dominant, which can be compared with the situation in the application in Niss [15] with 72 papers from three journals, where the first four categories attracted the most papers.
In the case Niss analyzed, 79% of all papers were in the first four paradigms. In NORMA17, 88% of all papers are in the first four categories. Papers in the category 6 Classroom and discourse studies are missing here, which may seem strange. Discourse is a concept that is visible in some of the papers, but they fall primarily into other categories. Classroom studies are important but of course in many ways demanding. Studies of mathematics in vocations and professions have been carried out in the Nordic countries as mentioned above, see also for example [71,72,73], but they are not present in this book.
The distribution of categories for choice of methods is presented in Table 4.

Table 4.
Categories for choice of methods for papers in NORMA17.
Thus, the empirical investigations are most common, and only two papers can mainly be seen as conceptual or theoretical investigations. In the choice of papers that Niss [15] explored, the qualitative investigations were 54% and the quantitative were 27%. Here, we have 56% and 38%, respectively. Thus, it seems that there is a somewhat higher degree of quantitative papers in NORMA17 than in the selection by Niss [15]. A closer look at the quantitative papers shows that all papers representing Finland except one are quantitative. One paper representing Sweden is quantitative. That paper is written by two authors coming from Finland. On the other hand, all papers from Sweden except one (the one by Finnish authors) are qualitative. Thus, the papers from both countries seem less balanced in preference of methods in this selection.
Now, the number of papers is small in both cases, and we may only see these conclusions as indications. From this overview of research study paradigms and choice of methods of the 32 papers, we proceed to a closer investigation of the papers.
6.3. Exposing a Background for the Further Characterization of Nordic Research in DM
A short exposé of the papers in the proceedings of NORMA17 will establish evidence for further claims about the current situation. Readers need to know the foundation for the conclusions made in the paper. To avoid a too general and abstract discussion, we need a rather concrete image of the content of the papers.
As the main structure for exposing the papers, we use three of the aspects that are evaluated in the reviews of the papers for NORMA conferences:
- Statement of problem/issue and discussion of its significance in the light of Nordic research in mathematics education or its general relevance for mathematics education research.
- Theoretical framework.
- Methodology and data analysis.
Based on this overview, an exploration of some specific aspects that are of interest to an international audience follows.
6.3.1. Aspect 1: Problems or Issues Presented in the Papers and the Significance of Them According to the Authors
For the first 20 of the 32 papers, a statement is made of what the authors see as their problems or issues and how they argue for the significance in the papers. The numbering of the papers will be used in the text and tables further down and is visible in the appendix and reference list, respectively, for each paper. The account here may seem to be a long story, but the intention is to help readers by a rather concrete and explicit picture of what the authors present in NORMA17.
Bommel and Palmér [40] study if and how the use of a digital application influenced the systematization and representation that the children spontaneously used when working on a combinatorial task. The aim is to elaborate on how the analogue and digital version of the task can be combined in teaching to contribute to children’s understanding and to explore the rationale for children’s choice of representation.
Fosse and Lossius [41] focus on the mathematical topics the kindergarten teachers find important to work with and their arguments for doing so. They refer to the tensions between what the official documents, including the framework (curriculum), prescribe and the kindergarten teachers’ own perceptions, meanings, and practices.
Dahl, Klemp, and Nilssen [42] explore collaborative tool-mediated talk in an example with two third graders working on a multiplicative task. They want to shed light on the idea that representations such as drawings are necessary mediational means in young learners’ collaborative talk.
Enge and Valenta [43] study students’ narratives on general properties of fractions. Starting with equal sharing, further teaching was built on students’ work and discussions. Videos were searched for narratives about generality of fraction properties.
Maugesten, Mosvold, and Fauskanger [44] examined second graders’ written responses to an open task to identify potential indications of emerging number sense. Implications of the findings for mathematical demands on teachers, when presenting tasks in lessons, are discussed.
Tossavainen and Hirsto [45] study expectancy value and self-efficacy from experiences of utilizing tablet computers for the learning of mathematics among primary and lower secondary students. Due to financial reasons, the implementation of use of tablets varies in different schools and subjects. Students’ beliefs and motivation to study mathematics is the interest of the authors.
Villalonga Pons and Andrews [39] study students’ problem solving when using a scaffolding mechanism, an orientation basis (OB). The OB consists of four dimensions: understand the problem, devise a plan, apply the plan, and review the task, each with three subareas or actions. The OB is meant to support the transition toward students being able to scaffold their own problem-solving actions.
Misfeldt, Jankvist, and Møllegaard Iversen [46] explores the phenomenon “mixed notation” as a result of the use of computer algebra system (CAS) in upper secondary school. The argument is that it is important to study the influence of CAS on mathematical writing and notation.
Larson and Pettersson [47] study university students’ use of proof by induction and especially the first step in such proofs. They argue that proof by induction is conceptually difficult.
Rensaa and Vos [48] investigate how university teachers interpret the teaching in a video on linear algebra in categories of procedural or conceptual knowledge. They claim that asking professionals in mathematics education may yield unreliable results if the notions are not carefully defined, explained, and discussed.
Viholainen, Lepik, Hemmi, Asikainen, and Hirvonen [49] investigate mathematics students’ views about proof. The countries Estonia and Finland are interesting to compare because earlier studies show differences in how proof and proof-related items are addressed in the school curricula of these countries.
The International Lexicon Project is led by Clarke [74], and here, Hannula [50] describes the Finnish part of it. The aim of the overarching project is to identify and compare lexica used by mathematics teachers for describing mathematics lesson events in Australia, Chile, China, the Czech Republic, Finland, France, Germany, Japan, and the USA.
Topphol [51] presents a correlation study of mathematics proficiency vs. reading and spelling proficiency. The motivation is to indicate that the correlation is not simple but may depend on other factors also, maybe working memory.
Opsal and Tonheim [52] study students with low reading abilities and word problems in mathematics. The motivation is to find out if students with low reading abilities struggle more with word problems than students with satisfactory reading abilities.
Hähkiöniemi, Nieminen, Lehesvuori, Fransisco, Hiltunen, Jokiranta, and Viiri [53] observe the processes of attending to and fostering in interaction between teacher andstudents in argumentation discussions. They argue that the concepts of attending to and fostering help understand how teachers can orchestrate argumentation discussions.
Hvalsøe Schou [54] studies how mathematical knowledge is presented to students in secondary school by means of symbols. She argues that mathematical symbols are essential in communicating, employing, and generalizing mathematical knowledge.
Petersson [55] investigated 259 grade 9 students solving two test items in algebra involving linear expressions. He argues that early arrived immigrants suffer from having larger parts of their mathematics education as second language students and struggle with advanced mathematics.
Kärki and Silfverberg [56] measured prospective class teachers’ attitudes toward learning mathematics and teaching mathematics. They are interested in whether there are differences in the prospective class teachers’ attitudes concerning mathematics in two programs with different entrance examinations.
Kacerja and Lode [57] analyze post-teaching conversations about mathematics in a school-based/practicum setting. They argue that finding the potentiality zone helps them get more insight into when and how to ask questions to foster student teachers’ reflections about mathematics.
Mosvold and Fauskanger [58] discuss the opportunities and challenges of using the MDI (mathematics discourse in instruction) framework for research in Norwegian teacher education. They suggest that the framework is relevant to use for analysis of classroom discourse that is problematic.
All the papers have clear research questions or aims, but when it comes to justification of the significance of the problem, the picture is more varying. In some cases, it is hard to find out what the authors see as the significance of the problem they analyze.
These 20 papers are a satisfactory basis for the later argumentation in the paper. Now, the theoretical approach and the most crucial concepts in these papers are exposed as they are described by the authors of the papers.
6.3.2. Aspect 2 Theoretical Framework as Presented by the Authors
The theoretical approach and the crucial concepts used in the papers as presented by the authors are shown in Table 5. One theoretical approach is common for several papers, namely statistical and measuring theory. Two papers claim use of a sociocultural theory, but for the rest, there are many different theoretical frameworks, and the number of different crucial concepts in the papers is even higher. The diversity and variation in theoretical approach is large. We note that the learning theories used changed from constructivism in 1994 to socio-cultural theory or theory of commognition in 2017. The research area of DM is widely spread when it comes to choosing theory, as is also the case internationally [75]. There is no specific Nordic preference concerning choice of topics or methods as far as can be seen from these papers, and there seems to be no homegrown Nordic theories in these papers.

Table 5.
Theoretical approach and crucial concepts used for the 20 first papers in NORMA17.
6.3.3. Aspect 3 Methods and Data Analysis
The data collected, methods used, and analysis outcomes are shown in Table 6. In 13 of the 20 papers, the data collected are written texts, such as questionnaires, responses, written problem solutions, written work, and so on. In three cases, the data consist of video recordings and in four cases, they consist of observations. The choices of methods are highly varying. The most common way to expose the analysis outcomes is in tables giving quantities of different statistical measures or coefficients.

Table 6.
Data, methods used, and outcome according to authors.
It is evident that Norén, Palmér, and Cooke [35] are right when they point to the variety of topics in the papers, and to the various methodologies and theoretical perspectives used by the researchers in NORMA17. Indeed, Nordic research in DM is a broad field.
6.4. The Literature Review in the Papers
Most of the papers start with an introduction including some review of literature. It is noticeable that few authors refer to other researchers in the Nordic countries. In almost half of the papers (15), there is no reference at all to other Nordic researchers (not including authors’ own papers or official Nordic documents). Six of the papers refer to one other Nordic paper, and one paper refers to two other Nordic papers. Ten papers have three or more other Nordic references. The impression is that Nordic research papers are not very visible among the references. As a curiosity, we note that only the three Danish papers refer to French didactical theories.
A conclusion could be that Nordic researchers are rather well acquainted with the international literature in DM, but they are not so keen on referring to other Nordic authors. One could suspect that the Nordic research is not so well known to them as research from outside the Nordic area, despite long-standing Nordic cooperation. It might also be that international research from outside the Nordic countries has higher status for the Nordic researchers. It would be an improvement of the collaboration among Nordic researchers and the links between them if they could choose to refer to other Nordic colleagues to a higher degree, when relevant. Possible cumulative effects might become more visible in that way. It would help to make Nordic research results better known abroad and be a counterweight to the international reports that often neglect Nordic studies.
6.5. The Role and Impact of Nordic Research in DM in Society
Examples from the overview of the papers in the NORMA17 proceedings will now feed the discussion of the corners of the socio-scientific triad and the links between them. A presentation of an image of the role and impact of Nordic research in society follows.
6.5.1. Corner 1 in the Triad: Researchers
Who are the persons in NORMA17 carrying out the studies on DM in the Nordic countries? The authors come from seven different Swedish universities, Chalmers Technology, Karlstad, Linnaeus, Luleå Technology, Mälardalen, Stockholm, and Uppsala. Expected to be represented are the universities of Gothenburg, Lund, Linköping, Malmö, and Umeå, together with some smaller institutions such as Kristianstad, Gävle, and Dalarna. Lund and Gothenburg are large universities, but neither of them has a department of DM. Historical reasons may have prevented the development of DM in these places [76]. That Umeå is absent is strange, as they used to have much activity in DM [77]. The reason for the absence here is not known. There are also seven represented universities in Norway. They are Agder, The Arctic, Norwegian Technology and Science, Stavanger, Volda, Western Norway, and Østfold. Here, the university of Oslo is missing. In Finland, the researchers come from the universities of Eastern Finland, Helsinki, Jyväskylä, Turkku, and Åbo Academy. The Danish authors are from the universities of Aalborg, Aarhus, and Southern Denmark, but no one is present from the University of Copenhagen. Finally, there are writers from the universities of Tallin and Iceland. In total, 21 universities are represented among the participants of NORMA17 compared to the 45 universities that were part of NoGSME [12]. Thus, only less than half of the institutions with doctoral students and supervisors in the Nordic Graduate School in DM were present here. That could mean that the research activities in DM in some of the former universities in NoGSME are no longer as lively as 15 years ago. That conclusion would need further investigation, as we are looking at a momentary exposition. A process of merging universities has been going on in the Nordic countries; therefore, the number of universities is smaller now, which also influences the situation.
A few authors come from outside the academic world: one Danish man works in the Ministry of Education, and one Estonian woman works in an upper secondary school. The positions of the researchers illustrate that the research activity is carried out with state money and is driven in official institutions. The researchers have positions at all levels of the academic system, from doctoral student to professor.
There is a balanced mixture of women and men among the authors in the proceedings, with a small overweight of women from Sweden and Norway and a small overweight of men from Finland and Denmark. The interests of the researchers are at all levels of the educational system from preschool to academic studies, and this probably exemplifies their work profiles.
There is some collaboration over the borders, as one professor works both in Sweden and Finland, a Swedish man is an assistant professor in Norway, a Finnish man is a professor in Sweden, an Englishman is a professor in Sweden, and a Dutch woman is a professor in Norway. Seven of the papers have authors from more than one country, which illustrates the closeness and cooperation of the Nordic countries. The links to countries outside the Nordic area indicate that research in DM is international, although some of the aspects that are studied are highly culturally bound.
Didactics of mathematics is a multidisciplinary research area, and mathematics should always be a central part of the studies [78], but they can in addition to that build on pedagogy, psychology, history, sociology, logic, philosophy, linguistics, educational sciences, or many other areas. To which disciplines do the researchers that we are discussing belong? Several of them have their roots in mathematics as such and have later become more interested in questions about education and teaching and moved to DM. Many of the authors are teacher educators or teachers of mathematics at universities in different programs. Some are more closely linked to pedagogy or have sociological interests. The researchers work in departments linked either to mathematics or to educational sciences and teacher education. The roots of the researchers are sometimes visible in the kind of questions they ask in their studies; for example, it is common that teacher educators study their own student–teachers.
From the papers in NORMA17, it is possible to get a sense of research from four of the Nordic and Baltic countries, but Iceland and Estonia are only vaguely discernible, and Latvia and Lithuania are not present at all. Thus, a few more words need to be said about those participants in NORME, the Nordic Society of Research in mathematics Education [79]. In Iceland and Estonia, there is research education and research studies going on that feature positions created and taken in DM. In Iceland, it was common for students to go abroad to get their doctorates or to have a foreign supervisor. However, there is promising development pointing to a more internal education [80]. Estonia had an impressive development after 1991, when it was free from the Soviet Republic, although mathematics education had always been based on Estonian language and textbooks also before 1991. Research in DM was strong at Tartu University, since long ago, but it is now also growing in Tallin. An additional professorship has just been announced. The two other Baltic countries, Latvia and Lithuania, are not visible in this selection of papers, but researchers from both countries have been active in the Nordic community of DM, and research studies are ongoing.
6.5.2. Corner 2 in the Triad: Messages from the Researchers
What researchers say as result of their work is called their messages. As an academic person, one of the obligations one has is to make one’s message clear and heard by those who can benefit from it. This dissemination process can take place in many ways, and one is what we discuss here, to publish in refereed conference proceedings. Other channels are scientific journals, lectures and presentations, books, seminars, and popular talks. What is the content of the messages that the authors are spreading in the NORMA17 proceedings?
At the preschool level, there is one message about the children and one about the preschool teachers. When the children solve a combinatorial problem, it is helpful for them to use both paper and pencil and a digital application. Using the digital application seems to lead to more systematic documentation and fewer duplications [40]. The second study at this level demonstrates that preschool teachers can have different views on why children should work with mathematics. They argue either with children’s interest or need for school preparation or both. Children’s possibilities to participate actively in a democratic society was another argument. The main topics the teachers prefer are in order counting, classification, concepts, shapes, and sets [41].
For early school years, there are several messages. For third graders, it is shown that representations such as drawings are necessary mediational means in the learner’s collaborative talk [42]. Another message concerns fourth graders and tells us that when they learn fractions, narratives can provide insights into their opportunities to learn as well as about the complexity of the topic [43]. When second graders were given an open task about the number 24, it became clear that the demands that teachers are faced with are challenging when teaching early number sense: to interpret students’ responses and often quickly, to figure out what students know and are able to do by looking at their responses, to know about quantity value and column value, and to know about models for important components of number sense [44]. For several age groups in primary and lower secondary school, the students’ motivation to learn mathematics is influenced by the use of tablet computers in school. Especially boys’ intrinsic value in studying mathematics increases, but both girls and boys rather disagree that computers made it easier to learn mathematics [45].
For secondary school, authors give several messages. For first year secondary students, it is probable that the use of an orientation basis (OB) when solving mathematical problems supports the development of students’ scaffolding behavior. The chances of completing a task successfully are enhanced if students address the two OB checking actions [39]. For upper secondary school, it is shown that students mix notations from ordinary writing and from the use of computer algebra systems (CAS). This mixed notation calls for an awareness of how this ongoing transformation of written mathematical texts influences students’ mathematical learning [46].
At the academic level, there are three messages. Students working with proof by induction used different cases as the induction basis, and it was common to use more than one case, which is superfluous for the tasks [47]. When university teachers are asked to judge if the teacher in a video is aiming for procedural or conceptual knowledge, it is revealed that there are divergent interpretations of conceptual knowledge. The recommendation is that the notions should be carefully defined and explained when used to evaluate the quality of teaching videos [48]. University students in both Finland and Estonia highly appreciate the importance of proof in school mathematics as well as in mathematics in general. Their reasons are that proofs give support for the understanding and development of thinking skills [49].
Concerning communication, language, and texts in DM, it is reported that Finnish mathematics teachers’ terminology is more focused on the interaction between teacher and students and on lesson organization rather than on mathematics specific aspects of teaching [50]. Mathematics proficiency is shown to correlate stronger with spelling proficiency than with reading proficiency. The correlation between language and mathematics is not simply a matter of the ability to read and understand the mathematics task [51]. Another part of the larger project SPEED (The function of special education) shows that text might be a barrier for students, but the context can also be a possible help in solving problems [52]. The concepts attending to and fostering were shown to be helpful in examining how teachers orchestrate the whole class discussions, when students were expected to argue for their mathematics [53]. A method is introduced for examining teacher instruction, especially to discover how mathematical knowledge is presented to students by means of symbols. Four different roles of symbols are identified [54]. Second language students have problems with advanced mathematics, and they suffer from having studied large parts of mathematics in a second language [55].
Measuring prospective class teachers’ attitudes to learning mathematics and teaching mathematics shows that attitudes toward teaching were more positive than toward learning. Students were more positive in a more mathematically focused program [56]. Post-teaching conversations in mathematics practicum reveal that there are ways to direct reflections to be more mathematics-based [57]. The mathematics discourse in instruction (MDI) framework provides opportunities for highlighting the complexities of mathematics teaching, but it does not distinguish between mathematically valid and invalid responses, which might limit its usefulness [58].
Already, these 20 messages from the 32 papers expose an impressive amount of new knowledge on teaching and learning mathematics. Expressing the messages in a few words or sentences, as done here, does of course not give justice to them, and they are in fact much more nuanced than shown here. However, to offer an overview, there is a need to simplify. The interested reader must go to the source to get a fair impression of the studies. In order to be able to benefit from the messages, educators would need to relate them to the knowledge used so far about the issues and consider if they demand some adjustments of what is going on in the process of teaching and learning mathematics. How can that be done? Are the authors able to link the new knowledge to earlier knowledge and indicate clear ways of how to proceed? How solid are the messages? “More research is needed” is a phrase we often find in the reports here. The researchers are humble and careful not to draw too definitive conclusions from their work. Then, that would be a prompt for other researchers to take up the investigation, replicate, or go further. We do not often find that such initiatives have been the starting point in the papers. Are researchers building enough on what has been discovered by other researchers? In some of the papers, the authors show that they are taking earlier knowledge further, but in some cases, the results are not linked to specific earlier findings.
6.5.3. Corner 3 in the Triad: Targets or Receivers of the Messages from Researchers
For academic teachers, there is a demand to publish (publish or perish), and thus, we need to realize that one strong driving force for many of the papers is that one must carry out research, present it, and publish. One target is the leaders in academia, who want to see research activity among the employees. However, once the researchers have chosen their problems to study, they also indirectly have chosen the main target group they will publish for. Target groups can be other researchers, students, mathematics teachers, teacher educators, textbook authors, politicians, curriculum and policy makers, educational administrators, etc. For example, students are addressed when researchers try out interventions that can work as direct help in the learning process. Among the papers, here we notice the observation basis [39] or the use of drawings in collaborative tasks in problem-solving [42]. Such messages are also relevant for teachers as they need to act as mediators for the message to the students. Messages on learning and cognition often go to teachers with the intention that they might want to develop their teaching or include recent research results in their profession. Such results are often used in professional development for teachers or in-service training of teachers. Many of the results concerning mathematics teaching are of interest both to teachers and to teacher educators. For about four decades, there has been a demand for teacher education to be research-based, which makes it necessary for teacher educators to follow the latest results in DM. There is also a demand from society in general that research in DM should deliver results that in some sense improve the teaching and learning of mathematics in schools. Björkqvist [5] (p. 38) writes that research in DM should remember that an important condition for its survival is to remain an organic part of the society that feeds the rest. That means to be sensitive to the expectations that society has and to do one’s best to meet these expectations. However, it is hard to discern the improvements of teaching and learning mathematics in society, and it often takes a long time before research results are accepted, implemented, and known more generally and can have an impact on the learners. The process of implementing results is much more complex than we understood earlier [75].
The messages in the papers most often are directed to more than one target group. All the papers are directed to other researchers and will hopefully be read and referred to in later studies, thus helping in creating cumulative knowledge in the field. A summary of the targets of the papers indicates that 4 messages are for the students, 3 messages are for prospective teachers, 22 messages are directed to mathematics teachers in school, and 4 are directed to university teachers. Teacher educators could be interested in at least 15 of the messages, and a couple of them would be of help for policy makers or politicians. An interesting investigation would be to explore to what extent these messages have reached the persons in the intended target groups.
6.6. Short Overview of the Results in This Paper
In Section 6.1, it is shown that 50% of the papers in NORMA17 are from Norway, 19% are from Finland, and 19% are from Sweden. From the authors, 45% are from Norway, 20% are from Finland, and 18% are from Sweden. There are about the same number of women as men among the authors. It is most common to have three authors or more for each paper. Seven papers have authors from more than one Nordic country. Norway dominates both concerning the number of papers in the proceedings and the number of authors in the conference proceedings. That is evidence of the efforts that have been made in Norway for two decades now to build up doctoral education and strong groups of researchers.
In Section 6.2, we find that about one-third of the papers in NORMA17 fall into the category studies of learning and cognition, including problem-solving strategies. One-third of the papers are categorized as studies of outcomes of interventions, including teaching approaches and experiments. The rest of the papers fall into four categories, 3 to 5 and 7, according the list of research study paradigms in Niss [15]. From the papers in NORMA17, 88% fall into the first four categories, compared to 79% of the papers in the cases reported by Niss [15].
Concerning choice of methods, 94% of the papers in NORMA17 are qualitative or quantitative empirical studies, and only two papers are conceptual or theoretical investigations. From Finland, quantitative studies dominate, and from Sweden, most studies are qualitative.
In Section 6.3.1, we find that the questions posed, or problems investigated in the papers from NORMA17 are as many as the papers and they span from the level of preschool to studies of teaching and learning mathematics at the tertiary level.
In Section 6.3.2, it is visible that the authors describe their choice of theoretical approach in a multitude of ways. The use of sociocultural theory or statistical theories are present in more than one study, but otherwise, most papers claim a different theoretical approach. The crucial concepts used in the papers are varied to a high degree. No specific Nordic preference can be found, and no homegrown theories are visible in the 20 papers.
In Section 6.3.3, the authors of papers in NORMA17 expose a manifold of ways of choosing what data to collect and the methods for analysis used in the studies. No specific Nordic preference is discernable.
In Section 6.4, it is shown that in almost half of the papers in NORMA17, there are no references to other Nordic publications. Less than one-third of the papers have three or more Nordic references.
In Section 6.5.1, the researchers reporting in NORMA17 are focused. They come from 21 universities in six different countries. Some of the universities that were expected to be visible because of their known research activity in DM are missing, such as authors from Copenhagen, Oslo, Gothenburg, and Umeå. The authors represent all levels of positions from doctoral student to professor.
In Section 6.5.2, the messages from the researchers are exposed. We notice that there are as many messages as there are papers in NORMA17. In some cases, it is explicitly made clear how a specific message adds to earlier knowledge, but in many cases, that is not visible. Researchers are humble, and they often express that more research is needed to confirm the findings exposed.
In Section 6.5.3, the targets of the messages from researchers are reported. Most of the messages are directed to mathematics teachers in school, but there are also messages to students, prospective teachers, university teachers, teacher educators, and policy makers. It is not known to what degree such messages reach the intended targets.
6.7. Limitations
In an overview of research from the Nordic countries, it is crucial to analyze what is selected as basis for the presentation. In this case, the research reports from the latest common Nordic conference in didactics of mathematics were chosen. This selection might be criticized for having some irregularities, but it is less biased than any personal selection. Thus, this was the choice made.
Another limitation is the rather small number of papers that are included in the investigation. One needs to be careful with the conclusions because of that, and the indicated results may have to be further tested if one wants to make more firm claims about them. The exploration of the papers was made by only one researcher, and it could be claimed that there are misinterpretations or misunderstandings of what the authors in NORMA17 are writing. I have given the paper to the main editor of the NORMA17 proceedings to read to get some confirmation of my interpretations. She responded and could add some facts and confirm that the picture I present is adequate. I am aware that just a few lines about longer papers concerning questions, theory, or methods cannot do justice to the work presented in that paper or to the conclusions drawn. However, the reader can go to the source and form her own opinion, as the book is available on the internet at the webpage of SMDF (Svensk förening för matematikdidaktisk forskning (Swedish Society for Research in Mathematics Education)).
The intention of the author is to make a fair and just presentation of Nordic research in DM.
7. Discussion
In this section, some perspectives on the findings will be discussed from an insider’s view. The author’s more personal emphases are guiding the aspects that are further corroborated here.
7.1. Nordic Collaboration
One characteristic feature of research in DM in the Nordic countries is the Nordic collaboration. This is visible in many ways. The Nordic umbrella organization NORME (Nordic Society for Research in Mathematics Education) created in 2008 as a heritage after NoGSME [79] cares for the NORMA conferences that take place regularly since 1994, and for the Nordic journal NOMAD. Nomad organizes yearly seminars for doctoral students around academic writing and publishing in journals. Nordic networks of researchers cooperate on specific topics or interest such as textbooks or students with special needs [33,34]. Among the papers we investigate from NORMA17, there are many with authors from more than one of the countries [45,47,49,53,67,68,69]. Research projects are carried out in collaboration over the borders, such as the collaborative project on teachers’ use of curriculum material [68,69] and the NorBa project (Nordic Baltic cooperation) [81,82]. Mentioned above already are the Nordic networks for research on mathematics textbooks and for studies on students with low achievement, and there are others, too. A strong reason for the Nordic cooperation is the need to reach a critical mass in research in DM. All the countries are small and can benefit from this cooperation. Other reasons are the common historical development as independent democratic countries, the societal systems, and the educational traditions and development, and the linguistic connections and culture. Research results in DM are not easily transferred to other countries with different teaching traditions and educational structures. The similarities between the Nordic countries from such perspectives could mean that Nordic research results are more relevant for neighboring countries than research from other parts of the world.
7.2. The Breadth of Nordic Research in Didactics of Mathematics
Another characteristic feature is that Nordic studies in DM show a breadth in research interests, theoretical approaches, and choice of methods that seems to be as wide as in the international case. There are no limitations in the research in DM that takes place in the Nordic countries. It is not possible the point to specific topics or areas of study that the Nordic researchers prefer. Above, I have mentioned a few areas that were clearly visible, such as the use of ICT, textbooks, mathematical reasoning, use of language and communication, feedback, students’ attitudes, and beliefs, and the concept of inquiry. In NORMA17, we find papers representing these areas. For example, the use of ICT is treated in papers [40,45,46], textbooks are addressed in [67,68,69], mathematical reasoning in papers [39,47,53,63], language and communication in papers [42,43,50,51,52], students’ attitudes and beliefs in papers [45,49,56], and inquiry in paper [70]. Teachers and teaching, also mentioned above, is the focus of many of the papers in NORMA17. However, we find many other areas of interest for the researchers. Thus, both continuity and breadth are present in the choice of questions.
7.3. Choice of Research Study Paradigms and Categories of Choice of Method
Most of the papers in NORMA17 fall into two of the research study paradigms used. Ten papers are categorized as studies of learning and cognition, including problem-solving strategies, and eleven papers are seen as studies of outcomes of interventions, including teaching approaches and experiments. Thus, only 11 of the papers were categorized in the other four research study paradigms appearing here. The variation is not so great in choosing a paradigm.
In the categorization Niss [15] made of research study paradigms, he expresses worries about the fact that just a few study paradigms are common. He says, “Since there are so many different things within and around mathematics teaching and learning that we, in the mathematics education community, don’t understand, we cannot allow our studies to congeal into a few hardened study paradigms already at this relatively early stage of development of our field” [15] (p. 406). He suggests that we need “more studies providing in-depth analyses of mathematical entities, topics and structures in an educational setting, more studies involving conceptual analyses (in addition to conceptual frameworks), more studies providing (civilized) critique and analysis of existing publications, more studies that compare curricula and syllabi, more studies of the historical development of mathematics teaching and learning as well as of mathematics education as a research domain, more replication studies of empirical investigations, more studies of the sociology of mathematics education, more studies that attempt to identify causal relationships and mechanism responsible for them, and so on and so forth” (p. 407). The selection of papers in NORMA17 still falls into just a few of the research study paradigms identified, and we see little of the kind of contributions Niss is asking for. We find one paper where a framework is criticized, questioned, and investigated further [58], and one paper where the authors try to synthesize existing studies of one specific phenomenon [70]. Otherwise, many of the papers are exploring one specific phenomenon without fully relating the outcomes to earlier knowledge and experience. In some cases, the authors present studies that are part of larger projects. In the larger research groups visible from the papers, it is more obvious how capacity is created to build on earlier results and gather results cumulatively. That is the case, for example for the papers [51,52], being part of the SPEED project (The function of special education, [83]) and the paper [42] being part of the project LaUDiM (Language use and Development in the Mathematics classroom). Another larger study is Mastering Ambitious Mathematics Teaching (MAM) mentioned in paper [61] and the project Quality in the Subjects Danish and Mathematics (KiDM) in paper [70]. Paper [67] presents part of a larger study on Swedish school algebra. With the impressive number of results that have been produced during the latest decades, we need summaries and overviews, synthesis, and analyses for new researchers to be able to enter the field with understanding of what we build on.
7.4. Some Topics, Theories, and Areas of Study in Nordic Research in DM
Fifteen years ago, results were found concerning studies of mathematics textbooks and texts, on mathematics teachers and teaching, of specific areas of the mathematics curriculum or development of mathematical concepts, of mathematics teaching and learning in the classroom, and of the history of mathematics related to learning and teaching [30]. From this overview of the papers in NORMA17, it is evident that all these areas are represented here except for the history of mathematics related to learning and teaching. That general picture would coincide with the international situation. Among the 20 papers we investigated closely, there is no use of specific Nordic theories. We can find use of the Danish competence model in three papers [62,66,70]. In earlier overviews [5,31,76], other Nordic theoretical approaches are mentioned, such as phenomenography and theory of variation, critical mathematics education, framework for mathematical reasoning, and the theoretical model for mathematics teachers’ development of a professional identity. Those frameworks are not present in NORMA17. The areas of study mentioned in earlier overviews [5,76] but not included here are for example mathematics education and democracy, gender and mathematics, the history of mathematics, and the teaching of mathematics. Missing are also some of the kinds of papers Niss is pointing to such as analytic and theoretical essays, synthesis of earlier research on a specific issue, studies on vocations and professions, and causal studies.
What topics inside school mathematics are visible in the papers? It is evident that not all papers deal with a certain mathematical topic. Some papers report on general educational issues, such as the use of tablet computers, attitudes to teaching and learning mathematics, post-teaching conversations, or similar issues. However, we can discover at least the following topics in mathematics: combinatorics, fractions, number sense, multiplication, problem-solving, word problems, mathematical symbols and notation, linear algebra, mathematical proof, proof by induction, linear expressions, school algebra, and so on. No special area of mathematics seems to be favored by Nordic researchers.
Some typical areas of study from DM are visible, such as self-efficacy, expectancy value, beliefs and motivation, proficiency, orientation basis, mixed notation, attending to and fostering argumentation, attitudes to mathematics, post-teaching conversations, mathematics discourse, inquiry-based learning, low-achieving students, and many others. The breadth is great, showing no specific feature or brand of Nordic character.
7.5. Nordic Research in DM and Society
Will society win or improve from the outcomes of research in MD? What would the common person consider the most urgent problems in mathematics education, and are they solved? As a result of the strong focus in the media on results in school mathematics from the TIMSS (Trends in Mathematics and Science Study) and PISA (Program for International Student Assessment) studies, one might fear that the public wants a higher mean value for the country in such international tests. It is commonly known that the results for Finland are slightly better than from the other Nordic countries. Finland also has a stronger teacher education with a master’s degree on all levels and a higher status for teachers. What are the relations between these facts? Not even the Finnish researchers are convinced about that. More relevant than points on written tests might be to ask for the long-term mathematical knowledge needed in the work force. However, there is no study among these papers about mathematics for work or in the profession, which is category 10 in Niss [15].
We might want to ask if all problems in education can be solved by research. For example, the lack of well-educated mathematics teachers in Sweden and Norway must be solved by politics and cannot be solved by researchers, as I see it [84]. Björkqvist [5] points to the fact that it seems as if research in DM is avoiding the “how” component in mathematics education, especially for typical large classes with a heterogeneous group of students. He claims that such studies would be seen as useful (p. 36). Are the needs of the educational system satisfied? We have introduced mathematics for all in the Nordic countries. However, are we able to handle students with special needs or highly talented students? Among the papers we investigate here, there are a few papers posing questions on low-achieving students. As mentioned, it has been an area of interest for Nordic researchers.
Is it visible for the receivers of the messages that research is systematic inquiry made public [85]? We see many different studies, and they must partly be perceived as giving fragmented results. The target groups would express a need for cumulative studies and results that enhance what earlier studies have shown. They must ask for summaries or overviews of studies to get a systematic and holistic description. Researchers need to stand on the shoulders of giants [86] and recognize the results of earlier studies when they carry on.
We have explored the corners of the socio-scientific triad carefully. The researchers, messages, and targets have been scrutinized above. The side on the bottom of the triad, inquiry, or questions, is represented in Section 6.3.1 with short descriptions of each question or issue in the papers. The right side of the triad, the dissemination, includes the papers from NORMA17, which the authors chose as their way of disseminating the outcomes of their investigations. They are the object of study in the whole paper here. The left side of the triad, the impact of the research, we cannot study in more detail in this paper if we mean actual impact. We can study possible impact but not what really happens. The impact of research is hard to discern, and it takes a long time before it is noticeable. When discussing the political pressure on mathematics education research, Niss [75] (p. 1298) concludes that “… it should be admitted that the nature of our results is not always easy to understand and use, because they are multifaceted and need substantial interpretation, and we are much better at demonstrating what does not work and at providing explanations of why, than the opposite.” As we know rather little about the actual impact of the results, I suggest that some efforts will be made to study the impact of research in DM on society in the Nordic countries.
8. Conclusions
What characterizes recent Nordic research in didactics of mathematics? The Nordic cooperation is a characteristic feature of research in DM in the Nordic countries. The Nordic collaboration is multifaceted and has long traditions, and it continues to be strong and visible in many ways. It can be strengthened if Nordic researchers more often value, use, and refer to the studies and results by their Nordic colleagues. It would also be valuable to show how knowledge on teaching and learning mathematics in the Nordic area is cumulative.
Nordic didactics of mathematics is a lively research field in a state of strong development with many new doctors and ongoing studies, especially in Norway. The field is broad, and the methods are varied in the same way as for international research in DM. No unified grand theory is valid, but there are influences of theory from many surrounding disciplines. Specific Nordic theories are sparsely used. The group of active researchers and of doctoral students is growing, and many new positions have been created over the last ten years. With this great expansion of research, the collected knowledge is growing and not easy for newcomers to comprehensively understand. The field is not cumulative enough, and there is a need to engage in work that synthesizes the field [17] (p. 80). As Niss [15] points out, there is also need for courageous researchers that are not in predominant paradigms.
The international research in DM has expanded from the 1960s to embrace all categories of learners, teaching on all levels in many situations, and a multitude of questions linked to mathematics teaching and learning [75]. The same has happened in the Nordic countries, only some decades later. The Nordic area is the little sister in DM and has not yet much to boast of. Björkqvist [5] has noted that the how-question when it comes to teaching and learning mathematics maybe has been neglected, and issues about teaching methods have not been popular. Still, this seems to be the case, and that should be a concern. As noted above, forces should go to creating overviews, syntheses, and analytic investigations.
I agree with Niss [15] (p. 407) when he says, “As a result of the impressive development of Nordic mathematics education research since the mid-1990s, the Nordic community now ought to be strong enough to engage in conducting and publishing such non-mainstream studies”, referring to the ones in the citation of him above. I repeat that it is still too early in the development of DM in the Nordic countries to discern what is going to be important, influential, and viable studies. Perhaps many decades later, we may see a Nordic version of DM as we now have the French DM, the Dutch DM, and so on. The Nordic collaboration will continue to support the development of research in DM as a broad field of study that deals with a multitude of questions of teaching and learning mathematics.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Proceedings of NORMA17. http://matematikdidaktik.org/wp-content/uploads/2019/05/NORMA-17-2018-papers-SMDF-skriftserie-f.pdf (accessed on 26 February 2021).
Acknowledgments
Thanks go to University of Agder for supporting the publication of the paper, and to Ann Sofi Röj-Lindberg, Trygve Breiteig and Kristin Bjarnadottir for supplying national facts. Thanks also to Eva Norén for facts about some presentations and for reading an earlier draft of the paper and confirming the picture described of NORMA17.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The content of the proceedings of NORMA17
Early years mathematics
Mathematics in Swedish and Australian Early Childhood Curricula
Audrey Cooke
Paper or and digital: A study of combinatorics in preschool class
Jorryt van Bommel, Hanna Palmér (1)
“I find that pleasurable and play-oriented mathematical activities create wondering and curiosity” Norwegian kindergarten teachers’ views on mathematics
Trude Fosse, Magni Hope Lossius (2)
Primary mathematics
Collaborative tool-mediated talk—an example from third graders
Heidi Dahl, Torunn Klemp, Vivi Nilssen (3)
Narratives constructed in the discourse on early fractions
Ole Enge, Anita Valenta (4)
Second graders’ reflections about the number 24
Marianne Maugesten, Reidar Mosvold, Janne Fauskanger (5)
Secondary mathematics
Tablet computers and Finnish primary and lower secondary students’ motivation in mathematics
Timo Tossavainen, Laura Hirsto (6)
Supporting students’ mathematical problem solving: The key role of different forms of checking as part of a self-scaffolding mechanism
Joana Villalonga Pons, Paul Andrews (7)
Negotiating mathematical meaning with oneself—snapshots from imaginary dialogues on recurring decimals
Eva Müller-Hill, Annika M. Wille
Upper secondary mathematics
Mixed notation and mathematical writing in Danish upper secondary school
Morten Misfeldt, Uffe Thomas Jankvist, Steffen Møllegaard Iversen (8)
University mathematics
Proof by induction—the role of the induction basis
Niclas Larson, Kerstin Pettersson (9)
Interpreting teaching for conceptual and for procedural knowledge in a teaching video about linear algebra
Ragnhild Johanne Rensaa, Pauline Vos (10)
Research study about Estonian and Finnish mathematics students’ views about proof
Antti Viholainen, Madis Lepik, Kirsti Hemmi, Mervi Asikainen, Pekka E. Hirvonen (11)
Communication, language and texts in mathematics education
The national validation of Finnish mathematics teachers’ Lexicon
Markku Hannula (12)
A correlation study of mathematics proficiency VS reading and spelling proficiency
Arne Kåre Topphol (13)
Students with low reading abilities and word problems in mathematics
Hilde Opsal, Odd Helge Mjellem Tonheim (14)
Attending to and fostering argumentation in whole class discussion
Markus Hähkiöniemi, Pasi Nieminen, Sami Lehesvuori, John Francisco, Jenna Hiltunen, Kaisa Jokiranta, Jouni Viiri (15)
The roles of mathematical symbols in teacher instruction
Marit Hvalsøe Schou (16)
Second language students’ achievement in linear expressions and time
since immigration
Jöran Petersson (17)
Mathematics teacher education
Prospective class teachers’ attitude profiles towards learning and teaching mathematics
Tomi Kärki, Harry Silfverberg (18)
An initial analysis of post-teaching conversations in mathematics practicum: Researching our own practice
Suela Kacerja, Beate Lode (19)
Opportunities and challenges of using the MDI framework for research in Norwegian teacher education
Reidar Mosvold, Janne Fauskanger (20)
Assessing prospective teachers’ development of MKT through their teacher education: A Malawian case Arne Jakobsen, Mercy Kazima, Dun Nkhoma Kasoka (21)
Continuing professional development
Towards an organizing frame for mapping teachers’ learning in professional development
Daniel Brehmer, Andreas Ryve (22)
Good mathematics teaching as constructed in Norwegian teachers’ discourses
Janne Fauskanger, Reidar Mosvold, Anita Valenta, Raymond Bjuland (23)
Teachers’ mathematical discussions of the Body Mass Index formula
Ragnhild Hansen, Rune Herheim, Inger Elin Lilland (24)
Teachers’ attention to student thinking, mathematical content and teachers’ role in a professional learning community
Odd Tore Kaufmann (25)
Teacher learning in Lesson Study: Identifying characteristics in teachers’ discourse on teaching
Anita Tyskerud (26)
Adopting the developmental research cycle in working with teachers
Jónína Vala Kristinsdóttir (27)
In-service teachers’ positioning when discussing the body mass index
Toril Eskeland Rangnes, Rune Herheim, Suela Kacerja (28)
Curricular aspects of mathematics education
Characterizing Swedish school algebra –initial findings from analyses of steering documents, textbooks and teachers’ discourses
Kirsti Hemmi, Kajsa Bråting, Yvonne Liljekvist, Johan Prytz, Lars Madej, Johanna Pejlare, Kristina Palm Kaplan (29)
A cross-cultural study of teachers’ relation to curriculum materials
Leila Pehkonen, Kirsti Hemmi, Heidi Krzywacki, Anu Laine (30)
Mathematics education in general
Estonian and Finnish teachers’ views about the textbooks in mathematics teaching
Leila Pehkonen, Sirje Piht, Käthlin Pakkas, Anu Laine, Heidi Krzywacki (31)
Inquiry-based Learning in Mathematics Education: Important Themes in the Literature
Jonas Dreyøe, Dorte Moeskær Larsen, Mette Dreier Hjelmborg, Claus Michelsen, Morten Misfeldt (32).
References
- Jonson, K.G. Undersökningar Rörande Problemräkningens Förutsättningar Och Förlopp. Akademisk Avhandling, Investigations About the Presuppositions and Course of Problem-Solving. Ph.D. Thesis, University Uppsala. A & W, Uppsala, Sweden, 1919. [Google Scholar]
- Nykänen, A. Alkeisgeometrian Opetuksesta Suomessa Erityisesti Oppikirjojen Kehitystä Silmällä Pitäen, On Beginner Education in Geometry in Finland with Special Focus on Textbook Development. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 1954. [Google Scholar]
- Lahti, A. Virheet Opetusopillisena Ongelmana: Lähinnä Matemaattiseen Tietoalueeseen Sijoittuva Opetusopillinen Tutkimus Mistakes as a Problem in Education: Research Related to the Mathematical Area of Knowing. Ph.D. Thesis, Kasvatusopillinen Korkeakoulu University, Kasvatusopillinen, Finland, 1949. [Google Scholar]
- Werdelin, I. The Mathematical Ability. Experimental and Factorial Studies. In Studia Psychologica et Paedagogica, Investigationes X; Gleerup: Lund, Sweden, 1958. [Google Scholar]
- Björkqvist, O. Matematikdidaktiken i Sverige en Lägesbeskrivning av Forskningen och Utvecklingsarbetet Didactics of Mathematics in Sweden—A Description of the State Regarding Research and Development; Kungliga Vetenskapsakademin: Stockholm, Sweden, 2003. [Google Scholar]
- Ahtee, M.; Vatanen, V. The Finnish Graduate School of Mathematics, Physics and Chemistry Education. In Research on Mathematics and Science Education. From Beliefs to Cognition, from Problem Solving to Understanding; Ahtee, M., Bjorkqvist, O., Pehkonen, E., Vatanen, V., Eds.; University of Jyväskylä: Kasvatusopillinen, Finland, 2001; pp. 5–10. [Google Scholar]
- Leder, G.C.; Brandell, G.; Grevholm, B. The Swedish Graduate School in Mathematics Education. Nord. Stud. Math. Educ. 2004, 9, 165–182. [Google Scholar]
- Brandell, G.; Grevholm, B.; Wallby, K.; Wallin, H. (Eds.) Matematikdidaktiska Frågor Resultat Från en Forskarskola Questions in Didactics of Mathematics Results from a Graduate School; SMDF & NCM: Göteborg, Sweden, 2009. [Google Scholar]
- Hodgson, B.R.; Rogers, L.F.; Lerman, S.; Lim-Teo, S.K. International Organizations in Mathematics Education. In Third International Handbook of Mathematics Education; Clements, M.A., Bishop, A.J., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Springer: New York, NY, USA, 2013; pp. 901–947. [Google Scholar]
- Grevholm, B. The Nordic Graduate School in Mathematics Education—A Growing Network. Nord. Stud. Math. Educ. 2005, 10, 61–62. [Google Scholar]
- Grevholm, B. The Nordic Graduate School in Mathematics Education. Nord. Stud. Math. Educ. 2007, 12, 79–83. [Google Scholar]
- Grevholm, B. Self-Evaluation of the Nordic Research Schools in the Humanities and Social Sciences 2004–2008. Available online: https://www.researchgate.net/publication/242494223 (accessed on 5 April 2021).
- Grevholm, B. The Nordic Graduate School in Mathematics Education—Planning for the Future. Nord. Stud. Math. Educ. 2008, 13, 93–98. [Google Scholar]
- Grevholm, B. Nordic Doctoral Programs in Didactics of Mathematics. In US Doctorates in Mathematics Education Developing Stewards of the Discipline; Reys, E., Dossey, J., Eds.; AMS: Providence, RI, USA; MAA: Washington, DC, USA, 2008; pp. 189–194. [Google Scholar]
- Niss, M. Dominant Study Paradigms in Mathematics Education Research—For better and for Worse. Global Trends and their Impact on Nordic Research. In Nordic Research in Didactics of Mathematics: Past, Present and Future; Grevholm, B., Hundeland, P.S., Juter, K., Kislenko, K., Persson, P.-E., Eds.; Cappelen Damm Akademisk: Oslo, Norway, 2013; pp. 395–408. [Google Scholar]
- Björkqvist, O.; Finne, L. (Eds.) Matematikdidaktik i Norden. Didactics of Mathematics in the Nordic Area. Rapporter Från Pedagogiska Fakultetenvid Åbo Akademi; Reports; Pedagogical Faculty at Åbo Academy: Vasa, Finland, 1994; p. 8. [Google Scholar]
- Björkqvist, O. Supervision of Mathematics Education Research in the Nordic Countries. In Nordic Research in Didactics of Mathematics: Past, Present and Future; Grevholm, B., Hundeland, P.S., Juter, K., Kislenko, K., Persson, P.-E., Eds.; Cappelen Damm Akademisk: Oslo, Norway, 2013; pp. 77–86. [Google Scholar]
- Bjarnadóttir, K. Recommendations of the Royaumont Seminar on Primary School Arithmetic. Influences in the Nordic countries. In Dig Where You Stand. 4. Proceedings of the fourth International Conference on the History of Mathematics Education; Bjarnadóttir, K., Furinghetti, F., Menghini, M., Prytz, J., Schubring, G., Eds.; Edizioni Nuova Cultura: Rome, Italy, 2017; pp. 47–59. [Google Scholar]
- Pehkonen, E. (Ed.) Proceedings of the NORMA-94 Nordic Conference on Mathematics Teaching (NORMA-94) in Lahti 1994; University of Helsinki: Helsinki, Finland, 1994. [Google Scholar]
- Breiteig, T.; Brekke, G. (Eds.) Theory into Practice in Mathematics Education. In Proceedings of the NORMA98 the Second Nordic Conference on Mathematics Education, Kristiansand, Faculty of Mathematics and Sciences, Kristiansand, Norway, 5–9 June 1998. [Google Scholar]
- Bergsten, C.; Grevholm, B. (Eds.) Conceptions of Mathematics. In Proceedings of the NORMA01 in Kristianstad, SMDF, Linköping, Sweden, 8–12 June 2001. [Google Scholar]
- Bergsten, C.; Grevholm, B.; Måsøval, H.S.; Rønning, F. (Eds.) Relating Practice and Research in Mathematics Education. In Proceedings of the Norma05, Fourth Nordic Conference on Mathematics Education, Trondheim, Norway, 2–6 September 2007; Tapir Academic Press: Trondheim, Norway, 2007. [Google Scholar]
- Winsløw, C. Nordic Research in Mathematics Education. In Proceedings of the NORMA08, Copenhagen, Denmark, 21–25 April 2008; Sense Publishers: Rotterdam, The Netherlands, 2009. [Google Scholar]
- Gunnarsdottir, G.; Hreinsdottir, F.; Palsdottir, G.; Hannula, M.; Hannula-Sormunen, M.; Jablonka, E.; Jankvist, U.T.; Ryve, A.; Valero, P.; Waege, K. (Eds.) NORMA11, Proceedings of the Sixth Nordic Conference on Mathematics Education, Reykjavik, Iceland, 11–14 May 2011; University of Iceland: Borgarnes, Iceland, 2012. [Google Scholar]
- Silfverberg, H.; Kärki, T.; Hannula, M.S. (Eds.) Nordic Research in Mathematics Education. In Proceedings of the NORMA14, Finnish Research Association for Subject Didactics. Helsinki, Finland, 3–6 June 2014. [Google Scholar]
- Gjone, G. Nomad—Nordic Studies in Mathematics Education. The First Eight Years. In Nordic Research in Didactics of Mathematics: Past, Present and Future; Grevholm, B., Hundeland, P.S., Juter, K., Kislenko, K., Persson, P.-E., Eds.; Cappelen Damm Akademisk: Oslo, Norway, 2013; pp. 182–198. [Google Scholar]
- Grevholm, B. Didactics of Mathematics a Nordic Perspective. In Matematikdidaktik–ett Nordiskt Perspektiv; Studentlitteratur: Lund, Sweden, 2001. [Google Scholar]
- Grevholm, B. Mathematics for School. In Matematikk for Skolen; Fagbokforlaget: Bergen, Norway, 2003. [Google Scholar]
- Pehkonen, E.; Brandell, G.; Winslöw, C. Nordic Presentations. In Proceedings of the Section Nordic Presentations at ICME-10, Copenhagen, Denmark, 12 July 2004. [Google Scholar]
- Grevholm, B. Some Examples of Recent Research in Mathematics Education–what it is About and How it is Done. In Pathways into Research-Based Teaching and Learning in Mathematics and Science Education; Asunta, T., Viiri, J., Eds.; University of Jyväskylä: Jyväskylä, Finland, 2006; pp. 50–74. [Google Scholar]
- Sriraman, B.; Bergsten, C.; Goodchild, S.; Palsdottir, G.; Dahl, B.; Haapasalo, L. The First Sourcebook on Nordic Research in Mathematics Education; Information Age Publishing: Charlotte, NC, USA, 2010. [Google Scholar]
- Grevholm, B.; Hundeland, P.S.; Juter, K.; Kislenko, K.; Persson, P.-E. Nordic Research in Didactics of Mathematics: Past, Present, and Future; Cappelen Damm Academic: Oslo, Norway, 2013. [Google Scholar]
- Grevholm, B. Mathematics Textbooks, Their Content, Use and Influences. In Research in Nordic and Baltic Countries; Cappelen Damm Akademisk: Oslo, Norway, 2017. [Google Scholar]
- Räsänen, P.; Daland, E.; Dalvang, T.; Engström, A.; Korhonen, J.; Kristinsdóttír, J.V.; Lindenskov, L.; Lindhardt, B.; Oskarsdottir, E.; Reikerás, E.; et al. Mathematical Learning and Its Difficulties: The Case of Nordic Countries. In International Handbook of Mathematical Learning Difficulties; Fritz, A., Haase, V.G., Räsänen, P., Eds.; Springer: Duisburg, Germany, 2019; pp. 107–126. [Google Scholar]
- Norén, E.; Palmér, H.; Cooke, A. Nordic Research in Mathematics Education. Papers of NORMA 17; Skrifter från SMDF; SMDF: Linköping, Sweden, 2018. [Google Scholar]
- Ödman, P.J. Tolkning, Förståelse, Vetande. Hermeneutik i Teori och Praktik. Interpretation, Understanding, Knowing. Hermeneutics in Theory and Practice; Almkvist & Wiksell: Stockholm, Sweden, 1979. [Google Scholar]
- Cooke, A. Mathematics in Swedish and Australian Early Childhood Curricula. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 1–10. [Google Scholar]
- Müller-Hill, E.; Wille, A.M. Negotiating Mathematical Meaning with Oneself Snapshots from Imaginary Dialogues on Recurring Decimals. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 79–88. [Google Scholar]
- Villalonga Pons, J.; Andrews, P. Supporting Students’ Mathematical Problem Solving: The Key Role of Different Forms of Checking as Part of a Self-Scaffolding Mechanism. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 69–78. [Google Scholar]
- Van Bommel, J.; Palmér, H. Paper or and Digital: A study of Combinatorics in Preschool Class. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 11–19. [Google Scholar]
- Fosse, T.; Hope Lossius, M. “I Find that Pleasurable and Play-Oriented Mathematical Activities Create Wondering and Curiosity” Norwegian Kindergarten Teachers’ Views on Mathematics. In Nordic Research in Mathematics Education. Papers of Norma 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 21–30. [Google Scholar]
- Dahl, H.; Klemp, T.; Nilssen, V. Collaborative Tool-Mediated Talk an Example from Third Graders. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 31–40. [Google Scholar]
- Enge, O.; Valenta, A. Narratives Constructed in the Discourse on Early Fractions. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 41–50. [Google Scholar]
- Maugesten, M.; Mosvold, R.; Fauskanger, J. Second Graders’ Reflections about the Number 24. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 51–58. [Google Scholar]
- Tossavainen, T.; Hirsto, L. Tablet Computers and Finnish Primary and Lower Secondary Students Motivation in Mathematics. In Nordic Research in Mathematics Education; Papers of NORMA, 17, Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 59–68. [Google Scholar]
- Misfeldt, M.; Jankvist, U.T.; Møllegaard Iversen, S. Mixed Notation and Mathematical Writing in Danish Upper Secondary School. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 89–98. [Google Scholar]
- Larson, N.; Pettersson, K. Proof by Induction the Role of the Induction Basis. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 99–107. [Google Scholar]
- Rensaa, R.J.; Vos, P. Interpreting Teaching for Conceptual and for Procedural Knowledge in a Teaching Video about Linear Algebra. In Nordic Research in Mathematics Education. Papers of NORMA 17; ENorén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 109–118. [Google Scholar]
- Viholainen, A.; Lepik, M.; Hemmi, K.; Asikainen, M.; Hirvonen, P.E. Research Study about Estonian and Finnish Mathematics Students’ Views about Proof. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 119–127. [Google Scholar]
- Hannula, M. The National Validation of Finnish Mathematics Teachers’ Lexicon. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 129–138. [Google Scholar]
- Topphol, A.K. A Correlation Study of Mathematics Proficiency VS Reading and Spelling Proficiency. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 139–147. [Google Scholar]
- Opsal, H.; Mjellem Tonheim, O.H. Students with Low Reading Abilities and Word Problems in Mathematics. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 149–157. [Google Scholar]
- Hähkiöniemi, M.; Nieminen Lehesvuori, S.; Francisco, J.; Hiltunen, J.; Jokiranta, K.; Viiri, J. Attending to and Fostering Argumentation in Whole Class Discussion. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 159–168. [Google Scholar]
- Hvalsøe Schou, M. The Roles of Mathematical Symbols in Teacher Instruction. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 169–178. [Google Scholar]
- Petersson, J. Second Language Students’ Achievement in Linear Expressions and Time Since Immigration. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 179–187. [Google Scholar]
- Kärki, T.; Silfverberg, S. Prospective Class Teachers’ Attitude Profiles Towards Learning and Teaching Mathematics. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 189–198. [Google Scholar]
- Kacerja, S.; Lode, B. An Initial Analysis of Post-Teaching Conversations in Mathematics Practicum: Researching our own Practice. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 199–208. [Google Scholar]
- Mosvold, R.; Fauskanger, J. Opportunities and Challenges of Using the MDI framework for Research in Norwegian Teacher Education. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 209–218. [Google Scholar]
- Jakobsen, A.; Kazima, M.; Nkhoma Kasoka, D. Assessing Prospective Teachers’ Development of MKT Through Their Teacher Education: A Malawian Case. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 219–227. [Google Scholar]
- Brehmer, D.; Ryve, A. Towards an Organizing Frame for Mapping Teachers’ Learning in Professional Development. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 229–237. [Google Scholar]
- Fauskanger, J.; Mosvold, R.; Valenta, A.; Bjuland, R. Good Mathematics Teaching as Constructed in Norwegian Teachers’ Discourses. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 239–248. [Google Scholar]
- Hansen, R.; Herheim, R.; Lilland, I.E. Teachers’ Mathematical Discussions of the Body Mass Index Formula. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter Från SMDF; SMDF: Linköping, Sweden, 2017; pp. 249–258. [Google Scholar]
- Kaufmann, O.T. Teachers’ Attention to Student Thinking, Mathematical Content and Teachers’ Role in a Professional Learning Community. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 259–268. [Google Scholar]
- Tyskerud, A. Teacher Learning in Lesson Study: Identifying Characteristics in Teachers’ Discourse on Teaching. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 269–278. [Google Scholar]
- Kristinsdóttir, J.V. Adopting the Developmental Research Cycle in Working with Teachers. In Nordic Research in Mathematics Education Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 279–288. [Google Scholar]
- Eskeland Rangnes, T.; Herheim, R.; Kacerja, S. In-Service Teachers’ Positioning when Discussing the Body Mass Index. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 289–298. [Google Scholar]
- Hemmi, K.; Bråting, K.; Liljekvist, Y.; Prytz, J.; Madej, L.; Pejlare, J.; Palm Kaplan, K. Characterizing Swedish School Algebra –Initial Findings from Analyses of Steering Documents, Textbooks and Teachers’ Discourses. In Nordic Research in Mathematics Education. Papers of NORMA 17, 30 May–2 June 2017; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2018; pp. 299–309. [Google Scholar]
- Pehkonen, L.; Hemmi, K.; Krzywacki, H.; Laine, A. A Cross-Cultural Study of Teachers’ Relation to Curriculum Materials. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 309–318. [Google Scholar]
- Pehkonen, L.; Piht, S.; Pakkas, K.; Laine, A.; Krzywacki, H. Estonian and Finnish Teachers’ Views About the Textbooks in Mathematics Teaching. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 319–327. [Google Scholar]
- Dreyøe, J.; Moeskær Larsen, D.; Dreier Hjelmborg, M.; Michelsen, C.; Misfeldt, M. Inquiry-based Learning in Mathematics Education: Important Themes in the Literature. In Nordic Research in Mathematics Education. Papers of NORMA 17; Norén, E., Palmér, H., Cooke, A., Eds.; Skrifter från SMDF; SMDF: Linköping, Sweden, 2017; pp. 329–341. [Google Scholar]
- FitzSimons, G.E.; Wedege, T. Developing Numeracy in the Workplace. Nord. Stud. Math. Educ. 2007, 12, 49–66. [Google Scholar]
- Lindberg, L. Matematiken i Yrkesutbildningen. Möjligheter och Begränsningar, Mathematics in Vocational Education. Opportunities and Constraints. Licentiate Thesis, Luleå University of Technology, Luleå, Sweden, 2010. [Google Scholar]
- Rensaa, R.J.; Grevholm, B. Engineers into Teachers of Mathematics: What Challenges are There? In Proceedings of NORMA11. The sixth Nordic Conference on Mathematics Education in Reykjavik, Iceland; Gunnarsdóttir, G.H., Hreinsdóttir, F., Pálsdóttir, G., Hannula, M., Hannula-Sormunen, M., Jablonka, E., Volmer Jankvist, U.T., Ryve, A., Valero, P., Wæge, K., Eds.; University of Iceland: Reykjavik, Iceland, 2012; pp. 523–532. [Google Scholar]
- Clarke, D.J. International Comparative Research into Educational Interaction. Constructing and Concealing Difference. In Interaction in Educational Settings; Tirri, K., Kuusisto, E., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2013; pp. 5–22. [Google Scholar]
- Niss, M. Reflections on the State of and Trends in Research on Mathematics Teaching and Learning. From Here to Utopia. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 1293–1312. [Google Scholar]
- Rönning, F. Didactics of Mathematics as a Research Field in Scandinavia. In European Traditions in Didactics of Mathematics; Blum, W., Artigue, M., Mariotti, M.A., Strässer, R., Van den Heuvel-Panhuizen, M., Eds.; ICME-13 Monographs; Springer: Cham, Switzerland, 2018; pp. 153–185. [Google Scholar] [CrossRef] [Green Version]
- Bergqvist, E.; Österholm, M.; Granberg, C.; Sumpter, L. In Proceedings of the 42nd International Group for the Psychology of Mathematics Education, PME, Umeå, Sweden, 3–8 July 2018; Volume 1.
- Grevholm, B. Matematikdidaktikens Möjligheter i en Forskningsbaserad Lärarutbildning. Opportunities for Didactics of Mathematics in a Research-Based Teacher Education. In Fag og Didaktik i Lärareutdanning Subject and Didactics in Teacher Education; Ongstad, S., Ed.; Universitetsforlaget: Oslo, Norway, 2006; pp. 183–206. [Google Scholar]
- Grevholm, B. Final Note: Creation of a Nordic Society for Research in Mathematics Education. In Nordic Research in Mathematics Education: Proceedings from NORMA08; Winsløw, C., Ed.; Sense Publishers: Rotterdam, Copenhagen, 2008; pp. 387–389. [Google Scholar]
- Bjarnadóttir, K.; Iceland University, Reykjavik, Iceland. Personal communication, 2021.
- Lepik, M.; Grevholm, B.; Viholainen, A. Using Textbooks in the Mathematics Classroom the Teachers’ View. Nord. Stud. Math. Educ. 2015, 20, 129–156. [Google Scholar]
- Lepik, M.; Pipere, A.; Hannula, M. Comparing Mathematics Teachers’ Beliefs about Good Teaching: The Cases of Estonia, Latvia, and Finland. Nord. Stud. Math. Educ. 2012, 17, 177–198. [Google Scholar]
- Haug, P. Spesialundervisning, Innhald og Funksjon; Special Education; Content and Function; Samlaget: Oslo, Norway, 2017. [Google Scholar]
- Grevholm, B. Mathematics Teacher Education–A Scandinavian Perspective. In Teachers of Mathematics: Recruitment, Retention, Professional Development and Identity; Anthony, G., Grevholm, B., Eds.; SMDFs Skriftserie: Linköping, Sweden, 2010; pp. 93–100. [Google Scholar]
- Stenhouse, L. An Introduction to Curriculum Research and Development; Heinemann: London, UK, 1975. [Google Scholar]
- Steen, L.A. On the Shoulders of Giants: New Approaches to Numeracy; Mathematical Sciences Education Board, National Research Council; National Academy Press: Washington, DC, USA, 1990. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).