Mexican Axolotl Optimization: A Novel Bioinspired Heuristic
Abstract
1. Introduction
2. Related Works on Bioinspired Optimization
- Fireflies are unisexual, so a firefly will be attracted to other fireflies regardless of their gender.
- The attractiveness is proportional to the brightness and both diminish as your distance increases. Therefore, for two flashing fireflies, the less bright will move to the brighter. If there is no one brighter than a particular firefly, it will move randomly.
- The brightness of a firefly is determined by the landscape of the objective feature.
3. Mexican Axolotl Variable Optimization
3.1. The Axolotl in Nature
3.2. The Artificial Axolotl
- We divide the individuals into males and females.
- We consider the females more important, due to the fact that for each female we find the best male according to tournament selection, to obtain the offspring.
- We have an elitist replacement procedure to include new individuals in the population. In such a procedure, the best individual is considered to be a female, and the second-best to be a male. That is, our procedure has the possibility of converting a male into a female, if the male is best.
4. Results and Discussion
4.1. Optimization Functions
4.2. Optimization Results of the Compared Algorithms
4.3. Statistical Tests
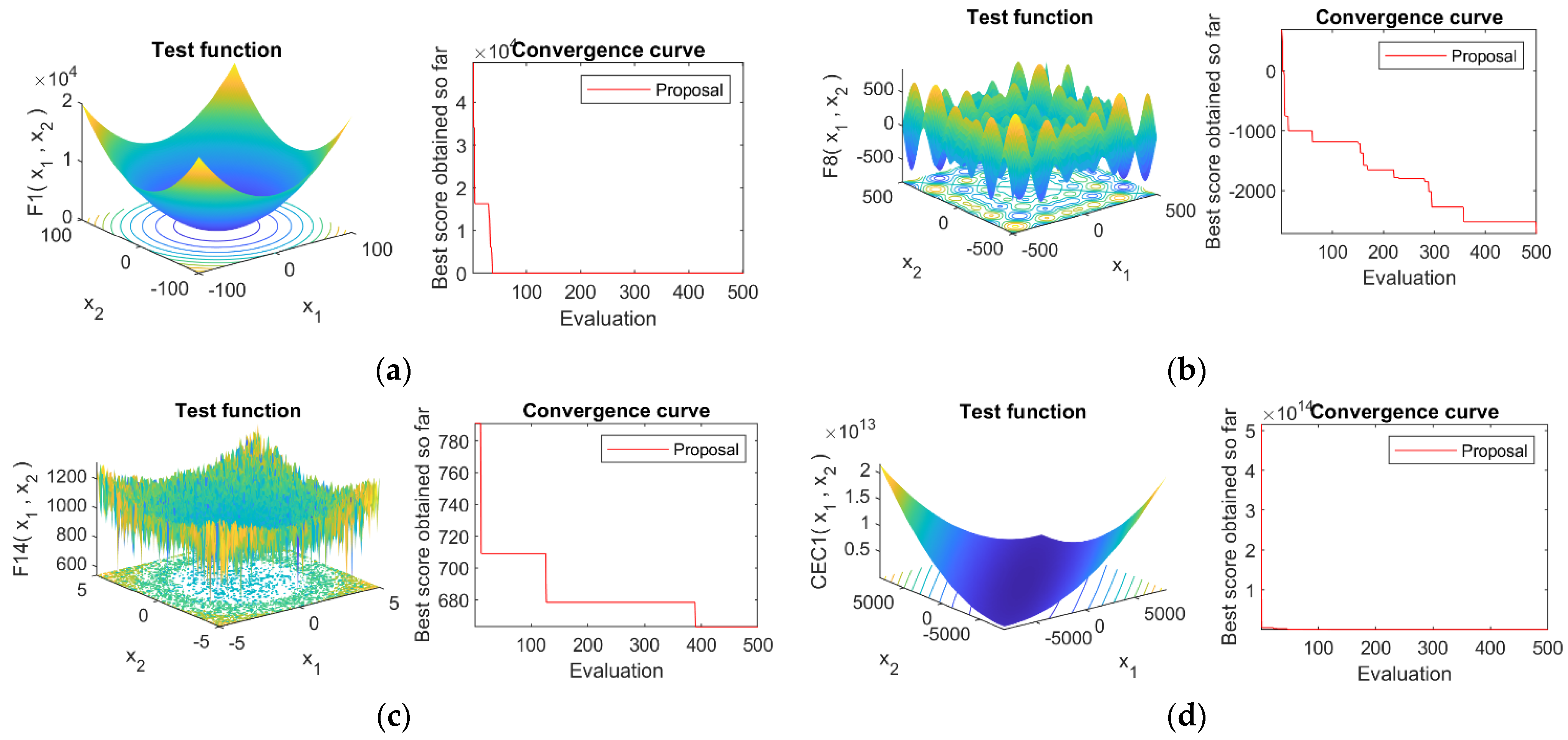
4.4. Convergence Analysis
4.5. Main differences of MAO with Respect Other Bioinspired Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
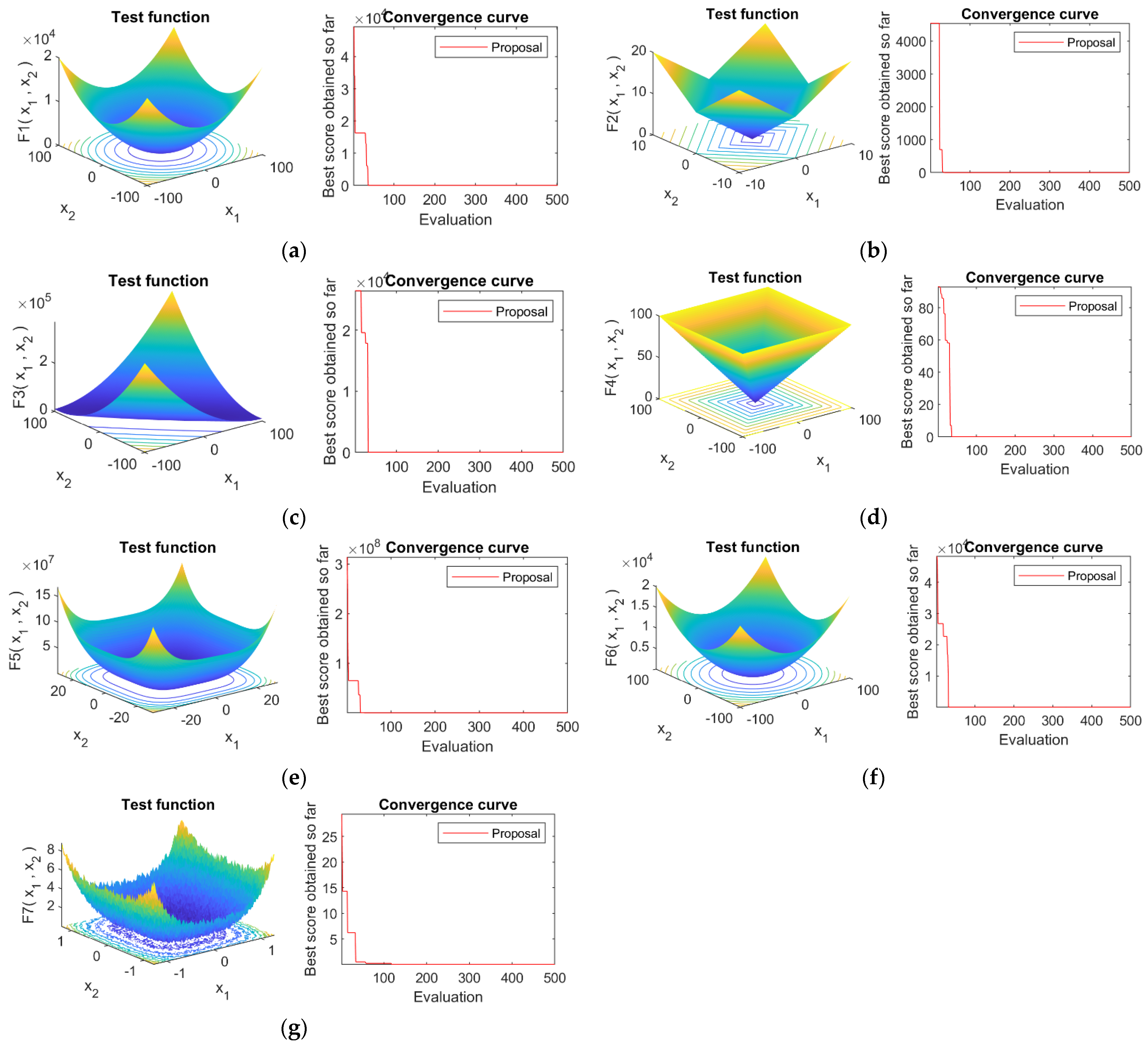
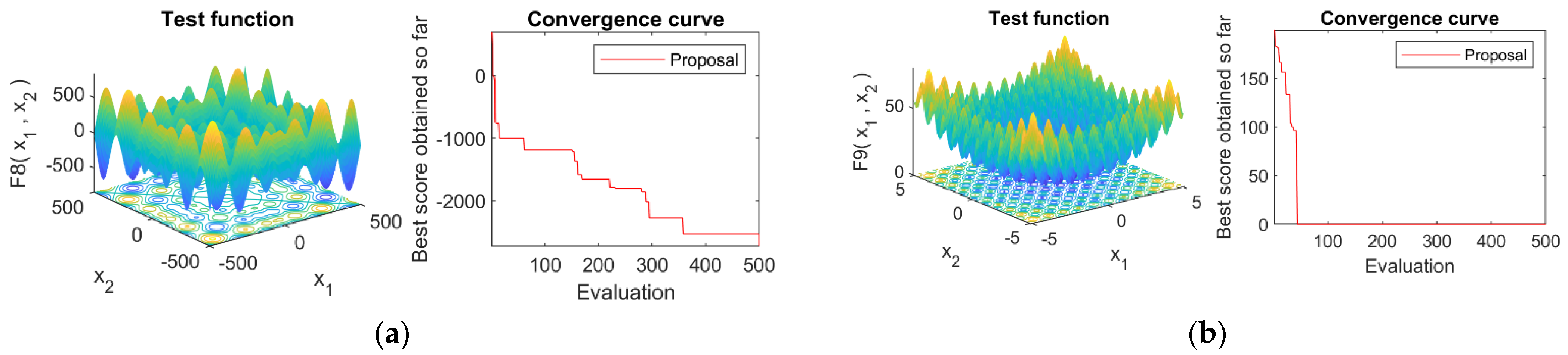
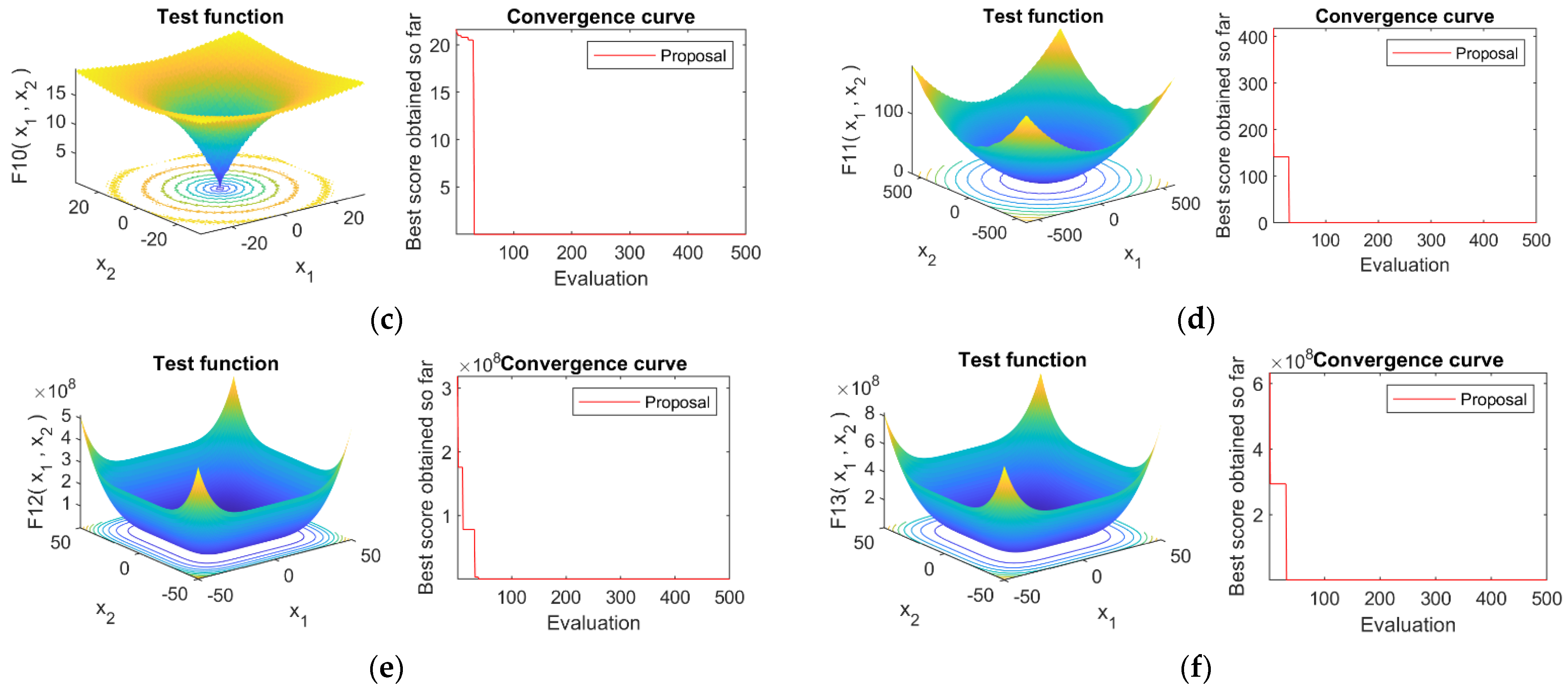
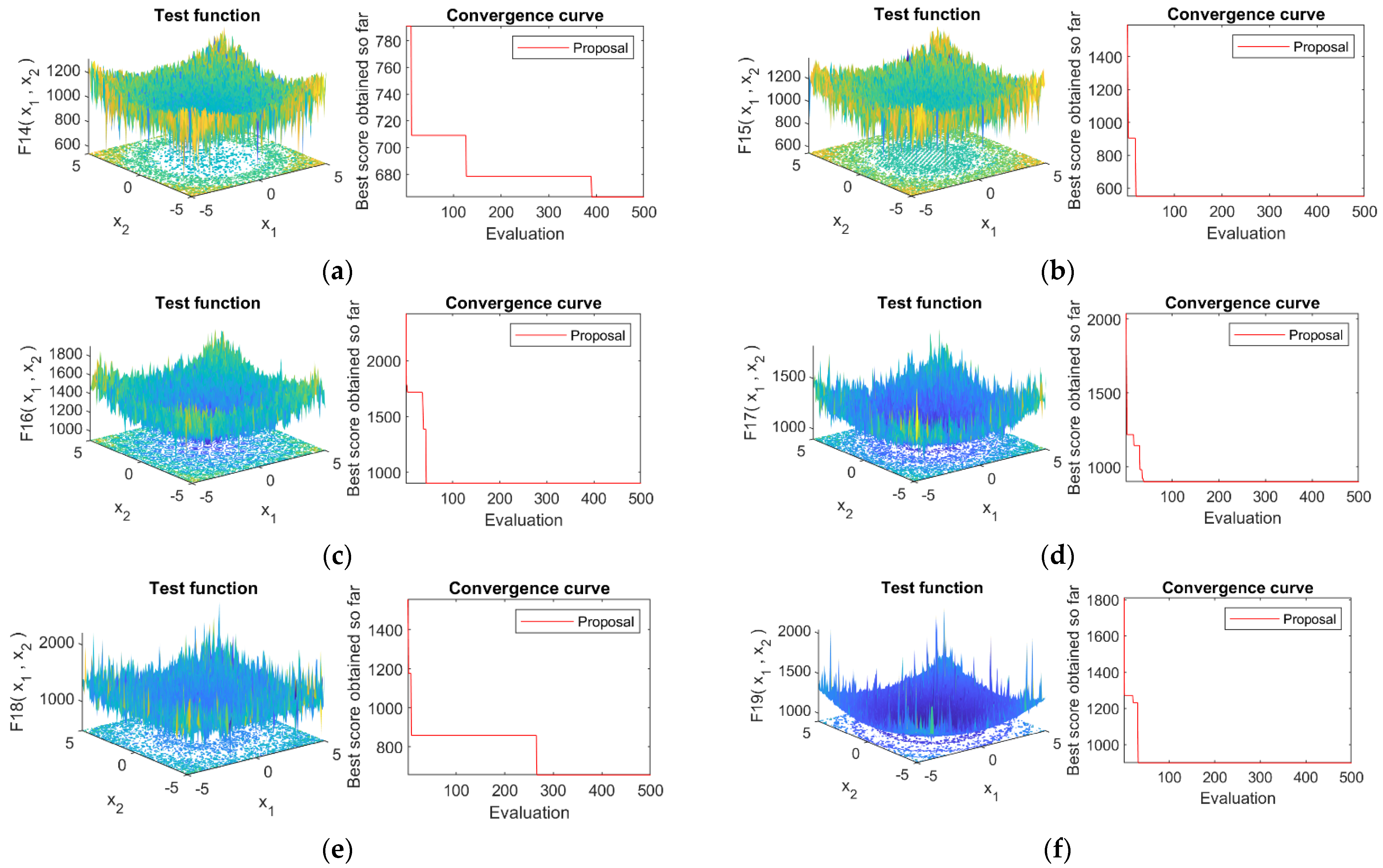

References
- Dinov, I.D. Function Optimization. In Data Science and Predictive Analytics; Springer: Cham, Switzerland, 2018; pp. 735–763. [Google Scholar]
- Flood, M.M. The traveling-salesman problem. Oper. Res. 1956, 4, 61–75. [Google Scholar] [CrossRef]
- Beckers, R.; Deneubourg, J.; Gross, S. Trail and U-turns in the Selection of the Shortest Path by the Ants. J. Theor. Biol. 1992, 159, 397–415. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to Solve Problems; Stanford University, Department of Computer Science: Stanford, CA, USA, 1990; Volume 34. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Fan, X.; Sayers, W.; Zhang, S.; Han, Z.; Ren, L.; Chizari, H. Review and classification of bio-inspired algorithms and their applications. J. Bionic Eng. 2020, 17, 611–631. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, I.; Singh, M. Exploiting grasshopper and cuckoo search bio-inspired optimization algorithms for industrial energy management system: Smart industries. Electronics 2020, 9, 105. [Google Scholar] [CrossRef]
- Abdelaziz, F.B.; Alaya, H.; Dey, P.K. A multi-objective particle swarm optimization algorithm for business sustainability analysis of small and medium sized enterprises. Ann. Oper. Res. 2020, 293, 557–586. [Google Scholar] [CrossRef]
- Phan, A.V.; Le Nguyen, M.; Bui, L.T. Feature weighting and SVM parameters optimization based on genetic algorithms for classification problems. Appl. Intell. 2017, 46, 455–469. [Google Scholar] [CrossRef]
- Santos, P.; Macedo, M.; Figueiredo, E.; Santana, C.J.; Soares, F.; Siqueira, H.; Maciel, A.; Gokhale, A.; Bastos-Filho, C.J. Application of PSO-based clustering algorithms on educational databases. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Almufti, S.; Marqas, R.; Ashqi, V. Taxonomy of bio-inspired optimization algorithms. J. Adv. Comput. Sci. Technol. 2019, 8, 23. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Kitakyushu, Japan, 15–17 December 2010; pp. 210–214. [Google Scholar]
- Yang, X.-S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm. Nat. Inspired Metaheuristic Algorithms 2008, 20, 79–90. [Google Scholar]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In Proceedings of the International Symposium on Stochastic Algorithms, Sapporo, Japan, 26–28 October 2009; pp. 169–178. [Google Scholar]
- Kumar, V.; Kumar, D. A Systematic Review on Firefly Algorithm: Past, Present, and Future. Arch. Comput. Methods Eng. 2020, 1–23. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Meraihi, Y.; Ramdane-Cherif, A.; Acheli, D.; Mahseur, M. Dragonfly algorithm: A comprehensive review and applications. Neural Comput. Appl. 2020, 32, 16625–16646. [Google Scholar] [CrossRef]
- Abdullah, J.M.; Ahmed, T. Fitness dependent optimizer: Inspired by the bee swarming reproductive process. IEEE Access 2019, 7, 43473–43486. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Gresens, J. An introduction to the Mexican axolotl (Ambystoma mexicanum). Lab Anim. 2004, 33, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Voss, S.R.; Woodcock, M.R.; Zambrano, L. A tale of two axolotls. BioScience 2015, 65, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Cortázar, J. End of the Game; In Spanish, Final del Juego; HarperCollins: New York, NY, USA, 1956. [Google Scholar]
- Herbert, F. Dune; Chilton Company: Boston, MA, USA, 1965. [Google Scholar]
- Tank, P.W.; Carlson, B.M.; Connelly, T.G. A staging system for forelimb regeneration in the axolotl, Ambystoma mexicanum. J. Morphol. 1976, 150, 117–128. [Google Scholar] [CrossRef]
- Demircan, T.; Hacıbektaşoğlu, H.; Sibai, M.; Fesçioğlu, E.C.; Altuntaş, E.; Öztürk, G.; Süzek, B.E. Preclinical molecular signatures of spinal cord functional restoration: Optimizing the metamorphic axolotl (Ambystoma mexicanum) model in regenerative medicine. OMICS J. Integr. Biol. 2020, 24, 370–378. [Google Scholar] [CrossRef]
- Vieira, W.A.; Wells, K.M.; McCusker, C.D. Advancements to the axolotl model for regeneration and aging. Gerontology 2020, 66, 212–222. [Google Scholar] [CrossRef]
- Nowoshilow, S.; Schloissnig, S.; Fei, J.-F.; Dahl, A.; Pang, A.W.; Pippel, M.; Winkler, S.; Hastie, A.R.; Young, G.; Roscito, J.G. The axolotl genome and the evolution of key tissue formation regulators. Nature 2018, 554, 50–55. [Google Scholar] [CrossRef]
- Pietsch, P.; Schneider, C.W. Vision and the skin camouflage reactions of Ambystoma larvae: The effects of eye transplants and brain lesions. Brain Res. 1985, 340, 37–60. [Google Scholar] [CrossRef]
- Griffiths, R.A.; Graue, V.; Bride, I.G. The axolotls of Lake Xochimilco: The evolution of a conservation programme. Axolotl News 2003, 30, 12–18. [Google Scholar]
- Khattak, S.; Murawala, P.; Andreas, H.; Kappert, V.; Schuez, M.; Sandoval-Guzmán, T.; Crawford, K.; Tanaka, E.M. Optimized axolotl (Ambystoma mexicanum) husbandry, breeding, metamorphosis, transgenesis and tamoxifen-mediated recombination. Nat. Protoc. 2014, 9, 529. [Google Scholar] [CrossRef] [PubMed]
- Price, K.; Awad, N.; Ali, M.; Suganthan, P. Problem Definitions and Evaluation Criteria for the 100-Digit Challenge Special Session and Competition on Single Objective Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2018. [Google Scholar]
- MATLAB. Matlab, version 9.8 (R2020a); The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Chen, Q.; Liu, B.; Zhang, Q.; Liang, J.; Suganthan, P.; Qu, B. Problem Definitions and Evaluation Criteria for CEC 2015 Special Session on Bound Constrained Single-Objective Computationally Expensive Numerical Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2014. [Google Scholar]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Triguero, I.; González, S.; Moyano, J.M.; García, S.; Alcalá-Fdez, J.; Luengo, J.; Fernández, A.; del Jesús, M.J.; Sánchez, L.; Herrera, F. KEEL 3.0: An open source software for multi-stage analysis in data mining. Int. J. Comput. Intell. Syst. 2017, 10, 1238–1249. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Earthworm optimisation algorithm: A bio-inspired metaheuristic algorithm for global optimisation problems. Int. J. Bio Inspired Comput. 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Coelho, L.D.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; pp. 1–5. [Google Scholar]
- Wang, G.G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]





| Function | Range | Shift Position | Min 1 |
|---|---|---|---|
| [−100, 100] | [−30, −30, …, −30] | 0 | |
| [−10, 10] | [−3, −3, …, −3] | 0 | |
| [−100, 100] | [−30, −30, …, −30] | 0 | |
| [−100, 100] | [−30, −30, …, −30] | 0 | |
| [−30, 30] | [−15, −15, …, −15] | 0 | |
| [−100, 100] | [−750, …, −750] | 0 | |
| [−1.28, 1.28] | [−0.25, …, −0.25] | 0 |
| Function | Range | Shift Position | Min 1 |
|---|---|---|---|
| [−500, 500] | [−300, …, −300] | −418.9829 | |
| [−5.12, 5.12] | [−2, −2, …, −2] | 0 | |
| [−32, 32] | − | 0 | |
| [−600, 600] | [−400, …, −400] | 0 | |
| [−50, 50] | [−30, −30, …,−30] | 0 | |
| [−50, 50] | [−100, …, −100] | 0 |
| Function | Range | Min 1 |
|---|---|---|
; ; | [−5, 5] | 0 |
; ; | [−5, 5] | 0 |
; ; | [−5, 5] | 0 |
| [−5, 5] | 0 | |
| [−5, 5] | 0 | |
| [−5, 5] | 0 |
| Function | Dimensions | Range | Min 1 |
|---|---|---|---|
| Storn’s Chebyshev polynomial fitting problem | 9 | [−8192, 8192] | 1 |
| Inverse Hilbert matrix problem | 16 | [−16,384, 16,384] | 1 |
| Lennard-Jones minimum energy cluster | 18 | [−4, 4] | 1 |
| Rastrigin’s function | 10 | [−100, 100] | 1 |
| Griewangk’s function | 10 | [−100, 100] | 1 |
| Weierstrasss function | 10 | [−100, 100] | 1 |
| Modified Schewefel’s function | 10 | [−100, 100] | 1 |
| Expanded Schafeer’s F6 function | 10 | [−100, 100] | 1 |
| Happy Cat function | 10 | [−100, 100] | 1 |
| Ackley function | 10 | [−100, 100] | 1 |
| Set | Function | ABC | CS | DE | FA | FDO | MBO | SMA | WOA | MAO |
|---|---|---|---|---|---|---|---|---|---|---|
| Unimodal | F1 | 5447.7037 | 9165.9901 | 8587.4237 | 2936.3110 | 2855.3899 | 2997.0703 | 13.0903 | 234.8699 | 321.0370 |
| F2 | 2.8086 | 31.3204 | 35.0858 | 14.5341 | 13.8453 | 13.6921 | 0.3195 | 3.2792 | 4.1843 | |
| F3 | 7228.5989 | 9879.7702 | 10,826.8313 | 4258.6261 | 5174.2327 | 6729.9519 | 5245.1086 | 13,758.8168 | 700.1304 | |
| F4 | 57.9899 | 54.8784 | 59.7082 | 29.7369 | 25.2446 | 23.4809 | 0.3670 | 41.7093 | 12.3571 | |
| F5 | 2.68 × 106 | 1.10 × 107 | 9.71 × 106 | 1.23 × 106 | 3.12 × 106 | 4.40 × 106 | 13.1924 | 3.51 × 104 | 1.84 × 104 | |
| F6 | 5928.5177 | 9269.7192 | 7336.3097 | 3043.6261 | 2771.3385 | 3193.3915 | 3.0798 | 246.8890 | 266.5308 | |
| F7 | 1.2196 | 2.3582 | 2.8935 | 0.6749 | 1.1486 | 2.5256 | 0.1911 | 0.2530 | 0.0484 | |
| Multimodal | F8 | −2407.4569 | −1809.7610 | −1950.2114 | −1531.2946 | −1483.9961 | −3132.3800 | −3293.9270 | −2635.7968 | −2843.8943 |
| F9 | 70.2922 | 91.3020 | 95.3271 | 67.2274 | 55.1742 | 44.5630 | 15.3040 | 56.0142 | 25.3499 | |
| F10 | 17.9524 | 18.7192 | 19.4404 | 15.1343 | 10.1403 | 11.3944 | 0.5564 | 7.3438 | 7.1662 | |
| F11 | 46.1170 | 83.3698 | 71.7901 | 27.2379 | 24.3820 | 22.7500 | 0.4801 | 2.5929 | 3.7582 | |
| F12 | 2.36 × 106 | 1.42 × 107 | 1.62 × 107 | 1.22 × 105 | 1.56 × 106 | 1.99 × 106 | 2.5396 | 5.96 × 103 | 5.95 | |
| F13 | 7.54 × 106 | 5.21 × 107 | 5.64 × 107 | 2.12 × 106 | 9.22 × 106 | 1.17 × 106 | 1.0523 | 3.03 × 104 | 3.28 × 103 | |
| Composite | F14 | 342.3150 | 354.0967 | 410.7029 | 758.6487 | 968.2830 | 393.5150 | 429.0229 | 395.7099 | 473.1349 |
| F15 | 476.2411 | 463.9622 | 468.3889 | 821.8865 | 1048.0255 | 478.9110 | 513.0348 | 457.5810 | 507.2991 | |
| F16 | 1072.7264 | 1052.7694 | 1056.7774 | 1491.2869 | 1393.0906 | 1087.9062 | 1062.6645 | 1114.6494 | 1147.8570 | |
| F17 | 990.3510 | 1003.4222 | 1026.9885 | 1077.1571 | 1050.0625 | 1001.3681 | 904.2288 | 999.8535 | 952.0442 | |
| F18 | 420.8507 | 424.6245 | 442.7791 | 894.0803 | 1136.6270 | 420.0096 | 508.7819 | 447.0013 | 524.1615 | |
| F19 | 1003.9296 | 996.0488 | 978.5206 | 974.7888 | 951.7356 | 933.2716 | 874.2914 | 933.4341 | 905.2780 | |
| Competition | CEC01 | 6.27 × 1011 | 1.13 × 1012 | 6.26 × 1011 | 1.04 × 1012 | 3.96 × 1011 | 8.13 × 1011 | 8.17 × 1011 | 1.01 × 1012 | 4.11 × 1010 |
| CEC02 | 10,208.4315 | 8666.1661 | 4254.8599 | 4408.7645 | 4833.2511 | 7174.2428 | 41.9309 | 479.6424 | 424.2248 | |
| CEC03 | 12.7058 | 12.7047 | 12.7039 | 12.7043 | 12.7037 | 12.7036 | 12.7035 | 12.7026 | 12.7026 | |
| CEC04 | 8564.8124 | 16,171.5930 | 9055.5641 | 11,536.6751 | 4962.4534 | 7862.3602 | 17,307.1928 | 5700.3273 | 4460.3403 | |
| CEC05 | 4.4837 | 5.4179 | 3.9627 | 3.8751 | 2.8207 | 3.4589 | 5.6967 | 3.1687 | 2.6745 | |
| CEC06 | 11.8186 | 13.0760 | 13.3387 | 14.3070 | 13.5259 | 11.4701 | 13.0106 | 13.1277 | 12.5090 | |
| CEC07 | 1016.2961 | 1318.4455 | 1425.1217 | 1635.1259 | 1506.3325 | 1057.3337 | 1204.1217 | 1275.5805 | 1184.9008 | |
| CEC08 | 6.9177 | 7.2169 | 7.4573 | 7.5103 | 7.0885 | 6.9756 | 7.4529 | 7.1778 | 6.8954 | |
| CEC09 | 2013.8642 | 3939.6893 | 2682.6881 | 1773.0340 | 1059.9142 | 1321.8686 | 4199.2309 | 1043.8402 | 431.0717 | |
| CEC10 | 20.6068 | 20.7581 | 20.8089 | 20.8308 | 20.8116 | 20.5595 | 20.7914 | 20.7122 | 20.6511 |
| Algorithm | Parameters 1 |
| ABC | Number of food sources: 30; Maximum number of failures which lead to the elimination: Number of food sources * dimension |
| CS | Number of nests: 30; Discovery rate of alien eggs/solutions: 10−5 |
| DE | Population Size: 30; Crossover probability: 0.8; Scaling factor: 0.85 |
| FA | Number of Fireflies: 30; Alpha: 0.5; Betamin: 0.2; Gamma: 1.0 |
| FDO | Scout bee number: 30; Weight Factor: 0.0 |
| MAO | Total population size: 30; damage probability dp = 0.5; regeneration probability rp = 0.1; tournament size k = 3; differentiation constant . |
| MBO | Total population size: 30; The percentage of population for MBO: 5/12; Elitism parameter: 2.0; Max Step size: 1.0; 12 months in a year: 1.2 |
| SMA | Number of search agent: 30; z: 0.03 |
| WOA | Number of search agents |
| Algorithm. | Ranking |
|---|---|
| MAO | 2.7069 |
| SMA | 3.4483 |
| WOA | 3.8448 |
| MBO | 4.1724 |
| ABC | 5.1724 |
| FDO | 5.5517 |
| FA | 6.4828 |
| CS | 6.7931 |
| DE | 6.8276 |
| i | Algorithm | Z | p-Value | Holm |
|---|---|---|---|---|
| 8 | DE | 5.729586 | 0.000000 | 0.006250 |
| 7 | CS | 5.68164 | 0.000000 | 0.007143 |
| 6 | FA | 5.250123 | 0.000000 | 0.008333 |
| 5 | FDO | 3.955572 | 0.000076 | 0.010000 |
| 4 | ABC | 3.428163 | 0.000608 | 0.012500 |
| 3 | MBO | 2.037719 | 0.041578 | 0.016667 |
| 2 | WOA | 1.582229 | 0.113597 | 0.025000 |
| 1 | SMA | 1.030846 | 0.302613 | 0.050000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villuendas-Rey, Y.; Velázquez-Rodríguez, J.L.; Alanis-Tamez, M.D.; Moreno-Ibarra, M.-A.; Yáñez-Márquez, C. Mexican Axolotl Optimization: A Novel Bioinspired Heuristic. Mathematics 2021, 9, 781. https://doi.org/10.3390/math9070781
Villuendas-Rey Y, Velázquez-Rodríguez JL, Alanis-Tamez MD, Moreno-Ibarra M-A, Yáñez-Márquez C. Mexican Axolotl Optimization: A Novel Bioinspired Heuristic. Mathematics. 2021; 9(7):781. https://doi.org/10.3390/math9070781
Chicago/Turabian StyleVilluendas-Rey, Yenny, José L. Velázquez-Rodríguez, Mariana Dayanara Alanis-Tamez, Marco-Antonio Moreno-Ibarra, and Cornelio Yáñez-Márquez. 2021. "Mexican Axolotl Optimization: A Novel Bioinspired Heuristic" Mathematics 9, no. 7: 781. https://doi.org/10.3390/math9070781
APA StyleVilluendas-Rey, Y., Velázquez-Rodríguez, J. L., Alanis-Tamez, M. D., Moreno-Ibarra, M.-A., & Yáñez-Márquez, C. (2021). Mexican Axolotl Optimization: A Novel Bioinspired Heuristic. Mathematics, 9(7), 781. https://doi.org/10.3390/math9070781








