Fuzzy Techniques Applied to the Analysis of the Causes and Effects of Tourism Competitiveness

Abstract

The aim of this research is to identify and analyze the causes and effects of tourism competitiveness, as well as cause–effect relationships from the perspective of two groups of experts, which are decision makers versus academics/researchers, both from the tourism sector. The purpose is to respond to the question: do decision makers in the tourism sector share the same perspective as academics/researchers regarding the relationship between the causes and effects of tourism competitiveness? The methodology used is the theory of expertons, the theory of forgotten effects and the Hamming distance. It was found that in most cases, the groups of experts share perspective, since their differences are small or non-existent. However, in all the relationships analyzed (cause–effect, cause–cause, and effect–effect), academic experts reported the highest assessment. The greatest difference in opinion is identified in the evaluation of the “Environmental Commitment” and “Tourist Demand” relationship. Decision makers in the tourism sector are ignoring the growing inclination and sensitivity that tourists are adopting towards the environment. It is necessary for the tourism sector to develop and consolidate its commitment to caring for and preserving the environment, which is an element that contributes to a destination’s competitiveness and has two main effects: tourism demand and customer satisfaction.

1. Introduction

Since the 80s and 90s, tourism has become a global economic phenomenon, which is a situation that has encouraged the search for competitive models that reveal what makes one destination more interesting than another [1]. Tourism is regarded as a sound alternative to achieve the economic development and social well-being of nations, but especially for developing or less developed ones [2]. However, tourism market trends and the life cycle of destinations bring about the need to undertake renovation processes [3]. Furthermore, the resources that position a destination as the most competitive today may not have any significance in the future [4].

The study of competitiveness became a topic of interest in tourism sector research in the 1990s, with the first researcher to conduct studies on tourism competitiveness being Poon [5]. Subsequently, to understand the role that competitiveness plays in tourism, researchers such as Ritchie and Crouch [6] defined a theoretical and conceptual framework to reveal how a tourist destination manages its competitiveness. The concept progressed from a perspective focused on tourist attractiveness to the strategic promotion of the tourism industry in a more holistic way, which considers different advantages of competitiveness [7].

Therefore, tourism competitiveness is presented as a key instrument to turn tourism into a factor of economic development [8,9,10]; it provides countries with the opportunity to maintain their position as leaders in the tourism activity [11] or to obtain a favorable position [12]. The continual interest of the tourism sector in competitiveness is due to the diversification that occurred in this activity; there are destinations competing to have more tourist arrivals or more tourism expenditure, which are indicators that reflect the economic prosperity of their residents [1].

Tourism competitiveness is defined as the ability of a destination to intensify tourism expenditure and gain more visitors while offering satisfying and memorable experiences in a profitable way, as well as improving the well-being of local residents and preserving the natural capital of the destination for future generations [6]. The concept proposed by Ritchie and Crouch [6] was adapted as the primary definition of tourism competitiveness [13], from which others arose such as the one proposed by Acerenza [14], who in a simple way defines tourism competitiveness as the ability of a destination to attract tourists. On the other hand, Dupeyras and MacCallum [15] conceptualize destination competitiveness as the ability of a place to take advantage of its attractiveness and offer quality and innovative tourist services, as well as to gain national and global market shares, while ensuring that the available resources that support tourism are used efficiently and sustainably.

In practice, tourism competitiveness is a construct in which various tangible and intangible factors participate, although it is only in a few, which are known as critical factors, where the greatest options for success or failure lie [16]. Tourism competitiveness brings about collective improvement, both in organizations and institutions, in favor of strengthening the tourism sector and focusing on increasing tourist flow and jobs [17]. It can also be said that destination competitiveness is the ability of the destination to conceive, integrate and provide tourist experiences, which include value-added goods and services that tourists consider substantial [18] and is characterized as a crucial element for the success of tourist destinations [19].

As a line of research, tourism competitiveness has had an interesting development in recent years, with one of its fields being the identification of the factors that affect it [2] and its relationship with variables such as tourism performance. Research papers in which this subject was addressed include those by Imali [20], Milicevic et al. [21], Hanafiah and Zulkifly [22]; Armenski et al. [23], Andradres and Dimanche [24], Amaya et al. [25], Cucculelli and Goffi [26], García and Siles [1], Decasper [27], Castellanos et al. [28], Leung and Baloglu [12], Goffi [19], Gandara et al. [17], Bolaky [29], Rodrigues and Carrasqueira [30] and Pascarella and Fontes [4], to name a few. Models have also been proposed to explain this phenomenon, including those developed by Poon [5], Hassan [31], Health [32], Ritchie and Crouch [6], Dwyer and Kim [33], Acerenza [14], Wei-Chiang [18], Alonso [16] and Jiménez and Aquino [34], among others.

Based on the research carried out to date on tourism competitiveness, it is possible to determine the causes that generate it and its effects on a tourist destination. However, a question arises: do decision makers in the tourism sector share the same perspective as academics/researchers regarding the relationship between the causes and effects of tourism competitiveness?

In this context, the aim of this paper is to compare the opinions held by two groups of experts, decision makers versus academics/researchers, both from the tourism sector, regarding the relationship between the causes and effects of tourism competitiveness. The methodology used to achieve these objectives is the experton and forgotten effects theories, and the Hamming distance.

This manuscript is structured in four sections. The first section establishes the bases of tourism competitiveness and its causes and effects, and sets out the objective of the research. The second section describes the materials and methods; the experton theory, the forgotten effects theory and the Hamming distance are discussed. In the third section, the results obtained are presented and discussed. In the fourth section, the conclusions of the paper are discussed.

2. Materials and Methods

Firstly, the causes and effects of tourism competitiveness were identified by reviewing the models proposed by Poon [5], Hassan [31], Health [32], Ritchie and Crouch [6], Dwyer and Kim [33], Acerenza [14], Wei-Chiang [18], Alonso [16], and Jiménez and Aquino [34]. The causes and effects found are shown in

Table 1. Causes of tourist competitiveness.

Causes	Definition
a.  Environmental commitment	The destination’s commitment to the environment [32].
b.  Legacy resources	The endogenous resources of the territory itself, among which are the natural resources (physiography, flora, climate and fauna, among others) and cultural resources (history, customs, architecture, music and dances, among others). They are the main attractions of a destination [33].
c.  Resources created	Tourist infrastructure (accommodation, meals, transport, travel agencies and car rentals, among others), tourist services (medical services, security and gas stations, among others), special events, recreational activities, sports, leisure and entertainment, and souvenir shops [33].
d.  General infrastructure	The variety and quality of local transport services, drinking water supply, sanitation, communication systems, public facilities, electricity, financial services and telecommunications, among others [6,35].
e.  Quality of service	The degree of conformity of the attributes and characteristics of a service with respect to customer expectations [36].
f.  Accessibility	Means of access to a destination; airports and roads, mainly [33].
g.  Hospitality	The kindness and warmth of the local population [33].
h.  Destination management	The activities that can improve resource attractiveness, as well as strengthen the quality and effectiveness of support factors (infrastructure), such as destination marketing management; policies, planning and development of the destination; management organization; human resources development and resource management [33].
i.  Ties to the market	Business relationships, migration flows, culture and language, among others [33].
j.  Location	The geographical area in which the destination is located [37].
k.  Security	The conditions of political stability, crime, terrorism and disease, among others [33].
l.  Price	A relationship that indicates the amount of money needed to acquire a given amount of a good or service [38].
m.  The microenvironment	The capacities and resources of tourism companies, this also includes the stakeholders of a destination [33].
n.  The macro environment	The conditions of the economic, demographic, social, political and legal environment, mainly [33].
o.  Demand conditions	The understanding of the perception and preferences of tourism [33].

Source: Reproduced from [39], Journal of Intelligent & Fuzzy Systems: 2021.

and

Table 2. Effects of tourist competitiveness.

Effects	Definition
A.  Sustainable development	The process of economic, human and environmental development that can be maintained without relying on external assistance [40].
B.  Tourist demand	A set of goods and services that tourists are willing to acquire in a certain destination [41].
C.  Customer satisfaction	Associated with the simple feeling of contentment, conditioned by a double human vision: utilitarian (to what extent the good of consumption or service fulfils the functions or tasks assigned to them) and hedonistic (activation of affective processes) [42].
D.  Customer loyalty	A favorable correspondence between the attitude of the individual towards an organization; in this case, the tourist destination and the behavior of purchasing the products and services thereof [43].
E.  Tourist spending	Total consumption expenses made by a visitor or on behalf of a visitor during their travel and tourist stay at the destination [41].
F.  Profitability	Return on investment [44].
G.  Prosperity	Favorable development, especially in the economic and social aspect.
H.  Arrival of tourist	Number of tourists arriving at a destination [41].
I.  Economic growth	Quantitative increase or expansion of income and value of goods and services produced in the economic system as measured through the growth rate of gross domestic product [45].

Source: Reproduced from [39], Journal of Intelligent & Fuzzy Systems: 2021.

.

At the same time, 8 experts were selected according to their academic and professional background; these people are directly immersed in the tourism sector, either offering a service or conducting research, as applicable. According to the purpose of this work, the government sector has been excluded. Two groups of experts were formed: the first group was made up of academics/researchers on the subject of tourism and competitiveness; the second group of experts was made up of people who work in the tourism sector. Next, both groups evaluated the cause–effect, cause–cause and effect–effect relationships based on the endecadary scale shown in

Table 3. Endecadary scale.

Degree	Meaning
0	It has no incidence
0.1	Virtually no incidence
0.2	Almost without incidence
0.3	It has a very weak incidence
0.4	Has a weak incidence
0.5	Median incidence
0.6	Has a noticeable incidence
0.7	It has a lot of incidence
0.8	It has a strong incidence
0.9	It has a very strong incidence
1	It has the highest incidence

Source: Kaufmann and Gil-Aluja [46].

, proposed by Kaufmann and Gil-Aluja [46]. It is worth mentioning that all the experts had the same weight in the evaluation.

Based on the evaluations conducted by the experts, six expert tables were constructed, with three for each group. To construct each experton, first the absolute frequencies were calculated (number of experts suggesting each result), then the data were normalized through relative frequencies (division of the absolute frequencies by the total number of experts) and finally, the accumulated relative frequencies were obtained [47,48,49]. This is done level by level for the 11-point endecadary scale [49] (Table 3).

The forgotten effects theory was used to identify the variables and relationships that remain hidden or generate an indirect impact. This was done for each group of experts, for which the constructed expertons M (cause–effect relationship), A (cause–cause relationship) and B (effect–effect relationship) were used, which correspond to the direct incidence matrices. The matrices M, A and B were convoluted in the following way: $A\circ M=AM$ and $AM\circ B=M^{*}$ ($M^{*}$ represents the accumulated effects matrix), then the forgotten effects matrix was calculated with the formula $O=M^{*}-M$.

Finally, the Hamming distance between expertons was used to compare the opinions that both groups of experts have regarding tourism competitiveness, particularly its causes, effects and the relationship between them. This last step follows a similar process to the Hamming distance between fuzzy subsets in the discrete domain. In this case, all expert evaluations are considered, except for the level α = 0, and the result is normalized by dividing by the number of n evaluations considered. The formulation of the Hamming distance between experts is as follows:

$$Distance to the left=d_I\left(A,B\right)=\frac{1}{2n}{\displaystyle \sum }_{j=1}^n\left|a_1\left({\alpha }_j\right)-b_1\left({\alpha }_j\right)\right|$$

(1)

$$Distance to the right=d_D\left(A,B\right)=\frac{1}{2n}{\displaystyle \sum }_{j=1}^n\left|a_2\left({\alpha }_j\right)-b_2\left({\alpha }_j\right)\right|$$

(2)

$$Total distance=d\left(A,B\right)= d_I\left(A,B\right)+ d_D\left(A,B\right)$$

(3)

It should be noted that only one of the distances was used (left or right), since the information was in individual data and not in intervals.

2.1. Theory of Expertons

There are phenomena in nature that humans evaluate through a subjective opinion and can hardly be classified according to whether or not a property is fulfilled [50]. In this regard, the theory of expertons suggests that to obtain realistic data of phenomena that cannot be measured directly, it is useful to have an aggregate set of the assessments given by experts [46,51].

The theory of expertons extends the probabilistic set concept [52] to uncertain environments that can be evaluated with interval numbers and allows for the analysis of group information considering all individual opinions, producing a single final result. Thus, it makes the information more robust because it is evaluated by several experts and the use of several experts in the analysis generally leads to better decisions [47].

An experton is defined as a generalization of a probabilistic set when the accumulated probabilities are replaced by intervals that decrease monotonically [53]. It arises as a result of a procedure of aggregation of different expert opinions regarding the degree of veracity of a statement and provides the percentage of experts who agree that the veracity of the statement is at least the given value [49].

The theory of expertons, which was developed by Kaufmann [51], is defined as follows:

Definition 1.

Let E be a referential set, finite or not; where r experts are required to express their subjective opinion about each element of E in the form of a confidence interval:

$$\forall x\in E: \left[a_{*}^j\left(x\right), a_j^{*}\left(x\right)\right]\subset \left[0, 1\right]$$

(4)

where ⊂ is an inclusion set and j is the expert. A cumulative complementary law$F_{*}\left(a,x\right)$can be established for all$a_{*}^j\left(x\right)$and$F^{*}\left(a,x\right)$for all$a_j^{*}\left(x\right)$, which is due to a statistic that indicates that for each$x\in E$, the lower limits are one way and the upper limits another way. By substituting this approach in Equation (4), the following is obtained:

$$\forall x\in E, \forall x\in \left[0, 1\right]:\tilde{A}\left(x\right)=\left[F_{*}\left(\alpha ,x\right) , F^{*}\left(\alpha ,x\right)\right]$$

(5)

The symbol $\tilde{A}$ that appears in Equation (5) recalls the nature of the concept.

So, the referential set E is the following experton:

$$\forall x\in E, \forall x\in \left[0, 1\right]:\left[F_{*}\left(\alpha ,x\right) , F^{*}\left(\alpha ,x\right)\right]=1$$

(6)

Additionally, an empty experton is given by:

$$\forall x\in E:\left[F_{*}\left(\alpha ,x\right) , F^{*}\left(\alpha ,x\right)\right]=\left\{\begin{array}{c}1, \alpha =0\\ 0, \alpha \ne 0\end{array}\right.$$

(7)

And it has the following properties:

$$\begin{array}{cc}\forall x\in E,\forall \alpha ,{\alpha }^{\prime }& \in \left[0,1\right]:\left(\alpha <{\alpha }^{\prime }\right) \\ & ⟹\left(\left[F_{*}\left({\alpha }^{\prime },x\right), F^{*}\left({\alpha }^{\prime },x\right)\right]{\subset }_i\left[F_{*}\left(\alpha ,x\right), F^{*}\left({\alpha }^{\prime },x\right)\right]\right)\end{array}$$

(8)

The expression ${\subset }_i$ that appears in Equation (8) is known as the inclusion interval. It can be expressed as follows:

$$\left(\alpha <{\alpha }^{\prime }\right) ⟹\left(\left(F_{*}\left({\alpha }^{\prime },x\right)\le F_{*}\left(\alpha ,x\right)\right) and \left(F^{*}\left({\alpha }^{\prime },x\right)\le F^{*}\left(\alpha ,x\right)\right)\right)$$

(9)

When a final consideration or interpretation of the phenomena is required, the experton can be reduced to a single representative value by reducing the entropy of the results. This can be obtained by calculating the mathematical expectation of the probabilistic set [53].

2.2. Forgotten Effects Theory

Any activity is subject to cause–effect incidents [54] and to the possibility of forgetting some causal relationships that are not explicit, obvious or visible [55]. In situations of uncertainty and volatility, there are variables that are not immediately detectable because they are hidden as a result of an accumulation of causes [46]. To identify the incidents that are not so evident between variables, but are fundamental for decision making, the theory of forgotten effects has proven to be an effective approach when seeking to maximize the information retrieved from the complex relationships between variables and to minimize errors that can occur in these processes [56].

The theory of forgotten effects is an extension of fuzzy logic applications [57]. This theory allows for an approach to the objective of globalizing the direct and indirect incidences between a set of causes and effects [46], since it suggests that all events, phenomena and facts that surround people are based on some type of system or subsystem. Therefore, they are subject to some type of cause–effect relationship, with the possibility that voluntarily or involuntarily some relationships are not directly perceived [58].

The theory of forgotten effects developed by Kaufmann and Gil-Aluja [46] is defined as follows:

Definition 2.

The existence of two sets,$A=\left\{\frac{a_i}{i}=1, 2,\dots ,n\right\}$and$B=\left\{\frac{b_j}{j}=1,2,\dots ,m\right\}$, is assumed. It is conjectured that an impact of$a_i$on$b_j$prevails if the value of the characteristic membership function of$\left(a_i, b_j\right)$is evaluated in a [0, 1] range, that is:

$$\forall \left(a_i,b_j\right)\Rightarrow \mu \left(a_i,b_j\right) \in \left[0,1\right]$$

(10)

The set of pairs of elements evaluated is the direct incidence matrix (M), which shows the cause–effect relationship in different degrees caused by the corresponding set A (causes) and set B (effects), as shown below:

		$b_1$	$b_2$	$b_3$	…	$b_m$
	$a_1$	${\mu }_{a_1{b}_1}$	${\mu }_{a_1{b}_2}$	${\mu }_{a_1{b}_3}$	…	${\mu }_{a_1{b}_m}$
	$a_2$	${\mu }_{a_2{b}_1}$	${\mu }_{a_2{b}_2}$	${\mu }_{a_2{b}_3}$	…	${\mu }_{a_2{b}_m}$
M =	$a_3$	${\mu }_{a_3{b}_1}$	${\mu }_{a_3{b}_2}$	${\mu }_{a_3{b}_3}$	…	${\mu }_{a_3{b}_m}$
	$⋮$	…	…	…	…	…
	$a_n$	${\mu }_{a_n{b}_1}$	${\mu }_{a_n{b}_2}$	${\mu }_{a_n{b}_3}$	…	${\mu }_{a_n{b}_m}$

The next step is to proceed to detecting the forgotten effects. For this, it is assumed that there is a third set of elements, called C, expressed in the following way $C=\left\{\frac{C_k}{k}=1, 2,\dots ,k\right\}$. This set consists of elements that are effects of set B and has an incidence matrix which is expressed as follows:

		$c_1$	$c_2$	$c_3$	…	$c_k$
	$b_1$	${\mu }_{b_1{c}_1}$	${\mu }_{b_1{c}_2}$	${\mu }_{b_1{c}_3}$	…	${\mu }_{b_1{c}_k}$
	$b_2$	${\mu }_{b_2{c}_1}$	${\mu }_{b_2{c}_2}$	${\mu }_{b_2{c}_3}$	…	${\mu }_{b_2{c}_k}$
N =	$b_3$	${\mu }_{b_3{c}_1}$.	${\mu }_{b_3{c}_2}$	${\mu }_{b_3{c}_3}$	…	${\mu }_{b_2{c}_k}$
	$⋮$	…	…	…	…	…
	$b_m$	${\mu }_{b_m{c}_1}$	${\mu }_{b_m{c}_2}$	${\mu }_{b_m{c}_3}$	…	${\mu }_{b_m{c}_k}$

So far, there are two incidence matrices, M and N, and they both have element B in common. This relationship is expressed as:

$$M\subset AxB y N\subset BxC$$

(11)

Next, the max–min operator (convolution) is used to detect the relationship between sets A and C using B. As a result, a new incidence matrix is generated, which is expressed by:

$$\begin{array}{c}M\circ N=P\\ P\subset AxC\end{array}$$

(12)

This new relationship is formulated in the following way:

$$\forall \left(a_i,c_z\in AxC\right)$$

(13)

$$\mu \left(a_i,c_z\right)M\circ N= {\forall }_{\mathit{bj}}\left({\mu }_M\left(a_i,b_j\right)\wedge {\mu }_N\left(b_j,c_z\right)\right)$$

(14)

The matrix that results from the max–min operation is:

		$c_1$	$c_2$	$c_3$	…	$c_k$
	$a_1$	${\mu }_{a_1{c}_1}$	${\mu }_{a_1{c}_2}$	${\mu }_{a_1{c}_3}$	…	${\mu }_{a_1{c}_k}$
	$a_2$	${\mu }_{a_2{c}_1}$	${\mu }_{a_2{c}_2}$	${\mu }_{a_2{c}_3}$	…	${\mu }_{a_2{c}_k}$
P =	$a_3$	${\mu }_{a_3{c}_1}$	${\mu }_{a_3{c}_2}$	${\mu }_{a_3{c}_3}$	…	${\mu }_{a_2{c}_k}$
	$⋮$	…	…	…	…	…
	$a_n$	${\mu }_{a_n{c}_1}$	${\mu }_{a_n{c}_2}$	${\mu }_{a_n{c}_3}$	…	${\mu }_{a_n{c}_k}$

Matrix P defines the causal relationships between the elements of the A and C sets, at the intensity or degree that B allows for.

2.3. The Hamming Distance between Fuzzy Subsets

The distance measurement plays a vital role in pattern recognition, information fusion, decision making and other fields [59]. It is an important issue in fuzzy sets and their extensions [60,61]. There are several distance measures that have been introduced by researchers to solve problems in various fields; among these distances, the Euclid distance and the Hamming distance are widely used [62]. Specifically, the Hamming distance was developed by Richard Wesley Hamming in 1950 and is defined as follows [63]:

Definition 3.

The distance$D\left(x,y\right)$between two x and y points is defined as the number of coordinates for which x and y are different. This function fulfils the three usual conditions for a metrics:

$$D\left(x,y\right)=0\hspace{1em}\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} x=y$$

(15)

$$D\left(x,y\right)=D\left(y,x\right)>0\hspace{1em}\mathrm{if} x\ne y$$

(16)

$$D\left(z,y\right) +D\left(y,z\right) \ge D\left(x,z\right) (\mathrm{triangular} \mathrm{inequality})$$

(17)

The Hamming distance, like the Theory of Expertons, is considered a fuzzy numerical model [64]; it is known for its ability to calculate the difference between two sets or elements and is identified as one of the multi-criteria decision-making approaches. Also, when counting the number of specific differences between two permutations, it is a natural choice to measure the distance between assignments or pairings [65]. This approach helps to solve many problems related to biology, science and technology due to its ability to construct some related distance measures, in particular, similarity and proximity, which usually become a norm in several problems [66].

Before defining the Hamming distance between fuzzy subsets in the discrete domain, it is necessary to understand the concepts of fuzzy sets and subsets, which in the words of Zadeh [67] are defined below:

Definition 4.

Let X be a universe of analysis, then a fuzzy set A in X is defined as a set of pairs established in the following way:

$$A=\left\{\langle x,{\mu }_A\left(x\right)\rangle :x\in X\right\}$$

(18)

where${\mu }_A:X\to \left[0, 1\right]$is the membership function that characterizes the universe of analysis A and${\mu }_A\left(x\right)$is the degree of membership of x in A.

Definition 5.

A fuzzy subset A of a universe of analysis X is characterized by a membership function${\mu }_A:X\to \left[0, 1\right]$which associates to each element x of X a number${\mu }_A\left(x\right)$in an interval [0, 1]; thus, ${\mu }_A\left(x\right)$ represents the degree of membership of x in A.

Regarding the degree of membership ${\mu }_A\left(x\right)$ shown in the two previous definitions, it can be interpreted as the degree of compatibility of x with the concept represented by A or as the degree of possibility of x given A. In these cases, the function ${\mu }_A:X\to \left[0, 1\right]$ can be referred to as a compatibility function. It should be noted that the meaning attributed to a particular numerical value of the membership function is purely subjective in nature [57]. From the above, it is possible to state that the degree of non-membership of x in A is equal to $1-{\mu }_A\left(x\right)$ [68].

Therefore, the Hamming distance of two fuzzy subsets is defined as follows [69]:

Definition 6.

Given two fuzzy subsets A and B with a reference set X = {$x_1$,$x_2$, …,$x_n$} and membership functions${\mu }_A$and${\mu }_B$, the Hamming distance is defined as:

$$d\left(A,B\right)={\displaystyle \sum }_{j=1}^n\left|{\mu }_A\left(x_j\right)-{\mu }_B\left(x_j\right)\right|$$

(19)

where${\mu }_A$and${\mu }_B$ ∈ [0, 1].

In this case, the Hamming distance measures the relationship between variables in a study of facts and how they fit a profile. Finally, it calculates the distance between the extremes of the intervals [64].

3. Results

To compare the perspectives that decision makers in the tourism sector and tourism academics/researchers have regarding the causes and effects of tourism competitiveness, as well as the relationship between them, the following tools were used: experton, forgotten effects and Hamming distance between experts, with the last tool showing numerical differences of opinion. Each expert evaluated the cause–effect, cause–cause and effect–effect relationships; the expertons shown in

Table 4. Expertons made up of the cause–effect valuation carried out by the group of experts from the tourism sector (Matrix M1).

Cause–Effect	A	B	C	D	E	F	G	H	I
a	0.75	0.40	0.38	0.53	0.28	0.50	0.58	0.58	0.40
b	0.50	0.63	0.50	0.60	0.45	0.55	0.48	0.73	0.50
c	0.53	0.63	0.55	0.55	0.58	0.50	0.55	0.65	0.53
d	0.70	0.70	0.78	0.68	0.70	0.73	0.75	0.78	0.70
e	0.38	0.85	0.93	0.93	0.75	0.83	0.70	0.85	0.58
f	0.35	0.63	0.65	0.60	0.55	0.55	0.60	0.83	0.63
g	0.25	0.75	0.88	0.83	0.70	0.50	0.48	0.83	0.48
h	0.38	0.83	0.55	0.68	0.75	0.60	0.55	0.75	0.50
i	0.50	0.65	0.63	0.58	0.50	0.58	0.78	0.70	0.68
j	0.45	0.70	0.75	0.73	0.50	0.75	0.70	0.78	0.78
k	0.45	0.83	0.90	0.90	0.80	0.83	0.90	0.93	0.88
l	0.33	0.80	0.78	0.78	0.90	0.88	0.80	0.75	0.80
m	0.65	0.68	0.68	0.65	0.60	0.73	0.65	0.65	0.65
n	0.60	0.70	0.48	0.50	0.53	0.70	0.65	0.60	0.68
o	0.55	0.93	0.68	0.58	0.78	0.70	0.63	0.80	0.43

Source: own elaboration.

,

Table 5. Expertons formed from the cause–effect evaluation carried out by the group of academic experts/researchers (Matrix M2).

Cause–Effect	A	B	C	D	E	F	G	H	I
a	0.83	0.78	0.68	0.53	0.63	0.48	0.53	0.63	0.53
b	0.70	0.73	0.63	0.65	0.68	0.65	0.70	0.83	0.60
c	0.60	0.63	0.60	0.55	0.65	0.65	0.65	0.75	0.58
d	0.60	0.70	0.83	0.78	0.75	0.75	0.78	0.75	0.78
e	0.65	0.83	0.90	0.90	0.90	0.85	0.80	0.88	0.73
f	0.65	0.68	0.68	0.60	0.58	0.58	0.50	0.68	0.58
g	0.58	0.78	0.88	0.85	0.80	0.63	0.55	0.80	0.55
h	0.63	0.80	0.75	0.75	0.78	0.65	0.63	0.73	0.53
i	0.60	0.65	0.63	0.65	0.68	0.55	0.68	0.68	0.58
j	0.58	0.70	0.78	0.78	0.65	0.75	0.73	0.85	0.78
k	0.73	0.88	0.90	0.90	0.80	0.83	0.83	0.83	0.85
l	0.60	0.68	0.73	0.75	0.73	0.78	0.75	0.75	0.73
m	0.53	0.68	0.63	0.70	0.68	0.75	0.68	0.68	0.58
n	0.55	0.60	0.58	0.55	0.58	0.68	0.60	0.58	0.60
o	0.58	0.75	0.78	0.75	0.75	0.80	0.70	0.73	0.65

Source: own elaboration.

,

Table 6. Expertons made up of the cause–cause valuation carried out by the group of experts from the tourism sector (Matrix A1).

Cause–Cause	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
a	1.00	0.53	0.55	0.58	0.55	0.33	0.20	0.35	0.43	0.40	0.28	0.30	0.35	0.48	0.45
b	0.53	1.00	0.55	0.63	0.48	0.60	0.35	0.60	0.55	0.38	0.43	0.53	0.68	0.43	0.45
c	0.58	0.43	1.00	0.68	0.68	0.70	0.58	0.63	0.58	0.45	0.58	0.60	0.68	0.55	0.45
d	0.45	0.40	0.50	1.00	0.45	0.68	0.25	0.50	0.40	0.28	0.65	0.63	0.60	0.38	0.50
e	0.45	0.38	0.58	0.65	1.00	0.60	0.88	0.48	0.63	0.43	0.73	0.73	0.70	0.55	0.68
f	0.40	0.30	0.55	0.55	0.63	1.00	0.55	0.48	0.48	0.63	0.63	0.53	0.65	0.60	0.65
g	0.25	0.30	0.55	0.50	0.88	0.60	1.00	0.55	0.58	0.30	0.55	0.58	0.68	0.45	0.70
h	0.23	0.45	0.65	0.53	0.78	0.60	0.40	1.00	0.70	0.65	0.75	0.65	0.60	0.55	0.60
i	0.38	0.40	0.55	0.55	0.73	0.55	0.75	0.78	1.00	0.48	0.60	0.58	0.58	0.48	0.65
j	0.33	0.60	0.68	0.65	0.60	0.83	0.35	0.68	0.70	1.00	0.60	0.68	0.58	0.53	0.65
k	0.28	0.35	0.75	0.58	0.85	0.58	0.60	0.85	0.88	0.63	1.00	0.70	0.75	0.65	0.68
l	0.25	0.33	0.75	0.80	0.80	0.73	0.40	0.80	0.70	0.58	0.65	1.00	0.65	0.55	0.63
m	0.35	0.38	0.58	0.50	0.70	0.58	0.55	0.68	0.60	0.45	0.60	0.58	1.00	0.73	0.50
n	0.43	0.35	0.65	0.73	0.60	0.70	0.53	0.58	0.63	0.60	0.83	0.68	0.85	1.00	0.63
o	0.45	0.40	0.63	0.73	0.73	0.68	0.60	0.78	0.63	0.63	0.73	0.73	0.63	0.53	1.00

Source: own elaboration.

,

Table 7. Expertons made up of the cause–cause valuation carried out by the group of academic experts/researchers (Matrix A2).

Cause– Cause	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
a	1.00	0.55	0.63	0.55	0.65	0.53	0.55	0.50	0.53	0.68	0.60	0.55	0.58	0.55	0.55
b	0.50	1.00	0.55	0.58	0.55	0.70	0.60	0.68	0.50	0.65	0.60	0.55	0.65	0.58	0.60
c	0.68	0.60	1.00	0.63	0.58	0.73	0.50	0.68	0.55	0.65	0.63	0.63	0.63	0.63	0.60
d	0.70	0.70	0.83	1.00	0.78	0.85	0.70	0.83	0.83	0.80	0.83	0.85	0.78	0.83	0.83
e	0.68	0.65	0.75	0.78	1.00	0.83	0.83	0.75	0.83	0.70	0.88	0.80	0.80	0.70	0.80
f	0.63	0.50	0.68	0.70	0.75	1.00	0.70	0.63	0.70	0.83	0.83	0.60	0.73	0.68	0.78
g	0.55	0.55	0.68	0.70	0.85	0.68	1.00	0.55	0.63	0.63	0.75	0.68	0.75	0.60	0.78
h	0.58	0.60	0.65	0.75	0.83	0.70	0.68	1.00	0.78	0.88	0.83	0.65	0.75	0.58	0.73
i	0.53	0.50	0.65	0.73	0.73	0.65	0.73	0.70	1.00	0.70	0.75	0.65	0.63	0.55	0.78
j	0.48	0.53	0.70	0.70	0.68	0.80	0.60	0.75	0.78	1.00	0.78	0.73	0.63	0.60	0.75
k	0.53	0.53	0.75	0.85	0.85	0.83	0.65	0.80	0.85	0.88	1.00	0.80	0.83	0.60	0.80
l	0.48	0.60	0.68	0.68	0.78	0.70	0.48	0.70	0.75	0.75	0.78	1.00	0.70	0.55	0.80
m	0.53	0.55	0.65	0.63	0.68	0.70	0.60	0.63	0.68	0.63	0.63	0.63	1.00	0.68	0.63
n	0.43	0.38	0.60	0.70	0.65	0.68	0.40	0.45	0.50	0.43	0.50	0.48	0.78	1.00	0.50
o	0.45	0.45	0.63	0.73	0.70	0.78	0.58	0.83	0.73	0.80	0.80	0.78	0.68	0.65	1.00

Source: own elaboration.

,

Table 8. Expertons made up of the effect–effect valuation carried out by the group of experts from the tourism sector (Matrix B1).

Effect–Effect	A	B	C	D	E	F	G	H	I
A	1.00	0.63	0.70	0.60	0.60	0.53	0.65	0.53	0.53
B	0.65	1.00	0.65	0.68	0.85	0.73	0.73	0.95	0.83
C	0.50	0.55	1.00	0.93	0.65	0.68	0.58	0.80	0.55
D	0.28	0.53	0.80	1.00	0.48	0.50	0.40	0.88	0.45
E	0.60	0.68	0.55	0.60	1.00	0.68	0.68	0.58	0.68
F	0.50	0.68	0.55	0.58	0.55	1.00	0.65	0.73	0.73
G	0.60	0.73	0.68	0.70	0.70	0.70	1.00	0.75	0.63
H	0.48	0.90	0.75	0.70	0.68	0.68	0.63	1.00	0.73
I	0.70	0.65	0.70	0.73	0.78	0.95	0.85	0.75	1.00

Source: own elaboration.

and

Table 9. Expertons made up of the effect–effect assessment carried out by the group of academic experts/researchers (Matrix B2).

Effect–Effect	A	B	C	D	E	F	G	H	I
A	1.00	0.65	0.65	0.50	0.58	0.60	0.58	0.58	0.55
B	0.60	1.00	0.60	0.55	0.53	0.43	0.50	0.48	0.38
C	0.65	0.68	1.00	0.85	0.68	0.70	0.65	0.78	0.63
D	0.78	0.83	0.85	1.00	0.73	0.83	0.80	0.93	0.80
E	0.80	0.80	0.58	0.78	1.00	0.68	0.60	0.73	0.65
F	0.53	0.78	0.63	0.73	0.68	1.00	0.58	0.78	0.60
G	0.53	0.65	0.68	0.60	0.58	0.50	1.00	0.60	0.65
H	0.70	0.83	0.88	0.85	0.75	0.73	0.63	1.00	0.70
I	0.50	0.75	0.58	0.53	0.45	0.78	0.45	0.55	1.00

Source: own elaboration.

were constructed based on these evaluations.

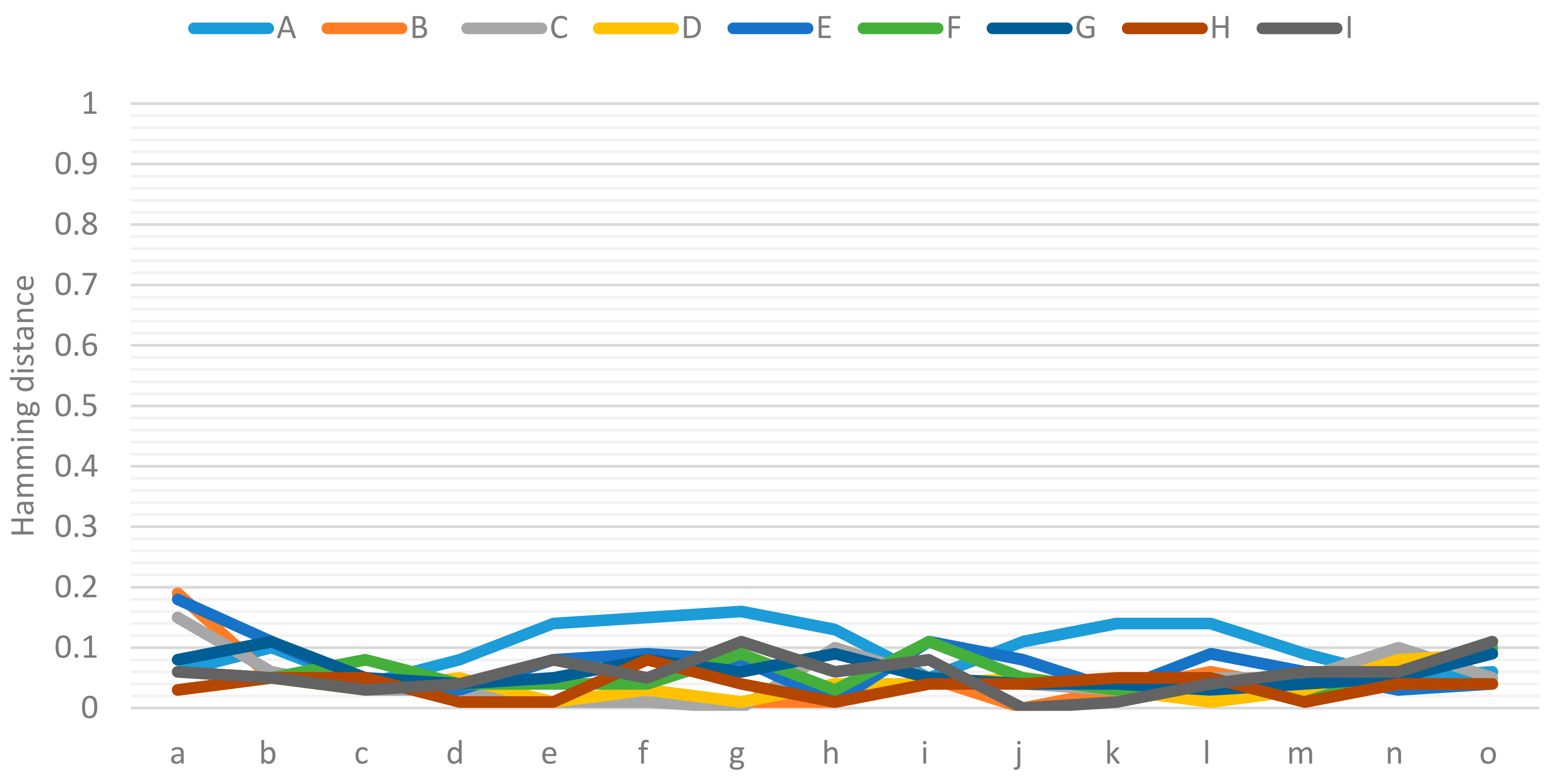
Figure 1 shows the Hamming distance between the two groups of experts regarding the evaluation of the relationship between the causes and effects of tourism competitiveness. The greatest distance, with a value of 0.19, occurs in the relationship between Environmental Commitment and Tourism Demand. The experton which was constructed based on the assessment of this relationship by the sector of academics/researchers was considerably higher than the one obtained by experts in the tourism sector.

In this regard, there is a growing acceptance of public and private stakeholders interested in tourism due to the assumption of a compatibility between the economic benefit and the minimization of the socio-cultural impacts on hosts and tourists with the protection of the natural environment; a situation that raises conflicting attitudes among the actors involved, which are favorable among administrators, researchers and environmental groups, but reluctant in the private sector [68]. It is visualized that this is one of the reasons why the group of academics/researchers reported a higher evaluation with respect to the experts of the tourism sector.

In Figure 1, it can also be seen that there are relationships in which the distance is zero in the evaluation of both groups of experts. This means that both groups agree on those evaluations; this is found in the relationships of Location–Tourist Demand, Hospitality–Customer Satisfaction and Location–Economic Growth. Regarding the Hospitality–Customer Satisfaction relationship, previous studies show the relationship between them, such as those developed by Oliver [70], who proposed that satisfaction is deduced from the guest’s perception of the attention given. Alves and Barcellos [71] indicated that experiences in hospitality and tourist services are the main product of the sector, with an impact and influence on its competitiveness.

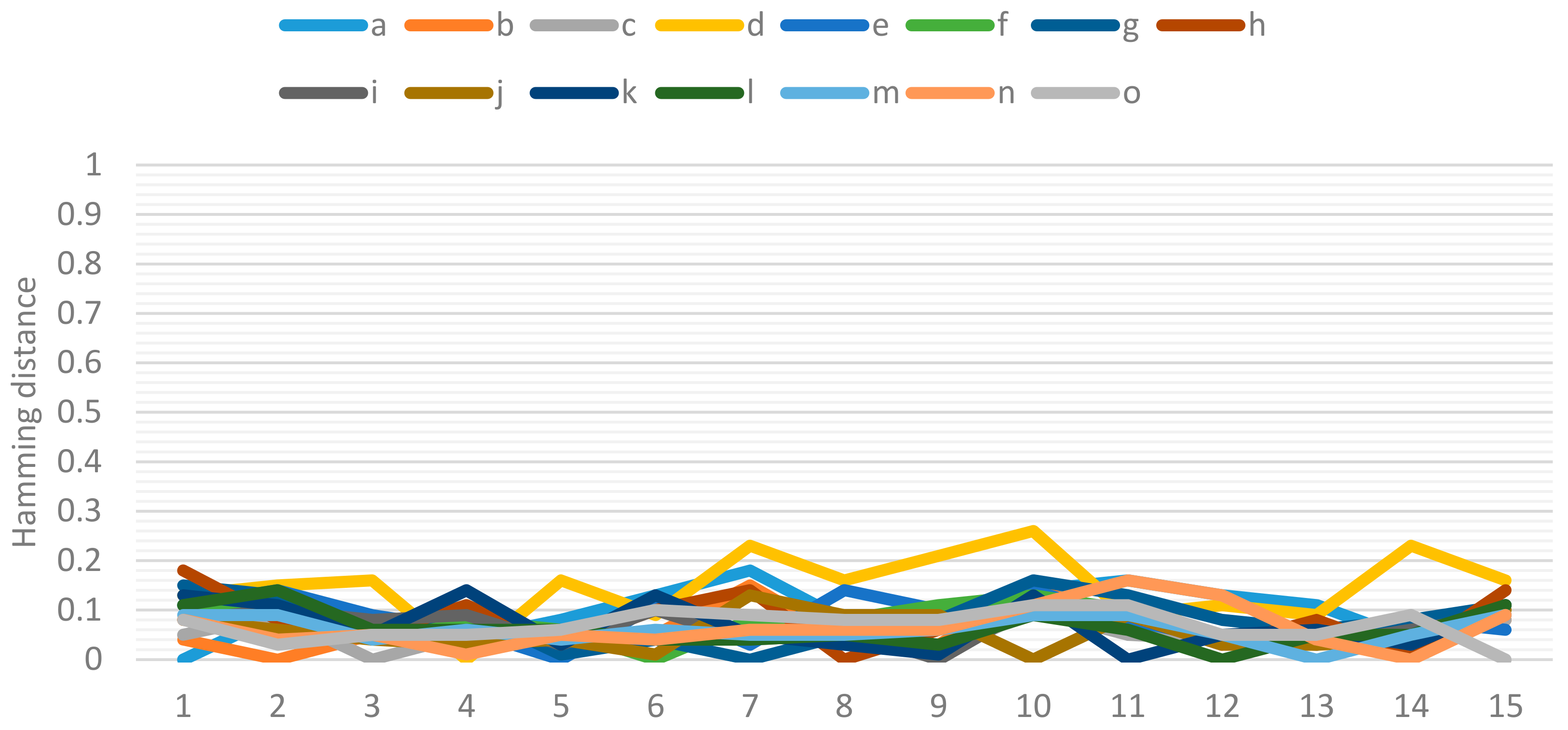
Figure 2 shows the Hamming distance between the two groups of experts regarding the evaluation of the relationship between causes and the cause of tourism competitiveness. The greatest distance, with a value of 0.26, occurs in the relationship found between General Infrastructure and Location, and again in this relationship, academic experts were the ones who gave a higher evaluation compared to the evaluations made by the tourism sector experts. In this matrix, there is a diagonal line of the relationships in which the distance is zero. However, this occurs because the evaluation of the cause–cause relationship produces a value of one when it is the same.

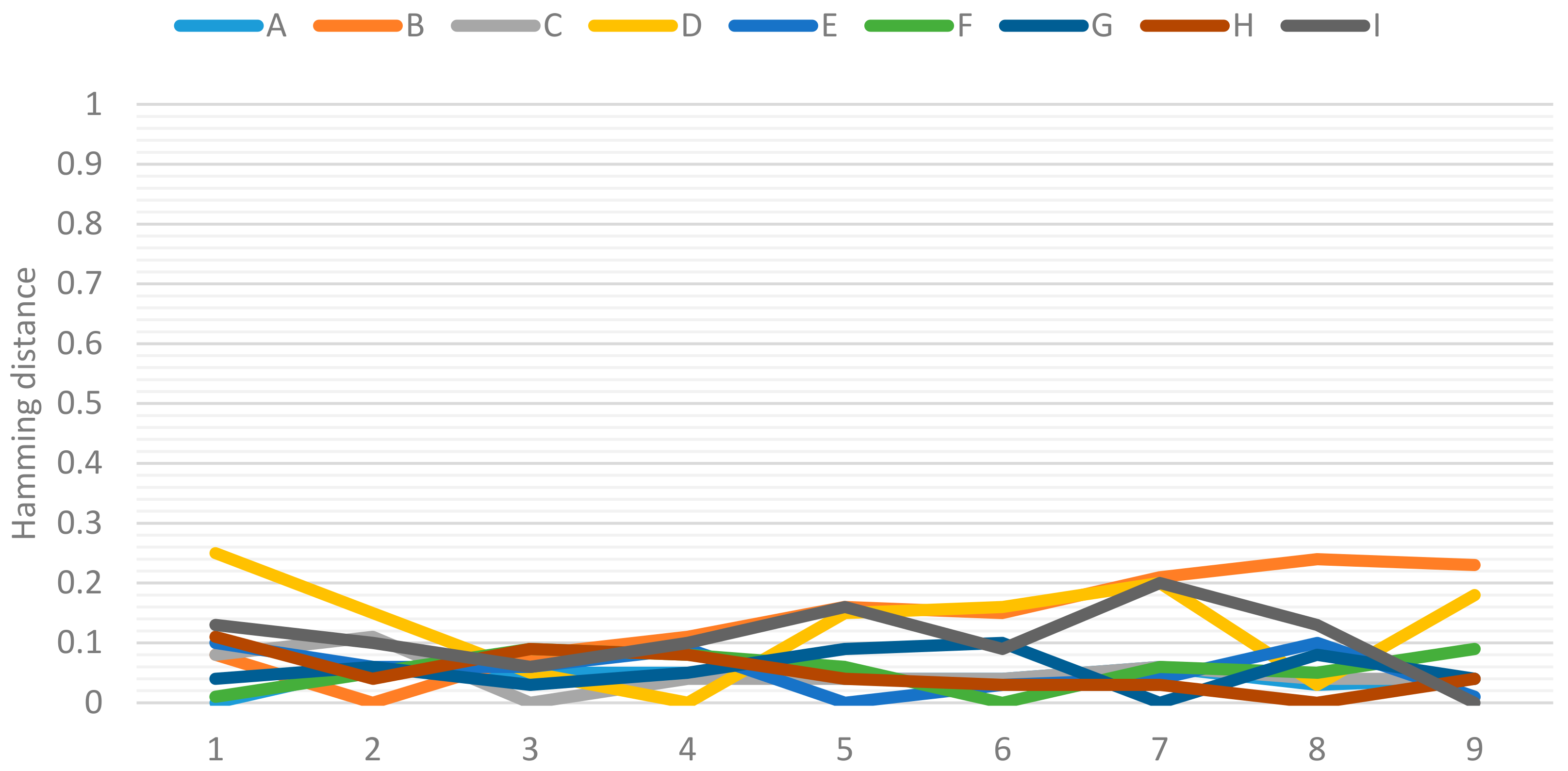
Figure 3 shows the Hamming distance between the two groups of experts regarding the evaluation of the relationship between effect–effect of tourism competitiveness. The greatest distance, with a value of 0.25, occurs in the relationship that is found between Customer Loyalty and Sustainable Development. This time, it was also academic experts who evaluated the relationship higher. Note that in this matrix there is also a diagonal line of the relationships in which the distance is zero, which is for the same reasons as in the previous figure.

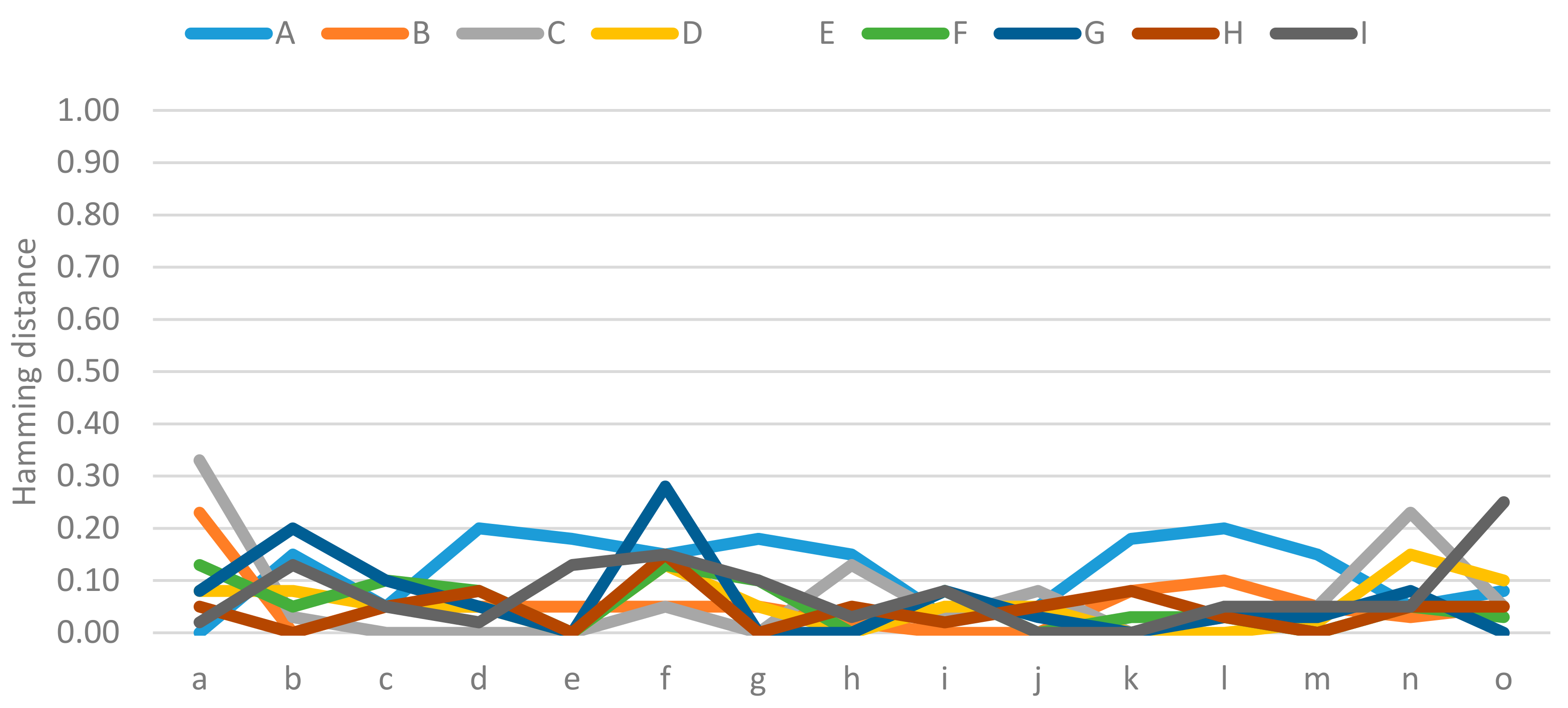
From the information shown in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, the forgotten effects were obtained by each group of experts and with these results. The Hamming distance of the forgotten effects was calculated, which is shown in Figure 4. The greatest distance, with a value of 0.33, occurs in the relationship between Environmental Commitment (cause) and Customer Satisfaction (effect). In this case, the forgotten effect by the academic sector was zero, while the forgotten effect by the tourism sector was 0.33, which indicates that the academic sector has clearly identified the impact of the environmental commitment that a tourist destination has on customer satisfaction, which is a situation in which people who work in the tourism sector have not yet recognized.

Figure 4 shows 30 relationships whose Hamming distance is zero. In this situation, all the effects and all the causes are present except for Accessibility and The Macroenvironment. Cumulatively, the Hamming distance of the effect that shows the highest value is the “Sustainable Development” effect with a value of 1.78, while for the Hamming distance of the causes, the causes with the highest values are “Environmental Commitment” and “Accessibility”, with both causes having a value of 1.18.

4. Conclusions

This research paper began by discussing the importance of the tourism sector in the economy, as well as the need to develop competitiveness in tourist destinations. An analysis from the perspective of two expert groups (decision makers from the tourism sector and academics/researchers) regarding the relationship between the causes and effects of tourism competitiveness using fuzzy techniques was presented, such as the Theory of Expertons, the Theory of Forgotten Effects and the Hamming distance between expertons.

The Theory of Expertons enabled us to group all of the experts’ opinions of each group into a single group result. The Forgotten Effects Theory helped to identify, for each group of experts, the variables and relationships that remained hidden or whose impact was indirect on cause–effect relationships. Finally, the Hamming distance between experts helped to detect differences of opinion between the perspective of a group of decision makers in the tourism sector versus the perspective of a group of academics/researchers regarding the relationship between the causes and effects of tourism competitiveness.

The results obtained showed that the experts’ perspectives regarding the cause–effect relationship have a distance that ranges from 0.00 to 0.19, with the value of 0.19 being the one corresponding to the relationship of Environmental Commitment (cause) and Tourist Demand (effect). Regarding the cause–cause relationship, a distance was found in a range of 0.00 to 0.26, with the value of 0.26 referring to the General Infrastructure and Location relationship. Regarding the effect–effect relationship, the resulting distance ranges from 0.00 to 0.25, which corresponds to the relationship between Customer Loyalty and Sustainable Development. Finally, the distances found in the Forgotten Effects fluctuate between 0.00 and 0.33, with the value of 0.33 present in the Environmental Commitment (cause) and Customer Satisfaction (effect) relationship. In all of the aforementioned relationships, academic experts gave the highest evaluation.

According to the experience of the group of academics/researchers, Environmental Commitment (cause) has a significant impact on Tourism Demand (effect) and on Customer Satisfaction (effect). When applying Forgotten Effects on these relationships, zero values were obtained, which indicates that academics/researchers have clearly defined these cause–effect relationships. On the other hand, decision makers in the tourism sector have a Forgotten Effects value of 0.23 in the Environmental Commitment–Tourism Demand relationship and the Forgotten Effects in the Environmental Commitment–Customer Satisfaction relationship is 0.33. In both cases, decision makers omitted the indirect impact that causes sustainable development. In the aforementioned cause–effect relationship, decision makers in the tourism sector do not share the same perspective as academics/researchers.

In most cases, decision makers in the tourism sector share the same perspective as academics regarding the relationship between the different causes and effects of tourism competitiveness. However, they are ignoring the growing inclination and sensitivity that the tourist is adopting towards the environment. The tourism sector must adopt an attitude of responsibility, protection and respect for the environment, pay special attention to the implementation of actions that minimize the environmental impact that the activity itself causes, in addition to joining the programs that are present in each tourist destination that pursue a sustainable use of resources. It is necessary for the tourism sector to develop and consolidate its commitment to caring for and preserving the environment, which is an element that contributes to the competitiveness of the destination and has two main effects: tourism demand and customer satisfaction.

With the results of this work, the tourism sector can benefit from knowing the elements of a destination, which beyond the attractiveness itself, today interest the tourist and to whom they must direct their actions based on the effect(s) they want to achieve. On the other hand, the benefit for academics/researchers is that based on these results, new works and lines of research are made visible that allow for finding a way to support the business sector to understand the changes that are experienced in the tourist environment and in the interest of the tourist. A joint work between academics/researchers and the tourism sector could close the perception gaps that exist and generate results for both.

The results of this research are a starting point for future research and for companies that are part of the tourism sector to make decisions and take actions that contribute to making the tourist destination a competitive place. Future lines of research could address the reasons that limit decision makers in the tourism sector to develop an environmental commitment. On the other hand, it would be worth expanding the studies on the subject by using other tools such as the Pichart algorithm and different distance measures, as well as including interval values, in order to support the results obtained. One of the limitations of this study lies in the number of experts that made up each group, as to identify a pattern of behavior or opinion more easily, a larger group is required in terms of quantity and in terms of the role played in tourism.