Graph Convolutional Network for Drug Response Prediction Using Gene Expression Data

Abstract

Genomic profiles of cancer patients such as gene expression have become a major source to predict responses to drugs in the era of personalized medicine. As large-scale drug screening data with cancer cell lines are available, a number of computational methods have been developed for drug response prediction. However, few methods incorporate both gene expression data and the biological network, which can harbor essential information about the underlying process of the drug response. We proposed an analysis framework called DrugGCN for prediction of Drug response using a Graph Convolutional Network (GCN). DrugGCN first generates a gene graph by combining a Protein-Protein Interaction (PPI) network and gene expression data with feature selection of drug-related genes, and the GCN model detects the local features such as subnetworks of genes that contribute to the drug response by localized filtering. We demonstrated the effectiveness of DrugGCN using biological data showing its high prediction accuracy among the competing methods.

1. Introduction

Cancer is a disease driven by the accumulation of somatic mutations. Mutations on specific genes that are called cancer driver genes can affect the transcription of the genes and cause the differential expression of the genes. As many of the driver genes are signaling molecules that control the expression of downstream genes, their differential gene expressions may impinge on the cell and contribute to the hallmarks of cancer such as sustained cell proliferation and resistance to cell death [1,2].

In the early stages of the analysis on differential gene expression in cancer, several research works focused on comparative studies between normal and cancer cells [1,3]. Since the era of precision medicine or personalized medicine, however, the analysis of the differential gene expression among individual patients has become popular, as researchers have observed heterogeneity for immune responses induced by the same cancer therapy due to the diverse genetic background of individuals [4,5]. A recent study suggested that only around 5% of patients benefit from precision oncology [6], which highlights the importance of improving the prediction accuracy of drug response.

As the number of molecular data from cancer patients increases, several large-scale database have been created including The Cancer Genome Atlas (TCGA) and the International Cancer Genome Consortium (ICGC) [7,8]. Although TCGA and the ICGC provide multi-platform genomic profiling data across cancer types, these databases do not include a large number of patient records with drug response or responses to multiple drugs as the data were collected from patients (donors). On the other hand, the Genomics of Drug Sensitivity in Cancer (GDSC) [9] database provides large-scale drug screening results for 266 drugs on around 1000 human cancer cell lines that can be utilized to learn and predict drug responses from gene expression by computational methods.

With a large number of cell line data, various computational methods based on machine learning have been proposed to predict drug response [10,11]. Drug response prediction is one of the supervised learning problems. Computational models are trained to compute a drug response value (output) of cell lines (m samples) with a genomic profile (n input features). Depending on the type of method, learning can be performed using data of the d entire drugs at once or for each drug separately. The genomic profile of cell lines is usually given as a matrix $C_{m\times n}$, and the responses to d drugs are given as a matrix $R_{m\times d}$. The purpose of learning here is to predict the response accurately when a new cell line is given for a known drug. Various types of genomic profiles of cell lines can be provided, among which the gene expression profile is the most frequently used one [10], owing to its representability of the cellular state and the amount of data released. Drug responses in $R_{m\times d}$ are often measured as the half maximal inhibitory concentration ($I{C}_{50}$). $I{C}_{50}$ represents the amount of drug needed to inhibit a cell’s activity by 50%. Another measure is the Area Under the concentration response Curve (AUC), where a lower AUC implies lesser effectiveness of the drug.

Reference [10] reviewed several computational methods for drug response prediction that utilized gene expression data including linear regression methods and their generalizations. The linear regression model learns a response function $r\left(x\right)=w·x$ with the coefficient vector $w\in {\mathbb{R}}^n$ where $x\in {\mathbb{R}}^n$ is a genomic profile vector of a cell line. Kernelized Ridge Regression (KRR) maps x to a vector in a high-dimensional feature space with a kernel function and computes w in the image vector space [12]. Reference [13] recently developed a method called Kernelized Ranked Learning (KRL) that recommends the k most sensitive drugs for each cell line, rather than the response value itself [13]. Response-Weighted Elastic Net (RWEN) is based on the linear regression model, but it incorporates additional weights to find a coefficient vector w that results in a good prediction for cell lines with low drug responses [14]. As shown in KRR and KRL, feature engineering such as feature selection or extraction can help improve the prediction accuracy. Recent studies on feature engineering included kernel principal component analysis integrated with bootstrapping [15] and rough set theory [16].

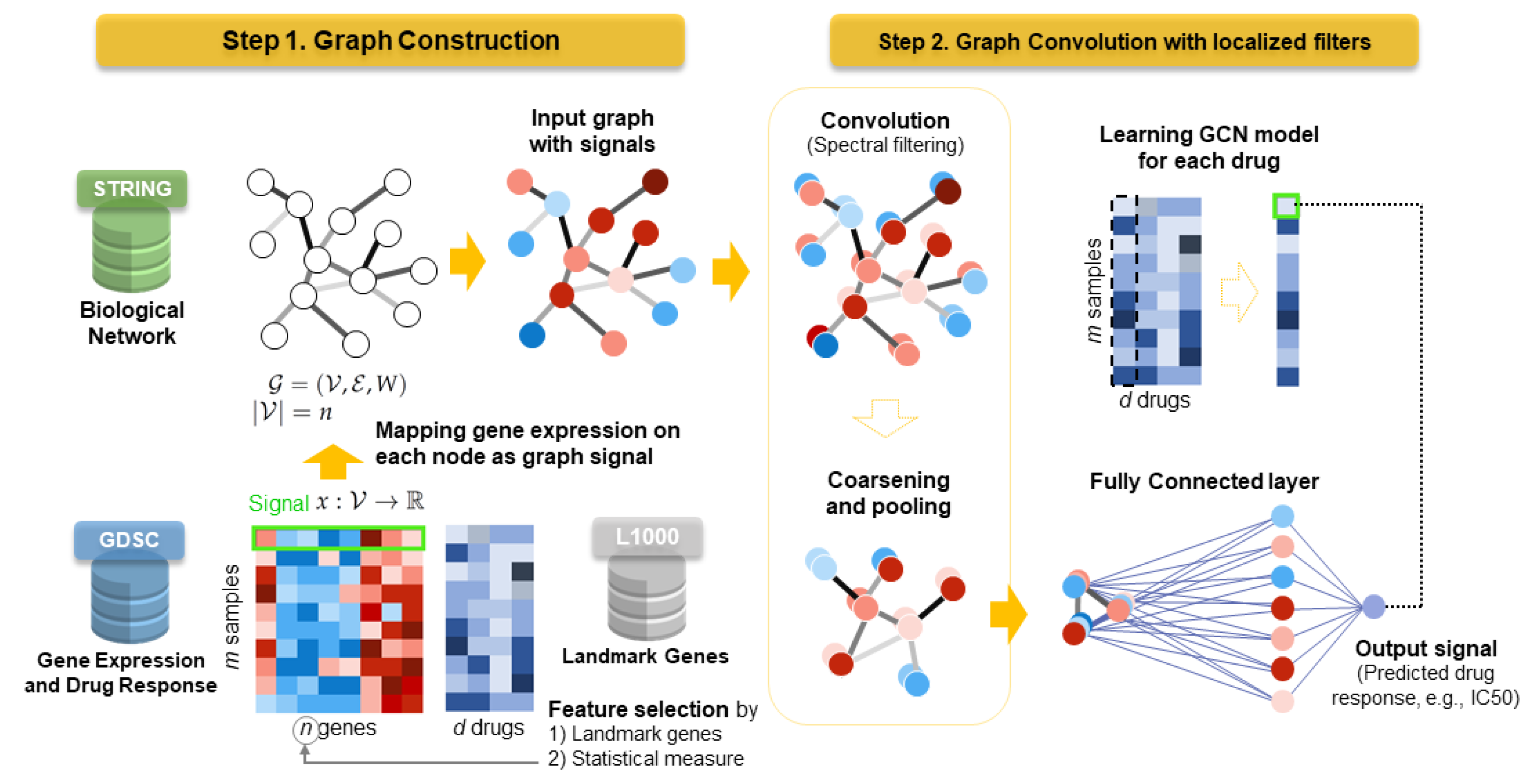
When gene expression is used as the genomic profile of a cell line, information on the relationship among genes can be incorporated into the drug response prediction process. The relationships among biological entities such as genes or proteins are usually represented as a biological network. STRING [17] is one of the databases that provides a Protein-Protein Interaction (PPI) network that corresponds to the gene-gene relationship. As biological processes in a cell are operated by certain groups of genes with interactions like binding or regulation, we can assume that expression values of genes located close to each other in a network may affect the cellular state of a cell line together, thereby contributing to the drug response. However, the computational models for drug response prediction mentioned above do not incorporate the prior knowledge of the biological network, which may enhance the prediction accuracy.

Deep learning with neural networks has shown remarkable achievements compared to the traditional machine learning methods in the field of drug development such as drug-drug interaction extraction [18], drug target prediction [19,20], drug side effect detection [21], and drug discovery [22]. For drug response prediction, a number of methods have been developed as well, each of which utilizes different input data for prediction [11]. Multi-omics Late Integration (MOLI) [23] is a deep learning model that uses multi-omics data including gene expression, Copy Number Variation (CNV), and somatic mutations to characterize a cell line. Three separate subnetworks of MOLI learn representations for each type of omics data, and a final network uses concatenated features and classifies the response of a cell as a responder or non-responder. Reference [24] proposed a deep autoencoder model for representation learning of cancer cells from input data consisting of gene expression, CNV, and somatic mutations. The latent variables learned from the deep autoencoder are used to train an elastic net or support vector machine to classify the response. Those methods share two characteristics in common: the integration of multiple input data (multi-omics) and binary classification of the drug response. Although the integration of multiple types of omics data can improve the learning of the status of the cell lines, it might limit the availability of the method for testing on different cell lines or patients as the model requires additional data other than gene expression. Furthermore, a certain threshold of the $I{C}_{50}$ values should be set before binary classification of the drug response, which may vary depending on the experimental condition such as drug or tumor types.

The Convolutional Neural Network (CNN) is one of the neural network models adopted for drug response prediction [11]. The CNN has been actively used for image, video, text, and sound data due to its strong ability to preserve the local structure of data and learn hierarchies of features [25]. Twin Convolutional Neural Network for drugs in SMILES format (tCNNS) [26] takes a one-hot encoded representation of drugs and feature vectors of cell lines as the inputs for two encoding subnetworks of a One-Dimensional (1D) CNN. One-hot encodings of drugs in tCNNS are derived from Simplified Molecular Input Line Entry System (SMILES) strings that describe the chemical structure of a drug compound. Binary feature vectors of cell lines represent 735 mutation states or CNVs of a cell. Cancer Drug Response profile scan (CDRscan) [27] proposes an ensemble model composed of five CNNs, each of which predicts the $I{C}_{50}$ values from the binary encoding of the genomic signature (mutation) and the drug signature (PaDEL-descriptors [28]). KekuleScope [29] adopts transfer learning, which uses a pre-trained CNN on ImageNet data. The pre-trained CNN is trained with images of drug compounds represented as Kekulé structures to predict the drug response. Recently, several algorithms have been proposed to extend CNNs for data on irregular or non-Euclidean domains represented as graphs [30,31,32]. Reference [33] proposed a method to predict drug response called GraphDRP, which integrates two subnetworks for drug and cell line features, similar to tCNNS [26]. Instead of one-hot encoding, GraphDRP uses a molecular graph to represent the drug structure converted from the SMILES string, and the Graph Convolutional Network (GCN) model from [32] is used to learn the features of drugs. Along with GraphDRP, there have been a number of approaches to use graphs to represent the structural properties of drug compounds for drug development and discovery [34].

Although the aforementioned CNN models incorporate a number of features in the input data, they do not include gene expression values in the genomic features because gene expression cannot be described as 1D binary sequences [26,27] or images [29] used in those CNN models. However, gene expression is known to be the most informative data type for drug response prediction [35,36], whereas mutation and the CNV profiles of cell lines added little to the performance in a comparative study [10]. Furthermore, most of the regression-based methods that utilize gene expression data in the prediction do not consider interactions between genes [12,13,14]. Recent studies successfully introduced a GCN model to use gene expression data for subtype classification of cancer [37,38], and a similar model can be transferred into the problem of drug response prediction. Thus, we propose an analysis framework, DrugGCN, for drug response prediction that can leverage gene expression data and network information using a GCN. DrugGCN constructs an undirected graph from a PPI network and maps gene expression values to each vertex (gene) as graph signals, which will be learned by the GCN to predict the drug response such as the $I{C}_{50}$ or AUC. In addition, DrugGCN incorporates the feature selection process to use genes that can possibly improve the prediction accuracy using prior knowledge. The main contributions of DrugGCN are as follows:

• We propose a novel framework for drug response prediction that uses a GCN model learning genomic features of cell lines with a graph structure, which is the first approach to our knowledge.
• DrugGCN generates a gene graph suitable for drug response prediction by the integration of a PPI network and gene expression data and the feature selection process of genes with high predictive power.
• DrugGCN with localized filters can detect the local features in a biological network such as subnetworks of genes that contribute together to the drug response, and its learning complexity is suitable for biological networks with a huge number of vertices and edges.
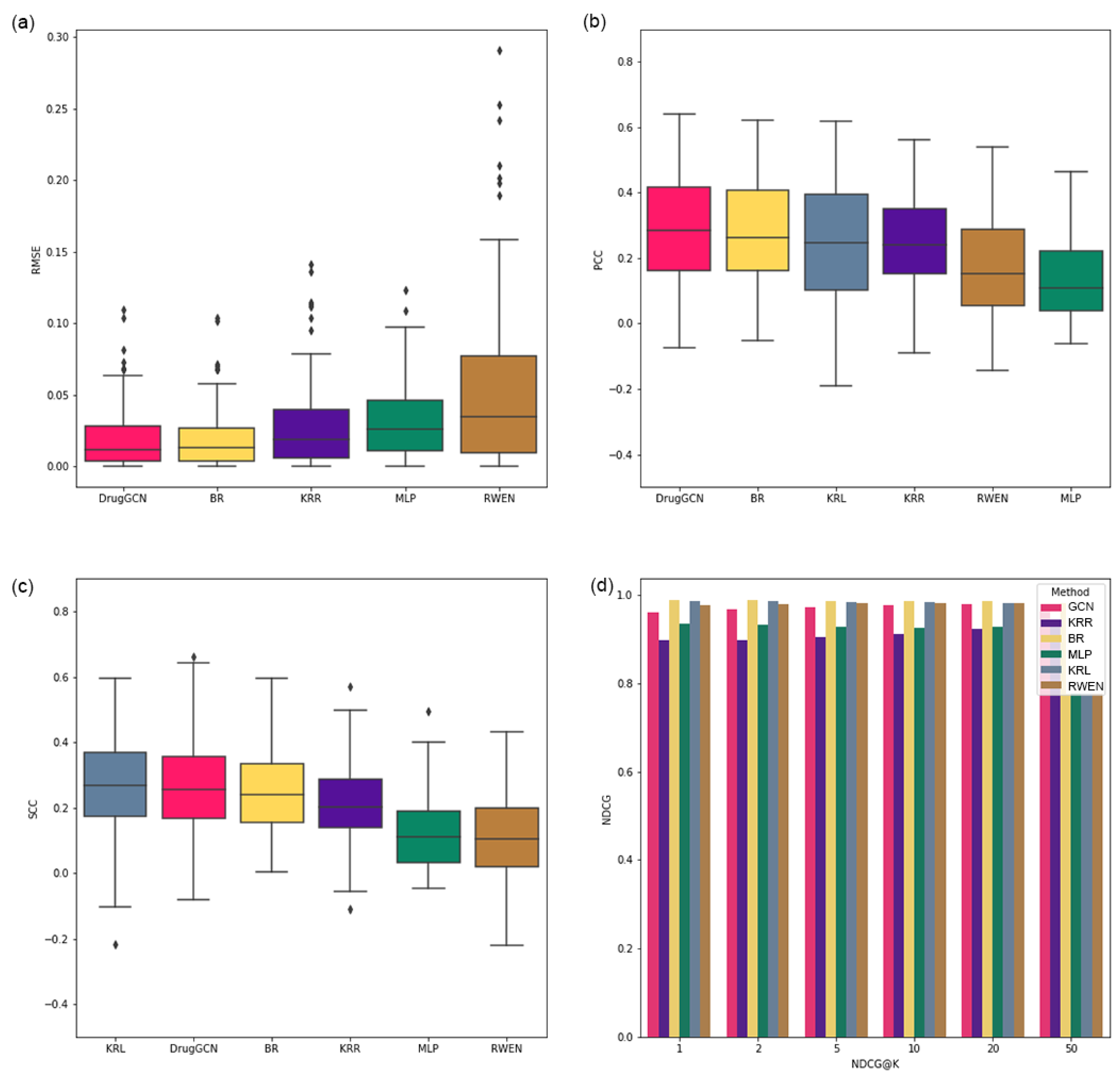
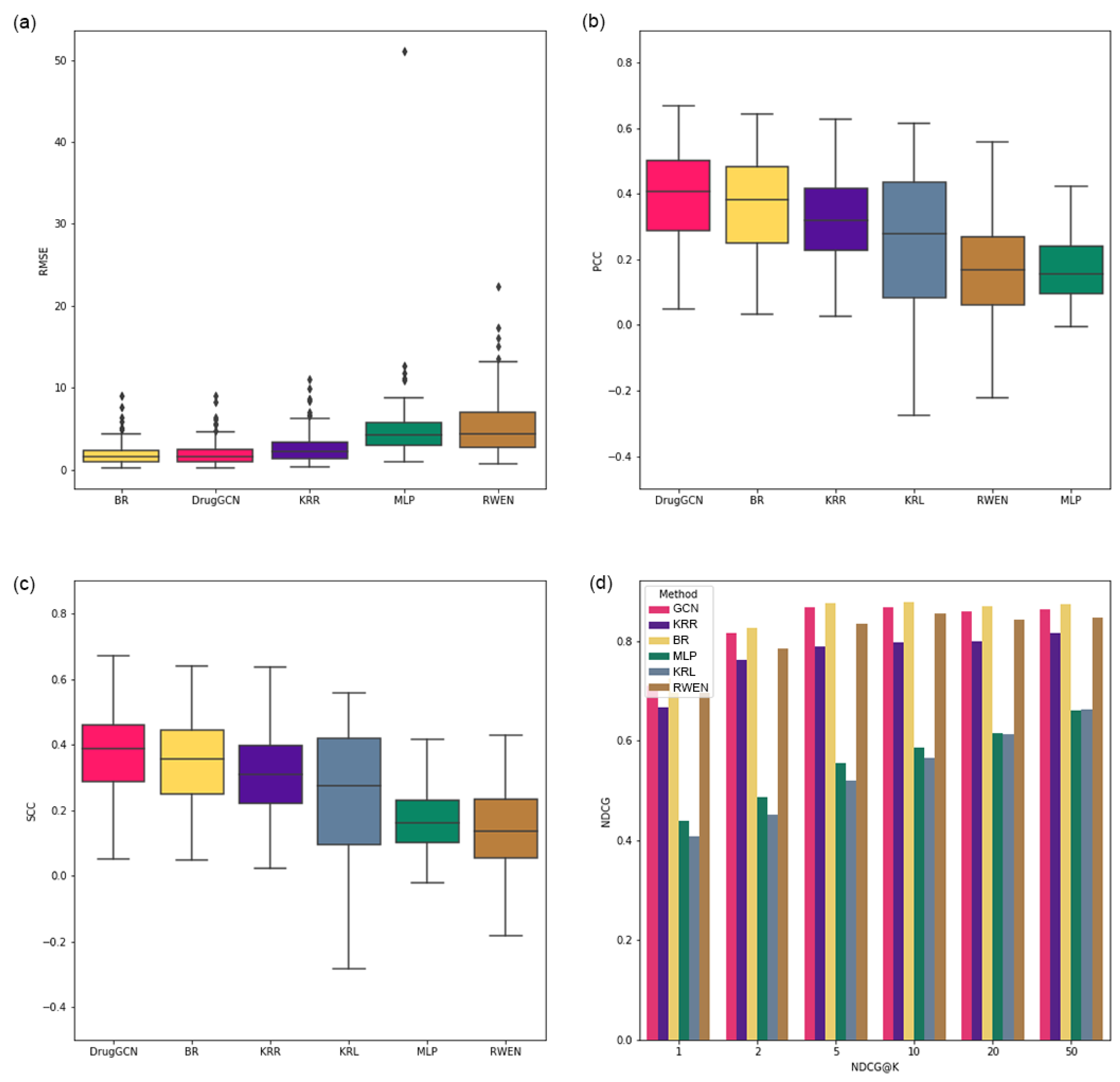
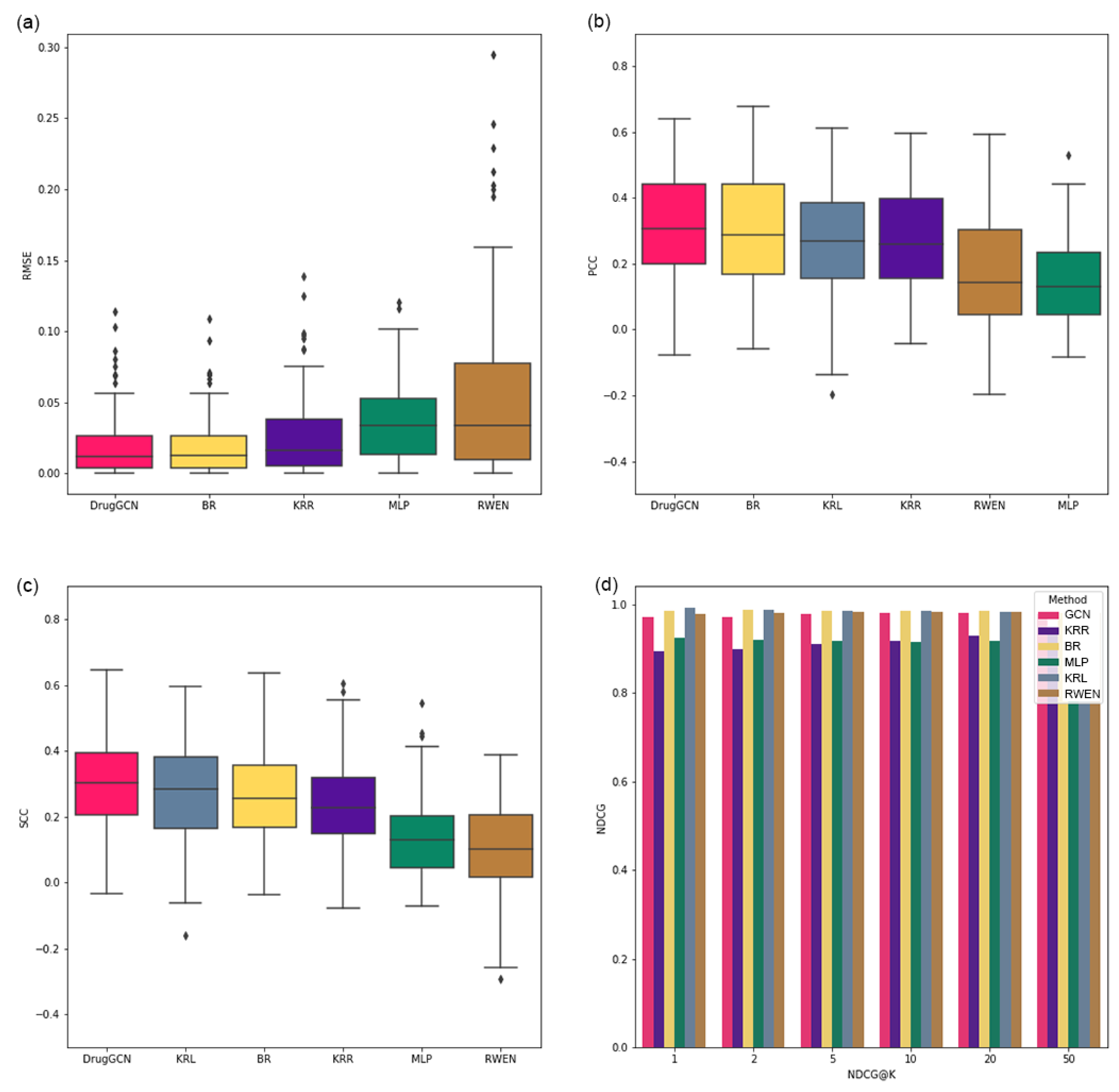
• The performance of the proposed approach is demonstrated by a GDSC cell line dataset, and DrugGCN shows high prediction accuracy among the competing methods.

2. Materials and Methods

Figure 1 shows the proposed DrugGCN framework. DrugGCN introduces a two-step approach for drug response prediction as follows: (1) construction of an input graph with signals and (2) learning a graph convolutional network with localized filters. The following sections describe the methods and evaluation criteria for the comparative analysis in Section 3.

2.1. Graph Construction for Drug Response Prediction

DrugGCN utilizes three biological databases, GDSC [9], L1000 [39], and STRING [17]. GDSC dataset retrieved from [10] includes gene expression matrix $C_{734\times 8046}$ of 8046 genes in 734 cell lines and drug response matrix $R_{734\times 201}$ of 201 drugs for the same cell lines with two measures, common logarithms of the $I{C}_{50}$ and AUC. Drugs with missing responses for 80% or more cell lines were removed from the initial 266 drugs.

2.1.1. Feature Selection on Gene Expression Data

To select effective features that potentially contribute to drug response, two criteria can be used in DrugGCN: prior knowledge on landmark genes or statistical measurement from the given data. A list of landmark genes is derived from Library of Integrated Network-Based Cellular Signatures (LINCS) L1000 project by the National Institutes of Health (NIH) [39]. In the LINCS L1000 project, nine-hundred seventy-eight landmark genes are selected as the assay targets of large-scale experiments on multiple time points, doses, perturbagens, and cell lines due to their representability of human genes. The landmark genes are known to be widely expressed across different cellular contexts and have good predictive power for inferring the expression of the other 22,268 human genes, based on the model built from Gene Expression Omnibus (GEO) data. After the feature selection on the GDSC dataset, six-hundred sixty-three common genes with landmark genes remained, leading to the final gene expression matrix $C_{734\times 663}$. As another criterion for feature selection, DrugGCN calculated the 1000 most variable genes from the GDSC dataset according to the variance of gene expression across cell lines. High variances of genes imply that the genes may be dependent on the heterogeneous cellular states and responsive to perturbation such as drug treatment. The criteria of feature selection can be selected by the user configuration in the DrugGCN framework.

2.1.2. Graph Construction with Gene Expression Data

The input of the GCN model is an undirected input graph $\mathcal{G}=(\mathcal{V},\mathcal{E},W)$ where $\mathcal{V}$ is a set of vertices, $\mathcal{E}$ is a set of edges, and W is a weighted adjacency matrix. We assumed that the vertices and edges of the graph indicate genes and interactions between genes, respectively. To construct the gene graph, biological network information was retrieved from the STRING database [17], which provides the known and predicted PPI corresponding to gene-gene interactions. The original STRING database contains 11,759,454 interactions among 19,566 genes for Homo sapiens, reduced as 25,069 interactions with 663 landmark genes after feature selection. STRING also provides the weights of the interactions that reflect the amount of available evidence of the interaction between two genes, which is used to construct a weighted adjacency matrix. A signal $x:\mathcal{V}\to \mathbb{R}$ is defined for each gene in the graph as a row vector $x\in {\mathbb{R}}^{663}$ of $C_{734\times 663}$ that represents the gene expression values in a certain cell line.

2.2. Localized Filters for the Graph Convolutional Network

To capture the localized patterns of the gene expression profile, convolution is performed on the input graph $\mathcal{G}$ with signal x. The graph Laplacian matrix L of $\mathcal{G}$ is defined as $L=D-A$ where D is the degree matrix and A is the adjacency matrix of the graph. With normalized Laplacian matrix $L=I_n-D^{-1/2}W{D}^{-1/2}$, L has a complete set of orthonormal eigenvectors ${\left\{u_l\right\}}_{l=0}^{n-1}\in {\mathbb{R}}^n$ and corresponding eigenvalues ${\left\{{\lambda }_l\right\}}_{l=0}^{n-1}$. The graph Laplacian can be diagonalized as $L=\mathrm{U}\mathsf{\Lambda }{\mathrm{U}}^T$ on the Fourier basis $\mathrm{U}=[u_0,\dots ,u_{n-1}]\in {\mathbb{R}}^{n\times n}$ where $\mathsf{\Lambda }=diag\left([{\lambda }_0,\dots ,{\lambda }_{n-1}]\right)\in {\mathbb{R}}^{n\times n}$. The graph Fourier transform of the signal $x\in {\mathbb{R}}^n$ is defined as $\widehat{x}={\mathrm{U}}^{T}x\in {\mathbb{R}}^n$, with its inverse as $x=\mathrm{U}\widehat{x}$ [40].

Based on the Fourier inversion theorem, the convolution operator on graph ${\ast }_{\mathcal{G}}$ can be defined in the Fourier domain as $x{\ast }_{\mathcal{G}}y=\mathrm{U}(\left({\mathrm{U}}^{T}x\right)\odot \left({\mathrm{U}}^{T}y\right))$ where ⊙ is the element-wise Hadamard product. A signal x filtered by $g_{\theta }$ is:

$$y=g_{\theta }\left(L\right)x=g_{\theta }\left(\mathrm{U}\mathsf{\Lambda }{\mathrm{U}}^T\right)x=\mathrm{U}{g}_{\theta }\left(\mathsf{\Lambda }\right){\mathrm{U}}^{T}x.$$

(1)

where $g_{\theta }\left(\mathsf{\Lambda }\right)$ is a diagonal matrix $diag\left([g_{\theta }\left({\lambda }_0\right),\cdots ,g_{\theta }\left({\lambda }_{n-1}\right)]\right)$. That is, only $g_{\theta }\left(\mathsf{\Lambda }\right)$ is used to define convolution filters as $\mathrm{U}$ is determined by the input graph. Reference [31] suggested a polynomial filter $g_{\theta }\left(\mathsf{\Lambda }\right)={\sum }_{k=0}^{K-1}{\theta }_k{\mathsf{\Lambda }}^k$ [31] that is localized in K hops from the central vertex where the parameter $\theta \in {\mathbb{R}}^K$ is a vector of polynomial coefficients. To reduce the learning complexity of the polynomial filter from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}\left(K\right|\mathcal{E})$, a fast filtering by Chebyshev expansion [41] is introduced [31]. A filter is parameterized as the expansion:

$$g_{\theta }\left(\mathsf{\Lambda }\right)=\sum _{k=0}^{K-1}{\theta }_k{T}_k\left(\tilde{\mathsf{\Lambda }}\right),$$

(2)

where the parameter $\theta \in {\mathbb{R}}^K$ is a vector of Chebyshev coefficients and $\tilde{\mathsf{\Lambda }}=2\mathsf{\Lambda }/{\lambda }_{max}-I_n$. $T_k\left(\tilde{\mathsf{\Lambda }}\right)$ is the Chebyshev polynomial of order k that can be computed by the recurrence relation $T_k\left(x\right)=2x{T}_{k-1}\left(x\right)-T_{k-2}\left(x\right)$ with $T_0=1$ and $T_1=x$. The filtering operation is learned by the backpropagation algorithm with a cost of $\mathcal{O}\left(K\right|\mathcal{E}\left|F_{in}{F}_{out}S\right)$ where $F_{in}$ and $F_{out}$ are the number of input and output convolution filters, respectively [31].

Coarsening of the graph is performed by the Graclus multilevel clustering algorithm, which is a greedy algorithm to compute coarser versions of a graph by picking a vertex i and its neighbor j that maximize the local normalized cut [42]. Graph signals are then coarsened as well by pooling with a structure of a balanced binary tree as proposed in [31]. Among the pooling methods, max pooling is selected empirically in DrugGCN.

2.3. Evaluation Criteria

In the following section, the performance of DrugGCN and other algorithms is evaluated by four metrics: Root Mean Squared Error (RMSE), Pearson Correlation Coefficient (PCC), Spearman Correlation Coefficient (SCC), and Normalized Discounted Cumulative Gain (NDCG). The metrics are based on the difference between the observed drug responses $y={\left(y_i\right)}_{i=1}^m$ ($I{C}_{50}$ or AUC) and the predicted drug responses $\widehat{y}={\left(\widehat{y_i}\right)}_{i=1}^m$ where m is the number of cell lines.

RMSE is defined as the square root of the mean squared error, which is the average squared difference between the true and predicted responses by a method:

$$RMSE(y,\widehat{y})=\sqrt{\frac{{\sum }_i{(y_i-{\widehat{y}}_i)}^2}{m}.}$$

(3)

PCC attempts to measure if there is a linear correlation between two variables. The PCC of y and $\widehat{y}$ is defined as follows where $\mu \left(X\right)$ is the mean of a random variable X:

$$PCC(y,\widehat{y})=\frac{{\sum }_i\left({\widehat{y}}_i-\mu \left(\widehat{y}\right)\right)\left(y_i-\mu \left(y\right)\right)}{\sqrt{{\sum }_i{\left({\widehat{y}}_i-\mu \left(\widehat{y}\right)\right)}^2}\sqrt{{\sum }_i{\left(y_i-\mu \left(y\right)\right)}^2}}.$$

(4)

The SCC between two variables is equivalent to the PCC between the rank values of the two variables. That is, the SCC assesses whether the two variables are monotonically related. Assume that $r\left(y\right)$ and $r\left(\widehat{y}\right)$ are the rank vector of y and $\widehat{y}$, respectively. SCC is defined as:

$$SCC(y,\widehat{y})=PCC(r\left(y\right),r\left(\widehat{y}\right)).$$

(5)

The Discounted Cumulative Gain (DCG) [43] is a measure of ranking quality.

$$DGG(y,\widehat{y})=\sum _{i=1}^m\frac{2^{-y_i}-1}{lo{g}_2(r(-{\widehat{y}}_i)+1)}.$$

(6)

To only consider the highest k scores in the ranking, m can be set as k. The NDCG is used to normalize the DCG by the ideal $DCG(y,y)$, as the DCG can be affected by the number of scores.

$$NDCG(y,\widehat{y})=\frac{DCG(y,\widehat{y})}{DCG(y,y)}.$$

(7)

3. Results and Discussion

3.1. Performance Evaluation on the GDSC Dataset

To assess the prediction accuracy of the proposed framework, gene expression and drug response data from the GDSC database including 734 cell lines and 201 drugs were used. Pre-processed GDSC data were retrieved from the paper by Chen and Zhang [10] where genes with little variation in expression and drugs with missing responses in 80% or more cell lines were removed. We generated four sets of data with two different gene sets (L1000 and Var1000) and two types of drug response values ($I{C}_{50}$ and AUC), referred to as the L1000-IC50, L1000-AUC, Var1000-IC50, and Var1000-AUC datasets. The L1000-IC50 and L1000-AUC datasets contained 663 genes that commonly exist in 978 landmark genes in L1000 and 8046 genes in the GDSC dataset. The Var1000-IC50 and Var1000-AUC datasets included the top 1000 genes with the largest variance of gene expression values among the entire cell lines, which might suggest that those genes can be expressed differently to generate diverse cellular statuses and consequent drug responses.

The computational models compared with DrugGCN were KRR, KRL [13], RWEN [14], a Multi-Layer Perceptron (MLP), and a Bagging Regressor (BR). The methods using gene expression data without considering the interaction between genes were selected to compare the prediction accuracy and to analyze the contribution of gene-gene interaction information utilized in DrugGCN. As for KRR, MLP, and BR, we used Python functions implemented in the scikit-learn library [44]. The hyperparameters of the methods were set as default values except the regularization parameter $\lambda$ in KRL. $\lambda$ was tuned with a line search with $\lambda \in 1.0,0.1,0.01,\dots ,1\times {10}^{-6}$ as described in the original paper and finally selected as one. The hyperparameters of DrugGCN are described in Appendix A

Table A1. Hyperparameters of DrugGCN used for the GDSC dataset.

Hyperparameters
GCN Layer = 2
Number of Kernels = [20, 10]
Kernel Size = [40, 20]
Polling size = [4, 4]
FC Size = [128, 1]
Reg = 0
Dropout = 1
l_rate = 0.02
Momentum = 0.9
Decay_rate = 0.95
Batch_size = 4

. In the learning process, a three-fold cross-validation with a 50% training set, a 25% validation set, and a 25% test set was carried out.

Figure 2 shows the result of the six methods with four measures, RMSE, PCC, SCC, and NDCG, using the L1000-IC50 dataset. k for NDCG was tested as $k\in 1,2,5,10,20,50$. As KRL calculates the predicted ranking of drugs to recommend for a given cell line rather than the exact drug response values for all potential drugs, KRL was not included in the plots of the RMSE results. As in Figure 2, the top three methods showed consistently high performance in all measures in the order of DrugGCN, BR, and KRR. The ranks of the other three methods changed depending on the measures.

To compare the result of the six methods using a statistical test, the RMSE, PCC, and SCC values for each drug predicted by the six methods were ranked from one (the smallest for RMSE and the largest for PCC and SCC) to six. The rank vectors of each method were generated with the ranks that each method gained for 201 drugs. If a method always predicted the drug response most correctly among the six methods, the rank vector would be $(1,1,\dots ,1)$. On the contrary, the worst rank vector would be $(6,6,\dots ,6)$ for a method whose prediction was always the worst. We performed the one-sided Wilcoxon signed-rank test [45], which compares two matched measurements and assesses whether their means differ, comparing pairs of rank vectors of DrugGCN and the other five methods. The p-values estimated by the Wilcoxon signed-rank test are shown in

Table 1. p-values of the one-sided Wilcoxon signed-rank test using the L1000-IC50 dataset comparing the ranks of DrugGCN and the other five methods.

Measure	BR	KRR	KRL	MLP	RWEN
RMSE	1.48 $\times {10}^{-10}$	9.44 $\times {10}^{-38}$	-	6.99 $\times {10}^{-37}$	2.77 $\times {10}^{-37}$
PCC	9.57 $\times {10}^{-15}$	5.03 $\times {10}^{-28}$	2.93 $\times {10}^{-31}$	1.38 $\times {10}^{-35}$	3.89 $\times {10}^{-35}$
SCC	5.77 $\times {10}^{-12}$	1.07 $\times {10}^{-25}$	1.31 $\times {10}^{-28}$	2.11 $\times {10}^{-35}$	9.28 $\times {10}^{-35}$

. As expected, in Figure 2, the mean rank of DrugGCN is significantly higher (smaller in number) than the other methods.

For the remaining three datasets, DrugGCN showed consistently high performance as shown in Appendix A Figure A1, Figure A2 and Figure A3 and

Table A2. p-values of the one-sided Wilcoxon signed-rank test using the L1000-AUC dataset comparing the ranks of DrugGCN and the other five methods.

Measure	BR	KRR	KRL	MLP	RWEN
RMSE	$0.0038$	9.91 $\times {10}^{-35}$	-	4.55 $\times {10}^{-46}$	1.99 $\times {10}^{-36}$
PCC	$0.0082$	1.43 $\times {10}^{-8}$	4.09 $\times {10}^{-9}$	1.01 $\times {10}^{-32}$	3.73 $\times {10}^{-23}$
SCC	$0.0025$	1.71 $\times {10}^{-8}$	$0.5151$	2.75 $\times {10}^{-30}$	3.28 $\times {10}^{-26}$

,

Table A3. p-values of the one-sided Wilcoxon signed-rank test using the Var1000-IC50 dataset comparing the ranks of DrugGCN and the other five methods.

Measure	BR	KRR	KRL	MLP	RWEN
RMSE	$0.9914$	4.87 $\times {10}^{-37}$	-	4.59 $\times {10}^{-36}$	2.34 $\times {10}^{-37}$
PCC	3.66 $\times {10}^{-14}$	2.39 $\times {10}^{-29}$	4.10 $\times {10}^{-26}$	1.31 $\times {10}^{-35}$	1.48 $\times {10}^{-35}$
SCC	6.01 $\times {10}^{-13}$	1.18 $\times {10}^{-27}$	1.03 $\times {10}^{-25}$	1.31 $\times {10}^{-35}$	9.06 $\times {10}^{-36}$

and

Table A4. p-values of the one-sided Wilcoxon signed-rank test using the Var1000-AUC dataset comparing the ranks of DrugGCN and the other five methods.

Measure	BR	KRR	KRL	MLP	RWEN
RMSE	$0.0957$	1.12 $\times {10}^{-32}$	-	5.76 $\times {10}^{-36}$	1.00 $\times {10}^{-36}$
PCC	$0.0001$	3.56 $\times {10}^{-11}$	1.08 $\times {10}^{-10}$	2.93 $\times {10}^{-33}$	9.47 $\times {10}^{-27}$
SCC	4.52 $\times {10}^{-6}$	8.06 $\times {10}^{-16}$	$0.0002$	5.81 $\times {10}^{-35}$	4.88 $\times {10}^{-33}$

. In most tests of the Wilcoxon signed-rank test from the RMSE, PCC, and SCC measures, DrugGCN predicted better than the other methods except two tests with KRL and BR, where the mean ranks of DrugGCN, KRL, and BR were nearly the same as in Appendix A Figure A1c and Figure A2a. In the NDCG results of the three other datasets, BR showed the highest accuracy.

In summary, DrugGCN and BR were the first and second methods that showed good prediction power for the GDSC datasets. KRR-KRL and RWEN-MLP showed similar results in the 3rd-4th and 5th-6th places. The high performance of DrugGCN and BR presumably stemmed from the power of network information and ensemble learning, respectively. From this result, we can suggest an ensemble model integrated with GCN, for which similar approaches have been made for other biological problems such as subtype classification of cancer [37,38]. Lee et al. [38] constructed an ensemble model from multiple GCNs of smaller subnetworks of PPI (biological pathways) with hundreds of genes, known to regulate a biological process together. In addition, the GCN model can be extended with other types of networks rather than PPI such as molecular graphs of drugs [33] and biological networks from multi-omics data [23], which can provide additional information for drug response prediction. As in [23,33], different types of input features can be integrated into a multi-modal neural network, and the contribution of each drug or genomic features can be measured and compared with the augmented model structure.

3.2. Case Study: ERK MAPK Signaling-Related Drugs

We investigated the L1000-IC50 dataset to uncover how the network of genes affected the accuracy of drug response prediction. First, drugs were classified into 23 drug groups depending on their target pathways, as defined by [10]. For each accuracy measure, two-hundred one drugs can be ranked from one (a drug predicted with the smallest RMSE or largest PCC or SCC) to 201. The ranks of drugs in the same drug group were collected, and a box plot showing the distribution of the ranks of each drug group was generated, as shown in Figure 3 and Figure 4. Figure 3 shows the distribution of ranks when ranks from all measures were put together, and Figure 4 is the individual box plots for the RMSE, PCC, and SCC. The overall prediction accuracy was high in a group of drugs targeting the ERK MAPK signaling pathway.

We assumed that high prediction accuracy of a drug response was derived by the information from the highly connected genes forming a subnetwork in the PPI network. On the contrary, lower prediction accuracy may result from the important genes scattered in the network, even though those drugs with high and low prediction accuracy have similar roles in a cell. To verify the hypothesis, we selected two drugs from the “ERK MAPK signaling pathway” group with the highest rank (refametinib, rank one) and the lowest rank (PLX-4720, rank 109) in terms of the PCC. For refametinib and PLX-4720, fifty genes that potentially contributed to predict the IC50 were selected by the correlation between their gene expression values and the IC50. That is, the gene expression of 50 genes had a relatively strong (positive or negative) correlation with the IC50 values across cell lines, among 663 genes. With those two sets of 50 genes, we performed a pathway enrichment analysis that assessed the ratio of query genes found together in the subnetworks of the PPI network called biological pathways. The DAVID platform [46] provided over-representation analysis, one of the pathway enrichment analyses [47] that conducts statistical tests on query genes based on the hypergeometric distribution.

The pathway analysis results of refametinib and PLX-4720-related genes are shown in

Table 2. Pathway enrichment test results with 50 genes for refametinib. QueryG indicates the number of query genes found in the pathway, and PathwayG is the number of total genes in the pathway.

Pathway	QueryG	PathwayG	%	p-Value	FDR
hsa05212:Pancreatic cancer	6	65	12.2449	7.65 $\times {10}^{-6}$	9.11 $\times {10}^{-4}$
hsa05210:Colorectal cancer	5	62	10.20408	1.38 $\times {10}^{-4}$	0.008185
hsa05220:Chronic myeloid leukemia	5	72	10.20408	2.46 $\times {10}^{-4}$	0.009764
hsa05200:Pathways in cancer	8	393	16.32653	0.001218	0.036235
hsa04380:Osteoclast differentiation	5	131	10.20408	0.002345	0.054046
hsa05214:Glioma	4	65	8.163265	0.002725	0.054046
hsa05166:HTLV-I infection	6	254	12.2449	0.004409	0.074948
hsa05205:Proteoglycans in cancer	5	200	10.20408	0.010509	0.156321
hsa04068:FoxO signaling pathway	4	134	8.163265	0.019992	0.26434
hsa04010:MAPK signaling pathway	5	253	10.20408	0.023081	0.264767
hsa05223:Non-small cell lung cancer	3	56	6.122449	0.024474	0.264767
hsa05206:MicroRNAs in cancer	5	286	10.20408	0.034222	0.32247
hsa04917:Prolactin signaling pathway	3	71	6.122449	0.037938	0.32247
hsa05218:Melanoma	3	71	6.122449	0.037938	0.32247
hsa04062:Chemokine signaling pathway	4	186	8.163265	0.046265	0.367033

and

Table 3. Pathway enrichment test results with 50 genes for PLX-4720. QueryG indicates the number of query genes found in the pathway, and PathwayG is the number of total genes in the pathway.

Pathway	QueryG	PathwayG	%	p-Value	FDR
hsa05010:Alzheimer’s disease	4	168	8	0.027233	1
hsa05120:Epithelial cell signaling in Helicobacter pylori infection	3	67	6	0.028047	1
hsa04912:GnRH signaling pathway	3	91	6	0.049052	1

, respectively. Fifty genes having a high correlation with refametinib were enriched (p-value under 0.05) in a number of biological pathways including MAPK signaling itself; even four pathways remained as significantly enriched after FDR correction of the p-values. On the other hand, genes selected for PLX-4720 had three or zero enriched pathways with p-values or FDR corrected p-values under 0.05. The results from pathway enrichment analysis supported our hypothesis that the gene network contributes to the prediction of drug response.

4. Conclusions

In this study, DrugGCN, a computational framework for drug response prediction, was proposed. DrugGCN incorporated PPI network and gene expression data into the GCN model to detect the local features in graphs by localized filtering. The effectiveness of DrugGCN was tested with four GDSC datasets, and it showed high prediction accuracy in terms of the RSME, PCC, and SCC. In the case study of ERK MAPK signaling-related drugs, we discovered supporting evidence of the hypothesis that the high accuracy of DrugGCN was due to the genes forming a subnetwork in the PPI network that provided much information to predict cellular states and consequent drug responses.

The prediction accuracy of DrugGCN can be further improved in terms of the current limitations pertaining to the model structure and input features as described below. Among the competing methods of DrugGCN, the bagging regressor showed high performance with the support of the ensemble model. An ensemble model consisting of multiple GCN was proposed in [38] for the cancer subtype classification problem where the original graph of the biological network was divided into smaller subnetworks with hundreds of genes using prior knowledge on which genes cooperated with each other for a certain biological process, such as biological pathways from the KEGG database [48]. The prediction accuracy of the DrugGCN model can be improved with the aforesaid ensemble model, as we showed the predictive power of subnetworks in the case study of ERK MAPK signaling.

The DrugGCN model also can be extended with additional genomic features from different omics data or drug features such as the chemical structures of drug compounds. In particular, the structural properties of drug compounds have been used for drug development and discovery as the form of a graph [34], which can be easily integrated into the GCN model. As in the similar models [23,26], learning from multiple types of features can be implemented with multiple GCN models, the learned representations of which are then concatenated and put into fully connected layers.