Abstract
Size mismatch is a serious problem in online footwear purchase because size mismatch implies an almost sure return. Not only foot measurements are important in selecting a size, but also user preference. This is the reason we propose several methodologies that combine the information provided by a classifier with anthropometric measurements and user preference information through user-based collaborative filtering. As novelties: (1) the information sources are 3D foot measurements from a low-cost 3D foot digitizer, past purchases and self-reported size; (2) we propose to use an ordinal classifier after imputing missing data with different options based on the use of collaborative filtering; (3) we also propose an ensemble of ordinal classification and collaborative filtering results; and (4) several methodologies based on clustering and archetype analysis are introduced as user-based collaborative filtering for the first time. The hybrid methodologies were tested in a simulation study, and they were also applied to a dataset of Spanish footwear users. The results show that combining the information from both sources predicts the foot size better and the new proposals provide better accuracy than the classic alternatives considered.
1. Introduction
Although online shopping is an emerging marketing channel, the footwear sector is not exploiting this channel enough if compared to other consumer goods. The main barrier is the impossibility of trying on the footwear before buying it. In footwear, fit is a key aspect to ensure the comfort of the product, so not choosing the correct size during the purchase process means a sure return in most cases. If the company has a zero cost policy for the customer, the cost of the return must be borne by the company itself. On the other hand, it also affects customer satisfaction since having to return items purchased on the Internet is considered frustrating by consumers, which reduces the likelihood that the customer will buy again. Furthermore, the fear of a poor fit is the main barrier to buying footwear online. According to Huang et al. [1], the return rate due to mismatches in shoe size in online purchases is much higher than that for traditional retail stores, it can be up to 35%.
Users could select the size based on their previous experience. However, each company has its own sizing, it can even change according to shoe styles, and, moreover, it can change over time. Companies usually provide a sizing chart to online customers and size is assigned according to foot length. However, the accuracy of the foot-length-based strategy is low: 33.7% according to Huang et al. [1] and 34.2% with our data. Therefore, other foot measurements besides foot length should be taken into account. However, not only anthropometric measurements are important, but also user preferences. Some customers prefer wearing shoes loose, i.e., they prefer a size larger than that predicted by their foot measurements [1]. This is the reason some approaches for size matching consider collaborative filtering based on past purchases [2,3], while other approaches require customers to provide their preferences [4].
As a consequence, our approach to footwear size matching is based on foot measurements and user preferences. To find out the user’s preferences, we consider both approaches. We use the information yielded by past purchases of the user and other customers, but we also require the customer to input his/her usual size.
Recommending the footwear size that best fits the user is a statistical ordinal classification problem [5], i.e., given a new user and his or her features (foot measurements and preferences), this new case should be assigned to one of the predefined ordered categories, i.e., sizes, based on a training set of cases whose features and size are known. However, it is not a typical classification problem. On the one hand, it is an ordinal classification problem, i.e., classes are ordered, they are not nominal labels. Therefore, ordinal methods should be used since their accuracy is higher than classical nominal classification techniques [6]. On the other hand, as we are using information on past purchases, we do not have complete cases, i.e., we only have the size bought by users of some shoe models, which are different for each user. We do not have the size selected by users for all possible shoe models in the dataset. In other words, the amount of missingness is high. This prevents the use of many classifiers, since many of them are not capable of handling missing values [7]. A previous step could be to use imputation; in fact, we consider it here. Finally, it is a difficult problem due to uncertainties [8]. The standard supervised classification paradigm supposes that classes are objectively formulated, with no uncertainty or arbitrariness about class labels. These are “laboratory conditions”, but this is not so in our case. In our real-world problem, classes are defined more quantitatively than qualitatively. In fact, class definition in our problem is based on each user’s subjective preference for each model. Moreover, it is possible that none of the sizes fits the user well for a given shoe model [1] or even that two sizes may be wearable [5]. Hand [8] argued that in real-world conditions the performance provided by simple classification techniques is usually as good as more modern sophisticated machine learning techniques, i.e., highly sophisticated techniques may only be apparently superior in accuracy because this is achieved in “laboratory conditions”, but this superiority may not translate in real-world conditions and may be illusory. In fact, this was confirmed in a garment matching problem [5].
Our contribution is to propose several methodologies that combine the information provided by anthropometric measurements with the information provided by user preference. This combination is carried out using several approaches. One of them is to use ordinal classifiers that can handle missing values. Another is to impute missing values and then use ordinal classifiers. For the imputation phase, we propose different options based on the use of collaborative filtering [9] for the first time, which are compared with previous imputation methodologies. Another approach consists of proposing an ensemble of the ordinal classifier results from complete features and the collaborative filtering results from features with missing values. Furthermore, another contribution consists of the use of methods based on clustering and archetype analysis as user-based collaborative filtering for the first time.
In summary, the main novelties of this work consist of:
- We design several recommendation systems that jointly combines 3D foot measurements extracted from a fast, portable and low-cost 3D foot digitizer with user preferences extracted from past purchases and self-reported usual size. To the best of our knowledge, this is the first time all this information is jointly taken into account for footwear size recommendation.
- We use methods based on clustering and archetype analysis as user-based collaborative filtering [9] for the first time.
- We use those and another collaborative filtering as imputation methods before the use of an ordinal classifier for the first time.
- We propose an ensemble of an ordinal classifier and collaborative filtering for the first time.
- We compared the performance of the proposed methodologies with that of well-known methods. These well-known methods are: ordinal classifiers that can handle missing values, such as random forests, and ordinal classifiers, such as ordered logistic regression, after using a well-known imputation method.
- We tested all these approaches in a simulation study and applying them to a novel dataset of Spanish users.
- We have made the code of our procedure and synthetic datasets available for reproducing the results (see the Data Availability Statement).
The outline of the paper is as follows. The data are described in Section 2, including real data and simulated data. Related work in footwear recommendation is surveyed in Section 3. Section 4 reviews machine learning background: ordinal classifiers, collaborative filtering and ensembles. The proposed methodology is explained in Section 5. The results are discussed in Section 6, where we present the application of the proposed methodologies to our real dataset and simulated datasets. Conclusions are given in Section 7.
2. Data
2.1. Real Data
In total, 36 right foot scans of Spanish men were measured with DomeScan. DomeScan is a small lightweight booth (35 × 45 × 45 cm) that consists of a U-shaped aluminum frame with a non-reflecting vinyl bottom surface and two mirrors on the sides equipped with a Raspberry Pi, camera, Bluetooth communication and illumination system mounted on a bridge over the frame. It is a fast, portable and low-cost 3D foot digitizer, which can be used in retail shops. From the images, DomeScan makes a 3D reconstruction of the foot and foot measurements are also returned. The complete details about how DomeScan operates can be found in [10], together with an analysis of the validity and reliability of its measurements.
The dataset was collected from 6 July 2018 to 10 October 2018 by Valencian Biomechanics Institute (Instituto de Biomecánica de Valencia (IBV)) under the project “Generación de una metodología de asignación de talla escalable por la industria para la venta por Internet. Aplicación en los sectores de ropa y calzado” (Generation of a methodology for assigning scalable size by industry for online sales. Application to the clothing and footwear sectors) (IMDEEA/2017/60) funded by the Valencian Region Government (i.e., Institut Valencià de la Competitivitat Empresarial, IVACE) under the program “Ayudas dirigidas a centros tecnológicos de la Comunitat Valenciana para proyectos de I + D en cooperación con empresas 2017” (Grants for technology centers in the Valencia Region for R&D projects in collaboration with companies 2017). All participants signed an informed consent document, complying with the applicable Spanish legislation (Organic Law 15/1999, of December 13, on Personal Data Protection, LOPD) granting the use of the data for research purposes. The data were collected by the IBV from volunteers. All of them declared that they usually wear shoe size 42.
We consider the same foot measurements as in [11], which are the variables that could most influence shoe fit, and are therefore the most relevant variables in shoe design according to footwear experts. In particular, the features are: Ball Position (BP) (distance from the rearmost location of the foot to the intersection of the ball area and the foot axis), Foot Length (FL) (distance between the fore and rearmost location, the foot axis), Ball Width (BW) (maximal distance between the extreme locations of the ball area projected onto the ground plane), Instep Height (IH) (maximal height of the instep area, located at 50% of the FL), Toe Height (TH) (maximal height of the toe area), Ball Girth (BG) (perimeter of the ball area), Instep to Heel Girth (IHG) (perimeter of the area that passes through the heel to the instep, located at 50% of the FL) and Instep Girth (IG) (perimeter of the instep area, located at 50% of FL).
Furthermore, we built a new variable called ‘pref’ for estimating preference, which is formed by the difference between his usually used size (42 in this case) and the technical size that should be used according to FL. This technical size is determined by the following equation: the smallest integer no less than . In this way, we can estimate users who prefer tight shoes, larger sizes or if his usually used size coincides with his technical size.
In addition, users tried on several models of different sizes. In particular, we have eight different models of shoes, which are referred as –. Users selected the size that fitted best for the models that they tried on. Users did not try on all the models. There was a time restriction for trying on the models due to resource constraints. The majority of users tried on the expected number of shoes (6 models × 3 sizes = 18 shoes). However, some users tried on the shoes slowly and they were unable to try on the expected number of shoes within the specified time. The majority of users (27) tried on six models and three sizes for each model, but seven men only tried on five models (with three sizes for each model), one man only tried on four models and another man only tried on three models (with three sizes for each model). The sizes selected ranged from 41 to 43. In other words, men who stated that they normally wear shoe size 42 selected sizes 41, 42 or 43, i.e., the same size that they usually use, one size up or one size down.
In summary, the data form a 36 × 17 matrix, where the columns are the following variables: eight anthropometric measurements, ‘pref’, and the other eight columns have the preferred size for each model. However, in these last eight columns, there are missing values. The percentage of missing values for these columns ranges from 22% to 39%, the mean percentage of missing values being 29%.
2.2. Simulated Data
Two scenarios were considered. In Scenario 1, the anthropometric part may have more influence on the selection of the size than preference, unlike Scenario 2, where the anthropometric part is not so relevant. Both scenarios are composed of an anthropometric predictor similar to FL, which is based on the summary statistics of the FL variable of the previous real data. Then, the ‘pref’ variable is built as explained in Section 2.1. Afterwards, the preferred size for four models – is generated in different ways for each scenario, according to Table 1. Those distributions are truncated to keep the sizes in the range of 41 to 43. In other words, if some of the sizes generated in variables – are lower (higher) than 41 (43), the value is changed to 41 (43, respectively). In total, 100 observations (users) were generated for each dataset. To establish the missing values, the following mechanism was followed: Entries 1–33 for , 34–66 for and 67–100 for were removed.

Table 1.
The variables are sampled independently from the following distributions. Tria(a, c, b) stands for the triangular distribution, with values in and mode in c; ceiling returns the smallest integer not less than the corresponding element; and round rounds the values.
Note that values are random and independently generated, so the deleting mechanism used in each shoe model is equivalent to a missing completely at random (MCAR) mechanism. However, the missing mechanism for the whole dataset is not MCAR, but missing not at random (MNAR). In real data, we need to have users who share some past purchases. This is the reason we used this missing mechanism.
In Scenarios 1 and 2, , and are related to one another, but in Scenario 1 they are also related to FL and ‘pref’ variable, unlike in Scenario 2. The scenarios were also built to test the influence of variability and average bias inside a model. This is the reason in both scenarios has more variability than , and is biased. was built to test whether having models where the size selection is somewhat biased influences the performance.
3. Related Work
In Section 1, some methods for footwear size recommendation are mentioned, but here we review those and other related methods in more detail.
The simplest method is using the foot length provided in companies’ sizing charts. However, this approach reports very low accuracy, as previously mentioned. Another approach would be to consider other foot measurements besides foot length. This is the idea in [12]. Nevertheless, user preferences are very important in this problem, since subjects with similar foot shapes have different size preferences, as shown in [1]. Some approaches examine only user preference. For example, users are asked what size they usually wear in [13], similarly to our ‘pref’ variable. Other approaches recommend a shoe size based on the best fitting shoes previously purchased by the user [3]; in this case, they consider the measurements of the inner dimensions of shoe sizes. Internal dimensions of footwear items are also considered in [4], together with self-reported preference about a more or less tight fit. This kind of subjective preference was also requested by Marks [14], who additionally considered information from 3D foot scans. Huang et al. [1] used 3D foot measurements too, in addition to 3D shoe last measurements and user’s preference, which is determined by comparing the user selection with the most frequently selected size for each shoe type and foot shape combination. Note that, in practice, this kind of information is not usually available.
The most similar method to our approach is the one by Lu and Stauffer [2], since they considered both anthropometric measurements and historical purchases. They clustered users by self-reported height, body-mass index and historical purchases and based their size recommendation on comparisons with other users in the same cluster. However, there are important differences with the approach in [2] and ours. Firstly, we do not use self-reported foot measurements, which could be very unreliable since common people are not expert in carrying out anatomical foot measurements. Secondly, our approach for carrying out the recommendation is also completely different.
To the best of our knowledge, our approach is the first method for footwear size recommendation that combines 3D anthropometric information obtained objectively by a low-cost 3D foot digitizer and user preferences by self-reported usual size and past purchases by the user and other customers.
4. Background
4.1. Ordinal Classifiers
In ordinal classification, classes are ordered, i.e., labels are levels of an ordinal variable. Although nominal classification is often used in ordinal classification problems, taking into account the order improves the performance, Gutiérrez et al. [6] surveyed ordinal classifiers with complete cases since the majority of methods do not handle missing values. We review here two methods for ordinal classification that yielded excellent performance in an extensive comparison with other methods carried out by Pierola et al. [5] in a garment matching problem.
4.1.1. Ordered Logistic Regression
Let be an matrix with M explanatory variables in N cases and a vector, an ordered factor with Q levels, with the values of the dependent variable. The cumulative link model was described in detail by Agresti [15] (Chapter 7). The model is () = , where each cumulative logit is yielded by parameters, the linear predictor + …+ is and the logit link function, = , is the inverse of the standard logistic cumulative distribution function. In our implementation, the model is selected by a forward stepwise model selection using Akaike’s information criterion (AIC). This model forecasts the class probabilities for a new case, once the parameters have been estimated. We carried out the implementation using the and functions from the R package MASS [16]. This method needs complete cases. We refer to this method as POLR. We assign a new case to the class with the highest probability.
If there are missing values, a classic way to handle them is to impute them and then apply POLR. A well-known imputation method is MICE (Multivariate Imputation by Chained Equations) implemented in from the R package MICE [17], which was a satisfactory imputation method in the comparison carried out by Hao and Blair [18]. We refer to this method as POLR-MICE.
4.1.2. Random Forests
Random forest (RF) is a classification and regression method where decision trees are combined. This method can handle missing values. If the response is an ordinal factor, the classic RF version proposed by Breiman [19] does not take into account the order, i.e., it is treated as a nominal classification problem. We refer to this method as ClassRF. We used the function from the R package randomForest [20] with the default parameters, which implements the RF algorithm of Breiman [21].
An alternative RF method based on a conditional inference framework that takes the ordering information of the response into account when building the trees is that proposed by Hothorn et al. [22]. We refer to this method as CondRF. We used the function with the default parameters from the R package party [23,24].
According to Janitza et al. [25], there are only small differences in prediction accuracy in favor of CondRF versus ClassRF when the response is ordinal. This is the reason we analyzed both alternatives.
As previously mentioned, RF are ensembles of trees. The growth of each tree is governed by random vectors. On the one hand, a group of m (mM) input variables is randomly selected to split at each node of the tree. On the other hand, it bootstraps training set samples. Therefore, the non-selected observations, which are called out-of-bag (OOB), can be used to estimate the error rate.
4.2. Collaborative Filtering
Collaborative filtering (CF) uses the known selections or preferences of a group of customers to predict the unknown selections or preferences for other customers. According to Su and Khoshgoftaar [9], CF tools are divided into memory-based techniques and model-based techniques, and hybrid techniques, which combine different techniques.
CF memory-based techniques rely on the computation of the similarity between users or items. We use the function with the default parameters from the R package recommenderlab [26], with the ’UBCF’ method, a user-based CF. User-based CF assumes that customers with similar selections will choose items similarly. It predicts the selection of a customer by first finding a neighborhood of similar customers and then aggregating the selections of these customers to give a prediction. We refer to this method as UBCF.
CF model-based techniques use unsupervised machine learning techniques, such as clustering. We propose the use of some unsupervised machine learning techniques for missing data as CF tools for the first time. Therefore, their use as CF is explained in Section 5. In particular, we use k-POD [27], a method for k-means clustering of missing data and AAcMDS and AAHP [28], two methods for carrying out archetypal analysis (AA) [29] with missing data.
k-POD obtained very accurate results even with a very high percentage of missingness in [27]. k-POD results were better or equivalent to those obtained after imputing and carrying out k-means, when imputation did not fail, since imputation fails at high levels of overall missingness. Similar to classic k-means, k-POD returns the centroids of each cluster and the assignations indicating the cluster to which each observation is allocated.
We chose AAcMDS and AAHP since both are based on projecting dissimilarities between cases and computing AA, and this kind of methodology provided the most accurate results with Rand score, even better or equivalent to k-POD in [28]. In AAcMDS and AAHP, pairwise Euclidean distances are estimated with missing data and then projected before AA is executed. The projection is carried out with classic multidimensional scaling and h-plot [30] for AAcMDS and AAHP, respectively. Similar to classic AA, AAcMDs and AAHP return the archetypes and, for each observation, a vector with the mixture coefficients that approximate the given observation by the weighted average (a convex combination) of the archetypes. The Euclidean distances are estimated using the function daisy from the R package cluster [31] that uses the Partial Distance Strategy (PDS) for missing data [32]. If some pairwise dissimilarities cannot be estimated because both users have not coincided in selecting any shoe model, then that dissimilarity is given a high value, larger than the other dissimilarities (a value of 10 is used in the experiments). If there is a missing value in an archetype, we impute it with the common size selected (usually 42 in the experiments).
Although we are dealing with a supervised problem, we can use CF as classifiers, despite being unsupervised tools. The response is treated as another predictor by CF. CF returns the recommended size as a real number, not a level of the ordered factor. Thus, we round the recommendation to the nearest integer in order to assign a new case to that size. Note that Spanish footwear sizes are integer numbers.
4.3. Ensembles
An ensemble of classifiers is a combination of classifiers whose individual predictions are merged somehow to predict the class of new observations. Greater accuracy is usually obtained by ensembles than that of the individual members that compose them. In order for an ensemble of classifiers to be more accurate than any of its individual classifiers, a necessary and sufficient condition is that the classifiers are accurate and diverse [33]. On the one hand, error rates of the individual classifiers should be lower than random guessing, i.e., the lower, the better. On the other hand, the more different are the errors they make on new observations, the more diverse the classifiers are, and the better they are for the ensemble. Pierola et al. [5] proposed an ensemble for two ordinal classifiers that return the predicted class probabilities. Soft voting is used. The predicted class probabilities for each classifier are mixed by a convex combination, i.e., they are weighted with values between zero and one and whose sum is one, and then aggregated. The final predicted class label is assigned based on the maximum of these weighted average probabilities. The weights are based on the ranked probability score (RPS) for probabilistic forecasts of ordered events [34,35]. RPS takes the order of the labels into account. With this measure, the cumulative density function (CDF) of a probabilistic forecast is compared with the CDF of the respective case over a given number of discrete probability levels. Moreover, we raise the scores to a power r to expand the effective range of weight values. Specifically, the weights of each classifier are = 1 − , where is the RPS associated with classifier i, with i = 1, 2. We considered r = 4, following the suggestion by Pierola et al. [5]. We refer to this method as EN.
5. Proposed Methodologies
We explain here our proposals about how the information provided by anthropometric measurements is combined with the information provided by user preference for footwear size matching.
POLR, POLR-MICE, CondRF, ClassRF and UBCF are well-known methods. However, k-POD, AAcMDS, AAHP, the respective CO-methods and the EN-methods are introduced for the first time, not only in the footwear size matching problem, but also in a classification problem.
- POLR POLR is applied to the anthropometric measurements and the variable ‘pref’, which are the variables with complete cases, without missing values.
- POLR-MICE POLR-MICE applies POLR to the anthropometric measurements, the variable ‘pref’ and the variables with the preferred size for each model except the variable used as output, after imputing the missing values with MICE.
- CondRF CondRF is applied to the anthropometric measurements, the variable ‘pref’ and the variables with the preferred size for each model, which contain missing values, except the variable used as output. This method handles missing values by using surrogate splits when predictors are missing [22].
- ClassRF ClassRF is applied to the anthropometric measurements, the variable ‘pref’ and the variables with the preferred size for each model, which contain missing values, except the variable used as output. For handling missing data, we use the function from the R package randomForest that imputes missing values in predictor data using proximity from randomForest, before using the function.
- UBCF UBCF is applied to the variables with the preferred size for each model, which contain missing values.
- k-PODk-POD is applied to the variables with the preferred size for each model, which contain missing values. We consider k = 3 since users select their usual size or one size up or one size down, as mentioned above. To give a recommendation, i.e., to predict a missing value of a given observation, we use the value for that variable of the cluster centroid of the cluster to which the given observation is assigned by k-POD.
- AAcMDS AAcMDS is applied to the variables with the preferred size for each model, which contain missing values. We consider k = 3, as with k-POD. To give a recommendation, i.e., to predict a missing value of a given observation, we use the approximation given by the archetypes to the referred observation.
- AAHP AAHP is applied to the variables with the preferred size for each model, which contain missing values. We consider k = 3, as with k-POD. To give a recommendation, i.e., to predict a missing value of a given observation, we use the approximation given by the archetypes to the referred observation.
- CO-POLR-UBCF CO-POLR-UBCF combines the information of the variables with complete cases with the user preference information with missing data using UBCF. UBCF is used as an imputation method. UBCF is used with the variables with the preferred size for each model to give a recommended size for the missing values. Then, we apply POLR to these data together with the anthropometric measurements and the variable ‘pref’.
- CO-POLR-k-POD CO-POLR-k-POD combines the information of the variables with complete cases with the user preference information with missing data using k-POD. k-POD is used as an imputation method. k-POD is used with the variables with the preferred size for each model to give a recommended size for the missing values. Then, we apply POLR to these data together with the anthropometric measurements and the variable ‘pref’.
- CO-POLR-AAcMDS CO-POLR-AAcMDS combines the information of the variables with complete cases with the user preference information with missing data using AAcMDS. AAcMDS is used as an imputation method. AAcMDS is used with the variables with the preferred size for each model to give a recommended size for the missing values. Then, we apply POLR to these data together with the anthropometric measurements and the variable ‘pref’.
- CO-POLR-AAHP CO-POLR-AAHP combines the information of the variables with complete cases with the user preference information with missing data using AAHP. AAHP is used as an imputation method. AAHP is used with the variables with the preferred size for each model to give a recommended size for the missing values. Then, we apply POLR to these data together with the anthropometric measurements and the variable ‘pref’.
- EN-POLR-UBCF EN-POLR-UBCF builds an ensemble of the two previous methods POLR and UBCF, as described in Section 4.3. EN needs the predicted class probabilities for each classifier. POLR returns them, but not UBCF. UBCF returns a real number as a recommendation. Thus, we recast these recommendations as the role of probabilities as follows. If the is between 41 and 42, we consider that the predicted probability for size 41 is 1 − (− 41), while the predicted probability for size 42 is 1 − (42- ) and zero for size 43. On the contrary, if the is between 42 and 43, we consider that the predicted probability for size 42 is 1 −(− 42), while the predicted probability for size 43 is 1 − (43−) and zero for size 41.
- EN-POLR-k-POD EN-POLR-k-POD builds an ensemble of the two previous methods, POLR and k-POD, as described in Section 4.3. As with UBCF, k-POD does not return probabilities but real numbers as recommendations. Therefore, we follow the same strategy with k-POD as with UBCF in EN-POLR-UBCF to obtain probabilities and build the ensemble.
- EN-POLR-AAcMDS EN-POLR-AAcMDS builds an ensemble of the two previous methods, POLR and AAcMDS, as described in Section 4.3. Again, we follow the same strategy as with UBCF in EN-POLR-UBCF to obtain probabilities and build the ensemble, since AAcMDS does not return probabilities either.
- EN-POLR-AAHP EN-POLR-AAHP builds an ensemble of the two previous methods, POLR and AAHP, as described in Section 4.3. Again, we follow the same strategy as with UBCF in EN-POLR-UBCF to obtain probabilities and build the ensemble, since AAHP does not return probabilities either.
POLR needs the response, the ordered factor, to have three or more levels. In one of the models, , users only selected two different sizes (41 and 42); therefore, POLR cannot be used. For that case, we use linear discriminant analysis (LDA) with stepwise variable selection instead, using the greedy.wilks function of the R package klaR [36].
Figure 1 presents an overview of the footwear size recommendation system framework. The well-known methods appear in bold font, while the proposed methodologies appear in normal font. As shown in Figure 1, the inputs are foot measurements, the ‘pref’ variable and past purchases and the information sources are different for each method. The recommendation size can be a single size if we only report the size with the highest probability, or we can return the probability of assignation to each size. In this way, the user can have more information and make a more informed decision.
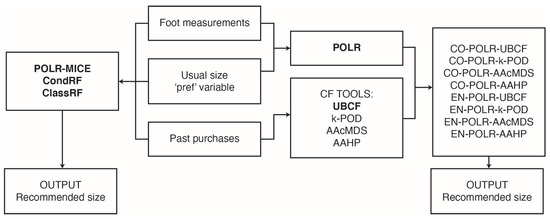
Figure 1.
Overview of the recommendation system framework.
Experimental Set-Up
To evaluate the methods of the shoe size recommendation system, the experimental set-up is as follows. We use the real data and the simulated data introduced in Section 2.1 and Section 2.2, respectively. In total, 10 datasets for Scenarios 1 and 2 were generated to assess the stability of the results. Table 2 shows the functions and parameter setting used in the implementation of the methods.

Table 2.
Summary of the implementation of each method. Default parameters are denoted by d.p.
To assess the performance of the methods, CondRF and ClassRF use the accuracy reported by the OOB samples, while the accuracy is estimated by leave-one-out (LOO) cross-validation for the other methods. In this case, in each trial, one subject is left out for all the methods involving POLR (POLR, CO-POLR-UBCF, CO-POLR-k-POD, CO-POLR-AAcMDS, CO-POLR-AAHP, EN-POLR-UBCF, EN-POLR-k-POD, EN-POLR-AAcMDS and EN-POLR-AAHP), which constitutes the test set, while the remaining subjects constitute the training set of that trial. For UBCF, k-POD, AAcMDS and AAHP, the following LOO strategy is followed: in each trial, each known value is replaced by a missing value and its value is predicted.
6. Results and Discussion
The performance estimates for the synthetic data from Scenarios 1 and 2 are shown in Table 3 and Table 4, respectively, while the estimated accuracies for the real data are shown in Table 5.

Table 3.
Mean and standard deviation, in brackets, of accuracy (percentage) over 10 simulations of the classifiers for the different models of Scenario 1 and their average. The maximum value in each column appears in bold.

Table 4.
Mean and standard deviation, in brackets, of accuracy (percentage) over 10 simulations of the classifiers for the different models of Scenario 2 and their average. The maximum value in each column appears in bold.

Table 5.
Accuracy (percentage) of the classifiers for the different models of shoes and their average for the real dataset. The maximum value in each column appears in bold. Underlined numbers indicate that LDA had to be used instead of POLR.
6.1. Synthetic Data Results
- Models where anthropometry and preference are relevant give the best performance: The best accuracies are achieved by the models that are more closely related to ‘pref’, i.e., M1 (89.1%) and M4 (88.9%) for Scenario 1 and M4 (88.8%) for Scenario 2. On the contrary, the models built without a relationship with ‘pref’ and anthropometric data (FL) give the worst results: M1 (60.8%), M2 (55.8%) and M3 (62.4%) for Scenario 2. This makes sense since these last models can only be predicted by the preferred sizes of other models. This is the reason accuracies for Scenario 1 are higher than for Scenario 2.
- Performance is more affected by high variability in size selection than by bias: The best accuracy for M3 in Scenario 1 (82.1%) is higher than that for M2 (69.1%) in Scenario 1. This also happens in Scenario 2. The data in M2 are generated with more variability, and therefore, less predictability.
- CO-methods and EN-methods are good alternatives to established tools: For Scenario 1, the CO-methods and EN-methods return very competitive results with the different CF strategies. This also happens in Scenario 2, but in this scenario CO-POLR-k-POD seems to be the best option. In both scenarios, the use of classic MICE for imputation yields worse results than using CF strategies for imputation, i.e., our proposed CO-methods are better. Our proposed CO-methods and EN-methods also provide better results than established tools, such as CondRF and ClassRF.
6.2. Real Data Results
- Accuracies depend on the shoe model: The best accuracies vary according to the shoe model, ranging from 57% for model M6 to 88% for model M2. This is also shown in Section 6.1. However, the average of the best accuracies for all the shoe models is 77%. In any case, these results are much higher than the accuracy obtained by the traditional foot-length-based strategy, which was 34.2%, as previously discussed in Section 1.
- The best result is obtained with different methods for each shoe model: There is no single method that is the best for all shoe models. For some of them, the information on past purchases is sufficient. Only for model M3 is the best classification obtained with the anthropometric measurements and ‘pref’ (its own preference, not relative to the other users), although for model M7 this comment could also be valid. Very good results are obtained with POLR and LDA for both with M3 and M7. For the other shoe models, the information given by the size selection made by other users is useful to the point that, in four of the shoe models, M1, M4, M6 and M7, the best classification is obtained without taking the anthropometric measurements and ‘pref’ into account, just the size selections. In the remaining models (M2, M5 and M8), both measurements and selections are useful for obtaining accurate predictions. In short, it is clear that the selections made by other users are important.
- EN-methods are very competitive: In global terms, if the mean accuracy for all the shoe models is analyzed, the best method is EN-POLR-AAcMDS (72.9%), followed by AAcMDS (71.9%), EN-POLR-AAHP (71.4%) and EN-POLR-UBCF (70.4%). On the one hand, the ensemble methodologies (EN-methods) provide excellent results. They are better than other ways of combining the different kinds of information, such as the use of RFs or classification by POLR after imputation (CO-methods). Furthermore, the ensemble methodologies improve the results of the individual classifiers in all cases when global results are analyzed: mean accuracy of EN-POLR-UBCF (70.4%) is higher than that of UBCF (66.5%), and the same happens for EN-POLR-k-POD (66%) versus k-POD (63%), EN-POLR-AAcMDS (72.9%) versus AAcMDS (71.9%) and EN-POLR-AAHP (71.4%) versus AAHP (68.9%).
- Collaborative filtering techniques with past purchases return very competitive results: The two techniques that we propose for the first time as collaborative filtering techniques, AAcMDS (71.9%) and AAHP (68.9%), provide higher mean accuracy than the well-established technique UBCF (66.5%).
- Suitability of CF tools in classification problems with uncertainties: Our results may seem to disagree with the message given by Hao and Blair [18]. They showed that user-based collaborative filtering was consistently inferior to logistic regression and random forests with different imputations on clinical prediction. However, there are relevant differences in both studies. First of all, Hao and Blair [18] indicated that CF may not be desirable in datasets where classification is an acceptable alternative, but this is not the case in our situation. Note that global accuracies for RFs (51.6% and 63.5% for CondRF and ClassRF, respectively) are lower than for CF in general (71.9%, 68.9%, 66.5% and 63% for AAcMDS, AAHP, UBCF and k-POD, respectively). Moreover, the problems are different. The responses and input variables of their clinical datasets are objective. However, in our problem, the size selection is quite subjective; each user has his own preferences even when they have similar anthropometric measurements. Therefore, ours is a difficult problem due to the presence of uncertainties in all parts of the problem: the outcome and the inputs. In fact, in other medical problems [38], their CF-based approach achieved a higher predictive accuracy than popular classification techniques such as logistic regression and support vector machines.
6.3. What Are the Advantages and Limitations of Our Proposal?
One of the advantages is the use of objective data for making footwear recommendation. In this way, we remove noise that could deteriorate the performance. On the one hand, some approaches use self-reported anthropometric measurements, which can be unreliable in the case of feet, since people are not experts in taking this kind of measurements at home. Instead, we use a low-cost 3D foot digitizer available in retail shops. We could have used Avatar3D, which is a smartphone app that acquires three images of each foot [10]. On the other hand, other approaches use self-reported opinion about tightness preference when wearing shoes. However, this opinion is not reliable either, since the perception is very subjective: there are people who say they prefer wearing loose shoes, when in fact they wear tight shoes according to a shoe expert. As limitations, we have to know the selected size of several users, although this is essential in any classification method. Our proposal depends partially on the information about historical purchases: the more information about past purchases we have, the better for our proposal.
Another advantage of our proposal is the good performance of the proposed methods that improve on the performance of well-known methods. As a limitation, in the case of big data, the computation could be slow for archetypal-based methods. In that case, we could use more efficient algorithms, as explained in [39] (e.g., [37,40,41,42,43]).
Another advantage is that the application of the proposed methods is not limited to footwear recommendation. The proposed procedures are not ad hoc, but they could also be applied to other real problems.
As positive impacts, the proposed methods based on clustering and archetypal analysis have proven to be excellent CF tools. Not only that, they have proven to be suitable for imputation. The results obtained are very satisfying and they improve on the performance of previous methods in on-line footwear size assignation. This is even more important in the current context, since the spread of COVID-19 makes customers seek more online services. Therefore, our proposal can help reduce the return rate.
7. Conclusions
We propose to combine information from a 3D foot measurements from low-cost 3D foot digitizer, past purchases and self-reported size. The results in Section 6.2 show that information on past purchases is very useful. In some cases, the information from 3D foot measurements is not very relevant, although in others it is.
We propose two approaches for combining information from those sources in the matching footwear size problem. On the one hand, we propose to use CF methodologies for imputing missing data before using a classifier (CO-methods). On the other hand, we propose an ensemble for joining the information from a classifier and CF methodologies (EN-methods). Furthermore, we propose the use of several unsupervised statistical learning techniques as CF methodologies for the first time: k-POD, AAcMDS and AAHP. We compares our proposals with several classic alternatives, such as the use of common imputation methods (MICE) and other techniques, such as RFs, with synthetic and real data. In both cases, our proposals returned better or comparable results to classical alternatives.
The EN-methods showed very good performance on the real dataset. EN-POLR-AAcMDS was the best method, with 72.9% accuracy. The ensemble methods outperform the results of each individual classifier in the ensemble.
We also show that the performance is more affected by high variability in size selection than bias.
As future work, the preliminary results on the real dataset could be tested with a larger dataset. The proposals could also be applied to other kinds of real problems, where uncertainties have a prominent role. Other classifiers could be also considered instead of POLR with CO-methods and EN-methods. Other recent CFs could be tested (e.g., [44,45,46]).
Author Contributions
Conceptualization, I.E.; data curation, J.V. and A.B.; formal analysis, A.A. and I.E.; funding acquisition, I.E. and A.B.; investigation, J.V. and A.B.; methodology, I.E.; resources, J.V. and A.B.; software, A.A. and I.E.; supervision, I.E.; visualization, A.A. and I.E.; writing—original draft preparation, I.E.; and writing—review and editing, A.A., I.E. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science, Innovation and Universities (AEI/FEDER, EU) grant number DPI2017-87333-R and Universitat Jaume I grant numbers UJI-B2017-13 and UJI-B2020-22.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
All participants signed an informed consent document, complying with the applicable Spanish legislation (Organic Law 15/1999, of 13 December, on Personal Data Protection, LOPD) granting the use of the data for research purposes.
Data Availability Statement
The code of our procedure and synthetic datasets for reproducing the results are available at http://www3.uji.es/~epifanio/RESEARCH/footwear.zip. Real data obtained through project IMDEEA/2017/60 are available on ibv@ibv.org.
Acknowledgments
The authors would like to thank IVACE for having promoted “Generación de una metodología de asignación de talla escalable por la industria para la venta por Internet. Aplicación en los 99 sectores de ropa y calzado” (Generation of a methodology for assigning scalable size by industry for online sales. Application to the clothing and footwear sectors) (IMDEEA/2017/60).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of the data; in the writing of the manuscript, or in the decision to publish the results.
References
- Huang, S.; Wang, Z.; Jiang, Y. Guess your size: A hybrid model for footwear size recommendation. Adv. Eng. Inform. 2018, 36, 64–75. [Google Scholar] [CrossRef]
- Lu, Z.; Stauffer, J. Fit Recommendation via Collaborative Inference. U.S. Patent 8,478,663, 2 July 2013. [Google Scholar]
- Dumke, M.A.; Briare, M.B. Recommending a Shoe Size Based on Best Fitting Past Shoe Purchases. U.S. Patent Application No. 12/655,553, 30 June 2011. [Google Scholar]
- Wilkinson, M.T.; Fresen, G.B.; End, N.B.; Wolodzko, E. Method and System for Recommending a Default Size of a Wearable Item Based on Internal Dimensions. U.S. Patent 9,366,530, 14 June 2016. [Google Scholar]
- Pierola, A.; Epifanio, I.; Alemany, S. An ensemble of ordered logistic regression and random forest for child garment size matching. Comput. Ind. Eng. 2016, 101, 455–465. [Google Scholar] [CrossRef]
- Gutiérrez, P.; Pérez-Ortiz, M.; Sánchez-Monedero, J.; Fernández-Navarro, F.; Hervás-Martínez, C. Ordinal Regression Methods: Survey and Experimental Study. IEEE Trans. Knowl. Data Eng. 2016, 28, 127–146. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. Data Mining, Inference and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Hand, D.J. Classifier Technology and the Illusion of Progress. Stat. Sci. 2006, 21, 1–14. [Google Scholar] [CrossRef]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009. [Google Scholar] [CrossRef]
- Ballester, A.; Piérola, A.; Parrilla, E.; Izquierdo, M.; Uriel, J.; Nácher, B.; Alemany, S. Fast, portable and low-cost 3D foot digitizers: Validity and reliability of measurements. In Proceedings of the 3DBODY, TECH 2017 8th International Conference and Exhibition on 3D Body Scanning and Processing Technologies, Montreal, QC, Canada, 11–12 October 2017; pp. 218–225. [Google Scholar]
- Alcacer, A.; Epifanio, I.; Ibá nez, M.V.; Simó, A.; Ballester, A. A data-driven classification of 3D foot types by archetypal shapes based on landmarks. PLoS ONE 2020, 15, e0228016. [Google Scholar] [CrossRef]
- Tran, B.; Tran, H. Systems and Methods for Footwear Fitting. U.S. Patent 9,460,557, 4 October 2016. [Google Scholar]
- Wilkinson, M.T.; End, N.B.; Fresen, G.B.; Wolodzko, E. Method and System for Recommending a Size of a Wearable Item. U.S. Patent 10,311,498, 4 June 2019. [Google Scholar]
- Marks, W.H. Footwear Recommendations From Foot Scan Data Describing Feet of a User. U.S. Patent 9,648,926, 16 May 2017. [Google Scholar]
- Agresti, A. Categorical Data Analysis; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef]
- Hao, F.; Blair, R.H. A comparative study: Classification vs. user-based collaborative filtering for clinical prediction. BMC Med. Res. Methodol. 2016, 16, 1–14. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Manual On Setting Up, Using, and Understanding Random Forests V4.0; Statistics Department, University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased Recursive Partitioning: A Conditional Inference Framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Hothorn, T.; Buehlmann, P.; Dudoit, S.; Molinaro, A.; Laan, M.V.D. Survival Ensembles. Biostatistics 2006, 7, 355–373. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional Variable Importance for Random Forests. BMC Bioinform. 2008, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Janitza, S.; Tutz, G.; Boulesteix, A.L. Random forest for ordinal responses: Prediction and variable selection. Comput. Stat. Data Anal. 2016, 96, 57–73. [Google Scholar] [CrossRef]
- Hahsler, M. Recommenderlab: Lab for Developing and Testing Recommender Algorithms. R Package Version 0.2-6. 2020. Available online: https://www.rdocumentation.org/packages/recommenderlab/versions/0.2-6 (accessed on 22 January 2021).
- Chi, J.T.; Chi, E.C.; Baraniuk, R.G. k-POD: A Method for k-Means Clustering of Missing Data. Am. Stat. 2016, 70, 91–99. [Google Scholar] [CrossRef]
- Epifanio, I.; Ibá nez, M.V.; Simó, A. Archetypal Analysis With Missing Data: See All Samples by Looking at a Few Based on Extreme Profiles. Am. Stat. 2020, 74, 169–183. [Google Scholar] [CrossRef]
- Cutler, A.; Breiman, L. Archetypal Analysis. Technometrics 1994, 36, 338–347. [Google Scholar] [CrossRef]
- Epifanio, I. h-plots for displaying nonmetric dissimilarity matrices. Stat. Anal. Data Min. 2013, 6, 136–143. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. Cluster: Cluster Analysis Basics and Extensions. R package version 2.1.1. 2021. Available online: https://cran.r-project.org/web/packages/cluster/index.html (accessed on 22 January 2021).
- Dixon, J.K. Pattern Recognition with Partly Missing Data. IEEE Trans. Syst. Man, Cybern. 1979, 9, 617–621. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Proceedings of the First International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; Springer: London, UK, 2000; pp. 1–15. [Google Scholar]
- Wilks, D. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- NCAR—Research Applications Laboratory. Verification: Weather Forecast Verification Utilities. R Package Version 1.42. 2015. Available online: https://rdrr.io/cran/verification/ (accessed on 22 January 2021).
- Weihs, C.; Ligges, U.; Luebke, K.; Raabe, N. klaR Analyzing German Business Cycles. Data Analysis and Decision Support; Springer: Berlin/Heidelberg, Germany, 2005; pp. 335–343. [Google Scholar]
- Vinué, G.; Epifanio, I. Robust archetypoids for anomaly detection in big functional data. Adv. Data Anal. Classif. 2020, 1–26. [Google Scholar] [CrossRef]
- Hassan, S.; Syed, Z. From netflix to heart attacks: Collaborative filtering in medical datasets. In Proceedings of the ACM International Health Informatics Symposium. ACM, Arlington, VA, USA, 11–12 November 2010; pp. 128–134. [Google Scholar]
- Cabero, I.; Epifanio, I.; Piérola, A.; Ballester, A. Archetype analysis: A new subspace outlier detection approach. Knowl.-Based Syst. 2021, 217, 106830. [Google Scholar] [CrossRef]
- Mørup, M.; Hansen, L.K. Archetypal analysis for machine learning and data mining. Neurocomputing 2012, 80, 54–63. [Google Scholar] [CrossRef]
- Chen, Y.; Mairal, J.; Harchaoui, Z. Fast and Robust Archetypal Analysis for Representation Learning. In Proceedings of the CVPR 2014—IEEE Conference on Computer Vision & Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1478–1485. [Google Scholar]
- Bauckhage, C.; Kersting, K.; Hoppe, F.; Thurau, C. Archetypal analysis as an autoencoder. In Proceedings of the Workshop New Challenges in Neural Computation, Aachen, Germany, 7–10 October 2015; pp. 8–15. [Google Scholar]
- Mair, S.; Boubekki, A.; Brefeld, U. Frame-based data factorizations. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2305–2313. [Google Scholar]
- Shahbazi, Z.; Hazra, D.; Park, S.; Byun, Y.C. Toward Improving the Prediction Accuracy of Product Recommendation System Using Extreme Gradient Boosting and Encoding Approaches. Symmetry 2020, 12, 1566. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Kudo, Y.; Murai, T.; Ren, Y.G. Enhancing Recommendation Accuracy of Item-Based Collaborative Filtering via Item-Variance Weighting. Appl. Sci. 2019, 9, 1928. [Google Scholar] [CrossRef]
- Sun, M.; Min, T.; Zang, T.; Wang, Y. CDL4CDRP: A Collaborative Deep Learning Approach for Clinical Decision and Risk Prediction. Processes 2019, 7, 265. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).