On Unification of Methods in Theories of Fuzzy Sets, Hesitant Fuzzy Set, Fuzzy Soft Sets and Intuitionistic Fuzzy Sets

Abstract

The main goal of this publication is to show that the basic constructions in the theories of fuzzy sets, fuzzy soft sets, fuzzy hesitant sets or intuitionistic fuzzy sets have a common background, based on the theory of monads in categories. It is proven that ad hoc defined basic concepts in individual theories, such as concepts of power set structures in these theories, relations or approximation operators defined by these relations are only special examples of applications of the monad theory in categories. This makes it possible, on the one hand, to unify basic constructions in all these theories and, on the other hand, to verify the legitimacy of ad hoc definitions of these constructions in individual theories. This common background also makes it possible to transform these basic concepts from one theory to another.

1. Introduction

Currently, there is a whole range of theories and theoretical structures that describe different types of non-probabilistic problems related to incomplete or inaccurate information. It is probably unnecessary to describe the history and versatile use of fuzzy sets, based on the pioneering work of L.A. Zadeh from 1964. The huge number of publications in the form of monographs and papers dealing with both theory and applications of fuzzy sets testifies to their extraordinary importance from both a theoretical and especially a practical point of view. Inspired by the theory of fuzzy sets, a number of theories were created, which dealt with the issue of incomplete or inaccurate information and which had developed their own theory and a specific range of potential applications. Let us mention here some well-known and frequently used methods, among which undoubtedly belong the theory of intuitionistic sets, the theory of soft sets and the theory of hesitant sets. The common feature of these three theories is, among other things, a large number of current publications dealing with both theoretical properties and application possibilities of these theories. For a basic overview of these theories, we will briefly mention some basic facts about these theories.

The oldest of these three theories is the intuitionistic fuzzy set theory, which was introduced by Atanassov [1] in 1983. Although several articles have emerged since its inception criticizing the name of this theory, which, in the authors’ views, is somewhat at odds with classical intuitionistic logic, the considerable range of publications and applications using the theory has led to the name still being actively used. Immediately after the emergence of this theory, Atanassov extended this theory to L-fuzzy intuitionistic sets [2] and also introduced the concept of intuitionistic fuzzy relation [3], which subsequently led to the expansion of the application possibilities of this theory. Currently, there are publications concerning the extension of this theory to other theoretical structures, such as the research of intuitionistic L-fuzzy metric spaces [4], and to the field of practical applications, such as [5,6,7].

The soft sets theory was introduced by Molodtsov [8] in 1999, who established the fundamental results and also proposed some applications of this theory. This theory was expanded to fuzzy soft sets theory in 2001 in [9]. In addition to the standard fuzzy sets theory, the fuzzy soft sets theory also uses a set of criteria. For each criterion, it defines, among other things, a special fuzzy set, which determines the extent to which the objects of the basic set meet the given criterion. Further extension of the theoretical results and possible application was subsequently published in, e.g., Maji et al. [9,10], Mushrif et al. [11], Feng et al. [12], Majumdar [13], Aktas [14], and many others.

The youngest of these theories is the theory of hesitant fuzzy sets, introduced by Torra and Narukawa [15] in 2009 and extended in [16]. A characteristic feature of this theory is that, unlike the classical fuzzy set, where the membership degree of an element is represented by a single value, the membership degree of an element in a hesitant fuzzy set is represented by a set of possible values. The motivation for this theory is the common difficulty that often appears when the membership degree of an element must be selected, and there are some possible values that make to hesitate about which one would be the right one. Even during its short existence, hesitant fuzzy sets have appeared in a number of publications, both of a theoretical and especially an application nature. As an example, let us mention at least an extensive monograph [17] with a number of theoretical and application results and an extensive bibliography, or the paper [18].

All three theories are connected by the use of fuzzy sets as key structures with which these theories work. It can therefore be expected that the tools and methods that are used in the theory of fuzzy sets can be also used in other theories with some modification. Examples of methods used by these theories are various tools for working with sets of fuzzy type objects, such as various analogies of Zadeh’s extension principle, various types of relations in these theories, or various types of approximation operators transforming objects of these theories. All these tools and methods are actively used, both in the theory of fuzzy sets and in the theory of fuzzy soft sets, hesitant fuzzy sets or intuitionistic fuzzy sets.

What is surprising, however, is that these methods are built adhoc in individual theories as separate independent methods. For example, without any interrelation new definitions of fuzzy soft relations [19,20], fuzzy hesitant relations [21,22] or intuitionistic fuzzy relations [23,24] are introduced independently and without justifying why these definitions were chosen and not others.

The aim of this paper is therefore to show that these new individual methods are, in fact, only special examples of methods from the theory of monads in categories. This statement has two practical consequences concerning both existing theories based on the fuzzy sets theory and possibly new, hitherto unused theories:

• In the case of existing theories and their tools, such as the already mentioned fuzzy soft sets or hesitant fuzzy sets and their special relations, transformation operators defined by these relations, or modifications of Zadeh’s extension principle, we can use these methods from monad theory to verify whether these special methods in individual theories are really consistent and correspond to the way of generalization of this theory in relationship to the classical theory of fuzzy sets. Using monads theory, we can also transform methods from one theory to methods from another.
• In the case of defining new theories, such as so far unused combinations of existing theories of fuzzy sets, hesitant sets, soft sets, rough sets or intuitionist sets, or in the case of underdeveloped theories, we can firstly verify if this theory defines a monad in an appropriate category. If the answer if affirmative, we do not need to define, for example, new types of relations, new transformation operators or look for ways how to define an analogy of Zadeh’s extension principle. We can simply introduce these definitions directly using tools from the monad theory.

The theory of monads, being an abstract and general theory, enables us to describe and present tools and methods from fuzzy sets, rough sets, hesitant set, intuitionistic sets or soft sets in an unified way. This makes it possible to eliminate the often and not always appropriately used method in the theory of fuzzy structures, namely, new ad hoc introduced definitions of basic tools in individual theories without any justification as to why such a definition has been chosen. Using this approach, we can define, for example, a general concept of a monadic relation in a category, which is then transformed into individual examples of relations in concrete fuzzy type theories. In many cases, it is also not necessary to prove basic properties for each of these new fuzzy type theories, because these can be derived from general properties of these constructions in monads.

There are many articles and monographs that deal with the issue of the category theory in the theory of fuzzy sets. For illustration, let us mention [25,26,27,28,29,30]. However, most of these articles deal only with applications of category theory to one type of fuzzy structures, most often classical fuzzy sets. Basically, there are no articles that deal with the application of category theory methods to various fuzzy type structures and use the category theory to unify methods in different fuzzy type structures. In this paper, we will therefore try to show how, using the category theory, we can unify some methods used in fuzzy set theory, hesitant fuzzy sets, fuzzy soft sets or intuitionistic fuzzy sets.

In order to work with this general theory, in the paper, we will use some methods from the category theory. In that way, we not only confirm that the four fuzzy type theories (i.e., including fuzzy set theory) use methods that are in fact only examples of a general method described in the category theory, but we also show how specific methods in one theory can be transformed into methods in another theory, using the language of the category theory.

Due to the limited scope of this article, we will focus only on some of the frequently used constructions in these theories. Namely, we will deal with

• An analogy of Zadeh’s extension principle applied to sets of objects from corresponding theory, i.e.,

  (a)

  sets of all intuitionistic L-fuzzy sets in a set X,

  (b)

  sets of all L-fuzzy soft set in a soft universe $(X,K)$, and

  (c)

  sets of all hesitant L-fuzzy sets in a set X,

• Analogies of L-fuzzy relations in these theories, i.e., intuitionistic L-fuzzy relations, hesitant L-fuzzy relations and L-fuzzy soft relations, and
• Transformation operators defined by the above analogies of L-fuzzy relations applied to sets of objects from these theories.

These methods represent one of the key tools in the fuzzy set theory, significantly used both in theory and in applications. Therefore, our goal will be to apply the general categorical core of these tools to the above three areas and thus unify the procedures in these four theories.

The main tool from the category theory that we will use for these purposes is related to the theory of monads and power set monads in categories. As we will see, power set monads in a category represent a key tool for all mentioned theories. In general, with the help of a power set monad in a cateogry $\mathbf{K}$, it is possible to define the concept of a cluster $T(X)$ of structures with uncertainty defined over objects X of a category $\mathbf{K}$ and to work with this cluster as a separate object in a category $\mathbf{K}$. With the help of these clusters with uncertainty, it is possible to define between two objects of a category $\mathbf{K}$ the concept of an uncertainty relation R, which is represented by a morphism $R:X\to T(Y)$ in a category $\mathbf{K}$. The monadic character of a power set theory then allows one to compose these relations using the Kleisli’s composition ◊. Both of these tools, i.e., the cluster of objects with uncertainty and the uncertainty relation, subsequently enable the use of one of the strongest tools in the theory of structures with uncertainty, namely the transformation of a given structure using the uncertainty relation.

Despite the undeniable importance of power set monads, very little is known about the specific existence of these theories for individual fuzzy type structures. At present, only the power set monad of classical fuzzy sets with values in various types of complete lattices can be considered as exhaustively processed (see, e.g., [29,30]). For the other structures with uncertainties mentioned above, there are only very partial results in this area. Our goal in this work is to at least partially supplement the lack of knowledge about the cluster structures of objects in the above mentioned theories and to show that analogously to classical fuzzy sets, these structures form power set monads. This result can then be used, for example, for the construction of uncertainty relations in these structures and for the approximation of objects of these structures.

The rest of the paper is organized as follows: The introductory section with basic notions from the residuated lattices theory and some definitions from the category theory are followed by three sections on fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets theories, respectively. In these sections, it is proven that the structures of sets of objects of these theories, including analogies of an extension principle, relations in these theories and transformation operators defined by these relations are only special examples of general methods in the theory of categories, presented in the introductory part. The last section is devoted to the issue of relationships represented by morphisms between individual theories. Using these morphisms, it is shown how some methods of one theory can be transferred to methods in another theory.

2. Preliminaries and Categorical Tools

A membership structure of fuzzy sets in the paper is a complete residuated lattice (see e.g., [31]), i.e., a structure $\mathcal{L}=(L,\wedge ,\vee ,\otimes ,\to ,0_L,1_L)$ such that $(L,\wedge ,\vee )$ is a complete lattice, $(L,\otimes ,1_L)$ is a commutative monoid with operation ⊗ isotone in both arguments and → is a binary operation which is residuated with respect to ⊗. Recall that a negation of an element a in $\mathcal{L}$ is defined by $\neg a=a\to 0_L$.

In the case of intuitionistic fuzzy sets, we use a special example of a residuated lattice $\mathcal{L}$, namely, an $MV$-algebra [32], i.e., a structure $\mathcal{L}=(L,\oplus ,\otimes ,\neg ,0_L,1_L)$ satisfying the following axioms:

(i)

$(L,\otimes ,1_L)$ is a commutative monoid,

(ii)

$(L,\oplus ,0_L)$ is a commutative monoid,

(iii)

$\neg \neg x=x$, $\neg 0_L=1_L$,

(iv)

$x\oplus 1_L=1_L$, $x\oplus 0_L=x$, $x\otimes 0_L=0_L$,

(v)

$x\oplus \neg x=1_L,x\otimes \neg x=0_L$,

(vi)

$\neg (x\oplus y)=\neg x\otimes \neg y$, $\neg (x\otimes y)=\neg x\oplus \neg y$,

(vii)

$\neg (\neg x\oplus y)\oplus y=\neg (\neg y\oplus x)\oplus x$,

For all $x,y\in X$.

If we put

$$x\vee y=(x\oplus \neg y)\otimes y,x\wedge y=(x\otimes \neg y)\oplus y,x\to y=\neg x\oplus y,$$

then $(L,\wedge ,\vee ,\otimes ,\to ,0_L,1_L)$ is a residuated lattice. $MV$-algebra is called a complete, if that lattice is a complete lattice.

$MV$-algebras have their origin in algebraic analysis of Lukasiewicz logic by Chang in [33] and represent a generalization of Boolean algebras. A standard example of an $MV$-algebra is the Lukasiewicz algebra ${\mathcal{L}}_L=([0,1],\oplus ,\otimes ,\neg ,0,1)$, where

$$x\otimes y=0\vee (x+y-1),\neg x=1-x,x\oplus y=1\wedge (x+y).$$

If $\mathcal{L}$ is a complete residuated lattice, an $\mathcal{L}$-fuzzy set in a crisp set X is a map $f:X\to L$. f is a non-trivial $\mathcal{L}$-fuzzy set, if f is not identical to the zero function.

In order not to increase the scope of this text beyond what is absolutely necessary, we will assume that the reader is acquainted at least with the basics of the category theory, i.e., the concepts of a category, a functor between categories and a natural transformation between two functors. For these pieces of information and many others, see [34,35]. In what follows, categories will be denoted by bold letters and morphisms in a category, $\mathbf{K}$ will be called $\mathbf{K}$-morphisms.

As we mentioned in the introduction, the main tool from the category theory that we will use is the monad. This concept was introduced in the 1960s and is now one of the powerful tools that connects computer science with mathematics. For details about the history and theory of monads, see [34,35,36]. The second tool from the category theory that we will use is the power set theory, which was introduced in its categorical background in [29,30]. It is not our goal to deal with these individual theories here, but for our purposes, it is important to use the properties of both of these theories at the same time. To this end, we will introduce a new structure called the power set monad in a category. In what follows by $\mathbf{Set}$, we denote the category of sets with mappings as morphisms. If $f:X\to Y$ and $g:Y\to Z$ are $\mathbf{K}$-morphisms, then $g.f:X\to Z$ is a composition of f and g. The following is the basic structure from the category theory, which we will use in the paper.

Definition 1.

A structure $\mathbf{T}=(T,◊,\eta ,W)$ is called a power set monad in a category $\mathbf{K}$, if

• $T:obj(\mathbf{K})\to obj(\mathbf{K})$ is mapping between objects of $\mathbf{K}$,
• $W:\mathbf{K}\to \mathbf{Set}$ is a functor,
• For an arbitrary object X in $\mathbf{K}$, a structure of a complete ⋁-semilattice is defined on a set $W(T(X))$,
• For $\mathbf{K}$-morphisms $f:X\to T(Y)$ and $g:Y\to T(Z)$ there exists their composition $g◊f:X\to T(Z)$, (called the Kleisli composition) which is associative,
• For arbitrary $\mathbf{K}$-morphisms $f,f^{\prime }:X\to T(Y)$ and $g,g^{\prime }:Y\to T(Z)$, the following implications hold

  $$\begin{array}{c}W(g){\le }_{Y}W(g^{\prime })\Rightarrow W(g◊f){\le }_{Z}W(g^{\prime }◊f),\\ W(f){\le }_{Y}W(f^{\prime })\Rightarrow W(g◊f){\le }_{Z}W(g◊f^{\prime }),\end{array}$$
  where ${\le }_Y,{\le }_Z$ are point-wise pre-order relations defined by ordering on $W(T(Y))$ or $W(T(Z))$, respectively.
• η is a system of $\mathbf{K}$-morphisms ${\eta }_X:X\to T(X)$, for any object X of $\mathbf{K}$,
• For any $\mathbf{K}$-morphism $f:X\to Y$, the $\mathbf{K}$-morphism

  $$f_T^{\to }:={\eta }_Y.f◊1_{T(X)}:T(X)\to T(Y)$$
  is such that $W(f_{\mathbf{T}}^{\to })$ is also ⋁-preserving map with respect to ordering defined in 3, where $1_{T(X)}$ is the identity $\mathbf{K}$-morphism $T(X)\to T(X)$ in $\mathbf{K}$.
• For any $\mathbf{K}$-morphism $f:X\to T(Y)$, ${\eta }_Y◊f=f$ holds,
• ◊ is compatible with composition of $\mathbf{K}$-morphisms, i.e., for $\mathbf{K}$-morphisms $f:X\to Y$, $g:Y\to T(Z)$, we have $g◊({\eta }_Y.f)=g.f$.

Remark 1.

• If ${\le }_Y$ is the order relation in a ⋁-semilattice $W(T(Y))$, for $W(f){\le }_{Y}W(g)$ we use only $f\le g$ for simplicity, if the object $T(Y)$ and a functor W are clear.
• Instead of a power set monad $\mathbf{T}$ in a category $\mathbf{K}$, we use sometimes an abbreviation ”power set monad $(\mathbf{K},\mathbf{T})$".

It should be mentioned that power set monad includes both a classical monad defined in References [34,35,36] and standard power set structure defined in Reference [29]. In fact, it is easy to see that if $(T,◊,\eta ,W)$ is a power set monad, $(T,◊,\eta )$ is a monad as follows from axioms 1,4,5,7,8. On the other hand, $(WT,\Rightarrow ,\xi )$ is a power set theory, where for a $\mathbf{K}$-morphism $f:X\to Y$, $f^{\Rightarrow }=W(f_T^{\to }):WT(X)\to WT(Y)$ and ${\xi }_X=W({\eta }_Y)$.

As we will see from results in the next section, it is natural to call the $\mathbf{K}$-morphism $f_T^{\to }:T(X)\to T(Y)$ by an analogy of Zadeh’s extension of $f:X\to Y$.

Let us consider the following classical example of a power set monad.

Example 1.

[30] Let $\mathcal{L}$ be a complete residuated lattice. The structure $\mathbf{Z}=(Z,⊞,\chi ,1_{\mathbf{Set}})$ is defined by

• $Z:obj(\mathbf{Set})\to obj(\mathbf{Set})$ is a function defined by $Z(X)=L^X$ and $1_{\mathbf{Set}}:\mathbf{Set}\to \mathbf{Set}$ is the identity functor,
• On $L^X$ the order relation is defined point-wise,
• For each $X\in \mathbf{Set}$, ${\chi }^X:X\to Z(X)$ is the characteristic map of elements from X, i.e.,

  $$x,y\in X,{\chi }^X(x)(y)={\chi }_{\left\{x\right\}}^X(y)=\left\{\begin{array}{cc}{1}_L,\hfill & x=y,\hfill \\ 0_L,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$
• For each $f:X\to Z(Y)$ and $g:Y\to Z(V)$ in $\mathbf{Set}$, $g⊞f:X\to Z(V)$ is defined by

  $$(g⊞f)(x)(z)=\underset{y\in Y}{\bigvee }f(x)(y)\otimes g(y)(z).$$

Then, $\mathbf{Z}$ is a power set monad.

It is easy to see that $f_Z^{\to }={\chi }^Y.f⊞1_{Z(X)}:Z(X)\to Z(Y)$ is a classical Zadeh’s extension $f_Z^{\to }$ of a map $f:X\to Y$, i.e.,

$$\begin{array}{c}s\in Z(X),y\in Y,f_Z^{\to }(s)(y)={\chi }^Y.f⊞1_{Z(X)}(s)(y)=\underset{x\in X,f(x)=y}{\bigvee }s(x).\end{array}$$

(1)

With the help of power set monad in a category, we can now define the concept of a monadic relation. This construction was first explicitly mentioned in the paper of Manes [37] and has recently proven to be an universal construction of relations for many fuzzy type structures (e.g., see [38]). We use the following form of a monadic relation in a category.

Definition 2

([37]). Let $\mathbf{K}$ be a category and let $\mathbf{T}=(T,◊,\eta ,W)$ be a power set monad in $\mathbf{K}$.

• A $\mathbf{T}$-relation R from an object X to an object Y in $\mathbf{K}$, in symbol $R:X⇝Y$, is a $\mathbf{K}$-morphism $R:X\to T(Y)$ in the category $\mathbf{K}$.
• If $R:X⇝Y$ and $S:Y⇝Z$ are $\mathbf{T}$-relations, their composition is a $\mathbf{T}$-relation $S◊R:X⇝Z$.

Using this general definition, we can now define some special types of monadic relations. For example, let us consider the following types of $\mathbf{T}$-relations.

Definition 3.

Let $\mathbf{K}$ be a category and let $\mathbf{T}=(T,◊,\eta ,W)$ be a power set monad in $\mathbf{K}$. Let $R:X⇝X$ be a $\mathbf{T}$-relation from X to X.

• R is called to be a $\mathbf{T}$-reflexive, if $R\le \eta$,
• R is called to be a $\mathbf{T}$-transitive, if $R◊R\le R$,

For $\mathbf{T}$-relations we can prove many important properties. For illustration, we present the following properties of a composition of $\mathbf{T}$-relations. The proof follows directly from Definition 1.

Proposition 1.

Let $\mathbf{K}$ be a category and let $\mathbf{T}=(T,◊,\eta ,W)$ be a power set monad in $\mathbf{K}$. Let $R,S:X⇝Y$ and $Q:Y⇝Z$ be $\mathbf{T}$-relations. Then,

• $Q◊(R\vee S)\ge (Q◊R)\vee (Q◊S)$,
• $Q◊(R\wedge S)\le (Q◊R)\wedge (Q◊S).$

In fuzzy mathematics and its applications, various types of approximation and transformation operators are very often used, which convert fuzzy objects defined over the basic structure X to fuzzy objects over the other structure Y. These operators undoubtedly include not only Zadeh’s extension principle, but also approximation operators based on different types of uncertainty relations, such as classical approximations of fuzzy sets using fuzzy relations or F-transformations defined using the so-called fuzzy partitions (for some examples, see [38]). As was proven in [38], many of these transformation operators are special examples of a general transformation operator defined by $\mathbf{T}$-relations, where $\mathbf{T}$ are suitable monads in categories, as it is defined in the following definition.

Definition 4.

[38] Let $\mathbf{T}=(T,◊,\xi ,W)$ be a power set monad in a category $\mathbf{K}$ and let $R:X⇝Y$ be a $\mathbf{T}$-relation from X to Y. The n an R-transformation of objects from $T(X)$ is a $\mathbf{K}$-morphism

$$R^{\uparrow }=R◊1_{T(X)}:T(X)\to T(Y).$$

Let us consider the following application of Definitions 2–4 in the power set monad $\mathbf{Z}$ from Example 1.

Example 2.

Recall that an $\mathcal{L}$-fuzzy relation from X to Y is an $\mathcal{L}$-fuzzy set R in a set $X\times Y$. It is easy to see that R is an $\mathcal{L}$-fuzzy relation if and only if $\overline{R}$ is a $\mathbf{Z}$-relation $X⇝Y$, where $\overline{R}(x)(y)=R(x,y)$. Moreover, R is a reflexive or transitive $\mathcal{L}$-fuzzy relation if and only if $\overline{R}$ is $\mathbf{Z}$-reflexive or $\mathbf{Z}$-transitive, respectively. For an $\mathcal{L}$-fuzzy relation $R:X\times Y\to L$ and an $\mathcal{L}$-fuzzy set $s\in L^X$, the upper approximation of s by R is a map $R^{\Uparrow }:L^X\to L^Y$ defined by $R^{\Uparrow }(s)(y)={\bigvee }_{x\in X}s(x)\otimes R(x,y)$. It is easy to see that $R^{\Uparrow }=\overline{R}⊞1_{Z(X)}={\overline{R}}^{\uparrow }$.

3. Results

In this section, we focus on the identification of a common background of tools and methods in the theory of fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets. Our goal is to show that tools defined in individual theories, such as power set objects, various types of fuzzy type relations, variants of Zadeh’s extension or transformation operators defined using various types of fuzzy relations are in fact only special examples of general constructions using monads in categories. This proves that all three theories, i.e., fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets, have a common background based on the theory of monads in categories.

3.1. $\mathcal{L}$-Fuzzy Soft Sets

In this part, we develop the power set monad of $\mathcal{L}$-fuzzy soft sets and we show that fuzzy soft relations are defined by this monad. We also prove that both analogies of Zadeh’s extension principle and approximation operators defined for fuzzy soft sets are defined by this monad. Hence, the power set theory of fuzzy soft set theory and its principal constructions represent special examples of methods from power set monads theory. Let us recall the basic definition of $\mathcal{L}$-fuzzy soft sets, which was introduced in a simplified way in Reference [9]. In what follows, $\mathcal{L}$ be a complete residuated lattice.

Definition 5.

Let X be a set of objects to be evaluated and let K be a set of all possible criteria. A pair $(E,s)$ is called an $\mathcal{L}$-fuzzy soft set in a space $(X,K)$, if $\varnothing \ne E\subseteq K$ and $s:E\to L^X$.

A space $(X,K)$ is referred to as a soft universe according to the conventional notation and terms in the literature and K is usually called parameter space. The basic category we use for $\mathcal{L}$-fuzzy soft sets monadic power set construction will be the subcategory ${\mathbf{Set}}_{*}$ of the product $\mathbf{Set}\times \mathbf{Set}$, where objects of ${\mathbf{Set}}_{*}$ are all soft universe pairs $(X,K)$, such that K contains a special object ★ (called a trivial criterium) and morphisms are pairs $(f,\alpha ):(X,K)\to (Y,M)$ such that $f:X\to Y$ and $\alpha :K\twoheadrightarrow M$ is a surjective map with $\alpha (★)=★$.

It should be mentioned that in Reference [39] we introduced a special power set monad for $\mathcal{L}$-fuzzy soft sets in the category $\mathbf{Set}$. The specificity of this power set monad was that instead of being defined for arbitrary soft universes $(X,K)\in {\mathbf{Set}}_{*}$; it was defined only for special soft unverses in the form $(U,K)$, where U is a fixed set of objects, i.e., for soft universes with the same sets U of objects to be evaluated. It follows that this construction represented a power set theory of criteria sets, on the contrary to a power set monad for a set of objects X in a soft universe $(X,K)$. The purpose of this special power set monad was to create a theoretical tool for possible applications in the field of image processing that we presented in References [40,41]. Hence, this special power set monad cannot be considered a power set monad representing general $\mathcal{L}$-fuzzy soft sets.

In the following theorem, we introduce a power set monad of $\mathcal{L}$-fuzzy soft sets. As in the classical theory of fuzzy sets, where the power set structure is formed by all fuzzy sets in a given set X, the monadic power set structure of $\mathcal{L}$-fuzzy soft sets will be formed by all $\mathcal{L}$-fuzzy soft sets defined in a soft universe $(X,K)$, for arbitrary soft universe $(X,K)\in {\mathbf{Set}}_{*}$.

In what follows, we use the following notation. If $f:X\to T(Y,M)$ is a map, where $T(Y,M)$ is defined in Theorem 1, then for $x\in X$, we set

$$\begin{array}{c}f(x)=(M_x^f,f_x)\in T(Y,M),M_x^f\subseteq M,f_x:M_x^f\to L^Y.\end{array}$$

(2)

Theorem 1.

Let $\tilde{\mathbf{T}}=(\tilde{T},\square ,\xi ,W)$ be defined by

• $\tilde{T}:obj({\mathbf{Set}}_{*})\to obj({\mathbf{Set}}_{*})$ is a mapping defined by $\tilde{T}(X,K)=(T(X,K),K)$, where

  $$T(X,K)=\{(E,s):★\in E\subseteq K,s:E\to L^X\}.$$
• $W:{\mathbf{Set}}_{*}\to \mathbf{Set}$ is the functor such that $W(X,K)=X$, $W(f,\alpha )=f$ for arbitrary object $(X,K)\in {\mathbf{Set}}_{*}$ and a ${\mathbf{Set}}_{*}$-morphism $(f,\alpha )$.
• An order relation ⊑ is defined on $T(X,K)=W(\tilde{T}(X,K))$ by

  $$\begin{array}{c}(E,s),(F,t)\in T(X,K),(E,s)⊑(F,t)\mathrm{iff}\\ E\subseteq F,(\forall e\in E)s(e)\le t(e)\mathrm{in}{L}^X.\end{array}$$
• If $(f,\alpha ):(X,K)\to \tilde{T}(Y,M)$ and $(g,\beta ):(Y,M)\to \tilde{T}(Z,N)$ are morphisms in ${\mathbf{Set}}_{*}$, using the notation (2), the Kleisli composition □ is defined by

  $$\begin{array}{c}(g,\beta )\square (f,\alpha )=(g\Delta f,\beta .\alpha ):(X,K)\to \tilde{T}(Z,N),\end{array}$$

  (3)

  $$\begin{array}{c}g\Delta f:X\to T(Z,N),(g\Delta f)(x)=(N_x^{g\Delta f},{(g\Delta f)}_x),\end{array}$$

  (4)

  $$\begin{array}{c}{N}_x^{g\Delta f}=\bigcup _{y\in Y}\beta (M_x^f)\cap N_y^g,\end{array}$$

  (5)

  $$\begin{array}{c}{(g\Delta f)}_x(n)(z)=\underset{\{(m,y)|m\in M_x^f,n=\beta (m)\in N_y^g\}}{\bigvee }{f}_x(m)(y)\otimes g_y(n)(z),\end{array}$$

  (6)
  for arbitrary $n\in N_x^{g\Delta f},z\in Z$.
• For $(X,K)\in {\mathbf{Set}}_{*}$, the ${\mathbf{Set}}_{*}$-morphism ${\xi }_{(X,K)}:(X,K)\to \tilde{T}(X,K)$ is defined by

  $$\begin{array}{c}{\xi }_{(X,K)}=({\xi }_X,1_K),{\xi }_X:X\to T(X,K),\\ x\in X,{\xi }_X(x)=(K,{\eta }_x^X),\end{array}$$
  where ${\eta }_x^X:K\to L^X$ is defined by

  $$k\in K,z\in X,{\eta }_x^X(k)(z)={\chi }_{\left\{x\right\}}^X(z).$$

Then, $\tilde{\mathbf{T}}$ is a power set monad in the category ${\mathbf{Set}}_{*}$.

Proof of Theorem 1.

It is clear that $W(\tilde{T}(X,K))=T(X,K)$ is a complete ⋁-semilattice with respect to ⊑, where for a system $\{(E_i,s_i):i\in I\}\subseteq T(X,K)$, we have

$$\begin{array}{c}\underset{i\in I}{\bigvee }(E_i,s_i)=(\bigcup _{i\in I}{E}_i,s),s:\bigcup _i{E}_i\to L^X\\ m\in \bigcup _i{E}_i,s(m)=\underset{j\in I,m\in E_j}{\bigvee }{s}_j(m).\end{array}$$

(1) We show that the operation □ is associative. Let $(f,\alpha ):(X,K)\to \tilde{T}(Y,M)$, $(g,\beta ):(Y,M)\to \tilde{T}(Z,N)$ and $(h,\omega ):(Z,N)\to \tilde{T}(V,P)$ be morphisms in ${\mathbf{Set}}_{*}$. According to (3), we have

$$\begin{array}{c}(h,\omega )\square ((g,\beta )\square (f,\alpha ))=(h\Delta (g\Delta f),\omega .\beta .\alpha ),\\ ((h,\omega )\square (g,\beta ))\square (f,\alpha )=((h\Delta g)\Delta f,\omega .\beta ,\alpha ).\end{array}$$

Hence, we need to prove that $h\Delta (g\Delta f)=(h\Delta g)\Delta f:X\to T(V,P)$. Let $x\in X$. According to (4)–(6), we obtain

$$\begin{array}{c}h\Delta (g\Delta f)(x)=(P_x^{h\Delta (g\Delta f)},(h\Delta {(g\Delta f)}_x),\\ (h\Delta g)\Delta f)(x)=(P_x^{(h\Delta g)\Delta f},{((h\Delta g)\Delta f)}_x).\end{array}$$

We prove that $P_x^{(h\Delta g)\Delta f}=P_x^{h\Delta (g\Delta f)}$. In fact, we have

$$\begin{array}{c}{P}_x^{h\Delta (g\Delta f)}=\bigcup _{z\in Z}\omega (N_x^{g\Delta f})\cap P_z^h=\bigcup _{z\in Z}(\omega (\bigcup _{y\in Y}\beta (M_x^f)\cap N_y^g)\cap P_z^h),\\ P_x^{(h\Delta g)\Delta f}=\bigcup _{y\in Y}\omega .\beta (M_x^f)\cap P_y^{h\Delta g}=\bigcup _{y\in Y}(\omega .\beta (M_x^f)\cap (\bigcup _{z\in Z}\omega (N_y^g)\cap P_z^h)).\end{array}$$

Let $p\in P_x^{(h\Delta g)\Delta f}$. Then, there exist $y\in Y,z\in Z$ and $n\in N_y^g$, such that $p=\omega \beta (m)=\omega (n)\in P_z^h$, and it follows that $p\in \omega .\beta (M_x^f)\cap \omega (N_y^g)\cap P_z^h$. Therefore, $P_x^{(h\Delta g)\Delta f}\subseteq P_x^{h\Delta (g\Delta f)}$.

On the other hand, for $p\in P_x^{h\Delta (g\Delta f)}$, there exist $y\in Y,z\in Z,m\in M_x^f,n\in N_z^g$, such that $p=\omega .\beta (m)=\omega (n)\in P_z^h$ and it follows that $P_x^{h\Delta (g\Delta f)}\subseteq P_x^{(h\Delta g)\Delta f}$ holds.

According to (6), for arbitrary $p\in P_x^{h\Delta (g\Delta f)},v\in V$, we have

$$\begin{array}{c}{(h\Delta (g\Delta f))}_x(p)(v)=\\ \underset{\{(n,z)|n\in N_x^{g\Delta f},\omega (n)=p\in P_z^h\}}{\bigvee }{(g\Delta f)}_x(n)(z)\otimes h_z(p)(v)=\\ \underset{\{(n,z)|n\in N_x^{g\Delta f},\omega (n)=p\in P_z^h\}}{\bigvee }\underset{\{(m,y)|m\in M_x^f,n=\beta (m)\in N_y^g\}}{\bigvee }{f}_x(m)(y)\otimes \\ g_y(n)(z)\otimes h_z(p)(v)=\\ \underset{\{(m,y,z)|y\in Y,z\in Z,m\in M_x^f,\beta (m)\in N_y^g,\omega .\beta (m)=p\in P_z^h\}}{\bigvee }{f}_x(m)(y)\otimes \\ g_y(\beta (m))(z)\otimes h_z(p)(v).\end{array}$$

On the other hand, we have

$$\begin{array}{c}{((h\Delta g)\Delta f)}_x(p)(v)=\\ \underset{\{(m,y)|m\in M_x^f,\omega .\beta (m)=p\in P_y^{h\Delta g}\}}{\bigvee }{f}_x(m)(y)\otimes {(h\Delta g)}_x(p)(v)=\\ \underset{\{(m,y)|m\in M_x^f,\omega .\beta (m)=p\in P_y^{h\Delta g}\}}{\bigvee }\underset{\{(n,z)|n\in N_y^g,p=\omega (n)\in P_z^h\}}{\bigvee }{f}_x(m)(y)\otimes \\ g_y(n)(z)\otimes h_z(p)(v)=\\ \underset{\{(m,y,z)|y\in Y,z\in Z,m\in M_x^f,\beta (m)\in N_y^g,\omega .\beta (m)=p\in P_z^h\}}{\bigvee }{f}_x(m)(y)\otimes \\ g_y(\beta (m))(z)\otimes h_z(p)(v),\end{array}$$

and it follows that $h\Delta (g\Delta f)=(h\Delta g)\Delta f$. Hence, the operation □ is associative.

(2) Let $(f,\alpha ):(X,K)\to \tilde{T}(Y,M)$ be a morphism in ${\mathbf{Set}}_{*}$. We show that the identity ${\xi }_{(Y,M)}\square (f,\alpha )=(f,\alpha )$ holds. For $x\in X$, we have

$$\begin{array}{c}{\xi }_{(Y,M)}\square (f,\alpha )=({\xi }_Y\Delta f,\alpha ),\\ {\xi }_Y\Delta f(x)=(M_x^{{\xi }_Y\Delta f},{({\xi }_Y\Delta f)}_x),\\ M_x^{{\xi }_Y\Delta f}=\bigcup _{y\in Y}{M}_x^f\cap M_y^{{\xi }_Y}=\bigcup _{y\in Y}{M}_x^f\cap M=M_x^f,\\ m\in M_x^f,y\in Y,{({\xi }_Y\Delta f)}_x(m)(y)=\\ \underset{\{(z,q)|q\in M_x^f,q=m\in M_z^{{\xi }_Y}\}}{\bigvee }{f}_x(q)(z)\otimes {\xi }_{Y,z}(m)(y)=f_x(m)(y),\end{array}$$

as follows from the definition of ${\xi }_{(Y,M)}$. Therefore, ${\xi }_Y\Delta f(x)=(M_x^f,f_x)=f(x)$ and the identity holds.

(3) Let $(f,\alpha ):(X,K)\to (Y,M)$ and $(g,\beta ):(Y,M)\to \tilde{T}(Z,N)$ be morphisms in ${\mathbf{Set}}_{*}$. We show that $(g,\beta )\square ({\xi }_{(Y,M)}.(f,\alpha ))=(g,\beta ).(f,\alpha )=(g.f,\beta .\alpha )$. According to (3)–(6), we have

$$\begin{array}{c}(g,\beta )\square ({\xi }_{(Y,M)}.(f,\alpha ))=(g\Delta {\xi }_Y.f,\beta .\alpha ),\\ g\Delta {\xi }_Y.f:X\to T(Z,N),\\ x\in X,g\Delta {\xi }_Y.f(x)=(N_x^{g\Delta {\xi }_Y.f},{(g\Delta {\xi }_Y.f)}_x),\\ N_x^{g\Delta {\xi }_Y.f}=\bigcup _{y\in Y}\beta (M_x^{{\xi }_y.f})\cap N_y^g=\bigcup _{y\in Y}\beta (M)\cap N_y^g=\bigcup _{y\in Y}{N}_y^g,\\ n\in N_x^{g\Delta {\xi }_Y.f},z\in Z,{(g\Delta {\xi }_Y.f)}_x(n)(z)=\\ \underset{\{(y,m)|m\in M_x^{{\xi }_Y.f},n=\beta (m)\in N_y^g\}}{\bigvee }{\eta }_{f(x)}^Y(m)(y)\otimes g_y(n)(z)=\\ \underset{\{(y,m)|m\in M_x^{{\xi }_Y.f},n=\beta (m)\in N_y^g\}}{\bigvee }{\chi }_{f(x)}^Y(y)\otimes g_y(n)(z)=g_{f(x)}(n)(z).\end{array}$$

On the other hand, we have $g.f(x)=g(f(x))=(N_{f(x)}^g,g_{f(x)})$. If $y\in Y,y\ne f(x)$ is such that there exists $n\in N_y^g\setminus N_{f(x)}^g$, for arbitrary $z\in Z$ we have ${(g\Delta {\xi }_Y.f)}_x(n)(z)=0_L$ and it follows that we can identify $N_x^{g\Delta {\xi }_Y.f}$ with $N_{f(x)}^g$. Therefore, the required identity holds.

(4) Let $(f,\alpha ):(X,K)\to (Y,M)$ be a morphism in ${\mathbf{Set}}_{*}$. We have

$$\begin{array}{c}{(f,\alpha )}_{\tilde{T}}^{\to }:=\\ {\xi }_{(Y,M)}.(f,\alpha )\square 1_{\tilde{T}(X,K)}=({\xi }_Y.f\Delta 1_{T(X,K)},\alpha ):\tilde{T}(X,K)\to \tilde{T}(Y,M).\end{array}$$

For simplicity, we put ${(f,\alpha )}_T^{\to }:={\xi }_Y.f\Delta 1_{T(X,K)}$, i.e.,

$$\begin{array}{c}{(f,\alpha )}_{\tilde{T}}^{\to }=({(f,\alpha )}_T^{\to },\alpha ).\end{array}$$

(7)

For $(E,s)\in T(X,K)$, using the notation (2) we have

$${(f,\alpha )}_T^{\to }(E,s)=(M_{(E,s)}^{{\xi }_Y.f\Delta 1_{T(X,K)}},{({\xi }_Y.f\Delta 1_{T(X,K)})}_{(E,s)}).$$

Because $1_{T(X,K)}(E,s)=(E,s)$ and $M_x^{{\xi }_Y.f}=M_{f(x)}^{{\xi }_Y}$, ${\xi }_Y(f(x))=(M,{\eta }_{f(x)}^Y)$, we obtain $M_x^{{\xi }_Y.f}=M$ and

$$M_{(E,s)}^{{\xi }_Y.f\Delta 1_{T(X,K)}}=\bigcup _{x\in X}\alpha (K_{(E,s)}^{1_{T(X,K)}})\cap M_x^{{\xi }_Y.f}=\bigcup _{x\in X}\alpha (E)\cap M=\alpha (E).$$

For $n\in \alpha (E),y\in Y$ we obtain

$$\begin{array}{c}{({\xi }_Y.f\Delta 1_{T(X,K)})}_{(E,s)}(n)(y)=\\ \underset{\{(m,x)|m\in K_{(E,s)}^{1_{T(X,K)}},n=\alpha (m)\in M_x^{{\xi }_Y.f}\}}{\bigvee }{1}_{T(X,K),(E,s)}(m)(x)\otimes {({\xi }_Y.f)}_x(n)(y)=\\ \underset{\{(m,x)|m\in E,n=\alpha (m),x\in X\}}{\bigvee }s(m)(x)\otimes {\eta }_{f(x)}^Y(n)(y)=\\ \underset{\{(m,x)|m\in E,n=\alpha (m),x\in X\}}{\bigvee }s(m)(x)\otimes {\chi }_{f(x)}^Y(y)=\\ \underset{(x,m)|m\in E,x\in X,f(x)=y,\alpha (m)=n)\}}{\bigvee }s(m)(x).\end{array}$$

Therefore, we can put

$$\begin{array}{c}{(f,\alpha )}_T^{\to }(E,s)=(\alpha (E),f_T^{\Rightarrow }(s)),\end{array}$$

(8)

$$\begin{array}{c}n\in \alpha (E),y\in Y,f_T^{\Rightarrow }(s)(n)(y)=\underset{\{(x,m)|m\in E,x\in X,f(x)=y,\alpha (m)=n\}}{\bigvee }s(m)(x).\end{array}$$

(9)

We show that ${(f,\alpha )}_T^{\to }$ is a ⋁-preserving mapping. Let $(E_i,s_i)\in T(X,K),i\in I$. Then, we have

$$\begin{array}{c}{(f,\alpha )}_T^{\to }(\underset{i\in I}{\bigvee }(E_i,s_i))={(f,\alpha )}_T^{\to }(\bigcup _{i\in I}{E}_i,s)=(\alpha (\bigcup _{i\in i}{E}_i),f_T^{\Rightarrow }(s)),\end{array}$$

where for $m\in {\bigcup }_{i\in I}{E}_i$, $s(m)(x)={\bigvee }_{j\in I,m\in E_j}{s}_j(m)(x)$. Hence, for $n\in \alpha ({\bigcup }_{i\in I}{E}_i)$, $y\in Y$ we have

$$\begin{array}{c}{f}_T^{\Rightarrow }(s)(n)(y)=\underset{\{(x,m)|m\in {\bigcup }_{i\in I}{E}_i,\alpha (m)=n,x\in X,f(x)=y\}}{\bigvee }s(m)(x)=\\ \underset{\{(x,m)|m\in {\bigcup }_{i\in I}{E}_i,\alpha (m)=n,x\in X,f(x)=y\}}{\bigvee }\underset{\{j\in I,m\in E_j\}}{\bigvee }{s}_j(m()(x).\end{array}$$

On the other hand, we have

$$\begin{array}{c}\underset{i\in I}{\bigvee }{(f,\alpha )}_T^{\to }(E_i,s_i)=(\bigcup _{i\in I}\alpha (E_i),t^{\to }),\\ t^{\to }(n)(y)=\underset{\{j\in I,n\in \alpha (E_j)\}}{\bigvee }{f}_T^{\Rightarrow }(s_j)(n)(y)=f_T^{\Rightarrow }(s)(n)(y).\end{array}$$

Therefore, ${(f,\alpha )}_T^{\to }$ is ⋁-preserving.

(5) If $(f,\alpha ):(X,K)\to \tilde{T}(Y,M)$ and $(g,\beta ),(g^{\prime },{\beta }^{\prime }):(Y,M)\to \tilde{T}(Y,N)$ are such that $g=W(g,\beta ){\le }_{(Z,N)}W(g^{\prime },{\beta }^{\prime })=g^{\prime }$, then $g\Delta f=W((g,\beta )\square (f,\alpha )){\le }_{(Z,N)}$$W((g^{\prime },{\beta }^{\prime })\square (f,\alpha ))=g^{\prime }\Delta f$ follows directly from (4)–(6). □

A notion of an $\mathcal{L}$-fuzzy soft relation between two sets or two soft universes was defined by various authors (see, e.g., [19,20,24]). Unfortunately, most of these definitions considered only rather special cases of fuzzy soft relations between soft universes $(X,K)$ and $(Y,K)$, i.e., for soft universes with the same sets of parameters. A typical example of these definitions is presented in [19], where $(E,R)$ is an $\mathcal{L}$-fuzzy soft relation from $(X,K)$ to $(Y,K)$ if $R:E\to L^{X\times Y}$, where $\ast \in E\subseteq K$. We use the following form of a fuzzy soft relation between two soft universes with the same set of criteria.

Definition 6.

An $\mathcal{L}$-fuzzy soft relation from $(X,K)$ to $(Y,K)$ is a couple $(E,R)$, where $\{\ast \}\times X\subseteq E\subseteq K\times X$, $R:E\times Y\to L$.

The definition of a fuzzy soft relation from [19] is a special example of an $\mathcal{L}$-fuzzy soft relation from Definition 6. In fact, if $(E,R)$ is a fuzzy soft relation between $(X,K)$ and $(Y,K)$, according to [19], where $R:E\to L^{X\times Y}$, $E\subseteq K$, then we can identify $(E,R)$ with the $\mathcal{L}$-fuzzy soft relation $(\overline{E},\overline{R})$ from Definition 6, where $\overline{E}=E\times X$ and $\overline{R}:\overline{E}\times Y\to L$ are such that $\overline{R}((e,x),y)=R(e)(x,y)$. Hence, we can consider the embedding

$$\begin{array}{c}\Lambda :\{(E,R)|(E,R)\mathrm{is}\mathrm{an}\mathcal{L}-\mathrm{fuzzy}\mathrm{soft}\mathrm{relation}\mathrm{according}\mathrm{to}\left[19\right]\}\hookrightarrow \\ \hookrightarrow \{(E,R)|(E,R)\mathrm{is}\mathrm{an}\mathcal{L}-\mathrm{fuzzy}\mathrm{soft}\mathrm{relation}\mathrm{according}\mathrm{to}\mathrm{Definition}6\}.\end{array}$$

In the following part of this section, we show that $\mathcal{L}$-fuzzy soft relations between soft universes defined in Definition 6 can be determined by the monadic structure of a fuzzy soft set theory; i.e., $\mathcal{L}$-fuzzy soft relations from Definition 6 can be represented as special $\tilde{\mathbf{T}}$-relations. We also show what the approximation operators defined using these $\tilde{\mathbf{T}}$-relations look like.

Lemma 1.

Let $(X,K)$ and $(Y,K)$ be soft universes. There exists a bijection mapping Ψ between the set

$$\{r|(r,1_K):(X,K)⇝(Y,K)\mathrm{is}\tilde{\mathbf{T}}-\mathrm{relation}\}$$

and the set of all $\mathcal{L}$-fuzzy soft relations from $(X,K)$ to $(Y,K)$ from Definition 6.

Proof of Lemma 1.

Let $(r,1_K):(X,K)\to \tilde{T}(Y,K)$ be a $\tilde{\mathbf{T}}$-relation. According to the notation (2), we have $W(r,1_K)(x)=r(x)=(K_x^r,r_x)\in T(Y,K)$. We define ${\Psi }^{-1}(r)=(E,R)$, where

$$\begin{array}{c}E=\bigcup _{x\in X}{K}_x^r\times \left\{x\right\}\subseteq K\times X,R:E\times Y\to L,\\ (m,x)\in E,y\in Y,R(m,x,y):=r_x(m)(y).\end{array}$$

Conversely, for an $\mathcal{L}$-fuzzy soft relation $(F,S)$ from $(X,K)$ to $(Y,K)$ according to Definition 6, we have $F={\bigcup }_{x\in X}{F}_x\times \left\{x\right\}$, where $F_x=\{m\in K:(m,x)\in F\}$. The n $(q,1_K):(X,K)⇝(Y,K)$ is defined by

$$\begin{array}{c}x\in X,q(x)=(F_x,q_x),q_x:F_x\to L^Y,\\ m\in F_x,y\in Y,q_x(m)(y)=S(m,x,y).\end{array}$$

It is straightforward to see that $(q,1_K)$ is a $\tilde{\mathbf{T}}$-relation from $(X,K)$ to $(Y,K)$ and we can put $\Psi (F,S)=q$. It is easy to see that $\Psi$ and ${\Psi }^{-1}$ are mutually inverse maps and this proof will be omitted. □

For fuzzy soft relations from [19,24], it is possible to define their compositions. We present this definition for $\mathcal{L}$-fuzzy soft versions of these relations.

Definition 7.

Let $(E,R):(X,K)\to (Y,K)$ and $(F,Q):(Y,K)\to (Z,K)$ be $\mathcal{L}$-fuzzy soft relations according to [19]. The ir composition $(F,Q)\circ (E,R)$ is defined as an $\mathcal{L}$-fuzzy soft relation $(E\cap F,Q\times R)$, where $Q\times R:E\cap F\to L^Z$ is defined by

$$k\in E\cap F,(x,z)\in X\times Z,(Q\times R)(k)(x,z)=\underset{y\in Y}{\bigvee }R(k)(x,y)\otimes Q(k)(y,z).$$

Using Lemma 1, we can show that there is a relationship between the composition of $\mathcal{L}$-fuzzy soft relations according to [19] and a composition defined by a monad $\tilde{\mathbf{T}}$.

Proposition 2.

Let $(E,R)$ be an $\mathcal{L}$-fuzzy soft relation from $(X,K)$ to $(Y,K)$ and $(F,Q)$ be an $\mathcal{L}$-fuzzy soft relation from $(Y,K)$ to $(Z,K)$. Then, we have

$$\Psi .\Lambda (F,Q)\Delta \Psi .\Lambda (E,R)=\Psi .\Lambda ((F,Q)\times (E,R)).$$

Proof of Proposition 2.

From the proof of Lemma 1, it follows that

$$\begin{array}{c}\Psi .\Lambda (E,R)=r:X\to T(Y,K),x\in X,r(x)=(E,r_x),\\ \Psi .\Lambda (F,Q)=s:Y\to T(Z,K),y\in Y,s(y)=(F,s_y),\\ k\in E,j\in F,z\in Z,r_x(k)(y)=R(k)(x,y),s_y(j)(z)=Q(j)(y,z).\end{array}$$

On the other hand, according to (4)–(6) and the proof of Lemma 1, we obtain

$$\begin{array}{c}(s\Delta r)(x)=(K_x^{s\Delta r},{(s\Delta r)}_x)=(E\cap F,{(s\Delta r)}_x),\\ k\in E\cap F,z\in Z,{(s\Delta r)}_x(k)(z)=\underset{y\in Y}{\bigvee }{r}_x(k)(y)\otimes s_y(k)(z)=\\ \underset{y\in Y}{\bigvee }R(k)(x,y)\otimes Q(k)(y,z)=(Q\times R)(k)(x,z),\end{array}$$

and this completes the proof. □

Using the power set monad $\tilde{\mathbf{T}}$, we can also define a general form of an $\mathcal{L}$-fuzzy soft relations between soft universes $(X,K)$ and $(Y,M)$ as a $\tilde{\mathbf{T}}$-relation $(r,\alpha ):(X,K)⇝(Y,K)$.

Lemma 1 can be used to construct an approximation operator ${(r,\alpha )}^{\uparrow }$ defined by a $\tilde{\mathbf{T}}$-relation $(r,\alpha )$, which is, in a general form, introduced in Definition 4.

Proposition 3.

Let $(r,\alpha ):(X,K)⇝(Y,K)$ be a $\tilde{\mathbf{T}}$-relation and let $\Psi (r)=(F,R)$. The $(r,\alpha )$-approximation operator ${(r,\alpha )}^{\uparrow }:\tilde{T}(X,K)\to \tilde{T}(Y,K)$ is such that

$$\begin{array}{c}{(r,\alpha )}^{\uparrow }=(r^{\uparrow },\alpha ):\tilde{T}(X,K)\to \tilde{T}(Y,K),\end{array}$$

where $r^{\uparrow }:T(X,K)\to T(Y,K)$ is defined by

$$\begin{array}{c}(E,s)\in T(X,K),r^{\uparrow }(E,s)=(\bigcup _{x\in X}\alpha (E)\cap F(x),R^{\uparrow }(s))\in T(Y,K),\\ \forall n\in \bigcup _{x\in X}\alpha (E)\cap F(x),y\in Y,\\ R^{\uparrow }(s)(n)(y)=\underset{\{(m,x)|x\in X,m\in E,\alpha (m)=n\in F(x)\}}{\bigvee }s(m)(x)\otimes R(n,x,y).\end{array}$$

Proof of Proposition 3.

According to Definition 4 and relations (3)–(6), the $\tilde{\mathbf{T}}$-operator ${(r,\alpha )}^{\uparrow }:\tilde{T}(X,K)\to \tilde{T}(Y,M)$ is defined by

$${(r,\alpha )}^{\uparrow }=(r,\alpha )\square 1_{\tilde{T}(X,K)}=(r,\alpha )\square (1_{T(X,K)},1_K)=(r\Delta 1_{T(X,K)},\alpha ).$$

We show that $r\Delta 1_{T(X,K)}=r^{\uparrow }$. Using the notation (2) and identity (5), for $(E,s)\in T(X,K)$ we have $r\Delta 1_{T(X,K)}(E,s)=(K_{(E,s)}^{r\Delta 1_{T(X,K)}},{(r\Delta 1_{T(X,K)})}_{(E,s)})$, where

$$K_{(E,s)}^{r\Delta 1_{T(X,K)}}=\bigcup _{x\in X}\alpha (K_{(E,s)}^{1_{T(X,K)}})\cap K_x^r=\bigcup _{x\in X}\alpha (E)\cap K_x^r=\bigcup _{x\in X}\alpha (E)\cap F(x).$$

Using the identity (6) and Lemma 1, for $n\in {\bigcup }_{x\in X}\alpha (E)\cap F(x)$ and $y\in Y$, we obtain

$$\begin{array}{c}{(r\Delta 1_{T(X,K)})}_{(E,s)}(n)(y)=\underset{\{(m,x)|x\in X,n=\alpha (m)\in M_x^r\}}{\bigvee }{1}_{T(X,K),(E,s)}(m)(x)\otimes r_x(n)(y)=\\ \underset{\{(m,x)|x\in X,n=\alpha (m)\in F(x)\}}{\bigvee }s(m)(x)\otimes R(n,x,y)=R^{\uparrow }(s)(n(y)).\end{array}$$

Therefore, $r\Delta 1_{T(X,K)}=r^{\uparrow }$. □

In the following example, we show that a classical upper approximation $R^{\uparrow }(s)$ of an $\mathcal{L}$-fuzzy set s by an $\mathcal{L}$-fuzzy relation R is only a special example of a $\tilde{\mathbf{T}}$-relation.

Example 3.

Let $(r,\alpha ):(X,\{★\})⇝(Y,\{★\})$ be a $\tilde{\mathbf{T}}$-relation from $(X,\{★\})$ to $(Y,\{★\})$. It follows that $\alpha :\{★\}\to \{★\}$ is a trivial map and $(r,\alpha )$ can be identified with $r:X\to T(Y,\{★\})$ only. According to Proposition 3, ${(r,\alpha )}^{\uparrow }:\tilde{T}(X,\{★\})\to \tilde{T}(Y,\{★\})$ equals to $(r^{\uparrow },\alpha )$ and it can be identified with $r^{\uparrow }:T(X,\{★\})\to T(Y,\{★\})$. If $\Psi (r)=(F,R)$, then for an $\mathcal{L}$-fuzzy set $s\in L^X$, according to Proposition 3 we obtain

$$r^{\uparrow }(\{★\},\overline{s})=(\{★\},R^{\uparrow }(\overline{s})),R^{\uparrow }(\overline{s}):\{★\}\to L^Y,$$

where $\overline{s}:\{\ast \}\to L^X$, $\overline{s}(\ast )(x)=s(x)$ and

$$\begin{array}{c}{R}^{\uparrow }(\overline{s})(★)(y)=\underset{\{x|★\in F(x)\}}{\bigvee }\overline{s}(★)(x)\otimes R(★,x,y)=\\ \underset{x\in X}{\bigvee }s(x)\otimes S(x,y)=S^{\uparrow }(s)(y),\end{array}$$

where $S(x,y)=R(★,x,y)$. Therefore, ${(r,\alpha )}^{\uparrow }$ can be identified with the approximation operator $S^{\uparrow }$ defined by an $\mathcal{L}$-fuzzy relation S. □

Example 4.

In this example, we show how $\mathcal{L}$-fuzzy soft set $(E,s)$ can be transformed to an $\mathcal{L}$-fuzzy set using an extension principle. Recall that according to (7), for arbitrary morphism $(f,\alpha ):(X,K)\to (Y,M)$, we have ${(f,\alpha )}_{\tilde{T}}^{\to }=(f_T^{\to },\alpha )$, and it follows that $f_T^{\to }:T(X,K)\to T(Y,M)$ can be considered a transformation of fuzzy soft sets in $(X,K)$ to fuzzy soft sets in $(Y,M)$. Now, let $(1_X,\alpha ):(X,K)\to (X,\{\ast \})$, where $\alpha :K\to \{\ast \}$ is a trivial map. According to (8) and (9), for a fuzzy soft set $(E,s)\in T(X,K)$, we obtain

$$\begin{array}{c}{(1_X,\alpha )}_T^{\to }(E,s)=(\{\ast \},1_{X,T}^{\Rightarrow }(s))=(\{\ast \},\overline{s}),\overline{s}:\{\ast \}\to L^X,\\ x\in X,\overline{s}(\ast )(x)=\underset{k\in K}{\bigvee }s(k)(x).\end{array}$$

Therefore, an $\mathcal{L}$-fuzzy soft set $(E,s)\in T(X,K)$ is transformed to an $\mathcal{L}$-fuzzy set $\overline{s}(\ast ):X\to L$. □

3.2. Hesitant $\mathcal{L}$-Fuzzy Sets

In this part, we develop the power set monad of hesitant $\mathcal{L}$-fuzzy sets and we show that hesitant $\mathcal{L}$-fuzzy relations are defined by this monad. We also prove that both an analogy of Zadeh’s extension principle and approximation operators for hesitant $\mathcal{L}$-fuzzy sets are defined by this monad. Hence, the power set theory of hesitant $\mathcal{L}$-fuzzy set theory and its principal constructions represent special examples of methods from power set monads theory.

We use the definition of hesitant fuzzy sets from Reference [15] which we extend to the hesitant $\mathcal{L}$-fuzzy sets.

Definition 8.

Let X be a set. A hesitant $\mathcal{L}$-fuzzy set in X is a mapping $h:X\to 2^L$, i.e., for $x\in X$, $h(x)\subseteq L$.

If h is a hesitant $\mathcal{L}$-fuzzy set in a set X, then an element $x\in X$ corresponds to this hesitant fuzzy set with any membership degree $\alpha \in h(x)$. In the next theorem, we prove that hesitant $\mathcal{L}$-fuzzy sets also define power set monad.

Theorem 2.

Let $\mathcal{L}$ be a complete residuated lattice and let the structure $\mathbf{H}=(H,\diamond ,\sigma ,1_{\mathbf{Set}})$ be defined by

• The mapping $H:obj(\mathbf{Set})\to obj(\mathbf{Set})$ is defined by $H(X)=\{h|h:X\to 2^L\}$.
• The set $H(X)$ is ordered by the relation

  $$h,g\in H(X),h⪯g\iff (\forall x\in X)h(x)\subseteq g(x).$$
• If $f:X\to H(Y)$ and $g:Y\to H(Z)$ are $\mathbf{Set}$-morphisms, we set

  $$\begin{array}{c}g\diamond f:X\to H(Z),\\ x\in X,z\in Z,g\diamond f(x)(z)=\bigcup _{y\in Y}f(x)(y)\otimes g(y)(z)\subseteq L,\end{array}$$
  where for $A,B\subseteq L$, $A\otimes B=\{\alpha \otimes \beta |\alpha \in A,\beta \in B\}$ and $A\otimes \varnothing =\varnothing$.
• For $X\in \mathbf{Set}$, ${\sigma }_X:X\to H(X)$ is defined by

  $$x,z\in X,{\sigma }_X(x)(z)=\left\{\begin{array}{cc}\left\{1_L\right\},\hfill & x=z\hfill \\ \varnothing ,\hfill & x\ne z\hfill \end{array}\right..$$

Then, $\mathbf{H}$ is a power set monad in the category $\mathbf{Set}$.

Proof of Theorem 2.

It is straightforward to see that the Kleisli composition ⋄ is associative and that $(H(X),⪯)$ is a complete ⋁-semilattice. For arbitrary $\mathbf{Set}$-morphism $f:X\to Y$, we obtain

$${\sigma }_Y\diamond f(x)(z)=\bigcup _{y\in Y}f(x)(y)\otimes {\sigma }_Y(y)(z)=f(x)(z)\cup \bigcup _{y\in Y,y\ne z}\varnothing =f(x)(z).$$

Analogously, for $\mathbf{Set}$-morphisms $f:X\to Y$ and $g:Y\to H(Z)$, we obtain

$$\begin{array}{c}x\in X,z\in Z,g\diamond ({\sigma }_Y.f)(x)(z)=\bigcup _{y\in Y}{\sigma }_Y(f(x))(y)\otimes g(y)(z)=\\ \bigcup _{y\in Y,y\ne f(x)}\varnothing \cup g(f(x)(z))=g(f(x))(z).\end{array}$$

Finally, we show that for arbitrary $\mathbf{Set}$-morphism $f:X\to Y$, the $\mathbf{Set}$-morphism $f_H^{\to }:={\sigma }_Y.f\diamond 1_{H(X)}:H(X)\to H(Y)$ is also a ⋁-preserving mapping. For $h\in H(X)$, we have

$$\begin{array}{c}y\in Y,f_H^{\to }(h)(y)=\bigcup _{x\in X}{1}_{H(X)}(h)(x)\otimes {\sigma }_Y.f(x)(y)=\bigcup _{x\in X,f(x)=y}h(x),\end{array}$$

(10)

and it follows that $f_H^{\to }$ is ⋁-preserving. Therefore, $\mathbf{H}$ is a power set monad in the category $\mathbf{Set}$. □

Hesitant fuzzy relations between two sets are introduced in several papers ([21,22], for example) in a natural way as a hesitant fuzzy sets in a cartesian product of two sets. We extend this definition to hesitant $\mathcal{L}$-fuzzy relations.

Definition 9.

• A hesitant $\mathcal{L}$-fuzzy relation from a set X to Y is a hesitant $\mathcal{L}$-fuzzy set in a set $X\times Y$.
• If R and S are hesitant $\mathcal{L}$-fuzzy relations from X to Y and from Y to Z, respectively, then their composition $S\times R$ is a hesitant $\mathcal{L}$-fuzzy relation from X to Z, such that $(S\times R)(x,z)={\bigcup }_{y\in Y}R(x,y)\otimes S(y,z)$.

In the following lemma, we show that hesitant $\mathcal{L}$-fuzzy relations are, in fact, $\mathbf{H}$-relations.

Lemma 2.

• Let $X,Y$ be sets. There exists a bijection map Φ between the set of $\mathbf{H}$-relations from X to Y and the set of all hesitant $\mathcal{L}$-fuzzy relations from X to Y.
• If R and S are $\mathbf{H}$-relations from X to Y and from Y to Z, respectively, then

  $$\Phi (S\diamond R)=\Phi (S)\times \Phi (R).$$

Proof of Lemma 2.

For a $\mathbf{H}$-relation R we set $\Phi (R)=r$, where $r\in H(X\times Y)$ is defined by $r(x,y)=R(x)(y)\subseteq L$. The rest of the proof follows directly from the definition of the operation ⋄. □

From Lemma 2, it follows that the hesitant $\mathcal{L}$-fuzzy relations are defined using the same principles that are used for definition of monadic relations and this also justifies a specific way of defining these concrete types of relations.

Using Lemma 2 and Definition 4, for arbitrary hesitant $\mathcal{L}$-fuzzy relation R from X to Y, we can construct the approximation operator

$$R^{\uparrow }=R\diamond 1_{H(X)}:H(X)\to H(Y).$$

Proposition 4.

Let $R:X\to H(Y)$ be a $\mathbf{H}$-relation from a set X to a set Y and let $\Phi (R)=r\in H(X\times Y)$. The n, the R-approximation operator $R^{\uparrow }=R\diamond 1_{H(X)}:H(X)\to H(Y)$ is such that

$$h\in H(X),y\in Y,R^{\uparrow }(h)(y)=\{\alpha \otimes \beta |\alpha \in h(x),\beta \in r(x,y),x\in X\}.$$

The proof follows directly from the definition of Kleisli composition ⋄ for $\mathbf{H}$ and it will be omitted.

Let us consider the following illustrative example.

Example 5.

Assume that a finite set of variants X is available for some decision-making problem. An expert according to his opinion how variants $x\in X$ met the required criteria evaluated these variants x with the number $s(x)\in [0,1]$ . Hence, $s\in L^X$, where $\mathcal{L}$ is, for example, the Lukasiewicz algebra. At the same time, however, a questionnaire was conducted among another selected group of m evaluator of how, for each pair of variants $(x,y)$, in their opinion, variant x is more suitable than a variant y. The answers of these m evaluators then formed a set of values $\{w^h(x,y)|x,y\in X,h=1,\cdots m\}$, where the value $w^h(x,y)\in [0,1]$ describes how, in the opinion of an evaluator h, variant x is more suitable than a variant y. The answers of these m evaluators then form a hesitant $\mathcal{L}$-fuzzy relation $R\in H(X\times X)$, where $R(x,y)=\{w^h(x,y)|h=1,\cdots ,m\}$. According to Lemma 2, ${\Phi }^{-1}(R):X\to H(X)$ is a $\mathbf{H}$-relation and because s can be considered a hesitant $\mathcal{L}$-fuzzy set with one-element value set, the R-approximation $R^{\uparrow }(s)$ can be considered a modification of the expert’s evaluation s on the basis of a questionnaire survey among other experts, i.e., the final evaluation of variants X is a hesitant fuzzy set $R^{\uparrow }(s)$ such that a variant $x\in X$ is evaluated by the following possible membership degrees

$$R^{\uparrow }(s)(x)=\{s(y)\otimes w^h(x,y)|y\in X,h=1,\cdots ,m\}.$$

3.3. Intuitionistic $\mathcal{L}$-Fuzzy Sets

In this part, we develop the power set monad of intuitionistic $\mathcal{L}$-fuzzy sets and we show that intuitionistic $\mathcal{L}$-fuzzy relations are defined by this monad. We also prove that both an analogy of Zadeh’s extension principle and approximation operators defined for intuitionistic $\mathcal{L}$-fuzzy sets are defined by this monad. Hence, the power set theory of intuitionistic $\mathcal{L}$-fuzzy set theory and its principal constructions represent special examples of methods from power set monads theory.

For simplicity, in this section, $\mathcal{L}=(L,\oplus ,\otimes ,\neg ,0_L,1_L)$ will be a complete $MV$-algebra, although some parts of the theory can be proven even for complete residuated lattices. The basic category for intuitionistic $\mathcal{L}$-fuzzy sets is the standard category $\mathbf{Set}$ of sets and mappings.

Definition 10.

[1]An intuitionistic $\mathcal{L}$-fuzzy set in a set X is a pair $(u,v)$ of $\mathcal{L}$-fuzzy sets on X, such that $\neg u\ge v$. By $J(X)$, we denote the set of all intuitionistic $\mathcal{L}$-fuzzy sets in X.

It should be mentioned that in the original Atanassov’s definition [1], the relation $u\le \neg v$ is used. Because $\mathcal{L}$ is an $MV$-algebra, both variants are equivalent. In the next theorem, we identify the power set monad for intuitionistic $\mathcal{L}$-fuzzy sets.

Remark 2.

We use the following notation. If $f:X\to J(Y)$ is a mapping, then for $x\in X$, the value $f(x)\in J(X)$ is denoted by $f(x)=(f^x,f_x)$, where $f^x,f_x\in L^Y$, $\neg f^x\ge f_x$.

Theorem 3.

Let the structure $\mathbf{J}=(J,⊠,\eta ,1_{\mathbf{Set}})$ be defined in the category $\mathbf{Set}$ by

• $J:obj(\mathbf{Set})\to obj(\mathbf{Set})$ is a mapping defined by

  $$J(X)=\{(u,v)|u,v\in L^X,\neg u\ge v\}.$$
• The set $J(X)$ is ordered by the relation ⊑ such that

  $$(u,v),(s,t)\in J(X),(u,v)⊑(s,t)\iff u\le s,v\ge t,$$
  where ≤ is a point-wise order relation on $L^X$.
• If $f:X\to J(Y)$ and $g:Y\to J(Z)$ are $\mathbf{Set}$-morphisms, $g⊠f:X\to J(Z)$ is defined by

  $$\begin{array}{c}x\in X,g⊠f(x)=({(g⊠f)}^x,{(g⊠f)}_x)\in J(Z),\end{array}$$

  (11)
  where for $z\in Z$,

  $$\begin{array}{c}{(g⊠f)}^x(z)=\underset{y\in Y}{\bigvee }{f}^x(y)\otimes g^y(z),{(g⊠f)}_x(z)=\underset{y\in Y}{\bigwedge }{f}_x(y)\oplus g_y(z).\end{array}$$

  (12)
• For $X\in \mathbf{Set}$, ${\eta }_X:X\to J(X)$ is defined by

  $$x\in X,{\eta }_X(x)=({\chi }_{\left\{x\right\}}^X,\neg {\chi }_{\left\{x\right\}}^X).$$

Then $\mathbf{J}$ is a power set monad in the category $\mathbf{Set}$.

Proof of Theorem 3.

It is easy to see that $(J(X),⊑)$ is a complete ⋁-lattice. In fact, for $\{(s_i,t_i):i\in I\}\subseteq J(X)$ we have ${\bigvee }_{i\in I}(s_i,t_i)=({\bigvee }_{i\in I}{s}_i,{\bigwedge }_{i\in I}{t}_i)\in J(X)$, as follows from the identity $\neg {\bigvee }_i{s}_i={\bigwedge }_i\neg s_i\ge {\bigwedge }_i{t}_i$.

The Kleisli composition is defined correctly. In fact, we have

$$\begin{array}{c}\neg {(g⊠f)}^x(z)=\underset{y\in Y}{\bigwedge }\neg (f^x(y)\otimes g^y(z))=\underset{y\in Y}{\bigwedge }\neg f^x(y)\oplus \neg g^y(z)\ge \\ \underset{y\in Y}{\bigwedge }{f}_x(y)\oplus g_y(z)={(g⊠f)}_x(z).\end{array}$$

Moreover, it is straightforward to prove that the Kleisli composition is associative and this proof will be omitted.

We show that for arbitrary $Y\in \mathbf{Set}$ and $f:X\to J(Y)$, ${\eta }_Y⊠f=f$ holds. In fact, for $x\in X$, we have ${\eta }_Y⊠f(x)=({({\eta }_Y⊠f)}^x,{({\eta }_Y⊠f)}_x)$, where ${({\eta }_Y⊠f)}^x(y)={\bigvee }_{z\in Y}{f}^x(z)\otimes {\chi }_{\left\{z\right\}}^Y(y)=f^x(y)$ and ${({\eta }_Y⊠f)}_x(y)={\bigwedge }_{z\in Y}{f}_x(z)\oplus \neg {\chi }_{\left\{z\right\}}^Y(y)=f_x(y)$.

Now, let $f:X\to Y$ and $g:Y\to J(Z)$ be mappings. For $x\in X,z\in Z$, we have

$$\begin{array}{c}{(g⊠{\eta }_Y.f)}^x(z)=\underset{y\in Y}{\bigvee }{({\eta }_Y.f)}^x(y)\otimes g^y(z)=\underset{y\in Y}{\bigvee }{\chi }_{\{f(x)\}}^Y(y)\otimes g^y(z)=g^{f(x)}(y),\\ {(g⊠{\eta }_Y.f)}_x(z)=\underset{y\in Y}{\bigwedge }{({\eta }_Y.f)}_x(y)\oplus g_y(z)=\underset{y\in Y}{\bigwedge }\neg {\chi }_{\{f(x)\}}^Y\oplus g_y(z)=g_{f(x)}(z).\end{array}$$

Therefore, $g⊠({\eta }_Y.f)=g.f$. Finally, we show that for arbitrary mapping $f:X\to Y$, the extension mapping $f_J^{\to }={\eta }_Y.f⊠1_{J(X)}:J(X)\to J(Y)$ is a ⋁-preserving mapping. In fact, for arbitrary $(s,t)\in J(X)$ and $y\in Y$,

$$\begin{array}{c}{f}_J^{\to }(s,t)(y)=(\underset{x\in X,f(x)=y}{\bigvee }s(x),\underset{x\in X,f(x)=y}{\bigwedge }t(x))\end{array}$$

(13)

holds, as follows directly from the definitions of ⊠ and ${\eta }_Y$. From (13) and the definition of suprema in $J(X)$, it is straightforward to see that $f_J^{\to }$ preserves ⋁-operation. □

Intuitionistic fuzzy relations were defined in several papers (see, e.g., [23,42]). We extend this definition to intuitionistic $\mathcal{L}$-fuzzy relation:

Definition 12.

• An intuitionistic $\mathcal{L}$-fuzzy relation from a set X to Y is an intuitionistic $\mathcal{L}$-fuzzy set in a set $X\times Y$.
• Let $(u,v)$ and $(p,q)$, respectively, be intuitionistic $\mathcal{L}$-fuzzy relations from X to Y and Y to Z, respectively. The ir composition $(p,q)\times (u,v)$ is an intuitionistic $\mathcal{L}$-fuzzy relation from X to Z such that for arbitrary $(x,z)\in X\times Z$,

  $$\begin{array}{c}(p,q)\times (u,v)=(p⊛u,q⊚v),\\ (p⊛u)(x,z)=\underset{y\in Y}{\bigvee }u(x,y)\otimes p(y,z),(q⊚v)(x,z)=\underset{y\in Y}{\bigwedge }v(x,y)\oplus q(y,z).\end{array}$$

This definition is correct, because $\neg (p⊛u)\ge (q⊚v)$. In the next lemma, we show that intuitionistic $\mathcal{L}$-valued fuzzy relations are also defined by the same principle as fuzzy relation, hesitat fuzzy relation or fuzzy soft relations, i.e., as monadic relations.

Lemma 3.

• Let $X,Y$ be sets. There exists a bijection map Γ between the set of all $\mathbf{J}$-relations from a set X to Y and the set of all intuitionistic $\mathcal{L}$-fuzzy relations from X to Y.
• Let R and S, respectively, be $\mathbf{J}$-relations from X to Y and from Y to Z, respectively. The n

  $$\Gamma (S⊠R)=\Gamma (S)\times \Gamma (R).$$

Proof of Lemma 3.

(1) Let $R:X\to J(Y)$ be an $\mathbf{J}$-relation. Using the notation from Remark 2, for $x\in X$ we have $R(x)=(R^x,R_x)$, where $R^x,R_x\in L^Y$ and $\neg R^x\ge R_x$. We set

$$\Gamma (R)=(\overline{R},\underline{R})\in J(X\times Y),$$

where $\overline{R}(x,y)=R^x(y)$ and $\underline{R}(x,y)=R_x(y)$. It is straightforward to verify that $\Gamma$ is a bijection map and it will be omitted.

(2) The proof follows directly from definitions of operations ⊠ and ×. □

As in the case of hesitant fuzzy sets and soft fuzzy sets, we can use Lemma 3 to construct an approximation operator defined by a $\mathbf{J}$-relation.

Proposition 5.

Let $R:X\to J(Y)$ be an $\mathbf{J}$-relation from X to Y and let $\Gamma (R)=(\overline{R},\underline{R})$. Then, the R-approximation $R^{\uparrow }=R⊠1_{J(X)}:J(X)\to J(Y)$ is such that

$$(s,t)\in J(X),y\in Y,R^{\uparrow }(s,t)(y)=({\overline{R}}^{\Uparrow }(s)(y),{\underline{R}}^{\Downarrow }(t)(y))$$

where ${\overline{R}}^{\Uparrow }$ is defined in Example 2 and ${\underline{R}}^{\Downarrow }(t)(y)={\bigwedge }_{x\in X}t(x)\oplus \underline{R}(x,y)$.

Proof of Proposition 5.

Using the notation from Remark 1, we have

$$\begin{array}{c}{R}^{\uparrow }(s,t)(y)=R⊠1_{J(X)}(s,t)(y)=({(R⊠1_{J(X)})}^{(s,t)}(y),{(R⊠1_{J(X)})}_{(s,t)}(y)),\\ {(R⊠1_{J(X)})}^{(s,t)}(y)=\underset{x\in X}{\bigvee }{1}_{J(X)}^{(s,t)}(x)\otimes R^x(y)=\underset{x\in X}{\bigvee }s(x)\otimes \overline{R}(x,y)={\overline{R}}^{\Uparrow }(s)(y),\\ {(R⊠1_{J(X)})}_{(s,t)}(y)=\underset{x\in X}{\bigwedge }{1}_{J(X),(s,t)}(x)\oplus R_x(y)=\underset{x\in X}{\bigwedge }t(x)\oplus \underline{R}(x,y)={\underline{R}}^{\Downarrow }(t)(y).\end{array}$$

□

In the following illustrative example, we show that an R-approximation $R^{\uparrow }$ defined by an $\mathbf{J}$-relation extends a standard upper approximation $r^{\Uparrow }$ of $\mathcal{L}$-fuzzy sets defined by an $\mathcal{L}$-fuzzy relation r.

Example 6.

Let s be an $\mathcal{L}$-fuzzy sets in a set X. The n s can be identified with the intuitionistic $\mathcal{L}$-fuzzy set $(s,\neg s)$ and an arbitrary $\mathcal{L}$-fuzzy relation r from X to Y can also be identified with the intuitionistic $\mathcal{L}$-fuzzy set $(r,\neg r)$ in $X\times Y$. According to Lemma 3, r then represents an $\mathbf{J}$-relation $R:X\to J(Y)$. We have

$$\begin{array}{c}{R}^{\uparrow }(s,\neg s)(y)=(r^{\Uparrow }(s)(y),{(\neg s)}^{\Downarrow }(\neg s)(y))=(r^{\Uparrow }(s)(y),\neg r^{\Uparrow }(s)(y)),\end{array}$$

which can be identified with $r^{\Uparrow }(s)(y)$.

3.4. Relationships among $\mathcal{L}$-Fuzzy Theories

Power set structures, relations and approximations by relations represent one of principal tools in fuzzy set theory. In previous sections, we saw that all these tools in various modifications of $\mathcal{L}$-fuzzy sets, such as $\mathcal{L}$-fuzzy soft set, hesitant $\mathcal{L}$-fuzzy sets or intuitionistic $\mathcal{L}$-fuzzy sets, are only special examples of general tools in power set monads in categories. Similarly, we have shown that fuzzy relations, fuzzy soft relations, hesitant fuzzy relations or intuitionistic fuzzy relations and their approximation operators are only special examples of monadic relations in these categories. It follows that we can use this common theoretical basis of all these constructions to determine more easily and clearly the relationships between these modifications of fuzzy sets and, moreover, to extend these relationships into relationships between approximation operators of these structures, defined by corresponding types of relations.

In order to effectively investigate relationships between these structures for individual modifications of fuzzy sets, we must introduce the concept of a morphism between two power set monads. In what follows, natural transformations between functors, we denote by small bold letter, i.e., for functors F and G from a category $\mathbf{K}$ to the category $\mathbf{L}$, $\mathbf{a}=\{{\mathbf{a}}_X:X\in obj(\mathbf{K})\}:F⤏G$ is a natural transformation if for arbitrary $\mathbf{K}$-morphism $f:X\to Y$, the following diagram commutes:

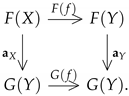
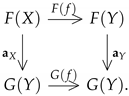
Definition 11.

Let $\mathbf{T}=(T,◊,\eta ,V)$ and $\mathbf{R}=(R,\square ,\mu ,W)$ be power set monads in categories $\mathbf{K}$ and $\mathbf{L}$, respectively.

• A pair $(U,\mathbf{a}):(\mathbf{K},\mathbf{T})\to (\mathbf{L},\mathbf{R})$ is a morphism of power set monads if

  (a)

  $U:\mathbf{K}\to \mathbf{L}$ is a functor, such that $W\circ U=V$,

  (b)

  $\mathbf{a}:U\circ T⤏R\circ U$ is a natural transformation between compositions of functors,

  (c)

  For each morphisms $f:A\to T(B),g:B\to T(C)$ in $\mathbf{K}$, the following relations hold:

  $$\begin{array}{c}{\mathbf{a}}_C.U(g◊f)\le ({\mathbf{a}}_C.U(g))\square ({\mathbf{a}}_B.U(f)),\end{array}$$

  (14)

  $$\begin{array}{c}X\in obj(\mathbf{K}),{\mathbf{a}}_X.U({\eta }_X)={\mu }_{U(X)}.\end{array}$$

  (15)

Using this definition, in the following theorem, we describe possible relationships between power set monads of fuzzy sets, fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets. We use the notation from definitions and theorems from previous sections

Theorem 4.

• Let $\mathcal{L}$ be a complete residuated lattice. There exist the following morphisms between power set monads:
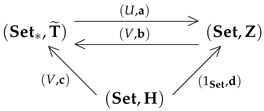
• If $\mathcal{L}$ is a complete $MV$-algebra; in addition, there exist the following morphisms between power set monads:

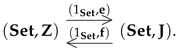
Proof of Theorem 4.

(1) The morphism $(U,\mathbf{a}):({\mathbf{Set}}_{*},\tilde{\mathbf{T}})\to (\mathbf{Set},\mathbf{Z})$ is defined by

• The functor $U:{\mathbf{Set}}_{*}\to \mathbf{Set}$ is such that $U(X,K)=X$, $U(f,\alpha )=f$,
• For $(X,K)\in {\mathbf{Set}}_{*}$, ${\mathbf{a}}_{(X,K)}:U\circ \tilde{T}(X,K)\to Z\circ U(X,K)$ is defined by

  $$(E,s)\in T(X,K),x\in X,{\mathbf{a}}_{(X,K)}(E,s)=\overline{s},\overline{s}(x)=\underset{k\in E}{\bigvee }s(k)(x).$$

Then, $\mathbf{a}:U\circ \tilde{T}⤏Z\circ U$ is a natural transformation as, for arbitrary morphism $(f,\alpha ):(X,K)\to (Y,M)$ in ${\mathbf{Set}}_{*}$ and element $(E,s)\in T(X,K)=U\circ \tilde{T}(X,K)$, it follows from the identity:

$$\begin{array}{c}{f}_Z^{\to }.{\mathbf{a}}_{(X,K)}(E,s)={\mathbf{a}}_{(Y,M)}.U({(f,\alpha )}_{\tilde{T}}^{\to })(E,s),\end{array}$$

which follows directly from Definitions (1),(7)–(9). Let $(f,\alpha ):(A,K)\to \tilde{T}(B,M)$ and $(g,\beta ):(B,M)\to \tilde{T}(C,N)$ be morphisms in ${\mathbf{Set}}_{*}$. We need to prove

$${\mathbf{a}}_{(C,N)}.U((g,\beta )\square (f,\alpha ))\le ({\mathbf{a}}_{(C,N)}.U(g,\beta ))⊞({\mathbf{a}}_{(B,M)}.U(f,\alpha )).$$

Using the notation (2) and Definitions (3)–(6), for $a\in A,c\in C$, we obtain

$$\begin{array}{c}{\mathbf{a}}_{(C,N)}.U((g,\beta )\square (f,\alpha ))(a)(c)={\mathbf{a}}_{(C,N)}((g\Delta f)(a))(c)=\underset{n\in N_a^{g\Delta f}}{\bigvee }{(g\Delta f)}_a(n)(c)=\\ \underset{\{(b,n,m)|b\in B,m\in M_a^f,n=\beta (m)\in N_b^g\}}{\bigvee }{f}_a(m)(b)\otimes g_b(n)(c)\le \\ \underset{\{(b,n,m)|b\in B,n\in N_b^g,m\in M_a^f\}}{\bigvee }{f}_a(m)(b)\otimes g_b(n)(c)=\\ \underset{b\in B}{\bigvee }{\mathbf{a}}_{(B.M)}.f(a)(b)\otimes {\mathbf{a}}_{(C,N)}.g(b)(c)=({\mathbf{a}}_{(B,M)}.g⊞{\mathbf{a}}_{(C,N)}.f)(a)(c)=\\ ({\mathbf{a}}_{(B,M)}.U(g,\beta )⊞{\mathbf{a}}_{(C,N)}.U(f,\alpha ))(a)(c).\end{array}$$

Therefore, the inequality (14) holds. The equality (15) follows directly from definitions of ${\xi }_{(X,K)}$ and ${\chi }^X$.

(2) The morphism $(V,\mathbf{b}):(\mathbf{Set},\mathbf{Z})\to ({\mathbf{Set}}_{*},\tilde{\mathbf{T}})$ is defined by

• The functor $V:\mathbf{Set}\to {\mathbf{Set}}_{*}$ is such that $V(X)=(X,\{\ast \})$ and $V(f)=(f,1_{\{\ast \}})$.
• For $X\in \mathbf{Set}$, ${\mathbf{b}}_X:V\circ Z(X)\to \tilde{T}\circ V(X)$ is defined by

  $$\begin{array}{c}{\mathbf{b}}_X=(b^X,1_{\{\ast \}}):(Z(X),\{\ast \})\to (T(X,\{\ast \}),\{\ast \}),\\ b^X:Z(X)\to T(X,\{\ast \}),\\ s\in Z(X),b^X(s)=(\{\ast \},\overline{s}),\\ \overline{s}:\{\ast \}\to L,\overline{s}(\ast )(x)=s(x).\end{array}$$

Then, $\mathbf{b}$ is a natural transformation, because for arbitrary morphism $f:X\to Y$ in $\mathbf{Set}$, using the identities (7)–(9), the following identity holds:

$$(f_T^{\Rightarrow }.b^X,1_{\{\ast \}})={(f,1_{\{\ast \}})}_{\tilde{T}}^{\to }.{\mathbf{b}}_X={\mathbf{b}}_Y.(f_Z^{\to },1_{\{\ast \}})=(b^Y.f_Z^{\to },1_{\{\ast \}}).$$

In fact, we have to prove $f_T^{\Rightarrow }.b^X=b^Y.f_Z^{\to }$, but it follows directly from identities (1), (7)–(9).

Let $f:A\to Z(B)$ and $g:B\to Z(C)$ be morphism in $\mathbf{Set}$. According to (14), we need to prove

$${\mathbf{b}}_C.V(g⊞f)\le {\mathbf{b}}_C.V(g)\square {\mathbf{b}}_B.V(f).$$

We have

$$\begin{array}{c}{\mathbf{b}}_C.V(g⊞f)=(b^C.(g⊞f),1_{\{\ast \}}):(A,\{\ast \})\to (T(C,\{\ast \}),\{\ast \}),\\ {\mathbf{b}}_C.V(g)\square {\mathbf{b}}_B.V(f)=(b^C.g,1_{\{\ast \}})\square (b^B.f,1_{\{\ast \}})=(b^C.g\Delta b^B.f,1_{\{\ast \}}).\end{array}$$

Using identities (1), (4) and (5), by a simple calculation, we can prove that $b^C.(g⊞f)\le b^C.g\Delta b^B.f$ and the inequality (14) holds. The equality (15) follows directly from definitions of $\xi$ and $\chi$.

(3) The morphism $(V,\mathbf{c}):(\mathbf{Set},\mathbf{H})\to ({\mathbf{Set}}_{*},\tilde{\mathbf{T}})$ is defined by

• V is the functor from the previous case (2),
• For $X\in \mathbf{Set}$, ${\mathbf{c}}_X:V\circ H(X)\to \tilde{T}\circ V(X)$ is defined by

  $$\begin{array}{c}{\mathbf{c}}_X=(c^X,1_{\{\ast \}}):(H(X),\{\ast \})\to (T(X,\{\ast \},),\{\ast \})\end{array}$$

  (16)

  $$\begin{array}{c}{c}^X:H(X)\to T(X,\{\ast \}),c^X(h)=(\{\ast \},\overline{h}),\end{array}$$

  (17)

  $$\begin{array}{c}\overline{h}:\{\ast \}\to L^X,\overline{h}(\ast )(x)=\underset{\alpha \in h(x)}{\bigvee }\alpha .\end{array}$$

  (18)

Then, $\mathbf{c}$ is a natural transformation. In fact, for a morphism $f:X\to Y$ in $\mathbf{Set}$, using the identity (7), we obtain:

$$\begin{array}{c}V{(f)}_{\tilde{T}}^{\to }.{\mathbf{c}}_X={(f,1_{\{\ast \}})}_{\tilde{T}}^{\to }.{\mathbf{c}}_X=({(f,1_{\{\ast \}})}_T^{\to },1_{\{\ast \}}).{\mathbf{c}}_X=({(f,1_{\{\ast \}})}_T^{\to }.c^X,1_{\{\ast \}}),\\ {\mathbf{c}}_Y.V(f_H^{\to })=(c^Y,1_{\{\ast \}}).(f_H^{\to },1_{\{\ast \}})=(c^Y.f_H^{\to },1_{\{\ast \}}).\end{array}$$

Using the identities (8)–(10), it is possible to show by a simple calculation that $V{(f)}_{\tilde{T}}^{\to }.{\mathbf{c}}_X={\mathbf{c}}_Y.V(f_H^{\to })$ and $\mathbf{c}$ are a natural transformation. We omit this simple proof.

Let $f:A\to H(B)$ and $g:B\to H(C)$ be morphism in $\mathbf{Set}$. According to (14), we need to prove

$${\mathbf{c}}_C.V(g\diamond f)\le {\mathbf{c}}_C.V(g)\square {\mathbf{c}}_B.V(f).$$

Using (16) and (3), we have

$$\begin{array}{c}{\mathbf{c}}_C.V(g\diamond f)=(c^C,1_{\{\ast \}}).(g\diamond f,1_{\{\ast \}})=(c^C.(g\diamond f),1_{\{\ast \}}),\\ {\mathbf{c}}_C.V(g)\square {\mathbf{c}}_B.V(f)=(c^C.g\Delta c^B.f,1_{\{\ast \}}).\end{array}$$

Using (4), (17) and (18), we obtain

$$\begin{array}{c}{c}^C.(g\diamond f)(a)=(\{\ast \},\overline{(g\diamond f)(a)}),\\ (c^C.g\Delta c^B.f)(a)=(\{\ast \},{(c^C.g\Delta c^B.f)}_a).\end{array}$$

Finally, using (6), (18) and definition of ⋄ from Theorem 2, we obtain that the above two expressions are identical. Therefore, the inequality (14) holds. The identity (15) can be simply proven directly from definitions of $\xi$ and $\sigma$ in Theorems 1 and 2.

(4) The morphism $(1_S,\mathbf{d}):(\mathbf{Set},\mathbf{H})\to (\mathbf{Set},\mathbf{Z})$ is defined such that for $X\in \mathbf{Set}$, ${\mathbf{d}}_X:H(X)\to Z(X)$ is defined by

$$h\in H(X),x\in X,{\mathbf{d}}_X(h)(x)=\underset{\alpha \in h(x)}{\bigvee }\alpha .$$

To prove that $\mathbf{d}$ is a natural transformation, we need to show that for arbitrary morphism $f:X\to Y$ in $\mathbf{Set}$, ${\mathbf{d}}_Y.f_H^{\to }=f_Z^{\to }.{\mathbf{d}}_X$ holds. Let $h\in H(X)$, $y\in Y$. According to (10), we obtain

$$\begin{array}{c}{\mathbf{d}}_Y.f_H^{\to }(h)(y)=\underset{\alpha \in f_H^{\to }(h)(y)}{\bigvee }\alpha =\underset{x\in X,f(x)=y,\alpha \in h(x)}{\bigvee }\alpha =f_Z^{\to }.{\mathbf{d}}_X(h)(y).\end{array}$$

Let $f:A\to H(B)$ and $g:B\to H(C)$ be morphisms in $\mathbf{Set}$. The inequality (14) is transformed to

$${\mathbf{d}}_C.(g\diamond f)\le {\mathbf{d}}_C.g⊞{\mathbf{d}}_B.f,$$

which follows directly from definitions of ⋄ and ⊞ and a simple proof will be omitted. The identity (15) follows directly from definition of $\sigma$ and $\chi$.

(5) Let $\mathcal{L}$ be a complete $MV$-algebra. The morphism $(1_{\mathbf{Set}},\mathbf{e}):(\mathbf{Set},\mathbf{Z})\to (\mathbf{Set},\mathbf{J})$ is such that for $X\in \mathbf{Set}$, ${\mathbf{e}}_X:Z(X)\to J(X)$ is defined by

$$s\in Z(X),{\mathbf{e}}_X(s)=(s,\neg s).$$

To prove that $\mathbf{e}$ is a natural transformation, we need to show that for arbitrary morphism $f:X\to Y$ in $\mathbf{Set}$, ${\mathbf{e}}_Y.f_Z^{\to }=f_J^{\to }.{\mathbf{e}}_X$ holds. For $s\in Z(X)$, $y\in Y$, using (11), we obtain

$$\begin{array}{c}{\mathbf{e}}_Y.f_Z^{\to }(s)(y)=(f_Z^{\to }(s)(y),\neg f_Z^{\to }(s)(y))=(\underset{x,f(x)=y}{\bigvee }s(x),\neg \underset{x,f(x)=y}{\bigvee }s(x))=\\ (\underset{x,f(x)=y}{\bigvee }s(x),\underset{x,f(x)=y}{\bigwedge }\neg s(x))=f_J^{\to }(s,\neg s)(y)=f_J^{\to }.{\mathbf{e}}_X(s)(y).\end{array}$$

Let $f:A\to Z(B)$ and $g:B\to Z(C)$ are morphisms ni $\mathbf{Set}$. To prove (14), we need to prove

$${\mathbf{e}}_C.(g⊞f)\le {\mathbf{e}}_C.g⊠{\mathbf{e}}_B.f.$$

For $a\in A,c\in C$, according to (11) and (12), we have

$$\begin{array}{c}{\mathbf{e}}_C.(g⊞f)(a)=((g⊞f)(a),\neg (g⊞f)(a)),\\ ({\mathbf{e}}_c.g⊠{\mathbf{e}}_B.f)(a)=({({\mathbf{e}}_C.g⊠{\mathbf{e}}_B.f)}^a,{({\mathbf{e}}_C.g⊠{\mathbf{e}}_B.f)}_a),\\ {({\mathbf{e}}_C.g⊠{\mathbf{e}}_B.f)}^a(c)=\underset{b\in B}{\bigvee }{({\mathbf{e}}_B.f)}^a(b)\otimes {({\mathbf{c}}_C.g)}^b(c)=\underset{b\in B}{\bigvee }f(a)(b)\otimes g(b)(c)=\\ (g⊞f)(a)(c),\\ {({\mathbf{e}}_C.g⊠{\mathbf{e}}_B.f)}_a(c)=\underset{b\in B}{\bigwedge }\neg f(a)(b)\oplus \neg g(b)(c)=\neg (g⊞f)(a)(c).\end{array}$$

Therefore, the inequality (14) holds and the equality (15) follows directly from definitions of $\chi$ (Example 1) and $\eta$ from Theorem 3.

(6) Let $\mathcal{L}$ be a complete $MV$-algebra. The morphism $(1_{\mathbf{Set}},\mathbf{f}):(\mathbf{Set},\mathbf{J})\to (\mathbf{Set},\mathbf{Z})$ is such that for $X\in \mathbf{Set}$, ${\mathbf{f}}_X:J(X)\to Z(X)$ is defined by

$$(s,t)\in J(X),{\mathbf{f}}_X(s,t)=s.$$

To prove that $\mathbf{f}$ is a natural transformation, we need to prove that for arbitrary morphism $g:X\to Y$, $g_Z^{\to }.{\mathbf{f}}_X={\mathbf{f}}_Y.g_J^{\to }$ holds. This follows directly from (1) and (13).

Let $g:A\to J(B)$ and $h:B\to J(C)$ be morphisms in $\mathbf{Set}$. To prove (14), we need to prove

$${\mathbf{f}}_C.(h⊠g)\le {\mathbf{f}}_C.h⊞{\mathbf{f}}_B.g.$$

Using Definitions (11) and (12), for $a\in A,c\in C$, we obtain

$$\begin{array}{c}{\mathbf{f}}_C.(h⊠g)(a)(c)={(h⊠g)}^a(c)=\underset{b\in B}{\bigvee }{g}^a(b)\otimes h^b(c)=\\ \underset{b\in B}{\bigvee }{\mathbf{f}}_B.g(a)(b)\otimes {\mathbf{f}}_C.h(b)(c)=({\mathbf{f}}_C.h⊞{\mathbf{f}}_B.g)(a)(c).\end{array}$$

The identity (15) follows directly from definitions of $\eta$ and $\chi$. □

Using morphisms between power set monads, we can transform some constructions in one theory to constructions in another. Let us consider the following simple proposition describing examples of these transformations.

Proposition 6.

Let $(U,\mathbf{a}):(\mathbf{K},\mathbf{T})\to (\mathbf{L},\mathbf{R})$ be a morphism of power set monads and let $S:X⇝Y$ be a $\mathbf{T}$-relation from X to Y.

• $Q={\mathbf{a}}_Y.U(S):U(X)⇝U(Y)$ is a $\mathbf{R}$-relation from $U(X)$ to $U(Y)$, which is called a transformation of S by $(U,\mathbf{a})$.
• If $S^{\uparrow }:T(X)\to T(Y)$ is an $\mathbf{T}$-approximation defined by a $\mathbf{T}$-relation S, then

  $$Q^{\uparrow }={\mathbf{a}}_Y.U(S)◊1_{RU(X)}:RU(X)\to RU(Y)$$
  is a $\mathbf{R}$-approximation defined by a $\mathbf{R}$-relation Q.

Let us consider the following example.

Example 7.

Let $(1_{\mathbf{Set}},\mathbf{d}):(\mathbf{Set},\mathbf{H})\to (\mathbf{Set},\mathbf{Z})$ be a morphism of power set monads from Theorem 4. Let $X,Y$ be sets and let S be a hesitant $\mathcal{L}$-fuzzy relation from X to Y, i.e., according to Definition 9, $S(x,y)\subseteq L$ for arbitrary $x\in X,y\in Y$. According to Lemma 2, S can be identified with the $\mathbf{H}$-relation $\overline{S}:X\to H(Y)$, such that $\overline{S}(x)(y)=S(x,y)\subseteq L$. Then, the transformation of S by $(1_{\mathbf{Set}},\mathbf{a})$ is a fuzzy relation $Q:X\times Y\to L$, such that

$$Q(x,y)={\underline{d}}_Y.S(x)(y)=\underset{\alpha \in S(x)(y)}{\bigvee }\alpha .$$

Example 8.

Let us consider the same morphism $(1_{\mathbf{Set}},\mathbf{d})$ of power set monads and the same hesitant fuzzy relation S from X to Y from Example 7. According to Theorem 2, the $\mathbf{H}$-approximation $S^{\uparrow }:H(X)\to H(Y)$ is defined by

$$h\in H(X),y\in Y,S^{\uparrow }(h)(y)=S\diamond 1_{H(X)}(h)(y)=\underset{\alpha \in h(x),\beta \in S(x)(y)}{\bigvee }\alpha \otimes \beta .$$

Let Q be a transformation of S by $(1_{\mathbf{Set}},\mathbf{d})$. Then, the $\mathbf{Z}$-approximation $Q^{\uparrow }:Z(X)\to Z(Y)$ defined by the $\mathbf{Z}$-relation Q is

$$s\in Z(X),y\in Y,Q^{\uparrow }(s)(y)=({\mathbf{d}}_Y.S⊞1_{Z(X)})(s)(y)=\underset{x\in X,\alpha \in S(x)(y)}{\bigvee }s(x)\otimes \alpha .$$

Therefore, the $\mathbf{Z}$-approximation $Q^{\uparrow }$ can be considered a transformation of a $\mathbf{H}$-approximation $S^{\uparrow }$ by a morphism $(1_{\mathbf{Set}},\mathbf{d})$.

4. Discussion

The main goal of this paper was to show that some of the key theoretical tools of fuzzy sets, fuzzy soft sets, hesitant fuzzy sets and intuitionistic fuzzy sets have a common theoretical background, based on the theory of monads in categories. For this purpose, we analyzed power set structures of objects of individual theories, fuzzy type relations in these theories and approximation operators defined by these fuzzy type relations and we proved that all these tools in all above mentioned theories are just special examples of general constructions in monads defined for corresponding theories. These results make it possible in many cases not only to perceive these theories as examples of one common theory, but also to verify some specific tools and definitions in individual theories that have been introduced ad hoc so far. A typical example of such an ad hoc procedure is the definition of fuzzy type relations in individual theories, which has so far been introduced without mutual relationships between individual theories. An additional justification for the consistency of these particular definitions can now be given by the fact that all these definitions are in fact an example of a relation defined by the monad in the relevant theory, i.e., all these definitions have a common basis. For further research in this area, it will be interesting to try to unify basic tools not only from these basic theories, but also tools from derived theories, such as e.g., hesitant intuitionistic fuzzy sets, hesitant intuitionistic fuzzy soft sets, fuzzy rough sets or ituitionistic fuzzy rough sets, etc. We also consider a possibility to apply this method to another tools in fuzzy type theories, such as approximation of fuzzy structures etc. The above procedures can be used for all fuzzy type structures, whose power sets can be extended to monads in an appropriate category. Of course, it can be assumed that some artificially created fuzzy type structures may not meet this assumption.