The Size, Multipartite Ramsey Numbers for nK₂ Versus Path–Path and Cycle

Abstract

For given graphs $G_1,G_2,\dots ,G_n$ and any integer j, the size of the multipartite Ramsey number $m_j(G_1,G_2,\dots ,G_n)$ is the smallest positive integer t such that any n-coloring of the edges of $K_{j\times t}$ contains a monochromatic copy of $G_i$ in color i for some i, $1\le i\le n$, where $K_{j\times t}$ denotes the complete multipartite graph having j classes with t vertices per each class. In this paper, we computed the size of the multipartite Ramsey numbers $m_j(K_{1,2},P_4,n{K}_2)$ for any $j,n\ge 2$ and $m_j(n{K}_2,C_7)$, for any $j\le 4$ and $n\ge 2$.

1. Introduction

In this paper, we were only concerned with undirected, simple and finite graphs. We followed [1] for terminology and notations not defined here. For a given graph G, we denoted its vertex set, edge set, maximum degree and minimum degree by $V\left(G\right)$, $E\left(G\right)$, $\mathsf{\Delta }\left(G\right)$ and $\delta \left(G\right)$, respectively. For a vertex $v\in V\left(G\right)$, we used ${deg}_G\left(v\right)$ and $N_G\left(v\right)$ to denote the degree and neighbours of v in G, respectively. The neighbourhood of a vertex $v\in V\left(G\right)$ are denoted by $N_G\left(v\right)=\{u\in V\left(G\right)|uv\in E\left(G\right)\}$ and $N_{X_j}\left(v\right)=\{u\in V\left(X_j\right)|uv\in E\left(G\right)\}$.

As usual, a cycle and a path on n vertices are denoted by $C_n$ and $P_n$, respectively. A complete graph on n vertices, denoted $K_n$, is a graph in which every vertex is adjacent, or connected by an edge, to every other vertex in G. By a stripe $m{K}_2,$ we mean a graph on $2m$ vertices and m independent edges. A clique is a subset of vertices such that there exists an edge between any pair of vertices in that subset of vertices. An independent set of a graph is a subset of vertices such that there exists no edges between any pair of vertices in that subset. Let C be a set of colors $\{c_1,c_2,...,c_m\}$ and $E\left(G\right)$ be the edges of a graph $G.$ An edge coloring $f:E\to C$ assigns each edge in $E\left(G\right)$ to a color in C. If an edge coloring uses k color on a graph, then it is known as a k-colored graph. The complete multipartite graph with the partite set $(X_1,X_2,\dots X_j)$, $|X_i|=s$ for $i=1,2,\dots j$, denoted by $K_{j\times s}$. We use $[X_i,X_j]$ to denote the set of edges between partite sets $X_i$ and $X_j$. The complement of a graph G, denoted by $\overline{G}$, is a graph with the same vertices as G and contains those edges which are not in G. Let $T\subseteq V\left(G\right)$ be any subset of vertices of G. Then, the induced subgraph G[T] is the graph whose vertex set is T and whose edge set consists of all of the edges in E(G) that have both endpoints in T.

Since 1956, when Erdös and Rado published the fundamental paper [2], major research has been conducted to compute the size of the multipartite and bipartite Ramsey numbers. A big challenge in combinatorics is to determining the Ramsey numbers for the graphs. We refer to [3] for an overview on Ramsey theory. Ramsey numbers are related to other areas of mathematics, like combinatorial designs [4]. In fact, exact or near-optimal values of several Ramsey numbers depend on the existence of some combinatorial designs like projective planes, which have been studied to date. Many of these connections are briefly described in [3,5]. There are many applications of Ramsey theory in various branches of mathematics and computer science, such as number theory, information theory, set theory, geometry, algebra, topology, logic, ergodic theory and theoretical computer science [6]. In particular, multipartite Ramsey numbers have applications in decision-making problems and communications [7]. There are many mathematicians who present the new results of multipartite Ramsey numbers every year. As a result of this vast range of applications, we were motivated to conduct research on multipartite Ramsey numbers.

For given graphs $G_1,G_2,\dots ,G_n$ and integer j, the size of the multipartite Ramsey number $m_j(G_1,G_2,\dots ,G_n)$ is the smallest integer t such that any n-coloring of the edges of $K_{j\times t}$ contains a monochromatic copy of $G_i$ in color i for some i, $1\le i\le n$, where $K_{j\times t}$ denotes the complete multipartite graph having j classes with t vertices per each class. G is n-colorable to $(G_1,G_2,\dots ,G_n)$ if there exist a t-edge decomposition of G say $(H_1,H_2,\dots ,H_n)$, where $G_i⊈H_i$ for each $i=1,2,\dots ,n.$

The existence of such a positive integer is guaranteed by a result in [2]. The size of the multipartite Ramsey numbers of small paths versus certain classes of graphs have been studied in [8,9,10]. The size of the multipartite Ramsey numbers of stars versus certain classes of graphs have been studied in [11,12]. In [13,14], Burger, Stipp, Vuuren, and Grobler investigated the multipartite Ramsey numbers $m_j(G_1,G_2)$, where $G_1$ and $G_2$ are in a completely balanced multipartite graph, which can be naturally extended to several colors. Recently, the numbers $m_j(G_1,G_2)$ have been investigated for special classes: stripes versus cycles; and stars versus cycles, see [10] and its references. In [15], authors determined the necessary and sufficient conditions for the existence of multipartite Ramsey numbers $m_j(G,H)$ where both G and H are incomplete graphs, which also determined the exact values of the size multipartite Ramsey numbers $m_j(K_{1,m},K_{1,n})$ for all integers $m,n\ge 1$ and $j=2,3$. Syafrizal et al. determined the size multipartite Ramsey numbers of path versus path [16]. $m_3(G,P_3)$ and $m_2(G,P_3)$ where G is a star forest, namely a disjoint union of heterogeneous stars have been studied in [17]. The exact values of the size Ramsey numbers $m_j(P_3,K_{2,n})$ and $m_j(P_4,K_{2,n})$ for $j\ge 3$ computed in [18].

In [12], Lusiani et al. determined the size of the multipartite Ramsey numbers of $m_j(K_{1,m},H)$, for $j=2,3$, where H is a path or a cycle on n vertices, and $K_{1,m}$ is a star of order $m+1$. In this paper, we computed the size of the multipartite Ramsey numbers $m_j(K_{1,2},P_4,n{K}_2)$ for $n,j\ge 2$ and $m_j(n{K}_2,C_7)$, for $j\le 4$ and $n\ge 2$ which are the new results of multipartite Ramsey numbers. Computing classic Ramsey numbers is very a difficult problem, therefore we can use multipartite and bipartite Ramsey numbers to obtain an upper bound for a classic Ramsey number. In particular, the first target of this work was to prove the following theorems:

Theorem 1.

$m_j(K_{1,2},P_4,n{K}_2)=\lfloor \frac{2n}{j}\rfloor +1$ where $j,n\ge 2$.

In [10], Jayawardene et al. determined the size of the multipartite Ramsey numbers $m_j(n{K}_2,C_m)$ where $j\ge 2$ and $m\in \{3,4,5,6\}$. The second goal of this work extends these results, as stated below.

Theorem 2.

Let $j\in \{2,3,4\}$ and $n\ge 2$. Then

$$m_j(n{K}_2,C_7)=\left\{\begin{array}{cc}\infty \hfill & j=2,n\ge 2,\hfill \\ 2\hfill & (j,n)=(4,2),\hfill \\ 3\hfill & (j,n)=(3,2),(4,3),\hfill \\ n\hfill & j=3,n\ge 3,\hfill \\ \lceil \frac{n+1}{2}\rceil \hfill & j=4,n\ge 4.\hfill \end{array}\right.$$

We estimate that this value of $m_j(n{K}_2,C_7)$ holds for every $j\ge 2$. We checked the proof of the main theorems into smaller cases and lemmas in order to simplify the idea of the proof.

2. Proof of Theorem 1

In order to simplify the comprehension, let us split the proof of Theorem 1 into small parts. We begin with a simple but very useful general lower bound in the following lemma:

Lemma 1.

$m_j(K_{1,2},P_4,n{K}_2)\ge \lfloor \frac{2n}{j}\rfloor +1$ where $j,n\ge 2$.

Proof. 

Consider $G=K_{j\times t}$ where $t=\lfloor \frac{2n}{j}\rfloor$ with partition sets $X_i$, $X_i=\{x_1^i,x_2^i,\dots ,x_t^i\}$ for $i\in \{1,2,\dots ,j\}$. Consider $x_1^1\in X_1$, decompose the edges of $K_{j\times t}$ into graphs $G_1,G_2$, and $G_3$, where $G_1$ is a null graph and $G_2=\overline{G_3}$, where $G_3$ is $G[X_1\backslash \left\{x_1^1\right\},X_2,\dots ,X_j]$. In fact $G_2$ is isomorphic to $K_{1,(j-1)t}$ and:

$$E\left(G_2\right)=\left\{x_1^1{x}_i^r\right|r=2,3,\dots ,j\mathrm{and}i=1,2\dots ,t\}.$$

Clearly $E\left(G_t\right)\cap E\left(G_{t^{\prime }}\right)=\mathsf{\varnothing }$, $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)\cup E\left(G_3\right)$, $K_{1,2}⊈G_1$ and $P_4⊈G_2$. Since $|V\left(K_{j\times t}\right)|=j\times \lfloor \frac{2n}{j}\rfloor \le 2n$, we have $\left|V\right(G_3\left)\right|\le 2n-1$, that is, $n{K}_2⊈G_3$, which means that $m_3(K_{1,2},P_4,n{K}_2)\ge \lfloor \frac{2n}{j}\rfloor +1$ and the proof is complete. □

Observation 1.

Let $G=K_{2,3}(or{K}_4-e)$. For any subgraph of G, say H, either H has a subgraph isomorphism to $K_{1,2}$ or $\overline{H}$ has a subgraph isomorphism to $P_4$.

Proof. 

Let $H\subseteq G=K_{2,3}$, for $G=K_4-e$ the proof is same. Without loss of generality (w.l.g.), let $X=\{x_1,x_2\}$ and $Y=\{y_1,y_2,y_3\}$ be a partition set of $V\left(G\right)$ and P be a maximum path in H. If $\left|P\right|\ge 3$, then H has a subgraph isomorphic to $K_{1,2}$, so let $\left|P\right|\le 2$. If $\left|P\right|=1$, then $\overline{H}(=G)$ has a subgraph isomorphic to $P_4$. Hence, we may assume that $\left|P\right|=2$, w.l.g., and let $P=x_1{y}_1$. Since $\left|P\right|=2$, $x_1{y}_2,x_1{y}_3$ and $x_2{y}_1$ are in $E\left(\overline{H}\right)$ and there is at least one edge of $\{x_2{y}_2,x_2{y}_3\}$ in $\overline{H}$, in any case, $P_4\subseteq \overline{H}$ and the proof is complete. □

We determined the exact value of the multipartite Ramsey number of $m_2(K_{1,2},P_4,n{K}_2)$ for $n\ge 2$ in the following lemma:

Lemma 2.

$m_2(K_{1,2},P_4,n{K}_2)=n+1$ for $n\ge 2$.

Proof. 

Let $X=\{x_1,x_2,\dots ,x_{n+1}\}$ and $Y=\{y_1,y_2,\dots ,y_{n+1}\}$ be a partition set of $G=K_{n+1,n+1}$. Consider a three-edge coloring $G^r$, $G^b$ and $G^g$ of G. By Lemma 1, the lower bound holds. Now, let M be the maximum matching in $G^g$. If $\left|M\right|\ge n$, then the lemma holds, so let $\left|M\right|\le n-1$. If $\left|M\right|\le n-2$, then we have $K_{3,3}\subseteq \overline{G^g}$ and by Observation 1, the lemma holds, so let $\left|M\right|=n-1$. W.l.g., we may assume that $M=\{x_1{y}_1,x_2{y}_2,\dots ,x_{n-1}{y}_{n-1}\}$. By considering the edges between $\{x_n,x_{n+1}\}$ and $Y\backslash \{y_n,y_{n+1}\}$ and the edges between $\{y_n,y_{n+1}\}$ and $X\backslash \{x_n,x_{n+1}\}$, we have $K_{3,2}\subseteq G^r\cup G^b$. Hence, by Observation 1, the lemma holds. □

In the next two lemmas, we consider $m_3(K_{1,2},P_4,n{K}_2)$ for certain values of n. In particular, we proved that $m_3(K_{1,2},P_4,n{K}_2)=n,$ for $n=2,3$ in Lemma 3 and $m_3(K_{1,2},P_4,4K_2)=3$ in Lemma 4.

Lemma 3.

$m_3(K_{1,2},P_4,n{K}_2)=n$ for $n=2,3$.

Proof. 

Let $X_i=\{x_1^i,x_2^i,\dots ,x_n^i\}$ for $i\in \{1,2,3\}$ be a partition set of $G=K_{3\times n}$. Consider a three-edge coloring $G^r$, $G^b$ and $G^g$ of G. By Lemma 1 the lower bound holds. Now, let M be the maximum matching in $G^g$ and consider the following cases:

Case 1: $n=2$. If $\left|M\right|\ge 2$ then $n{K}_2\subseteq G^g$ and the proof is complete. So let $\left|E\right(M\left)\right|\le 1$. W.l.g., we may assume that $x_1^1{x}_1^2\in E\left(M\right)$, hence, we have $K_4-e\cong G[x_2^1,x_2^2,X_3]\subseteq G^r\cup G^b$ and by Observation 1, the proof is complete.

Case 2: $n=3$. In this case, if $\left|E\right(M\left)\right|\le 1$ or $\left|E\right(M\left)\right|\ge 3$, then the proof is the same as case 1. So let $\left|E\right(M\left)\right|=2$ and w.l.g., we may assume that $E\left(M\right)=\{e_1,e_2\}$—considering any $e_1$ and $e_2$ in $E\left(G\right)$. In any case, we have $G^r\cup G^b$ has a subgraph isomorphic to $K_{3,2}$, hence, by Observation 1, the lemma holds. Therefore, we have $m_3(K_{1,2},P_4,3K_2)=3$. Now, through cases 1 and 2, the proof is complete. □

Lemma 4.

$m_3(K_{1,2},P_4,4K_2)=3$.

Proof. 

Let $X_i=\{x_1^i,x_2^i,x_3^i\}$ for $i\in \{1,2,3\}$ be a partition set of $G=K_{3\times 3}$. By Lemma 1, the lower bound holds. Consider a three-edge coloring ($G^r$, $G^b$, $G^g$) of G where $4K_2⊈G^g$. Let M be a maximum matching in $G^g$, if $\left|M\right|\le 2$, then the proof is same as Lemma 3. Hence, we may assume that $\left|M\right|=3$ and w.l.g., let $E\left(M\right)=\{e_1,e_2,e_3\}$. By Observation 1, there is at least one edge between $X_1$ and $X_2$ in $G^g$, say $e_1=x_1^1{x}_1^2$, and similarly, there is at least one edge between $X_3$ and $\{x_2^1,x_3^1\}$ in $G^g$, say $e_2=x_2^1{x}_1^3$, otherwise $K_{3,2}\subseteq G^r\cup G^b$ and the proof is complete. Now, by Observation 1, there is at least one edge between $\{x_3^1,x_2^3,x_3^3\}$ and $\{x_2^2,x_3^2\}$ in $G^g$, and let $e_3$ be this edge. If $x_3^1\notin V\left(e_3\right)$ (say $e_3=x_2^2{x}_2^3$ ), then $K_3\subseteq G^r\cup G^b[x_3^1,x_3^2,x_3^3]$.

Now, consider the vertex $x_1^1$ and $x_1^2$, since $\left|M\right|=3$ and $e_1=x_1^1{x}_1^2$, it is easy to check that $x_1^1{x}_3^3,x_1^2{x}_3^3\in E\left(G^g\right)$ and $x_1^1{x}_3^2,x_1^2{x}_3^1\in E\left(\overline{G^g}\right)$, otherwise $K_4-e\subseteq \overline{G^g}$ and the proof is complete. Similarly, we have $x_2^1{x}_3^2,x_1^3{x}_3^2\in E\left(G^g\right)$ and $x_2^1{x}_3^3,x_1^3{x}_3^1\in E\left(\overline{G^g}\right)$. Now, by considering the edges of $G[X_1,x_1^2,x_3^2,x_1^3,x_3^3]$, it is easy to check that $K_4-e\subseteq G^r\cup G^b$ and the lemma holds. Hence, we have $x_3^1\in V\left(e_3\right)$ (say $e_3=x_3^1{x}_2^2$), in this case, and we have $K_{2,2}\cong G[x_2^2,x_3^2,x_2^3,x_3^3]\subseteq G^r\cup G^b$, otherwise, if there exists at least one edge between $\{x_2^3,x_3^3\}$ and $\{x_2^2,x_3^2\}$ in $G^g$, say e, then set $e=e_3$ and the proof is the same. Hence, by considering the vertex $x_1^1$ and $x_1^2$, since $\left|M\right|=3$ and $e_1=x_1^1{x}_1^2$, it is easy to check that $K_{3,2}\subseteq G^r\cup G^b$ and by Observation 1 the proof is complete. □

Lemma 5.

$m_3(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{3}\rfloor +1$ for each $n\ge 2$.

Proof. 

Let $X_i=\{x_1^i,x_2^i,\dots ,x_t^i\}$ for $i\in \{1,2,3\}$ be a partition set of $G=K_{3\times t}$ where $t=\lfloor \frac{2n}{3}\rfloor +1$. We will prove this Lemma by induction. For the base step of the induction, since $\lfloor \frac{2\times 2}{3}\rfloor +1=2,\lfloor \frac{2\times 3}{3}\rfloor +1=3$ and $\lfloor \frac{2\times 4}{3}\rfloor +1=3$, lemma holds by Lemmas 3 and 4. Suppose that $n\ge 5$ and $m_3(K_{1,2},P_4,n^{\prime }{K}_2)\le \lfloor \frac{2n^{\prime }}{3}\rfloor +1$ for each $n^{\prime }<n$. We will show that $m_3(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{3}\rfloor +1$. By contradiction, we may assume that $m_3(K_{1,2},P_4,n{K}_2)>\lfloor \frac{2n}{3}\rfloor +1$, that is, $K_{3\times (\lfloor \frac{2n}{3}\rfloor +1)}$ is three-colorable to $(K_{1,2},P_4,n{K}_2)$. Consider a three-edge coloring $(G^r,G^b,G^g)$ of G, such that $K_{1,2}⊈G^r$, $P_4⊈G^b$ and $n{K}_2⊈G^g$. By the induction hypothesis and Lemma 1, we have $m_3(K_{1,2},P_4,(n-1)K_2)=\lfloor \frac{2(n-1)}{3}\rfloor +1\le \lfloor \frac{2n}{3}\rfloor +1$. Therefore, since $K_{1,2}⊈G^r$ and $P_4⊈G^b$, we have $(n-1)K_2\subseteq G^g$. Now, we have the following cases:

Case 1: $\lfloor \frac{2n}{3}\rfloor =\lfloor \frac{2(n-1)}{3}\rfloor +1$.

Since $\lfloor \frac{2n}{3}\rfloor =\lfloor \frac{2(n-1)}{3}\rfloor +1$, we have a copy of $H=K_{3\times (\lfloor \frac{2(n-1)}{3}\rfloor +1)}$ in G. In other words, for each $i\in \{1,2,3\}$, there is a vertex, say $x\in X_i$, such that $x\in V\left(G\right)\backslash V\left(H\right)$. W.l.g., we may assume that $A=\{x_1^1,x_1^2,x_1^3\}$ would be these vertices. Since $H\subseteq G$, we have $K_{1,2}⊈G^r\left[V\left(H\right)\right]$ and $P_4⊈G^b\left[V\left(H\right)\right]$. Hence, by the induction hypothesis, we have $M=(n-1)K_2\subseteq G^g\left[V\left(H\right)\right]\subseteq G^g$. We consider that the three vertices do not belong to $V\left(H\right)$, i.e., A. Since $n{K}_2⊈G^g$, we have $G\left[A\right]\subseteq G^r\cup G^b$. Now, we consider the following Claim:

Claim 1.

$n\in B\cup D$ where $B=\left\{3k\right|k=1,2,...\}$ and $D=\{3k+2|k=1,2,...\}$.

Proof of the Claim. By contradiction, we may assume that $n\notin B\cup D$. In other words, let $n=3k+1$, then we have:

$$2k=\lfloor \frac{6k}{3}\rfloor =\lfloor \frac{6k}{3}+\frac{2}{3}\rfloor =\lfloor \frac{6k+2}{3}\rfloor =\lfloor \frac{2(3k+1)}{3}\rfloor$$

$$=\lfloor \frac{2n}{3}\rfloor =\lfloor \frac{2(n-1)}{3}\rfloor +1=\lfloor \frac{2\left(3k\right)}{3}\rfloor +1=2k+1,$$

which is a contradiction implying that $n\in B\cup D$.

Claim 2.

There is at least one vertex in $V\left(H\right)\backslash V\left(M\right)$.

Proof of the Claim. Let $M=(n-1)K_2\subseteq G^g$, then $\left|V\right(M\left)\right|=2(n-1)=2n-2$. Since $\lfloor \frac{2n}{3}\rfloor =\lfloor \frac{2(n-1)}{3}\rfloor +1$, by Claim 1, if $n\in B$, we have $n=3k$ for $k\ge 2$. Now, we have:

$$\lfloor \frac{2(n-1)}{3}\rfloor +1=\lfloor \frac{2(3k-1)}{3}\rfloor +1=\lfloor \frac{2\left(3k\right)}{3}-\frac{2}{3}\rfloor +1=2k-1+1=2k.$$

Hence, we have $\left|V\right(H\left)\right|=3\times \left(2k\right)=6k=2n$ and thus $\left|V\right(H)\backslash V(M\left)\right|=2$. If $n\in D$ then we have:

$$\lfloor \frac{2(n-1)}{3}\rfloor +1=\lfloor \frac{2(3k+1)}{3}\rfloor +1=\lfloor \frac{2\left(3k\right)}{3}+\frac{2}{3}\rfloor +1=2k+1.$$

Hence, $\left|V\right(H\left)\right|=3\times (2k+1)=6k+3=2n-1$. Therefore, $\left|V\right(H)\backslash V(M\left)\right|=1$.

By Claim 2, let $x\in V\left(H\right)\backslash V\left(M\right)$. Since $n{K}_2⊈G^g$, we have $K_4-e\cong G[A\cup \left\{x\right\}]\subseteq G^r\cup G^b$. Hence, by Observation 1, we again have a contradiction.

Case 2: $\lfloor \frac{2n}{3}\rfloor =\lfloor \frac{2(n-1)}{3}\rfloor$.

In this case, by Claim 1 we have $n=3k+1$. Since $K_{1,2}⊈G^r$ and $P_4⊈G^b$, by the induction hypothesis, we have $M=(n-1)K_2\subseteq G^g$. Now, we have the following claim:

Claim 3.

$\left|V\right(G)\backslash V(M\left)\right|=3$.

Proof of the Claim. Let $M=(n-1)K_2\subseteq G^g$. Since $|V\left(X_j\right)|=\lfloor \frac{2n}{3}\rfloor +1$ and $n=3k+1$, we have $\lfloor \frac{2n}{3}\rfloor +1=\lfloor \frac{2(3k+1)}{3}\rfloor +1=\lfloor \frac{6k}{3}+\frac{2}{3}\rfloor +1=2k+1$ and therefore, $\left|V\right(G\left)\right|=3\times (2k+1)=6k+3=2(3k+1)+1=2n+1$, that is, $\left|V\right(G)\backslash V(M\left)\right|=(2n+1)-(2n-2)=3$.

By Claim 3, we have $\left|V\right(G)\backslash V(M\left)\right|=3$. W.l.g., we may assume that $A^{\prime }=\{x,y,z\}$ has three vertices, since $n{K}_2⊈G^g$, and we have $G\left[A^{\prime }\right]\subseteq G^r\cup G^b$. We consider the three vertices belonging to $A^{\prime }$, and now, we have the following subcases:

Subcase 2-1: $A^{\prime }\subseteq X_j$ for only one $j\in \{1,2,3\}$. W.l.g. we may assume that $A^{\prime }\subseteq X_1$ and $E\left(M\right)=\left\{e_i\right|i=1,2,\dots ,(n-1)\}$. Since $k\ge 2$ and $3k+1=n\ge 7$ we have $|X_j|\ge 5$ and $|E\left(M\right)\cap E(G[X_2,X_3]\left)\right|\ge 3$, otherwise, $K_{3,3}\subseteq G^r\cup G^b$ and by Observation 1; a contradiction. W.l.g. we may assume that $\left\{x_i^2{x}_i^3\right|i=1,2,3\}\subseteq (E\left(M\right)\cap E\left(G^g[X_2,X_3]\right))$. Consider $G^{\prime }=G[A^{\prime },x_1^2,x_2^2,x_3^2,x_1^3,x_2^3,x_3^3]\cong K_{3\times 3}$. Since $n{K}_2⊈G^g$, if $M^{\prime }$ is a maximum matching in $G^{\prime g}$, then $|M^{\prime }|\le 3$, otherwise we have $n{K}_2=M\backslash \{e_1,e_2,e_3\}\cup M^{\prime }\subseteq G^g$; a contradiction again. Since $m_3(K_{1,2},P_4,4K_2)=3$ and $|M^{\prime }|\le 3$, we have $K_{1,2}\subseteq G^{\prime r}\subseteq G^r$ or $P_4\subseteq G^{\prime b}\subseteq G^b$; also a contradiction.

Subcase 2-2: $|A^{\prime }\cap X_j|=1$ for each $j\in \{1,2,3\}$. W.l.g., we may assume that $x\in X_1,y\in X_2$ and $z\in X_3$. Hence $G\left[A^{\prime }\right]\cong K_3\subseteq G^r\cup G^b$. Since $|X_j|\ge 5$, we have $|E\left(M\right)\cap E(G^g[X_i,X_j]\left)\right|\ge 2$ for each $i,j\in \{1,2,3\}$. W.l.g., we may assume that $x^{\prime }{y}^{\prime }\in E\left(M\right)\cap E\left(G^g[X_1\backslash \left\{x\right\},X_2\backslash \left\{y\right\}]\right)$, $x^{\prime }\in X_1$ and $y^{\prime }\in X_2$. If $x^{\prime }y$ and $x^{\prime }z\in E(G^r\cup G^b)$ then we have $K_4-e\subseteq G^r\cup G^b$ and by Observation 1; a contradiction. So let $x^{\prime }y$ or $x^{\prime }z\in E\left(G^g\right)$. If $x^{\prime }y\in E\left(G^g\right)$, then, since $n{K}_2⊈G^g$, we have $y^{\prime }x,y^{\prime }z\in E(G^r\cup G^b)$, that is, $K_4-e\subseteq G^r\cup G^b$; we have a contradiction again. So let $x^{\prime }z\in E\left(G^g\right)$ and $x^{\prime }y\in E(G^r\cup G^b)$. Since $n{K}_2⊈G^g$, we have $y^{\prime }x\in E(G^r\cup G^b)$. If $|E\left(G^r\right)\cap E\left(G\left[A^{\prime }\right]\right)|\ne 0$, then we have $P_4\subseteq G^b$. So let $xy,yz,zx\in E\left(G^b\right)$ and $x{y}^{\prime },y{x}^{\prime }\in E\left(G^r\right)$. Since $|E\left(M\right)\cap E(G^g[X_i,X_j]\left)\right|\ge 2$ there is at least one edge, say $y^{″}{z}^{″}\in E\left(M\right)\cap E\left(G^g[X_2\backslash \left\{y\right\},X_3\backslash \left\{z\right\}]\right)$. W.l.g., we may assume that $y^{″}\in X_2$ and $z^{″}\in X_3$. Since $K_{1,2}⊈G^r$ and $P_4⊈G^b$ we have $y^{″}x,z^{″}y\in E\left(G^g\right)$. Hence, we had a $n{K}_2=M\backslash \left\{y^{″}{z}^{″}\right\}\cup \{y^{″}x,z^{″}y\}$; a contradiction.

Subcase 2-3: $|A^{\prime }\cap X_j|=2$ for only one $j\in \{1,2,3\}$. W.l.g., we may assume that $x,y\in X_1$ and $z\in X_2$. Hence, we have $G^{\prime }\left[A^{\prime }\right]\cong P_3\subseteq G^r\cup G^b$. Since $k\ge 2$, we have $|X_j|\ge 5$, that is, $|E\left(M\right)\cap E(G^g[X_2,X_3]\left)\right|\ge 3$. W.l.g., we may assume that $vu,v^{\prime }{u}^{\prime }\in E\left(M\right)\cap G^g[X_2,X_3]$ where $v,v^{\prime }\in X_2$ and $u,u^{\prime }\in X_3$. Now, we have the following claim:

Claim 4.

$|N_{G^g}\left(x\right)\cap \{v,v^{\prime }\}|=|N_{G^g}\left(y\right)\cap \{v,v^{\prime }\}|=0$.

Proof of the Claim. By contradiction, w.l.g., we may assume that $xv\in E\left(G^g\right)$. Since $n{K}_2⊈G^g$, we have $yu,zu\in E(G^r\cup G^b)$. Consider $A^{″}=\{y,z,u\}$ and $M^{\prime }=M\backslash \left\{vu\right\}\cup \left\{xv\right\}$. Hence, $M^{\prime }=(n-1)K_2\subseteq G^g$ and $|A^{″}\cap X_j|\ne 0$ for each $j\in \{1,2,3\}$; we have a contradiction to subcase 2-2.

Now, by Claim 4, we have $K_{2,3}=G[A^{\prime }\cup \{v,v^{\prime }\}]\subseteq G^r\cup G^b$. In this case, by Observation 1, we have $K_{1,2}\subseteq G^r$ or $P_4\subseteq G^b$; we have a contradiction again.

Therefore, by Cases 1 and 2, we have $m_3(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{3}\rfloor +1$ for $n\ge 2$. □

Now, by Lemmas 1 and 5, we have the following lemma:

Lemma 6.

$m_3(K_{1,2},P_4,n{K}_2)=\lfloor \frac{2n}{3}\rfloor +1$ for $n\ge 2$.

In the next two lemmas, we consider $m_j(K_{1,2},P_4,n{K}_2)$ for each values of $n\ge 2$ and $j\ge 4$. In particular, we proved that $m_j(K_{1,2},P_4,n{K}_2)=\lfloor \frac{2n}{j}\rfloor +1$ for $n\ge 2$ and $j\ge 4$. We started with the following lemma:

Lemma 7.

Let $j\ge 4$ and $n\ge 2$. Given that $m_j(K_{1,2},P_4,(n-1)K_2)=\lfloor \frac{2(n-1)}{j}\rfloor +1$, it follows that $m_j(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{j}\rfloor +1.$

Proof. 

Let $j\ge 4$ and $n\ge 2$. For $i\in \{1,2,\dots ,j\}$ let $X_i=\{x_1^i,x_2^i,\dots ,x_t^i\}$ be partition set of $G=K_{j\times t}$ where $t=\lfloor \frac{2n}{j}\rfloor +1$. Assume that $m_j(K_{1,2},P_4,(n-1)K_2)=\lfloor \frac{2(n-1)}{j}\rfloor +1$ is true. To prove $m_j(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{j}\rfloor +1$. Consider three-edge coloring $(G^r,G^b,G^g)$ of G. Suppose that $n{K}_2⊈G^g$, we prove that $K_{1,2}\subseteq G^r$ or $P_4\subseteq G^b$. Let $M^{\ast }$ be the maximum matching in $G^g$. Hence, by the assumption, $|M^{\ast }|\le n-1$, that is $|V\left(K_{j\times t}\right)\cap V\left(M^{\ast }\right)|\le 2(n-1)$. Now, we have the following claim:

Claim 5.

$|V\left(K_{j\times t}\right)\backslash V\left(M^{\ast }\right)|\ge 3$.

Proof of the Claim. Consider the following cases:

Case 1: Let $2n=jk(2n\equiv 0(modj\left)\right)$. In this case, we have:

$$\left|V\left(G\right)\right|=j\times t=j\times (\lfloor \frac{2n}{j}\rfloor +1)=j\times \lfloor \frac{2n}{j}\rfloor +j=jk+j=j(k+1).$$

Hence:

$$|V\left(G\right)\backslash V\left(M^{\ast }\right)|\ge j(k+1)-2(n-1)=jk+j-2n+2=j+2\ge 6(j\ge 4).$$

Case 2: Let $2n=jk+r(2n\equiv r(modj)$ where $r\in \{1,2,\dots ,j-1\})$. In this case, we have:

$\left|V\left(G\right)\right|=j\times (\lfloor \frac{2n}{j}\rfloor +1)=j\times (\lfloor \frac{jk+r}{j}\rfloor +1)=j\times (\lfloor \frac{jk}{j}+\frac{r}{j}\rfloor +1)=j\times \lfloor \frac{jk}{j}\rfloor +j=jk+j.$

Hence we have:

$|V\left(G\right)\backslash V\left(M^{\ast }\right)|\ge j(k+1)-2(n-1)=jk+j-2n+2=jk+j-jk-r+2=j-r+2\ge 3.$

By Claim 5, G contains three vertices, say $x,y$ and z in $V\left(K_{j\times t}\right)\backslash V\left(M^{\ast }\right)$. Consider the vertex set $\{x,y,z\}$ and let $\{x,y,z\}\subseteq A=V\left(G\right)\backslash V\left(M^{\ast }\right)$. Now, we have the following cases:

Case 1: Let $x\in X_1$, $y\in X_2$ and $z\in X_3$, where $X_i$ for $i=1,2,3$ are distinct partition sets of $G=K_{j\times t}$. Note that all vertices of A are adjacent to each other in $\overline{G^g}$. Since $t\ge 2$, we have $|X_i|\ge 2$. Consider the partition $X_j$ for $j\ge 4$. Since $|X_j|\ge 2$, if $|A\cap X_j|\ge 1$ for at least one $j\ge 4$, then we have $K_4\subseteq G^r\cup G^b$ and the proof is complete by Observation 1. Now, let $|A\cap X_j|=0$ for each $j\ge 4$. Hence, for $x_1^4\in X_4$ there exists a vertex, say u such that $x_1^{4}u\in E\left(M^{\ast }\right)$. Consider $N_{G^g}\left(x_1^4\right)\cap \{x,y,z\}$. If $|N_{G^g}\left(x_1^4\right)\cap \{x,y,z\}|\le 1$, then we have $K_4-e\subseteq G^r\cup G^b$ and by Observation 1, the proof is complete. Therefore, let $|N_{G^g}\left(x_1^4\right)\cap \{x,y,z\}|\ge 2$. W.l.g., we may assume that $\{x,y\}\subseteq N_{G^g}\left(x_1^4\right)\cap \{x,y,z\}$. In this case, we have $|N_{G^g}\left(u\right)\cap \{x,y,z\}|=0$. On the contrary, let $xu\in E\left(G^g\right)$ and set $M^{\prime }=M^{\ast }\backslash \left\{x_1^{4}u\right\}\cup \{x_1^{4}y,ux\}$. Clearly $M^{\prime }$ is a match where $|M^{\prime }|>|M^{\ast }|$, which contradicts the maximality of $M^{\ast }$. Hence, we have $|N_{G^g}\left(u\right)\cap \{x,y,z\}|=0$. Therefore, we have $K_4-e\subseteq G^r\cup G^b[x,y,z,u]$ and, by Observation 1, the proof is complete.

Case 2: Let $x,y\in X_i$ and $z\in X_{i^{\prime }}$ where $X_i,X_{i^{\prime }}$ are distinct partition sets of G. W.l.g., let $i=1$ and $i^{\prime }=2$. Consider the partition $X_j(j\ne 1,2)$. Since $|X_j|\ge 2$, if $|A\cap X_j|\ge 1$, then we have $K_4-e\subseteq G^r\cup G^b$ and by Observation 1, the proof is complete. So let $|A\cap X_j|=0$ for each $j\ge 3$. Now, we have the following claim.

Claim 6.

Let $e=v_1{v}_2\in E\left(M^{\ast }\right)$, and w.l.g. let $|N_{G^g}\left(v_1\right)\cap \{x,y,z\}|\ge |N_{G^g}\left(v_2\right)\cap \{x,y,z\}|$. If $|N_{G^g}\left(v_1\right)\cap \{x,y,z\}|\ge 2$, then $|N_{G^g}\left(v_2\right)\cap \{x,y,z\}|=0$. If $|N_{G^g}\left(v_1\right)\cap \{x,y,z\}|=|N_{G^g}\left(v_2\right)\cap \{x,y,z\}|=1$, then $v_1,v_2$ has the same neighbor in $\{x,y,z\}$.

Proof of the Claim. Let $|N_{G^g}\left(v_1\right)\cap \{x,y,z\}|\ge 2$. W.l.g., we may assume that $\{w,w^{\prime }\}\subseteq N_{G^g}\left(v_1\right)\cap \{x,y,z\}$. By contradiction, let $|N_{G^g}\left(v_2\right)\cap \{x,y,z\}|\ne 0$, w.l.g., let $w{}^{″}\in N_{G^g}\left(v_2\right)\cap \{x,y,z\}$. In this case, we set $M^{\prime }=(M^{\ast }\backslash \left\{v_1{v}_2\right\})\cup \{v_{1}w,v_{2}w{}^{″}\}$. Clearly $M^{\prime }$ is a match with $|M^{\prime }|>|M^{\ast }|$, which contradicts the maximality of $M^{\ast }$. Thus, let $|N_{G^g}\left(v_i\right)\cap \{x,y,z\}|=1$ for $i=1,2$, if $v_i$ has a different neighbor, then the proof is same.

Claim 7.

There is at least one edge, say $e=u_i{u}_j\in E\left(M^{\ast }\right)$, such that $u_i,u_j\notin X_1,X_2$.

Proof of the Claim. If $|X_j|\ge 3$, then there is at least one edge, say $e=u_i{u}_j\in E\left(M^{\ast }\right)$, such that $u_i,u_j\notin X_1,X_2$. Otherwise, we have $K_{3,2}\subseteq G^r\cup G^b[X_j,X_{j^{\prime }}]$ where $j,j^{\prime }\ge 3$, hence, by Observation 1; we have a contradiction. So, let $|X_j|=2$. In this case, if $j\ge 5$, then the proof is same. Now, let $j=4$. We have $|M^{\ast }|\le 2$, that is, $n\le 3$. Hence, there is at least one vertex, say $w\in (X_3\cup X_4)\cap A$; a contradiction to $|A\cap X_j|=0$.

By Claim 7, there is at least one edge, say $e=u_i{u}_j\in E\left(M^{\ast }\right)$, such that $u_i,u_j\notin X_1,X_2$. W.l.g., let $e=u_1{u}_2\in E\left(M^{\ast }\right)$ such that $u_i\notin X_1,X_2$, also, w.l.g., assume that $|N_{G^g}\left(u_1\right)\cap \{x,y,z\}|\ge |N_{G^g}\left(u_2\right)\cap \{x,y,z\}|$. If $|N_{G^g}\left(u_1\right)\cap \{x,y,z\}|\ge 2$, then by Claim 7, we have $|N_{G^g}\left(u_2\right)\cap \{x,y,z\}|=0$. Hence, we have $K_4-e\subseteq G^r\cup G^b$. So, let $|N_{G^g}\left(u_1\right)\cap \{x,y,z\}|=|N_{G^g}\left(u_2\right)\cap \{x,y,z\}|=1$, in this case, by Claim 7, we have $N_{G^g}\left(u_1\right)\cap \{x,y,z\}=N_{G^g}\left(u_2\right)\cap \{x,y,z\}$, and if x or y is this vertex, then $K_4-e\subseteq G^r\cup G^b$; otherwise, $K_{3,2}\subseteq G^r\cup G^b$. In any case, by Observation 1, the proof is complete.

Case 3: Let $x,y,z\in X_i$ where $X_i$ is a partition set of $G=K_{j\times t}$, say $i=1$. If there exists a vertex, say $w\in X_j\cap A$, where $j\ne 1$, then the proof is the same as Case 2. Hence, let $|A\cap X_j|=0$. Since $|X_j|\ge 3$, there exists an edge, say $e=vu\in E\left(M^{\ast }\right)$, such that $v,u\notin X_1$. Consider the neighbors of vertices v and u in $X_1$. W.l.g., let $|N_{G^g}\left(v\right)\cap \{x,y,z\}|\ge |N_{G^g}\left(u\right)\cap \{x,y,z\}|$. If $|N_{G^g}\left(v\right)\cap \{x,y,z\}|=0$, then we have $K_{3,2}\subseteq G^r\cup G^b$, so let $|N_{G^g}\left(v\right)\cap \{x,y,z\}|\ge 1$. In this case, by Claim 7, we had $|N_{G^g}\left(u\right)\cap \{x,y,z\}|\le 1$. Hence, w.l.g., we may assume that $yu$ and $zu$ be in $E(G^r\cup G^b)$ and $x\in N_{G^g}\left(v\right)$. Now, set $M^{\ast \ast }=(M^{\ast }\backslash \left\{vu\right\})\cup \left\{vx\right\}$ and $A^{\prime }=(A\backslash \left\{x\right\})\cup \left\{u\right\}$, the proof is the same as Case 2 and the proof is complete.

According to the Cases $1,2$ and 3 we have $m_j(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{j}\rfloor +1$. □

The results of Lemmas 1, 2, 6 and 7, concludes the proof of Theorem 1.

3. Proof of Theorem 2

In this section, we investigate the size multipartite Ramsey numbers $m_j(n{K}_2,C_7)$ for $j\le 4$ and $n\ge 2$. In order to simplify the comprehension, let us split the proof of Theorem 2 into small parts. For $j=2$, since the bipartite graph has no odd cycle, we have $m_2(n{K}_2,C_7)=\infty$. For other cases, we start with the following proposition:

Proposition 1.

$m_3(n{K}_2,C_7)=3$ where $n=2,3$.

Proof. 

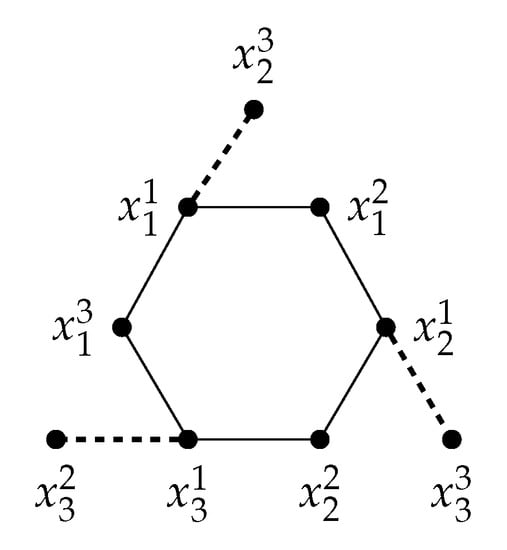
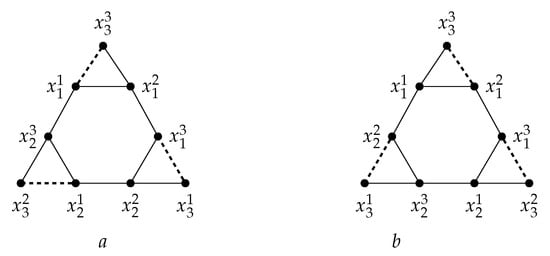
Clearly, $m_3(n{K}_2,C_7)\ge 3$. Consider $K_{3\times 3}$ with the partition set $X_i=\{x_1^i,x_2^i,x_3^i\}$ for $i=1,2,3$. Let G be a subgraph of $K_{3\times 3}$. For $n=2$, if $2K_2\subseteq G$, then proof is complete, so let $2K_2⊈G$. In this case, we have $K_{3,2,2}\subseteq \overline{G}$, hence $C_7\subseteq \overline{G}$, that is, $m_3(2K_2,C_7)=3$. For $n=3$ by contradiction, we may assume that $m_3(3K_2,C_7)>3$, that is, $K_{3\times 3}$ is 2-colorable to $(3K_2,C_7)$, say $3K_2⊈G$ and $C_7⊈\overline{G}$. Since $m_3(3K_2,C_6)=3$ [10], and $3K_2⊈G$, we have $C_6\subseteq \overline{G}$. Let $A=V\left(C_6\right)$ and $Y_i=A\cap X_i$ for $i=1,2,3$. If there exists $i\in \{1,2,3\}$ such that $|Y_i|=0$, say $i=1$, then we have $A=X_2\cup X_3$ and $C_6\subseteq \overline{G}[X_2,X_3]$. Let $C_6=w_1{w}_2\dots w_6{w}_1$. Since $C_7⊈\overline{G}$, for each $x_i\in X_1$ in $\overline{G}$, $x_i$ cannot be adjacent to $w_i$ and $w_{i+1}$ for $i=1,2,\dots ,6$. Hence, we have $|N_G\left(x_i\right)\cap V\left(C_6\right)|\ge 3$ for each $x_i\in X_1$. One can easily check that in any case, we have $3K_2\subseteq G$; a contradiction, hence, let $|Y_i|\ge 1$ for each $i=1,2,3$. Set $B=\left(\right|Y_1|,|Y_2|,|Y_3\left|\right)$. Now, we have the following cases:

Case 1: $B=(3,2,1)$. Let $A=X_1\cup \{x_1^2,x_2^2,x_1^3\}$. In this case, we have $C_6\cong x_1^1{x}_1^2{x}_2^1{x}_2^2{x}_3^1{x}_1^3{x}_1^1$. Consider the vertex set $A^{\prime }=V\left(K_{3\times 3}\right)\backslash A=\{x_3^2,x_2^3,x_3^3\}$. Since $C_7⊈\overline{G}$, we have $|N_{\overline{G}}\left(x_2^3\right)\cap \{x_1^1,x_1^2\}|\le 1$. Hence, $|N_G\left(x_2^3\right)\cap \{x_1^1,x_1^2\}|\ge 1$. W.l.g., let $x_2^3{x}_1^1\in E\left(G\right)$. By similarity, we have $|N_G\left(x_3^3\right)\cap \{x_2^1,x_2^2\}|\ge 1$ and $|N_G\left(x_3^2\right)\cap \{x_3^1,x_1^3\}|\ge 1$, see Figure 1. In any case, we have $3K_2\subseteq G$; a contradiction again.

Figure 1. $B=(3,2,1)$.

Case 2: $B=(2,2,2)$. W.l.g., let $Y_i=\{x_1^i,x_2^i\}$ for $i=1,2,3$. In this case, we have $C_6\cong w_1{w}_2{w}_3{w}_4{w}_5{w}_6{w}_1$. W.l.g., let $w_1=x_1^1,w_2=x_1^2$. Since $|Y_3|=2$ and $w_4{w}_5\in E\left(C_6\right)$, we have $|\{w_3,w_6\}\cap Y_3|\ge 1$. If $|\{w_3,w_6\}\cap Y_3|=2$, then considering Figure 2a, the proof is the same as case 1. So let $|\{w_3,w_6\}\cap Y_3|=1$. W.l.g., let $w_3=x_1^3$, $x_2^3=w_5$, $x_2^1=w_4,x_2^2=w_6$. In this case, consider Figure 2b and the proof is the same as case 1. Hence, in any case, we have $3K_2\subseteq G$; again a contradiction.

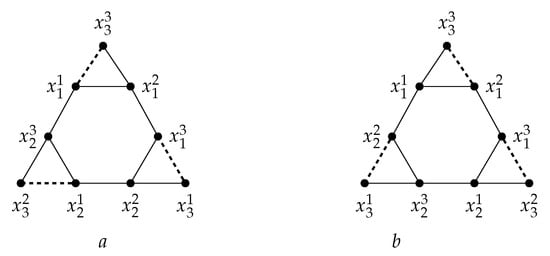
Figure 2. (a) $|\{w_3,w_6\}\cap Y_3|=2$, (b) $|\{w_3,w_6\}\cap Y_3|=1$.

By Cases 1 and 2, we have $3K_2\subseteq G$. Thus, the proof is complete and the proposition holds. □

We determine the exact value of the multipartite Ramsey number $m_3(n{K}_2,C_7)$ for $n\ge 3$ in the following lemma:

Lemma 8.

For each $n\ge 3$ we have $m_3(n{K}_2,C_7)=n$.

Proof. 

First, we show that $m_3(n{K}_2,C_7)\ge n$. Consider the coloring given by $K_{3\times (n-1)}=G^r\cup G^b$ where $G^r\cong K_{n-1,n-1}$ and $G^b\cong K_{n-1,2(n-1)}$. Since $|V\left(G^r\right)|=2(n-1)$ and $G^b$ is bipartite, we have $n{K}_2⊈G^r$ and $C_7⊈G^b$, that is, $m_3(n{K}_2,C_7)\ge n$. For the upper bound, consider $K_{3\times n}$ with partite sets $X_i=\{x_1^i,x_2^i,\dots ,x_n^i\}$ for $i=1,2,3$. We will prove this by induction. For $n=3$, by Proposition 1, the lemma holds. Suppose that $m_3(n{K}_2,C_7)\le n$ for each $n\ge 4$. We will show that $m_3((n+1)K_2,C_7)\le n+1$, as follows: by contradiction, we may assume that $m_3((n+1)K_2,C_7)>n+1$, that is, $K_{3\times (n+1)}$ is 2-colorable to $((n+1)K_2,C_7)$, say $(n+1)K_2⊈G$ and $C_7⊈\overline{G}$. Let $X_i^{\prime }=X_i\backslash \left\{x_1^i\right\}$. Hence, by the induction hypothesis, we have $m_3(n{K}_2,C_7)\le n$. Therefore, since $|X_i^{\prime }|=n$ and $C_7⊈\overline{G}[X_1^{\prime },X_2^{\prime },X_3^{\prime }]$, we have $M=n{K}_2\subseteq G[X_1^{\prime },X_2^{\prime },X_3^{\prime }]$. If there exists i and j such that $x_1^i{x}_1^j\in E\left(G\right)$, then we have $(n+1)K_2\subseteq G$; a contradiction. Hence, we have $x_1^i{x}_1^j\in E\left(\overline{G}\right)$ for $i,j\in \{1,2,3\}$. Let $A=V\left(K_{3\times n}\right)\backslash V\left(M\right)$. Hence, we have $\left|A\right|=3n-2n=n$. Since $(n+1)K_2⊈G$, we have $G[A,x_1^1,x_1^2,x_1^3]\subseteq \overline{G}$. Since $\left|A\right|=n\ge 4$, one can easily check that, in any case, we have $H\subseteq \overline{G}$, where, $H\in \{K_{5,1,1},K_{4,2,1},K_{3,3,1},K_{3,2,2}\}$. If $H\in \{K_{3,3,1},K_{3,2,2}\}$, one can easily observe that we have $C_7\subseteq H\subseteq \overline{G}$; a contradiction again. So let $H\in \{K_{5,1,1},K_{4,2,1}\}$ and consider the following cases:

Case 1: $A\subseteq X_i$ for only one i, that is, $H=K_{5,1,1}$. W.l.g., let $A\subseteq X_1$ and $\{x_2^1,x_3^1,\dots ,x_5^1\}\subseteq A$. Then, we have $K_{n+1,1,1}\subseteq \overline{G}$ and $M\subseteq G[X_2,X_3]$. Since $n\ge 4$, we have $\left|M\right|\ge 4$, that is, there exists at least two edges, say $e_1=x_1{y}_1$ and $e_2=x_2{y}_2$ in $E\left(M\right)$, where $\{x_1,x_2,y_1,y_2\}\subseteq X_2\cup X_3$. W.l.g., let $|N_G\left(x_i\right)\cap A|\ge |N_G\left(y_i\right)\cap A|$ for $i=1,2$. One can easily check that $|N_G\left(y_i\right)\cap A|\le 1$, otherwise, we have $(n+1)K_2\subseteq G$; a contradiction. Since $|N_G\left(y_i\right)\cap A|\le 1$ and $\left|A\right|\ge 5$, we have $|N_{\overline{G}}\left(y_i\right)\cap A|\ge 4$. Hence, we have $|N_{\overline{G}}\left(y_1\right)\cap N_{\overline{G}}\left(y_2\right)\cap A|\ge 3$. W.l.g., we may assume that $\{x_1^1,x_2^1,x_3^1\}\subseteq N_{\overline{G}}\left(y_1\right)\cap N_{\overline{G}}\left(y_2\right)\cap A$. In this case, we have $C_7\subseteq \overline{G}[x_1^1,x_2^1,x_3^1,x_1^2,x_1^3,y_1,y_2]\subseteq \overline{G}$; a contradiction again.

Case 2: $H=K_{4,2,1}$. W.l.g., let $|A\cap X_1|=n-1$ and $|A\cap X_2|=2$. Let $\{x_2^1,x_3^1,\dots ,x_4^1\}\subseteq A\cap X_1$ and $x_2^2\in A\cap X_2$, that is, we have $K_{4,2,1}\subseteq K_{n,2,1}=G[A,x_1^1,x_2^1,x_3^1]\subseteq \overline{G}$ and $M\subseteq K_{1,n-1,n}$. That is, there exists at least one edge, say $e=xy$, where $x\in X_2$ and $y\in X_3$. W.l.g., let $|N_G\left(x\right)\cap A|\ge |N_G\left(y\right)\cap A|$. One can easily check that $|N_G\left(y\right)\cap A|\le 1$. Hence, we have $|N_{\overline{G}}\left(y\right)\cap A|\ge 3$ and the proof is same as case 1.

By cases 1 and 2, we have the assumption that $m_3((n+1)K_2,C_7)>n+1$ does not hold. Now we have $m_3(n{K}_2,C_7)=n$ for each $n\ge 3$. This completes the induction step and the proof. □

Lemma 9.

For $j\ge 3$ and $n\ge j$, we have $m_j(n{K}_2,C_7)\ge \lceil \frac{2n+2}{j}\rceil$.

Proof. 

To show that $m_j(n{K}_2,C_7)\ge \lceil \frac{2n+2}{j}\rceil$, assume that $\lceil \frac{2n+2}{j}\rceil \ge 1$. Consider the coloring given by $K_{j\times t_0}=G^r\cup G^b$ where $t_0=\lceil \frac{2n+2}{j}\rceil -1$ such that $G^r\cong K_{(j-1)\times t_0}$ and $G^b\cong K_{t_0,(j-1)t_0}$. Since $G^b$ is bipartite, we have $C_7⊈G^b$, and

$$|V\left(G^r\right)|=(j-1)\times t_0=(j-1)(\lceil \frac{2n+2}{j}\rceil -1)=(j-1)\left(\lceil \frac{2n+2}{j}\rceil \right)-(j-1)$$

$$\le (j-1)(\frac{2n+2}{j}+1)-(j-1)=j\times \left(\frac{2n+2}{j}\right)-\frac{2n+2}{j}.$$

Since $n\ge j$, we have $\left|V\right(G^r\left)\right|<2n$. Hence, we have $n{K}_2⊈G^r$. Since $K_{j\times t_0}=G^r\cup G^b$, we have $m_j(n{K}_2,C_7)\ge \lceil \frac{2n+2}{j}\rceil$ for $n\ge j\ge 3$. □

Lemma 10.

$m_4(4K_2,C_7)=3$.

Proof. 

By Lemma 9, we have $m_4(4K_2,C_7)\ge 3$. For the upper bound, consider the coloring given by $K_{4\times 3}=G^r\cup G^b$ such that $C_7⊈G^b$. Since $m_3(3K_2,C_7)=3$, we have $3K_2\subseteq G^r[X_1,X_2,X_3]\subseteq G^r$. Let $M=3K_2$; hence, we have $|V(X_1\cup X_2\cup X_3)\backslash V\left(M\right)|=3$. W.l.g., let $A=\{w_1,w_2,w_3\}$ be these vertices. If $E\left(G^r\right)\cap E\left(G[X_4,A]\right)\ne \mathsf{\varnothing }$, then we have $4K_2\subseteq G^r$. So let $K_{3,3}\subseteq G[X_4,A]\subseteq G^b$. Consider the edge $e=v_1{v}_2\in E\left(M\right)$, and it is easy to show that $|N_{G^b}\left(v_i\right)\cap X_4|\ge 2$ for some $i\in \{1,2\}$, otherwise, we have $4K_2\subseteq G^r$. In any case, one can easily check that $C_7\subseteq G^b$; which is a contradiction. Thus, we obtain $m_4(4K_2,C_7)=3$. □

Lemma 11.

For $n\ge 4$ we have $m_4(n{K}_2,C_7)=\lceil \frac{n+1}{2}\rceil$.

Proof. 

By Lemma 9, we have $m_4(n{K}_2,C_7)\ge \lceil \frac{n+1}{2}\rceil$. To prove $m_4(n{K}_2,C_7)\le \lceil \frac{n+1}{2}\rceil$, consider $K_{4\times t}$ with partite set $X_i=\{x_1^i,x_2^i,\dots ,x_t^i\}$ for $i=1,2,3,4$, where $t=\lceil \frac{n+1}{2}\rceil$. We will prove this by induction. For $n=4$ by Lemma 10, the lemma holds. Now, we consider the following cases:

Case 1: $n=2k$, where $k\ge 3$. Suppose that $m_4(n^{\prime }{K}_2,C_7)\le \lceil \frac{n^{\prime }+1}{2}\rceil$ for each $n^{\prime }<n$. We will show that $m_4(n{K}_2,C_7)\le \lceil \frac{n+1}{2}\rceil$ as follows: by contradiction, we may assume that $m_4(n{K}_2,C_7)>\lceil \frac{n+1}{2}\rceil$, that is, $K_{4\times t}$ is 2-colorable to $(n{K}_2,C_7)$, say $n{K}_2⊈G$ and $C_7⊈\overline{G}$. Let $X_i^{\prime }=X_i\backslash \left\{x_1^i\right\}$ for $i=1,2,3,4$. Hence, by the induction hypothesis, we have $m_4((n-1)K_2,C_7)\le \lceil \frac{n}{2}\rceil =k$. Therefore, since $|X_i^{\prime }|=k=\frac{n}{2}$ and $C_7⊈\overline{G}$, we have $M=(n-1)K_2\subseteq G[X_1^{\prime },X_2^{\prime },X_3^{\prime },X_4^{\prime }]$. If there exists $i,j\in \{1,2,3,4\}$, where $x_1^i{x}_1^j\in E\left(G\right)$, then $n{K}_2\subseteq G$; a contradiction. Now, we have $K_4\cong \overline{G}[x_1^1,x_1^2,x_1^3,x_1^4]\subseteq \overline{G^g}$. Since $n{K}_2⊈G$ and $\lceil \frac{n+1}{2}\rceil =\lceil \frac{2k+1}{2}\rceil =k+1$, we have $|V\left(K_{4\times k}\right)\backslash V\left(M\right)|=2n-2(n-1)=2$, that is, there exists two vertices, say $w_1$ and $w_2$ in $V\left(K_{4\times k}\right)\backslash V\left(M\right)$. Since $n{K}_2⊈G$, we have $G\left[S\right]\subseteq \overline{G}$, where $S=\left\{x_1^i\right|i=1,2,3,4\}\cup \{w_1,w_2\}$. Hence, we have the following claim:

Claim 8.

Let $e=v_1{v}_2\in E\left(M\right)$ and w.l.g., we may assume that $|N_G\left(v_1\right)\cap S|\ge |N_G\left(v_2\right)\cap S|$. If $|N_G\left(v_1\right)\cap S|\ge 2$ then $|N_G\left(v_2\right)\cap S|=0$. If $|N_G\left(v_1\right)\cap S|=1$ then $|N_G\left(v_2\right)\cap S|\le 1$. If $|N_G\left(v_i\right)\cap S|=1$ then $v_1$ and $v_2$ have the same neighbor in S.

Proof of the Claim. By contradiction. We may assume that $\{w,w^{\prime }\}\subseteq N_G\left(v_1\right)\cap S$ and $w^{″}\in N_G\left(v_2\right)\cap S$, in this case, we set $M^{\prime }=(M\backslash \left\{v_1{v}_2\right\})\cup \{v_{1}w,v_2{w}^{″}\}$. Clearly, $M^{\prime }$ is a match with $|M^{\prime }|>|M|=n-1$, which contradicts the $n{K}_2⊈G$. If $|N_G\left(v_i\right)\cap S|=1$ and $v_i$ has a different neighbor, then the proof is same.

Since $n\ge 4$ and $\left|M\right|\ge 3$. If $\{w_1,w_2\}\subseteq X_i$, say $X_1$, then there is at least one edge, say $e=vu\in E\left(M\right)$ such that $v,u\notin X_1$. Otherwise, we have $C_7\subseteq K_{3\times 3}\subseteq \overline{G}[X_2,X_3,X_4]$; we again have a contradiction. W.l.g., let $|N_G\left(v\right)\cap S|\ge |N_G\left(u\right)\cap S|$. Now, by Claim 8 we have $|N_G\left(u\right)\cap S|\le 1$. One can easily check that in any case, we have $C_7\subseteq \overline{G}[S\cup \left\{u\right\}]$; again a contradiction. So w.l.g., let $w_1\in X_1$ and $w_2\in X_2$. In this case, since $|N_G\left(u\right)\cap S|\le 1$, we have $C_7\subseteq \overline{G}[S\cup \left\{u\right\}]$; a contradiction again.

Case 2: $n=2k+1$ where $k\ge 2$, $|X_i|=k+1$. Suppose that $m_4((n-2)K_2,C_7)\le \lceil \frac{n-2+1}{2}\rceil$ for $n\ge 2$. We show that $m_4(n{K}_2,C_7)\le \lceil \frac{n+1}{2}\rceil$ as follows: by contradiction, we may assume that $m_4(n{K}_2,C_7)>\lceil \frac{n+1}{2}\rceil$, that is, $K_{4\times t}$ is 2-colorable to $(n{K}_2,C_7)$, say $n{K}_2⊈G$ and $C_7⊈\overline{G}$. Let $X_i^{\prime }=X_i\backslash \left\{x_1^i\right\}$. By the induction hypothesis, we have $m_4((n-2)K_2,C_7)\le \lceil \frac{n-1}{2}\rceil =\lceil \frac{2k}{2}\rceil =k$. Therefore, since $|X_i^{\prime }|=k$ and $C_7⊈\overline{G}$, we have $M=(n-2)K_2\subseteq G[X_1^{\prime },X_2^{\prime },X_3^{\prime },X_4^{\prime }]$ and thus, we have the following claim:

Claim 9.

There exist two edges, say $e_1=uv$ and $e_2=u^{\prime }{v}^{\prime }$ in $E\left(M\right)=E\left((n-2)K_2\right)$, such that $v,v^{\prime },u$ and $u^{\prime }$ are in different partites.

Proof of the Claim. W.l.g., assume that $v\in X_1^{\prime }$ and $u\in X_2^{\prime }$. By contradiction, assume that $|E\left(M\right)\cap E(G[X_3^{\prime },X_4^{\prime }]\left)\right|=0$, that is, $G[X_3^{\prime },X_4^{\prime }]\subseteq \overline{G}$. Since $\left|V\right(M\left)\right|=2(n-2)$ and $|X_i^{\prime }|=k$, we have $|V\left(M\right)\cap X_i^{\prime }|\ge k-2$. Since $k\ge 3$, $|V\left(M\right)\cap X_j^{\prime }|\ge 1(j=3,4)$. W.l.g., let $e_j^{\prime }=x_j{y}_j\in E\left(M\right)$ where $x_j\in V\left(M\right)\cap X_j^{\prime }$. W.l.g., we may assume that $y_3\in V\left(M\right)\cap X_1^{\prime }$. Hence, we have $y_4\in V\left(M\right)\cap X_1^{\prime }$. In other words, take $e_1=x_3{y}_3$ and $e_2=x_4{y}_4$ and the proof is complete. Hence, we have $|E\left(M\right)\cap E(G[X_2^{\prime },X_j^{\prime }]\left)\right|=0$ for $j=3,4$, in other words, if there exists $e^{″}\in E\left(M\right)\cap E\left(G[X_2^{\prime },X_j^{\prime }]\right)$, then set $e_1=e_1^{\prime }$ and $e_2=e^{″}$ and the proof is complete. Therefore, for each $e\in E\left(M\right)$ we have $v\left(e\right)\cap X_1^{\prime }\ne \mathsf{\varnothing }$ which means that $\left|M\right|\le X_1^{\prime }=k$; a contradiction to $\left|M\right|$.

Now, by Claim 9 there exist two edges, say $e_1=uv$ and $e_2=u^{\prime }{v}^{\prime }$ in $E\left(M\right)=E\left((n-2)K_2\right)$, such that $v,v^{\prime },u$ and $u^{\prime }$ are in different partite. W.l.g., let $e_1=x_1{x}_2$ and $e_2=x_3{x}_4$, since are these edges, and let $x_i\in X_i^{\prime }$ for $i=1,2,3,4$. Set $X_i^{″}=X_i\backslash \left\{x_i\right\}$, hence, we have $|X_i^{″}|=k$. Since $C_7⊈\overline{G}$, we have $C_7⊈\overline{G}[X_1^{″},X_2^{″},X_3^{″},X_4^{″}]$. Therefore, by the induction hypothesis, we have $(n-2)K_2\subseteq G[X_1^{″},X_2^{″},X_3^{″},X_4^{″}]$. Let $M=(n-2)K_2\subseteq G[X_1^{″},X_2^{″},X_3^{″},X_4^{″}]$, set $M^{\ast }=M\cup \{e_1,e_2\}$ hence $|M^{\ast }|=n$, that is, $n{K}_2\subseteq G$; again a contradiction. Hence, the assumption that $m_4(n{K}_2,C_7)>\lceil \frac{n+1}{2}\rceil$ does not hold and we have $m_4(n{K}_2,C_7)\le \lceil \frac{n+1}{2}\rceil$. This completes the induction step and the proof is complete. By Cases 1 and 2, we have $m_4(n{K}_2,C_7)=\lceil \frac{n+1}{2}\rceil$ for $n\ge 4$. □

The results of Proposition 1 as well as Lemmas 8 and 11 concludes the proof of Theorem 2.

4. Concluding Remarks and Further Works

There are several papers in which the multipartite Ramsey numbers have been studied. In this paper, as a first target, we compute the size of the multipartite Ramsey number $m_j(K_{1,2},P_4,n{K}_2)$ for $n,j\ge 2$. To approach this purpose, we prove four lemmas as follows:

• $m_j(K_{1,2},P_4,n{K}_2)\ge \lfloor \frac{2n}{j}\rfloor +1$ where $j,n\ge 2$;
• $m_2(K_{1,2},P_4,n{K}_2)=n+1$ for $n\ge 2$;
• $m_3(K_{1,2},P_4,n{K}_2)=\lfloor \frac{2n}{3}\rfloor +1$ for $n\ge 2$;
• Let $j\ge 4$ and $n\ge 2$. Given that $m_j(K_{1,2},P_4,(n-1)K_2)=\lfloor \frac{2(n-1)}{j}\rfloor +1$, it follows that $m_j(K_{1,2},P_4,n{K}_2)\le \lfloor \frac{2n}{j}\rfloor +1.$

We computed the size of the multipartite Ramsey numbers $m_j(n{K}_2,C_7)$, for $j\le 4$ and $n\ge 2$ as the second purpose of this paper. This extended the result of [10]. To approach this purpose, we proved the following:

• $m_3(n{K}_2,C_7)=3$ where $n=2,3$;
• For each $n\ge 3$ we have $m_3(n{K}_2,C_7)=n$;
• For $n\ge 4$ we have $m_4(n{K}_2,C_7)=\lceil \frac{n+1}{2}\rceil$; We estimated our result for $m_j(n{K}_2,C_7)$ which holds for every $j\ge 2$, so it could be a good problem to work on.

In addition, one can compute $m_j(K_{1,2},P_4,m_1{K}_2,m_2{K}_2)$ and also $m_j(n{K}_2,C_7)$, for $j\ge 5$ and $n\ge 2$ in the future, using the idea of proofs in this paper.