A Family of Functionally-Fitted Third Derivative Block Falkner Methods for Solving Second-Order Initial-Value Problems with Oscillating Solutions
Abstract
1. Introduction
2. Development of the BFFM
2.1. Derivation of the BFFM
2.2. Specification of the BFFM
3. Analysis of the BFFM
3.1. Algebraic Order, Local Truncation Errors and Consistency of the BFFM
3.1.1. Local Truncation Error of BFFM
3.1.2. Consistency of the BFFM
3.2. Stability of the BFFM
3.2.1. Zero Stability of BFFM
3.2.2. Convergence of BFFM
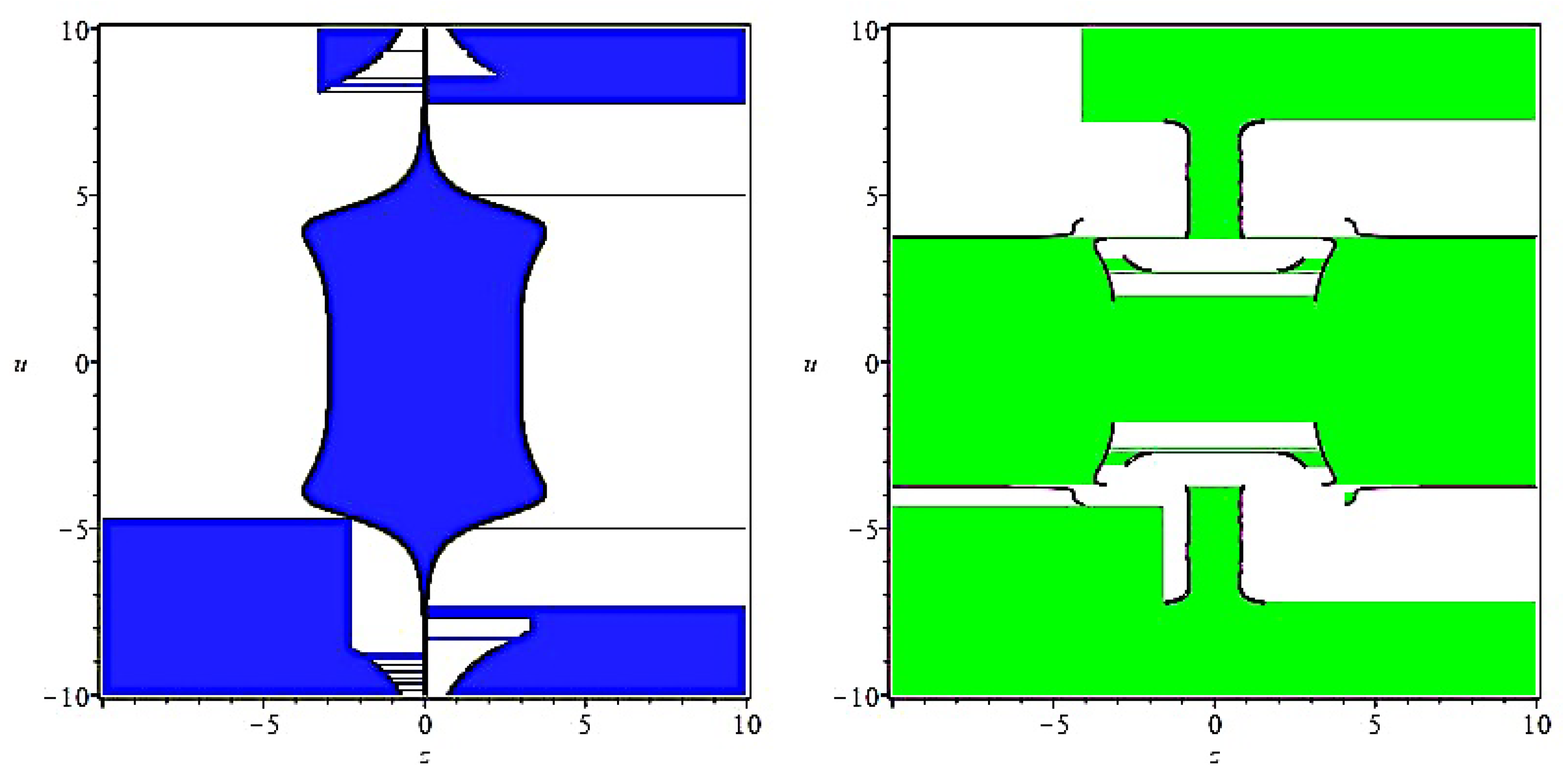
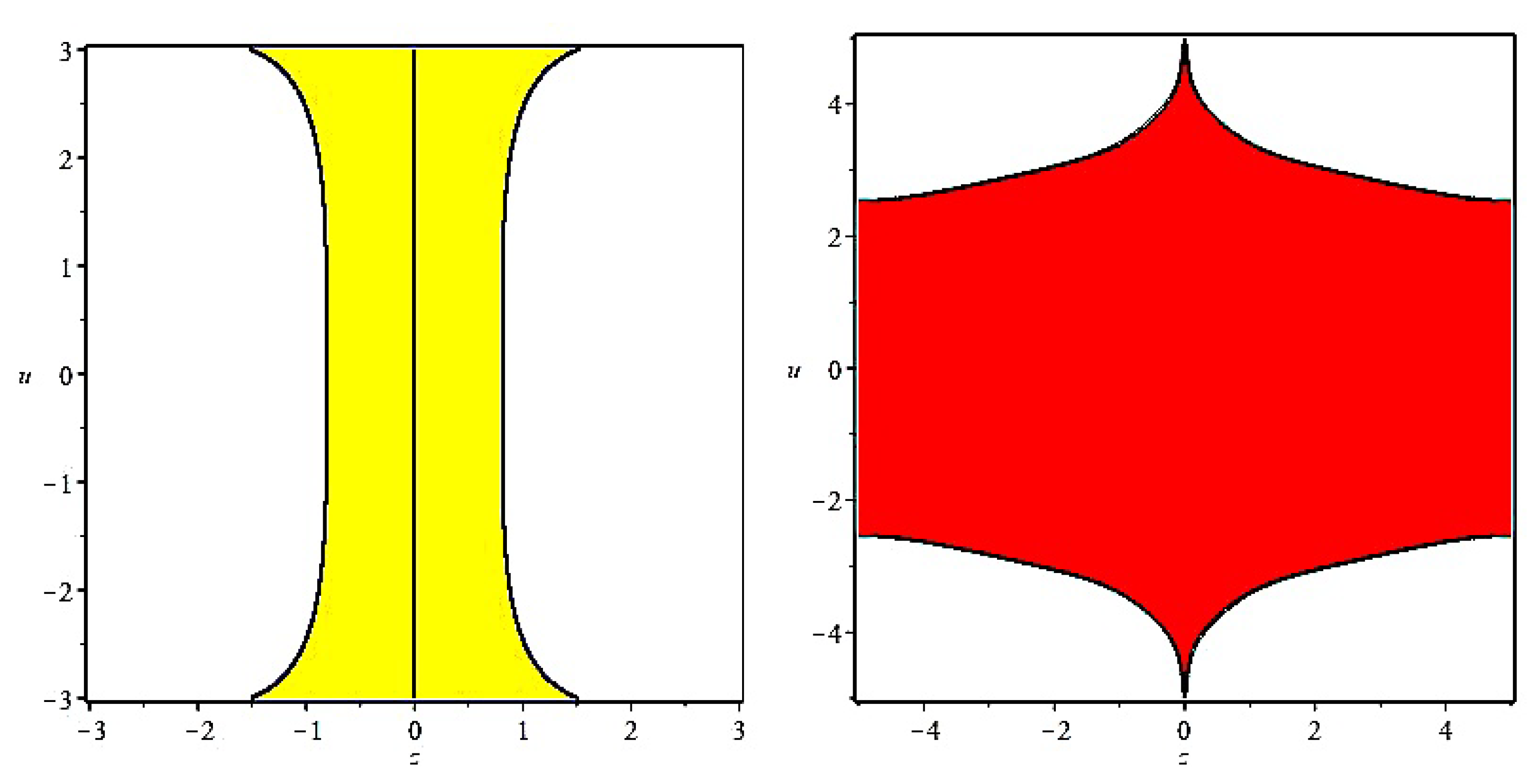
3.2.3. Linear Stability and Region of Stability of BFFM
4. Implementation and Numerical Experiments
4.1. Implementation of BFFM
- 64 bit Windows 10 Pro Operating System,
- Intel (R) Celeron CPU N3060 @ 1.60 GHz processor, and
- 4.00GB RAM memory.
4.2. Numerical Examples
4.3. Problems Where the First Derivative Appears Explicitly
4.3.1. Example 1
4.3.2. Example 2
4.3.3. Example 3
4.4. Problems Where the First Derivative Does Not Appear Explicitly
4.4.1. Example 4
4.4.2. Example 5
4.4.3. Example 6
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Specification of Entries of Matrix Π, the Determinant of Π and Determinants of Πi
Appendix B. Coefficients of the Main Methods of the BFFM for k = 2
Appendix C. Matrices RA1 − A0 for k = 2 and k = 3
Appendix D. Illustration of Step 2 of the Implementation for k = 2 When n = 0 and n = 2
References
- Lambert, J.D.; Watson, I.A. Symmetric multistip methods for periodic initial value problems. IMA J. Appl. Math. 1976, 18, 189–202. [Google Scholar] [CrossRef]
- Anantha Krishnaiah, U. P-stable Obrechkoff methods with minimal phase-lag for periodic initial value problems. Math. Comput. 1987, 49, 553–559. [Google Scholar] [CrossRef]
- Simos, T. Dissipative trigonometrically-fitted methods for second order IVPs with oscillating solution. Int. J. Mod. Phys. C 2002, 13, 1333–1345. [Google Scholar] [CrossRef]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I. Nonstiff Problems; Springer: Berlin, Germany, 1993. [Google Scholar]
- Tsitouras, C. Explicit eighth order two-step methods with nine stages for integrating oscillatory problems. Int. J. Mod. Phys. C 2006, 17, 861–876. [Google Scholar] [CrossRef]
- Tsitouras, C.; Simos, T. Trigonometric-fitted explicit numerov-type method with vanishing phase-lag and its first and second derivatives. Mediterr. J. Math. 2018, 15, 168. [Google Scholar] [CrossRef]
- Wang, B.; Liu, K.; Wu, X. A Filon-type Asymptotic Approach to Solving Highly Oscillatory Second-Order Initial Value Problems. J. Comput. Phys. 2013, 243, 210–223. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; You, X.; Wu, X. Two-step extended RKN methods for oscillatory systems. Comput. Phys. Commun. 2011, 182, 2486–2507. [Google Scholar] [CrossRef]
- Franco, J. New methods for oscillatory systems based on ARKN methods. Appl. Numer. Math. 2006, 56, 1040–1053. [Google Scholar] [CrossRef]
- Franco, J. Runge–Kutta methods adapted to the numerical integration of oscillatory problems. Appl. Numer. Math. 2004, 50, 427–443. [Google Scholar] [CrossRef]
- Ramos, H.; Patricio, M. Some new implicit two-step multiderivative methods for solving special second-order IVP’s. Appl. Math. Comput. 2014, 239, 227–241. [Google Scholar] [CrossRef]
- Chen, Z.; You, X.; Shi, W.; Liu, Z. Symmetric and symplectic ERKN methods for oscillatory Hamiltonian systems. Comput. Phys. Commun. 2012, 183, 86–98. [Google Scholar] [CrossRef]
- Shi, W.; Wu, X. On symplectic and symmetric ARKN methods. Comput. Phys. Commun. 2012, 183, 1250–1258. [Google Scholar] [CrossRef]
- Fang, Y.; Song, Y.; Wu, X. A robust trigonometrically fitted embedded pair for perturbed oscillators. J. Comput. Appl. Math. 2009, 225, 347–355. [Google Scholar] [CrossRef][Green Version]
- Senu, N.; Suleiman, M.; Ismail, F.; Othman, M. A new diagonally implicit Runge-Kutta-Nyström method for periodic IVPs. WSEAS Trans. Math. 2010, 9, 679–688. [Google Scholar] [CrossRef]
- Guo, B.Y.; Yan, J.P. Legendre–Gauss collocation method for initial value problems of second order ordinary differential equations. Appl. Numer. Math. 2009, 59, 1386–1408. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ramos, H. Variable stepsize implementation of multistep methods for y″ = f(x,y,y′). J. Comput. Appl. Math. 2006, 192, 114–131. [Google Scholar] [CrossRef]
- Jator, S.N. Implicit third derivative Runge-Kutta-Nyström method with trigonometric coefficients. Numer. Algorithms 2015, 70, 133–150. [Google Scholar] [CrossRef]
- Ngwane, F.; Jator, S. A trigonometrically fitted block method for solving oscillatory second-order initial value problems and Hamiltonian systems. Int. J. Differ. Equ. 2017, 2017, 9293530. [Google Scholar] [CrossRef]
- Mahmoud, S.; Osman, M.S. On a class of spline-collocation methods for solving second-order initial-value problems. Int. J. Comput. Math. 2009, 86, 616–630. [Google Scholar] [CrossRef]
- Awoyemi, D. A new sixth-order algorithm for general second order ordinary differential equations. Int. J. Comput. Math. 2001, 77, 117–124. [Google Scholar] [CrossRef]
- Liu, K.; Wu, X. Multidimensional ARKN methods for general oscillatory second-order initial value problems. Comput. Phys. Commun. 2014, 185, 1999–2007. [Google Scholar] [CrossRef]
- You, X.; Zhang, R.; Huang, T.; Fang, Y. Symmetric collocation ERKN methods for general second-order oscillators. Calcolo 2019, 56, 52. [Google Scholar] [CrossRef]
- Li, J.; Lu, M.; Qi, X. Trigonometrically fitted multi-step hybrid methods for oscillatory special second-order initial value problems. Int. J. Comput. Math. 2018, 95, 979–997. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, Z.; Li, J.; You, X. Two-derivative Runge-Kutta-Nyström methods for second-order ordinary differential equations. Numer. Algorithms 2015, 70, 897–927. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Lu, M. A class of linear multi-step method adapted to general oscillatory second-order initial value problems. J. Appl. Math. Comput. 2018, 56, 561–591. [Google Scholar] [CrossRef]
- You, X.; Zhao, J.; Yang, H.; Fang, Y.; Wu, X. Order conditions for RKN methods solving general second-order oscillatory systems. Numer. Algorithms 2014, 66, 147–176. [Google Scholar] [CrossRef]
- Falkner, V.L. A method of numerical solution of differential equations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1936, 21, 624–640. [Google Scholar] [CrossRef]
- Collatz, L. The Numerical Treatment of Differential Equations; Springer Science & Business Media: Berlin, Germany, 2012; Volume 60. [Google Scholar]
- Ramos, H.; Mehta, S.; Vigo-Aguiar, J. A unified approach for the development of k-step block Falkner-type methods for solving general second-order initial-value problems in ODEs. J. Comput. Appl. Math. 2017, 318, 550–564. [Google Scholar] [CrossRef]
- Ramos, H.; Lorenzo, C. Review of explicit Falkner methods and its modifications for solving special second-order IVPs. Comput. Phys. Commun. 2010, 181, 1833–1841. [Google Scholar] [CrossRef]
- Ramos, H.; Singh, G.; Kanwar, V.; Bhatia, S. An efficient variable step-size rational Falkner-type method for solving the special second-order IVP. Appl. Math. Comput. 2016, 291, 39–51. [Google Scholar] [CrossRef]
- Ramos, H.; Rufai, M.A. Third derivative modification of k-step block Falkner methods for the numerical solution of second order initial-value problems. Appl. Math. Comput. 2018, 333, 231–245. [Google Scholar] [CrossRef]
- Li, J.; Wu, X. Adapted Falkner-type methods solving oscillatory second-order differential equations. Numer. Algorithms 2013, 62, 355–381. [Google Scholar] [CrossRef]
- Li, J. A family of improved Falkner-type methods for oscillatory systems. Appl. Math. Comput. 2017, 293, 345–357. [Google Scholar] [CrossRef]
- Ehigie, J.; Okunuga, S. A new collocation formulation for the block Falkner-type methods with trigonometric coefficients for oscillatory second order ordinary differential equations. Afr. Mat. 2018, 29, 531–555. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 1961, 3, 381–397. [Google Scholar] [CrossRef]
- Lyche, T. Chebyshevian multistep methods for ordinary differential equations. Numer. Math. 1972, 19, 65–75. [Google Scholar] [CrossRef]
- Franco, J. An embedded pair of exponentially fitted explicit Runge–Kutta methods. J. Comput. Appl. Math. 2002, 149, 407–414. [Google Scholar] [CrossRef][Green Version]
- Franco, J. Exponentially fitted explicit Runge–Kutta–Nyström methods. J. Comput. Appl. Math. 2004, 167, 1–19. [Google Scholar] [CrossRef]
- Ixaru, L.G.; Berghe, G.V.; De Meyer, H. Frequency evaluation in exponential fitting multistep algorithms for ODEs. J. Comput. Appl. Math. 2002, 140, 423–434. [Google Scholar] [CrossRef]
- Berghe, G.V.; Van Daele, M. Exponentially-fitted Numerov methods. J. Comput. Appl. Math. 2007, 200, 140–153. [Google Scholar] [CrossRef][Green Version]
- Jator, S.N.; Swindell, S.; French, R. Trigonometrically fitted block Numerov type method for y″ = f(x,y,y′). Numer. Algorithms 2013, 62, 13–26. [Google Scholar] [CrossRef]
- Jator, S. Block third derivative method based on trigonometric polynomials for periodic initial-value problems. Afr. Mat. 2016, 27, 365–377. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. On the frequency choice in trigonometrically fitted methods. Appl. Math. Lett. 2010, 23, 1378–1381. [Google Scholar] [CrossRef]
- Vigo-Aguiar, J.; Ramos, H. On the choice of the frequency in trigonometrically-fitted methods for periodic problems. J. Comput. Appl. Math. 2015, 277, 94–105. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. Variable-stepsize Chebyshev-type methods for the integration of second-order IVP’s. J. Comput. Appl. Math. 2007, 204, 102–113. [Google Scholar] [CrossRef]
- Coleman, J.P.; Duxbury, S.C. Mixed collocation methods for y″ = f(x,y). J. Comput. Appl. Math. 2000, 126, 47–75. [Google Scholar] [CrossRef]
- Coleman, J.P.; Ixaru, L.G. P-stability and exponential-fitting methods for y″ = f(x,y). IMA J. Numer. Anal. 1996, 16, 179–199. [Google Scholar] [CrossRef]
- Nguyen, H.S.; Sidje, R.B.; Cong, N.H. Analysis of trigonometric implicit Runge–Kutta methods. J. Comput. Appl. Math. 2007, 198, 187–207. [Google Scholar] [CrossRef]
- Ozawa, K. A functionally fitted three-stage explicit singly diagonally implicit Runge-Kutta method. Jpn. J. Ind. Appl. Math. 2005, 22, 403–427. [Google Scholar] [CrossRef]
- Franco, J.; Gómez, I. Trigonometrically fitted nonlinear two-step methods for solving second order oscillatory IVPs. Appl. Math. Comput. 2014, 232, 643–657. [Google Scholar] [CrossRef]
- Wu, J.; Tian, H. Functionally-fitted block methods for ordinary differential equations. J. Comput. Appl. Math. 2014, 271, 356–368. [Google Scholar] [CrossRef]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; Wiley: Hoboken, NJ, USA, 1973. [Google Scholar]
- Simeon, O.F. Numerical Methods for Initial Value Problems in Ordinary Differential Equations; Academic Press: Cambridge, UK, 1988. [Google Scholar]
- Ola Fatunla, S. Block methods for second order ODEs. Int. J. Comput. Math. 1991, 41, 55–63. [Google Scholar] [CrossRef]
- Jator, S.; Oladejo, H. Block Nyström method for singular differential equations of the Lane–Emden type and problems with highly oscillatory solutions. Int. J. Appl. Comput. Math. 2017, 3, 1385–1402. [Google Scholar] [CrossRef]
- Ngwane, F.; Jator, S. Solving the telegraph and oscillatory differential equations by a block hybrid trigonometrically fitted algorithm. Int. J. Differ. Equ. 2015, 2015. [Google Scholar] [CrossRef]
- Andersen, C.; Geer, J.F. Power series expansions for the frequency and period of the limit cycle of the van der Pol equation. SIAM J. Appl. Math. 1982, 42, 678–693. [Google Scholar] [CrossRef]
- Vehrulst, F. Nonlinear Differential Equations and Dynamical Systems, Universitext; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Jator, S.N.; King, K.L. Integrating oscillatory general second-order initial value Problems using a block hybrid method of order 11. Math. Probl. Eng. 2018, 2018, 3750274. [Google Scholar] [CrossRef]
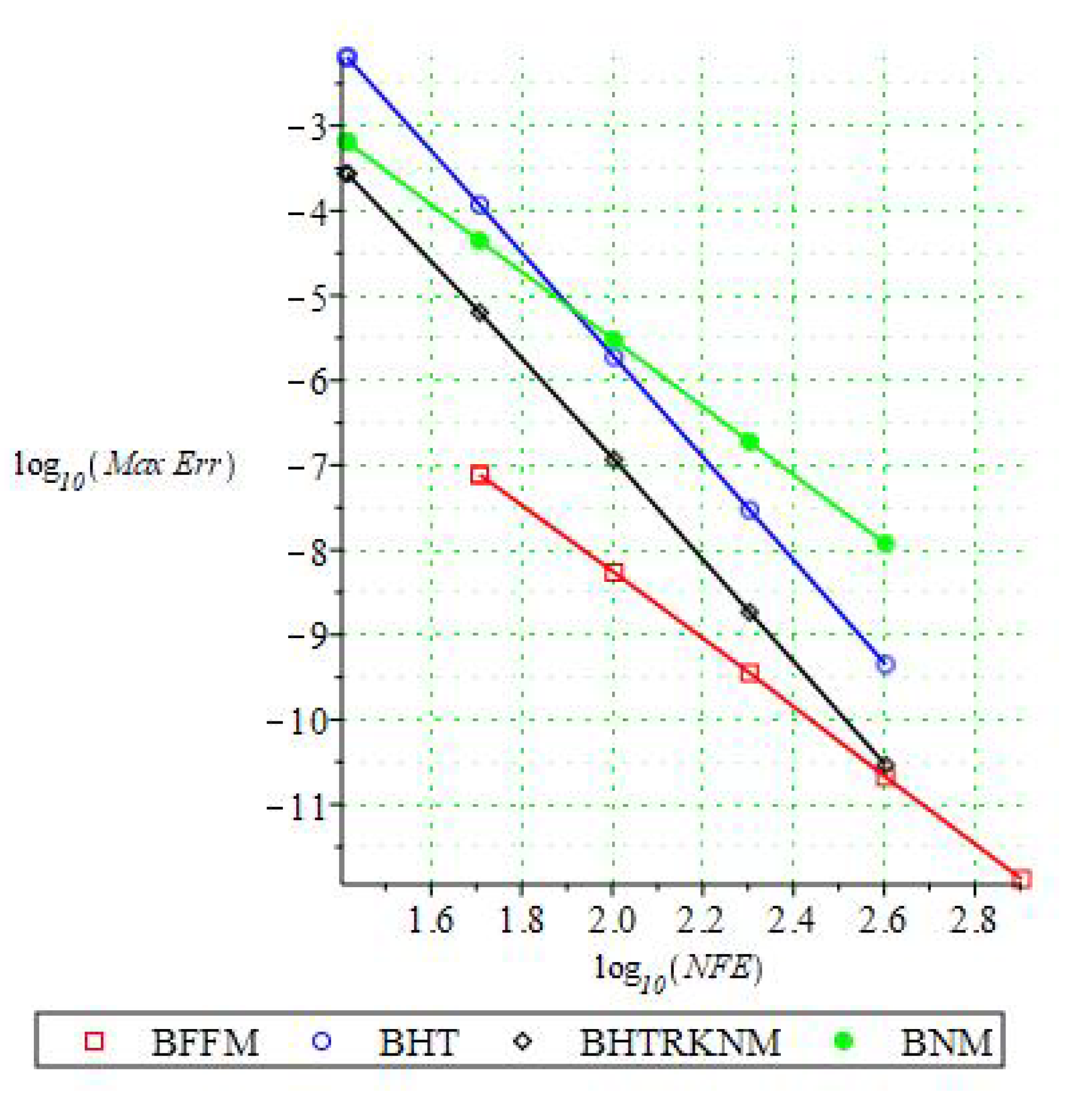
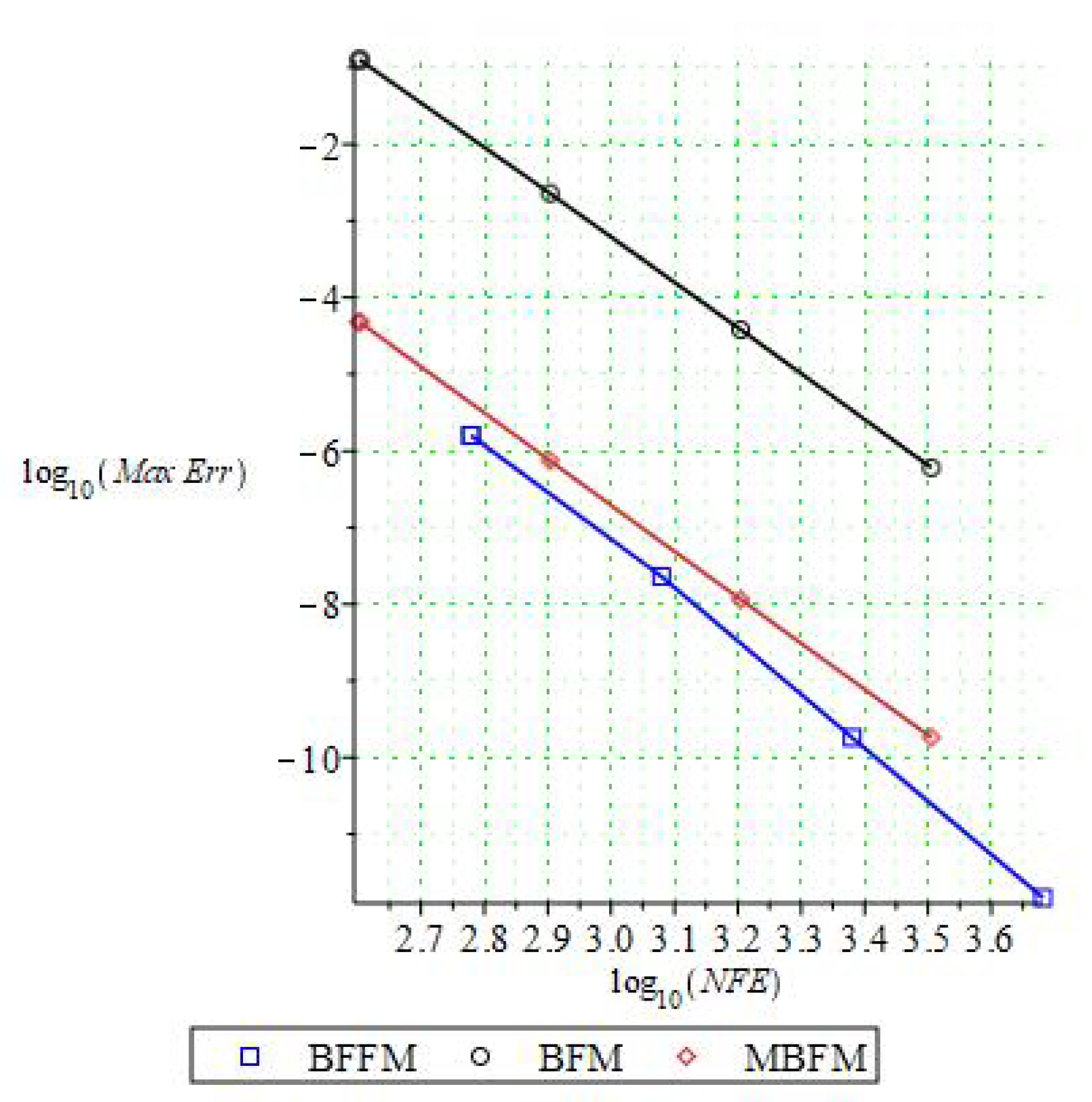


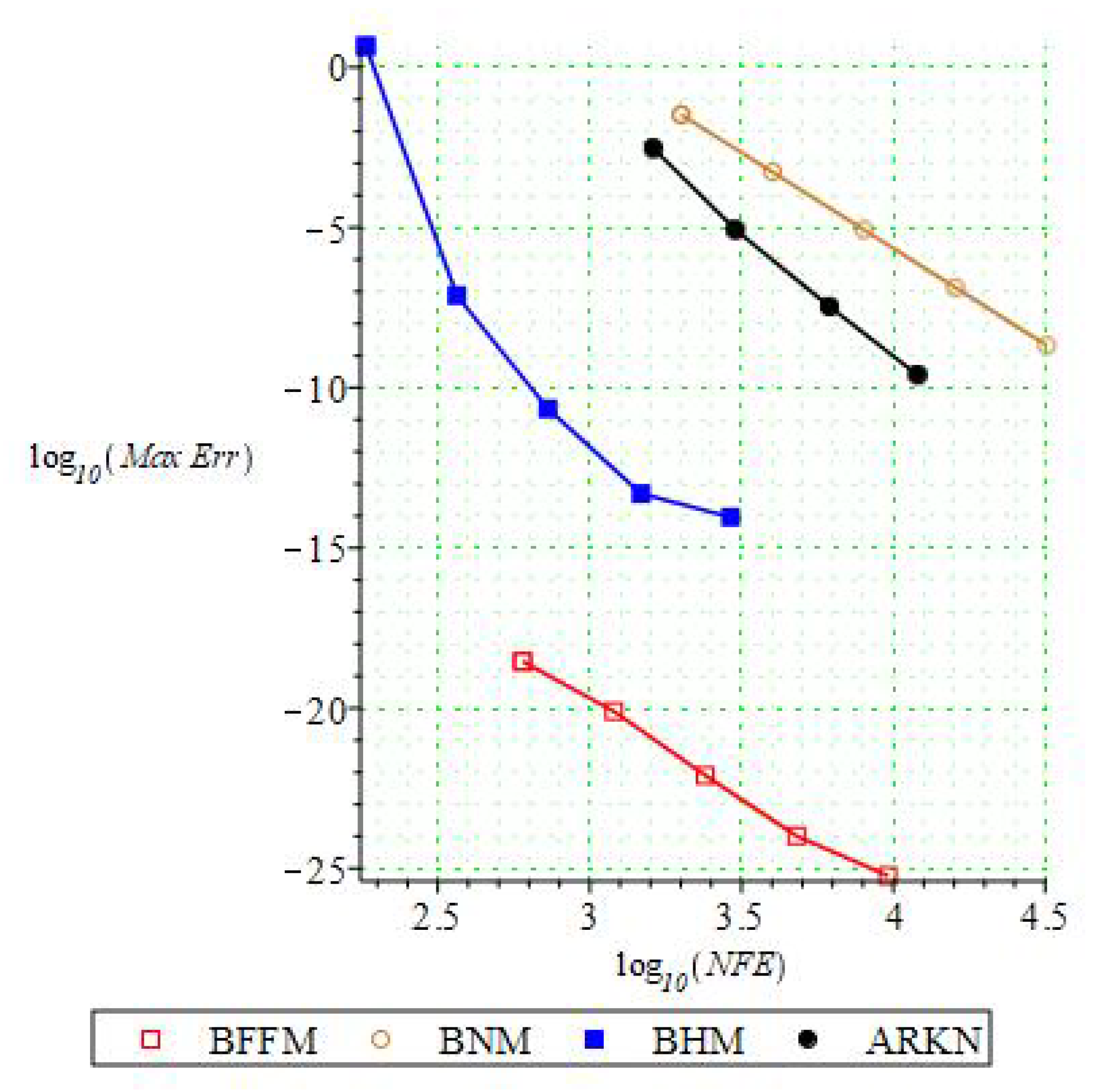
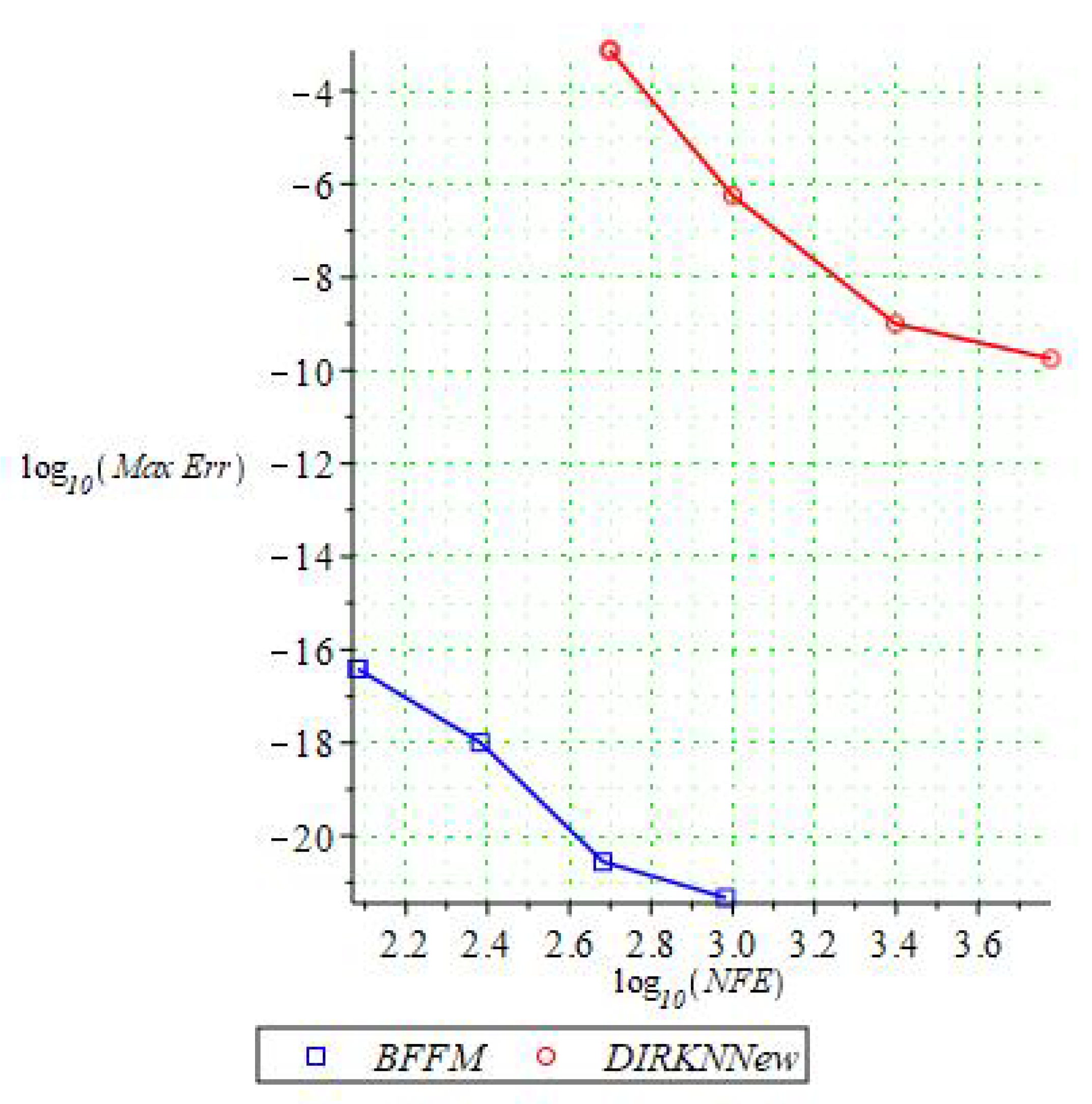
| h | BFFM | BHT | BHTRKNM | BNM | ||||
|---|---|---|---|---|---|---|---|---|
| Error | NFE | Error | NFE | Error | NFE | Error | NFE | |
| 2 | 51 | 26 | 26 | 26 | ||||
| 1 | 101 | 51 | 51 | 51 | ||||
| 201 | 101 | 101 | 101 | |||||
| 401 | 201 | 201 | 201 | |||||
| 801 | 401 | 401 | 401 | |||||
| h | BFFM | BFM | MBFM | |||
|---|---|---|---|---|---|---|
| Error | NFE | Error | NFE | Error | NFE | |
| 601 | 401 | 401 | ||||
| 1201 | 801 | 801 | ||||
| 2401 | 1601 | 1601 | ||||
| 4801 | 3201 | 3201 | ||||
| h | BFFM | BFM | MBFM | TDRKN2 | TDRKN3 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Error | NFE | Error | NFE | Error | NFE | Error | NFE | Error | NFE | |
| 151 | 101 | 101 | 603 | 631 | ||||||
| 301 | 201 | 201 | 1202 | 1230 | ||||||
| 601 | 401 | 401 | 2344 | 2455 | ||||||
| 1201 | 801 | 801 | 4786 | 5012 | ||||||
| BFFM | TFARKN | EFRK | EFRKN | ||||
|---|---|---|---|---|---|---|---|
| Error | NFE | Error | NFE | Error | NFE | Error | NFE |
| 301 | 300 | 8000 | 2000 | ||||
| 601 | 400 | 14,000 | 5000 | ||||
| 1201 | 600 | 22,000 | 9000 | ||||
| 2401 | 4200 | 38,000 | 19,000 | ||||
| BFFM | BNM | BHM | ARKN | ||||
|---|---|---|---|---|---|---|---|
| Error | NFE | Error | NFE | Error | NFE | Error | NFE |
| 601 | 2001 | 183 | 1621 | ||||
| 1201 | 4001 | 365 | 3020 | ||||
| 2401 | 8001 | 728 | 6166 | ||||
| 4801 | 16,001 | 1476 | 12,022 | ||||
| 9601 | 32,001 | 2910 | NIL | NIL | |||
| BFFM | DIRKNNew | ||
|---|---|---|---|
| Error | NFE | Error | NFE |
| 121 | 5000 | ||
| 241 | 10,000 | ||
| 481 | 25,000 | ||
| 961 | 60,000 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, H.; Abdulganiy, R.; Olowe, R.; Jator, S. A Family of Functionally-Fitted Third Derivative Block Falkner Methods for Solving Second-Order Initial-Value Problems with Oscillating Solutions. Mathematics 2021, 9, 713. https://doi.org/10.3390/math9070713
Ramos H, Abdulganiy R, Olowe R, Jator S. A Family of Functionally-Fitted Third Derivative Block Falkner Methods for Solving Second-Order Initial-Value Problems with Oscillating Solutions. Mathematics. 2021; 9(7):713. https://doi.org/10.3390/math9070713
Chicago/Turabian StyleRamos, Higinio, Ridwanulahi Abdulganiy, Ruth Olowe, and Samuel Jator. 2021. "A Family of Functionally-Fitted Third Derivative Block Falkner Methods for Solving Second-Order Initial-Value Problems with Oscillating Solutions" Mathematics 9, no. 7: 713. https://doi.org/10.3390/math9070713
APA StyleRamos, H., Abdulganiy, R., Olowe, R., & Jator, S. (2021). A Family of Functionally-Fitted Third Derivative Block Falkner Methods for Solving Second-Order Initial-Value Problems with Oscillating Solutions. Mathematics, 9(7), 713. https://doi.org/10.3390/math9070713







