An Extended SEIR Model with Vaccination for Forecasting the COVID-19 Pandemic in Saudi Arabia Using an Ensemble Kalman Filter
Abstract
1. Introduction
2. Model and Assimilation Scheme
2.1. Extended SEIR Model
2.2. Ensemble Kalman Filter (EnKF)
3. Mathematical Analysis of the COVID-19 Model
3.1. Non-Negativity of the Model
3.2. Boundedness of the Model
3.3. Epidemic Equilibrium and Basic Reproduction Number of the Model
3.4. Existence and Uniqueness of the Endemic Equilibrium
4. Results and Discussion
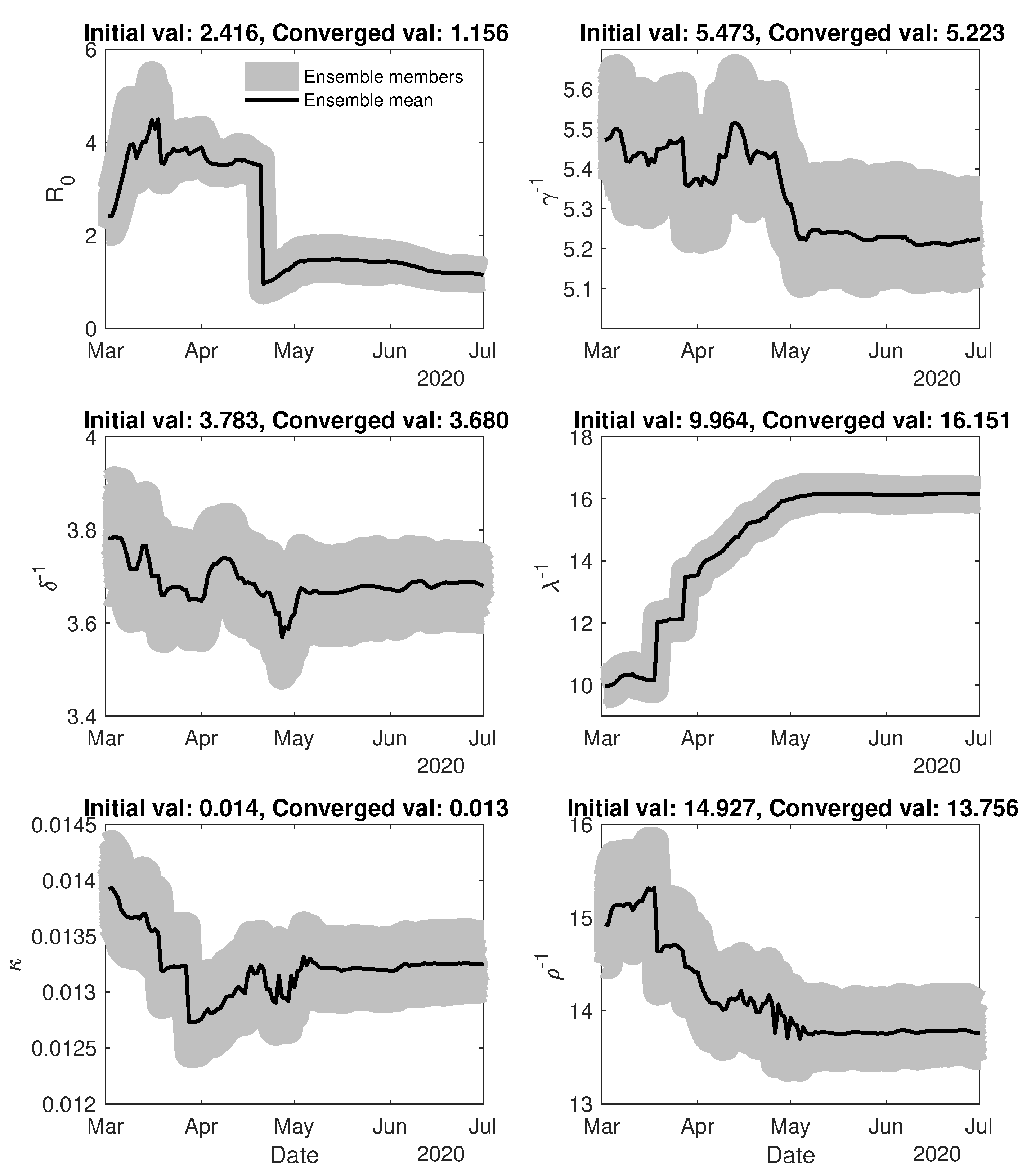
4.1. Assimilation Settings
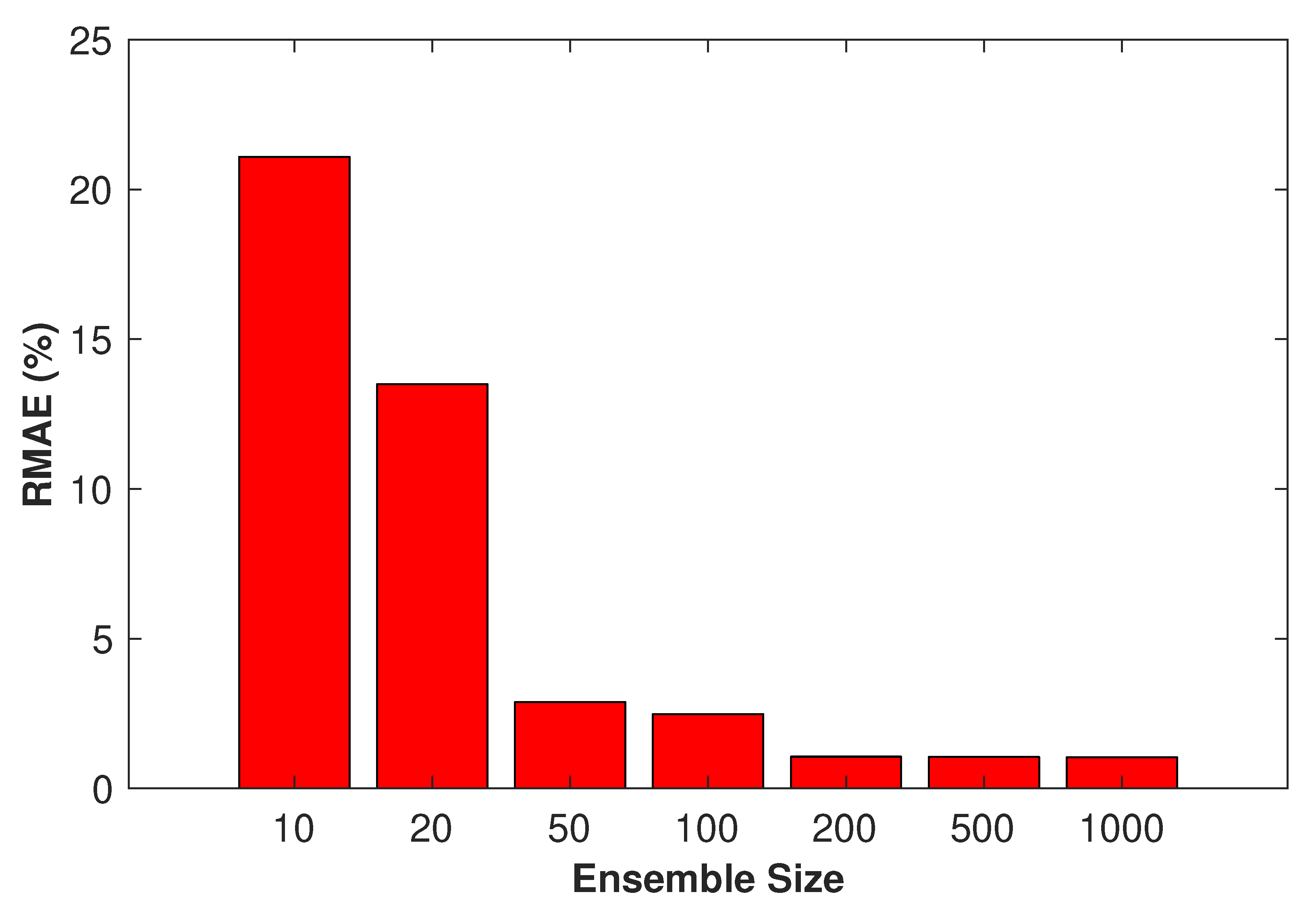
4.2. Sensitivity to Ensemble Size
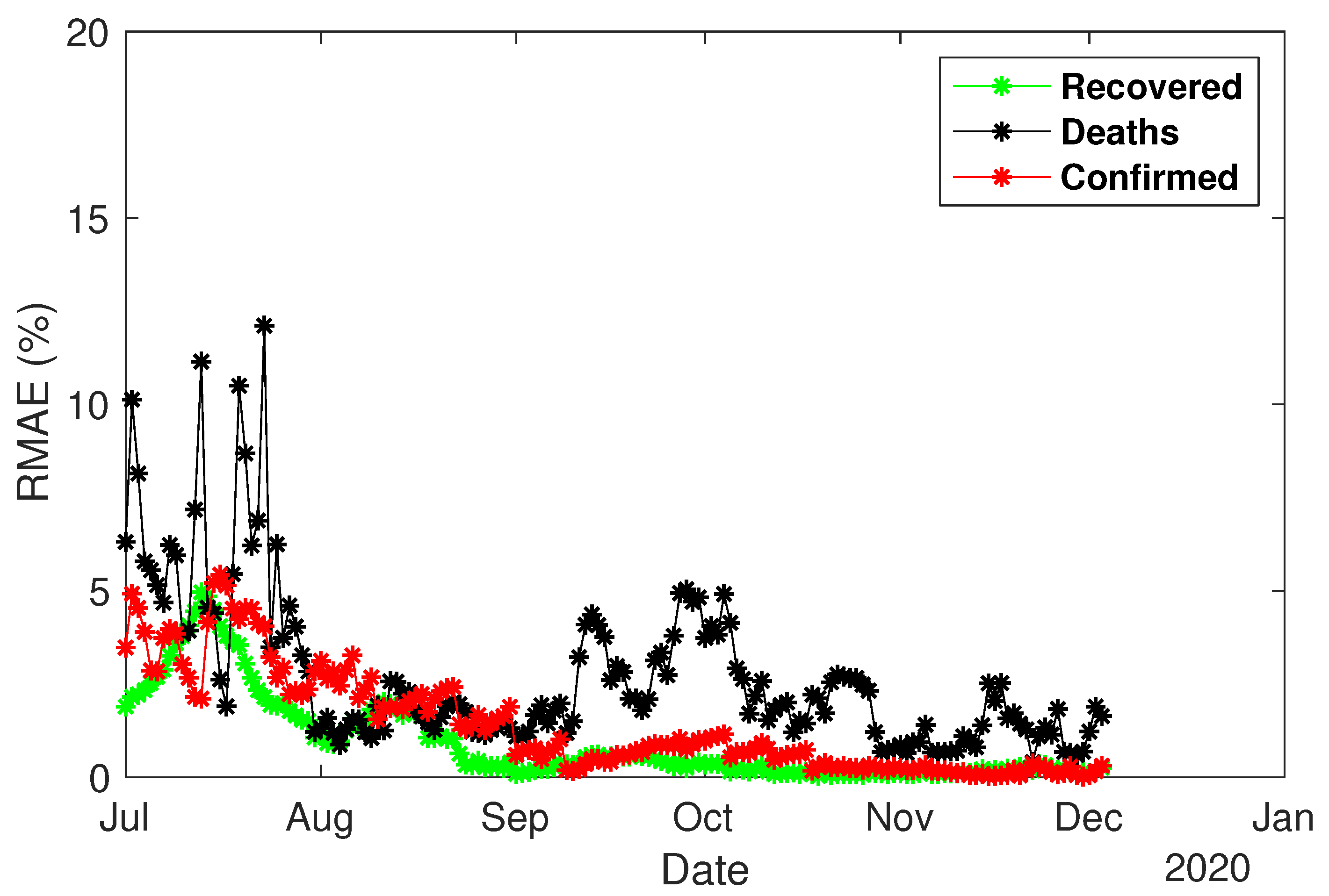
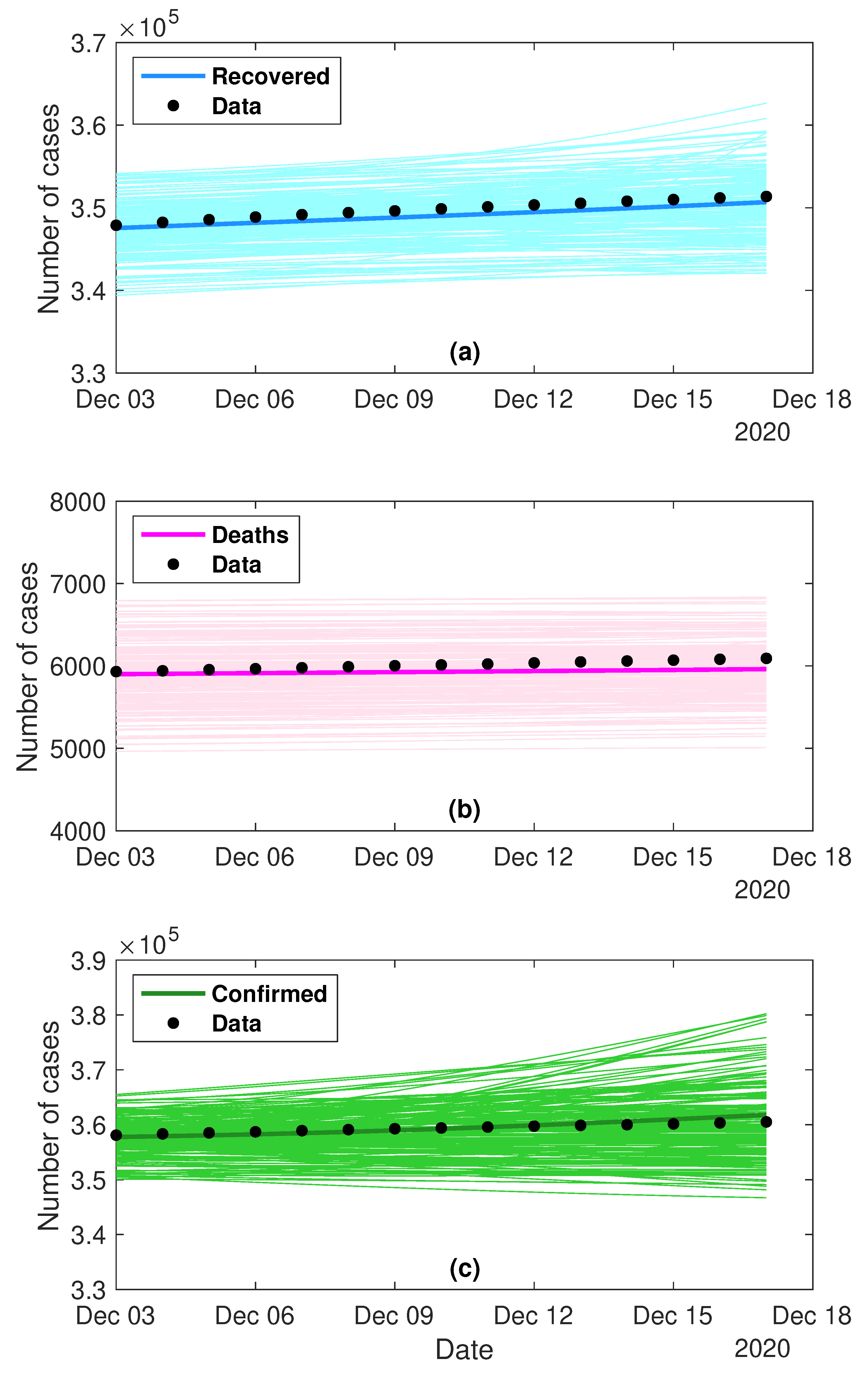
4.3. Predictability Experiment
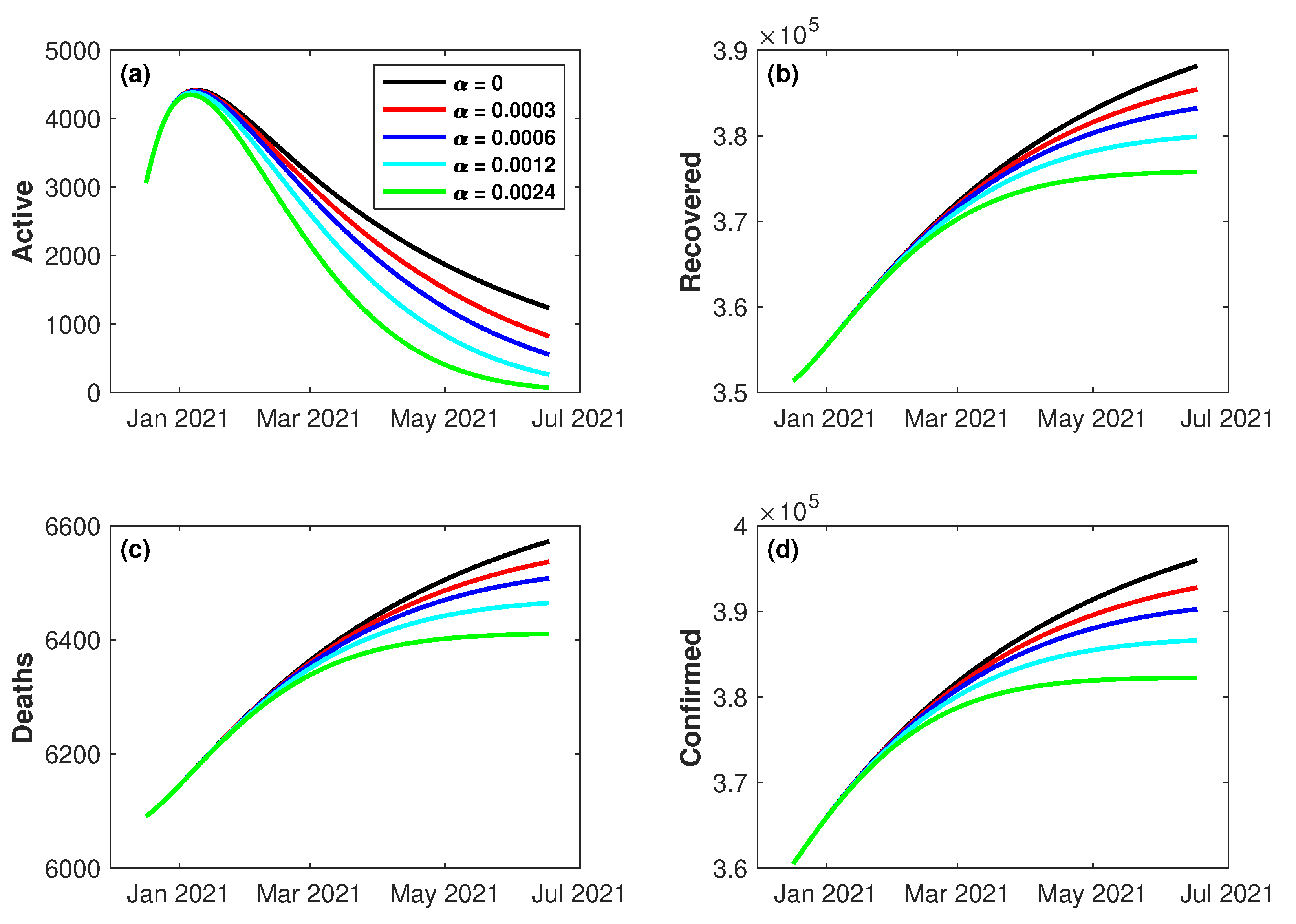
4.4. Impact of Vaccination
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization (WHO). Coronavirus Disease (COVID-19) Outbreak Situation. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 17 December 2020).
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. 1927, 115, 700–721. [Google Scholar]
- Giraldo, J.O.; Palacio, D.H. Deterministic SIR (Susceptible–Infected–Removed) models applied to varicella outbreaks. Epidemiol. Infect. 2008, 136, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Fung, I.C.H. Cholera transmission dynamic models for public health practitioners. Emerg. Themes Epidemiol. 2014, 11, 1–11. [Google Scholar] [CrossRef]
- Trawicki, M.B. Deterministic SEIRs epidemic model for modeling vital dynamics, vaccinations, and temporary immunity. Mathematics 2017, 5, 7. [Google Scholar] [CrossRef]
- Bjørnstad, O.N.; Shea, K.; Krzywinski, M.; Altman, N.S. The SEIRS model for infectious disease dynamics. Nat. Methods 2020, 17, 557–558. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmadian, A.; Kumar, R.; Kumar, D.; Singh, J.; Baleanu, D.; Salimi, M. An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics 2020, 8, 558. [Google Scholar] [CrossRef]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020, 139, 110057. [Google Scholar] [CrossRef]
- Bärwolff, G. Mathematical modeling and simulation of the COVID-19 pandemic. Systems 2020, 8, 24. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Torres, D.F. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 135, 109846. [Google Scholar] [CrossRef]
- Sarkar, K.; Khajanchi, S.; Nieto, J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals 2020, 139, 110049. [Google Scholar] [CrossRef] [PubMed]
- Ghil, M. Meteorological data assimilation for oceanographers. Part I: Description and theoretical framework. Dynam. Atmos. Ocean 1989, 13, 171–218. [Google Scholar] [CrossRef]
- Holland, W.R.; Malanotte-Rizzoli, P. Assimilation of altimeter data into an ocean circulation model: Space versus time resolution studies. J. Phys. Oceanogr. 1989, 19, 1507–1534. [Google Scholar] [CrossRef]
- Edwards, C.A.; Moore, A.M.; Hoteit, I.; Cornuelle, B.D. Regional ocean data assimilation. Ann. Rev. Mar. Sci. 2015, 7, 21–42. [Google Scholar] [CrossRef] [PubMed]
- Hoteit, I.; Pham, D.T.; Blum, J. A simplified reduced order Kalman filtering and application to altimetric data assimilation in Tropical Pacific. J. Mar. Syst. 2002, 36, 101–127. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Mar. Syst. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Altaf, M.; Butler, T.; Mayo, T.; Luo, X.; Dawson, C.; Heemink, A.; Hoteit, I. A comparison of ensemble Kalman filters for storm surge assimilation. Mon. Weather Rev. 2014, 142, 2899–2914. [Google Scholar] [CrossRef][Green Version]
- Buehner, M.; McTaggart-Cowan, R.; Heilliette, S. An ensemble Kalman filter for numerical weather prediction based on variational data assimilation: VarEnKF. Mon. Weather Rev. 2017, 145, 617–635. [Google Scholar] [CrossRef]
- Raboudi, N.F.; Ait-El-Fquih, B.; Dawson, C.; Hoteit, I. Combining Hybrid and One-Step-Ahead Smoothing for Efficient Short-Range Storm Surge Forecasting with an Ensemble Kalman Filter. Mon. Weather Rev. 2019, 147, 3283–3300. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the ensemble Kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Gharamti, M.; Kadoura, A.; Valstar, J.; Sun, S.; Hoteit, I. Constraining a compositional flow model with flow-chemical data using an ensemble-based Kalman filter. Water Resour. Res. 2014, 50, 2444–2467. [Google Scholar] [CrossRef]
- Gharamti, M.; Ait-El-Fquih, B.; Hoteit, I. An iterative ensemble Kalman filter with one-step-ahead smoothing for state-parameters estimation of contaminant transport models. J. Hydrol. 2015, 527, 442–457. [Google Scholar] [CrossRef]
- Ait-El-Fquih, B.; Gharamti, M.E.; Hoteit, I. A Bayesian consistent dual ensemble Kalman filter for state-parameter estimation in subsurface hydrology. Hydrol. Earth Syst. Sci. 2016, 20, 3289–3307. [Google Scholar] [CrossRef]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I.; Forootan, E.; Awange, J.; Kuhn, M. A two-update ensemble Kalman filter for land hydrological data assimilation with an uncertain constraint. J. Hydrol. 2017, 555, 447–462. [Google Scholar] [CrossRef]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I. Calibrating land hydrological models and enhancing their forecasting skills using an ensemble Kalman filter with one-step-ahead smoothing. J. Hydrol. 2020, 584, 124708. [Google Scholar] [CrossRef]
- Hoteit, I.; Hoar, T.; Gopalakrishnan, G.; Collins, N.; Anderson, J.; Cornuelle, B.; Köhl, A.; Heimbach, P. A MITgcm/DART ensemble analysis and prediction system with application to the Gulf of Mexico. Dynam. Atmos. Ocean 2013, 63, 1–23. [Google Scholar] [CrossRef]
- Triantafyllou, G.; Hoteit, I.; Luo, X.; Tsiaras, K.; Petihakis, G. Assessing a robust ensemble-based Kalman filter for efficient ecosystem data assimilation of the Cretan Sea. J. Mar. Syst. 2013, 125, 90–100. [Google Scholar] [CrossRef]
- Gharamti, M.; Tjiputra, J.; Bethke, I.; Samuelsen, A.; Skjelvan, I.; Bentsen, M.; Bertino, L. Ensemble data assimilation for ocean biogeochemical state and parameter estimation at different sites. Ocean Model. 2017, 112, 65–89. [Google Scholar] [CrossRef]
- Toye, H.; Kortas, S.; Zhan, P.; Hoteit, I. A fault-tolerant HPC scheduler extension for large and operational ensemble data assimilation: Application to the Red Sea. J. Comput. Sci. 2018, 27, 46–56. [Google Scholar] [CrossRef]
- Yu, L.; Fennel, K.; Bertino, L.; El Gharamti, M.; Thompson, K.R. Insights on multivariate updates of physical and biogeochemical ocean variables using an Ensemble Kalman Filter and an idealized model of upwelling. Ocean Model. 2018, 126, 13–28. [Google Scholar] [CrossRef]
- Neal, J.C.; Atkinson, P.M.; Hutton, C.W. Flood inundation model updating using an ensemble Kalman filter and spatially distributed measurements. J. Hydrol. 2007, 336, 401–415. [Google Scholar] [CrossRef]
- Kimura, N.; Hsu, M.H.; Tsai, M.Y.; Tsao, M.C.; Yu, S.L.; Tai, A. A river flash flood forecasting model coupled with ensemble Kalman filter. J. Flood Risk Manag. 2016, 9, 178–192. [Google Scholar] [CrossRef]
- Ziliani, M.G.; Ghostine, R.; Ait-El-Fquih, B.; McCabe, M.F.; Hoteit, I. Enhanced flood forecasting through ensemble data assimilation and joint state-parameter estimation. J. Hydrol. 2019, 577, 123924. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Ribeiro, R.M.; Chowell, G.; Lant, T.; Castillo-Chavez, C. Towards real time epidemiology: Data assimilation, modeling and anomaly detection of health surveillance data streams. In NSF Workshop on Intelligence and Security Informatics; Springer: Berlin, Germany, 2007; pp. 79–90. [Google Scholar]
- Rhodes, C.; Hollingsworth, T.D. Variational data assimilation with epidemic models. J. Theor. Biol. 2009, 258, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.; Verma, K.K.; Sharma, P. Using data assimilation technique and epidemic model to predict tb epidemic. Int. J. Comput. Appl. 2015, 128, 5. [Google Scholar] [CrossRef]
- Eksin, C.; Paarporn, K.; Weitz, J.S. Systematic biases in disease forecasting – the role of behavior change. Epidemics 2019, 27, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Engbert, R.; Rabe, M.M.; Kliegl, R.; Reich, S. Sequential data assimilation of the stochastic SEIR epidemic model for regional COVID-19 dynamics. Bull. Math. Biol. 2021, 83, 1–16. [Google Scholar] [CrossRef]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef] [PubMed]
- Van Wees, J.D.; Osinga, S.; Van Der Kuip, M.; Tanck, M.W.; Tutu-van Furth, A. Forecasting hospitalization and ICU rates of the COVID-19 outbreak: An efficient SEIR model. Bull World Health Organ 2020. [Google Scholar] [CrossRef]
- Evensen, G.; Amezcua, J.; Bocquet, M.; Carrassi, A.; Farchi, A.; Fowler, A.; Houtekamer, P.; Jones, C.K.; de Moraes, R.; Pulido, M.; et al. An international assessment of the COVID-19 pandemic using ensemble data assimilation. medRxiv 2020. [Google Scholar] [CrossRef]
- Yang, Q.; Yi, C.; Vajdi, A.; Cohnstaedt, L.W.; Wu, H.; Guo, X.; Scoglio, C.M. Short-term forecasts and long-term mitigation evaluations for the COVID-19 epidemic in Hubei Province, China. Infect. Dis. Model. 2020, 5, 563–574. [Google Scholar]
- Nkwayep, C.H.; Bowong, S.; Tewa, J.; Kurths, J. Short-term forecasts of the COVID-19 pandemic: Study case of Cameroon. Chaos Solitons Fractals 2020, 140, 110106. [Google Scholar] [CrossRef] [PubMed]
- Sesterhenn, J.L. Adjoint-based data assimilation of an epidemiology model for the covid-19 pandemic in 2020. arXiv 2020, arXiv:2003.13071. [Google Scholar]
- Armstrong, E.; Runge, M.; Gerardin, J. Identifying the measurements required to estimate rates of COVID-19 transmission, infection, and detection, using variational data assimilation. Infect. Dis. Model. 2020, 6, 133–147. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: Berlin, Germany, 2015; Volume 61. [Google Scholar]
- Saudi Center for Diseases Prevention and Control. Available online: https://covid19.cdc.gov.sa/daily-updates/ (accessed on 17 December 2020).
- Saudi Ministry of Health. Available online: https://www.moh.gov.sa/en/Ministry/Statistics/Indicator/Pages/Indicator-1440.aspx (accessed on 17 December 2020).
- Saudi Health Council. Available online: https://coronamap.sa (accessed on 19 January 2021).
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef]
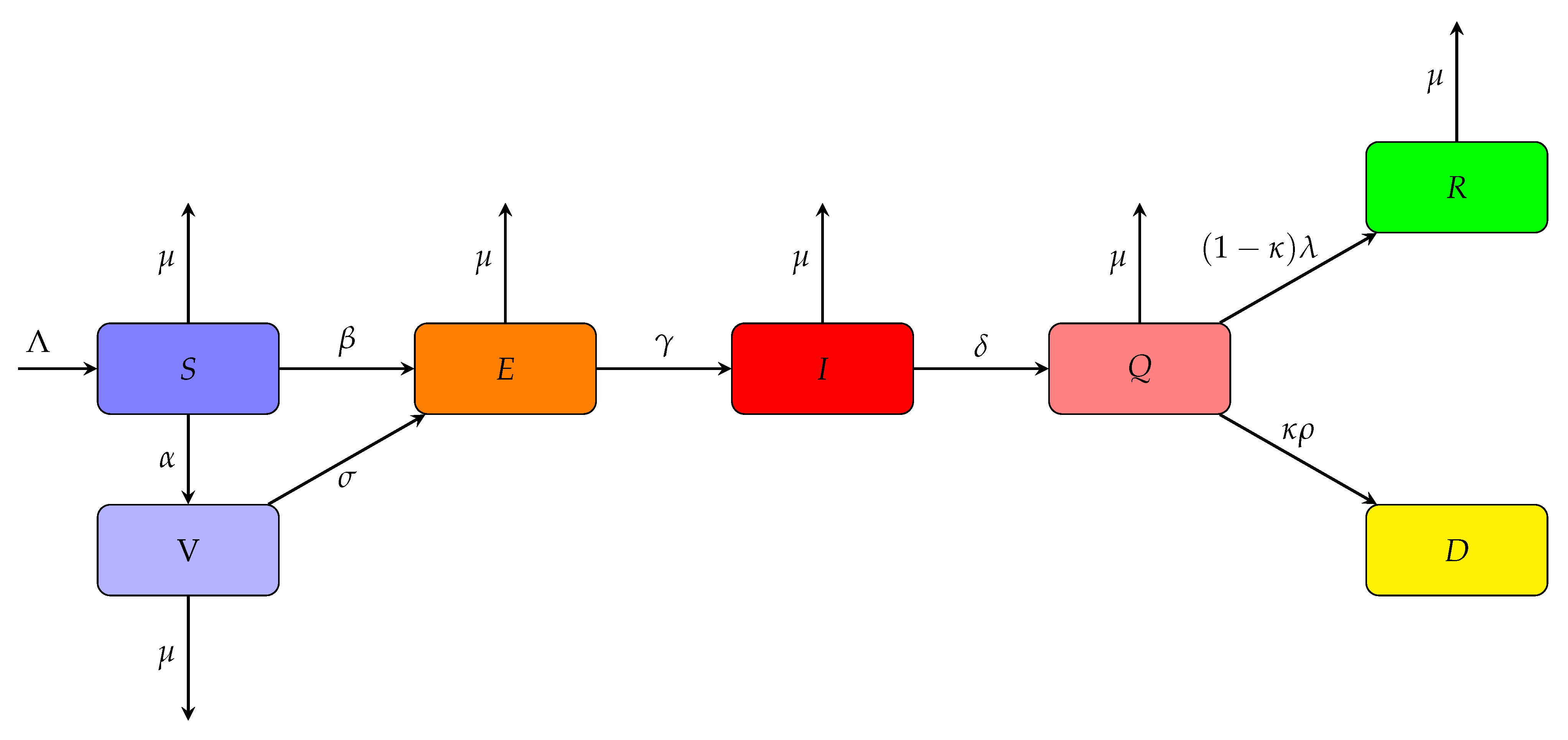

| Parameter | Initial Value | Description | Reference |
|---|---|---|---|
| 2300 persons/day | New births and new residents | [51] | |
| day | Transmission rate before intervention | Assumed | |
| day | Transmission rate during and after intervention | Assumed | |
| day | Vaccination rate | [52] | |
| persons/day | Natural death rate | [51] | |
| 5.5 days | Incubation period | [42] | |
| 0.05 | Vaccine inefficacy | [53] | |
| 3.8 days | Infection time | [42] | |
| 0.014 | Case fatality rate | [50] | |
| 10 days | Recovery time | [42] | |
| 15 days | Time until death | [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. An Extended SEIR Model with Vaccination for Forecasting the COVID-19 Pandemic in Saudi Arabia Using an Ensemble Kalman Filter. Mathematics 2021, 9, 636. https://doi.org/10.3390/math9060636
Ghostine R, Gharamti M, Hassrouny S, Hoteit I. An Extended SEIR Model with Vaccination for Forecasting the COVID-19 Pandemic in Saudi Arabia Using an Ensemble Kalman Filter. Mathematics. 2021; 9(6):636. https://doi.org/10.3390/math9060636
Chicago/Turabian StyleGhostine, Rabih, Mohamad Gharamti, Sally Hassrouny, and Ibrahim Hoteit. 2021. "An Extended SEIR Model with Vaccination for Forecasting the COVID-19 Pandemic in Saudi Arabia Using an Ensemble Kalman Filter" Mathematics 9, no. 6: 636. https://doi.org/10.3390/math9060636
APA StyleGhostine, R., Gharamti, M., Hassrouny, S., & Hoteit, I. (2021). An Extended SEIR Model with Vaccination for Forecasting the COVID-19 Pandemic in Saudi Arabia Using an Ensemble Kalman Filter. Mathematics, 9(6), 636. https://doi.org/10.3390/math9060636








