Local Convergence of the Continuous and Semi-Discrete Wavelet Transform in $L^p\left(\mathbb{R}\right)$

Abstract

The smoothness of functions f in the space $L^p\left(\mathbb{R}\right)$ with $1<p<\infty$ is studied through the local convergence of the continuous wavelet transform of f. Additionally, we study the smoothness of functions in $L^p\left(\mathbb{R}\right)$ by means of the local convergence of the semi-discrete wavelet transform.

1. Introduction

In order to study the local regularity of functions in $L^2\left(\mathbb{R}\right)$ by means of the local convergence of the continuous wavelet transform (CWT), we apply its inversion formula, which is usually considered in the weak sense [1]. The same concept is applied for the case of CWT with rotations in $L^2\left(R^n\right)$ [2]. Concerning distributions u with compact support, the regular points of u can be found again by using the convergence of the CWT by means of the $L^2-machinery$, [3].

When we move to the space $L^p\left({\mathbb{R}}^n\right)$, the inversion formula for the CWT is obtained with norm convergence in $L^p\left({\mathbb{R}}^n\right)$, where $1\le p<\infty$, [4,5]. For a.e. convergence in $L^p\left({\mathbb{R}}^n\right),1<p<\infty$, see [6]. For the convergence at every Lebesgue point x for functions in $L^p\left({\mathbb{R}}^n\right),1\le p<\infty$, see [7], and for the convergence on the entire Lebesgue set of $f\in L^p\left(\mathbb{R}\right)$, $1\le p<\infty$, see [8]. Moreover, in [9,10], the continuous wavelet transform $L_h:L^p\left(\mathbb{R}\right)\to L^p(\mathbb{R},L^2((0,\infty ),\frac{da}{a})):=W^p$, $1<p<\infty$ with respect to a wavelet $h\in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ is a bounded linear operator and

$${∥L_{h}f∥}_{W^p}:={\left({\int }_{\mathbb{R}}{\left[{\int }_0^{\infty }{\left|\left(L_{h}f\right)(a,b)\right|}^2\frac{da}{a}\right]}^{\frac{p}{2}}db\right)}^{\frac{1}{p}}\le A_p{\parallel f\parallel }_p,$$

where $A_p$ depends on p and h.

For the discrete wavelet transform, wavelets become an unconditional bases for $L^p\left(\mathbb{R}\right)$, $1<p<\infty$. Thus, there is a characterization for functions in $L^p\left(\mathbb{R}\right)$ using only absolute values of the wavelet coefficients of f, [11].

In this paper, we extend the results of local regularity of functions $f\in L^2\left(\mathbb{R}\right)$ to the space $L^p\left(\mathbb{R}\right)$, $1<p<\infty$, by means of the local convergence of the CWT. To study the regularity of functions in $L^p\left(\mathbb{R}\right)$, $1<p<\infty$ via the CWT, we give the necessary conditions to define the CWT for f in $L^p\left(\mathbb{R}\right)$ with respect to an admissible function h in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$.

Finally, we introduce the semi-discrete wavelet transform (SDWT) to show that there is a relationship between the local regularity of functions in $L^p\left(\mathbb{R}\right)$ and the local convergence of the SDWT. That is, if the dilation parameter takes only discrete values, namely $a:=a^m$, where a is fixed and $a>1$ with $m\in \mathbb{Z}$, and the translation parameter b is any value in $\mathbb{R}$, we get the SDWT. With respect to the reconstruction formula in the semi-discrete case, we will consider two functions, $h_1$ and $h_2$, instead of one h, one for the decomposition and the other one for the inversion formula, in such a way that the admissibility condition will depend on $h_1$ and $h_2$ [12,13].

This research led us to establish a relationship between the local existence of the limit of derivatives for the CWT and SDWT, and the derivatives of functions in $L^p\left(\mathbb{R}\right)$.

Some experiments are included to illustrate our results. In particular, we study the sigmoidal function, widely used in artificial neural networks, since its derivatives can be expressed in terms of itself and Stirling numbers of second order, that allow us to implement computer experiments to show graphical representations of the wavelet transform behaviour.

The reported results become relevant in research areas such as analytical chemistry, where wavelet functions can be used for derivative calculation through CWT [14,15], neural networks with wavelets to extract features from data [16], and to propose novel architectures [17], image processing with wavelets, where all their derivatives are admissible functions, such as the Beta function [18], computer vision via Shearlet Networks that take advantage of sparse representations of shearlets in biometric applications [19], and its convergence properties [20,21], as well as differential equations for numerical solutions [22], among other areas. Indeed, one of the projections of the results shown in this paper can be applied, for example, to study the regularity of weak solutions under elliptic partial differential operators.

2. Notations and Definitions

In this section, we give the definition for an admissible function. We also define the continuous wavelet transform for functions in $L^p\left(\mathbb{R}\right)$, where $1<p<\infty$ with respect to an admissible function, and we give the inversion formula for the continuous wavelet transform.

Definition 1.

For h in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$, the dilation operator $J_a$ and the translation operator $T_b$ are defined respectively, as:

(1) $\left(J_{a}h\right)\left(x\right)=a^{-1}h\left(a^{-1}x\right)$, where $a>0$ and $x\in \mathbb{R}$,

(2) $\left(T_{b}h\right)\left(x\right)=h(x-b)$, where $x,b\in \mathbb{R}$.

Notice that $J_{a}h$ and $T_{b}h$ are also in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$. In fact, $\parallel J_a{h\parallel }_1={\parallel h\parallel }_1$.

The admissibility condition is now given.

Definition 2.

The function h in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ is admissible (wavelet) if

$$0<C_h:={\int }_{{\mathbb{R}}^{+}}\frac{|\widehat{h}{\left(w\right)|}^2}{w}dw<\infty ,$$

(1)

where $\widehat{h}$ is the Fourier transform of h, and where ${\mathbb{R}}^{+}=(0,\infty )$.

Remark 1.

Following (1), note that if $h\in C_0^{\infty }\left(\mathbb{R}\right)$, then $h^{\left(n\right)}$ is admissible if and only if

$$C_{h^{\left(n\right)}}={\left(2\pi \right)}^{2n}{\int }_{{\mathbb{R}}^{+}}{w}^{2n-1}{\left|\widehat{h}\left(w\right)\right|}^{2}dw<\infty .$$

(2)

Given the admissibility condition, we extend the continuous wavelet transform on $L^2(\mathbb{R},dx)$ to $L^p(\mathbb{R},dx)$, where $1<p<\infty$, and interpret its images as elements of the space $W^p$, as above. For this, we give the following definition.

Definition 3.

Consider a measurable set X with measure μ and a Banach space B with norm ${\parallel ·\parallel }_B$. The space $L^p{((X,d\mu );(B,\parallel ·\parallel }_B\left)\right)$ consists of those elements, $F:X\to B$, F is strongly measurable and such that

$${\int }_X{\parallel F\left(x\right)\parallel }_B^{p}d\mu \left(x\right)<\infty .$$

According to Definition 3, if $X=\mathbb{R}$ is a measurable space with measure $db$ and $B=L^2({\mathbb{R}}^{+},\frac{da}{a})$ is a normed space with norm ${\parallel ·\parallel }_2$, then

$$W^p:=L^p\left((\mathbb{R},db);L^2({\mathbb{R}}^{+},\frac{da}{a})\right)$$

consists of those elements $F(·,b)\in L^2({\mathbb{R}}^{+},\frac{da}{a})$ such that

$${\int }_{\mathbb{R}}{\parallel F(·,b)\parallel }_{L^2({\mathbb{R}}^{+},\frac{da}{a})}^{p}db<\infty .$$

In this case,

$${\parallel F\parallel }_{W^p}:={\left({\int }_{\mathbb{R}}{\parallel F(·,b)\parallel }_{L^2({\mathbb{R}}^{+},\frac{da}{a})}^{p}db\right)}^{\frac{1}{p}}={\left({\int }_{\mathbb{R}}{\left({\int }_{{\mathbb{R}}^{+}}{\left|F(a,b)\right|}^2\frac{da}{a}\right)}^{\frac{p}{2}}db\right)}^{\frac{1}{p}}.$$

(3)

Thus, by using the space $W^p$, we give the definition of the continuous wavelet transform for functions in $L^p\left(\mathbb{R}\right)$ with respect to an admissible function in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$.

Definition 4.

Let f be in $L^p\left(\mathbb{R}\right)$ with $1<p<\infty$. Consider $a>0$ and $b\in \mathbb{R}$. Let h be an admissible function in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$. The continuous wavelet transform of f with respect to h is defined as the map

$$L_h:L^p(\mathbb{R},dx)\to W^p$$

so that

$$\left(L_{h}f\right)(a,b)={\int }_{\mathbb{R}}f\left(x\right)\overline{T_b{J}_{a}h\left(x\right)}dx={\int }_{\mathbb{R}}f\left(x\right)\frac{1}{a}\overline{h\left(\frac{x-b}{a}\right)}dx.$$

(4)

Note that the continuous wavelet transform can be written as

$$\left(L_{h}f\right)(a,b)=\left[{\left(J_a\overline{h}\right)}^{\sim }\ast f\right]\left(b\right),$$

(5)

where ∗ means convolution and $h^{\sim }$ means $h^{\sim }\left(x\right)=h(-x).$

Remark 2.

According to (5), and since $J_{a}h\in L^1\left(\mathbb{R}\right)$ and $f\in L^p\left(\mathbb{R}\right)$, it follows from Young’s Inequality that ${\left(J_a\overline{h}\right)}^{\sim }\ast f\in L^p\left(\mathbb{R}\right)$ and $\parallel {\left(J_a\overline{h}\right)}^{\sim }{\ast f\parallel }_p\le {\parallel h\parallel }_1{\parallel f\parallel }_p$. That is,

$$\parallel \left(L_{h}f\right)(a,·){\parallel }_p\le {\parallel h\parallel }_1{\parallel f\parallel }_p.$$

Additionally, note that from (3),

$$\parallel L_h{f\parallel }_{W^p}={\left({\int }_{\mathbb{R}}{\parallel L_{h}f(·,b)\parallel }_{L^2({\mathbb{R}}^{+},\frac{da}{a})}^{p}db\right)}^{\frac{1}{p}}={\left({\int }_{\mathbb{R}}{\left({\int }_{{\mathbb{R}}^{+}}{\left|\left(L_{h}f\right)(a,b)\right|}^2\frac{da}{a}\right)}^{\frac{p}{2}}db\right)}^{\frac{1}{p}},$$

where

$${∥L_{h}f∥}_{W^p}\le A_p{\parallel f\parallel }_p,$$

and where the constant $A_p$ depends only on p and h. Thus, the continuous wavelet transform is a bounded linear operator, [10].

The inversion formula of the continuous wavelet transform for f in $L^p\left(\mathbb{R}\right)$ with $1<p<\infty$ is now given.

Lemma 1.

Consider $f\in L^p\left(\mathbb{R}\right)$ with $1<p<\infty$, and $h\in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ admissible with real values. Then,

$$f\left(x\right)=\frac{1}{C_h}{\int }_{{\mathbb{R}}^{+}}{\int }_{\mathbb{R}}\left(L_{h}f\right)(a,b)h\left(\frac{x-b}{a}\right)db\frac{da}{a^2}.$$

(6)

The equality holds in the $L^p$ sense, and the integrals on the right-hand side have to be taken in the sense of distributions.

Proof. 

See [10]. □

3. Convergence of the Continuous Wavelet Transform in $L^p\left(\mathbb{R}\right)$

First, we give a result about the derivative of the continuous wavelet transform with respect to the translation parameter $b\in \mathbb{R}$.

Lemma 2.

If $f\in L^p\left(\mathbb{R}\right)$ with $1<p<\infty$ and if $h\in C_0^{\infty }\left(\mathbb{R}\right)$ is admissible, then for any integer $n>0$, $h^{\left(n\right)}$ is admissible. Moreover,

$$\frac{{\partial }^n}{\partial b^n}\left(L_{h}f\right)(a,b)=\frac{{(-1)}^n}{a^n}\left(L_{h^{\left(n\right)}}f\right)(a,b).$$

(7)

Proof. 

From (5), and since $f\in L^p\left(\mathbb{R}\right)$ and $h\in C_0^{\infty }\left(\mathbb{R}\right)$, then ${\left(J_a\overline{h}\right)}^{\sim }\ast f\in C^{\infty }\left(\mathbb{R}\right)$, and

$$\frac{{\partial }^n}{\partial b^n}\left[{\left(J_a\overline{h}\right)}^{\sim }\ast f\right]\left(b\right)=\left[\frac{{\partial }^n}{\partial b^n}{\left(J_a\overline{h}\right)}^{\sim }\ast f\right]\left(b\right)=\frac{{(-1)}^n}{a^n}\left[{\left(J_a\overline{h^{\left(n\right)}}\right)}^{\sim }\ast f\right]\left(b\right).$$

(8)

This proves Lemma 2. □

Then, we have the following result.

Lemma 3.

Suppose that $h\in C_0^{\infty }\left(\mathbb{R}\right)$ is a non-zero function where $\widehat{h}\left(0\right)=0$. Consider f in $L^p\left(\mathbb{R}\right)$, $1<p<\infty$. If f is of class $C^{\infty }$ in a neighborhood of $x=b_0$ in $\mathbb{R}$, then for each non-negative integer n, we have the existence of ${\displaystyle \underset{(a,b)\to (0,b_1)}{lim}\left({\mathcal{W}}_h^{n}f\right)(a,b)}$ for each $b_1$ in a neighborhood of $b_0\in \mathbb{R}$, where

$$\left({\mathcal{W}}_h^{n}f\right)(a,b):=\frac{1}{a}\frac{{\partial }^n}{\partial b^n}\left(L_{h}f\right)(a,b).$$

(9)

Proof. 

Suppose f is $C^{\infty }$ in a neighborhood of $x=b_0$ containing $[b_0-ϵ,b_0+ϵ]$, where $ϵ>0$. Take $b_1$ in $(b_0-ϵ/2,b_0+ϵ/2)$ and choose b in $(b_0-ϵ/2,b_0+ϵ/2)$.

Now since $h\in C_0^{\infty }\left(\mathbb{R}\right)$, there is $L>0$ such that $supph\subset [-L,L]$. Then, for $a\in (0,ϵ/2L)$, we have $[b-aL,b+aL]\subset [b_0-ϵ,b_0+ϵ]$. Hence, f is $C^{\infty }$ in $[b-aL,b+aL]$.

Following Lemma 2, and since $f\in L^p\left(\mathbb{R}\right)$, it follows from (4) that,

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_h^{n}f\right)(a,b)& =\frac{1}{a}\frac{{(-1)}^n}{a^n}{\int }_{b-aL}^{b+aL}f\left(x\right)\frac{1}{a}\overline{h^{\left(n\right)}\left(\frac{x-b}{a}\right)}dx=\frac{1}{a}{\int }_{-L}^L{f}^{\left(n\right)}(b+ay)\overline{h\left(y\right)}dy.\hfill \end{array}$$

(10)

Since f is $C^{\infty }$ at points in the region of integration, then for y in $[-L,L]$,

$$f^{\left(n\right)}(b+ay)=f^{\left(n\right)}\left(b\right)+ay{f}^{(n+1)}\left(b\right)+{\int }_b^{b+ay}(b+ay-t)f^{(n+2)}\left(t\right)dt.$$

Hence,

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_h^{n}f\right)(a,b)& =\frac{1}{a}{f}^{\left(n\right)}\left(b\right){\int }_{-L}^L\overline{h\left(y\right)}dy+f^{(n+1)}\left(b\right){\int }_{-L}^{L}y\overline{h\left(y\right)}dy+R(a,b),\hfill \end{array}$$

where

$$R(a,b)=\frac{1}{a}{\int }_{-L}^L\left({\int }_b^{b+ay}(b+ay-t)f^{(n+2)}\left(t\right)dt\right)\overline{h\left(y\right)}dy.$$

Now, set $M=su{p}_{x\in [b_0-ϵ,b_0+ϵ]}\left|f^{(n+2)}\left(x\right)\right|$. Then,

$$\left|R(a,b)\right|\le \frac{1}{2}aM{\int }_{-L}^L{y}^2\left|h\left(y\right)\right|dy.$$

Thus, $R(a,b)\to 0$ as $(a,b)\to (0,b_1)$ for any $b_1$ in $(b_0-ϵ/2,b_0+ϵ/2)$.

Then, since $\widehat{h}\left(0\right)=0$ and since $f^{(n+1)}$ is continuous near $b_1$, we have

$$\left({\mathcal{W}}_h^{n}f\right)(a,b)\to f^{(n+1)}\left(b_1\right){\int }_{-L}^{L}y\overline{h\left(y\right)}dy\mathrm{as}(a,b)\to (0,b_1).$$

(11)

□

4. Main Result 1

Now, let us prove the converse of Lemma 3, which is our first main result.

Theorem 1.

Suppose $h\in C_0^{\infty }\left(\mathbb{R}\right)$ satisfies condition (1). Consider f in $L^p\left(\mathbb{R}\right)$ with $1<p<\infty$. If, for each non-negative integer n, the limit of $\left({\mathcal{W}}_h^{n}f\right)(a,b)$ exists as $(a,b)\to (0,b_1)$ for each $b_1$ in an open neighborhood of $x=b_0\in \mathbb{R}$, then f is of class $C^{\infty }$ in an open neighborhood of $b_0\in \mathbb{R}$.

Proof. 

Suppose that for each non-negative integer n,

$$F_h^n\left(b_1\right)\underset{(a,b)\to (0,b_1)}{lim}\left({\mathcal{W}}_h^{n}f\right)(a,b)$$

exists for each $b_1$ in an open neighborhood containing the closed interval $[b_0-B,b_0+B]$, where $B>0$.

Now, for fixed x in $[b_0-B,b_0+B]$ and $y\in \mathbb{R}$, let

$$\left({\mathcal{I}}_h^{n}f\right)(a,x,y)=\left\{\begin{array}{c}h(-y)\left({\mathcal{W}}_h^{n}f\right)(a,x+ay)\mathrm{if}a>0\hfill \\ h(-y)F_h^n\left(x\right)\mathrm{if}a=0.\hfill \end{array}\right.$$

Note that for x in $[b_0-B,b_0+B]$, the function ${\mathcal{I}}_h^{n}f$ is well-defined for all $a\ge 0$ and all y in $\mathbb{R}$. Furthermore, for fixed $y\in \mathbb{R}$ and $a\ne 0$, the function ${\mathcal{I}}_h^{n}f$ is infinitely differentiable in the variable x by virtue of the definition of ${\mathcal{W}}_h^{n}f$.

Then we have the following Lemma (see Appendix A for the proof).

Lemma 4.

For x in $(b_0-B,b_0+B)$, let

$$w\left(x\right)={\int }_0^{\infty }{\int }_{\mathbb{R}}\left({\mathcal{I}}_h^{0}f\right)(a,x,y)dyda,$$

and let

$$\left(I_h^{n}f\right)\left(x\right)={\int }_0^{\infty }{\int }_{\mathbb{R}}\left({\mathcal{I}}_h^{n}f\right)(a,x,y)dyda.$$

Then for each non-negative integer n,

$$\frac{d^n}{d{x}^n}w\left(x\right)=\left(I_h^{n}f\right)\left(x\right).$$

(12)

That is, the function w is of class $C^{\infty }$ on $(b_0-B,b_0+B)$.

Back to the proof of Theorem 1, for any x in $\mathbb{R}$ and $\lambda >0$, define

$$u_{\lambda }\left(x\right):={\int }_{\frac{1}{\lambda }}^{\lambda }{\int }_{\mathbb{R}}h(-y)\frac{1}{a}\left(L_{h}f\right)(a,x+ay)dyda.$$

Then from Lemma 4, for $x\in (b_0-B,b_0+B)$,

$$\underset{\lambda \to \infty }{lim}{u}_{\lambda }\left(x\right)=w\left(x\right).$$

That is, $u_{\lambda }\to w$ pointwise on $(b_0-B,b_0+B)$ as $\lambda \to \infty .$

On the other hand, by (6), we have $u_{\lambda }\to C_{h}f$ in the $L^p$ sense as $\lambda \to \infty$. Then, $f={\left(C_h\right)}^{-1}w$ almost everywhere on $(b_0-B,b_0+B)$.

Finally, since from (12) the function w is $C^{\infty }$ on $(b_0-B,b_0+B)$, it follows that f is of class $C^{\infty }$ on $(b_0-B,b_0+B)$. □

5. The Semi-Discrete Wavelet Transform

In this section, we define the semi-discrete wavelet transform (SDWT) of functions $f\in L^p\left(\mathbb{R}\right)$, and we will prove the local convergence of the SDWT of f via the local regularity of f. For this purpose, we will use the reconstruction formula given in [12]. Thus, we will define the corresponding dilation operator for discrete values.

Definition 5.

For a function $h\in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$, and for fixed $a>1$, the dilation operator $J_{a^m}$ is now given by

$$\left(J_{a^m}h\right)\left(x\right)=\frac{1}{a^m}h\left(\frac{x}{a^m}\right),\mathit{where}m\in \mathbb{Z},\mathit{and}x\in \mathbb{R}.$$

(13)

Thus, we have the following definition for the semi-discrete wavelet transform for functions in $L^p\left(\mathbb{R}\right)$.

Definition 6.

Suppose that h in $L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ is an admissible function. Then, the semi-discrete wavelet transform for a function f in $L^p\left(\mathbb{R}\right)$ with respect to h is defined as:

$$\left(L_{h}f\right)(a^m,b)=\left({\left(J_{a^m}\overline{h}\right)}^{\sim }\ast f\right)\left(b\right)={\int }_{\mathbb{R}}f\left(x\right)\frac{1}{a^m}\overline{h}\left(\frac{x-b}{a^m}\right)dx,$$

(14)

where $a>1$ is fixed, $m\in \mathbb{Z}$, and $b\in \mathbb{R}$.

See [12] for Remark 3 with N any natural number. In this paper, $N=1$.

Remark 3.

In order to get a reconstruction formula for the semi-discrete wavelet transform in $L^p\left(\mathbb{R}\right)$, a function $h\in L^2\left(\mathbb{R}\right)$ must satisfy the following condition: Given an Unconditional Martingale Difference (UMD) space X with Fourier type $r\in (1,2]$ and $l:=[1/r]+1$, for all $\alpha \in \{0,1\}$ with $\left|\alpha \right|\le l$ and $a>1$, the distributional derivatives $D^{\alpha }\overline{\widehat{h}}$ are represented by measurable functions, and

$$Su{p}_{1\le \left|\omega \right|<a}{\left(\sum _{m\in \mathbb{Z}}{a}^{2m\left|\alpha \right|}{\left|\left(D^{\alpha }\overline{\widehat{h}}\right)\left(a^m\omega \right)\right|}^2\right)}^{1/2}<\infty .$$

(15)

Remark 4

(Reconstruction formula, see [12]). Suppose that $h_1,h_2\in L^1\left(\mathbb{R}\right)\cap L^2\left(\mathbb{R}\right)$ are admissible and satisfy the condition (15) with

$$\sum _{m=-\infty }^{\infty }{\widehat{h}}_2\left(a^m\omega \right)\overline{{\widehat{h}}_1}\left(a^m\omega \right)=1$$

(16)

for almost all $\omega \in \mathbb{R}\backslash \left\{0\right\}$. Then for any $f\in L^p\left(\mathbb{R}\right),1<p<\infty$,

$$f=\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }\left(J_{a^m}{h}_2\right)\ast \left(J_{a^m}\overline{h_1^{\sim }}\right)\ast f,$$

(17)

where the equality holds in the $L^p$ sense. In this paper, Formulas (15)–(17) based on [12] have been adapted to match with our nomenclature on the wavelet transform definition.

Then we have the following result concerning the continuity of the semi-discrete wavelet transform.

Note 1.

From Definition 6, if $f\in L^p\left(\mathbb{R}\right)$ and h in $C_0\left(\mathbb{R}\right)$ is admissible, then $\left(L_{h}f\right)(a^m,b)$ is continuous at $(a^{m_1},b_1)$ for all $(m_1,b_1)\in \mathbb{Z}\times \mathbb{R}.$

6. Main Result 2

Now we give our second main result. That is, we will prove the existence of the limit of $\left({\mathcal{W}}_{h_1}^{n}f\right)(a^m,b):=\frac{1}{a^m}\frac{{\partial }^n}{\partial b^n}\left(L_{h_1}f\right)(a^m,b)$ as $(a^m,b)\to (0,b_1)$ for any $b_1$ in a neighborhood of some point $x=b_0$ under the hypothesis that f is of class $C^{\infty }$ in a neighborhood of $x=b_0$, and where $h_1$ is admissible in $C_0^{\infty }\left(\mathbb{R}\right)$. Note that $a^m\to 0$ if and only if $m\to -\infty$. Thus, we have the following result.

Theorem 2.

Suppose $h_1,h_2\in C_0^{\infty }\left(\mathbb{R}\right)$ are admissible functions that satisfy the condition (16). Consider $f\in L^p\left(\mathbb{R}\right),1<p<\infty$. Then f is $C^{\infty }$ in a neighborhood of $x=b_0$ if, and only if for each non-negative integer n,

$$\underset{(m,b)\to (-\infty ,b_1)}{lim}\left({\mathcal{W}}_{h_1}^{n}f\right)(a^m,b)\mathit{exists}\mathit{for}\mathit{each}{b}_1\mathit{in}\mathrm{a}\mathit{neighborhood}\mathit{of}x=b_0.$$

Proof. 

First, suppose f is $C^{\infty }$ in a neighborhood of $x=b_0$. Then by Lemma 3, it follows that for each non-negative integer n,

$$\underset{(m,b)\to (-\infty ,b_1)}{lim}\left({\mathcal{W}}_{h_1}^{n}f\right)(a^m,b)\mathrm{exists}\mathrm{for}\mathrm{each}{b}_1\mathrm{in}\mathrm{a}\mathrm{neighborhood}\mathrm{of}x=b_0.$$

This completes the proof of the first part of Theorem 2.

For the second part, we will use similar arguments to the ones given in the proof of Theorem 1. Suppose then that for each non-negative integer n,

$$\underset{(m,b)\to (-\infty ,b_1)}{lim}\left({\mathcal{W}}_{h_1}^{n}f\right)(a^m,b):=S_{h_1}^n\left(b_1\right)$$

exists for each $b_1$ in an open neighborhood containing the closed interval $[b_0-B,b_0+B],B>0$.

Then we have the following Lemma (see Appendix A for the proof).

Lemma 5.

For any x in $(b_0-B,b_0+B)$, let

$$v\left(x\right):=\sum _{m=-\infty }^{\infty }(\left(J_{a^m}{h}_2\right)\ast \left(J_{a^m}\overline{h_1^{\sim }}\right)\ast f)\left(x\right),$$

and let

$$v_n\left(x\right)=\sum _{m=-\infty }^{\infty }(\left(J_{a^m}{h}_2\right)\ast \frac{{\partial }^n}{\partial x^n}\left(J_{a^m}\overline{h_1^{\sim }}\right)\ast f)\left(x\right).$$

Then for any non-negative integer n, we have

$$\frac{d^n}{d{x}^n}v\left(x\right)=v_n\left(x\right).$$

That is, the function v is of class $C^{\infty }$ on $(b_0-B,b_0+B)$.

Now, back to the proof of Theorem 2, for an integer $M\ge 0$ and any x in $(b_0-B,b_0+B)$, define

$$V_M\left(x\right):=\sum _{m=-M}^M(\left(J_{a^m}{h}_2\right)\ast \left(J_{a^m}\overline{h_1^{\sim }}\right)\ast f)\left(x\right).$$

(18)

Then by Lemma 5, for any $x\in (b_0-B,b_0+B)$,

$$\underset{M\to \infty }{lim}{V}_M\left(x\right)=v\left(x\right).$$

That is, $V_M\to v$ pointwise as $M\to \infty$.

On the other hand, from the reconstruction formula given in (17),

$$\begin{array}{cc}\hfill f\left(x\right)& =\frac{1}{2\pi }\sum _{m=-\infty }^{\infty }(\left(J_{a^m}{h}_2\right)\ast (J_{a^m}\overline{h_1^{\sim }}\ast f)\left(x\right)),\hfill \end{array}$$

hence, we have $V_M\to \left(2\pi \right)f$ as $M\to \infty$ for almost every x in $(b_0-B,b_0+B)$.

That is, $f={\left(2\pi \right)}^{-1}v$ pointwise almost everywhere. Thus, by Lemma 5, the function f is of class $C^{\infty }$ on $(b_0-\frac{B}{2},b_0+\frac{B}{2})$.

This completes the proof of Theorem 2. □

7. Examples

Example 1.

First we give an example for Lemma 3. Let $Q>1$ be a constant and consider the logistic function

$$f\left(x\right)=\left\{\begin{array}{cc}\frac{1}{1+e^{-x}},\hfill & x\in [-Q,Q]\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Then $f\in L^p\left(\mathbb{R}\right)$, $1<p<\infty$ and f is of class $C^{\infty }\left(\mathbb{R}\right)$ in any neighborhood of $x=b_0$ with $b_0\in (-Q,Q)$. As an admissible function consider the Haar function $h\left(x\right)$. Then $supph=[0,1]$, and hence $h\in L^1\left(\mathbb{R}\right)$.

Then from (10),

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_h^{n}f\right)(a,b)& =\frac{1}{a}{\int }_0^1{f}^{\left(n\right)}(b+ay)\overline{h\left(y\right)}dy\hfill \\ & =\frac{1}{a}{\int }_0^{\frac{1}{2}}{f}^{\left(n\right)}(b+ay)dy-\frac{1}{a}{\int }_{\frac{1}{2}}^1{f}^{\left(n\right)}(b+ay)dy\hfill \\ & =\frac{1}{a^2}{\left[f^{(n-1)}(b+ay)\right]}_0^{\frac{1}{2}}-\frac{1}{a^2}{\left[f^{(n-1)}(b+ay)\right]}_{\frac{1}{2}}^1\hfill \\ & =\frac{2f^{(n-1)}(b+\frac{a}{2})-f^{(n-1)}\left(b\right)-f^{(n-1)}(b+a)}{a^2}.\hfill \end{array}$$

By using the Taylor series with integral remainder

$$\begin{array}{cc}\hfill f^{(n-1)}(b+at)=& f^{(n-1)}\left(b\right)+at{f}^{\left(n\right)}\left(b\right)+\frac{1}{2}{a}^2{t}^2{f}^{(n+1)}\left(b\right)+\hfill \\ & \frac{1}{2}{\int }_b^{b+at}(b+at-\xi )f^{(n+2)}\left(\xi \right)d\xi ,\hfill \end{array}$$

and then taking $t=\frac{1}{2}$ and $t=1$, we have

$$\frac{2f^{(n-1)}(b+\frac{a}{2})-f^{(n-1)}\left(b\right)-f^{(n-1)}(b+a)}{a^2}\to -\frac{1}{4}{f}^{(n+1)}\left(b_1\right)\mathrm{as}(a,b)\to (0,b_1).$$

This result matches with (11) and shows that for any positive integer n and any $b_1$ in a neighborhood of $x=b_0$, a limit of $\left({\mathcal{W}}_h^{n}f\right)(a,b)$ exists as $(a,b)\to (0,b_1).$ Note that despite $h\left(x\right)$ having no derivatives, the result is consistent with Lemma 3. This example suggests that the results could apply with other wavelets that are not smooth.

According to [23], we can express $f^{(n+1)}\left(x\right)$ as a function of $f\left(x\right)$. In this case,

$$\underset{(a,b)\to (0,b_1)}{lim}\left({\mathcal{W}}_h^{n}f\right)(a,b)=-\frac{1}{4}\sum _{k=1}^{n+2}{(-1)}^{k-1}(k-1)!S(n+2,k){\left[f\left(b_1\right)\right]}^k,$$

(19)

where $S(n+2,k)$ are the Stirling numbers of the second kind.

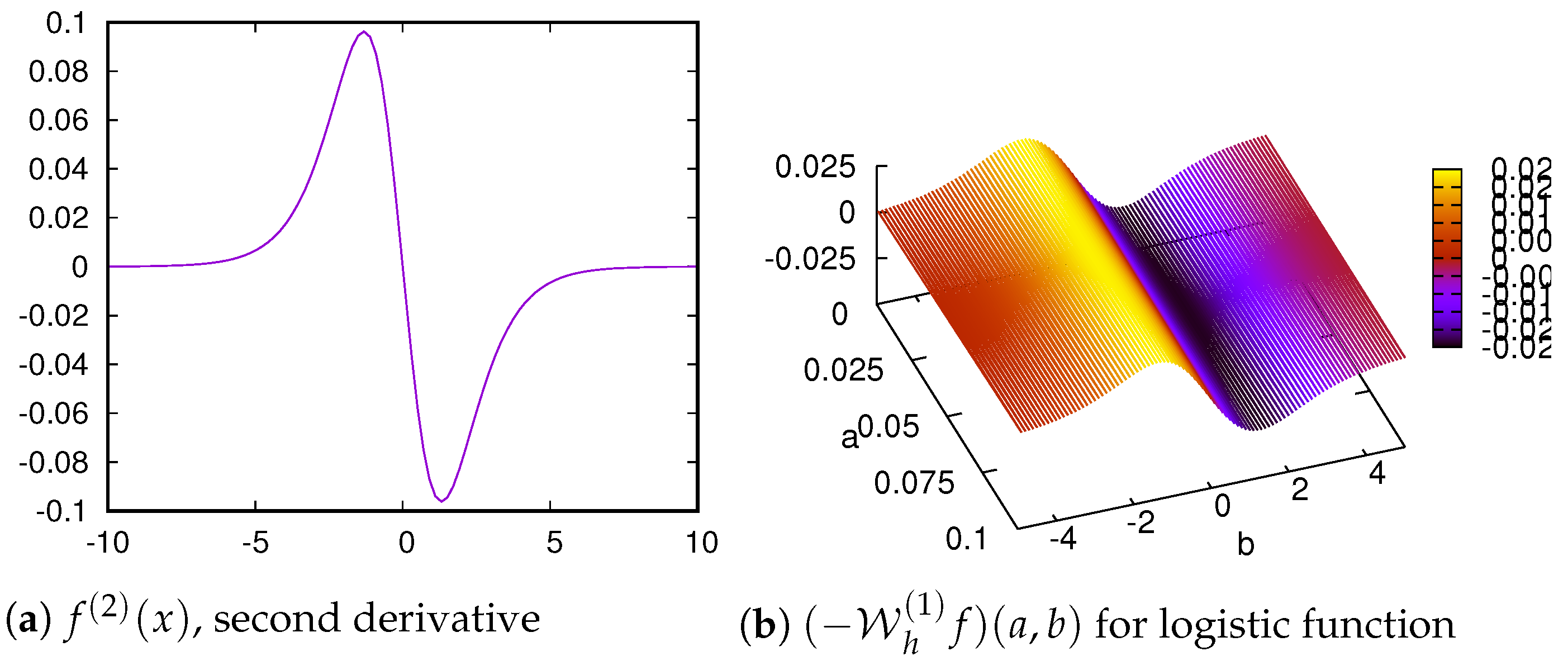
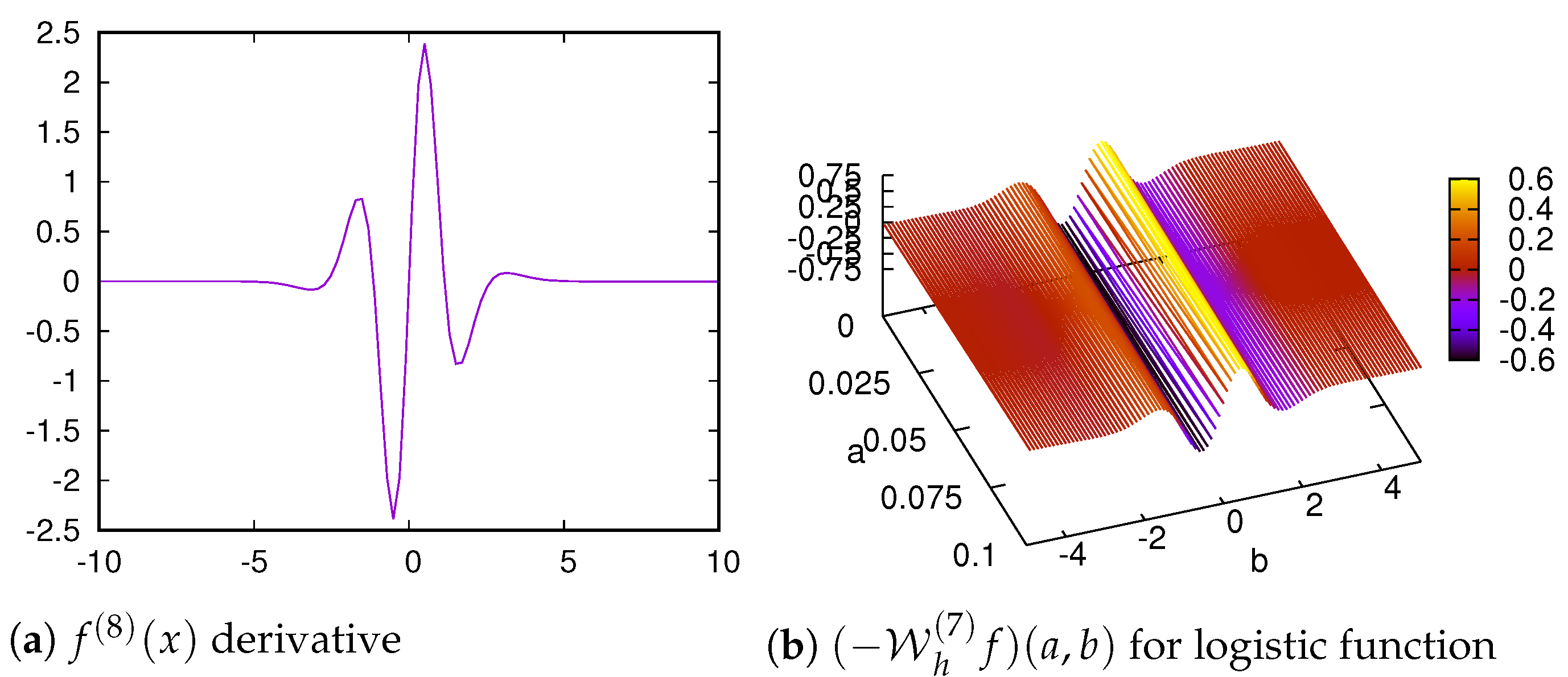
In fact, logistic function is widely used in the context of artificial neural networks [24,25,26] because of its mathematical properties. Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show the $(n+1)-$th derivatives of $f\left(x\right)$ and the $n-$th derivatives of $\left({-\mathcal{W}}_{h}f\right)(a,b)$ for $n = 0 , 1 , 2 , 6$, and 7. We are plotting $\left({-\mathcal{W}}_{h}f\right)(a,b)$ to illustrate that graphs in $2D$ and $3D$ match. Left sides show $2D$ plots with the same behaviour as the $3D$ plots of the right sides given the regularity of this function, as is indicated by Lemma 3.

Table 1. ${lim}_{(a,b)\to (0,b_1)}\left({\mathcal{W}}_h^{n}f\right)(a,b)$ for logistic function.

${\mathit{b}}_{\mathbf{1}}$
n	0	2	4	8
0	−0.0625	−0.02624	−0.00441	−0.00008
1	0	0.01999	0.00425	0.00008
2	0.03125	-0.00971	−0.00394	−0.00008
3	0	−0.00519	0.00335	0.00008
4	−0.0625	0.02170	−0.00224	−0.00008
5	0	−0.02660	0.00022	0.00008
6	0.265625	−0.01200	0.00321	−0.00008
7	0	0.13528	−0.00847	0.00007
8	−1.93750	−0.28892	0.01458	−0.00006

shows some values of $\left({\mathcal{W}}_h^{n}f\right)(a,b)$ for points $b_1=\{0 , 2 , 4 , 8\}$ as $a\to 0$ and for $n = 0 , 1 , 2 , \cdots , 8$. The limit values are consistent (negative values) with those of Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5. For example, for $n = 0$ and $b_1 = 0$ in Table 1, the value is $-0.0625$, and the graph of Figure 1 shows a maximum at this point, and moreover, it can be appreciated a consistent behaviour in Figure 1 as $a\to 0$.

For $n=1$ and $b_1=0$, $\left({\mathcal{W}}_h^{n}f\right)(a,b)\to 0$, and this is consistent with Figure 2. For $n=2$ and $b_1$ moving from 0 to 8, the value of $\left({\mathcal{W}}_h^{n}f\right)(a,b)$ tends to zero, and the graph of Figure 3 also shows a vanishing behaviour. As n increases, $f^{\left(n\right)}\left(x\right)$ and $\left({\mathcal{W}}_h^{n}f\right)(a,b)$ have more oscillations (see Figure 4 and Figure 5) but they always keep the regularity, as stated by Lemma 3.

Example 2.

Now we give an example for Theorem 2 in the case $b_0=0$. Let $h_1=(1-x^2)ex{p}^{-\frac{x^2}{2}}$. Consider $f\left(x\right)=\left|x\right|$ if $\left|x\right|\le 1$ and $f\left(x\right)=0$ otherwise. Then, $suppf=[-1,1]$ and therefore, $f\in L^p\left(\mathbb{R}\right)$, $1<p<\infty$. Take $a>1,b\in \mathbb{R}$ and $m\in \mathbb{Z}$.

Then from (7), (9) and (10),

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{h_1}^{n}f\right)(a^m,b)& =\frac{1}{a^m}\frac{{\partial }^n}{\partial b^n}\left(L_{h}f\right)(a^m,b)=\frac{1}{a^m}\frac{{(-1)}^n}{{\left(a^m\right)}^n}\left(L_{h^{\left(n\right)}}f\right)(a^m,b)\hfill \\ & =\frac{1}{a^m}\frac{{(-1)}^n}{{\left(a^m\right)}^n}{\int }_{b-aL}^{b+aL}f\left(x\right)\frac{1}{a^m}\overline{h^{\left(n\right)}\left(\frac{x-b}{a^m}\right)}dx.\hfill \end{array}$$

We have, for $n=1$,

$$h_1^{\left(1\right)}\left(x\right)=(-3x+x^3)e^{-\frac{x^2}{2}}$$

and since $h_1$ is a wavelet with real values,

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{h_1}^{1}f\right)(a^m,b)& =\frac{-1}{a^{2m}}{\int }_{b-a^{m}L}^{b+a^{m}L}\left|x\right|h^{\left(1\right)}\left(\frac{x-b}{a^m}\right)dx.\hfill \end{array}$$

With a change of variable, $y=\frac{x-b}{a^m}$, then $x=b+a^{m}y$, and consequently,

$$\begin{array}{cc}\hfill \left({\mathcal{W}}_{h_1}^{1}f\right)(a^m,b)& =\frac{-1}{a^{2m}}{\int }_{-L}^L|b+a^{m}y|h^{\left(1\right)}\left(y\right)dy\hfill \\ & =\frac{-1}{a^{2m}}\left[{\int }_{-L}^{-\frac{b}{a^m}}(-b-a^{m}y)h^{\left(1\right)}\left(y\right)dy+{\int }_{-\frac{b}{a^m}}^L(b+a^{m}y)h^{\left(1\right)}\left(y\right)dy\right]\hfill \\ & =\frac{-2b}{a^{2m}}\left[(1-L^2)e^{-\frac{L^2}{2}}-e^{-\frac{b^2}{2a^{2m}}}\right].\hfill \end{array}$$

We analyze $\left({\mathcal{W}}_h^{1}f\right)(a^m,b)$ involving the limit for $b\to 0$ and $a^m\to 0$ (i.e., $m\to -\infty$).

Note that, for $b=0$,

$$\underset{m\to -\infty }{lim}\left({\mathcal{W}}_{h_1}^{1}f\right)(a^m,0)=0$$

while, for $b=a^{2m}$

$$\underset{m\to -\infty }{lim}\left({\mathcal{W}}_{h_1}^{1}f\right)(a^m,a^m)=-2((1-L^2)e^{-\frac{L^2}{2}}-1),$$

consequently, this limit does not exist, and f is not $C^{\infty }$.

Note that in Example 2, we have used a function $h_1$ that does not have compact support (but it has a fast decay) and the result is consistent with Theorem 2, so the example shows that the results could apply with wavelets with no compact support.

In Figure 6 we show a plot for $f\left(x\right)$ in the left side, and a $3D$ plot in the right side for ${\mathcal{W}}_{h_1}^{\left(1\right)}f)(a^m,b)$ where it is possible to see how the graph loses smoothness and produces “two peaks” close to $b=0$ while $a^m\to 0$.