Meshing Drive Mechanism of Double Traveling Waves for Rotary Piezoelectric Motors
Abstract
1. Introduction
2. Materials and Methods
2.1. Input Parameters and Boundary Conditions for FEM
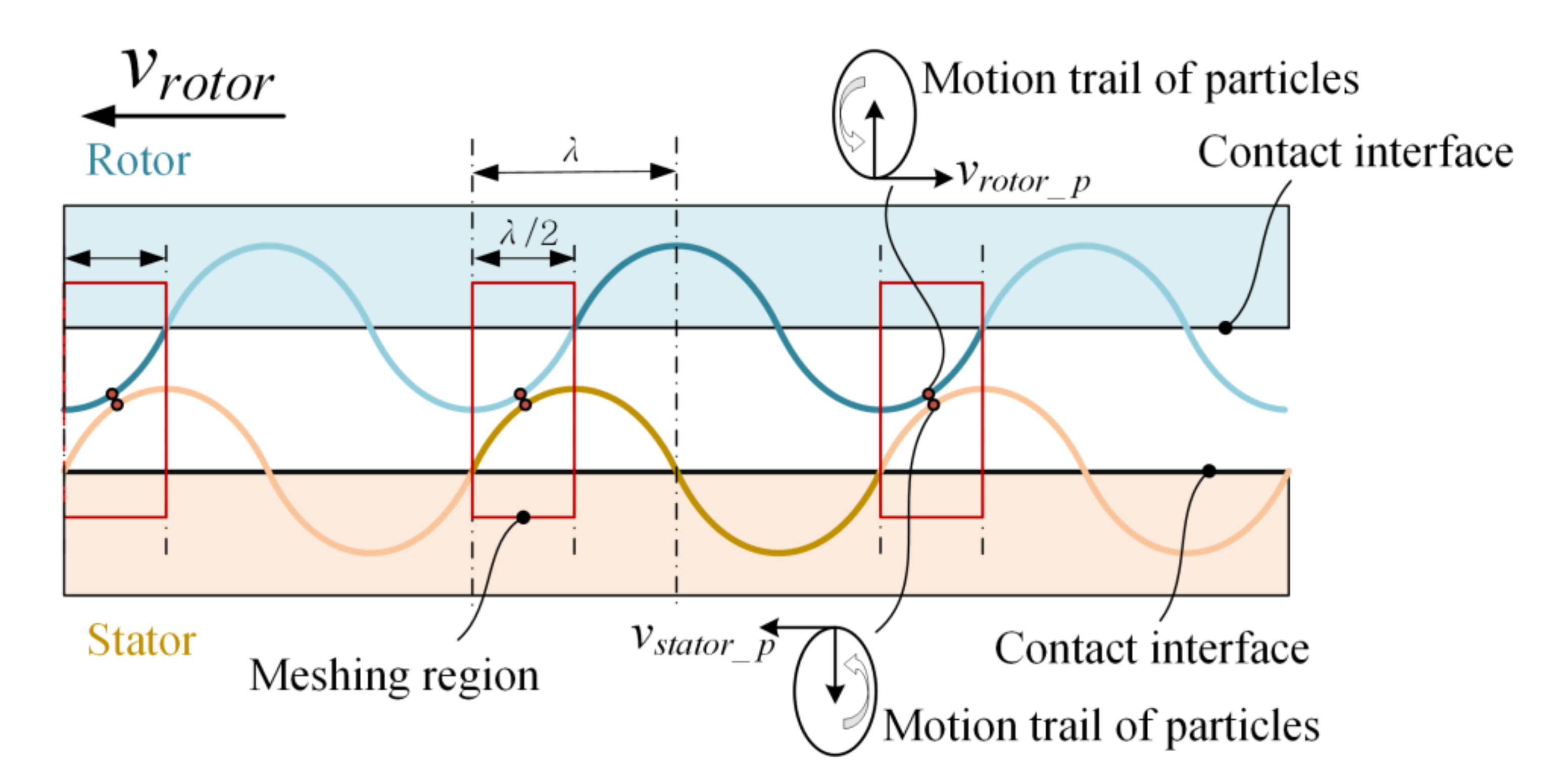
2.2. Theoretical Derivation for Wave Generating
3. Results and Discussion
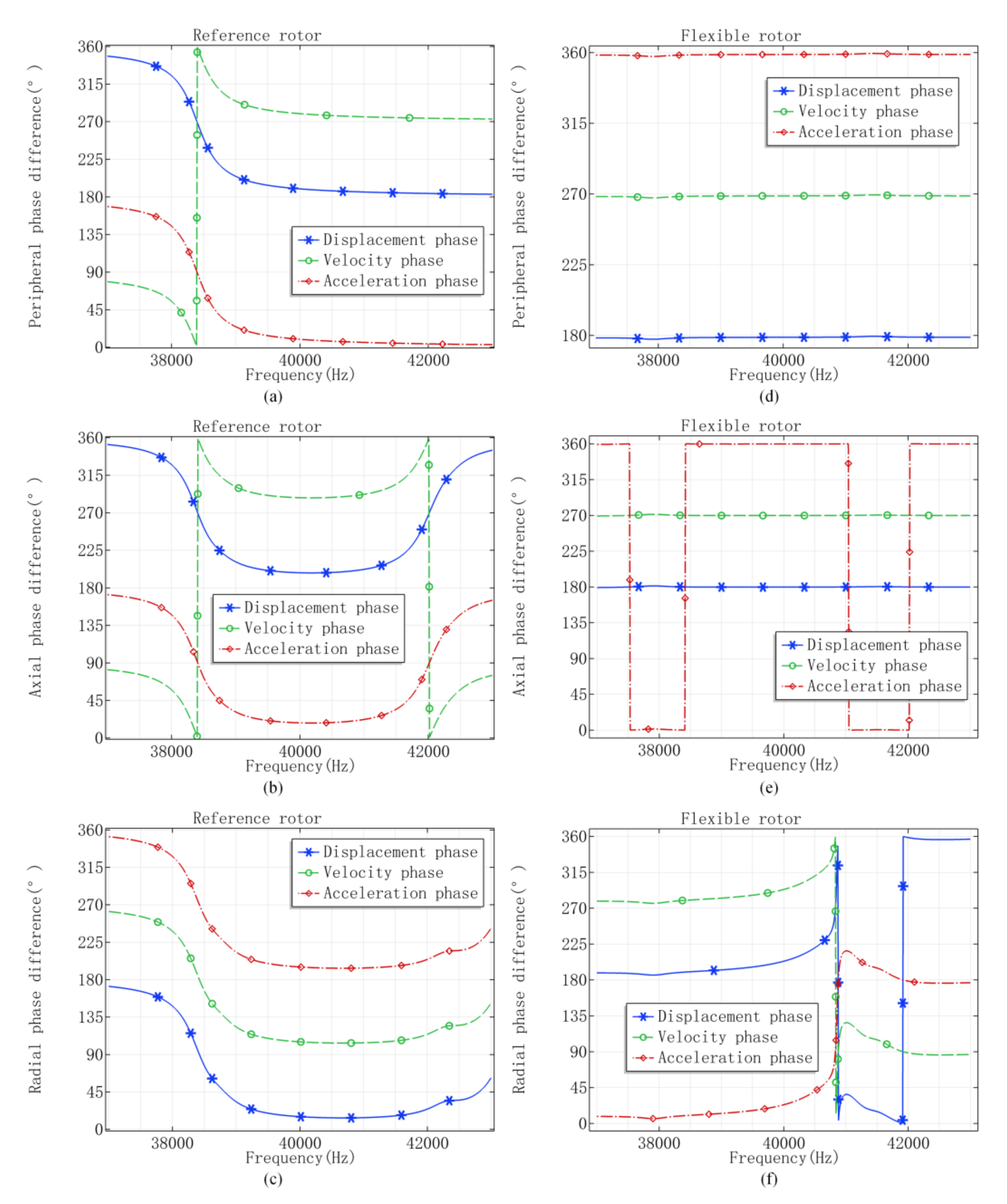
3.1. Numerical Results of FEM
3.2. Prototype Experimental Results
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Storck, H.; Littmann, W.; Wallaschek, J.; Mracek, M. The Effect of Friction Reduction in Presence of Ultrasonic Vibrations and Its Relevance to Travelling Wave Ultrasonic Motors. Ultrasonics 2002, 40, 379–383. [Google Scholar] [CrossRef]
- Giraud, F.; Semail, B. A Torque Estimator for a Traveling Wave Ultrasonic Motor-Application to an Active Claw. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1468–1477. [Google Scholar] [CrossRef]
- Chen, X.F.; Huang, W.Q.; Luo, J.Q.; Xu, J.J. Design of a Kind of Non-Resonant Linear Piezoelectric Motor. AMM 2013, 459, 418–423. [Google Scholar] [CrossRef]
- Chen, X.; Lu, Q.; Huang, W.; Wang, Y. Working Mechanism of Nonresonance Friction in Driving Linear Piezoelectric Motors with Rigid Shaking Beam. Math. Probl. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Peng, Y.; Peng, Y.; Gu, X.; Wang, J.; Yu, H. A Review of Long Range Piezoelectric Motors Using Frequency Leveraged Method. Sens. Actuators A Phys. 2015, 235, 240–255. [Google Scholar] [CrossRef]
- Cheon, S.-K.; Jeong, S.-S.; Ha, Y.-W.; Lee, B.-H.; Park, J.-K.; Park, T.-G. Driving Characteristics of an Ultrasonic Rotary Motor Consisting of Four Line Contact Type Stators. Ceram. Int. 2015, 41, S618–S624. [Google Scholar] [CrossRef]
- Li, S.; Li, D.; Yang, M.; Cao, W. Parameters Identification and Contact Analysis of Traveling Wave Ultrasonic Motor Based on Measured Force and Feedback Voltage. Sens. Actuators A Phys. 2018, 284, 201–208. [Google Scholar] [CrossRef]
- An, D.; Yang, M.; Zhuang, X.; Yang, T.; Meng, F.; Dong, Z. Dual Traveling Wave Rotary Ultrasonic Motor with Single Active Vibrator. Appl. Phys. Lett. 2017, 110, 143507. [Google Scholar] [CrossRef]
- An, D.; Huang, W. Inherent Mechanism of Frequency Drift Affected by Constraint Conditions for Rotary Piezoelectric Motors. Rev. Sci. Instrum. 2020, 91, 035002. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Bao, Q.; Zhang, J.; Ning, Q.; Chen, C.; Huang, J.; Wu, C. Design and Experimental Verification of a PZT Pump with Streamlined Flow Tubes. Appl. Sci. 2019, 9, 3881. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, J.; Tang, M.; Huang, Z.; Lai, L.; Huang, J.; Wu, C. A Novel PZT Pump with Built-in Compliant Structures. Sensors 2019, 19, 1301. [Google Scholar] [CrossRef] [PubMed]
- He, X.-T.; Yang, Z.-X.; Li, Y.-H.; Li, X.; Sun, J.-Y. Application of Multi-Parameter Perturbation Method to Functionally-Graded, Thin, Circular Piezoelectric Plates. Mathematics 2020, 8, 342. [Google Scholar] [CrossRef]
- Liu, T.; Li, C.; Wang, C.; Lai, J.W.; Cheong, K.H. A Simple-FSDT-Based Isogeometric Method for Piezoelectric Functionally Graded Plates. Mathematics 2020, 8, 2177. [Google Scholar] [CrossRef]
- Yuan, T.; Dong, X.; Shekhani, H.; Li, C.; Maida, Y.; Tou, T.; Uchino, K. Driving an Inductive Piezoelectric Transducer with Class E Inverter. Sens. Actuators A Phys. 2017, 261, 219–227. [Google Scholar] [CrossRef]
- Jang, J.H.; Chang, C.; Rasumssen, M.F.; Brenner, K.; Stedman, Q.; Ergun, A.S.; Khuri-Yakub, B.T. Dual-Mode Capacitive Micromachined Ultrasonic Transducer Arrays for High Intensity Focused Ultrasound and Imaging. J. Acoust. Soc. Am. 2018, 144, 1698. [Google Scholar] [CrossRef]
- Sun, X.; Li, S.; Dun, X.; Li, D.; Li, T.; Guo, R.; Yang, M. A Novel Characterization Method of Piezoelectric Composite Material Based on Particle Swarm Optimization Algorithm. Appl. Math. Model. 2019, 66, 322–331. [Google Scholar] [CrossRef]
- Guo, R.; Li, S.; An, D.; Han, T.; Chen, J.; Cao, W. Comprehensive Analysis of Mn:PIN-PMN-PT Single Crystals for Class IV Flextensional Transducer. Ceram. Int. 2018, 44, 2864–2868. [Google Scholar] [CrossRef]
- Wu, J.; Mizuno, Y.; Nakamura, K. Structural Parameter Study on Polymer-Based Ultrasonic Motor. Smart Mater. Struct. 2017, 26, 115022. [Google Scholar] [CrossRef]
- Wu, J.; Mizuno, Y.; Nakamura, K. Polymer-Based Ultrasonic Motors Utilizing High-Order Vibration Modes. IEEE/ASME Trans. Mechatron. 2018, 23, 788–799. [Google Scholar] [CrossRef]
- Cao, T.; Li, X.; Wang, B.; Mi, Y.; Zhao, G.; Twiefel, J.; Wu, D. Viscoelastic Analytical Model and Design of Polymer-Based Bimodal Piezoelectric Motor. Mech. Syst. Signal Process. 2020, 145, 106960. [Google Scholar] [CrossRef]
- Shi, M.; Liu, X.; Feng, K.; Zhang, K. Experimental and Numerical Investigation of a Self-Adapting Non-Contact Ultrasonic Motor. Tribol. Int. 2021, 153, 106624. [Google Scholar] [CrossRef]
- Yin, Z.; Dai, C.; Cao, Z.; Li, W.; Chen, Z.; Li, C. Modal Analysis and Moving Performance of a Single-Mode Linear Ultrasonic Motor. Ultrasonics 2020, 108, 106216. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Yashiro, D.; Yubai, K.; Komada, S. Torque Control of a Series Elastic Actuator Using an Ultrasonic Motor with Angular-velocity Saturation. Electr. Eng. Jpn. 2020, eej.23297. [Google Scholar] [CrossRef]
- Koc, B. Operating Frequency Tracking of Single Phase Driving Type Piezoelectric Motors. J. Electroceram. 2009, 23, 262. [Google Scholar] [CrossRef]
- Mustafa, A.; Morita, T. Fundamental Study of Preload Control for Rotary Ultrasonic Motors. In Proceedings of the 2018 JSPE Semestrial Meeting, Hachioji, Tokyo, Japan, 15–17 March 2018; pp. 713–714. Available online: https://www.jstage.jst.go.jp/article/pscjspe/2018S/0/2018S_713/_article/-char/ja/.
- Mustafa, A.; Morita, T. Efficiency Optimization of Rotary Ultrasonic Motors Using Extremum Seeking Control with Current Feedback. Sens. Actuators A Phys. 2019, 289, 26–33. [Google Scholar] [CrossRef]
- Lu, X.; Hu, J.; Zhao, C. Analyses of the Temperature Field of Traveling-Wave Rotary Ultrasonic Motors. Ieee Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2708–2719. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Hu, J.; Yang, L.; Zhao, C. Principle and Experimental Verification of Novel Dual Driving Face Rotary Ultrasonic Motor. Chin. J. Mech. Eng. 2013, 26, 1006–1012. [Google Scholar] [CrossRef]
- Li, S.; Ou, W.; Yang, M.; Guo, C.; Lu, C.; Hu, J. Temperature Evaluation of Traveling-Wave Ultrasonic Motor Considering Interaction between Temperature Rise and Motor Parameters. Ultrasonics 2015, 57, 159–166. [Google Scholar] [CrossRef]
- Ou, W.; Yang, M.; Meng, F.; Xu, Z.; Zhuang, X.; Li, S. Continuous High-Performance Drive of Rotary Traveling-Wave Ultrasonic Motor with Water Cooling. Sens. Actuators A Phys. 2015, 222, 220–227. [Google Scholar] [CrossRef]
- Hagood, N.W.; McFarland, A.J. Modeling of a Piezoelectric Rotary Ultrasonic Motor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 210–224. [Google Scholar] [CrossRef]
- Fang, Z.; Yang, T.; Zhu, Y.; Li, S.; Yang, M. Velocity Control of Traveling-Wave Ultrasonic Motors Based on Stator Vibration Amplitude. Sensors 2019, 19, 5326. [Google Scholar] [CrossRef] [PubMed]
- Mohd Romlay, F.R.; Wan Yusoff, W.A.; Mat Piah, K.A. Increasing the Efficiency of Traveling Wave Ultrasonic Motor by Modifying the Stator Geometry. Ultrasonics 2016, 64, 177–185. [Google Scholar] [CrossRef]
- Peng, T.; Shi, H.; Liang, X.; Luo, F.; Wu, X. Experimental Investigation on Sandwich Structure Ring-Type Ultrasonic Motor. Ultrasonics 2015, 56, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Shi, S.; Liu, Y.; Li, P. A New Traveling Wave Ultrasonic Motor Using Thick Ring Stator with Nested PZT Excitation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1160–1168. [Google Scholar] [CrossRef]
- Hagedorn, P.; Wallaschek, J. Travelling Wave Ultrasonic Motors, Part I: Working Principle and Mathematical Modelling of the Stator. J. Sound Vib. 1992, 155, 31–46. [Google Scholar] [CrossRef]
- Hagedorn, P.; Wallaschek, J.; Konrad, W. Travelling Wave Ultrasonic Motors, Part II: A Numerical Method For The Flexural Vibrations Of The Stator. J. Sound Vib. 1993, 168, 115–122. [Google Scholar] [CrossRef]
- Zhao, C. Ultrasonic Motors Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Rajkumar, R.; Nogai, T. A New Method of Improving the Torque of a Travelling Wave Ultrasonic Motor. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Atlanta, GA, USA, 19–23 September 1999; pp. 109–113. [Google Scholar]
- Bai, D.; Ishii, T.; Nakamura, K.; Ueha, S.; Yonezawa, T.; Takahashi, T. An Ultrasonic Motor Driven by the Phase-Velocity Difference between Two Traveling Waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 680–685. [Google Scholar] [PubMed]
- Dong, Z.; Yang, M.; Chen, Z.; Xu, L.; Meng, F.; Ou, W. Design and Performance Analysis of a Rotary Traveling Wave Ultrasonic Motor with Double Vibrators. Ultrasonics 2016, 71, 134–141. [Google Scholar] [CrossRef]
- Sana, M.; Mustahsan, M. Finite Element Approximation of Optimal Control Problem with Weighted Extended B-Splines. Mathematics 2019, 7, 452. [Google Scholar] [CrossRef]
- Vlase, S.; Negrean, I.; Marin, M.; Nastac, S. Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method. Mathematics 2020, 8, 805. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]

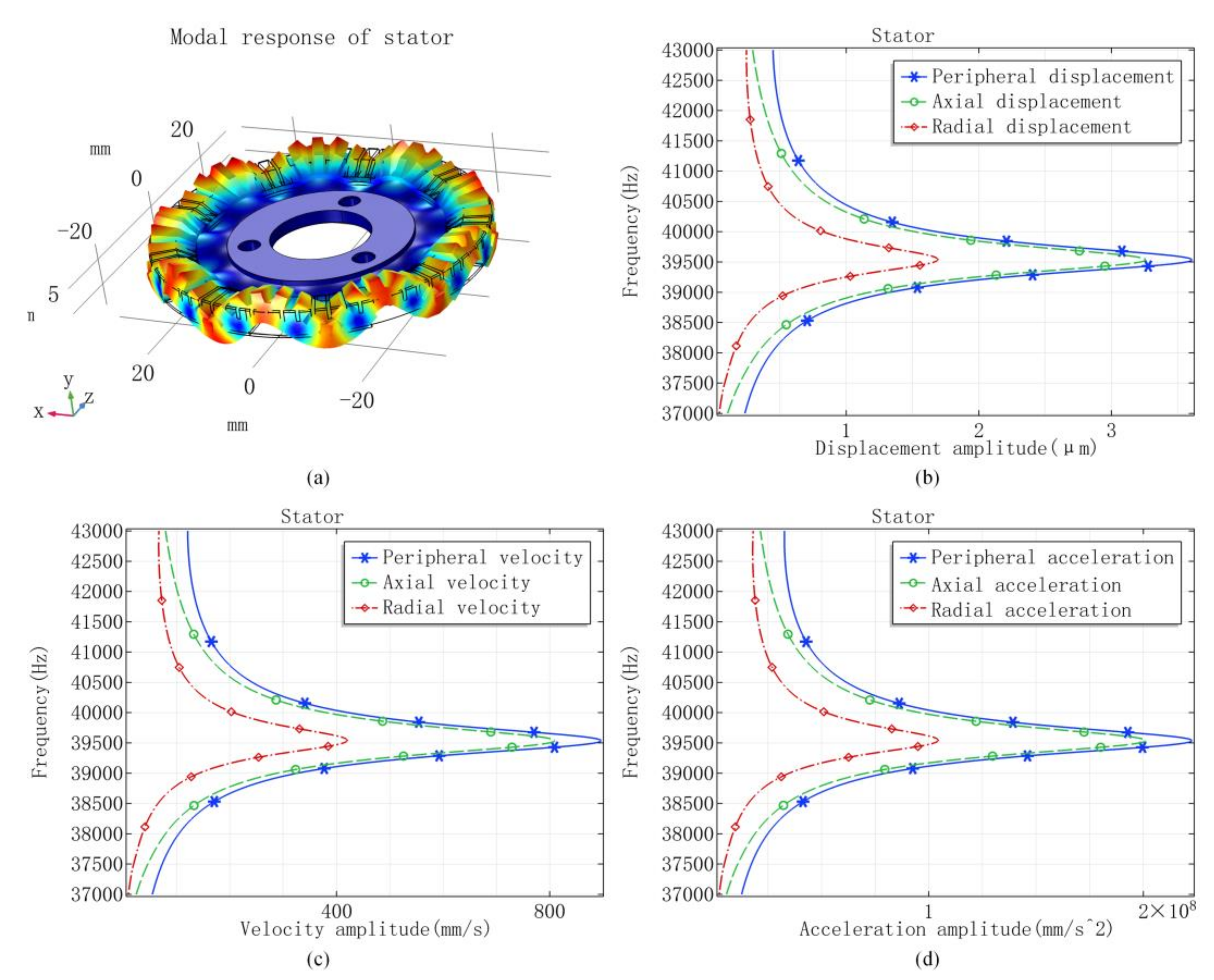


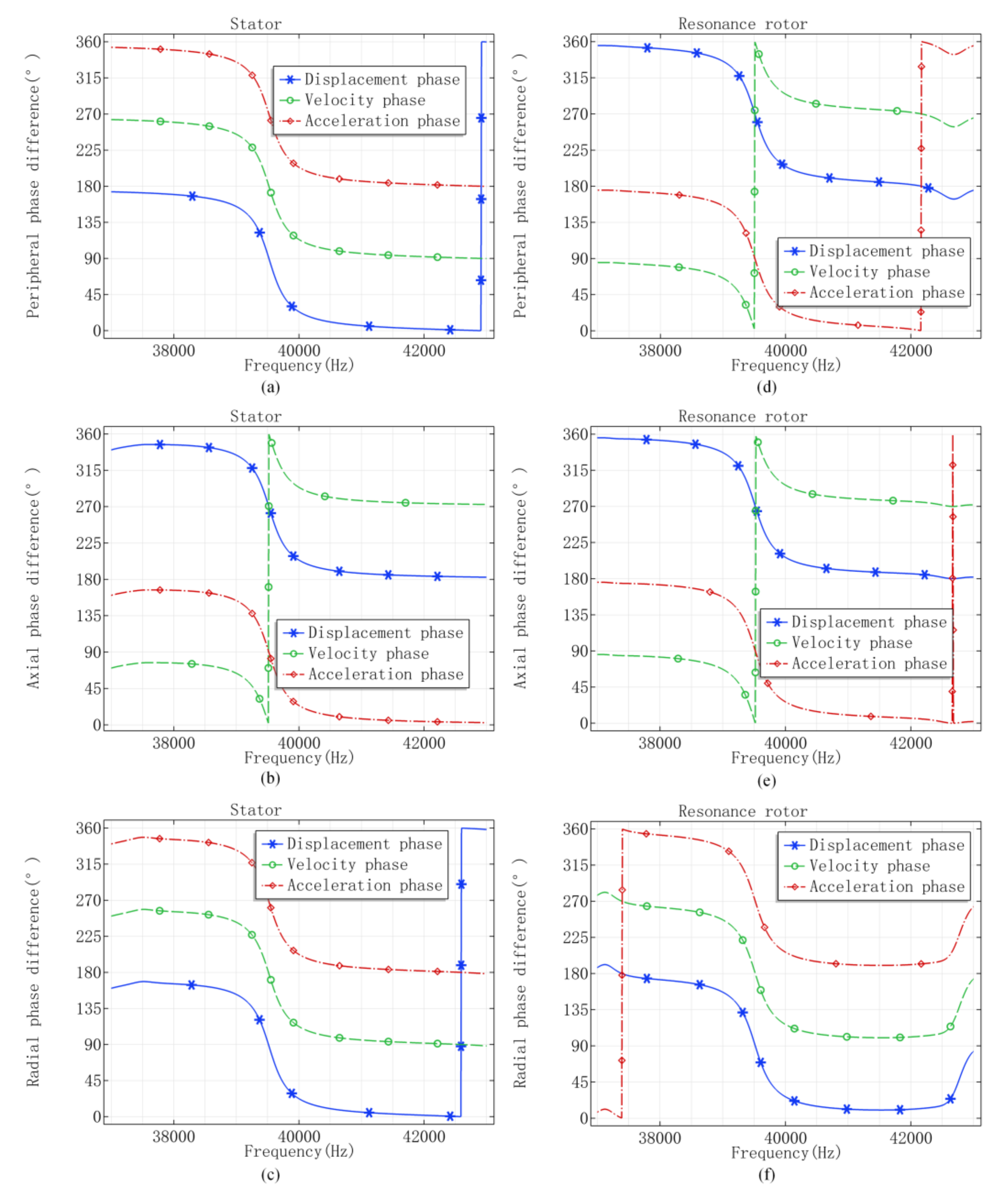
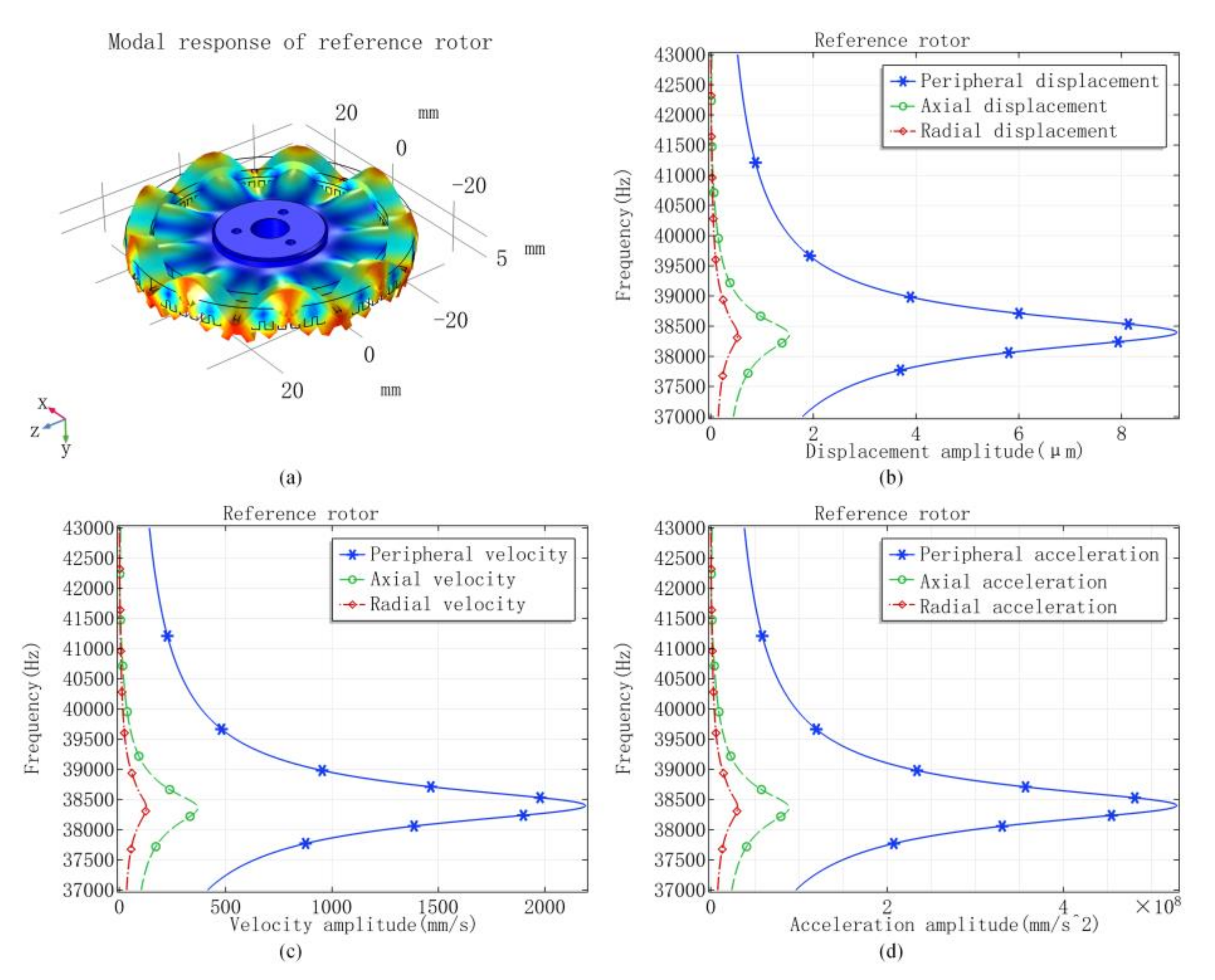
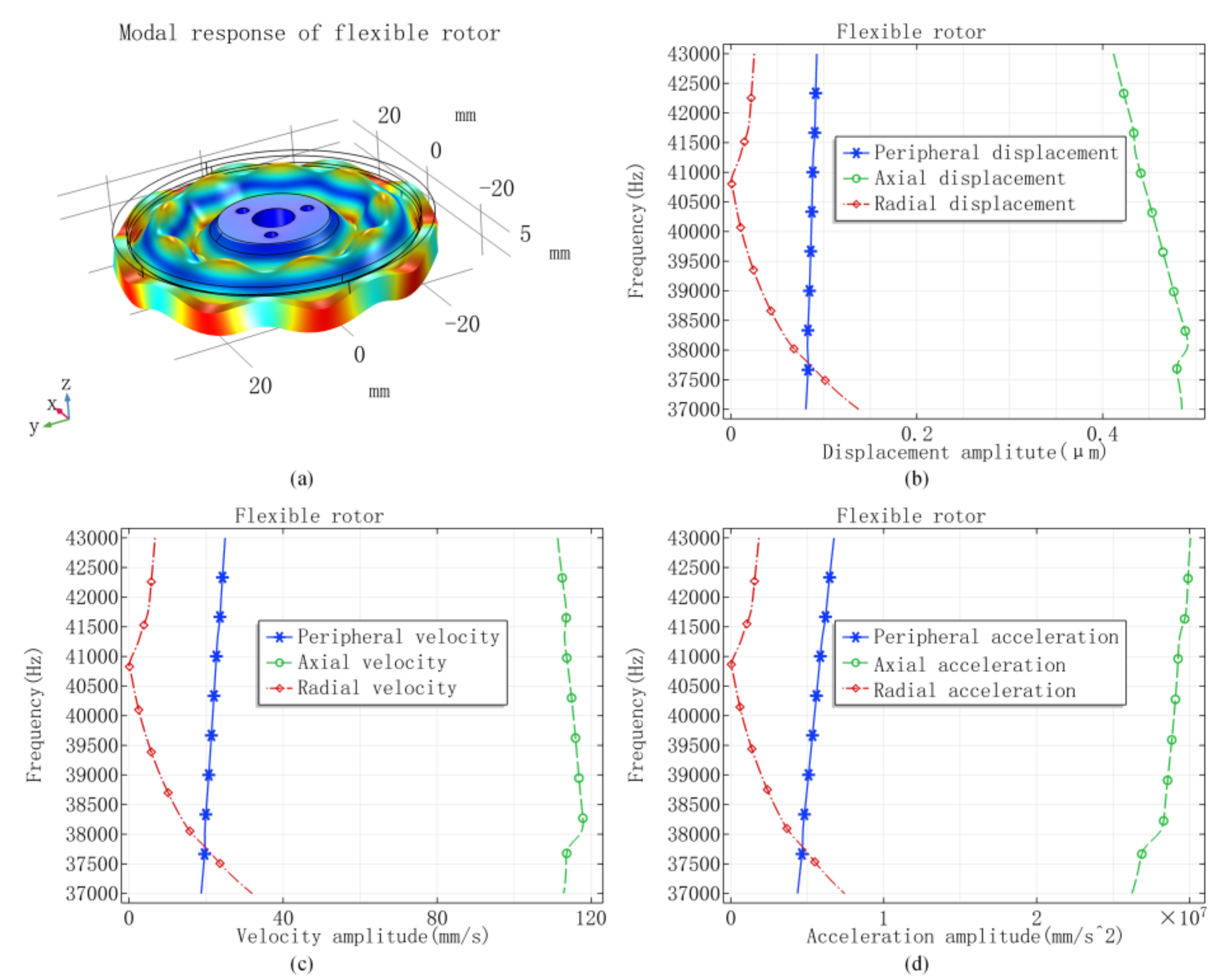

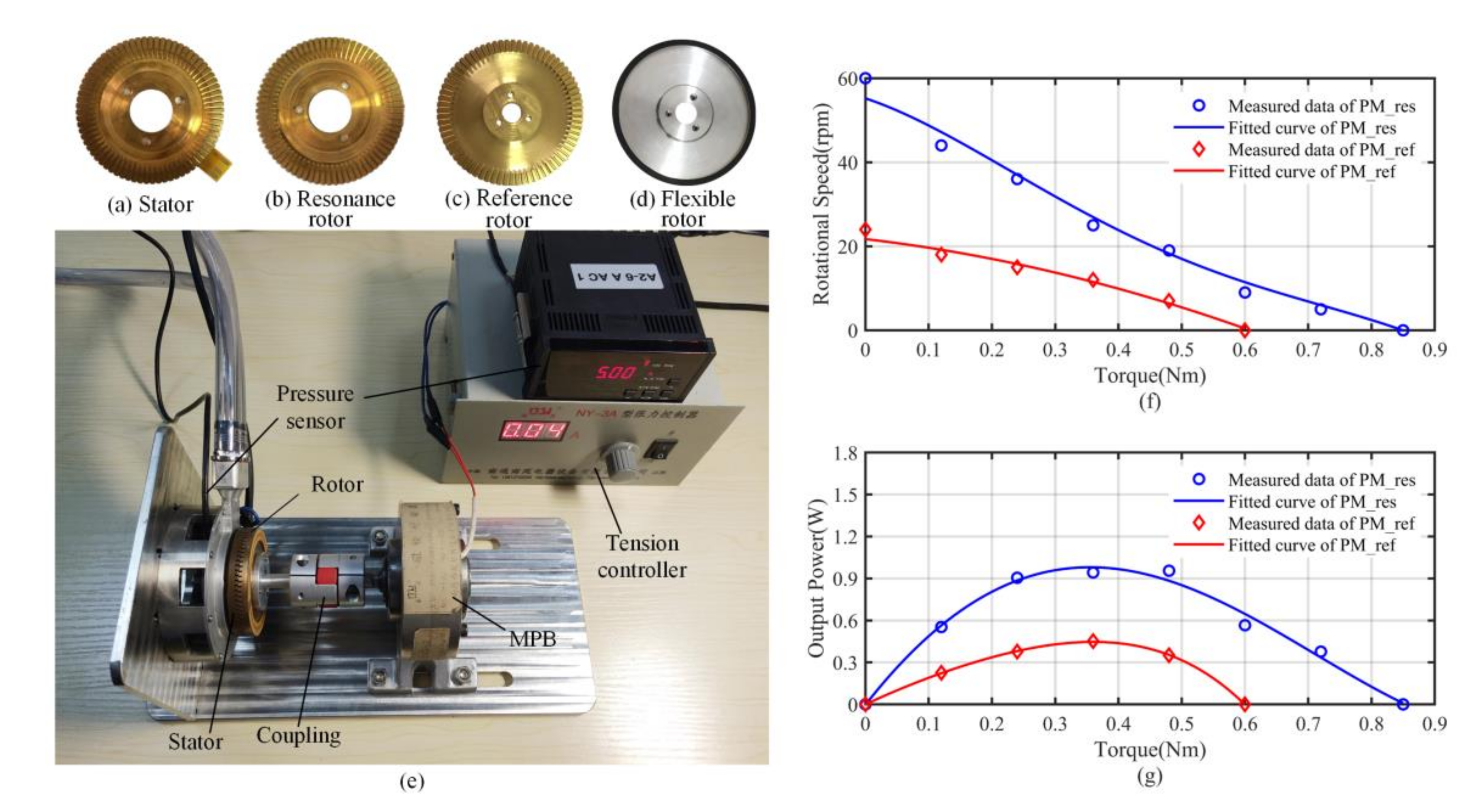
| Vibrators | Materials | Outer Diameter (mm) | Inner Diameter (mm) | Total Height (mm) |
|---|---|---|---|---|
| Stator | Phosphor bronze & PZT-8H | 60 | 18 | 4.5 + 0.5 |
| Resonance rotor | 18 | 4.5 + 0.5 | ||
| Reference rotor | Phosphor bronze | 8 | 5 | |
| Flexible rotor | Aluminum | 8 | 5 |
| Parameters | Phosphor Bronze | Aluminum | PZT-8H |
|---|---|---|---|
| Mass density (kg/m3) | 8780 | 2770 | 7600 |
| Poisson’s ratio | 0.341 | 0.3 | — |
| Young’s modulus (N/m2) | 1.1E11 | 7.17E10 | — |
| Calculated Results | Stator | Resonance Rotor | Reference Rotor | Flexible Rotor | |
|---|---|---|---|---|---|
| 9th modal frequency (Hz) | 39,535 | 39,514 | 38,419 | — | |
| Adjacent modal frequency (Hz) | — | — | 38,756 | 37,912 41,136 | |
| Displacement amplitude (μm) 1 | Peripheral | 3.608 | 3.716 | 2.139 | 0.466 |
| Axial | 3.258 | 2.255 | 0.243 | 0.085 | |
| Radial | 1.691 | 0.699 | 0.105 | 0.020 | |
| Velocity amplitude (mm/s) 1 | Peripheral | 896.5 | 923.1 | 531.3 | 115.9 |
| Axial | 809.6 | 560.3 | 60.49 | 21.27 | |
| Radial | 420.3 | 173.8 | 26.10 | 5.035 | |
| Acceleration amplitude (mm/s2) 1 | Peripheral | 2.227 × 108 | 2.293 | 1.319 × 108 | 0.288 × 108 |
| Axial | 2.011 × 108 | 1.391 | 0.150 × 108 | 0.052 × 108 | |
| Radial | 1.044 × 108 | 0.431 | 0.064 × 108 | 0.012 × 108 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, D.; Huang, W.; Liu, W.; Xiao, J.; Liu, X.; Liang, Z. Meshing Drive Mechanism of Double Traveling Waves for Rotary Piezoelectric Motors. Mathematics 2021, 9, 445. https://doi.org/10.3390/math9040445
An D, Huang W, Liu W, Xiao J, Liu X, Liang Z. Meshing Drive Mechanism of Double Traveling Waves for Rotary Piezoelectric Motors. Mathematics. 2021; 9(4):445. https://doi.org/10.3390/math9040445
Chicago/Turabian StyleAn, Dawei, Weiqing Huang, Weiquan Liu, Jinrui Xiao, Xiaochu Liu, and Zhongwei Liang. 2021. "Meshing Drive Mechanism of Double Traveling Waves for Rotary Piezoelectric Motors" Mathematics 9, no. 4: 445. https://doi.org/10.3390/math9040445
APA StyleAn, D., Huang, W., Liu, W., Xiao, J., Liu, X., & Liang, Z. (2021). Meshing Drive Mechanism of Double Traveling Waves for Rotary Piezoelectric Motors. Mathematics, 9(4), 445. https://doi.org/10.3390/math9040445









