1. Introduction
All graphs considered in this paper are finite, simple, and undirected. Let and be the vertex set and edge set of a graph G, respectively. The open neighborhood of a vertex v in G is the set of all vertices that are adjacent to v, the closed neighborhood is the set , and the set of edges incident with v is The degree of a vertex v is the number of vertices in . The maximum degree among all vertices of G is denoted by . The union of simple graphs G and H is the graph with vertex set and edge set . A star of order is the complete bipartite graph . The center of the star is the vertex of maximum degree.
A leaf of G is a vertex with degree one and a support vertex is a vertex adjacent to a leaf. For a vertex subset , we denote by the subgraph induced by S. A subdivision of an edge is obtained by removing the edge , adding a new vertex w, and adding edges and . Throughout this paper, when an edge is subdivided, the subdivision vertex for e is denoted by . For a set F of edges in a graph G, we use to denote the graph obtained from G by subdividing every edge in Note that for every two different edges
A set
is a
paired-dominating setof
G, PD-set for short, if each vertex in
has at least one neighbor in
S and
contains a perfect matching. The minimum cardinality of a PD-set of
G is called the
paired-domination number of
G and is denoted by
. Let
S be a PD-set of
G with a perfect matching
M. Then, two vertices
u and
v are called
partners (or paired) in
S if the edge
. Paired domination in graphs was first studied in [
1] and has been studied since then by several authors (for example, see [
2,
3,
4,
5,
6]). The literature on the subject of paired domination has been detailed in the recent book chapter [
7].
As good models of many practical problems, graphs sometimes have to be changed to adapt the changes in reality. Thus, we must pay attention to the change of graph parameters under graph modifications, such as deletion of vertices, deletion or addition of edges, and subdivision of edges. For example, Kok and Mynhardt [
8] introduced the reinforcement number, which is the minimum number of edges which must be added to
G in order to decrease the domination number of
G. Fink et al. [
9] introduced the bondage number of a graph, which is the minimum number of edges in which removal increases the domination number. For the subdivision of edges, Velammal [
10], in his thesis, introduced the domination subdivision number which is the minimum number of edges that must be subdivided (where each edge can be subdivided at most once) in order to increase the domination number. The study of this kind of problems has been extended to other domination parameters (see, for instance [
11,
12,
13,
14,
15,
16,
17,
18]).
In this paper, we are interested in studying the paired-domination subdivision number introduced by Favaron et al. in [
19]. In order to increase the paired-domination number of
G, the minimum number of edges that must be subdivided (where each edge in
G can be subdivided no more than once) is called the
paired-domination subdivision number and is denoted by
. We note that the subdivision of the unique edge of a path of order 2 does not increase the paired-domination number. Thus, we always assume that all graphs involved have a component of order at least 3. The minimum cardinality of a set
such that
is called an
-set. The paired-domination subdivision number has been studied by several authors (see, for instance [
20,
21]).
Let
G be a connected graph of order at least 3. Favaron et al. [
19] posed the following question: Is it true that, for any edge
? A negative answer to this question was given by Egawa et al. [
22]. However, they approved the question in the affirmative if the following additional condition is added: each edge
satisfies
. We can further specify that, if
for some edge
, then the difference
can be arbitrary large. To see this, consider the connected graph
obtained from
disjoint
by adding a new vertex attached to one vertex of each
Now, for two leaves
x and
y of
, one can easily see that
, while
and
.
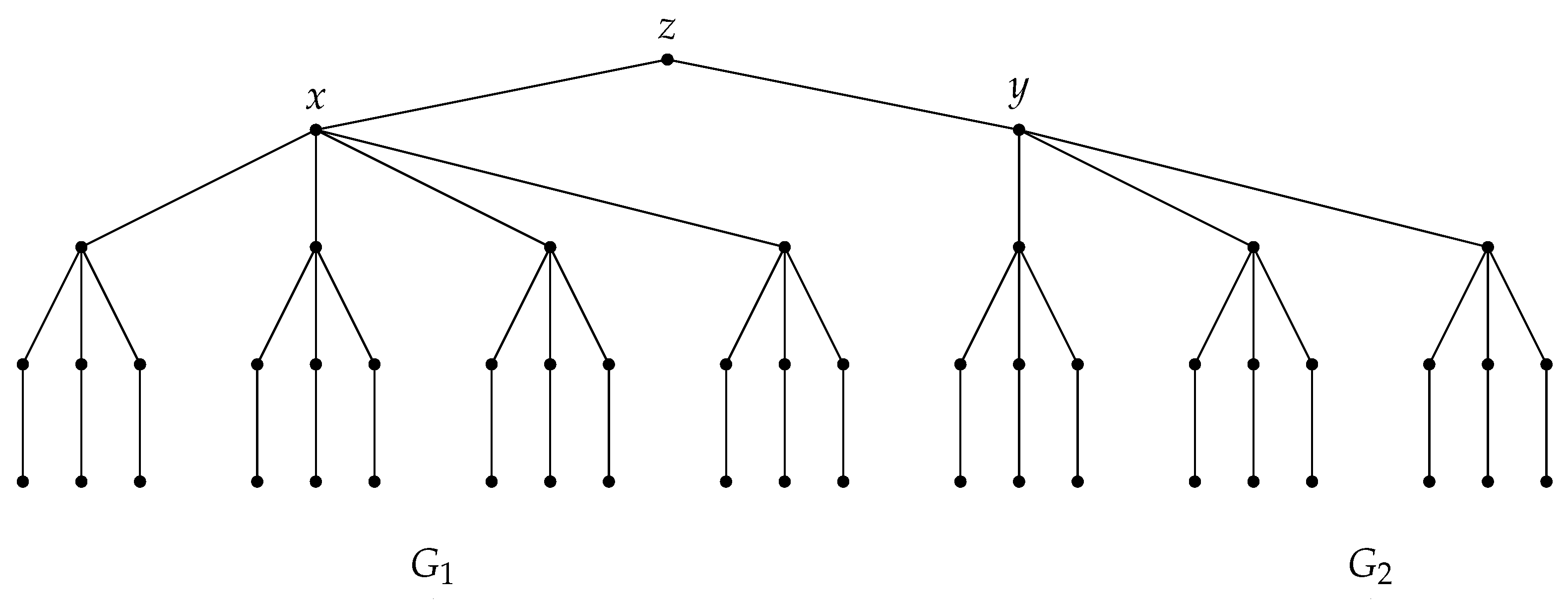
Let
denote the subdivided star obtained from a star
of order
t by subdividing all edges of
. Let
be obtained from
t copies of
by adding a new vertex
x and joining
x to the central vertices of subdivided stars,
be obtained from
copies of
by adding a new vertex
y and joining
y to the central vertices of subdivided stars and adding a pendant edge
, and let
be the union
. Note that
. It is not hard to verify that
and
, where the graph
for
is illustrated in
Figure 1. Hence, the difference of
can be arbitrary large for some edge
. Thus, an interesting problem is to find good bounds on
in terms of
and
if
.
In this paper, we provide an upper bound for
for any
in terms of
and
, the proof of which will be given in
Section 3. More precisely, we mainly show the following.
Theorem 1. Let G be an isolated-free graph different from Then, for every , Furthermore, this bound is sharp.
We close this section by recalling three useful results.
Proposition 1 ([
19])
. For any connected graph G of order at least three and any graph formed from G by subdividing an edge , . Proposition 2 ([
22])
. Let G be a graph with no isolated vertex. Then, for every edge , either or . Proposition 3 ([
22])
. Let G be a connected graph of order at least three, and let satisfy . Then, . 2. Preliminary Results
In this section, we give some preliminary results useful for the proof of Theorem 1. We begin by extending the result of Proposition 3 to disconnected graphs different from and having no isolated vertices.
Proposition 4. Let G be an isolated-free graph different from . If for some edge then .
Proof. Let F be an -set and observe that . We shall show that . Assume that and let P be a -set. If or , and they are not partners in P, then, clearly, P is a PD-set of , so . Hence, we assume that . First, let be two partners in P. Since P is a -set, we may assume that . Let . If y has a neighbor , then the set (in which x and y are partners with and respectively) is a PD-set of ; thus, .
Hence, we can assume that Then, the set (in which x and are partners) is a PD-set of , and the result follows as above. Finally, let . Without loss of generality, assume that . If y has a neighbor in P other than x, then P is a PD-set of and the result follows as above. Now, if x is the unique neighbor of y in then, by considering a vertex , one can see that the set (in which y and are partners) is a PD-set of ; thus, . In either case, implying that , which completes the proof. □
Lemma 1. Let G be an isolated-free graph different from . If for some edge then .
Proof. Assume that and let and . We denote by the graph formed from by subdividing the three edges and adding three new vertices , respectively. In addition, we denote by the graph formed from G by subdividing the two edges and adding two new vertices , respectively, and we denote by the graph formed from G by subdividing only the edge and adding a new vertex . Let P be a -set. If , then P is a PD-set of , so . Hence, assume that , and let, without loss of generality, x be the partner of in P.
Assume first that . If x has a neighbor w in such that , then is a PD-set of , and, as before, we have . Thus, we can assume that all neighbors of x in belong to P. Then, clearly, is a PD-set of , and, as before, . Assume now that . Then, we have . If x has a neighbor w in such that , then is a PD-set of , and, as above, one can easily see that . Finally, if all neighbors of x in belongs to P, then is a PD-set of ; thus, . Therefore, . □
As an immediate consequence of Proposition 4 and Lemma 1, we, therefore, have the following result.
Corollary 1. Let G be an isolated-free graph different from . If for some edge then .
Lemma 2. For any isolated-free graph G different from , let F be a set of edges of G in which subdivision increases , , and let be the graph formed from by subdividing the edges in If P is a -set such that or , then Proof. According to Proposition 4, we may assume that (otherwise, the result is straightforward from this proposition). If , then, clearly, P is a PD-set of ; thus, . Hence, assume that . Since, by assumption, , we may assume, without loss of generality, that x and are partners in P. If all neighbors of x in belong to P, then is a PD-set of ; thus, . Now, if x has a neighbor w in , then is a PD-set of , and, as before, , which completes the proof. □
Lemma 3. Let G be an isolated-free graph different from , and let F be an -set. If such that and , then Proof. If , then by Corollary 1, the assertion is trivial. So, in the following, we may assume that . Since and , let and be the neighbors of x and respectively, such that . Let be the graph formed from by subdividing the edges in . We denote by P a -set. According to Lemma 2, we may assume that and (otherwise, the result is straightforward from this lemma). Without loss of generality, assume that x is the partner of .
First, let . If x has a neighbor w in such that , then, clearly, is a PD-set of which is obtained from G by subdividing the edges of It follows that . Hence, we assume that all neighbors of x in belong to P. In this case, is a PD-set of , and, as before, we obtain .
Assume now that . Therefore, (to paired-dominates ). If x has a neighbor w in such that , then, clearly, is a PD-set of which is obtained from G by subdividing the edges of , and as before one can see that . Hence, we can assume that all neighbors of x in belong to P. In this case, is a PD-set of ; thus, In either case, □
Lemma 4. Let G be an isolated-free graph different from . If such that x or y is a support vertex, then Proof. If , then the result follows from Proposition 4. Hence, we assume that . Without loss of generality, let x be a support vertex, and let be a pendant edge. Suppose that F is an -set. We denote by the graph formed from G by subdividing the edges in F. In addition, we denote by the graph formed from G by subdividing the edges in , and we denote by the graph formed from by subdividing the edges in . Let P be a -set. By Lemma 2, we may assume that and (otherwise, the result is straightforward from this lemma).
First, let x be the partner of in P. Then, we must have . If , then the set in which x and are partners, is a PD-set of yielding . Hence, assume that and let w be a neighbor of y in Then, the set in which x and y are partners with and respectively, is a PD-set of As before, we get .
Now, assume that y is the partner of in P. Clearly, (to paired-dominates ). If y has a neighbor w in such that , then is a PD-set of ; thus, . Now, if all neighbors of y in belong to P, then is a PD-set of , and, as before, we obtain . In either case, □
Before going further, we give some notation and definitions. For a vertex , the set of isolated vertices in the subgraph induced by is denoted by . We also denote by the set of pairs of non-adjacent vertices in G. Moreover, for a pair , let in other words, is the set of edges incident with x in which end vertices are neighbors of In addition, we consider two functions and on as follows.
- (a)
defined by
if neither
nor
is independent, and
otherwise. Note that
if and only if
x or
y is a support vertex.
- (b)
defined by
if there exits an sd
-set
M such that
and
, and
otherwise.
Lemma 5. Let G be an isolated-free graph different from , and let .
- 1.
If neither nor is independent, then - 2.
If F is an -set such that , and is not independent, then - 3.
If , then
Proof. According to Proposition 4, we may assume that . Note that since G is isolated-free and different from We now show items of the lemma one by one.
If there is an
-set
F such that
and
, then
, and, by Lemma 3, we have
Hence, we may assume that, for every
-set
F,
or
. In that case, it is clear that
. Now, let
F be an
-set with, without loss of generality,
. Since, by assumption, neither
nor
is independent, let
be two adjacent vertices of
likewise
two adjacent vertices of
In addition, consider the graph
formed from
by subdividing the edges in
and all edges in
and let
P be a
-set. If
or
, then, by Lemma 2, we have
. Hence, we may assume that
and
. We claim that
is the unique subdivision vertex adjacent to
x belonging to
P. Suppose, to the contrary, that
is a subdivision vertex adjacent to
x such that
. If
x is the partner of
, then the set
in which
x and
z are partners, is a PD-set of
which is obtained from
by subdividing all edges in
and the edges of
It follows that
; thus,
Hence, we can now assume that
y is the partner of
If all neighbors of
y in
are in
P, then
is a PD-set of
which is obtained from
G by subdividing all edges in
and the edges of
It follows that
; thus,
If
y has a neighbor
w in
with
, then
is a PD-set of
(defined before) and the desired result follows as before. Thus,
is indeed the unique subdivision vertex adjacent to
x that belongs to
P. We now claim that
is the unique subdivision vertex adjacent to
y belonging to
P. Suppose, to the contrary, that
is a subdivision vertex adjacent to
y such that
. If
y is the partner of
, then the set
in which
y and
z are partners, is a PD-set of
which is obtained from
by subdividing all edges in
and the edges of
It follows that
; thus,
Therefore, we may now suppose that
x is the partner of
If all neighbors of
x in
are in
P, then
is a PD-set of
(defined before), and the desired result follows. If
x has a neighbor
w in
with
, then
is a PD-set of
, and the desired result follows as before. Thus,
is indeed the unique subdivision vertex adjacent to
y that belongs to
P. Moreover, to paired-dominate vertices
and
, we may assume that
. In this case,
(if
y is the partner of
) or
(if
x is the partner of
) is a PD-set of
which is obtained from
G by subdividing the edges of
, implying that
. Therefore,
We first note that, since
, we have
. In addition, since, by assumption,
and
is not independent, let
, and let
be two adjacent vertices of
. We denote by
the graph formed from
by subdividing the edges of
and all edges in
, and we denote by
the graph formed from
by further subdividing the edge
Now, let
P be a
-set, and let
be the set of all subdivided edges of
, except
, such that their subdivision vertices belong to
P. We denote by
the graph formed from
G by subdividing the edges of
. It is easy to check that, if
or
, then, by Lemma 2,
Hence, we may assume that
and
. As in the proof of Item 1, we can see that
is the unique subdivision vertex adjacent to
x and
y that belongs to
P. To paired-dominate vertex
, we may assume that
. Now, if
x and
are partners in
P and
is a subdivision vertex adjacent to
x, then
is a PD-set of
which is formed from
G by subdividing the edges in
, as well as the edges of
. It follows that
. However, if
y and
are partners in
P, then, clearly,
; thus,
is a PD-set of
, so
. In either case,
Let
. If there is an
-set
F such that
and
, then
, and, by Lemma 3, we have
Hence, we can assume that, for every
-set
F,
or
. Clearly, in this case,
. Now, let
F be an
-set, such that, without loss of generality,
. We denote by
the graph formed from
by subdividing the edges of
. Let
P be a
-set, and let
be the set of all subdivided edges of
except
in which subdivision vertices belong to
If
or
, then, by Lemma 2,
. Hence, we assume that
and
. As in the proof of Item 1, we can see that
is the unique subdivision vertex adjacent to
x and
y that belongs to
P. Then, clearly,
(to paired-dominate either
or
, thus,
is a PD-set of the graph
which is obtained from
G by subdividing only the edges of
Consequently,
; hence,
The proof is completed.
□
3. Proof of Theorem 1
In this section, we prove Theorem 1.
Proof of Theorem 1. We start by noting that since G is isolated-free and different from Now, let If then, by Proposition 4. Hence, we assume that . By Lemma 5-(3), we can assume that for, otherwise, the result is obviously valid. If , then x or y is support vertex; thus, the result follows by Lemma 4. Now, we consider two cases.
Case 1..
Without loss of generality, assume that where . Clearly, in this case v has degree two. Let z be the neighbor of v different from x. Moreover, let F be an -set such that is minimized. We can assume without loss of generality that (otherwise, the result follows from Lemma 3). Let . Consider the graph and let P be a -set, and let be a subset of F in which subdivision vertices are in P. According to Lemma 2, we can assume that and that . As in the proof of item 1 of Lemma 5, one can see that is the unique subdivision vertex adjacent to x and y that belongs to P.
First, let and . If , then ; thus, the set is a PD-set of the graph which is obtained from G by subdividing the edges of It follows that ; thus, Now, if , then is the partner of v in P; thus, the set in which v and x are partners, is a PD-set of the graph defined before, which leads to . Now, let and . Then, we must have ; thus, the set is a PD-set of which is obtained from by subdividing the edges in , yielding as above.
Case 2..
Assume that there exists some -set F satisfying and . By Lemma 3, the result follows. Hence, we assume that, for every -set F, either or . By Lemma 5-(3 and 1), we may assume that and either or is independent. Let z be a vertex in such that or . Moreover, let F be an -set. We denote by the graph formed by subdividing the edges of . Note that since either or , the number of subdivided edges is at most . Let P be a -set. Among all edges of G that have been subdivided resulting in the graph , let be the set of those in which subdivision vertices are in P. If or , then, clearly, the result follows from Lemma 2. Hence we may assume that and . In addition, we assume, without loss of generality, that and .
By the similar method to the proof of Lemma 5-(1), we may assume that no subdivision vertex adjacent to x or y other than belongs to P. Since , we have . First, let . Then, and it has as a partner a subdivision vertex, say . In this case, one can easily see that the set in which y and z are partners, is a PD-set of the graph which is obtained from by subdividing all edges in It follows that . Now, let . Then, P contains a subdivision vertex that may have as a partner either z or If then let , and if , then let Regardless the situation that occurs, is a PD-set of the graph which is obtained from by subdividing all edges in ; thus, again. This completes the proof. □