1. Introduction
Selected limit theorems, which we shall deal with in the article, are well known from Kolmogorov’s classical probability theory. Kolmogorov’s work [
1] introduced the theoretical axiomatic model in which events connected with the experiment form the Boolean
-algebra of subsets
of the set
. Thus, the probability is that for the
-additive, nonnegative final function
on
, with values in the interval
, if
is a sequence of mutually exclusive events from
, then
and
. Limit theorems have a wide range of use in this theory. Their validity has already been proven for other structures (spaces), e.g., MV-algebras defined in [
2]. We want to extend their use; therefore, in this article we prove that they also apply to sets in which we are working with incomplete data. Specifically, they also apply to Fuzzy quantum space, and that is the most significant finding in this article.
After some time, it became apparent that Kolmogorov’s classical model of the probability theory was not sufficient for describing quantum mechanics situations. Birkhoff and von Neumann [
3] referred to the fact that the set of experimentally verifiable statements about the quantum mechanical system does not have the same algebraic structure as Boolean algebra. Heisenberg [
4] and Schrödinger [
5] put forth the earliest attempts at the mathematical formulation of quantum mechanics. Schrödinger presented the formalism of wave mechanics, while Heisenberg proposed the formalism of matrix mechanics.
Zadeh [
6] wrote about the theory of fuzzy sets in the 1960s. The current quantum theory, basic mathematical model is that of von Neumann, grounded in the geometry of Hilbert space (Varadarajan, [
7]). If we define all closed subspaces of a given Hilbert space (where, according to Varadarajan, the notion “a state of system” means a measure of probability on
) as system
, and such a definition is compared with that of the
-measure on fuzzy sets (according to Piasecki [
8]), it follows that both objects have a similar algebraic structure. Piasecki submitted a model called soft
-algebra in the fuzzy set theory in 1985. His model demonstrated several characteristics identical to quantum logics. That comparison was first noted by Riečan [
9] and then by Pykacz [
10], and it led us to the idea to build a quantum theory based on fuzzy sets. If
is a non-empty set called a universum and
is a system of fuzzy subsets of universum
, i.e., the system of functions on
with values in the interval
, then according to Riečan [
9] we say that
is an
-quantum space, also referred to by Dvurečenskij and Chovanec [
11] as a fuzzy quantum space, or by Dvurečenskij [
12] as a fuzzy measurable space.
Many writers have attempted to prove some known assertions from the classical probability theory in the theory of fuzzy quantum spaces. For example, Dvurečenskij [
12], Navara [
13], and Navara and Pták [
14,
15] studied the existence of a fuzzy state on fuzzy quantum space while Dvurečenskij and Riečan [
16,
17] examined joint fuzzy observables and joint distributions of fuzzy observables. The representation theorem was proved by Dvurečenskij, Kôpka, and Riečan [
18]; it also includes the case in fuzzy quantum space. Riečan [
19,
20] looked at the theory of an indefinite integral on fuzzy quantum space. Mesiar [
21,
22,
23], Piasecki [
24,
25], and Piasecki and Svitalski [
26] investigated the extension of the validity of the Bayes formula for fuzzy sets. Markechová [
27,
28,
29] researched the entropy on fuzzy quantum space, and Tirpáková and Markechová [
30] investigated the fuzzy analogies of some ergodic theorems and Birkhoff’s individual ergodic theorem and maximal ergodic theorem for fuzzy dynamical systems [
31].
The existence of the sum of fuzzy observables is a key fact for the analysis of many assertions in the fuzzy sets theory. The existence of the sum of compatible fuzzy observables was proved by Harman and Riečan [
32].
Among the vital concepts of probability theory are the different kinds of convergence of random variables. They are especially significant for parts dealing with the validity of various forms of the law, the central limit theorem, and big numbers. As a result, the problem of generalizing different types of convergence for fuzzy quantum space
became topical. A few authors studied particular types of convergences on quantum logic. Here, we mention the writings which were the basic material for the study of various types of convergences of fuzzy observables on fuzzy quantum space
: Dvurečenskij and Pulmanová [
33], Jajte [
34], Ochs [
35,
36], Cushen [
37], Gudder [
38], and Révesz [
39]. Some types of convergences of fuzzy observables on fuzzy quantum space were dealt with by Dvurečenskij [
40], Riečan [
41,
42], Chovanec and Kôpka [
43], Kôpka and Chovanec [
44], and others.
We formulated convergences and consequently proved many familiar limit theorems [
34,
36,
45] for fuzzy quantum space on the basis of the analogy of the probability theory notions. As the central limit theorem refers to the limit distribution of the averages of independent, equally-distributed random variables, extreme value theory (EVT) addresses the limit distribution of the maximums of the independent, equally-distributed random variables [
45,
46]. EVT’s principal objective is to know or predict the statistical probabilities of events that have never or rarely been observed. Kotz and Nadarajah [
47] indicated that the extreme value distributions could be traced back to Bernoulli’s 1709 work [
48]. The theory of max-stable distribution functions, the counterpart of Feller stable distributions [
49], formed the basis of the probability background. First, the statistical analysis of extreme values was performed in order to study flood levels. These days, the areas of application include finance, meteorological events, insurance, industry, or the environmental sciences [
50]. Allow
,
, …,
to be a sequence of
, independently and identically distributed random variables with distribution function
. The corresponding ordered sequence in non-decreasing order is indicated by
,
, …,
, where
,
represents the
-th order statistic.
and
stand for the sample minimum and the sample maximum, respectively. Then, examine the sequence of maxima
,
, for
, obtained from the above sequence. All the sequence minimum results can be obtained from those of the sequence maximum since
.
’ s exact distribution can be obtained from the distribution function
. In fact, for all
:
For a single process, the behavior of the maxima can be described by the three extreme value distributions: Gumbel, Fréchet and reversed Weibull distribution as suggested by the Fisher–Tippett–Gnedenko theorem. One can combine these three distributions into a single family of continuous cumulative distribution functions, known as the generalized extreme value (GEV) distributions [
50]. A GEV can be identified by the real parameter
and the extreme value index, and as a stable distribution it is a characteristic exponent
. Subsequently, several researchers have provided useful applications of extreme value distributions. They may be found in several works [
51,
52,
53,
54].
2. Fuzzy Quantum Space
First, we recall the definitions of basic notions and some facts that will be used in the following text. In the quantum space approach to the fuzzy quantum theory, the triple is replaced by the couple where is a nonempty set, is fuzzy -algebra of fuzzy subsets of , such that the following conditions are satisfied:
- (i)
if for any then
- (ii)
if , then
- (iii)
, for any
- (iv)
if for any then
Elements of the set
are called fuzzy subsets of the universe
. In particular, if
is the characteristic function, we call it a crisp set. The symbols
and
indicate a fuzzy union and a fuzzy intersection of the sequence of fuzzy sets
. The event
is the so-called fuzzy complement. By Piasecki [
8], the system
is called a soft
-algebra.
To define and prove the law of large numbers and the central limit theorem, we need the following basic notions:
Definition 1. A fuzzy state on fuzzy quantum spaceis a mapping, such that
- (i)
for every
- (ii)
ifis a sequence of pairwise orthogonal fuzzy subsets from, i.e.,, , whenever, then
According to Piasecki [
8], a fuzzy state is called the
-measure. The triplet
where
is a
-measure is called a fuzzy probability space. This structure was studied in [
55,
56].
For illustration, we give the following example of a nontrivial fuzzy quantum space [
55].
Example 1. Considerwhere,,,for every. It is evident that. We define the mappingby the equalities,, and. Then the tripletis a fuzzy probability space.
Definition 2. A fuzzy observable on fuzzy quantum spacemaps to, satisfying the following properties:
- (i)
for every
- (ii)
if , then
wheredenotes the Borel-algebra of the real lineanddenotes the complement of a setin.
Definition 3. Let. The mappingis defined byfor everythere is a fuzzy observable of fuzzy quantum spacecalled the indicator of fuzzy set.
In particular, the null fuzzy observable of fuzzy quantum space
maps to
defined by
where
.
If is a Borel measurable function and is a fuzzy observable, then is a fuzzy observable, too. In this way, we define the functional calculus of fuzzy observables. For example, if , we write and the like. In particular, if then for any .
Let
x be a fuzzy observable of fuzzy quantum space
and let
,
. Dvurečenskij and Tirpáková [
57] proved that the system
of fuzzy sets of fuzzy quantum space
is a one-to-one correspondence to fuzzy observable
. Due to this result, the sum of any pair
and
of fuzzy observables of
can be introduced as follows:
Definition 4. Letandbe two fuzzy observables of fuzzy quantum space. If the systemwhereis the set of all rational numbers, then we determine fuzzy observableof. We call it the sum ofandand write.
In the text [
57], it was proved that the sum of two observables always exists, and it coincides with the pointwisely-defined sum of observables for
-algebra of crisp subsets. Moreover,
,
for fuzzy observables
,
and
. The subtraction of fuzzy observables
and
is defined as follows:
, where
. The mean value of a fuzzy observable on fuzzy quantum space
was defined by Riečan [
58] as follows: Let
be a fuzzy observable, and let
be a fuzzy state. If the integral
exists, then
is called the mean value of
in
, where
,
is a probability measure on
. In addition, if
is a Borel measurable function, then
in the sense that if one side exists, then the second side exists too, and they are equal. Specially, if
, then
is called the dispersion of fuzzy observable
x in fuzzy state
.
3. Convergences on a Fuzzy Space
Various types of convergences of random variables belong among important concepts of the probability theory. Therefore, the notion of a fuzzy observable is an analogy to the notion of a random variable. When defining different types of convergence and for the proof of limit theorems on fuzzy quantum space
we used the method of
-
-ideals, which enabled us to reformulate and prove many of the known limit theorems of the classical probability theory for the fuzzy quantum space
. The basic idea of the
-
-ideals method is described in [
54], and we can shortly describe it as follows: Let
be a fuzzy state on fuzzy quantum space
. Denote
. Dvurečenskij and Riečan [
16] proved that
is a
-algebra of fuzzy quantum space
. The relation “
” defined on fuzzy quantum space
via
if and only if
is the congruence, and, moreover,
is the Boolean
-algebra (in the sense of Sikorski [
59]), where complementation “
” in
is defined with properties
,
and
,
,
. Then, according to these properties, the mapping
defined by
is a
-homomorphism from
onto
. The mapping
from a Boolean
-algebra
into the interval
, defined by
for every
, is a probability measure on the Boolean
-algebra
. According to the Loomis–Sikorski theorem in [
60], there is a measurable space
and
-homomorphism
from
onto
, and due to Varadarajan [
7] there are functions
such that
where
is an observable of a Boolean
-algebra
. Moreover, mapping
, defined as
, is a probability measure on
.
Gudder and Mullikin [
51] introduced many types of convergences for observables in quantum logics. Inspired by their definition, Dvurečenskij and Tirpaková introduced [
57] the following definition:
Definition 5. We say that sequenceof fuzzy observables on fuzzy quantum spaceconverges to fuzzy observable
- (i)
in fuzzy state, if for every, we have - (ii)
almost everywhere in the fuzzy state, if for every
, we have - (iii)
- (iv)
in a mean, where, if - (v)
- (vi)
uniformly on, if for every, there is an integer, such that - (vii)
uniformly, if for every, there is an integer, such that - (viii)
almost uniformly in fuzzy state, if for everythere is an elementsuch thatand a sequenceconverges uniformly to on .
To prove the law of large numbers and the central limit theorem on fuzzy quantum space
, we also need the next theorem, which was proved in Dvurečenskij and Tirpaková [
57].
Theorem 1. Letbe a fuzzy state of fuzzy quantum space,be fuzzy observables ofandbe functions with properties (1) and (2). Then,
- (A)
The sequence of fuzzy observablesconverges to fuzzy observable
- (i)
in fuzzy stateif and only if the sequence of functionsconverges toin measure,
- (ii)
almost uniformly in fuzzy stateif and only if the sequence of functionsconverges almost uniformly toin measure,
- (iii)
almost everywhere in fuzzy stateif and only if the sequence of functionsconverges almost everywhere toin measure,
- (iv)
in meanif and only ifconverges toin meanin measure.
- (B)
If the sequence of fuzzy observablesconverges to fuzzy observable
- (v)
everywhere, then there issuch thatand the sequenceconverges toeverywhere on,
- (vi)
uniformly, then there issuch thatand the sequenceconverges touniformly on,
- (vii)
uniformly on, then there issuch thatand the sequenceconverges touniformly on.
Conversely, if the sequence of functionsdefined by (1), (2) converges to
- (viii)
everywhere, thenconverges to fuzzy observableeverywhere on, where
- (ix)
uniformly, thenconverges to fuzzy observableuniformly on, where
- (x)
uniformly on, , then fuzzy observablesconverges to fuzzy observableuniformly on, where.
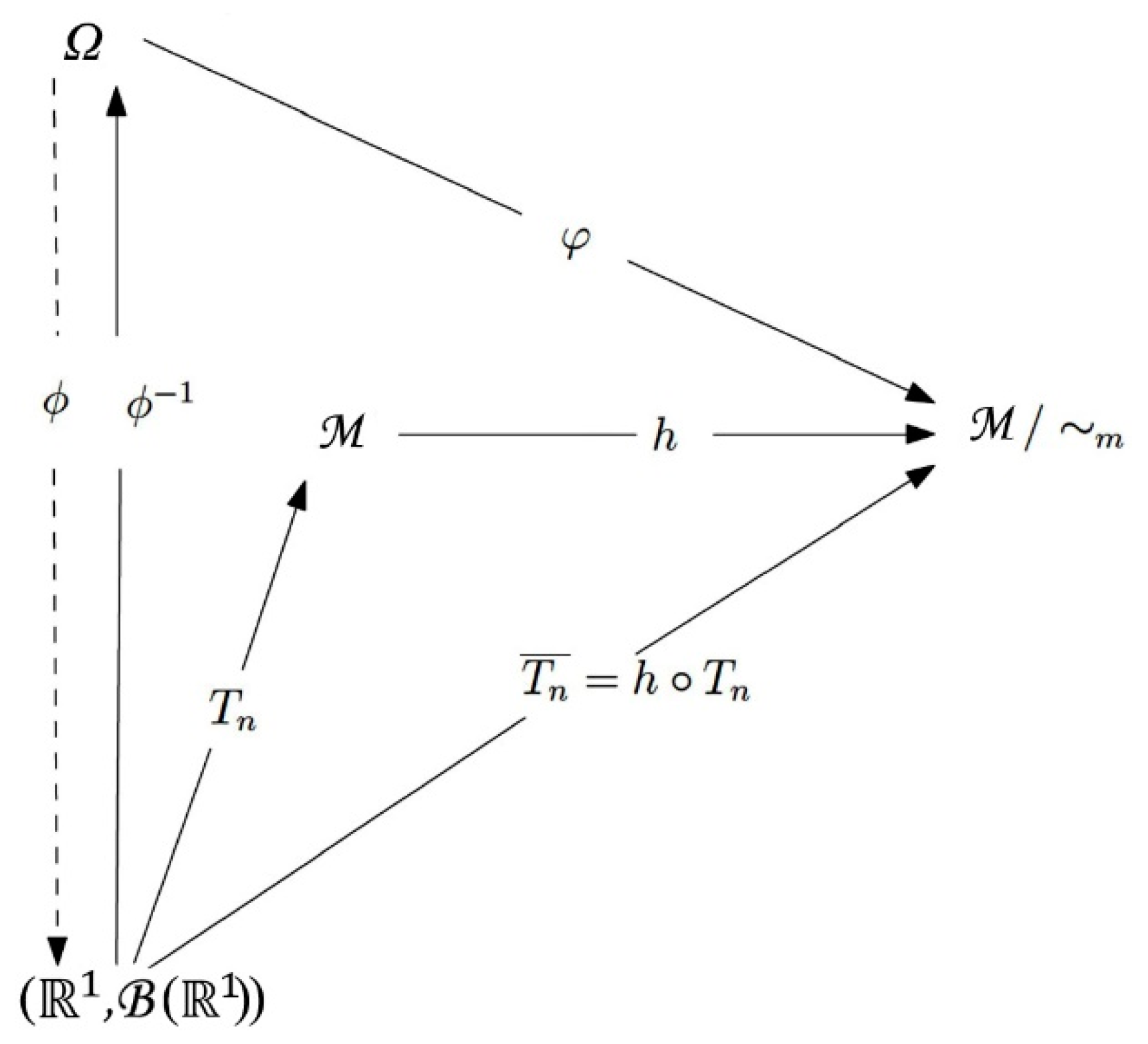
In the following, we will continue to introduce the notion of the independence of fuzzy observables in fuzzy state . Now, we define the joint fuzzy observable of fuzzy observables.
Definition 6. Let,, be a finite system of fuzzy observables on fuzzy quantum space. A joint fuzzy observable of fuzzy observablesis a-homomorphism, such that
- (i)
for every
- (ii)
- (iii)
for every
whereis the projection into the-th coordinate.
In accordance with Riečan [
61] and Riečan and Neubrunn [
62], a sufficient condition for the existence of the joint fuzzy observable of fuzzy observables
,
, meets the condition
for every
.
Definition 7. Fuzzy observableson fuzzy quantum spaceare independent in fuzzy stateif for everythere exists joint fuzzy observableandfor any.
According to the assumption of independence of the sequence of fuzzy observables
for every
there exists joint fuzzy observable
. To each fuzzy observable
,
exists the observable
and a real function
, such that
. We define function
such that
. If
, then
. The main idea of the proof can be illustrated by
Figure 1.
5. Extreme Value Theorems for Fuzzy Quantum Space
Let
be a sequence of independent, identically-distributed fuzzy observables of fuzzy quantum space
. For any
we define the real function
as follows:
Let
be the joint fuzzy observable of fuzzy observables
. We define the maximum fuzzy observables of
as
where
is the fuzzy observable.
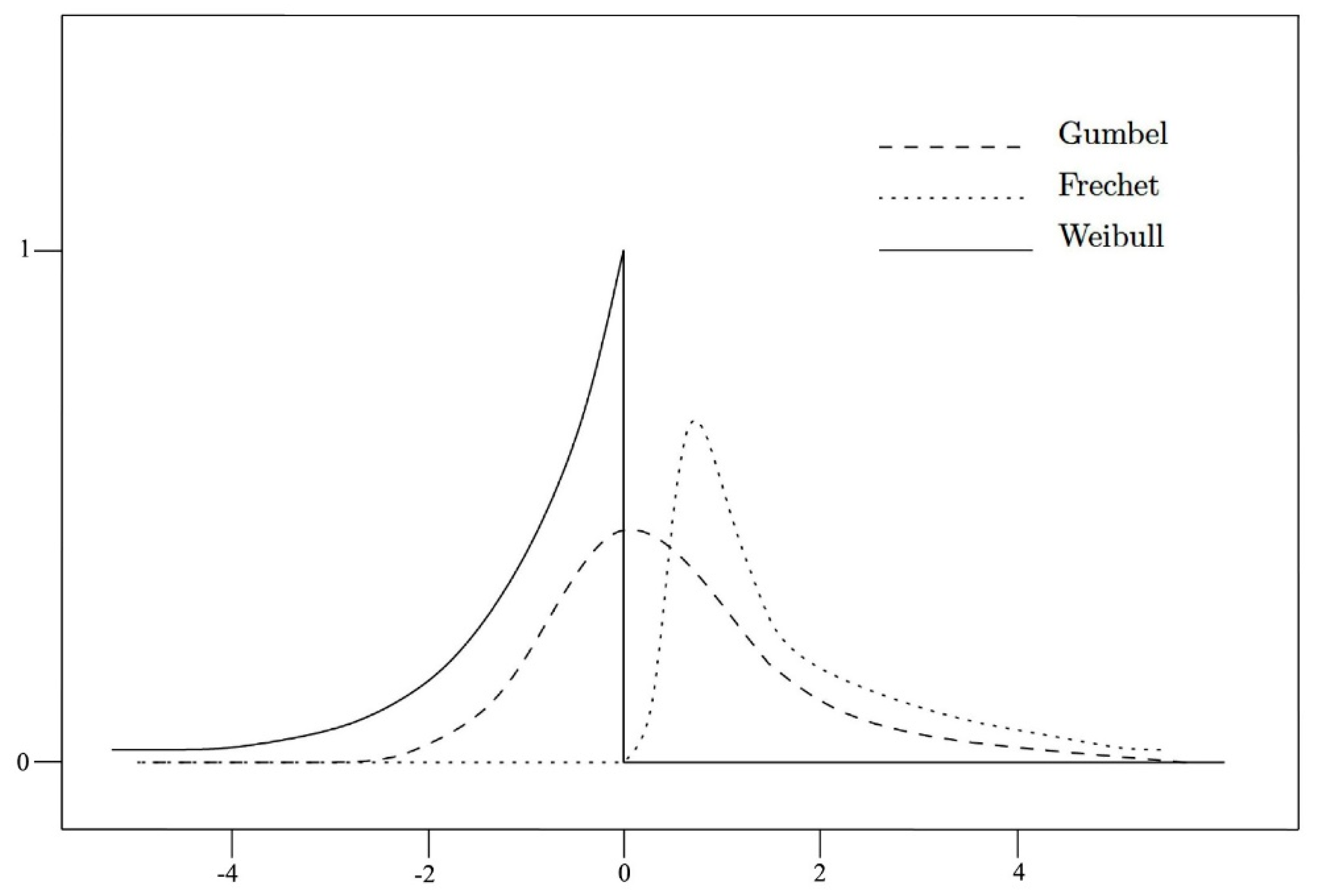
Theorem 5. Letbe a sequence of independent random variables with the same distribution functionin fuzzy state. Put. Let there exist,such thatwhereis a continuous distribution function, increasing on an interval. Then,has one of three distributions with parameters(Figure 2):
- 1.
Gumbel
- 2.
Fréchet
- 3.
Weibull
Proof of Theorem 5 can be found in [
63].
Theorem 6 (Fisher–Tippett–Gnedenko theorem). Letbe a sequence of fuzzy independent observables identically distributed in fuzzy state. Let there exist norming constants,and some non-degenerate distribution functionsuch that Then,belongs to the type of one of the following three types of standard extreme value distributions: Gumbel, Fréchet, or Weibull.
Proof.
We define the real function
as follows:
Then
and
Then, according to Theorem 5, the validity of the arguments is obvious. □
Now, we define the distribution function and excess distribution function on fuzzy quantum space .
Definition 8. Letbe a fuzzy state andbe a fuzzy observable on fuzzy quantum space. For anywe define functionas Functionis called the distribution function of an observable x on fuzzy quantum space.
Proposition 1. If the functionis the distribution function of an observableon fuzzy quantum space, then it satisfies the following conditions:
- (i)
is non-decreasing
- (ii)
is left continuous
- (iii)
- (iv)
Proof.
- (i)
Let
then
it follows that
We proved that the function is non-decreasing.
- (ii)
Let
then
it follows that
We proved that the function is left continuous.
- (iii)
Let
then
, it follows that
We proved that
- (iv)
Let
then
, it follows that
We proved that □
Now we define the excess distribution function on fuzzy quantum space .
Definition 9. Forwe define excess distribution functionon fuzzy quantum spaceasfor everyValueis called the right endpoint of distribution function.
Theorem 7 (Balkema, de Haan–Pickands). For a sufficiently large, the excess distributionconverges to the generalized pareto distribution. Parameteris dependent on threshold, and for every Proof.
Let
M,
be fuzzy observables. Then, there exist observables
and real functions
such that
. Then,
is the distribution function of real random variable
. It is obvious that
□
6. Conclusions
The seminal theoretical results in probability theory are limit theorems. When using random samples to estimate distributional parameters, we would like to know that as the sample size gets larger, the estimates are probably close to the parameters that they are estimating. In statistical inference, the central limit theorem is the dominant and most useful theorem. It allows us to make the assumption that, for a population, a normal distribution will occur regardless of what the initial distribution looks like for a sufficiently large sample size. When the distribution shape is not known or the population is not normally distributed, the theorem is used to make assumptions. The law of large numbers is an invaluable tool that is expected to state definite things about the real-world results of unexpected events. The law of large numbers is the postulate of statistics and probability theory that states that the greater the number of samples are used from an event, the closer the monitoring results will be to the average population. Thus, the law of large numbers describes the stability of big random variables. Both the strong and weak laws refer to the convergence of the sample mean to the population mean as the sample size gets bigger.
This paper generalizes the central limit theorem, the law of large numbers, and extreme value theorems of classical probability theory to fuzzy quantum spaces. Extreme value theory models rare events outside the range of allowable observations with high impact. This method has become a widely-used tool for risk assessment in recent years. It is used in the areas of insurance, banking, operational risk, market risk, and credit risk [
52]. By applying these limit theorems to the Atanassov set, it gives us the space to work with incomplete data, which we can use in the area of finance. The basic advantage of fuzzy logic is the ability to mathematically express information expressed verbally. Thanks to this, fuzzy logic proves to be a very good tool for working with behavioral data. Behavioral finance takes into account the human factor when making financial decisions. For this reason, behavioral finance often uses linguistic data, and therefore it is appropriate to use methods based on fuzzy logic to describe them. Behavioral finance is a financial field examining the effect of social, cognitive, and emotional factors on the economic decisions of individuals and institutions as well as the consequences of these decisions on market prices [
64].