Fractional Vertical Infiltration
Abstract
1. Introduction
2. Fractional Calculus
3. Fractional Horizontal Infiltration
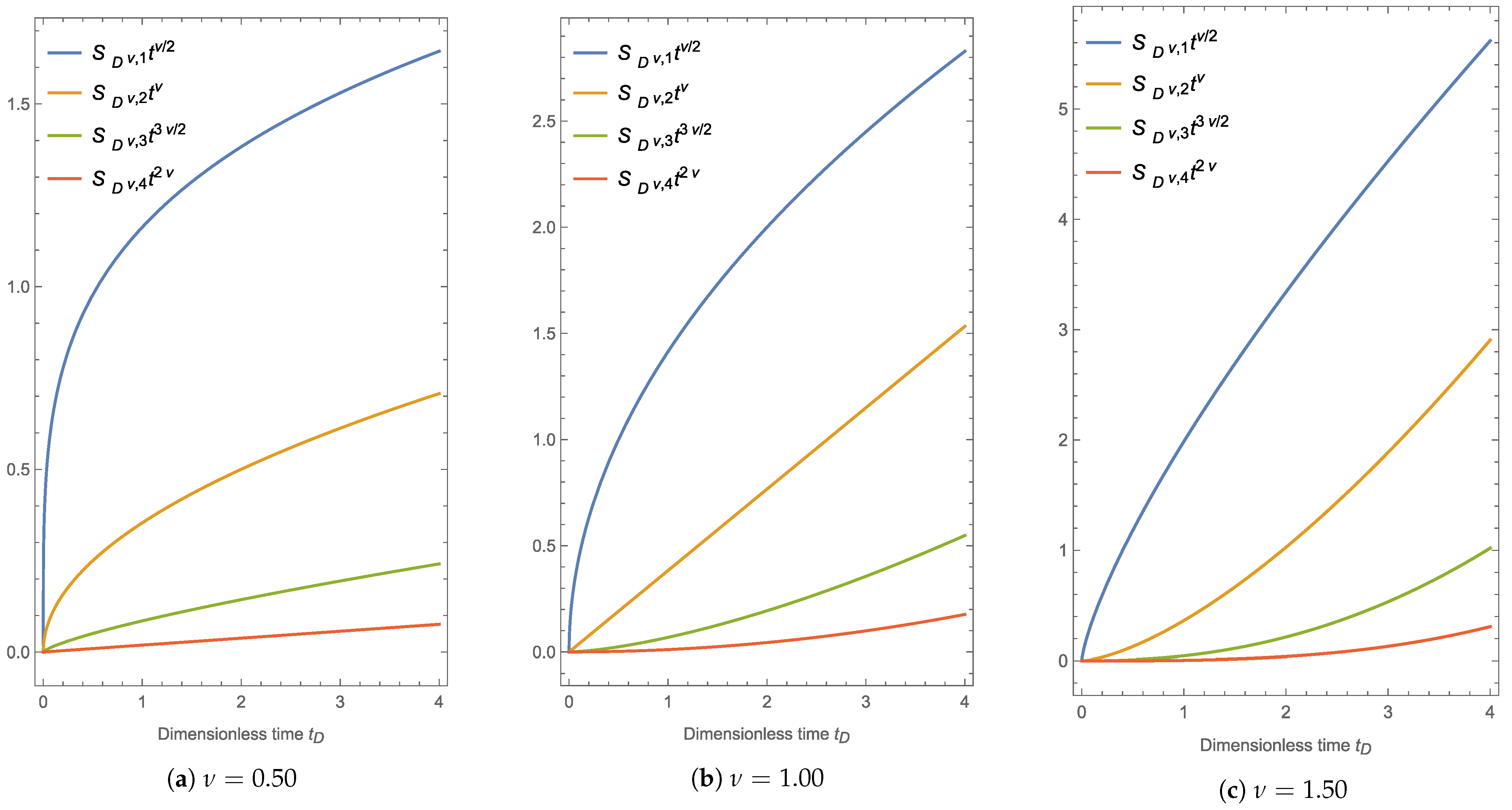
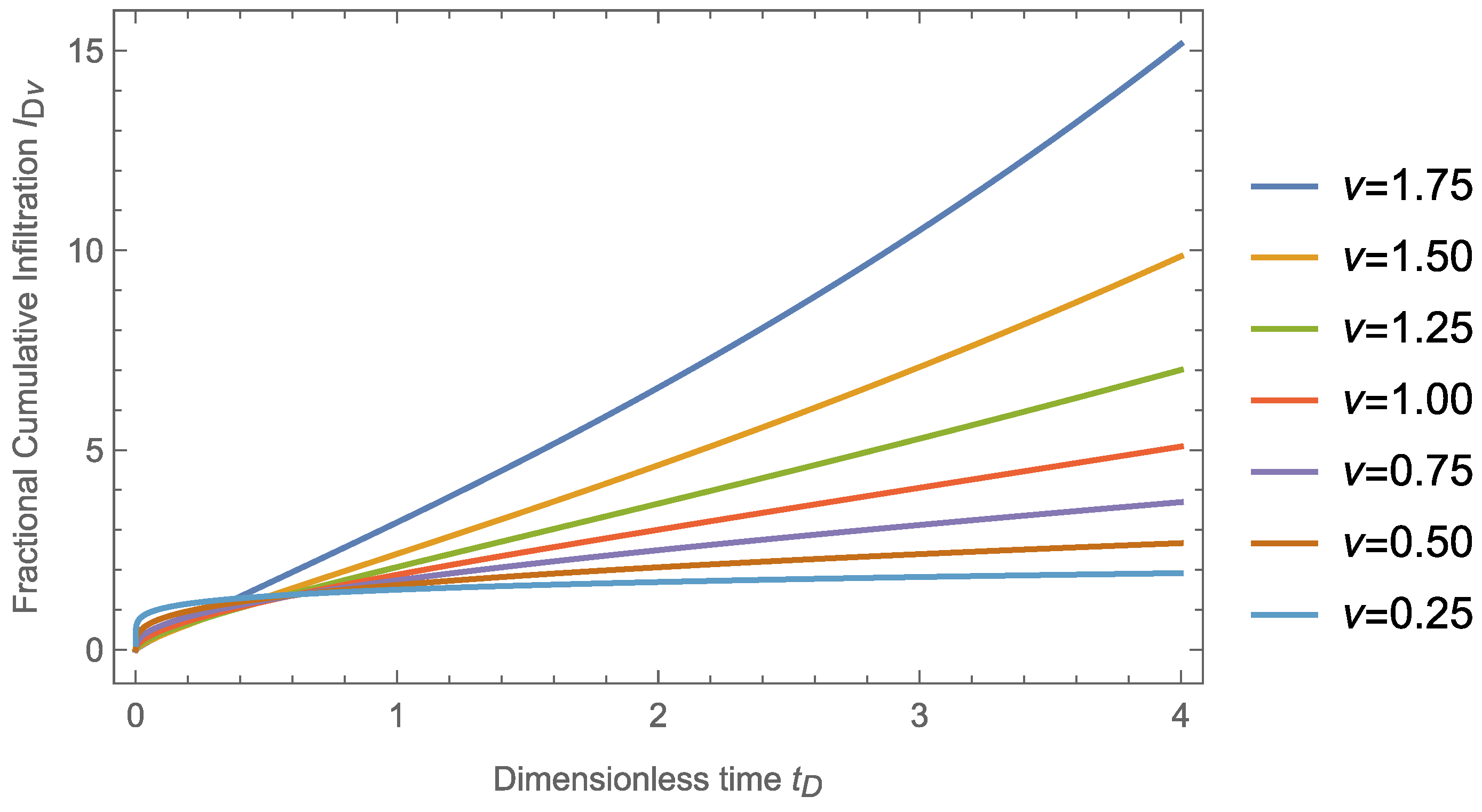
4. Fractional Vertical Infiltration
4.1. Short-Time Approximation
4.2. Long-Time Approximation
5. Fractional Parlange Solution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Green, W.H.; Ampt, G. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall infiltration modeling: A review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur integration der diffusionsgleichung bei variabeln diffusionscoefficienten. Annalen der Physik 1894, 289, 959–964. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Talsma, T.; Parlange, J. One dimensional vertical infiltration. Soil Res. 1972, 10, 143–150. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Lisle, I.; Braddock, R.; Smith, R. The three-parameter infiltration equation. Soil Sci. 1982, 133, 337–341. [Google Scholar] [CrossRef]
- Haverkamp, R.; Parlange, J.Y.; Starr, J.; Schmitz, G.; Fuentes, C. Infiltration under ponded conditions: 3. A predictive equation based on physical parameters. Soil Sci. 1990, 149, 292–300. [Google Scholar] [CrossRef]
- Haverkamp, R.; Kutilek, M.; Parlange, J.Y.; Rendon, L.; Krejca, M. Infiltration under ponded conditions: 2. infiltration equations tested for parameter time-dependence and predictive use. Soil Sci. 1988, 145, 317–329. [Google Scholar] [CrossRef]
- Fuentes, C.; Haverkamp, R.; Parlange, J.Y. Parameter constraints on closed-form soilwater relationships. J. Hydrol. 1992, 134, 117–142. [Google Scholar] [CrossRef]
- Fuentes, C.; Parlange, J.Y.; Haverkamp, R.; Vauclin, M. La solución cuasi-lineal de la infiltración vertical. Tecnología y Ciencias del Agua 2001, 16, 25–33. [Google Scholar]
- Saucedo, H.; Fuentes, C.; Zavala, M. El sistema de ecuaciones de Saint-Venant y Richards del riego por gravedad: 3. verificación numérica de la hipótesis del tiempo de contacto en el riego por melgas. Tecnología y Ciencias del Agua 2006, 21, 135–143. [Google Scholar]
- Mollerup, M.; Hansen, S. Power series solution for falling head ponded infiltration with evaporation. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Mollerup, M. Philip’s infiltration equation for variable-head ponded infiltration. J. Hydrol. 2007, 347, 173–176. [Google Scholar] [CrossRef]
- Mollerup, M.; Hansen, S. Power series solution for ponded infiltration on sloping surfaces. J. Hydrol. 2012, 464, 431–437. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, X.; Zhu, Y.; Yang, Q. Effects of pressure heads and soil bulk density on infiltration characteristics of vertically inserted moistube irrigation. Environ. Earth Sci. Res. J. 2019, 6, 119–124. [Google Scholar] [CrossRef]
- Castanedo, V.; Saucedo, H.; Fuentes, C. Modeling Two-Dimensional Infiltration with Constant and Time-Variable Water Depth. Water 2019, 11, 371. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C. Analytic Representation of the Optimal Flow for Gravity Irrigation. Water 2020, 12, 2710. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Holtan, H.N. Concept for Infiltration Estimates in Watershed Engineering; USDA Bulletin: Washington, DC, USA, 1961.
- Sihag, P.; Tiwari, N.; Ranjan, S. Estimation and inter-comparison of infiltration models. Water Sci. 2017, 31, 34–43. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Timashev, S.F.; Polyakov, Y.S.; Misurkin, P.I.; Lakeev, S.G. Anomalous diffusion as a stochastic component in the dynamics of complex processes. Phys. Rev. E 2010, 81, 041128. [Google Scholar] [CrossRef] [PubMed]
- Parlange, J.Y.; Haverkamp, R.; Rand, R.; Rendon, L.; Schmitz, G. Water Movement in Soils-The Role of Analytical Solutions. Future Dev. Soil Sci. Res. 1978, 11–21. [Google Scholar] [CrossRef]
- Bhattacharya, R.N.; Gupta, V. On a statistical theory of solute transport in porous media. SIAM J. Appl. Math. 1979, 37, 485–498. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F.; Vivoli, A. Continuous-time random walk and parametric subordination in fractional diffusion. Chaos Solitons Fractals 2007, 34, 87–103. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Bagley, R.L. The thermorheologically complex material. Int. J. Eng. Sci. 1991, 29, 797–806. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Timlin, D.; Rawls, W. Generalized Richards’ equation to simulate water transport in unsaturated soils. J. Hydrol. 2003, 272, 3–13. [Google Scholar] [CrossRef]
- Sun, H.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. A fractal Richards’ equation to capture the non-Boltzmann scaling of water transport in unsaturated media. Adv. Water Resour. 2013, 52, 292–295. [Google Scholar] [CrossRef]
- Su, N. Theory of infiltration: Infiltration into swelling soils in a material coordinate. J. Hydrol. 2010, 395, 103–108. [Google Scholar] [CrossRef]
- Su, N. Distributed-order infiltration, absorption and water exchange in mobile and immobile zones of swelling soils. J. Hydrol. 2012, 468, 1–10. [Google Scholar] [CrossRef]
- Su, N. Mass-time and space-time fractional partial differential equations of water movement in soils: Theoretical framework and application to infiltration. J. Hydrol. 2014, 519, 1792–1803. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Parlange, J.Y. On solving the flow equation in unsaturated soils by optimization: Horizontal infiltration. Soil Sci. Soc. Am. J. 1975, 39, 415–418. [Google Scholar] [CrossRef]
- Fuentes, C. Unidimensional infiltration theory: 2. Vertical infiltration. Agrociencia 1989, 78, 119–153. [Google Scholar]
- Fuentes, C.; Parlange, J.Y.; Palacios-Vélez, O. Infiltration Theory. In Gravity Irrigation, 1st ed.; Fuentes, C., Rendón, L., Eds.; National Association of Irrigation Specialists: México, México, 2017; Chapter 3; pp. 154–211. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuentes, C.; Alcántara-López, F.; Quevedo, A.; Chávez, C. Fractional Vertical Infiltration. Mathematics 2021, 9, 383. https://doi.org/10.3390/math9040383
Fuentes C, Alcántara-López F, Quevedo A, Chávez C. Fractional Vertical Infiltration. Mathematics. 2021; 9(4):383. https://doi.org/10.3390/math9040383
Chicago/Turabian StyleFuentes, Carlos, Fernando Alcántara-López, Antonio Quevedo, and Carlos Chávez. 2021. "Fractional Vertical Infiltration" Mathematics 9, no. 4: 383. https://doi.org/10.3390/math9040383
APA StyleFuentes, C., Alcántara-López, F., Quevedo, A., & Chávez, C. (2021). Fractional Vertical Infiltration. Mathematics, 9(4), 383. https://doi.org/10.3390/math9040383







