Abstract
The infiltration phenomena has been studied by several authors for decades, and numerical and approximate results have been shown through the asymptotic solution in short and long times. In particular, it is worth highlighting the works of Philip and Parlange, who used time and volumetric content as independent variables and space as a dependent variable, and found the solution as a power series in that is valid for short times. However, several studies show that these models are not applicable to anomalous flows, in which case the application of fractional calculus is needed. In this work, a fractional time derivative of a Caputo type is applied to model anomalous infiltration phenomena. Fractional horizontal infiltration phenomena are studied, and the fractional Boltzmann transform is defined. To study fractional vertical infiltration phenomena, the asymptotic behavior is described for short and long times considering an arbitrary diffusivity and hydraulic conductivity. Finally, considering a constant flux-dependent relation and a relation between diffusivity and hydraulic conductivity, a fractional cumulative infiltration model applicable to various types of soil is built; its solution is expressed as a power series in , where is the order of the fractional derivative. The results show the effect of superdiffusive and subdiffusive flows in different types of soil.
1. Introduction
More than a century ago, Green and Ampt [1] laid the bases for describing the infiltration process; to this day, there are still open problems in the area, where existing models in the literature cannot explain laboratory results [2]. As one of the pioneers in the area, Philip [3] describes the infiltration phenomenon as a Fokker–Planck type equation. In a semi-infinite domain, homogeneous, its form is
where is the volumetric water content, is the hydraulic diffusivity, is the hydraulic conductivity, is the initial volumetric water content, is the volumetric water content at saturation, t is the time, and z is the spatial variable taken positive downward.
In particular, when considering horizontal infiltration:
with initial conditions
On the other hand, when considering vertical infiltration,
Philip [5] applied the implicit function theorem and rewrote Equation (6) as
where is the Darcy flow; Philip proved that, for short times, the solution of Equation (8) is sought in the form
where each term function of in the series is defined from integro-differential equations whose expression considering fractional calculus will be shown in Section 4. In particular, the first term in the series (9), , matches the solution of the horizontal infiltration problem, Equation (4).
However, Philip did not work with the radius of convergence of the series, a problem that remains open to date, but suggests that the range of useful convergence is , where it is obtained from dimensional analysis that gravity effects are as great as capillarity effects, namely,
where is the hydraulic conductivity at saturation, is the initial hydraulic conductivity, and S is the sorptivity defined by
where is the Boltzmann transform defined by the differential Equation (4).
Likewise, Philip [5] proves that, for long times, the solution of Equation (8) has the form
where is a function of volumetric water content and can be expressed in terms of diffusivity and hydraulic conductivity as
where and is a definite small positive quality; the calculus of , Equation (13), should be done carefully since, in general, has singularities at .
Philip showed that, when water is applied to uniform soils, it is sufficient to retain only two terms of the series to obtain an adequate description of the vertical infiltration. Talsma and Parlange [6] proved that sorptivity S and conductivity at saturation were the soil parameters necessary for the two terms of the Philip series; in addition, the one-dimensional infiltration equation is more sensitive to soil heterogeneity than its equivalents in two or three dimensions.
Later, Parlange et al. [7] showed that adding a third parameter to the series is sufficient to describe cumulative infiltration accurately, where this extra parameter is representative of the type of soil in which water infiltration takes place.
Haverkamp et al. [8] recognize that the infiltration process can be described either by solving the Richards equation or by considering cumulative infiltration. They chose the second option. Since previous models used highly time-dependent parameters [9], they developed an equation for infiltration subject to head boundary conditions considering time-independent parameters, which takes into account the possibility of an infinite diffusivity near saturation.
Fuentes et al. [10] analyzed the constraints on different fitting parameters used in a water retention equation and hydraulic conductivity using the infiltration equations to describe several soils types. Later, Fuentes et al. [11] calculated the analytical solution for vertical infiltration considering a constant diffusivity and a hydraulic conductivity resulting from a linear combination of linear and quadratic functions of volumetric water content. They showed that their model can also be applied to soils that do not necessarily meet the hypotheses for his deduction. On the other hand, using a numerical approximation, Saucedo et al. [12] verified the contact time hypothesis to describe water transfer in melgas irrigation by coupling the Saint– Venant and Richards equations.
Over the years, the Philip power series has been applied in different contexts, such as falling head ponded infiltration [13], variable head ponded infiltration on flat surfaces [14], and variable head ponded infiltration on sloping surfaces [15], to name a few. In particular, in the last work, they showed that sorptivity is independent of the slope angle and that cumulative infiltration normal to the slope decreases with increasing slope angles.
Recently, cumulative infiltration was used to describe the effect of pressure head and soil bulk density on moistube irrigation [16]. It was concluded that infiltration index is negatively correlated with pressure head but positively with soil bulk density, while the infiltration coefficient K was positively correlated with the pressure head but negatively with the soil bulk density.
Likewise, water infiltration has been used to calculate infiltrated depth evolution and humidity profiles by coupling the Saint–Venant and Richards equations with furrow boundary conditions [17]. Considering this model, the relationship between the optimal irrigation flow and the length of the border for different types of soil was found [18].
These examples show the wide range of applications that the Philip power series has for water infiltration in different types of soil; in this sense, it goes without saying how useful infiltration models are in developing an effective design and evaluating surface irrigation systems, whether they are physical (such as Philip’s [5] and Richards’ [19] models), semi-empirical (such as Holtan’s [20] model) or empirical models (such as Sihag’s [21] model) [22].
When studying non-heterogeneous soils, the transport phenomenon in soils is recognized as being fundamentally stochastic [23,24]. Moreover, to apply equations, e.g., Richards or Philip power series, it is necessary to assume that water moves in a Brownian motion [25]; however, several studies have shown that this assumption is not valid and that anomalous flows can be created. The reason behind these anomalous flows is explained by several authors; they argue that constraints can be imposed by the structure of the porous media or by solute–surface interactions, resulting in Lévy flights due to the presence of highly conductive fractures, channels, or macropores or because the infiltration front undergoes jerky movements [26,27,28]. Thus, the application of fractional derivatives was considered to explain the anomalous behavior.
Pachepsky et al. [29] considered water transport in horizontal soil columns and generalized the Richards equation to include a fractional time derivative and solved it by generalizing the Boltzmann transform. Sun et al. [30] considered the same problem; however, noting that the fractional derivative fails with the chain rule, they considered a fractal derivative and showed that their results exhibited an anomalous Boltzmann transform, attributed to the fractal nature of the heterogeneous media.
Generalizing the Fokker–Planck type equation, Su [31] applied the fractional derivative to present a fractional cumulated infiltration into swelling soils where convection dominates, applying the most linear hydraulic conductivity. Subsequently [32], he generalized these results to include mobile and immobile zones with and without gravity effects. Later [33], he introduced mass–time fractional derivatives for swelling-shrinking soils and space–time fractional derivatives for non-swelling soils, applying for mobile zones with or without immobile zones by using power functions for diffusivity and hydraulic conductivity. Physically, the spatial fractional derivative means that the concentration change at the point of observation depends on upstream concentrations, while the temporal fractional derivative implies that the concentration change at the point of observation depends on the prior concentration loading [34].
In the present work, a model for infiltration is developed using a fractional calculation as a tool to incorporate the anomalous behavior in the flow of water. Anomalous horizontal infiltration will first be studied to later extend these results to study anomalous vertical infiltration, where asymptotic solutions will be given for short and long times. Finally, a relationship between conductivity and diffusivity will be assumed to yield a valid anomalous infiltration model for all times.
The work is developed in the following way: Section 2 describes the mathematical tools from fractional calculus that will be implemented; Section 3 develops the equation for the fractional horizontal infiltration considering as the dependent variable and , t as independent variables; Section 4 extends the results of the previous section by studying vertical infiltration phenomena for both arbitrary diffusivity and hydraulic conductivity through the asymptotic solution in short times and long times; Section 5 considers, as additional hypotheses, a constant flux-dependant relationship and a relation between diffusivity and hydraulic conductivity to build a model for fractional cumulative infiltration, where its solution is developed for short times expressed as a power series of , where is the order of the time fractional derivative with ; finally, Section 6 summarizes the conclusions reached in this work.
2. Fractional Calculus
At present, there is a great diversity of fractional derivatives such as Riemann–Liouville, Caputo, Grünwald, Marchaud, and Riez, among many others. In this section, the basis of fractional calculus that will be applied for the development of this work will be described. For more information regarding these properties, see [35,36,37].
Definition 1.
Let . The Riemann–Liouville fractional integral of order is defined by
where is the gamma function applied to α defined by
The fractional integral is the basis from which various forms of fractional derivative are defined:
Definition 2.
The Riemann–Liouville fractional derivative of order is defined by
where with .
Definition 3.
The Caputo fractional derivative of order is defined by
where with and is the n-th derivative.
The Riemann–Liouville fractional derivative and the Caputo fractional derivative are two of the most widely used definitions in fractional calculus; the first because it can be implemented numerically with ease due to the Grünwald-Letnikov algorithm, although it does not allow for the use of the usual initial conditions, while the second allows the classical initial conditions to be implemented when solving fractional differential equations.
In addition, both definitions of the fractional derivative are related by
it follows from Equation (18) that both definitions of the fractional derivative are equivalent if for .
In particular, if , it can be verified directly from definitions 2 and 3 that
Likewise, the Caputo fractional derivative and the Riemann–Liouville fractional integral act among themselves, generalizing the fundamental theorem of calculus, where, for sufficiently good conditions of , it is satisfied that
3. Fractional Horizontal Infiltration
In this section, the fractional horizontal infiltration equation is developed and solved by replacing the time derivative by the Caputo fractional derivative and neglecting the term associated with the gravitational field.
Note that applying the implicit function theorem to Equation (2), to express and t as independent variables and as a dependent variable, it follows that
where is the Darcy flow.
Therefore, the fractional differential equation that describes the anomalous horizontal infiltration is
where is the order of the fractional derivative, and is a constant introduced to maintain dimensional balance with units of time and initial and boundary conditions shown in Equation (3).
It can be verified that the solution to anomalous horizontal infiltration, Equation (22), is
where can be called the fractional Boltzmann transform and is defined by the following ordinary differential equation:
In addition, fractional cumulative infiltration for fractional horizontal infiltration is defined by
where can be called the -sorptivity.
4. Fractional Vertical Infiltration
The fractional differential equation that describes the complete anomalous infiltration is obtained analogously to the previous section, namely,
expressing it in closed form, we obtain
with initial and boundary conditions as in (7).
This equation has been analytically solved for considering particular behaviors for diffusivity and hydraulic conductivity; however, considering arbitrary behavior for D and K, the asymptotic behavior for infiltration can be deduced.
4.1. Short-Time Approximation
As a solution for the fractional differential equation, Equation (31), we consider the ansatz given by the convergent finite radius convergent series:
where for are defined through the ordinary differential equations that are obtained from substituting the series (32) into the differential Equation (31) and matching terms, considering
where . In particular, it can be seen that , as in (23). Likewise, similar to Philip, defining , , , and , the first four terms of series (32) satisfy the following integro-differential equations:
with , , , and .
Note that, with , Equations (35)–(38) become the equations given by Philip [3].
Furthermore, integrating the continuity equation, Equation (31), it follows that the Darcy flow becomes
the infiltration flow is calculated as Darcy’s law at the entry position of water into the soil, i.e., , by
Thereby, by substituting the series (33) in the previous equation, we have
where for .
In this case, the fractional cumulative infiltration for an anomalous vertical infiltration considering both an arbitrary diffusivity and hydraulic conductivity is defined by
Since
it is concluded that
4.2. Long-Time Approximation
We now find the long-time asymptotic behavior of fractional vertical infiltration, Equation (31); note that, from initial conditions, Equation (7), it follows that when ; from Darcy’s law, when . Therefore, assuming that, when , is independent of time, we have
consequently,
where is a function from volumetric water content.
Note that, when , the vertical infiltration, Equation (46), has the same behavior described by Philip in [5], Equation (12).
Finally, from Equation (42), the asymptotic behavior at long times for fractional cumulative infiltration is
5. Fractional Parlange Solution
In the previous sections, the fractional equation that describes the behavior of anomalous infiltration was deduced by neglecting the term associated with the gravitational field, generalizing the Boltzmann transform, as well as the anomalous cumulative infiltration and its relationship with the expressions corresponding to the non-anomalous case; otherwise, for both an arbitrary diffusivity and hydraulic conductivity, the fractional equation was deduced to describe the full anomalous vertical infiltration, and the asymptotic behavior was found for fractional cumulative infiltration in short and long times. Next, considering an arbitrary but related hydraulic diffusivity and conductivity, as well as the approximation of sorptivity given by Parlange [38], the explicit form of fractional equation for anomalous vertical infiltration will be deduced, and its solution will be given in terms of a power series in with .
Starting from the flow–concentration relationship applied to fractional flow, Equations (39) and (40) are
with . Substituting Darcy’s law and making a first integration, it follows that
Considering the previous expression, the fractional cumulative infiltration is obtained by substituting in Equation (42), namely,
Considering this, in long times, the flow concentration relationship behaves as follows:
assuming that this behavior is valid for all times. We consider the following relationship between diffusivity and hydraulic conductivity [7]:
where is a parameter associated with the soil type that satisfies . Equation (52) interpolates between the Green and Ampt model and the Talsma and Parlange model, for which and 1, respectively; moreover, can be calculated from the experimentally measured hydrodynamic characteristics data using the relation [39]
In fact, Parlange et al. [7] recommend to represent the two soil types sand and clay. Hereafter, will be considered as a fixed but arbitrary constant parameter.
By substituting Equations (51) and (52) into Equation (50), we have
where S is the sorptivity defined by the following approximation [38]:
Considering the dimensionless variables
the fractional cumulative infiltration, Equation (54), is expressed through the following dimensionless fractional differential equation:
with initial condition .
Note that, for , and Equation (56) can be integrated to obtain the following result:
as in [7], where, for , the last equation is reduced to , as in [1]; for , the last equation is reduced to , as in [6].
The asymptotic behavior of Equation (57) is, for short times,
for long times, it is
where, for the singular value , the last expression becomes .
Note that, for , the integral equation equivalent to Equation (56) is
Equation (60) expresses the general solution to fractional cumulative infiltration before different types of soil considering an anomalous flow. However, since the integral term has a singularity for , its solution requires numerical methods; nevertheless, an approximate solution in short times can yield useful information.
As in Equation (44), consider the approximation of through the dimensionless power series
where for are obtained by matching terms.
Thus, by substituting the approximation of Equation (61) into the right hand side of Equation (56), we have
where, the first four terms are
By introducing the approximation shown in Equation (62) into the fractional differential equation, Equation (56), we have
where the following coefficients relationship between the series is found:
Since depends on for and , it is necessary to solve non-linear equations to find the coefficients of the series . The expressions for the first four coefficients of are shown below:
It can be seen that the short-time asymptotic behavior shown in Equation (58) is obtained from Equations (67) and (68), making .
Figure 1 shows the first four terms of the series , for , where is as in Equations (67)–(70). In particular, it can be observed that the first two terms of the series provide the main contribution to , which is why it is understood that the approximation to two terms used in the literature is considered sufficient to approximate the cumulative infiltration; however, it is from the fourth term that the contribution provided by is less than of the cumulative infiltration value.
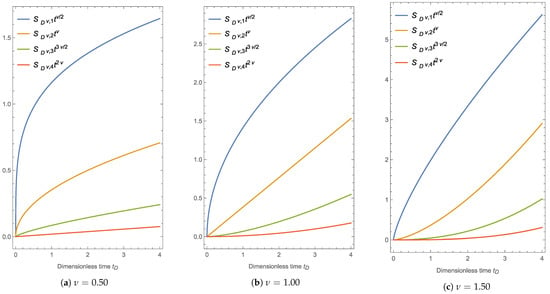
Figure 1.
First four terms from Series (61), for the solution in short times to the fractional cumulative infiltration given by the fractional
differential Equation (56), considering subdiffusive flow , classic flow , and superdiffusive flow for a soil type
represented by β = 0.85, which is valid for both sands and clays and τcD = 1.
Figure 2 shows the behavior of anomalous infiltration for different values of , where is the classic case solved in [7,40]. The phenomena described by the anomalous infiltration with are known as subdifusive phenomena, which indicate that the flow modifies the porous media such that particles blocking fractures or channels are moved, where, for a lower value of , there is greater blockage to the flow, showing a lower value to fractional cumulative infiltration. The phenomena described with is known as superdiffusive phenomena, where the flow modifies the porous media such that the particles create new fractures or channels that allow greater mobility to the fluid, where, for a higher value of , there is a greater flow and therefore greater fractional cumulative infiltration.
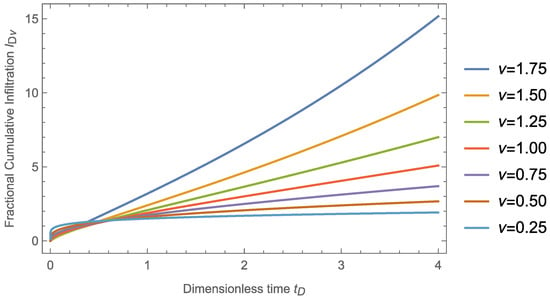
Figure 2.
Short-time-approximated solution given by Series (61) for fractional cumulative infiltration considering subdiffusive flows , classical flows , and superdiffusive flows , for a soil type represented by that is valid for sands and clays and .
Figure 3 shows the effect of on the fractional accumulated infiltration for several values of . As previously described, is associated with hydrodynamic characteristics of the soil type, where corresponds to a linear soil type solved in [1] for . corresponds to the solution given by Talsma and Parlange solved in [6] for . Further, Figure 3 shows how the effect of is greater than in determining the value of the fractional cumulative infiltration ; that is, the anomalous soil behavior has a greater impact on the cumulative infiltration compared to the soil type. On the other hand, it can be observed that, for a fixed value of , the extreme values of limit the behavior for cumulative infiltration.
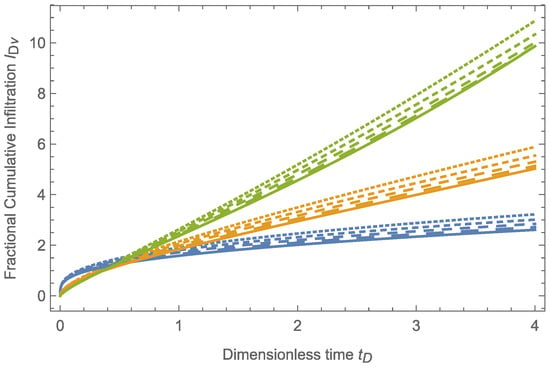
Figure 3.
Short-time-approximated solution for fractional cumulative infiltration considering different soil types represented by , with and subdiffusive, classical, and superdiffusive flows represented by , respectively. Results in green correspond to , results in orange to , and results in blue to , where a more dashed line indicates a lower value of .
6. Conclusions
A new model is proposed to capture the phenomenon of anomalous infiltration through the use of fractional calculus considering time t and volumetric water content as dependent variables and space z as an independent variable. We began the study of fractional horizontal infiltration phenomena by neglecting the term associated with the gravitational field, finding as a solution the fractional Boltzmann transform and the corresponding accumulated infiltration. For the study of fractional vertical infiltration phenomena, the asymptotic solution is found in short and long times for both an arbitrary diffusivity and hydraulic conductivity; the short-time approximation was expressed as a power series in , where is the order of fractional derivative, and the first terms are expressed as integro-differential equations. Finally, a constant flow–concentration relationship and a relation between diffusivity and hydraulic conductivity were considered to construct a fractional accumulated infiltration model that is valid for all times and for different soil types. The model was solved through a series that was valid for short times. It is shown that the first two terms of the series provide the main contribution to the anomalous infiltration. It is shown that, for subdifusive flows, there is less accumulated infiltration than in the classic case; for superdifusive flows, the accumulated infiltration is greater than the classic case. The effect of considering different types of soils is also shown, concluding that, for a fixed value of , the extreme values of limit the behavior of cumulative infiltration, and the anomalous soil behavior has a greater impact on cumulative infiltration compared to the soil type.
Author Contributions
Conceptualization, C.F.; Software, C.F. and F.A.-L.; Supervision, A.Q. and C.C.; Writing—original draft, C.F.; Writing—review & editing, F.A.-L. All authors have read and agreed to the published version of the manuscript.
Funding
The corresponding author of this work is grateful to CONACYT for the scholarship grant, scholarship number 548429.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Green, W.H.; Ampt, G. Studies on Soil Phyics. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall infiltration modeling: A review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur integration der diffusionsgleichung bei variabeln diffusionscoefficienten. Annalen der Physik 1894, 289, 959–964. [Google Scholar] [CrossRef]
- Philip, J. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Talsma, T.; Parlange, J. One dimensional vertical infiltration. Soil Res. 1972, 10, 143–150. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Lisle, I.; Braddock, R.; Smith, R. The three-parameter infiltration equation. Soil Sci. 1982, 133, 337–341. [Google Scholar] [CrossRef]
- Haverkamp, R.; Parlange, J.Y.; Starr, J.; Schmitz, G.; Fuentes, C. Infiltration under ponded conditions: 3. A predictive equation based on physical parameters. Soil Sci. 1990, 149, 292–300. [Google Scholar] [CrossRef]
- Haverkamp, R.; Kutilek, M.; Parlange, J.Y.; Rendon, L.; Krejca, M. Infiltration under ponded conditions: 2. infiltration equations tested for parameter time-dependence and predictive use. Soil Sci. 1988, 145, 317–329. [Google Scholar] [CrossRef]
- Fuentes, C.; Haverkamp, R.; Parlange, J.Y. Parameter constraints on closed-form soilwater relationships. J. Hydrol. 1992, 134, 117–142. [Google Scholar] [CrossRef]
- Fuentes, C.; Parlange, J.Y.; Haverkamp, R.; Vauclin, M. La solución cuasi-lineal de la infiltración vertical. Tecnología y Ciencias del Agua 2001, 16, 25–33. [Google Scholar]
- Saucedo, H.; Fuentes, C.; Zavala, M. El sistema de ecuaciones de Saint-Venant y Richards del riego por gravedad: 3. verificación numérica de la hipótesis del tiempo de contacto en el riego por melgas. Tecnología y Ciencias del Agua 2006, 21, 135–143. [Google Scholar]
- Mollerup, M.; Hansen, S. Power series solution for falling head ponded infiltration with evaporation. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Mollerup, M. Philip’s infiltration equation for variable-head ponded infiltration. J. Hydrol. 2007, 347, 173–176. [Google Scholar] [CrossRef]
- Mollerup, M.; Hansen, S. Power series solution for ponded infiltration on sloping surfaces. J. Hydrol. 2012, 464, 431–437. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, X.; Zhu, Y.; Yang, Q. Effects of pressure heads and soil bulk density on infiltration characteristics of vertically inserted moistube irrigation. Environ. Earth Sci. Res. J. 2019, 6, 119–124. [Google Scholar] [CrossRef]
- Castanedo, V.; Saucedo, H.; Fuentes, C. Modeling Two-Dimensional Infiltration with Constant and Time-Variable Water Depth. Water 2019, 11, 371. [Google Scholar] [CrossRef]
- Fuentes, C.; Chávez, C. Analytic Representation of the Optimal Flow for Gravity Irrigation. Water 2020, 12, 2710. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Holtan, H.N. Concept for Infiltration Estimates in Watershed Engineering; USDA Bulletin: Washington, DC, USA, 1961.
- Sihag, P.; Tiwari, N.; Ranjan, S. Estimation and inter-comparison of infiltration models. Water Sci. 2017, 31, 34–43. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Timashev, S.F.; Polyakov, Y.S.; Misurkin, P.I.; Lakeev, S.G. Anomalous diffusion as a stochastic component in the dynamics of complex processes. Phys. Rev. E 2010, 81, 041128. [Google Scholar] [CrossRef] [PubMed]
- Parlange, J.Y.; Haverkamp, R.; Rand, R.; Rendon, L.; Schmitz, G. Water Movement in Soils-The Role of Analytical Solutions. Future Dev. Soil Sci. Res. 1978, 11–21. [Google Scholar] [CrossRef]
- Bhattacharya, R.N.; Gupta, V. On a statistical theory of solute transport in porous media. SIAM J. Appl. Math. 1979, 37, 485–498. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F.; Vivoli, A. Continuous-time random walk and parametric subordination in fractional diffusion. Chaos Solitons Fractals 2007, 34, 87–103. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Bagley, R.L. The thermorheologically complex material. Int. J. Eng. Sci. 1991, 29, 797–806. [Google Scholar] [CrossRef]
- Pachepsky, Y.; Timlin, D.; Rawls, W. Generalized Richards’ equation to simulate water transport in unsaturated soils. J. Hydrol. 2003, 272, 3–13. [Google Scholar] [CrossRef]
- Sun, H.; Meerschaert, M.M.; Zhang, Y.; Zhu, J.; Chen, W. A fractal Richards’ equation to capture the non-Boltzmann scaling of water transport in unsaturated media. Adv. Water Resour. 2013, 52, 292–295. [Google Scholar] [CrossRef]
- Su, N. Theory of infiltration: Infiltration into swelling soils in a material coordinate. J. Hydrol. 2010, 395, 103–108. [Google Scholar] [CrossRef]
- Su, N. Distributed-order infiltration, absorption and water exchange in mobile and immobile zones of swelling soils. J. Hydrol. 2012, 468, 1–10. [Google Scholar] [CrossRef]
- Su, N. Mass-time and space-time fractional partial differential equations of water movement in soils: Theoretical framework and application to infiltration. J. Hydrol. 2014, 519, 1792–1803. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Parlange, J.Y. On solving the flow equation in unsaturated soils by optimization: Horizontal infiltration. Soil Sci. Soc. Am. J. 1975, 39, 415–418. [Google Scholar] [CrossRef]
- Fuentes, C. Unidimensional infiltration theory: 2. Vertical infiltration. Agrociencia 1989, 78, 119–153. [Google Scholar]
- Fuentes, C.; Parlange, J.Y.; Palacios-Vélez, O. Infiltration Theory. In Gravity Irrigation, 1st ed.; Fuentes, C., Rendón, L., Eds.; National Association of Irrigation Specialists: México, México, 2017; Chapter 3; pp. 154–211. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).