Hesitant Fuzzy Linguistic Agglomerative Hierarchical Clustering Algorithm and Its Application in Judicial Practice

Abstract

The fuzzy clustering algorithm has become a research hotspot in many fields because of its better clustering effect and data expression ability. However, little research focuses on the clustering of hesitant fuzzy linguistic term sets (HFLTSs). To fill in the research gaps, we extend the data type of clustering to hesitant fuzzy linguistic information. A kind of hesitant fuzzy linguistic agglomerative hierarchical clustering algorithm is proposed. Furthermore, we propose a hesitant fuzzy linguistic Boole matrix clustering algorithm and compare the two clustering algorithms. The proposed clustering algorithms are applied in the field of judicial execution, which provides decision support for the executive judge to determine the focus of the investigation and the control. A clustering example verifies the clustering algorithm’s effectiveness in the context of hesitant fuzzy linguistic decision information.

1. Introduction

Clustering refers to dividing a collection of physical or abstract objects into different classes or clusters according to some specific standards, which makes the objects in the class similar to each other but different from the objects outside the class [1]. Unlike traditional clustering with an either-or nature, fuzzy clustering is a mathematical method to classify things with both-and characteristics. The fuzzy clustering method has been widely used in multi-attribute decision-making problems such as image processing [1], risk assessment [2] and energy planning [3].

Ruspini [4] proposed the concept of fuzzy division and introduced fuzzy set theory into cluster analysis. Subsequently, scholars have successively proposed fuzzy clustering analysis methods, such as a transitive closure algorithm based on fuzzy equivalence relation [2,5,6], a fuzzy c-means clustering algorithm [7,8,9] and a hierarchical clustering algorithm [3,10]. The hierarchical clustering algorithm is a representative and essential clustering method. Hierarchical clustering decomposes or gathers the data set layer by layer by a particular method until all the classified data in the last layer meet the requirements. According to the different decomposition principles or aggregation principles, hierarchical clustering can be divided into agglomerative and divisive methods, and the agglomerative hierarchical clustering algorithm is more widely used [11].

It is known from the literature that the existing research on fuzzy data types of clustering mainly involves intuitionistic fuzzy information [12,13], type-2 fuzzy information [14,15] and hesitant fuzzy information [16,17]. There are few studies on the clustering of hesitant fuzzy linguistic information. In addition, uncertainty analysis methods such as intuitionistic fuzzy sets, soft multi-set topology and hesitant fuzzy linguistic term sets (HFLTSs) have been widely used in multi-attribute decision-making problems, such as optimal recommendation [18,19,20], risk assessment [21,22] and pattern recognition [23]. The application of the HFLTSs clustering method in the field of judicial execution is rare.

In practical decision-making, the hesitant fuzzy linguistic term sets (HFLTSs) have significant advantages in expressing experts’ qualitative judgment. For example, in judicial practice, many attributes of many persons subjected to execution cannot be described quantitatively. However, they can only be assessed qualitatively. The possibility of the hidden property of the persons subjected to execution is mostly presented in the form of linguistic expressions or sentences. At this time, the HFLTSs can scientifically represent the executive judge’s qualitative decision information. Therefore, it is of practical significance to study the clustering analysis method for processing HFLTSs.

Based on the above analysis, the main contributions are as follows. (1) The data type of clustering to hesitant fuzzy linguistic information is extended. (2) A hesitant fuzzy linguistic agglomerative hierarchical (HFLAH) clustering algorithm and hesitant fuzzy linguistic Boole matrix (HFLBM) clustering algorithm are proposed, and the two clustering algorithms are compared and analyzed. (3) The fuzzy cluster analysis method is applied in judicial execution, which helps the executive judge determine the critical points of investigation and control scientifically and objectively and realizes the subject’s classification of investigation and control under the hesitant fuzzy linguistic environment.

The structure of this paper is as follows. Section 2 reviews some of the related concepts, distance and similarity measures and integrated operations of the HFLTSs. In Section 3, the agglomerative hierarchical clustering algorithm is introduced in detail. On this basis, a kind of HFLAH clustering algorithm is proposed. Section 4 introduces the identification principle and realization steps of the person’s concealed property behavior subjected to execution. An example of a cluster analysis of the person subjected to execution based on hesitant fuzzy linguistic decision information is given. The validity of the HFLAH clustering algorithm is verified. Furthermore, an HFLBM clustering algorithm is proposed, and the two clustering algorithms are compared and analyzed. The conclusion is given in Section 5.

2. Distance and Similarity Measure and Integration Operation of Hesitant Fuzzy Linguistic Decision Information

2.1. Hesitant Fuzzy Linguistic Term Sets

Definition 1

[24,25].Suppose$X\ne \varnothing$, and let$S=\{s_t\mid t=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$be a linguistic term set. The mathematical expression of HFLTS on$X$is

$$H_s=\{<x_i,h_s(x_i)>\mid x_i\in X\}$$

(1)

where the hesitant fuzzy linguistic number (HFLN)$h_s(x_i)$is a set of values in the linguistic term set$S$, considering$x_i$: $h_s(x_i)=\{s_{\phi l}(x_i)\mid s_{\phi l}(x_i)\in S,l=1,\cdots ,L\}$, $L$is the number of linguistic terms and$S$admits the following definitions:

(1)

For any$s_{\alpha },s_{\beta }\in S$, $s_{\alpha }>s_{\beta }$if$\alpha >\beta$;

(2)

The negation operator is defined by$neg(s_{\alpha })=s_{-\alpha }$, and especially$neg(s_0)=s_0$.

Definition 2

[26,27].Let$h_s(x_i)$, $h_s^1(x_i)$and$h_s^2(x_i)$be three HFLNs with$h_s(x_i)$, simply written as$h_s^i$. The continuous linguistic term set is$\overline{S}=\{s_{\vartheta }\mid \vartheta \in [-q,q]\}$, where$q(q>\tau )$is a sufficiently large positive integer. For any two linguistic terms$s_{\alpha },s_{\beta }\in \overline{S}$and$\lambda ,{\lambda }_1,{\lambda }_2\in [0,1]$, there are operation rules, which are defined as follows:

• Lower bound:$h_s^{-}=\min ({\mathrm{s}}_t)={\mathrm{s}}_k,{\mathrm{s}}_t\in h_s$if$s_t\ge s_k$, $\forall t$;
• Upper bound: $h_s^{+}=\max ({\mathrm{s}}_t)={\mathrm{s}}_k,{\mathrm{s}}_t\in h_s$if$s_t\le s_k$, $\forall t$;
• $h_s^c=S-h_s=\{s_t\mid s_t\in S\hspace{0.17em}and\hspace{0.17em}{s}_t\ne h_s\}$;
• $h_s^1\cup h_s^2=\{{\mathrm{s}}_t\mid {\mathrm{s}}_t\in h_s^1\hspace{0.17em}or\hspace{0.17em}{\mathrm{s}}_t\in h_s^2\}$;
• $h_s^1\cap h_s^2=\{{\mathrm{s}}_t\mid {\mathrm{s}}_t\in h_s^1\hspace{0.17em}and\hspace{0.17em}{\mathrm{s}}_t\in h_s^2\}$;
• $s_{\alpha }\oplus s_{\beta }=s_{\alpha +\beta }$;
• $\lambda s_{\alpha }=s_{\lambda \alpha }$;
• $({\lambda }_1+{\lambda }_2)s_{\alpha }={\lambda }_1{s}_{\alpha }\oplus {\lambda }_2{s}_{\alpha }$;
• $\lambda (s_{\alpha }\oplus s_{\beta })=\lambda s_{\alpha }\oplus \lambda s_{\beta }$.

Definition 3

[26].Let$S$be a linguistic term set. A context-free grammar$G_H=(V_N,V_T,I,P)$is defined by its elements as follows:

• $V_N=\{<primary\hspace{0.17em}\hspace{0.17em}term>,<composite\hspace{0.17em}\hspace{0.17em}term>,<unary\hspace{0.17em}\hspace{0.17em}relation>,<binary\hspace{0.17em}\hspace{0.17em}relation>,<conjunction>\}$,
• $V_T=\{lower than,greater than,at least,at most, between,and,s_{-\tau },\cdots ,s_{-1},s_0,s_1,\cdots ,s_{\tau }\}$, $I\in V_N$,
• $\begin{array}{l}P=\{I::=<primary term>\mid <composite term><composite term>::=<unary relation>\\ <primary term>\mid <binary relation><conjunction><primary term><primary term>\\ ::=s_{-\tau }\mid \cdots \mid s_{-1}\mid s_0\mid s_1\mid \cdots \mid s_{\tau }<unary relation>::=lower than\mid greater than\\ <binary relation>::=between<conjunction>::=and\}\end{array}$

In the definitions above, the brackets enclose optional elements, and the $\mid$ symbol indicates alternative elements.

Definition 4

[26].Let$E_{G_H}$be a function that transforms the linguistic expression generated by$G_H$into the HFLTSs$h_s\in H_s$:

$$E_{G_H}:S_{\parallel }\to H_s$$

(2)

where$S_{\parallel }$is the expression domain generated by$G_H$. The linguistic expression generated by$G_H$can be converted to HFLTSs by the following conversion formula:

• $E_{G_H}(s_t)=\{s_t\mid s_t\in S\}$;
• $E_{G_H}(at\hspace{0.17em}most\hspace{0.17em}{s}_m)=\{s_t\mid s_t\in S\hspace{0.17em}and\hspace{0.17em}{s}_t\le s_m\}$;
• $E_{G_H}(lower\hspace{0.17em}than\hspace{0.17em}{s}_m)=\{s_t\mid s_t\in s\hspace{0.17em}and\hspace{0.17em}{s}_t<s_m\}$;
• $E_{G_H}(at\hspace{0.17em}least\hspace{0.17em}{s}_m)=\{s_t\mid s_t\in s\hspace{0.17em}and\hspace{0.17em}{s}_t\ge s_m\}$;
• $E_{G_H}(greater\hspace{0.17em}than\hspace{0.17em}{s}_m)=\{s_t\mid s_t\in s\hspace{0.17em}and\hspace{0.17em}{s}_t>s_m\}$;
• $E_{G_H}(between\hspace{0.17em}{s}_m\hspace{0.17em}and\hspace{0.17em}{s}_n)=\{s_t\mid s_t\in s\hspace{0.17em}and\hspace{0.17em}{s}_m\le s_t\le s_n\}$.

Definition 5

[28].For a given HFLN$h_s(x_i)=\{s_{\phi l}(x_i)\mid s_{\phi l}(x_i)\in S,l=1,\cdots ,L\}$, $s_{\phi l}^{+}(x_i)$and$s_{\phi l}^{-}(x_i)$are the maximum and minimum linguistic terms in$h_s(x_i)$, respectively, and$\varsigma (0\le \varsigma \le 1)$is an arbitrary parameter. Then, we can add the following linguistic term to HFLNs with fewer elements:

$$s_{\phi l}^{\ast }(x_i)=\varsigma s_{\phi l}^{+}(x_i)+\left(1-\varsigma \right)s_{\phi l}^{-}(x_i)$$

(3)

2.2. Distance and Similarity Measures of Hesitant Fuzzy Linguistic Decision Information

Definition 6

[29].For a given linguistic term set$S=\{s_t\mid t=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$, and for two given HFLNs$h_s^1$and$h_s^2$defined for$S$, the distance measure$d(h_s^1,h_s^2)$between$h_s^1$and$h_s^2$is a real number that satisfies the following conditions:

• $0\le d(h_s^1,h_s^2)\le 1$;
• $d(h_s^1,h_s^2)=0$, if and only if$h_s^1=h_s^2$;
• $d(h_s^1,h_s^2)=d(h_s^2,h_s^1)$.

Definition 7

[29].For a given term set$S=\{s_t\mid t=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$, and for given values$h_s^1$and$h_s^2$defined for$S$, the similarity measure$\rho (h_s^1,h_s^2)$between$h_s^1$and$h_s^2$is a real number that satisfies the following:

• $0\le \rho (h_s^1,h_s^2)\le 1$;
• $\rho (h_s^1,h_s^2)=1$if and only if$h_s^1=h_s^2$;
• $\rho (h_s^1,h_s^2)=\rho (h_s^2,h_s^1)$.

Definition 8

[30].For a given term set$S=\{{\mathrm{s}}_t\mid \mathrm{t}=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$, assume that$h_s^1(x_i)=\{s_{{\delta }_l^1}\mid l=1,\cdots ,L_1\}$and$h_s^2(x_i)=\{s_{{\delta }_l^2}\mid l=1,\cdots ,L_2\}$are two HFLNs on$X$with$L_1$and$L_2$as the numbers of the linguistic terms in$h_s^1(x_i)$and$h_s^2(x_i)$, respectively. If$L_1=L_2=L$(otherwise, linguistic terms can be added to the HFLTSs with fewer elements according to Equation (3)), then the generalized distance between$h_s^1(x_i)$and$h_s^2(x_i)$is defined as

$$d_{gd}\left(h_s^1(x_i),h_s^2(x_i)\right)={\left[\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}\right)}^{\lambda }}\right]}^{1/\lambda }$$

(4)

where$\lambda >0$. In particular, if$\lambda =1$, the Hamming distance between$h_s^1(x_i)$and$h_s^2(x_i)$can be obtained:

$$d_{hd}\left(h_s^1(x_i),h_s^2(x_i)\right)=\frac{1}{L}{\displaystyle \sum _{l=1}^L\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}}$$

(5)

If$\lambda =2$, the Euclidean distance between$h_s^1(x_i)$and$h_s^2(x_i)$can be obtained:

$$d_{ed}\left(h_s^1(x_i),h_s^2(x_i)\right)={\left[\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}\right)}^2}\right]}^{1/2}$$

(6)

Since the relationship between the distance and similarity measures satisfies$\rho (h_s^1,h_s^2)=1-d(h_s^1,h_s^2)$ [25], the generalized, Hamming and Euclidean similarities between $h_s^1(x_i)$ and $h_s^2(x_i)$ can be defined as

$${\rho }_{gd}\left(h_s^1(x_i),h_s^2(x_i)\right)=1-{\left[\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}\right)}^{\lambda }}\right]}^{1/\lambda }$$

(7)

$${\rho }_{hd}\left(h_s^1(x_i),h_s^2(x_i)\right)=1-\frac{1}{L}{\displaystyle \sum _{l=1}^L\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}}$$

(8)

$${\rho }_{ed}\left(h_s^1(x_i),h_s^2(x_i)\right)=1-{\left[\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^1-{\delta }_l^2\mid }{2\tau +1}\right)}^2}\right]}^{1/2}$$

(9)

Definition 9

[30].For$S=\{{\mathrm{s}}_t\mid \mathrm{t}=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$and for two collections of HFLTSs$H_s^1=\{h_s^{11},h_s^{12},\cdots ,h_s^{1m}\}$and$H_s^2=\{h_s^{21},h_s^{22},\cdots ,h_s^{2m}\}$with the associated weighting vector$\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_m)}^T$, where$0\le {\omega }_j\le 1$and${\displaystyle \sum _{j=1}^m{\omega }_j}=1$, the generalized weighted distance of$H_s^1$and$H_s^2$is defined as

$$d_{gwd}(H_s^1,H_s^2)={\left[{\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}\right)}^{\lambda }}\right)}\right]}^{1/\lambda }$$

(10)

where$\lambda >0$. In particular, if$\lambda =1$, then Equation (10) is converted to the weighted Hamming distance:

$$d_{whd}(H_s^1,H_s^2)={\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}}\right)}$$

(11)

If$\lambda =2$, then Equation (10) is converted to the weighted Euclidean distance:

$$d_{wed}(H_s^1,H_s^2)={\left[{\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}\right)}^2}\right)}\right]}^{1/2}$$

(12)

Similarly, the generalized weighted similarity, weighted Hamming similarity and weighted Euclidean similarity between$H_s^1$and$H_s^2$can be expressed as

$${\rho }_{gwd}(H_s^1,H_s^2)=1-{\left[{\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}\right)}^{\lambda }}\right)}\right]}^{1/\lambda }$$

(13)

$${\rho }_{whd}(H_s^1,H_s^2)=1-{\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}}\right)}$$

(14)

$${\rho }_{wed}(H_s^1,H_s^2)=1-{\left[{\displaystyle \sum _{j=1}^m{\omega }_j\left(\frac{1}{L}{\displaystyle \sum _{l=1}^L{\left(\frac{\mid {\delta }_l^{1j}-{\delta }_l^{2j}\mid }{2\tau +1}\right)}^2}\right)}\right]}^{1/2}$$

(15)

2.3. Hesitant Fuzzy Linguistic Bonferroni Mean Operator

Definition 10

[31].Let$S=\{{\mathrm{s}}_t\mid \mathrm{t}=-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$be a finite and ordered discrete linguistic term set,$h_s(x_i)=\{s_t\mid t\in [-\tau ,\tau ]\}$be an HFLN and$H=\{\gamma \mid \gamma \in [0,1]\}$be a hesitant fuzzy set. The conversion function between the linguistic variable$s_t$and the membership degree$\gamma$is defined as follows:

$$g:[-\tau ,\tau ]\to [0,1] , g(s_t)=\frac{t}{2\tau }+\frac{1}{2}=\gamma$$

(16)

The image of the function$g(s_t)$ is

$$g:[-\tau ,\tau ]\to [0,1], g(h_s)=\left\{g(s_t)=\frac{t}{2\tau }+\frac{1}{2}\mid t\in [-\tau ,\tau ]\right\}=h_{\gamma }$$

(17)

Since$g(\tau )$is monotone, the inverse is obtained as follows:

$$g^{-1}:[0,1]\to [-\tau ,\tau ] , g^{-1}(\gamma )=s_{(2\gamma -1)\tau }=s_t$$

(18)

The image of the inverse function defined in Equation (18) is obtained as follows:

$$g^{-1}:[0,1]\to [-\tau ,\tau ] , g^{-1}(h_{\gamma })=\{g^{-1}(\gamma )=s_{(2\gamma -1)\tau }\mid \gamma \in [0,1]\}=h_s$$

(19)

Definition 11

[31].Let$p,q>0$, $h_{s_i}(i=1,2,\cdots ,m)$be a collection of HFLNs. Then, the hesitant fuzzy linguistic Bonferroni mean operator can be defined as

$$\begin{array}{l}HFL{B}^{p,q}(h_{s_1},h_{s_2},\cdots ,h_{s_m})\\ =g^{-1}\left({\left(\frac{1}{m(m-1)}\left(\underset{\underset{i\ne j}{i,j=1}}{\overset{m}{\oplus }}\left({\left(g(h_{s_i})\right)}^p\otimes {\left(g(h_{s_j})\right)}^q\right)\right)\right)}^{\frac{1}{p+q}}\right)\\ =\underset{{\xi }_{i,j}\in {\sigma }_{i,j},i\ne j}{\cup }\left\{g^{-1}\left({\left(1-{\displaystyle \prod _{\underset{i\ne j}{i,j=1}}^m{\left(1-{\xi }_{i,j}\right)}^{\frac{1}{m(m-1)}}}\right)}^{\frac{1}{p+q}}\right)\right\}\end{array}$$

(20)

where${\sigma }_{i,j}={\left(g(h_{s_i})\right)}^p\otimes {\left(g(h_{s_j})\right)}^q$reflects the interrelationship between$g(h_{s_i})$and$g(h_{s_j})$,$(i,j=1,2,\cdots ,m;i\ne j)$.

3. Hesitant Fuzzy Linguistic Agglomerative Hierarchical Clustering Algorithm

3.1. Agglomerative Hierarchical Clustering Algorithm

Agglomerative hierarchical clustering is a bottom-up strategy that treats each object as a cluster first, then merges these atomic clusters into larger and larger clusters until all objects are in a cluster or some terminal condition is satisfied. Most of the hierarchical clustering methods belong to this class, and they just differ in the definition of the similarity between clusters. The steps of the traditional agglomerative hierarchical clustering algorithm are as follows [32]:

• Step 1: Take a sample $A_i(i=1,2,\cdots ,n)$ as the initial set of clusters $A=\{A_1,A_2,\cdots ,A_n\}$. Then, calculate the distance $d(A_i,A_j), (A_i,A_j\in A)$ between each pair of clusters;
• Step 2: Find the minimum distance $d(A_p,A_q)=\arg {\min }_{A_i,A_j\in A}d(A_i,A_j)$, merge clusters $A_p$ and $A_q$ into a new cluster $A_r$ and generate a new set of clusters: $A^{\prime }=\left\{\left\{A_p,A_q\right\},A_k\mid k\ne p,q\right\}$;
• Step 3: Calculate the distance $d(A_r,A_l),(A_l\in A)$ between the new cluster $A_r$ and the other clusters. Repeat Step 2 until all samples cluster to the target category number.

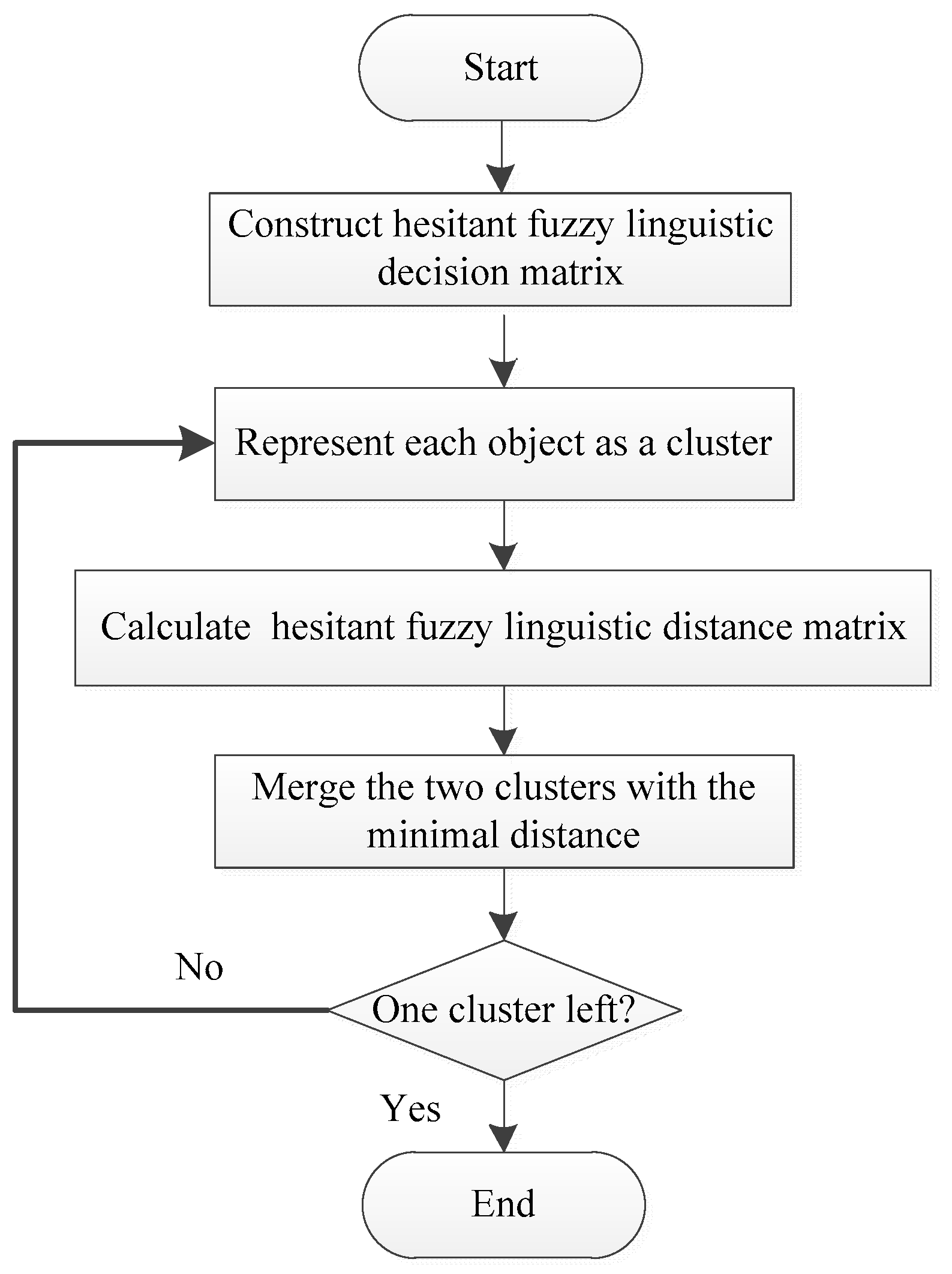
3.2. Hesitant Fuzzy Linguistic Agglomerative Hierarchical Clustering Algorithm

This paper proposes a hesitant fuzzy linguistic agglomerative hierarchical (HFLAH) clustering algorithm based on the above analysis. The algorithm flow is shown in Figure 1, and the specific implementation steps are as follows:

• Step 1: Supposing that the scheme set of a certain multi-attribute problem is $A=\{A_1,A_2,\cdots ,A_n\}$, then the attribute set is $X=\{x_1,x_2,\cdots ,x_m\}$, and the attribute weight vector is $\omega ={({\omega }_1,{\omega }_2,\cdots ,{\omega }_m)}^T$, satisfying $0\le {\omega }_j\le 1$ and ${\displaystyle \sum _{j=1}^m{\omega }_j}=1$. The decision-maker uses linguistic expressions or statements to evaluate the series of decision schemes $A_i$ under each attribute $x_j$. According to context-free grammar rules, the transformation function $E_{G_H}$ is used to transform the linguistic decision information into the HFLNs $h_s^{ij}=\{s_{{\delta }_l^{ij}}\mid l=1,\cdots ,L\}(i=1,2,\cdots ,n; \mathrm{j}=1,2,\cdots ,m)$, and the hesitant fuzzy linguistic decision matrix $H=(h_s^{ij}{)}_{n\times m}$ is obtained;
• Step 2: Take each object $A_i(i=1,2,\cdots ,n)$ as a class, and use Equations (11) or (12) to calculate the distance $d(A_i,A_j), (A_i,A_j\in A)$ between the classes. Then, get the hesitant fuzzy linguistic distance matrix $H_d=(d_s^{ij}{)}_{n\times n}$;
• Step 3: Find the minimum distance $d(A_p,A_q)=\arg {\min }_{A_i,A_j\in A}d(A_i,A_j)$ in the hesitant fuzzy linguistic distance matrix $H_d=(d_s^{ij}{)}_{n\times n}$, merge $A_p$ and $A_q$ into a new class $A_{pq}$ and calculate the center of class $A_{pq}$ using Equation (20);
• Step 4: Calculate the distance between the new class $A_{pq}$ and the other classes to obtain a new hesitant fuzzy linguistic distance matrix;
• Step 5: Repeat Steps 3 and 4 until all classes are grouped into one class.

4. Cluster Analysis of the Person Subjected to Execution Based on Hesitant Fuzzy Linguistic Decision Information

With the substantial increase in litigation cases, some useful legal documents cannot be implemented, which is referred to by people as difficult to execute. Unenforceable legal documents are called a mere scrap of paper. A person subjected to execution who can repay the debt but refuses to do so is called a deadbeat or laolai (a derogatory term in Chinese used for diehard debtors). The degree of realizing the legitimate rights and interests of the winning parties needs to be improved urgently. In many cases, the prominent phenomenon of hidden properties and limited human resources have become the prominent characteristics of problematic execution.

In judicial practice, the executive judge’s measures to the person subjected to execution mainly rely on the experience of handling cases, which is often restricted by subjective and objective factors such as cognitive bias, information asymmetry and personal bias. Many attributes of the executed person can only be evaluated qualitatively. The evaluation results of the possibility of concealing property by the person subjected to execution are presented in the form of linguistic expressions or statements. Avoiding the drawbacks of empirical judicature and scientifically representing the hesitation and qualitative decision information of executive judges is of great significance to improving decision-making.

4.1. Screening the Path of Concealment of Property by the Person Subjected to Execution

The quantitative probability of the concealed property was estimated based on the number of samples of laolai and non-laolai in the category to be identified. The specific screening steps for the person subjected to execution for concealing property are as follows:

• Step 1: Suppose that the executive judge needs to judge the possibility of concealing property for $n$ persons subjected to execution $A_i(i=1,2,\cdots ,n)$, respectively. $A_j(j=1,2,\cdots ,m)$ is the sample of $m$ representative persons subjected to execution extracted by the executive judge from the case database of court enforcement, among which the sample number of persons subjected to execution (laolai) who have concealed property behavior is $m/2$;
• Step 2: According to the behavior characteristics of the concealment of property by the person subjected to execution, the executive judges use linguistic expressions or statements to conduct a multidimensional evaluation of $m+n$ persons subjected to execution and give corresponding hesitant fuzzy linguistic decision information;
• Step 3: $k(k=1,2,\cdots ,n)$ samples to be identified are added to the known sample $A_j(j=1,2,\cdots ,m)$ of m subjects to perform fuzzy clustering on $m+k$ subjects $A_j(j=1,2,\cdots ,m+k)$. To improve the accuracy of clustering and discrimination, it is assumed that one sample $A_i$ of the subject to be identified is added to m known samples at a time, and then fuzzy clustering is carried out for these $m+1$ subjects $A_j(j=1,2,\cdots ,m+1)$;
• Step 4: According to the clustering results, $A_j(j=1,2,\cdots ,m+1)$ is divided into classes $C_{\gamma }(\gamma =1,2,\cdots ,m+1)$. If the subject $A_i$ belongs to class $C_{\gamma }$, the sample number of laolai individuals in $C_{\gamma }$ is $u$, and the sample number of non-Laolai individuals is $v$. Then, the quantified probability of the subject $A_i$ concealing property can be expressed as $u/(u+v)$;
• Step 5: Repeat Steps 3 and 4 until the quantified probability value of the concealed property of the subject $A_i(i=1,2,\cdots ,n)$ to be identified is obtained in turn. The greater the probability value is, the greater the concealed property’s possibility, and the greater the corresponding control force is. According to the reasonable allocation of execution resources, complete the classification of the person under execution.

4.2. Numerical Example

Assume that there are four samples $A_i(i=1,2,3,4)$ of the person subjected to execution. It is known that the persons $A_1$ and $A_4$ have hidden property involved, and the persons $A_2$ and $A_3$ have no property available for execution. Now it is necessary to distinguish the possibility of the person $A_{\ast }$ subjected to execution concealing property. According to the evaluation system of the person subjected to execution’s behavior characteristics, the executive judge conducted a multidimensional comprehensive evaluation on the possibility of five persons subjected to execution $A_i(i=1,2,3,4,\ast )$ concealing property. The evaluation dimension mainly considers three attributes of the person subjected to execution. The first is a demographic attribute ($x_1$), which includes the five subattributes of age ($x_{11}$), gender ($x_{12}$), education ($x_{13}$), occupation ($x_{14}$) and relatives ($x_{15}$). The second is the behavior attribute ($x_2$), which includes the three subattributes of typical performance ($x_{21}$), consumption habits ($x_{22}$) and trading behavior ($x_{23}$). The third is the credit attribute ($x_3$), which includes two subattributes: personal credit ($x_{31}$) and judicial proceedings ($x_{32}$). The attribute weight vector is given as $\omega ={(0.25,0.38,0.37)}^T$. The linguistic term set corresponding to the attribute is $S=\{s_{-3}=non-Laolai,s_{-2}=very small,s_{-1}=smaller,s_0=medium,s_1=larger,s_2=very large,s_3=Laolai\}$. According to the linguistic term set $S$ and the context-free grammar $G_H$, the executive judge uses the linguistic expression to give the corresponding evaluation information, as shown in

Table 1. The evaluation results given by the executive judge in linguistic expressions.

Person Subjected to Execution	Attributes
	$x_1$	$x_2$	$x_3$
$A_1$	Between very small and smaller	Greater than very large	Between smaller and medium
$A_2$	At least very large	Between smaller and medium	Smaller
$A_3$	Larger	At most very small	Very small
$A_4$	Between smaller and medium	Lower than very small	Very large
$A_{\ast }$	Very large	Between medium and larger	At least larger

.

• Step 1: According to the conversion function $E_{G_H}$, the following hesitant fuzzy linguistic evaluation matrix $H_1=(h_s^{ij}{)}_{5\times 3}$ can be generated:

  $$H_1=\left(\begin{array}{ccc}\{s_{-2},s_{-1}\}& \left\{s_3\right\}& \{s_{-1},s_0\}\\ \{s_2,s_3\}& \{s_{-1},s_0\}& \left\{s_{-1}\right\}\\ \left\{s_1\right\}& \{s_{-3},s_{-2}\}& \left\{s_{-2}\right\}\\ \{s_{-1},s_0\}& \left\{s_{-3}\right\}& \left\{s_2\right\}\\ \left\{s_2\right\}& \{s_0,s_1\}& \{s_1,s_2,s_3\}\end{array}\right)$$

  (21)
  To calculate the distance between two HFLTSs more accurately, the HFLTSs with fewer elements add linguistic terms by Equation (3). The following standardized hesitant fuzzy linguistic evaluation matrix $H_2=(h_s^{ij}{)}_{5\times 3}$ can be obtained:

  $$H_2=\left(\begin{array}{ccc}\{s_{-2},s_{-1}\}& \{s_3,s_3\}& \{s_{-1},s_{-0.5},s_0\}\\ \{s_2,s_3\}& \{s_{-1},s_0\}& \{s_{-1},s_{-1},s_{-1}\}\\ \{s_1,s_1\}& \{s_{-3},s_{-2}\}& \{s_{-2},s_{-2},s_{-2}\}\\ \{s_{-1},s_0\}& \{s_{-3},s_{-3}\}& \{s_2,s_2,s_2\}\\ \{s_2,s_2\}& \{s_0,s_1\}& \{s_1,s_2,s_3\}\end{array}\right)$$

  (22)
• Step 2: Take each executed person $A_i(i=1,2,3,4,\ast )$ as classes $\left\{A_1\right\}$, $\left\{A_2\right\}$, $\left\{A_3\right\}$, $\left\{A_4\right\}$ and $\left\{A_{\ast }\right\}$, and calculate the distance between the classes by using Equation (12) to get the hesitant fuzzy linguistic distance matrix $H_3=(d_s^{ij}{)}_{5\times 5}$:

  $$H_3=\left(\begin{array}{ccccc}0.0000& 0.3496& 0.4450& 0.4878& 0.3530\\ 0.3496& 0.0000& 0.1917& 0.3636& 0.2826\\ 0.4450& 0.1917& 0.0000& 0.3632& 0.4193\\ 0.4878& 0.3636& 0.3632& 0.0000& 0.3029\\ 0.3530& 0.2826& 0.4193& 0.3029& 0.0000\end{array}\right)$$

  (23)
• Step 3: In the hesitant fuzzy linguistic distance matrix $H_3$, the minimum distance is $d(A_2,A_3)=0.1917$. Therefore, $\left\{A_2\right\}$ and $\left\{A_3\right\}$ are merged into a new class, and the subjects $A_i(i=1,2,3,4,\ast )$ are divided into four classes: $\left\{A_1\right\}$, $\{A_2,A_3\}$, $\left\{A_4\right\}$ and $\left\{A_{\ast }\right\}$. Use Equation (20) to calculate the center of each new class:

  $$c\{A_2,A_3\}=A_{23}=HFL{B}^{1,0}(h_s^2,h_s^3)=\{<x_1,\{s_{1.59},s_3\}>,<x_2,\{s_{-1.9},s_{-1.2},s_{-1},s_{-0.5}\}>,<x_3,\left\{s_{-1.5}\right\}>\}$$

  (24)

  $$c\left\{A_1\right\}=A_1, c\left\{A_4\right\}=A_4, c\left\{A_{\ast }\right\}=A_{\ast }$$

  (25)
  By adding linguistic terms to the HFLTSs with fewer elements, a standardized hesitant fuzzy linguistic evaluation matrix $H_4=(h_s^{ij}{)}_{4\times 3}$ can be obtained:

  $$H_4=\left(\begin{array}{ccc}\{s_{-2},s_{-1}\}& \{s_3,s_3,s_3,s_3\}& \{s_{-1},s_{-0.5},s_0\}\\ \{s_{1.59},s_3\}& \{s_{-1.9},s_{-1.2},s_{-1},s_{-0.5}\}& \{s_{-1.5},s_{-1.5},s_{-1.5}\}\\ \{s_{-1},s_0\}& \{s_{-3},s_{-3},s_{-3},s_{-3}\}& \{s_2,s_2,s_2\}\\ \{s_2,s_2\}& \{s_0,s_{0.5},s_{0.5},s_1\}& \{s_1,s_2,s_3\}\end{array}\right)$$

  (26)
• Step 4: Calculate the distance between class $\{A_2,A_3\}$ and classes $\left\{A_1\right\}$, $\left\{A_4\right\}$ and $\left\{A_{\ast }\right\}$, respectively, and get $d(A_1,A_{23})=0.4885$, $d(A_{23},A_4)=0.3965$ and $d(A_{23},A_{\ast })=0.3502$. The updated hesitant fuzzy linguistic distance matrix is $H_5=(d_s^{ij}{)}_{4\times 4}$:

  $$H_5=\left(\begin{array}{cccc}0.0000& 0.4885& 0.4878& 0.3530\\ 0.4885& 0.0000& 0.3965& 0.3577\\ 0.4878& 0.3965& 0.0000& 0.3029\\ 0.3530& 0.3577& 0.3029& 0.0000\end{array}\right)$$

  (27)
• Step 5: In the hesitant fuzzy linguistic distance matrix $H_5$, the minimum distance is $d(A_4,A_{\ast })=0.3029$. Therefore, $\left\{A_4\right\}$ and $\left\{A_{\ast }\right\}$ are merged into a new class, $\{A_4,A_{\ast }\}$, and the subjects $A_i(i=1,2,3,4,\ast )$ are divided into the following three categories: $\left\{A_1\right\}$, $\{A_2,A_3\}$ and $\{A_4,A_{\ast }\}$. Use Equation (14) to calculate the center of each new class:

  $$\begin{gathered} c\left\{A_1\right\}=A_1, c\{A_2,A_3\}=A_{23}, \\ c\{A_4,A_{\ast }\}=A_{4\ast }=HFL{B}^{1,0}(h_s^4,h_s^{\ast })=\{<x_1,\{s_1,s_{1.3}\}>,<x_2,\left\{s_3\right\}>,<x_3,\{s_{1.6},s_2,s_3\}>\} \end{gathered}$$

  (28)

The standardized hesitant fuzzy linguistic evaluation matrix is $H_6=(h_s^{ij}{)}_{3\times 3}$:

$$H_6=\left(\begin{array}{ccc}\{s_{-2},s_{-1}\}& \{s_3,s_3,s_3,s_3\}& \{s_{-1},s_{-0.5},s_0\}\\ \{s_{1.59},s_3\}& \{s_{-1.9},s_{-1.2},s_{-1},s_{-0.5}\}& \{s_{-1.5},s_{-1.5},s_{-1.5}\}\\ \{s_1,s_{1.3}\}& \{s_3,s_3,s_3,s_3\}& \{s_{1.6},s_2,s_3\}\end{array}\right)$$

(29)

The distance between class $\{A_4,A_{\ast }\}$ and classes $\left\{A_1\right\}$ and $\{A_2,A_3\}$ is calculated as $d(A_1,A_{4\ast })=0.2823$ and $d(A_{23},A_{4\ast })=0.5405$, respectively. Then, the updated hesitant fuzzy linguistic distance matrix is $H_7=(d_s^{ij}{)}_{3\times 3}$:

$$H_7=\left(\begin{array}{ccc}0.0000& 0.4885& 0.2823\\ 0.4885& 0.0000& 0.5405\\ 0.2823& 0.5405& 0.0000\end{array}\right)$$

(30)

According to the hesitant fuzzy linguistic distance matrix $H_7$, it is easy to know that the minimum distance is $d(A_1,A_{4\ast })=0.2823$, so $\left\{A_1\right\}$ and $\{A_4,A_{\ast }\}$ are merged into a new class, $\{A_1,A_4,A_{\ast }\}$. So far, $A_i(i=1,2,3,4,\ast )$ has been divided into two categories: $\{A_1,A_4,A_{\ast }\}$ and $\{A_2,A_3\}$.

Finally, $\{A_1,A_4,A_{\ast }\}$ and $\{A_2,A_3\}$ can be further merged into a class, $\{A_1,A_2,A_3,A_4,A_{\ast }\}$, and the clustering ends here. The process of HFLAH clustering is shown in Figure 2.

The clustering results show that the executed person $A_{\ast }$ was classified as class $C_2$, and it is known that the executed person $A_1$ in this class had the behavior of concealing property while $A_4$ did not conceal property. Therefore, the quantified probability of the executed person $A_{\ast }$ concealing property was 50%. When the number of samples was large, if the sample number of the person subjected to execution (laolai) who had the act of concealing property in $C_2$ was $u$, the sample number of the person subjected to execution (non-laolai) who did not have the act of concealing property was $v$. Then, the quantified probability of the executed person $A_{\ast }$ concealing the property was $u/(u+v)$, and the greater the probability value, the greater the possibility of the person subjected to execution $A_{\ast }$ concealing property.

The clustering results show the effectiveness of the concealed property behavior evaluation system and the clustering algorithm, especially when the number of cases was large, as scientific cluster analysis of the person subjected to execution could effectively help the executive judge objectively determine the focus of the investigation and control, which is conducive to improving the execution’s quality and efficiency.

4.3. Contrastive Analysis

Inspired by the intuitionistic fuzzy clustering algorithm based on the Boole matrix proposed by Xu [33], we further propose the hesitant fuzzy linguistic Boole matrix (HFLBM) clustering algorithm. The HFLBM clustering algorithm was used to analyze the above examples, and the result of the HFLBM clustering algorithm was compared with that of the HFLAH clustering algorithm. Some basic definitions follow:

Definition 12

[33].Let$A=\{A_1,A_2,\cdots ,A_n\}$be a collection of$n$HFLTSs. Then,$\rho ={({\rho }_{ij})}_{n\times n}$is called a hesitant fuzzy linguistic similarity matrix, where the hesitant fuzzy linguistic similarity measure${\rho }_{ij}=\rho (A_i,A_j)$satisfies the following properties:

• $0\le {\rho }_{ij}\le 1$for all$i,j=1,2,\cdots ,n$;
• ${\rho }_{ij}=1$if and only if$A_i=A_j$;
• ${\rho }_{ij}={\rho }_{ji}$for all$i,j=1,2,\cdots ,n$.

Definition 13

[33].Let$\rho ={({\rho }_{ij})}_{n\times n}$be a hesitant fuzzy linguistic similarity matrix. Then,$\rho$satisfies the following:

• $\rho$is reflexive (i.e.,$I\subseteq \rho$);
• $\rho$is symmetric (i.e.,${\rho }^T=\rho$);
• $\rho$is transitive (i.e.,${\rho }^2\subseteq \rho$).

Then,$\rho ={({\rho }_{ij})}_{n\times n}$is called an equivalent hesitant fuzzy linguistic similarity matrix, where${\rho }^2=\rho \circ \rho ={({\stackrel{-}{\rho }}_{ij})}_{n\times n}$is a composition matrix of$\rho$, whose element${\stackrel{-}{\rho }}_{ij}$satisfies${\stackrel{-}{\rho }}_{ij}=\max \left\{\underset{k}{\min }\right\{{\rho }_{ik},{\rho }_{ki}\left\}\right\}$,$i,j=1,2,\cdots ,n$.

Definition 14

[33].Let$\rho ={({\rho }_{ij})}_{n\times n}$be a hesitant fuzzy linguistic similarity matrix. Then, we call${\rho }_{\lambda }={\left({\rho }_{ij}^{\lambda }\right)}_{n\times n}$the$\lambda$-cutting matrix of$\rho$:

$${\rho }_{ij}^{\lambda }=\{\begin{array}{ll}0,& {\rho }_{ij}<\lambda \\ 1,& {\rho }_{ij}\ge \lambda \end{array} (i,j=1,2,\cdots ,n)$$

(31)

where$\lambda$is the confidence level with$\lambda \in [0,1]$.

Definition 15

[33].Let$\rho$be a Boole matrix. Then,$\rho$is an equivalent Boole matrix if and only if$\rho$does not have the following special sub-matrices:

$$\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right),\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right),\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)$$

(32)

According to the above definition, the concrete implementation steps of the HFLBM clustering algorithm are as follows:

• Step 1: Assume that $A=\{A_1,A_2,\cdots ,A_n\}$ is the set of clustering objects. Use Equations (14) or (15) to calculate the similarity between classes, and the hesitant fuzzy linguistic similarity matrix $\rho ={({\rho }_{ij})}_{n\times n}$ is obtained;
• Step 2: Given the confidence level $\lambda$, the $\lambda$-cutting matrix ${\rho }_{\lambda }={\left({\rho }_{ij}^{\lambda }\right)}_{n\times n}$ is constructed by Equation (31);
• Step 3: Judge whether ${\rho }_{\lambda }$ is an equivalent Boole matrix. If ${\rho }_{\lambda }$ is an equivalent Boole matrix, skip to Step 4. If not, then ${\rho }_{\lambda }$ exists as a special submatrix in Definition 1 under a particular arrangement. In this case, as long as the 0 of the special submatrices is changed to 1, until no unique form of the submatrices is produced, then a new equivalent Boole matrix ${\rho }_{\lambda }^{\ast }$ can be obtained;
• Step 4: If all the elements in row $i$ (column) and row $j$ (column) in ${\rho }_{\lambda }$ are the same, then the cluster objects $A_i$ and $A_j$ can be combined into one class. According to the principle, the $n$ objects $A_i(i=1,2,\cdots n)$ are classified.

By using the above HFLBM clustering algorithm to cluster the person subjected to execution $A_i(i=1,2,3,4,\ast )$, the similarity matrix $\rho$ can be obtained:

$$\rho =\left(\begin{array}{ccccc}1.0000& 0.6504& 0.5550& 0.5122& 0.6470\\ 0.6504& 1.0000& 0.8083& 0.6364& 0.7174\\ 0.5550& 0.8083& 1.0000& 0.6368& 0.5807\\ 0.5122& 0.6364& 0.6368& 1.0000& 0.6971\\ 0.6470& 0.7174& 0.5807& 0.6971& 1.0000\end{array}\right)$$

(33)

The clustering process is shown in Figure 3.

The clustering results of the two clustering algorithms are shown in

Table 2. The clustering results obtained by different algorithms.

Clusters	HFLAH Clustering Algorithm	HFLBM Clustering Algorithm
5	$\left\{A_1\right\}$,$\left\{A_2\right\}$,$\left\{A_3\right\}$,$\left\{A_4\right\}$,$\left\{A_{\ast }\right\}$	$\left\{A_1\right\}$,$\left\{A_2\right\}$,$\left\{A_3\right\}$,$\left\{A_4\right\}$,$\left\{A_{\ast }\right\}$
4	$\left\{A_1\right\}$,$\{A_2,A_3\}$,$\left\{A_4\right\}$,$\left\{A_{\ast }\right\}$	$\left\{A_1\right\}$,$\{A_2,A_3\}$,$\left\{A_4\right\}$,$\left\{A_{\ast }\right\}$
3	$\left\{A_1\right\}$,$\{A_2,A_3\}$,$\{A_4,A_{\ast }\}$	$\left\{A_1\right\}$,$\{A_2,A_3,A_{\ast }\}$,$\left\{A_4\right\}$
2	$\{A_1,A_4,A_{\ast }\}$,$\{A_2,A_3\}$	$\left\{A_1\right\}$,$\{A_2,A_3,A_4,A_{\ast }\}$
1	$\{A_1,A_2,A_3,A_4,A_{\ast }\}$	$\{A_1,A_2,A_3,A_4,A_{\ast }\}$

.

By comparison, it can be seen that when the classification number was $\gamma (\gamma =1,2,5)$, the classification results of the two algorithms were identical. When the classification number was $\gamma (\gamma =3,4)$, the classification results of the two algorithms were different. The reason for this is that the HFLAH clustering algorithm was based on the distance measure of the hesitant fuzzy linguistic term sets and the integrated operation of the hesitant fuzzy linguistic information. In contrast, the HFLBM clustering algorithm was based on the similarity measure of the hesitant fuzzy linguistic term sets and the Boole matrix. The clustering principles of the two algorithms are different. Both of the two clustering algorithms have a small amount of computation and cannot lose the decision information. Therefore, both of them can effectively cluster the hesitant fuzzy linguistic data.

5. Conclusions

To avoid the drawbacks of empirical judicature and improve the quality and efficiency of execution, this paper applied the clustering idea of birds of a feather flock together to the field of judicial execution. It proposed a method for the evaluation of the concealed property behavior of a person subjected to execution. Given the executive judge’s fuzzy uncertainty in screening the property behavior involved in concealment, the executive judge’s qualitative decision information is represented by the hesitant fuzzy linguistic term sets. The data type of clustering is extended to the hesitant fuzzy linguistic information, and an HFLAH clustering algorithm and HFLBM clustering algorithm are proposed. The evaluation method’s effectiveness and the clustering algorithm were verified by the process of clustering analysis of the executors under the background of hesitant fuzzy linguistic decision information. The hesitant fuzzy linguistic clustering algorithms effectively avoided losing decision information and improved the clustering accuracy and decision quality. The cluster analysis results provided decision support for the executive judge to scientifically and objectively determine the focus of the investigation and control, reduce the judicial cost and have specific practical significance and application value.

Due to the limitation of the objective conditions, the sample size of the subjects used for clustering analysis in this paper was small. Only the running process of the clustering algorithm was demonstrated. The research conclusion may be relatively one-sided, and the research results can be further improved on the premise of a sufficient data sample size in the future.