Life Insurance and Subsistence Consumption with an Exponential Utility

Abstract

In this paper, we derive an explicit solution to the utility maximization problem of an individual with mortality risk and subsistence consumption constraint. We adopt an exponential utility for the individual’s consumption and the martingale and duality method is employed. From the explicit solution, we exhibit how the mortality intensity and subsistence consumption constraint affect, separately and together, portfolio, consumption and life insurance purchase.

1. Introduction

In portfolio selection problems, considering some constraints create difficulties in solving the relevant optimization problems but increase the realism. Borrowing constraints restrict individual’s financing only up to a partial amount of the individual’s human capital or do not allow any amount of borrowing. Borrowing constraints lead individual to reduce investment in the risky asset and to decrease consumption. Mathematical finance literature that mainly focuses on the effects of partial borrowing constraints on optimal decisions for individuals includes [2,3,5,15,16,17]. References [12,14] consider the case where an individual cannot borrow against future labor income at all, and especially the last one investigates how the borrowing constraints and job choice flexibility affect on portfolio selection and consumption.

Subsistence consumption constraints imply that an individual must consume at least a minimum level of consumption rate, for example a minimum level of consumption rate required to keep up life. Subsistence consumption constraints also have significant effects on the optimal decisions for individuals. Restrictions on subsistence level of consumption also make an individual’s portfolio strategy less aggressive and leads decrease in consumption. References [4,18,19] study an infinitely lived individual’s consumption, portfolio strategies while considering subsistence consumption constraints. Working individuals who face subsistence consumption decide retirement wealth levels differently from those who do not have such restrictions, as the analytical results from [6,9,10,11,13] imply.

This paper is an extension of literature that investigates how the existence of subsistence consumption constraints affect individual’s lifetime investment and consumption strategy. We assume an exponential utility function for consumption and consider an individual’s mortality risk by adopting an exponential distribution for the death time. Based on martingale and duality method, we derive optimal consumption, portfolio, and life insurance strategies explicitly and exhibit how the force of mortality and subsistence level of consumption affect, separately and together, on the individual’s decision making. Numerical illustrations reveal that a strong force of mortality and a high subsistence level of consumption result in reduced consumption and small investment in the risky asset. Numerical illustrations also show that life insurance demand increases with force of mortality and decreases with subsistence level of consumption. However, the effect of subsistence consumption constraint on demand for life insurance seems to be marginal. We also observe that an individual with a large coefficient of absolute risk aversion purchases more life insurance.

This paper proceeds as follows. Section 2 introduces financial and life insurance markets and our model. The utility function and the optimization problem we seek to solve is defined in Section 3, followed by Section 4 where we use the martingale and duality method to obtain explicit solution to the optimization problem. Section 5 illustrates numerical examples from which we examine effectcs of force of mortality and subsistence consumption constraint on an individual’s decision making, and Section 6 sums up and concludes.

2. The Market and Model

We assume that the individual participates in the financial market and can hedge the mortality risk. The financial market is simply consists of a risky asset and a riskless asset (money market account). The risk factor of the risky asset and that of mortality are uncorrelated. Denote by ${\left(W_t\right)}_{t\ge 0}$ a standard Brownian motion for a given probability space $(\Omega ,\mathcal{F},\mathbb{P})$. The individual’s death time $\tau$ has an exponential distribution with the parameter $\lambda >0$, called mortality intensity or force of mortality. The probability density function $f_{\tau }\left(t\right)$ of $\tau$ is given by

$$f_{\tau }\left(t\right)=\lambda e^{-\lambda t},t\ge 0.$$

Denote by $\mathbb{F}\triangleq {\left({\mathcal{F}}_t\right)}_{t\ge 0}$ the $\mathbb{P}$-augmentation of filtration generated by the standard Brownian motion ${\left(W_t\right)}_{t\ge 0}$ and ${\mathbf{1}}_{\{t\le {\tau }_d\}}$. In financial markets, there exist a riskless asset and a risky asset whose prices are $M_t$ and $S_t$ at time t, respectively.

At time $t\ge 0$, the risky asset price $S_t$ follows a log-normal distribution as follows

$$d{S}_t/S_t=\mu dt+\sigma d{W}_t,$$

where $\mu >0$ and $\sigma >0$. The risky asset’s mean rate of return per unit time, $\mu$, and its volatility $\sigma$ are assumed to be constants. The riskless asset price $M_t$ is assumed to follows

$$d{M}_t/M_t=rdt,$$

where $r<\mu$ is the risk free interest rate and it is also constant.

Let ${\pi }_t$ be the amount of money invested in the risky asset. If

$${\int }_0^t{\pi }_t^{2}dt<\infty \mathrm{for all}t\ge 0\mathrm{a}.\mathrm{s}.,$$

(1)

and if $\mathbf{\pi }\triangleq {\left({\pi }_t\right)}_{t\ge 0}$ is $\mathbb{F}$- adapted, we call $\mathbf{\pi }$ a portfolio process. In this paper, we consider the case where the individual has a subsistence consumption constraint. We call the minimum consumption rate the individual must consume the subsistence level of consumption $R>0$. If $c_t$ is the consumption rate at time t, it is satisfied that

$$c_t\ge R,0\le t\le \tau .$$

If

$${\int }_0^t{c}_{t}dt<\infty ,c_t\ge R,\mathrm{for all}0\le t\le \tau \mathrm{a}.\mathrm{s}.,$$

and $\mathbf{c}\triangleq {\left(c_t\right)}_{t\ge 0}$ is $\mathbb{F}$, we call $\mathbf{c}\triangleq {\left(c_t\right)}_{t\ge 0}$ a consumption process.

We assume that life insurance contracts we are considering cover mortality risk and they are actuarially fair. We denote by $p_t$ and $L_t$ the instantaneous life insurance premium rate paid by the individual and insurance benefit paid by the insurer, respectively. Since the life insurance contracts are fair, the insurance premium paid by the policyholder during the infinitesimal time $dt$ is equal to the insurance benefit multiplied by the probability of death during the infinitesimal time $dt$. Thus we have

$$p_t=\lambda L_t,$$

and the bequest $B_t$ received by the individual’s heir is given by

$$B_t=X_t+L_t=X_t+p_t/\lambda ,$$

(2)

where $X_t$ is the wealth level. The individual’s labor income rate is constantly $y>0$. Thus, we have the following wealth level process

$$\begin{array}{cc}\hfill d{X}_t& =(X_t-{\pi }_t)\frac{d{M}_t}{M_t}+(y-c_t-p_t)dt+{\pi }_t\frac{d{S}_t}{S_t}\hfill \\ \hfill & =\left\{r{X}_t+y-c_t-p_t+{\pi }_t(\mu -r)\right\}dt+\sigma {\pi }_{t}d{W}_t\hfill \\ \hfill & =\left\{(r+\lambda )X_t+y+{\pi }_t(\mu -r)-c_t-\lambda B_t\right\}dt+\sigma {\pi }_{t}d{B}_t,0\le t\le \tau ,\hfill \end{array}$$

(3)

where the 3rd equality follows from (2). A control variable $p_t$ is replaced by the bequest $B_t$. We say the $\mathbf{B}\triangleq {\left(B_t\right)}_{t\ge 0}$ the bequest process if it is $\mathbb{F}$- adapted and satisfies

$${\int }_0^t{B}_{t}dt<\infty ,\mathrm{for}\mathrm{all}t\ge 0a.s..$$

3. Utility Function and the Optimization Problem

While living, the individual enjoys from consumption and its utility function is given by an exponential form as follows

$$u\left(c\right)=-\frac{1}{\alpha }{e}^{-\alpha c},\alpha >0.$$

This type of utility is called the constant absolute risk aversion (CARA) utility and we call $\alpha$ the coefficient of absolute risk aversion. We assume that the utility of bequest is given by a constant relative risk aversion (CRRA) utility

$$V_B\left(x\right)=K\frac{x^{1-\gamma }}{1-\gamma },\gamma >0,\gamma \ne 1,K>0,$$

where $\gamma$ is the coefficient of relative risk aversion of the utility of bequest and K is the bequest motive which measures the importance of the utility of bequest (See [7]). Therefore, the individual’s lifetime discounted expected utility is given by

$$\begin{array}{cc}\hfill J(x;c,\mathbf{\pi },\mathbf{B})& \triangleq \mathbb{E}\left[{\int }_0^{\tau }{e}^{-\beta t}u\left(c_t\right)dt+e^{-\beta \tau }{V}_B\left(B_{\tau }\right)\right]\hfill \\ \hfill & =\mathbb{E}\left[{\int }_0^{\infty }{e}^{-(\beta +\lambda )t}u\left(c_t\right)dt+\lambda {\int }_0^{\infty }{e}^{-(\beta +\lambda )t}{V}_B\left(B_t\right)dt\right],\hfill \end{array}$$

(4)

where $\beta$ is the time preference of the individual. The expected discounted future income is given by

$$\mathbb{E}{\int }_0^{\tau }{e}^{-rt}ydt=\frac{y-R}{r+\lambda },$$

which is the maximum amount of money (considering subsistence level of consumption) the individual can finance if there is no restriction on borrowing. We call $\left(\mathbf{\pi },\mathbf{c},\mathbf{B}\right)$ admissible at $X_0=x\ge -(y-R)/(r+\lambda )$ if $X_t$ of (3) satisfies

$$X_t\ge -\frac{y-R}{r+\lambda },\mathrm{for all}t\le {\tau }_d\mathrm{a}.\mathrm{s}.$$

(5)

Now we formulate the individual’s optimization problem. For a given initial wealth $X_0=x\ge -(y-R)/(r+\lambda )$, the objective is to select the control $(\mathbf{c},\mathbf{\pi },\mathbf{B})\in \mathcal{A}$ for finding out the value function $V\left(x\right)$, which is defined as follows

$$\begin{array}{c}\hfill V\left(x\right)=\underset{\left(\mathbf{c},\mathbf{\pi },B\right)\in \mathcal{A}\left(x\right)}{max}J(x;\mathbf{c},\mathbf{\pi },\mathbf{B}),\end{array}$$

(6)

where $\mathcal{A}\left(x\right)$ the set of all admissible controls at x.

4. The Martingale Method and the Solution

A dynamic programming method can be applied to solve the optimization problem (6). However, the value function’s Bellman equation relevant to this problem is highly nonlinear. We use the martingale and duality method to convert the primal optimization problem into a dual maximization problem which solves a linear equation. Let us define the market price of risk $\theta$ and the state price density $H_t$ as follows

$$\theta \triangleq \frac{\mu -r}{\sigma },H_t\triangleq e^{-(r+\lambda )t}{e}^{-\frac{1}{2}{\theta }^{2}t-\theta W_t},$$

respectively. Applying the Itô’s lemma to the product of $e^{-(r+\lambda )t}$ and $\left(X_t+y/(r+\lambda )\right)$, which is lower bounded if (5) is satisfied, and with monotone convergence theorem we derive the following static budget constraint

$$\begin{array}{c}\hfill \mathbb{E}\left[{\int }_0^{\infty }{H}_t\left(c_t+\lambda B_t\right)dt\right]\le x+\frac{y}{r+\lambda },\end{array}$$

(7)

for any $\left(\mathbf{c},\mathbf{\pi },\mathbf{B}\right)\in \mathcal{A}\left(x\right)$.

To construct the dual value functioin of $V\left(x\right)$, let us define a convex dual function $\tilde{u}(·)$ of $u(·)$ as follows

$$\tilde{u}\left(z\right)\triangleq \underset{c\ge R}{max}\left[u\left(c\right)-zc\right],z>0.$$

(8)

So the convex dual function $\tilde{u}\left(z\right)$ is given by

$$\begin{array}{cc}\hfill \tilde{u}\left(z\right)& =\frac{z}{\alpha }\left[logz-1\right]{\mathbf{1}}_{\{0<z<\tilde{z}\}}-\left[\frac{1}{\alpha }+Rz\right]{\mathbf{1}}_{\{z\ge \tilde{z}\}},\tilde{z}=e^{-R\alpha },\hfill \end{array}$$

with the maximizing $c=c^{*}\left(z\right)$ is given by

$$c^{*}\left(z\right)\triangleq -\frac{1}{\alpha }logz{\mathbf{1}}_{\{0<z<\tilde{z}\}}+R{\mathbf{1}}_{\{z\ge \tilde{z}\}}.$$

(9)

Analogously, we define a convex dual function $\widetilde{V_B}(·)$ of $V_B(·)$ as follows

$$\widetilde{V_B}\left(z\right)\triangleq \underset{B\ge 0}{max}\left[V_B\left(B\right)-zB\right],z>0.$$

(10)

Thus we have

$$\begin{array}{cc}\hfill \widetilde{V_B}\left(z\right)& =\frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}{z}^{\frac{\gamma -1}{\gamma }},z>0,\hfill \end{array}$$

where the maximizing $B=B^{*}\left(z\right)$ is given by

$$B^{*}\left(z\right)\triangleq {\left(\frac{z}{K}\right)}^{-\frac{1}{\gamma }}>0.$$

By the definitions of $\tilde{u}\left(z\right)$ and $\widetilde{V_B}\left(z\right)$ and the static budget constraint (7), for any control $\left(\mathbf{c},\mathbf{\pi },\mathbf{B}\right)\in \mathcal{A}\left(x\right)$ and any $z>0$, we have

$$\begin{array}{c}\hfill J(x;\mathbf{c},\mathbf{\pi },\mathbf{B})\le \mathrm{\Phi }(x;z),\end{array}$$

(11)

where

$$\mathrm{\Phi }(x;z)\triangleq \mathbb{E}\left[{\int }_0^{\infty }{e}^{-(\beta +\lambda )t}\left\{\tilde{u}\left(z_t\right)+\lambda \widetilde{V_B}\left(z_t\right)\right\}dt\right]+z\left(x+\frac{y}{r+\lambda }\right),$$

(12)

and $z_t\triangleq z{e}^{(\beta +\lambda )t}{H}_t$.

We call ${\Phi }(x;z)$ the dual value function. The following duality relation between $V\left(x\right)$ and ${\Phi }(x;z)$ is due to Theorem 1 of [8]

Lemma 1.

If $z^{*}>0$ is the solution to the following minimization problem

$$\underset{z>0}{min}{\Phi }(x;z),$$

then the value function $V\left(x\right)$ of the primal maximization problem (6) is given by

$$V\left(x\right)={\Phi }(x;z^{*})=\underset{z>0}{min}{\Phi }(x;z).$$

(13)

For the pair $\left({\mathbf{c}}^{x,z^{*}},{\mathbf{B}}^{x,z^{*}}\right)$ of consumption and bequest processes given by

$$c_t^{x,z^{*}}=c^{*}\left(z_t^{z^{*}}\right),B_t^{x,z^{*}}=B^{*}\left(z_t^{z^{*}}\right),$$

(14)

where $z_t^{z^{*}}=z^{*}{e}^{(\beta +\lambda )t}{H}_t$, there exists a portfolio process ${\mathbf{\pi }}^{x,z^{*}}$ such that $\left({\mathbf{c}}^{x,z^{*}},{\mathbf{\pi }}^{x,z^{*}},{\mathbf{B}}^{x,z^{*}}\right)\in \mathcal{A}\left(x\right)$ and $\left({\mathbf{c}}^{x,z^{*}},{\mathbf{\pi }}^{x,z^{*}},{\mathbf{B}}^{x,z^{*}}\right)$ is the optimal strategy.

We define ${\displaystyle \psi \left(z\right)\triangleq {\Phi }(x;z)-z\left(x+\frac{y}{r+\lambda }\right)}$. Noting that $d{z}_t=(\beta -r)z_{t}dt-\theta d{W}_t,z_0=z,$$\psi \left(z\right)$ solves the following linear equation by the Feynman–Kac formula

$$\begin{array}{cc}\hfill & \frac{1}{2}{\theta }^2{z}^2{\psi }^{\prime \prime }\left(z\right)+(\beta -r)z{\psi }^{\prime }\left(z\right)-(\beta +\lambda )\psi \left(z\right)+\frac{z}{\alpha }\left[logz-1\right]+\lambda \frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}{z}^{\frac{\gamma -1}{\gamma }}=0,0<z<\tilde{z},\hfill \\ \hfill & \frac{1}{2}{\theta }^2{z}^2{\psi }^{\prime \prime }\left(\lambda \right)+(\beta -r)z{\psi }^{\prime }\left(z\right)-(\beta +\lambda )\psi \left(z\right)-\left[\frac{1}{\alpha }+Rz\right]+\lambda \frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}{z}^{\frac{\gamma -1}{\gamma }},z\ge \tilde{z}.\hfill \end{array}$$

(15)

Let $n_{+}>1$ and $n_{-}<0$ are two distinct roots to the following equation

$$\frac{1}{2}{\theta }^2{n}^2+\left(\beta -r-\frac{1}{2}{\theta }^2\right)n-(\beta +\lambda )=0.$$

(16)

Then we obtain $\psi \left(z\right)$ as in the following proposition.

Proposition 1.

$\psi \left(z\right)$ of (15) is given by

$$\begin{array}{c}\hfill \psi \left(z\right)=\left\{\begin{array}{cc}{\displaystyle A{z}^{n_{+}}+\frac{1}{\alpha (r+\lambda )}zlogz+\frac{\frac{1}{2}{\theta }^2-2r+\beta -\lambda }{\alpha {(r+\lambda )}^2}z+\frac{\lambda }{r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2}\frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}{z}^{1-\frac{1}{\gamma }},}\hfill & 0<z<\tilde{z},\\ {\displaystyle B{z}^{n_{-}}-\frac{R}{r+\lambda }z-\frac{e^{-\alpha R}}{\alpha (\beta +\lambda )}+\frac{\lambda }{r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2}\frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}{z}^{1-\frac{1}{\gamma }},}\hfill & z\ge \tilde{z},\end{array}\right.\end{array}$$

(17)

where the coefficients are determined by

$$\begin{array}{cc}\hfill A& =\frac{\frac{1-n_{-}}{\alpha (r+\lambda )}\tilde{z}log\tilde{z}+\left[\frac{1}{\alpha (r+\lambda )}+\frac{1-n_{-}}{\alpha {(r+\lambda )}^2}\left\{\frac{1}{2}{\theta }^2-2r+\beta -\lambda +(r+\lambda )\alpha R\right\}\right]\tilde{z}-\frac{n_{-}{e}^{-\alpha R}}{\alpha (\beta +\lambda )}}{(n_{-}-n_{+}){\tilde{z}}^{n_{+}}},\hfill \\ \hfill B& =\frac{\frac{1-n_{+}}{\alpha (r+\lambda )}\tilde{z}log\tilde{z}+\left[\frac{1}{\alpha (r+\lambda )}+\frac{1-n_{+}}{\alpha {(r+\lambda )}^2}\left\{\frac{1}{2}{\theta }^2-2r+\beta -\lambda +(r+\lambda )\alpha R\right\}\right]\tilde{z}-\frac{n_{+}{e}^{-\alpha R}}{\alpha (\beta +\lambda )}}{(n_{-}-n_{+}){\tilde{z}}^{n_{-}}}.\hfill \end{array}$$

Proof. 

For $0<z<\tilde{z}$, we discard the homogeneous part $z^{n-}$, which grows rapidly as z approaches 0. Similarly, we only choose the $z^{n_{-}}$ part if $z\ge \tilde{z}$. With particular parts, we derive (17). The coefficients A and B are determined by the $C^1$ condition at $z=\tilde{z}$. □

Theorem 1.

Suppose that ${\psi }^{\prime }\left(y\right)$ is a strictly increasing function that maps $(0,\infty ]$ onto $(-\infty ,0]$ with $y{\psi }^{\prime }\left(y\right)$ and $y^2{\psi }^{\prime \prime }\left(y\right)$ are bounded for $y\in (0,\infty ],$ where ${\psi }^{\prime }(\infty )\triangleq {lim}_{y\to \infty }{\psi }^{\prime }\left(y\right).$ Define

$$\mathcal{X}\left(z\right)\triangleq -{\psi }^{\prime }\left(z\right)-\frac{y}{r+\lambda },z>0,$$

(18)

and denote by $\mathcal{Z}$ be the inverse function of $\mathcal{X}.$ Then the value function $V\left(x\right)$ is given by

$$\begin{array}{ccc}\hfill V\left(x\right)& =& \psi \left(\mathcal{Z}\left(x\right)\right)+\mathcal{Z}\left(x\right)\left(x+\frac{y}{r+\lambda }\right)\hfill \\ & =& \left\{\begin{array}{c}{\displaystyle A\mathcal{Z}{\left(x\right)}^{n_{+}}+\frac{1}{\alpha (r+\lambda )}\mathcal{Z}\left(x\right)log\mathcal{Z}\left(x\right)+\frac{\frac{1}{2}{\theta }^2-2r+\beta -\lambda }{\alpha {(r+\lambda )}^2}\mathcal{Z}\left(x\right)}\hfill \\ {\displaystyle +\frac{\lambda }{r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2}\frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}\mathcal{Z}{\left(x\right)}^{1-\frac{1}{\gamma }}+\mathcal{Z}\left(x\right)\left(x+\frac{y}{r+\lambda }\right),}\hfill & x>\mathcal{X}\left(\tilde{z}\right),\hfill \\ \\ {\displaystyle B\mathcal{Z}{\left(x\right)}^{n_{-}}-\frac{R}{r+\lambda }\mathcal{Z}\left(x\right)-\frac{e^{-\alpha R}}{\alpha (\beta +\lambda )}}\hfill \\ {\displaystyle +\frac{\lambda }{r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2}\frac{\gamma }{1-\gamma }{K}^{\frac{1}{\gamma }}\mathcal{Z}{\left(x\right)}^{1-\frac{1}{\gamma }}+\mathcal{Z}\left(x\right)\left(x+\frac{y}{r+\lambda }\right),}\hfill & {\displaystyle -\frac{y-R}{r+\lambda }<x\le \mathcal{X}\left(\tilde{z}\right).}\hfill \end{array}\right.\hfill \end{array}$$

The optimal strategy $\left({\mathbf{\pi }}^{*},{\mathbf{c}}^{*},{\mathbf{B}}^{*}\right)$ is given by

$$\begin{array}{cc}\hfill c_t^{*}& =c^{*}\left(\mathcal{Z}\left(X_t\right)\right)=\left\{\begin{array}{cc}{\displaystyle -\frac{1}{\alpha }log\mathcal{Z}\left(X_t\right),}\hfill & x>\mathcal{X}\left(\tilde{z}\right),\\ R,\hfill & {\displaystyle -\frac{y-R}{r+\lambda }<x\le \mathcal{X}\left(\tilde{z}\right),}\end{array}\right.\hfill \\ \hfill {\pi }_t^{*}& =\frac{\theta }{\sigma }\mathcal{Z}\left(X_t\right){\psi }^{\prime \prime }\left(\mathcal{Z}\left(X_t\right)\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}{\displaystyle \frac{\theta }{\sigma }{n}_{+}(n_{+}-1)A{\mathcal{Z}\left(X_t\right)}^{n_{+}-1}+\frac{\theta }{\sigma \alpha (r+\lambda )}+\frac{\theta \lambda K^{\frac{1}{\gamma }}}{\sigma \gamma \left(r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2\right)}\mathcal{Z}{\left(x\right)}^{-\frac{1}{\gamma }},}\hfill & x>\mathcal{X}\left(\tilde{z}\right),\\ \\ {\displaystyle \frac{\theta }{\sigma }{n}_{-}(n_{-}-1)B{\mathcal{Z}\left(X_t\right)}^{n_{-}-1}+\frac{\theta \lambda K^{\frac{1}{\gamma }}}{\sigma \gamma \left(r+\lambda +\frac{\beta -r}{\gamma }+\frac{1}{2}\frac{\gamma -1}{{\gamma }^2}{\theta }^2\right)}\mathcal{Z}{\left(x\right)}^{-\frac{1}{\gamma }},}\hfill & {\displaystyle -\frac{y-R}{r+\lambda }<x\le \mathcal{X}\left(\tilde{z}\right).}\end{array}\right.\hfill \\ \hfill B_t^{*}& {\displaystyle =B^{*}\left(\mathcal{Z}\left(X_t\right)\right)={\left(\frac{\mathcal{Z}\left(X_t\right)}{K}\right)}^{-\frac{1}{\gamma }},x>-\frac{y-R}{r+\lambda },}\hfill \end{array}$$

and from (2) the optimal insurance premium process ${\mathbf{p}}^{*}\triangleq {\left(p_t^{*}\right)}_{t\ge 0}$ is given by

$${\displaystyle p_t^{*}=\lambda (B_t^{*}-X_t)=\lambda \left({\left(\frac{\mathcal{Z}\left(X_t\right)}{K}\right)}^{-\frac{1}{\gamma }}-X_t\right),x>-\frac{y-R}{r+\lambda }.}$$

Proof. 

The expression of the value function and the optimality of the strategy $\left({\mathbf{\pi }}^{*},{\mathbf{c}}^{*},{\mathbf{B}}^{*}\right)$ follows from Theorem 2 of [8]. □

5. Numerical Illustrations

In this section, we examine the effects of the force of mortality $\lambda$ and the subsistence level of consumption R on decision making of the individual. The wealth level threshold $\tilde{x}\triangleq \mathcal{X}\left(\tilde{z}\right)$ corresponds to the subsistence level of consumption R. The expected value of the individual’s death time $\tau$ is $1/\lambda .$ We use $\lambda =0.01,0.03,$ and $0.05$ those correspond to the expected lifetime 100 year, $33.3$ year, and 20 year, respectively. As to the subsistence level of consumption R, we use $0.05,0.1,$ and $0.15$ those correspond to the minimum percentage of the consumption rate to the income stream $16.67\%$, $33.33\%$, and $50\%$, respectively. As to the other parameters, we use a reasonable set of values for the financial market.

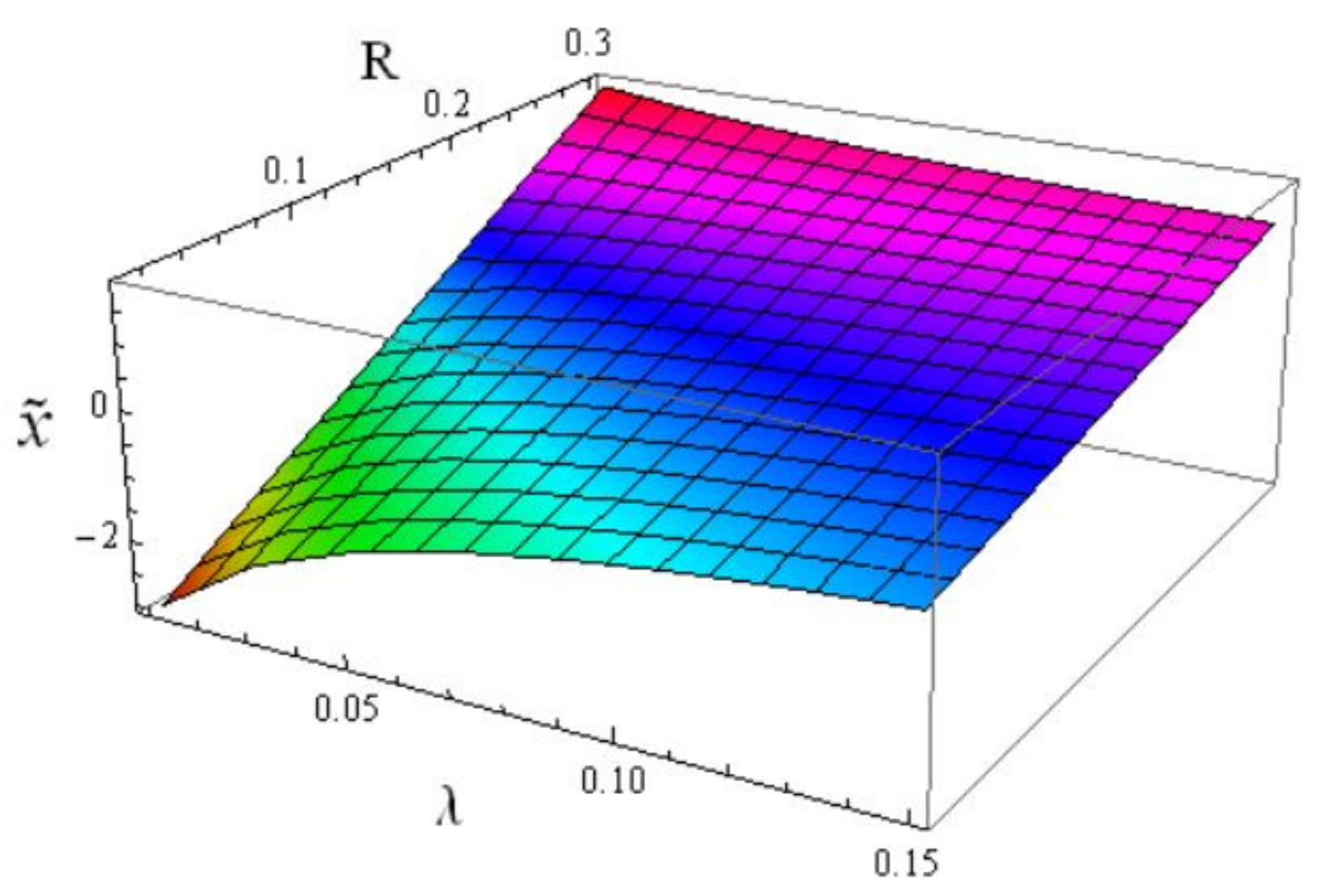
Figure 1 illustrates $\tilde{x}$ against $\lambda$ and R. Since R is the mininum rate the individual must consume, the wealth threshold $\tilde{x}$ increases with R. An individual with a large force of mortality $\lambda$ likely tends to consume less than does an individual with a small $\lambda .$ Therefore, $\tilde{x}$ increases also with $\lambda$.

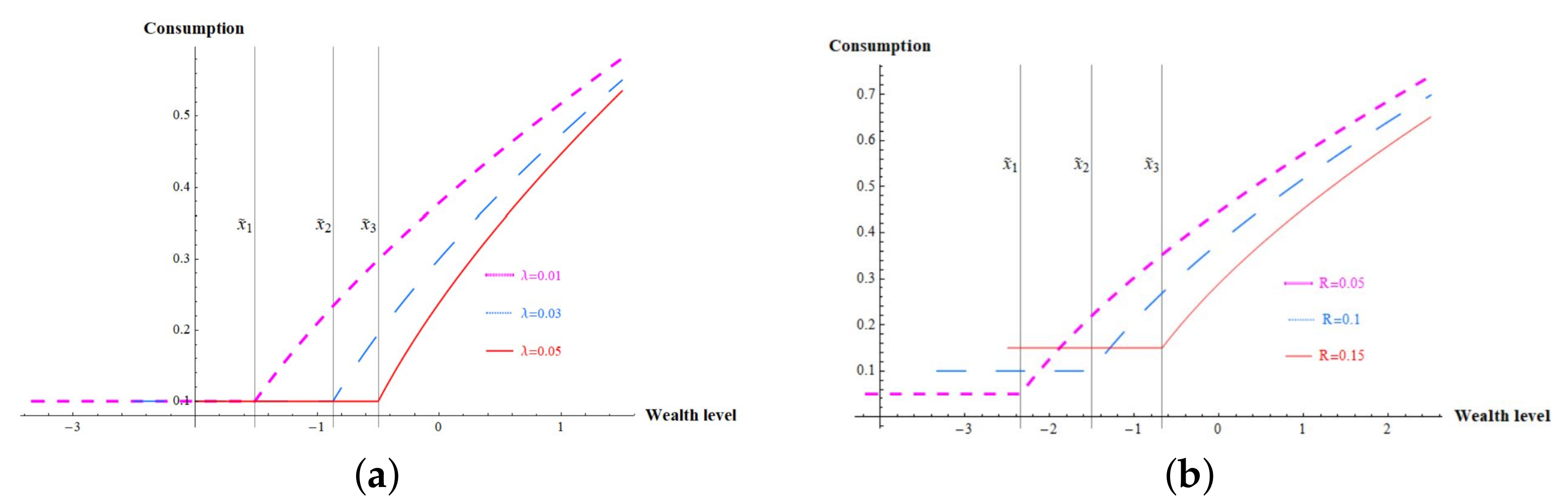
For Figure 2a,Figure 3a,Figure 4a wealth level threshold ${\tilde{x}}_1$, ${\tilde{x}}_2$, and ${\tilde{x}}_3$ stand for $\tilde{x}$ with $\lambda =0.01$, $\lambda =0.03$, and $\lambda =0.05$, respectively. For Figure 2b,Figure 3b, Figure 4b wealth level threshold ${\tilde{x}}_1$, ${\tilde{x}}_2$, and ${\tilde{x}}_3$ stand for $\tilde{x}$ with $R=0.05,R=0.1$, and $R=0.15$, respectively.

Figure 2 shows individual’s optimal consumption for various force of mortality $\lambda$ and subsistence level consumption R. For a given wealth level, an individual with a large force of mortality consume less than does an individual with a small force of mortality. A large force of mortality force an individual reduce consumption. The effect of R on consumption shows the same pattern as that of $\lambda$. A strong restriction on minimum consumption level makes an individual to decrease consumption.

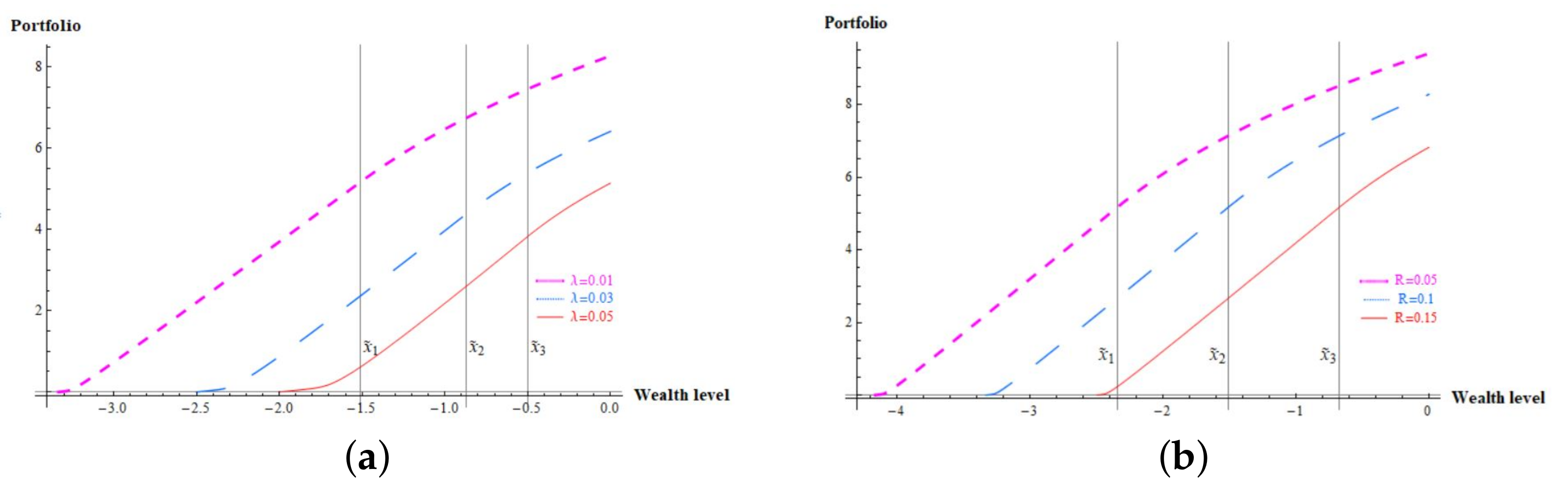
Individual’s preferences for the risky asset for different force of mortality or subsistence level of consumption are exhibited in Figure 3. As we can see, a large force of mortality leads an individual to conservative investing. An individual who are more likely to be exposed to the mortality risk may have more demand for hedging the risk so the individual is not unwilling to be exposed the market risk. A large subsistence level of consumption also force an individual to reduce investment in the risky asset. An individual with a strong subsistence consumption constraint is reluctant to take more market risk which may potentially results in lack of the individual’s wealth to meet the subsistence level of consumption.

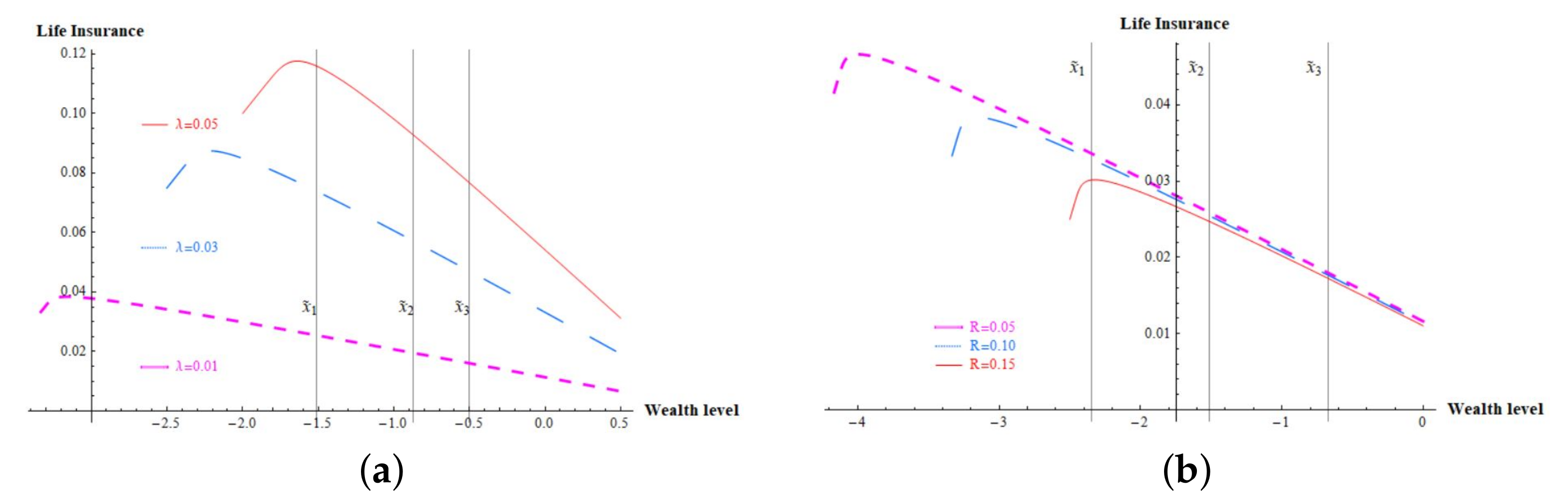
With a large mortality risk, an individual has a strong demand for life insurance coverage. This is well illustrated in Figure 4a. On the other hand, a large subsistence level of consumption leads to a less demand for life insurance coverage. However, the effect of subsistence level of consumption on life insurance demand is rather marginal, especially for higher wealth levels.

Differently from our study, Ref. [1] employs a CRRA utility to investigate effects of consumption habit on life-contingent claims using term structure of mortality intensity and labor income for considering age effects. The way how the life insurance purchase decision is affected by subsistence consumption (this paper) and consumption habit ([1]; the demand for life insurance increases with consumption habit level but also decrease with the level, if the level is very high) are different from each other. Nevertheless, both of the studies reveal that demand for life insurance increases with risk aversion. 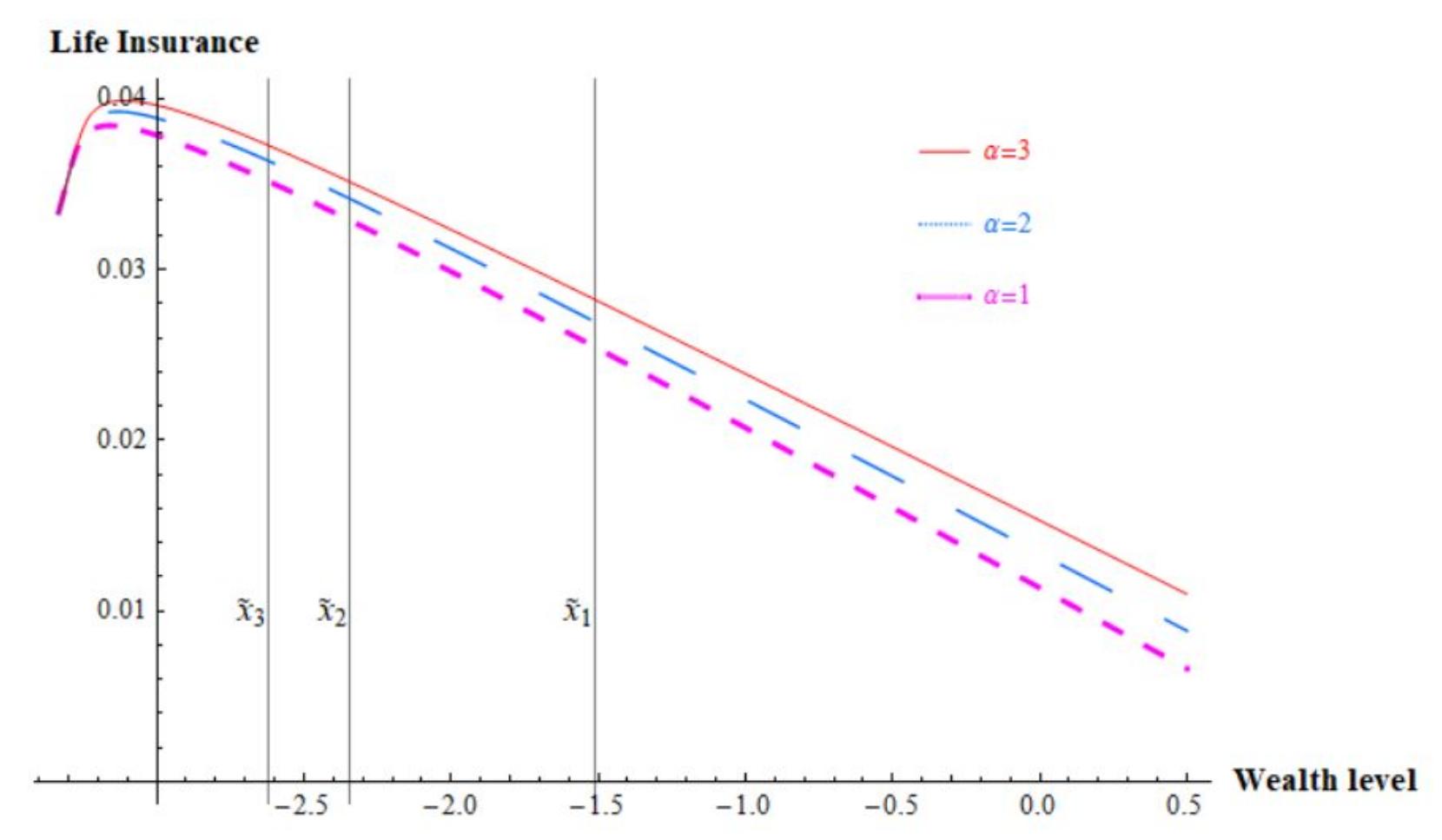In Figure 5, we present life insurance purchase against wealth level for diffrent coefficients of absolute risk aversion. A large risk aversion tends to induce more demand for hedging instrument to mitigate income loss due to mortality.

6. Conclusions

The purpose this paper is to examine effects of force of mortality and subsistence level of consumption on an individual’s decision making. With an exponential utility of consumption while living, we obtain optimal consumption, portfolio, and life insurance coverage strategies using the martingale and duality method. Numerical illustrations based on our explicit solution show that a strong force of mortality and a high subsistence level of consumption lead an individual to reduce exposure to the market risk and to consume less. An individual with a large mortality risk demands more life insurance coverage as an individual with a low subsistence level of consumption does. For example, during a pandemic outbreak, such as COVID-19, the force of mortality increases so the individual must lessen consumption and have lower risky asset shares, but buy more life insurance. If successful vaccines are developed, the force of mortality decreases so the individual consume more, increases long position in the risky asset, and reduce life insurance purchase. However, our numerical illustrations reveal that the effect of subsistence consumption constraint on demand for life insurance seems to be marginal. Lastly, we observe that the demand for life insurance increases with risk aversion.