Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time
Abstract
1. Introduction
2. Time and Shape Related Performance Measures
- (a)
- No connection to real-time control: by evaluating data obtained from experiments on real processes, we cannot determine the actual values of the sensitivity functions;
- (b)
- (c)
- Potential counterproductivity: in terms of robust control design, the use of sensitivity functions can lead to counterproductive results [10].
2.1. Monotonicity-Based Shape Related Measures
2.2. Optimization Problem
2.3. Speed-Effort and Speed-Wobbling Characteristics
3. PID Controller According to the MRDP Method
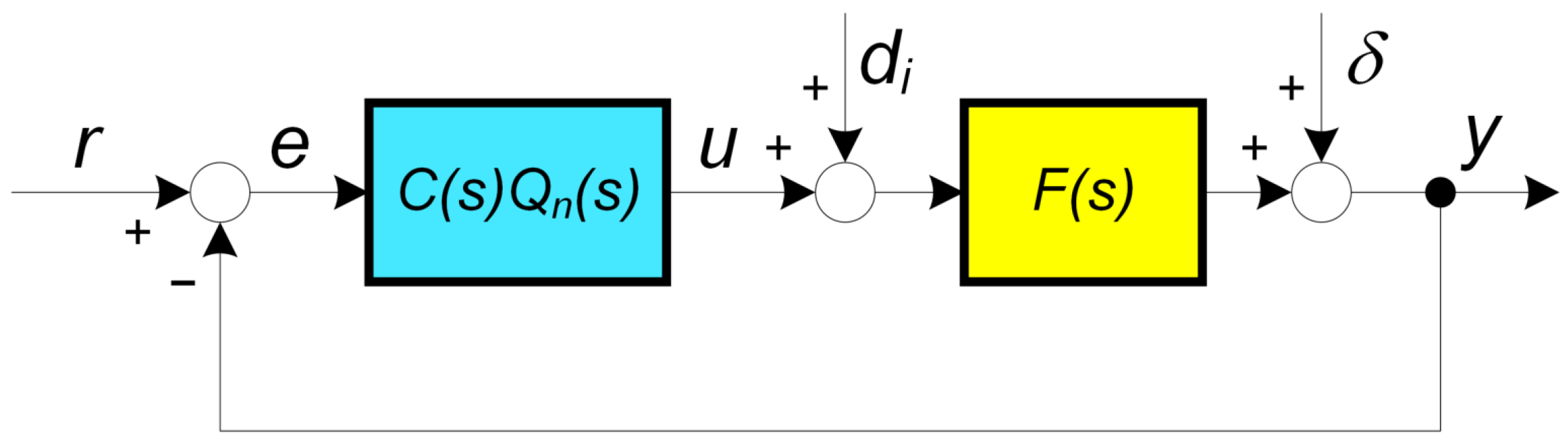
4. Equivalent Delay Based Controller Tuning
- The ideal PID controller may not be realized—to be causal, it must be extended by at least a first-order low-pass filter (18);
- A more effective attenuation of the measurement noise can be achieved by the filter order ;
- The included filters modify the loop dynamics, which must be taken into account in the controller tuning.
- After identifying the system model parameters and , select an appropriate value of the tuning parameter corresponding to the required degree of filtration;
- Select a filter order n and specify the filter time constant by a suitable delay equivalence described below, defined as
- Check that the computed value satisfies the requirement in (18), where represents the sampling period used for the quasi-steady control implementation.
- If not, either decrease , or n, which must still fulfill the condition .
- By experimentally evaluating the noise attenuation characteristics for different n, choose an optimal controller that guarantees the optimal control loop performance.
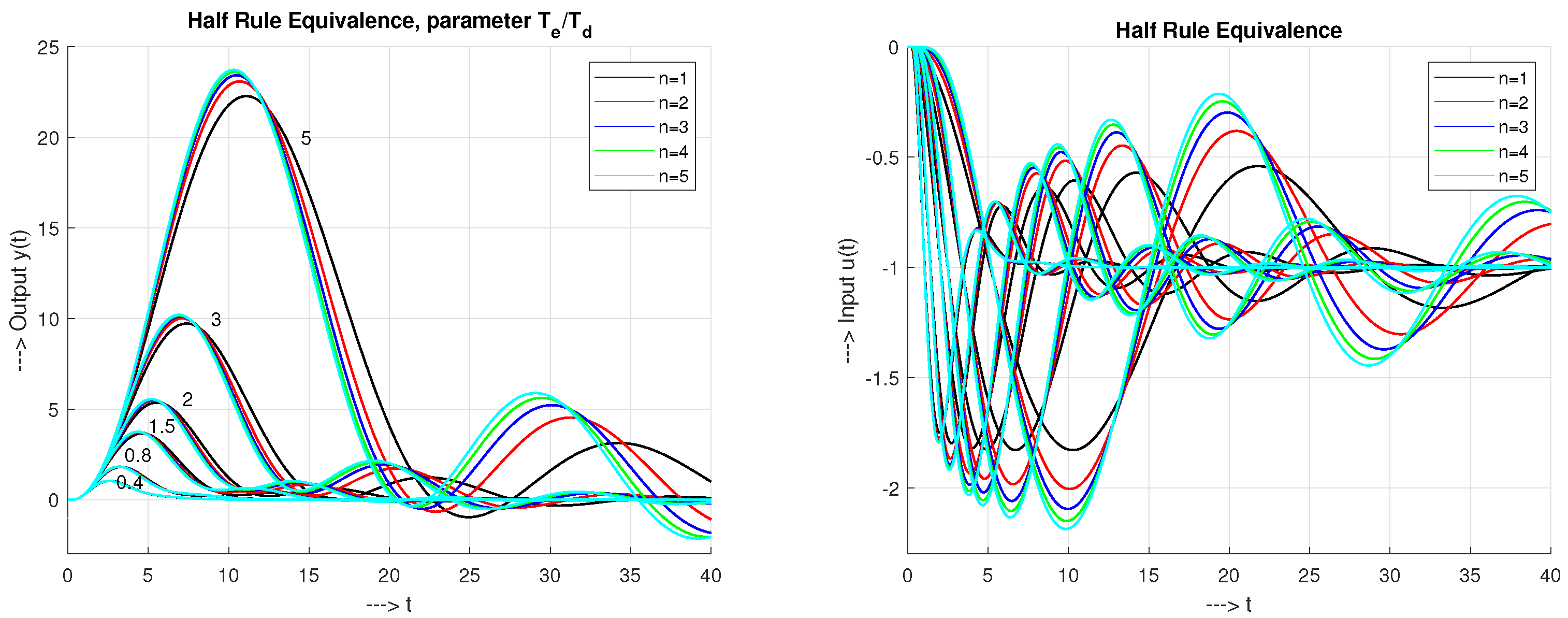
4.1. Half-Rule Equivalence (HRE)
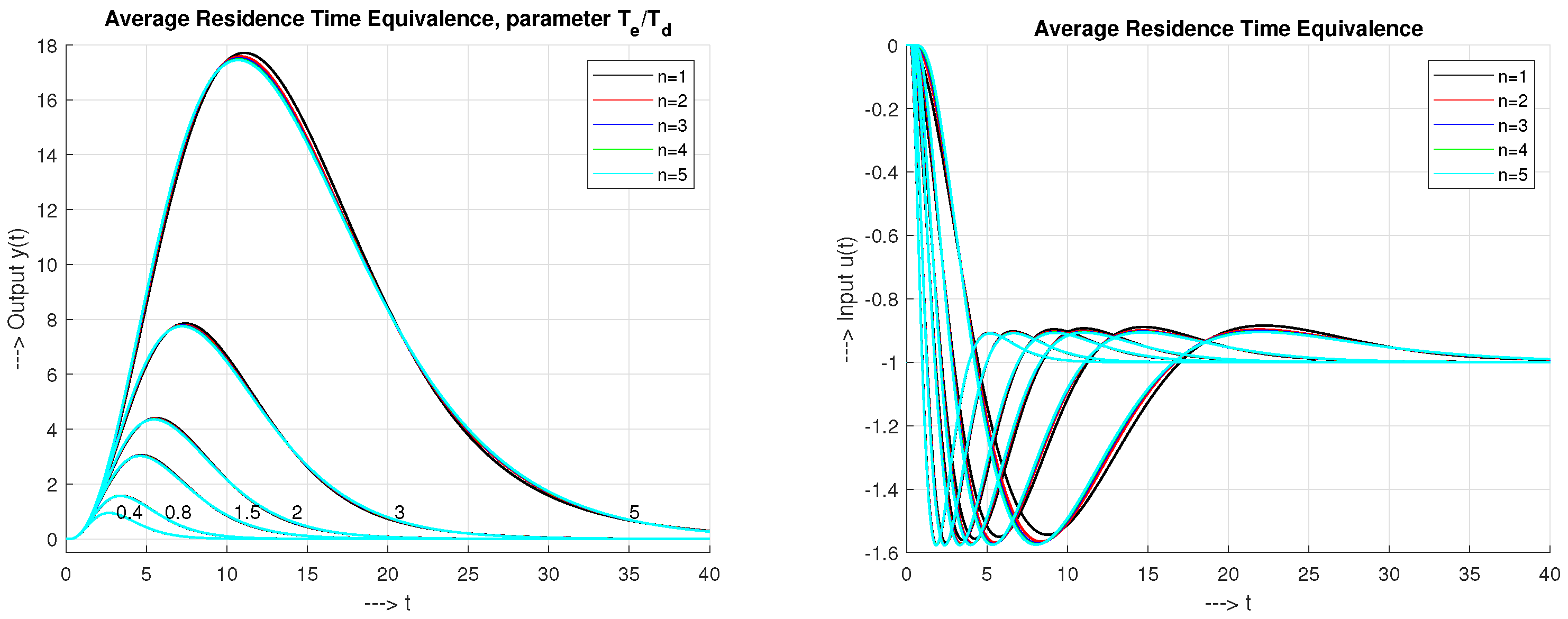
4.2. Average Residence Time Equivalence (ARTE)
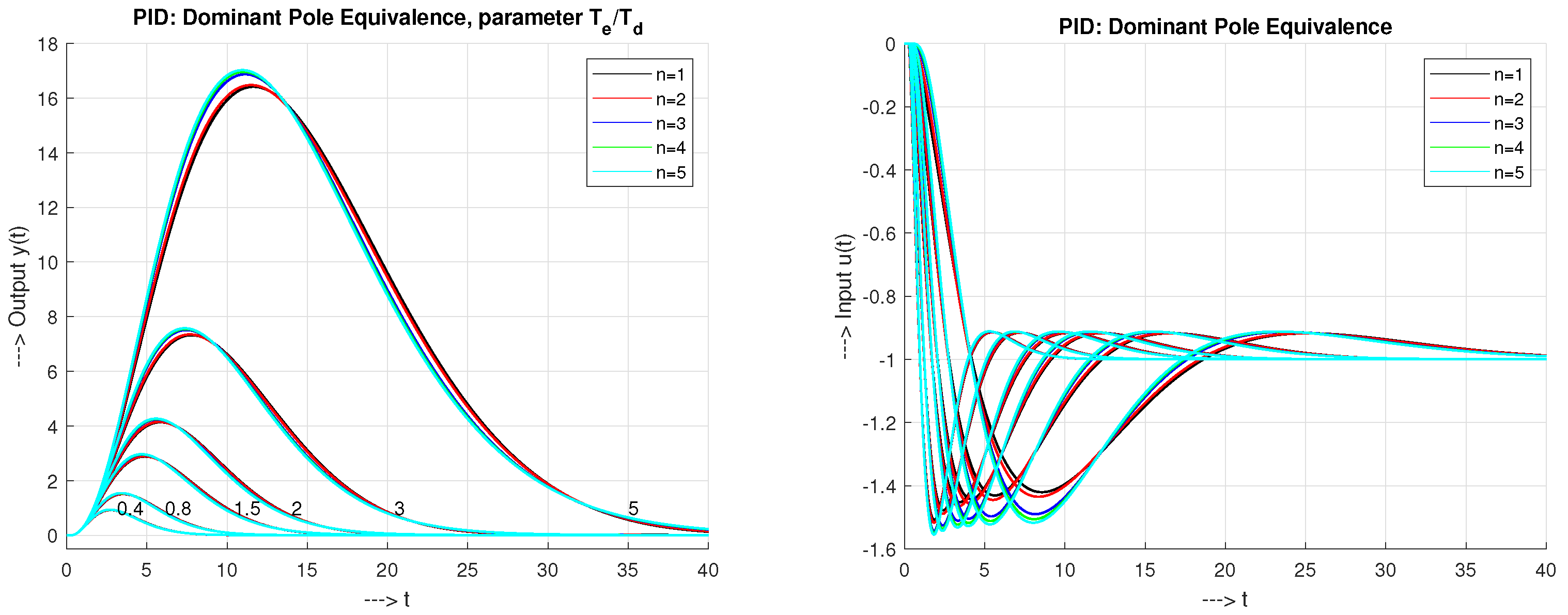
4.3. Dominant Poles Equivalence (DPE)
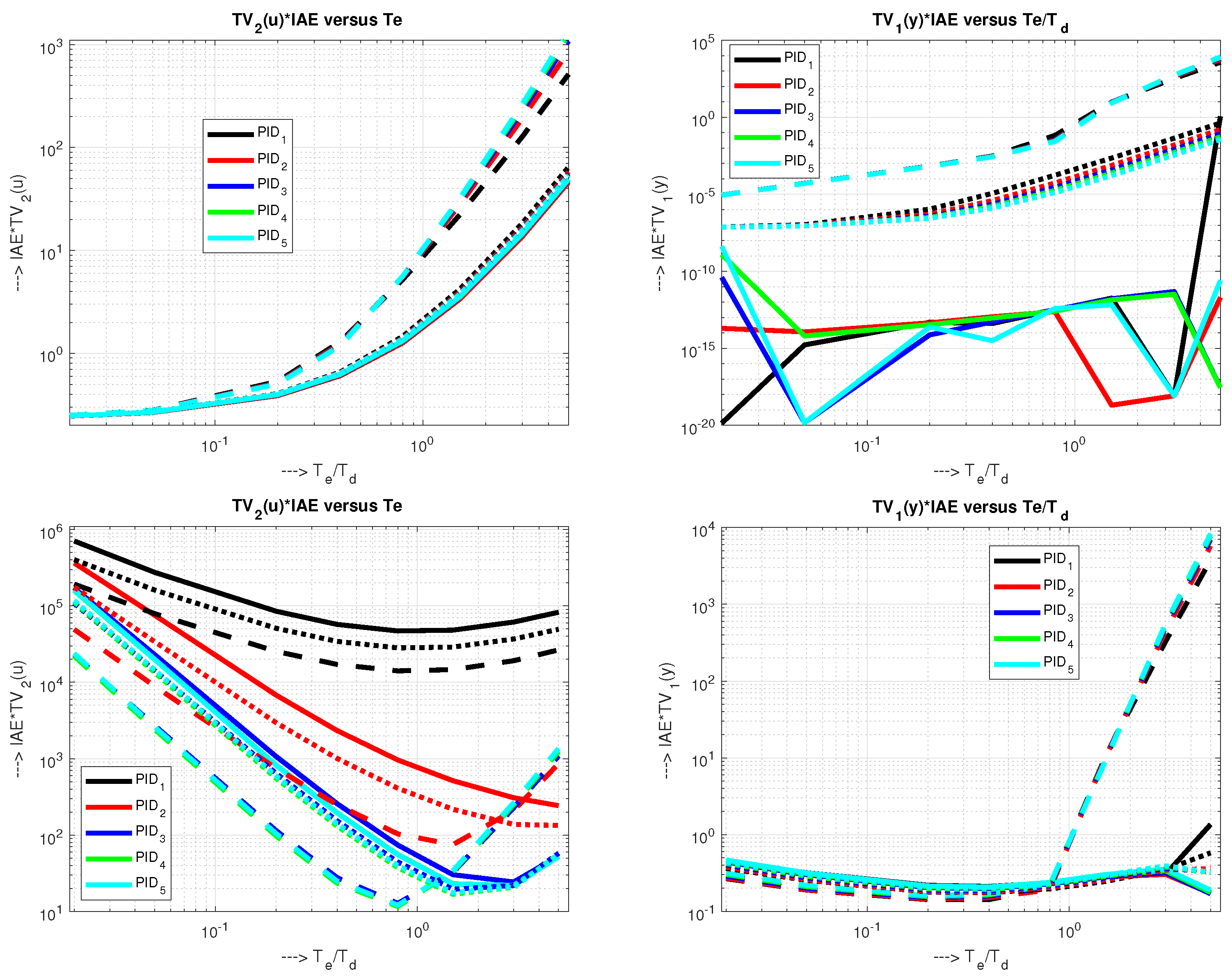
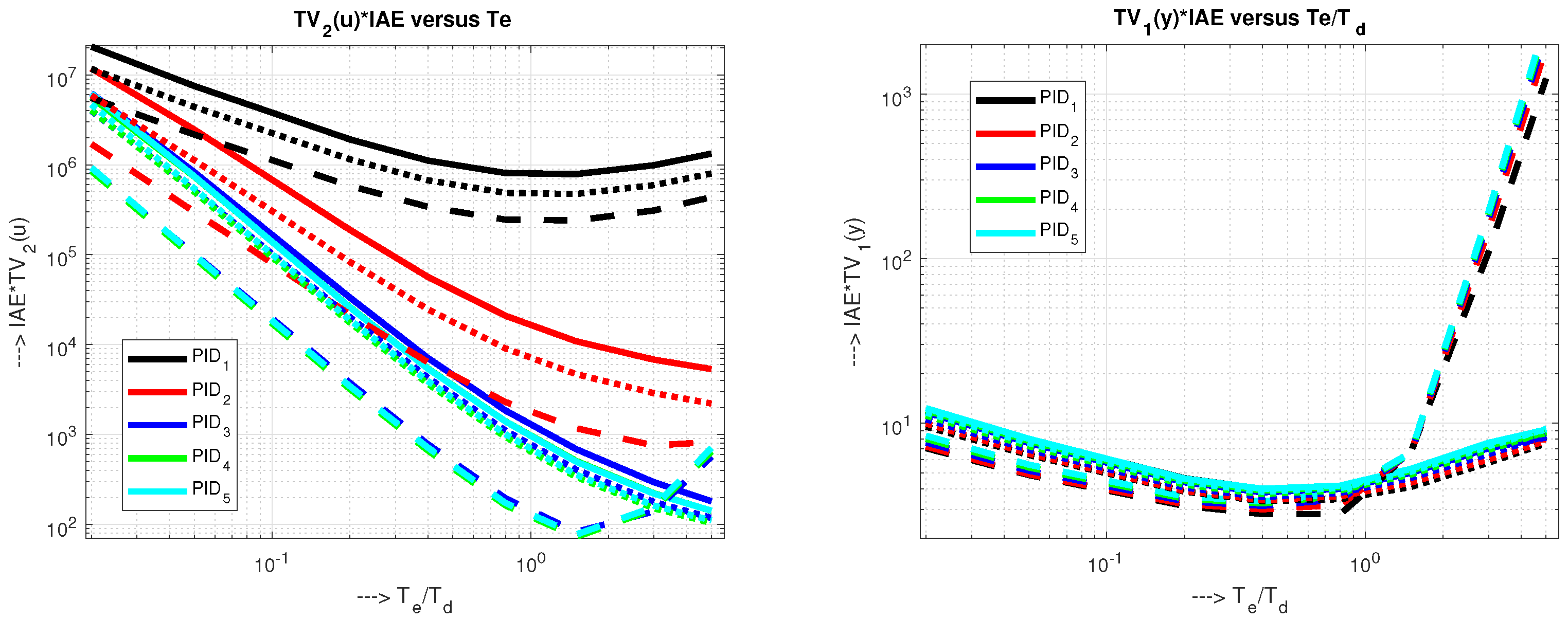
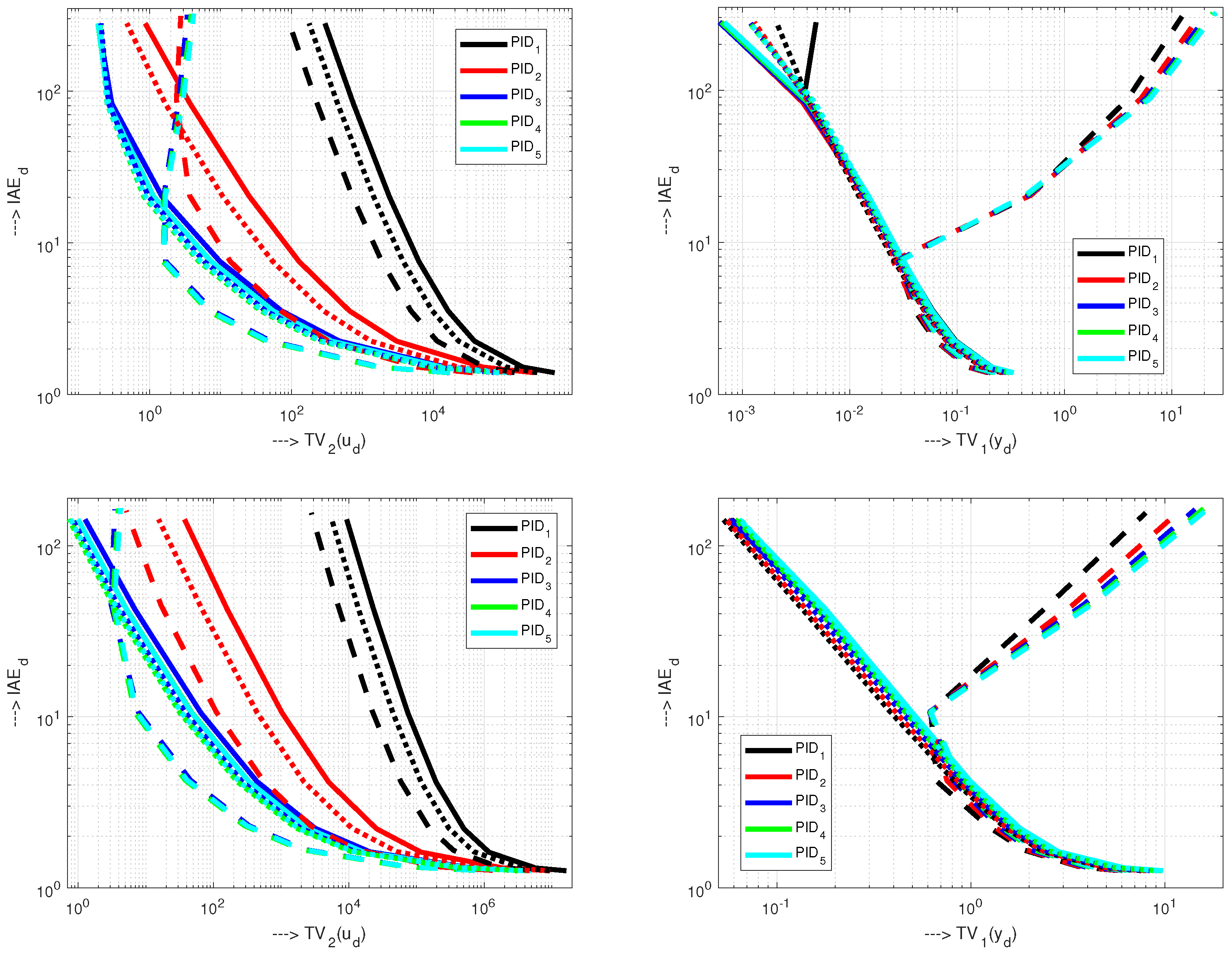
5. Evaluation of the Results
5.1. Holistic Cost Functions versus Equivalent Delay
5.2. Interpretation Is SE/SW Planes
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 1P | One-Pulse, response with 2 monotonic segments (1 extreme point) |
| 2P | Two-Pulse, response with 3 monotonic segments (2 extreme points) |
| ADRC | Active Disturbance Rejection Control |
| DIPDT | Double Integrator Plus Dead-Time |
| FO | Fractional Order |
| HO | Higher Order |
| IAE | Integral Absolute Error |
| IPDT | Integrator Plus Dead-Time |
| ISE | Integral Square Error |
| LESO | Linear Extended State Observer |
| MRDP | Multiple Real Dominant Pole |
| nP | n-Pulse, response with monotonic segments (n extreme points) |
| PID | Proportional-Integrative-Derivative |
| PID | generalized PID with mth order derivative action and nth order low-pass filter |
| SE | Speed-Effort |
| SW | Speed-Wobbling |
| TV | Total Variation |
| TV | Deviation from monotonicity (0P shape) |
| TV | Deviation from 1P shape |
| TV | Deviation from 2P shape |
References
- Richard, J.P. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; Imperial College Press: London, UK, 2009. [Google Scholar]
- O’Dwyer, A. An Overview of Tuning Rules for the PI and PID Continuous-Time Control of Time-Delayed Single-Input, Single-Output (SISO) Processes. In PID Control in the Third Millennium. Lessons Learned and New Approaches; Vilanova, R., Visioli, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chen, S.; Xue, W.; Zhong, S.; Huang, Y. On comparison of modified ADRCs for nonlinear uncertain systems with time delay. Sci. China Inf. Sci. 2018, 61, 70223. [Google Scholar] [CrossRef]
- Zhao, S.; Gao, Z. Modified active disturbance rejection control for time-delay systems. ISA Trans. 2014, 53, 882–888. [Google Scholar] [CrossRef]
- Pekař, L. On Simple Algebraic Control Design and Possible Controller Tuning for Linear Systems with Delays. Int. J. Mech. 2018, 12, 178–191. [Google Scholar]
- Pekař, L.; Gao, Q. Spectrum Analysis of LTI Continuous-Time Systems With Constant Delays: A Literature Overview of Some Recent Results. IEEE Access 2018, 6, 35457–35491. [Google Scholar] [CrossRef]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.; HosseinNia, S.H.; Petlenkov, E. FOPID Controllers and Their Industrial Applications: A Survey of Recent Results. IFAC Pap. 2018, 51, 25–30. [Google Scholar] [CrossRef]
- Huba, M.; Vrančič, D.; Bisták, P. Control for IPDT Plants. Part 1: Disturbance Response. In Proceedings of the 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018. [Google Scholar]
- Huba, M.; Vrančić, D.; Bisták, P. PID Control with Higher Order Derivative Degrees for IPDT Plant Models. IEEE Access 2020, 9, 2478–2495. [Google Scholar] [CrossRef]
- Jung, S.; Dorf, R.C. Novel Analytic Technique for PID and PIDA Controller Design. IFAC Proc. Vol. 1996, 29, 1146–1151. [Google Scholar] [CrossRef]
- Ukakimaparn, P.; Pannil, P.; Boonchuay, P.; Trisuwannawat, T. PIDA Controller designed by Kitti’s Method. In Proceedings of the 2009 ICCAS-SICE, Fukuoka City, Japan, 18–21 August 2009; pp. 1547–1550. [Google Scholar]
- Guha, D.; Roy, P.K.; Banerjee, S. Multi-verse optimisation: A novel method for solution of load frequency control problem in power system. IET Gener. Transm. Distrib. 2017, 11, 3601–3611. [Google Scholar] [CrossRef]
- Kumar, M.; Hote, Y.V. Robust CDA-PIDA Control Scheme for Load Frequency Control of Interconnected Power Systems. IFAC Pap. 2018, 51, 616–621. [Google Scholar] [CrossRef]
- Kumar, M.; Hote, Y.V. Robust PIDD2 Controller Design for Perturbed Load Frequency Control of an Interconnected Time-Delayed Power Systems. IEEE Trans. Control. Syst. Technol. 2020, 1–8. [Google Scholar] [CrossRef]
- Huba, M. Filtered PIDA Controller for the Double Integrator Plus Dead Time. In Proceedings of the 16th IFAC International Conference on Programmable Devices and Embedded Systems, High Tatras, Slovakia, 29–31 October 2019. [Google Scholar]
- Huba, M.; Bisták, P.; Skachová, Z.; Žáková, K. P- and PD-Controllers for I1 and I2 Models with Dead Time. In Proceedings of the 6th IEEE Mediterranean Conference on Control and Automation, Sardinia, Italy, 9–11 June 1998; Volume 11, pp. 514–519. [Google Scholar]
- Huba, M.; P.Bisták, Z.; Žáková, K. Predictive Antiwindup PI and PID-Controllers Based on I1 and I2 Models with Dead Time. IEEE Mediterr. Conf. 1998, 11, 532–535. [Google Scholar]
- Grimholt, C.; Skogestad, S. Optimal PID control of double integrating processes. IFAC Pap. 2016, 49, 127–132. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process. Control. 2003, 13, 291–309. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-free control. Int. J. Control. 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. Ind. Electron. IEEE Trans. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 2399–2405. [Google Scholar]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef]
- Huba, M.; Škrinárová, J.; Dudáš, A.; Bisták, P. Optimal PID controller tuning for the time delayed double integrator. In Proceedings of the 21st International Carpathian Control Conference—ICCC, Starý Smokovec, Slovak Republic, 27–29 May 2020. [Google Scholar]
- Huba, M. Designing Robust Controller Tuning for Dead Time Systems. In International Conference on System Structure and Control; IFAC: Ancona, Italy, 2010. [Google Scholar]
- Huba, M. Performance Measures and the Robust and Optimal Control Design. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 960–965. [Google Scholar]
- Shinskey, F. How good are Our Controllers in Absolute Performance and Robustness. Meas. Control. 1990, 23, 114–121. [Google Scholar] [CrossRef]
- Begum, K.G.; Rao, A.S.; Radhakrishnan, T. Maximum sensitivity based analytical tuning rules for PID controllers for unstable dead time processes. Chem. Eng. Res. Des. 2016, 109, 593–606. [Google Scholar] [CrossRef]
- Boskovic, M.C.; Sekara, T.B.; Rapaic, M.R. Novel tuning rules for PIDC and PID load frequency controllers considering robustness and sensitivity to measurement noise. Int. J. Electr. Power Energy Syst. 2020, 114, 105416. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 11, 759–768. [Google Scholar] [CrossRef]
- Feldbaum, A. Optimal Control Systems; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Pontrjagin, L.; Boltjanskij, V.; Gamkrelidze, R.; Miščenko, J. The Mathematical Theory of Optimal Processes; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Föllinger, O. Regelungstechnik. 8. Auflage; Hüthig Buch Verlag: Heidelberg, Germany, 1994. [Google Scholar]
- Kuo, B. Discrete-Data Control Systems; Prentice-Hall: Upper Saddle River, NY, USA, 1970. [Google Scholar]
- Huba, M. Performance measures, performance limits and optimal PI control for the IPDT plant. J. Process. Control. 2013, 23, 500–515. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Huba, M.; Šimunek, M. Modular Approach to Teaching PID Control. IEEE Trans. Ind. Electr. 2007, 54, 3112–3121. [Google Scholar] [CrossRef]
- Huba, M. Open flexible PD-controller design for different filtering properties. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON), Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Oldenbourg, R.; Sartorius, H. Dynamik Selbsttätiger Regelungen, 2nd ed.; R.Oldenbourg-Verlag: München, Germany, 1951. [Google Scholar]
- Vítečková, M.; Víteček, A. 2DOF PI and PID controllers tuning. In Proceedings of the 9th IFAC Workshop on Time Delay Systems, Prague, Czech Republic, 7–9 June 2010; Volume 9, pp. 343–348. [Google Scholar]
- Vítečková, M.; Víteček, A. 2DOF PID controller tuning for integrating plants. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016; pp. 793–797. [Google Scholar]
- Viteckova, M.; Vitecek, A.; Janacova, D. Robustness and Muliple Dominant Pole Method. In Proceedings of the 2020 21th International Carpathian Control Conference (ICCC), Star Smokovec, Slovak Republic, 27–29 October 2020; pp. 1–4. [Google Scholar]
- Huba, M. Comparing 2DOF PI and Predictive Disturbance Observer Based Filtered PI Control. J. Process. Control. 2013, 23, 1379–1400. [Google Scholar] [CrossRef]
- Bélai, I.; Huba, M.; Burn, K.; Cox, C. PID and filtered PID control design with application to a positional servo drive. Kybernetika 2019, 55, 540–560. [Google Scholar] [CrossRef]
- Huba, M. Filter choice for an effective measurement noise attenuation in PI and PID controllers. In Proceedings of the ICM2015, Nagoya, Japan, 6–8 March 2015. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA: Research Triangle Park, NC, USA, 2006. [Google Scholar]
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.667 | 0.5 | 0.4 | 0.333 | 0.286 | |
| 1 | 0.5 | 0.333 | 0.25 | 0.2 | 0.167 | 0.143 | |
| 0.601 | 0.373 | 0.271 | 0.213 | 0.176 | 0.149 | 0.130 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huba, M.; Vrancic, D. Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time. Mathematics 2021, 9, 328. https://doi.org/10.3390/math9040328
Huba M, Vrancic D. Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time. Mathematics. 2021; 9(4):328. https://doi.org/10.3390/math9040328
Chicago/Turabian StyleHuba, Mikulas, and Damir Vrancic. 2021. "Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time" Mathematics 9, no. 4: 328. https://doi.org/10.3390/math9040328
APA StyleHuba, M., & Vrancic, D. (2021). Delay Equivalences in Tuning PID Control for the Double Integrator Plus Dead-Time. Mathematics, 9(4), 328. https://doi.org/10.3390/math9040328







