On a Retarded Nonlocal Ordinary Differential System with Discrete Diffusion Modeling Life Tables
Abstract
1. Introduction
2. Properties of Solutions of Non-Local Diffusion Problems with Finite Delay
- for all .
- .
- for .
2.1. A Finite Number of Equations
2.2. An Infinite Number of Equations
- There exist and such that for all and
- There exists such that for all
3. Application to Life Tables
3.1. Dynamical Kernel Graduation with Delay
3.1.1. Procedure by Steps
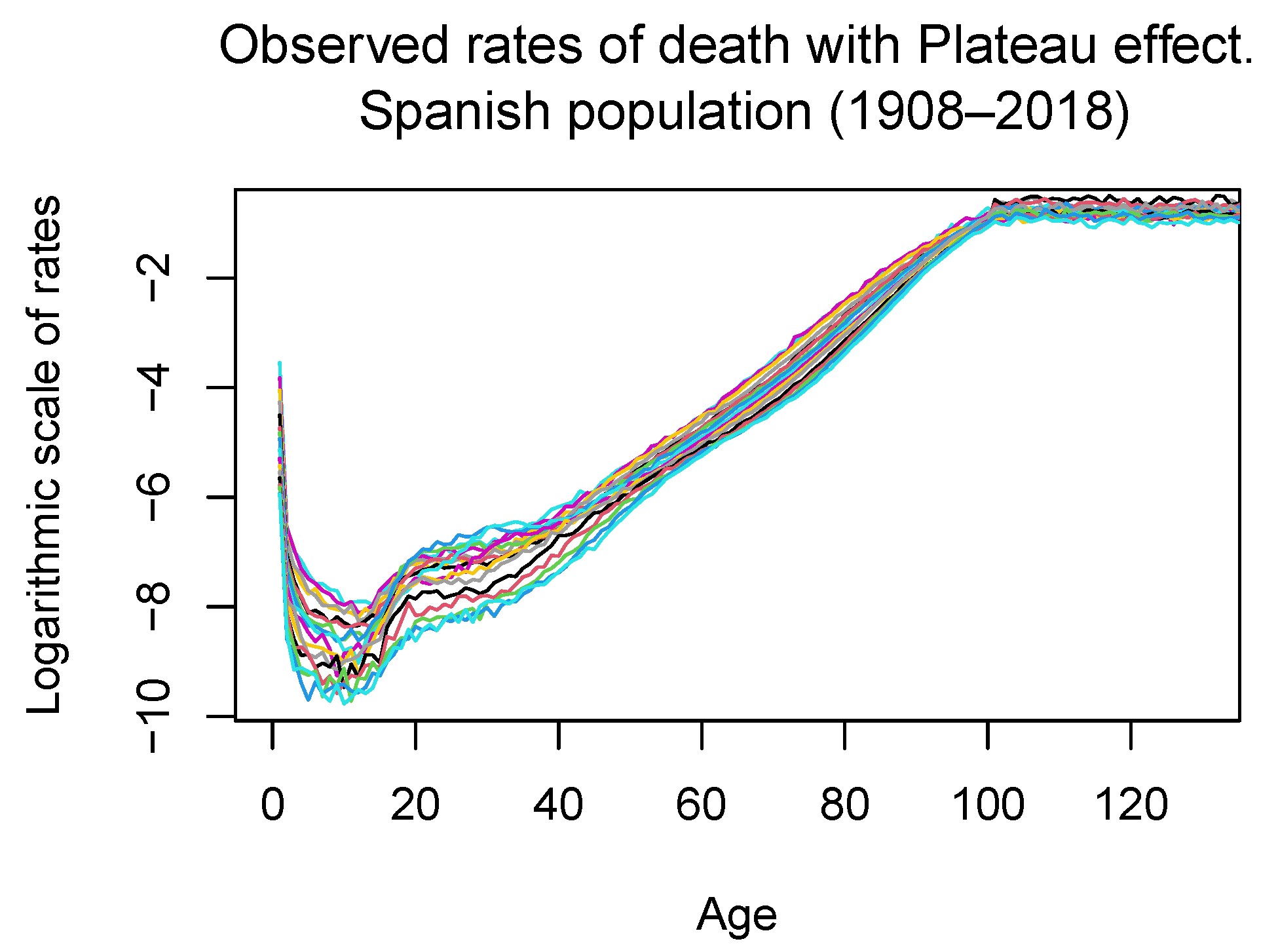
- We consider the observed mortality rates at each age (from to 100) and each year in the considered period (from 1908 to 2019), and denote them by , , . Additionally, we consider the values of , which is the rate of death either at “negative ages” or after the actuarial infinite (we have chosen it to be equal to 100).
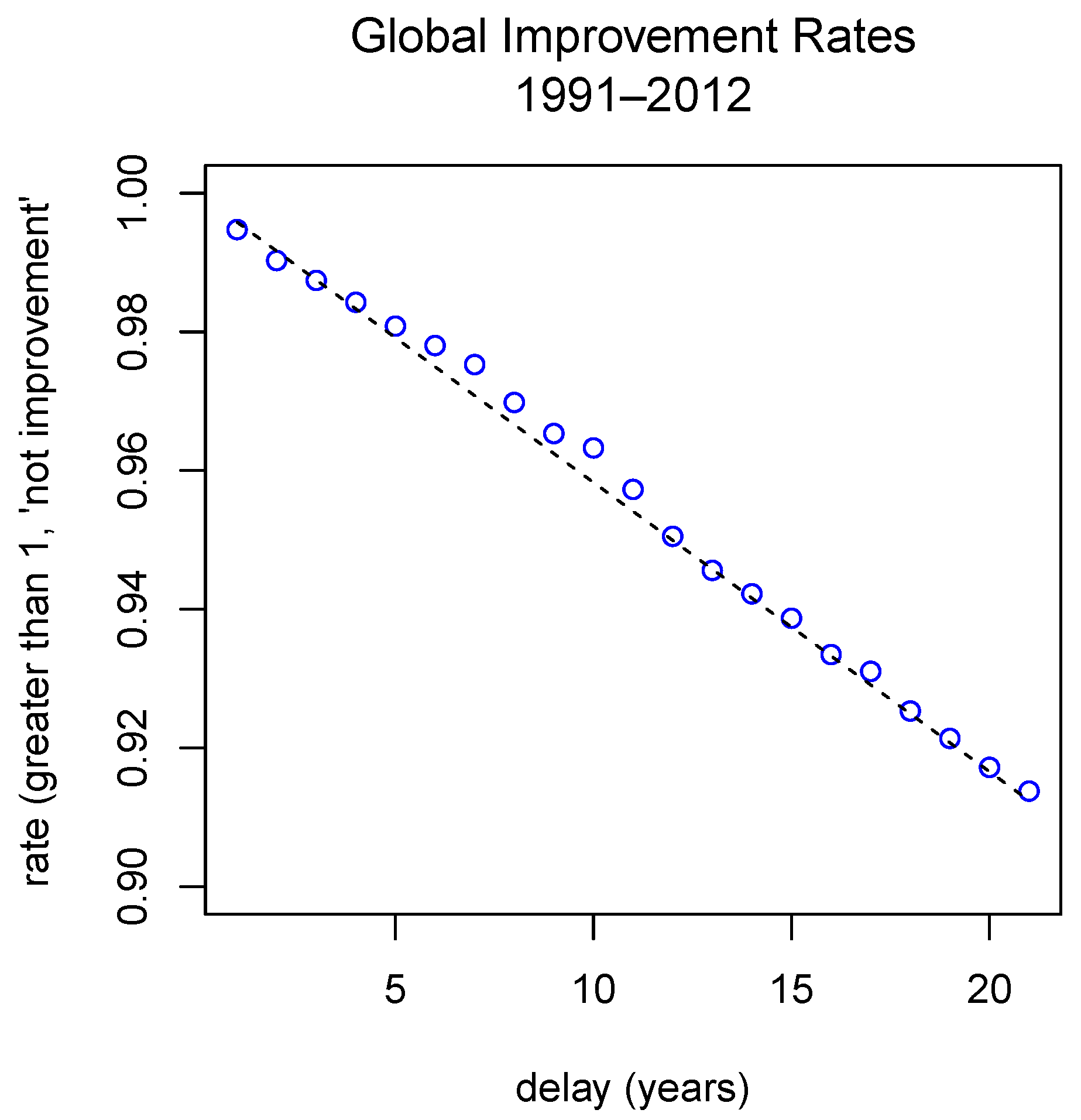
- We estimate the improvement rates by age and delays, that is:
- We estimate the mean, with respect to the delay, of the improvement rates:being the number of couples such that . We will refer to these values as the global improvement rates for the delayd.
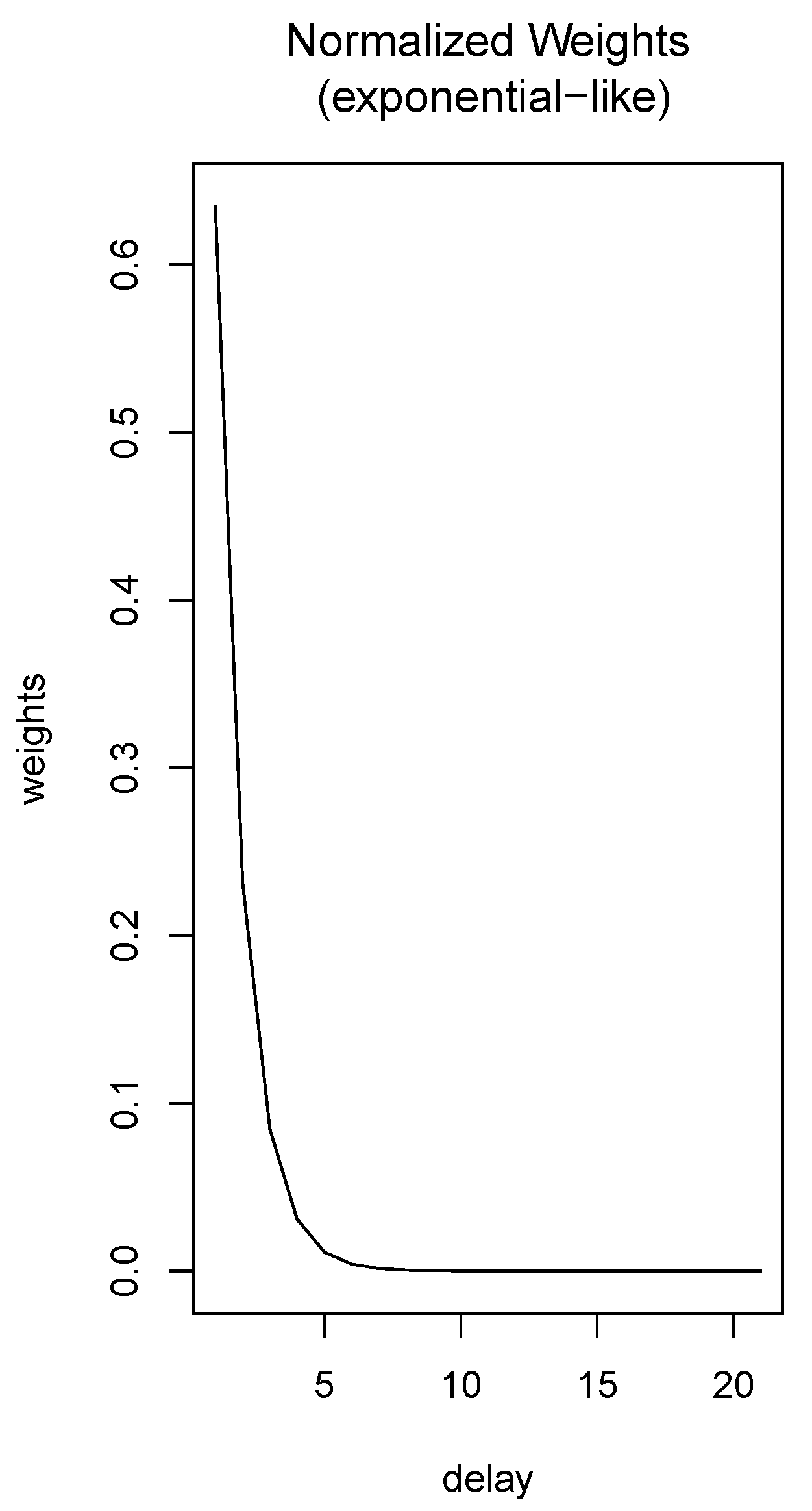
- The annual improvement rates by delay, , play an important role in the procedure because they contain previous information of the mortality process. However, the experience of studying this phenomenon allows us to assure that the importance of these rates are not the same for all delays, and it is clear (under usual conditions such as non-pandemic ones) that the behavior of the improvement rates become more important if they are close to the time of prediction. Using this realistic assumption, we assume that the importance of these rates is modulated by a probability distribution function. In particular, we consider a modified exponential function. To do this, we consider the exponential probability density function with the formand obtain a density function in the interval by puttingThen, we define the density function from (6) by forIn the particular case when in the numerical approximations we consider only integer delays, we can discretize the interval by using a finite number of integer delays , where is the maximum delay to be considered. Thus, instead of (17), we will use the discretized probability functionwhich approximates (17) at .Remark 3.We could also use the values of the function at to define the approximative function , but we have used (18) because the results in the numerical simulations were quite good. The use of the exponential function to derive is arbitrary. Thus, it is reasonable to think that the selected function is not optimal. In this sense, we consider that this topic could be a possible new line of investigation to improve the work.
- Using the annual improvement rates, and the exponential distribution, we define the weighted improvement rates as
- Using the improvement rates by delay, , we can define the functions from (6), by puttingwhere , and then defininig at other points by linear interpolation, that is,This procedure can be implemented for a non-integer step as well. Namely, let b be a divisor of . Then, we define in a similar way as above the improvement rates for . We observe that in this particular situation, the functions are independent of .
- H1.
- For each age x, for an arbitrary moment t and for a small time step , the graduate value at , denoted by , depends on:
- all graduate values at moment t, , (via Gaussian kernel graduation, see [17]).
- all previous moments of time , (via the exponential probability density function and the improvement rates).
- H2.
- The relation between and , is:where is a suitable kernel (in this work a Gaussian kernel), is the rate of death either at “negative ages” or after the actuarial infinite, and is defined above using the annual improvement rates from the past.
3.1.2. Application of Theoretical Results
3.2. Details and Example
3.2.1. Data, Period and Software
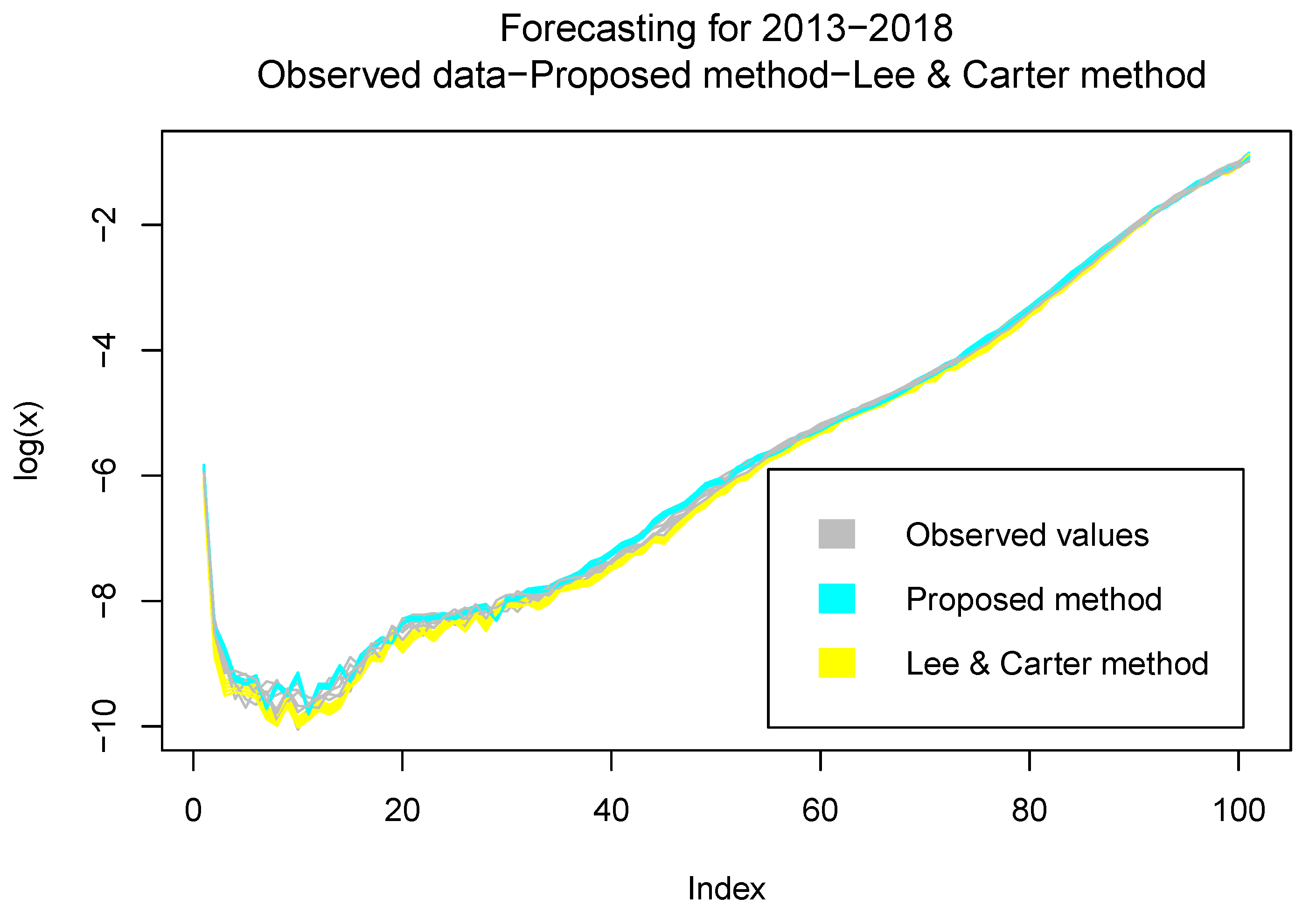
3.2.2. Validation
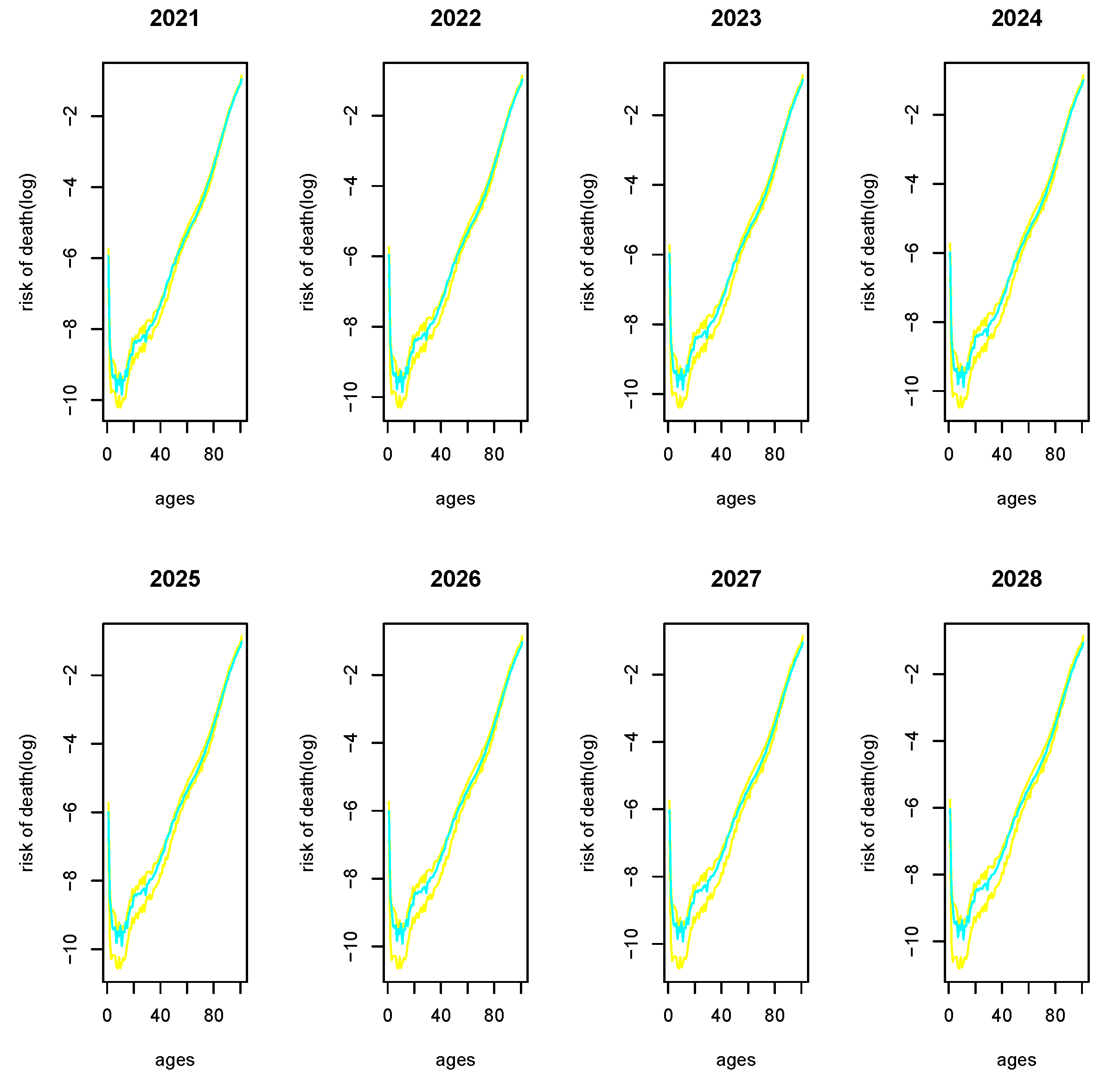
3.2.3. Estimations and Results
- In the model of this paper, we have considered the influence of the values of the variable in the past and not only in the current moment of time, as in [10].
- The functions are new in this paper and we have approximated them via the improvement rates
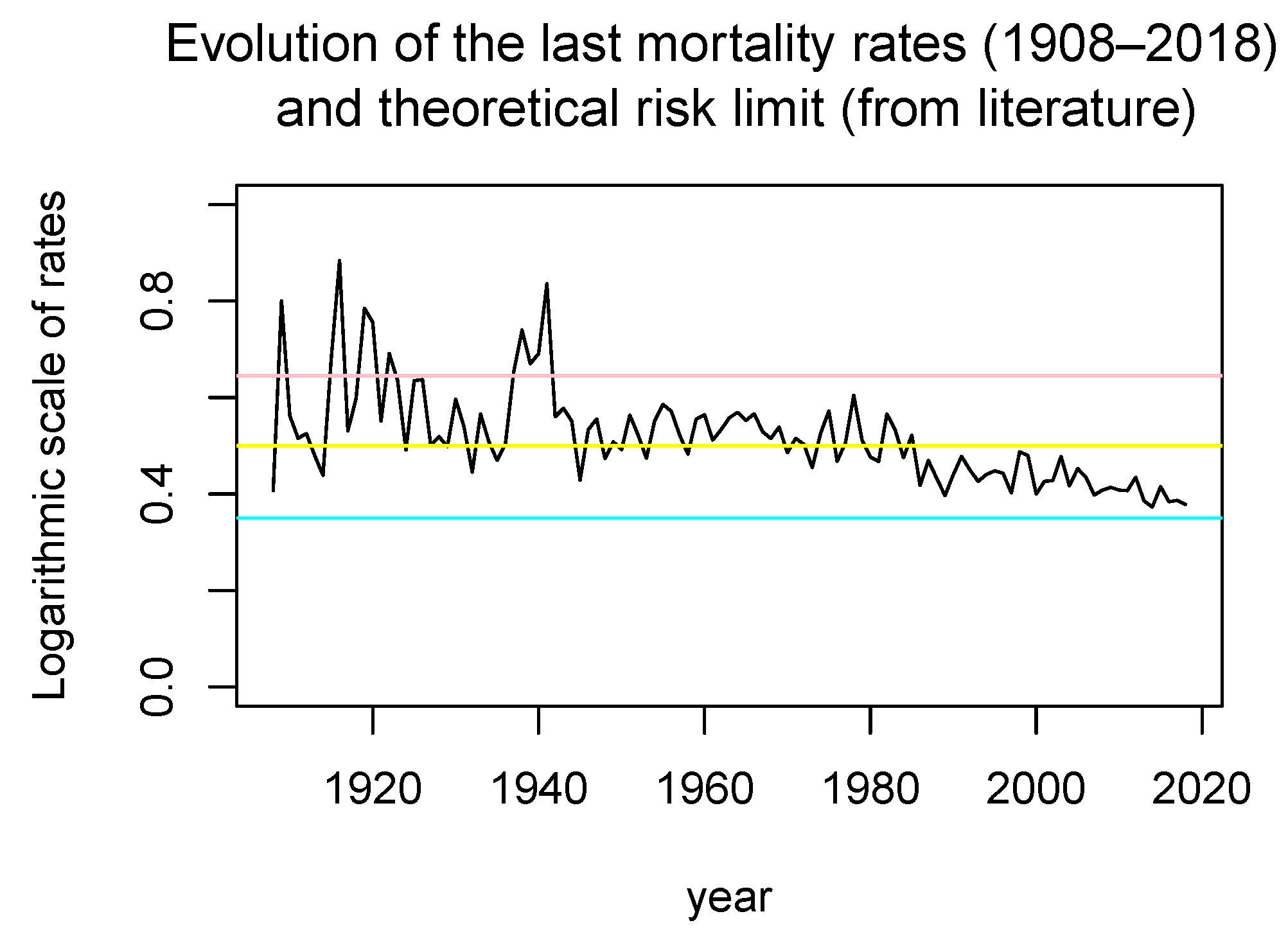
- In [10], the value of the function g was taken to be equal to 0 outside the domain D, whereas in the present work, the value of g for ages greater than 100 was taken to be equal to a positive number due to the “Plateau effect”.
- The numerical simulations show that the predictions are good enough for at least a period of 8 years, whereas in the model without delay, the predictions were good for a period of 3 years.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fife, P. Some nonclassical trends in parabolic and parabolic-like evolutions. In Trends in Nonlinear Analysis; Springer: Berlin, Germany, 2003; pp. 153–191. [Google Scholar]
- Cortazar, C.; Elgueta, M.; Rossi, J.D. Nonlocal diffusion problems that approximate the heat equations with Dirichlet boundary conditions. Israel J. Math. 2009, 170, 53–60. [Google Scholar] [CrossRef]
- Pérez-Llanos, M.; Rossi, J.D. Numerical approximations for a nonlocal evolution equations. SIAM J. Numer. Anal. 2012, 49, 2103–2123. [Google Scholar] [CrossRef]
- Bates, P.; Fife, P.; Ren, X.; Wang, X. Travelling waves in a convolution model for phase transitions. Arch. Ration. Mech. Anal. 1997, 138, 105–136. [Google Scholar] [CrossRef]
- Bates, P.; Chmaj, A. A discrete convolution model for phase transitions. Arch. Ration. Mech. Anal. 1999, 150, 281–305. [Google Scholar] [CrossRef]
- Bates, P.; Chmaj, A. An integrodifferential model for phase transitions: Stationary solutions in higher dimensions. J. Stat. Phys. 1999, 95, 1119–1139. [Google Scholar] [CrossRef]
- Bates, P.; Han, J. The Dirichlet boundary problem for a nonlocal Cahn-Hilliard equation. J. Math. Anal. Appl. 2005, 311, 289–312. [Google Scholar] [CrossRef]
- Chasseigne, E.; Chaves, M.; Rossi, J.D. Asymptotic behavior for nonlocal diffusion equations. J. Math. Pures Appl. 2006, 86, 271–291. [Google Scholar] [CrossRef]
- Bogoya, M.; Gómez S., C.A. Discrete model of a nonlocal diffusion equation. Rev. Colomb. Mat. 2013, 47, 83–94. [Google Scholar]
- Morillas, F.G.; Valero, J. On a nonlocal discrete diffusion system modeling life tables. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. RACSAM 2014, 108, 935–955. [Google Scholar] [CrossRef]
- Cairns, A.J.G.; Blake, D.; Dowd, K. Modelling and management of mortality risk: A review. Scand. Actuar. J. 2008, 2008, 79–113. [Google Scholar] [CrossRef]
- Hale, J.K. Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Amigó, J.M.; Giménez, A.; Morillas, F.; Valero, J. Attractors for a lattice dynamical system generated by non-newtonian fluids modelling suspensions. Internat. J. Bifur. Chaos 2010, 20, 2681–2700. [Google Scholar] [CrossRef]
- European Parliament and of the Council. Risk Management and Supervision of Insurance Companies (Solvency II)-Consolidated text: Directive 2009/138/EC of the European Parliament and of the Council of 25 November 2009 on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance. Available online: https://eur-lex.europa.eu/ (accessed on 6 December 2020).
- Chiang, C.L. The Life Tables and Its Applications; Krieger Publishing Company: Malabar, FL, USA, 1984. [Google Scholar]
- Benjamin, B.; Pollard, J.H. The Analysis of Mortality and Other Actuarial Statistics; Institute of Actuaries and the Faculty of Actuaries: Oxford, UK, 1993. [Google Scholar]
- Ayuso, M.; Corrales, H.; Guillén, M.; Perez-Marín, A.M.; Rojo, J.L. Estadística Actuarial Vida; Universitat de Barcelona, Edicions: Barcelona, Spain, 2007. [Google Scholar]
- University of California, Berkeley (USA); Max Planck Institute for Demographic Research (Germany). Human Mortality Database. Series of Death Rates of Spain. Available online: www.mortality.org (accessed on 1 December 2020).
- Instituto Nacional de Estadística (Statistics National Institute of Spain). Life Tables: Methodolgy. Available online: https://ine.es/en/metodologia/t20/t2020319a_en.pdf (accessed on 6 December 2020).
- Gompertz, B. On the nature of the function of the law of human mortality and on a new mode of determining the value of life contingencies. Trans. R. Soc. 1825, 115, 513–585. [Google Scholar]
- London, D. Graduation: The Revision of Estimates; ACTEX Publications: New Hartford, CT, USA, 1985. [Google Scholar]
- Beer, J. Dealing with uncertainty in population forecasting (Statistics Netherlands). Available online: https://www.cbs.nl/-/media/imported/documents/2000/24/dealing-with-uncertainty.pdf (accessed on 21 December 2020).
- Helligman, L.M.A.; Pollard, J.H. The age pattern of mortality. J. Inst. Actuar. 1980, 107, 49–82. [Google Scholar] [CrossRef]
- Forfar, D.O.; McCutcheon, M.A.; Wilkie, M.A. On graduation by mathematical formula. J. Inst. Actuar. 1988, 115, 1–149. [Google Scholar] [CrossRef]
- Gavin, J.; Haberman, S.; Verrall, R. Moving weighted average graduation using kernel estimation. Insur. Math. Econ. 1993, 12, 113–126. [Google Scholar] [CrossRef]
- Debón, A.; Montes, F.; Sala, R. A comparison of parametric models for mortality graduation. Application to mortality data for the Valencia Region (Spain). SORT Stat. Oper. Res. 2005, 29, 269–288. [Google Scholar]
- Villegas, A.M.; Kaishev, V.K.; Millossovich, P. StMoMo: A R package for stochastic mortality modeling. J. Stat. Softw. 2018, 84, 1–38. [Google Scholar] [CrossRef]
- Lee, R.; Carter, L. Modelling and forecasting US mortality. J. Am. Stat. Assoc. 1992, 87, 659–671. [Google Scholar]
- Debón, A.; Montes, F.; Sala, R. A comparison of models for dynamic life tables. Application to mortality data from the Valencia Region (Spain). Lifetime Data Anal. 2006, 12, 223–244. [Google Scholar] [CrossRef]
- Debón, A.; Montes, F.; Puig, F. Modelling and forecasting mortality in Spain. Eur. J. Oper. Res. 2008, 189, 624–637. [Google Scholar] [CrossRef][Green Version]
- Haberman, S.; Renshaw, A. On age-period-cohort parametric mortality rate projections. Insur. Math. Econ. 2009, 45, 255–270. [Google Scholar] [CrossRef]
- Dodd, E.; Forster, J.J.; Bijak, J.; Smith, P.W.F. Smoothing mortality data: Producing the English life table, 2010–2012. J. R. Stat. Soc. Ser. A Stat. Soc. 2016, 181, 1–19. [Google Scholar] [CrossRef]
- Copas, J.B.; Haberman, S. Non-parametric graduation using kernel methods. J. Inst. Actuar. 1983, 110, 135–156. [Google Scholar] [CrossRef]
- Morillas, F.G.; Baeza, I.; Pavia, J.M. Risk of death: A two-step method using wavelets and piecewise harmonic interpolation. Estadística Española 2016, 58, 245–264. [Google Scholar]
- Morillas, F.G.; Sampere, I.B. Using wavelet techniques to approximate the subjacent risk of death. In Modern Mathematics and Mechanics; Sadovnichiy, V.A., Zgurovsky, M.Z., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Chapter 28; pp. 541–557. [Google Scholar]
- Brouhns, N.; Denuit, M.; Keilegom, I.V. Bootstrapping the Poisson log-bilinear model for mortality forecasting. Scand. Actuar. J. 2005, 2005, 212–224. [Google Scholar] [CrossRef]
- Dodd, E.; Forster, J.J.; Bijak, J.; Smith, P.W.F. Stochastic modelling and projection of mortality improvements using a hybrid parametric/semi-parametric age–period–cohort model. Scand. J. 2020. [Google Scholar] [CrossRef]
- Haberman, S.; Renshaw, A. Parametric mortality improvement rate modelling and projecting. Insur. Math. Econ. 2012, 50, 309–333. [Google Scholar] [CrossRef]
- Haberman, S.; Renshaw, A. Modelling and projecting mortality improvement rates using a cohort perspective. Insur. Math. Econ. 2013, 53, 150–168. [Google Scholar] [CrossRef]
- Albarrán Lozano, I.; Ariza Rodríguez, F.; Cóbreces Juárez, V.M.; Durbán Reguera, M.L.; Rodríguez-Pardo del Castillo, J.M. Riesgo de Longevidad y su aplicación práctica a Solvencia II. VIII International Awards “Julio Castelo Matrán”, Fundación Mapfre. Available online: https://www.fundacionmapfre.org/fundacion/es_es/publicaciones/diccionario-mapfre-seguros/r/riesgo-de-longevidad.jsp (accessed on 21 December 2020).
- Montes, M.J. Las Culturas del Nacimiento. Ph.D. Thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2007. [Google Scholar]
- Lledó, J.; Pavía, J.M.; Morillas, F.G. Transformaciones en la distribución semanal de nacimientos. Un análisis temporal 1940–2010. Revista Española Investigaciones Sociológicas 2017, 159, 151–162. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 21 December 2020).
- Hyndman, R.J. (with Contributions from Heather Booth, Leonie Tickle and John Maindonald). Package Demography: Forecasting Mortality, Fertility, Migration and Population Data (R Package Version 1.22). 2019. Available online: https://CRAN.R-project.org/package=demography (accessed on 21 December 2020).
- Dolgin, E. Longevity data hint at no natural limit on lifespan. Nature 2018, 559, 14–15. [Google Scholar] [CrossRef]
- Barbi, E.; Lagona, F.; Marsili, M.; Vaupel, J.W.; Kenneth, W.W. The plateau of human mortality: Demography of longevity pioneers. Science 2018, 360, 1459–1461. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Milholland, B.; Vijg, J. Evidence for a limit to human lifespan. Nature 2016, 538, 257–259. [Google Scholar] [CrossRef] [PubMed]

| Model | ||||||
| Lee-Carter | ||||||
| %Improve. | ||||||
| Model | ||||||
| Lee-Carter | ||||||
| %Improve. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morillas, F.; Valero, J. On a Retarded Nonlocal Ordinary Differential System with Discrete Diffusion Modeling Life Tables. Mathematics 2021, 9, 220. https://doi.org/10.3390/math9030220
Morillas F, Valero J. On a Retarded Nonlocal Ordinary Differential System with Discrete Diffusion Modeling Life Tables. Mathematics. 2021; 9(3):220. https://doi.org/10.3390/math9030220
Chicago/Turabian StyleMorillas, Francisco, and José Valero. 2021. "On a Retarded Nonlocal Ordinary Differential System with Discrete Diffusion Modeling Life Tables" Mathematics 9, no. 3: 220. https://doi.org/10.3390/math9030220
APA StyleMorillas, F., & Valero, J. (2021). On a Retarded Nonlocal Ordinary Differential System with Discrete Diffusion Modeling Life Tables. Mathematics, 9(3), 220. https://doi.org/10.3390/math9030220





