A Study of ψ-Hilfer Fractional Boundary Value Problem via Nonlinear Integral Conditions Describing Navier Model

Abstract

This paper investigates existence, uniqueness, and Ulam’s stability results for a nonlinear implicit $\psi$-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s. By Banach’s fixed point theorem, the unique property is established. Meanwhile, existence results are proved by using the fixed point theory of Leray-Schauder’s and Krasnoselskii’s types. In addition, Ulam’s stability results are analyzed. Furthermore, several instances are provided to demonstrate the efficacy of the main results.

1. Introduction

Hundreds of years ago, fractional calculus began and has been widely interested by researchers in branches of applied mathematics, science, engineering, and so on (see References [1,2,3]). It is also known as the non-integer order (fractional-order) of differential and integral operators. Various definitions of novel fractional integral and derivative operators are currently prominent tools in numerous publications. Normally, the real-world problems were simulated using differential equations and solved the difficulties using powerful techniques (see References [4,5]). The fractional calculus has been used to examine differential equations with non-integer order (fractional differential equations ($\mathbb{FDE}$s)). $\mathbb{FDE}$s via initial/boundary conditions have also been used to solve the problems since fractional-order has more additional degrees of freedom than integer-order, allowing for more precise and realistic solutions. Researchers have considered a variety of mathematical approaches in relation to $\mathbb{FDE}$s in a large number of papers (see References [6,7,8,9,10,11,12,13,14,15,16,17,18,19]).

Elastic beams are an essential element required in structural problems, including aircraft, ships, bridges, buildings, and so on (see References [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]). In the sense of mathematical analysis, the deformation of the beam can be analyzed using the fourth-order boundary value problem ($\mathbb{BVP}$) describing the Navier model [37]:

$$\left\{\begin{array}{c}{\displaystyle u^{\left(4\right)}\left(\tau \right)=g(\tau ,u\left(\tau \right),u^{\prime \prime }\left(\tau \right)),\tau \in (0,1),}\hfill \\ {\displaystyle u\left(0\right)=u\left(1\right)=u^{\prime \prime }\left(0\right)=u^{\prime \prime }\left(1\right)=0,}\hfill \end{array}\right.$$

(1)

where $g\in \mathcal{C}([0,1]\times {\mathbb{R}}^2,\mathbb{R})$. Problem (1) has attracted the attention of many researchers due to its dominance in the field of mechanics. It simulates the bending equilibrium of a beam supported at both ends by an elastic basis. We will go through some important works on the subject shortly below. For instance, in 1986, Aftabizadeh [38] converted (1) into a second-order integro-differential equation with f is bounded on $[0,1]\times {\mathbb{R}}^2$. The existence results were analyzed by Schauder’s fixed point theorem. In 1997, Ma et al. [39] examined the existence of a solution for (1) by applying the upper and lower solutions method. After that, in 2004, Bai et al. [40] developed upper and lower solutions of (1). Dang et al. [41] examined the problem (1) by reducing it to an operator equation and using some simply confirmed conditions. In recent years, many literature examples pay attention to $\mathbb{BVP}$s under many kinds of fractional derivatives; for instance, in 2020, Bachar and Eltayeb [42] studied the Navier $\mathbb{BVP}$ under Riemann-Liouville ($\mathbb{RL}$) fractional derivative type:

$$\left\{\begin{array}{c}{\displaystyle {}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^{\alpha }\left({}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^{\beta }u\right)\left(\tau \right)=g(\tau ,u\left(\tau \right),{}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^{\beta }u\left(\tau \right)),\tau \in (0,1),}\hfill \\ {\displaystyle u\left(0\right)={}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^{\beta }u\left(0\right)=u\left(1\right)={}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^{\beta }u\left(1\right)=0,}\hfill \end{array}\right.$$

(2)

where ${}^{\mathbb{RL}}{\mathfrak{D}}_{0^{+}}^q$ denotes the $\mathbb{RL}$-fractional derivative of order $q=\{\alpha ,\beta \}\in (1,2]$ and $g\in \mathcal{C}([0,1],{\mathbb{R}}^2)$. The Green properties and helpful inequality technique are used to establish the uniqueness result of positive solutions for (2). $\mathbb{FDE}$s have been discussed in depth by several researchers. Clearly, the existence, uniqueness, and stability analysis of solutions are some important properties of $\mathbb{FDE}$s. Because the exact solution to differential equations or $\mathbb{FDE}$s is quite difficult, several researchers have attempted to identify the best technique to access the existence results. To establish the existence and stability of solutions for $\mathbb{FDE}$s, several analytical techniques, including fixed-point theory, have been investigated. Ulam’s stability is one of the most useful strategies which guarantee that there exists a close exact solution. Ulam’s stability has four types, such as Ulam–Hyers ($\mathbb{UH}$), generalized Ulam–Hyers ($\mathbb{GUH}$), Ulam–Hyers–Rassias ($\mathbb{UHR}$), and generalized Ulam–Hyers–Rassias ($\mathbb{GUHR}$) stabilities; see References [43,44,45,46,47,48,49,50,51,52,53,54] and references cited therein. However, to the authors’ knowledge, a few papers involving the Navier model in sense of $\psi$-Hilfer fractional operators have been concerned.

As a result of the preceding debates, we discuss a new class of nonlinear implicit $\psi$-Hilfer $\mathbb{FBVP}$ describing Navier model with nonlinear integral boundary conditions ($\mathbb{NIBC}$s):

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\right)\left(\tau \right)=f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right)),\tau \in (a,b),}\hfill \\ {\displaystyle u\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\left(a\right)=0,}\hfill \\ {\displaystyle \sum _{i=1}^m{\xi }_{i}u\left({\eta }_i\right)={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right)),\sum _{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }u\left({\lambda }_j\right)={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right)),}\hfill \end{array}\right.$$

(3)

where ${}^H{\mathfrak{D}}_{a^{+}}^{q,\rho ;\psi }$ denotes $\psi$-Hilfer fractional derivative of order $q=\{\alpha ,\beta ,{\varphi }_j\}$, $\alpha$, $\beta$, ${\varphi }_j\in (1,2]$, $j=1,2,\dots ,n$, $\rho \in [0,1]$, ${\mathcal{I}}_{a^{+}}^{v;\psi }$ denotes $\psi$-$\mathbb{RL}$-fractional integral of order $v=\{\phi ,\nu \}>0$, $f\in \mathcal{C}(\mathcal{J}\times {\mathbb{R}}^3,\mathbb{R})$, $\mathcal{G}$, $\mathcal{H}\in \mathcal{C}(\mathcal{J},\mathbb{R})$, $\mathcal{J}:=[a,b]$, $b>a>0$, $\sigma$, $\zeta$, ${\xi }_i$, ${\mu }_j\in \mathbb{R}$, $\sigma$, $\zeta$, ${\eta }_i$, ${\lambda }_j\in (a,b)$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$, and

$$\begin{array}{ccc}\hfill \left(\mathcal{K}u\right)\left(\tau \right)& =& \frac{1}{\mathrm{\Gamma }\left(\theta \right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{\theta -1}{\psi }^{\prime }\left(s\right)k(\tau ,s)u\left(s\right)ds,\tau \in \mathcal{J},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \left(\mathcal{W}u\right)\left(\tau \right)& =& \frac{1}{\mathrm{\Gamma }\left(\delta \right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{\delta -1}{\psi }^{\prime }\left(s\right)w(\tau ,s)u\left(s\right)ds,\tau \in \mathcal{J},\hfill \end{array}$$

(5)

where k, $w\in \mathcal{C}({\mathcal{J}}^2,[a,\infty ))$. The existence and uniqueness property is proved by using Banach’s fixed point theorem (Lemma 5), and the existence properties are derived by applying Leray-Schauder’s nonlinear alternative (Lemma 8) and Krasnoselskii’s fixed point theorems (Lemma 9) for the $\psi$-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3). We employ $\mathbb{UH}$, $\mathbb{GUH}$, $\mathbb{UHR}$, and $\mathbb{GUHR}$ stables to investigate the stability of (3). Finally, we give some numerical examples of various functions that were explored in order to confirm the theoretical results. In addition, we give our findings on a broad platform that covers a wide area of specific situations for different values $\rho$ and $\psi$. For example, $\psi$-Riemann-Liouville problem if $\rho =0$, $\psi$-Caputo problem if $\rho =1$, Riemann-Liouville $\mathbb{BVP}$ if $\rho =0$, $\psi \left(\tau \right)=\tau$, Caputo problem if $\rho =1$, $\psi \left(\tau \right)=\tau$, Hilfer problem if $\psi \left(\tau \right)=\tau$, Katugampola problem if $\psi \left(\tau \right)={\tau }^q$, Hilfer-Hadamard problem if $\psi \left(\tau \right)=log\left(\tau \right)$, and so on. The received results are improved: if $\alpha =2$, $\beta =2$, $\rho =1$, and $\psi \left(t\right)=t$, then we obtained Reference [41]; if $\rho =1$ and $\psi \left(t\right)=t$, then we obtained Reference [42].

This paper is structured the continuing parts of the paper as follows: In Section 2, we provide an essential system of symbols, definitions, and lemmas of $\psi$-Hilfer fractional calculus. Next, we state a lemma which is used in proving the main results. In Section 3, fixed point theorems are used to obtain the existence results of the proposed problem. By helping with the nonlinear analysis method, in Section 4, we analyze various of Ulam’s stability for the problem. Examples illustrate to confirm the effectiveness of the acquired theoretical results in Section 5. Finally, the conclusion and discussion of this paper are presented in Section 6.

2. Preliminaries

We provide the basic concepts of $\psi$-Hilfer fractional calculus, as well as important crucial results that will be engaged in this paper. Assume that $\mathcal{E}=\mathcal{C}(\mathcal{J},\mathbb{R})$ is the Banach space of continuous functions on $\mathcal{J}$ with $\parallel u\parallel ={sup}_{\tau \in \mathcal{J}}\left\{\right|u\left(\tau \right)\left|\right\}$. Assume that ${\mathcal{AC}}^n(\mathcal{J},\mathbb{R})$ is the space of n-times absolutely continuous functions with ${\mathcal{AC}}^n(\mathcal{J},\mathbb{R})=\{u:\mathcal{J}\to \mathbb{R};u^{(n-1)}\in \mathcal{AC}(\mathcal{J},\mathbb{R})\}$.

Definition 1.

(Reference [3]). Assume that $\psi \left(\tau \right)\in {\mathcal{C}}^1(\mathcal{J},\mathbb{R})$ is an increasing function with ${\psi }^{\prime }\left(\tau \right)\ne 0$ for each $\tau \in \mathcal{J}$. The ψ-$\mathbb{RL}$-fractional integral of order α of f depending on ψ on $\mathcal{J}$ is defined by

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }f\left(\tau \right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{\alpha -1}{\psi }^{\prime }\left(s\right)f\left(s\right)ds,\tau >a>0,\alpha >0,$$

where $\mathrm{\Gamma }(·)$ is the Gamma function.

Definition 2.

(Reference [3]). Assume that $\psi \left(\tau \right)$ is defined as in Definition with ${\psi }^{\prime }\left(\tau \right)\ne 0$. The ψ-$\mathbb{RL}$-fractional derivative of f depending on ψ is defined as ${\mathfrak{D}}_{a^{+}}^{\alpha ;\psi }f\left(\tau \right)={\left(\frac{1}{{\psi }^{\prime }\left(\tau \right)}\frac{d}{d\tau }\right)}^n{\mathcal{I}}_{a^{+}}^{n-\alpha ;\psi }f\left(\tau \right)$ or

$${\mathfrak{D}}_{a^{+}}^{\alpha ;\psi }f\left(\tau \right)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\left(\frac{1}{{\psi }^{\prime }\left(\tau \right)}\frac{d}{d\tau }\right)}^n{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{n-\alpha -1}{\psi }^{\prime }\left(s\right)f\left(s\right)ds,\alpha >0,$$

where $n=\left[\alpha \right]+1$, and $\left[\alpha \right]$ is an integer part of $Re\left(\alpha \right)$.

Definition 3.

(Reference [55]). Assume that $\gamma =\alpha +\rho (n-\alpha )$, $\alpha \in (n-1,n)$ with $n\in \mathbb{N}$, $f\in {\mathcal{C}}^n(\mathcal{J},\mathbb{R})$ and $\psi \left(\tau \right)\in {\mathcal{C}}^1(\mathcal{J},\mathbb{R})$ is increasing with ${\psi }^{\prime }\left(\tau \right)\ne 0$ for each $\tau \in \mathcal{J}$. Then, the ψ-Hilfer fractional derivative of type $\rho \in [0,1]$ of f depending on ψ is defined as

$${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }f\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\rho (n-\alpha );\psi }{\left(\frac{1}{{\psi }^{\prime }\left(\tau \right)}\frac{d}{d\tau }\right)}^n{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\gamma -\alpha ;\psi }{}^{}{\mathfrak{D}}_{a^{+}}^{\gamma ;\psi }f\left(\tau \right),$$

where ${}^{}{\mathfrak{D}}_{a^{+}}^{\gamma ;\psi }f\left(\tau \right)={}^{}{\mathfrak{D}}_{a^{+}}^{n;\psi }{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(\tau \right)$.

Lemma 1.

(Reference [3]). Assume that $\alpha ,\beta >0$. Then, ${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{I}}_{a^{+}}^{\beta ;\psi }f\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }f\left(\tau \right)$, $\tau >a$.

Proposition 1.

(References [3,55]). Assume that $\tau >a$ and ${\mathcal{G}}^{\upsilon }\left(\tau \right)={\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{\upsilon }$. Then, for $\upsilon >0$, $\alpha \ge 0$, we have

(i) 

${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{\mathcal{G}}^{\upsilon -1}\left(\tau \right)=\frac{\mathrm{\Gamma }\left(\upsilon \right)}{\mathrm{\Gamma }(\upsilon +\alpha )}{\mathcal{G}}^{\upsilon +\alpha -1}\left(\tau \right)$;

(ii) 

${\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }{\mathcal{G}}^{\upsilon -1}\left(\tau \right)=\frac{\mathrm{\Gamma }\left(\upsilon \right)}{\mathrm{\Gamma }(\upsilon -\alpha )}{\mathcal{G}}^{\upsilon -\alpha -1}\left(\tau \right)$;

(iii) 

${{}^H\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }{\mathcal{G}}^{\upsilon -1}\left(\tau \right)=\frac{\mathrm{\Gamma }\left(\upsilon \right)}{\mathrm{\Gamma }(\upsilon -\alpha )}{\mathcal{G}}^{\upsilon -\alpha -1}\left(\tau \right),\upsilon >\gamma =\alpha +\rho (n-\alpha )$.

Lemma 2.

(Reference [55]) Assume that $f\in {\mathcal{C}}^n(\mathcal{J},\mathbb{R})$, $\alpha \in (n-1,n)$, $\rho \in [0,1]$, $\gamma =\alpha +\rho (n-\alpha )$. Then, we obtain

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }f\left(\tau \right)=f\left(\tau \right)-\sum _{k=1}^n\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{q-k}}{\mathrm{\Gamma }(q-k+1)}{f}_{\psi }^{[n-k]}{\mathcal{I}}_{a^{+}}^{(1-\rho )(n-\alpha );\psi }f\left(a\right),$$

for all $\tau \in \mathcal{J}$, where $f_{\psi }^{\left[n\right]}f\left(\tau \right):={\left(\frac{1}{{\psi }^{\prime }\left(\tau \right)}\frac{d}{dt}\right)}^{n}f\left(\tau \right)$.

Lemma 3.

(Reference [51]) Assuming that $\alpha \in (m-1,m)$, $\beta \in (n-1,n)$, n, $m\in \mathbb{N}$, $n\le m$, $\rho \in [0,1]$, and $\alpha >\beta +\rho (n-\beta )$. If $f\in {\mathcal{C}}_{1-\gamma ,\psi }(\mathcal{J},\mathbb{R})$, then ${{}^H\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }{\mathcal{I}}_{a^{+}}^{\alpha ;\psi }f\left(\varsigma \right)={\mathcal{I}}_{0^{+}}^{\alpha -\beta ;\psi }f\left(\varsigma \right)$.

Lemma 4.

Let α, β, ${\varphi }_j\in (1,2]$, $(j=1,2,\dots ,n)$, $\rho \in [0,1]$, ${\gamma }_1=\alpha +\rho (2-\alpha )$, ${\gamma }_2=\beta +\rho (2-\beta )$, ω, φ, $\nu >0$. Suppose that $h\in \mathcal{E}$ and $\mathrm{\Omega }={\mathrm{\Omega }}_{11}{\mathrm{\Omega }}_{22}-{\mathrm{\Omega }}_{12}{\mathrm{\Omega }}_{21}\ne 0$. Then, $u\in {\mathcal{C}}^2(\mathcal{J},\mathbb{R})$ is a solution of

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\right)\left(\tau \right)=h\left(\tau \right),\tau \in (a,b),}\hfill \\ {\displaystyle u\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\left(a\right)=0,}\hfill \\ {\displaystyle \sum _{i=1}^m{\xi }_{i}u\left({\eta }_i\right)={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right)),\sum _{i=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }u\left({\lambda }_j\right)={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right)),}\hfill \end{array}\right.$$

(6)

if and only if u verifies the integral equation

$$\begin{array}{c}\hfill \begin{array}{ccc}u\left(\tau \right)\hfill & =\hfill & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Omega }\mathrm{\Gamma }({\gamma }_1+\beta )}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left({\eta }_i\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left({\lambda }_j\right)\right)]\hfill \\ \hfill & \hfill & +\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Omega }\mathrm{\Gamma }\left({\gamma }_2\right)}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left({\lambda }_j\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left({\eta }_i\right)\right)],\hfill \end{array}\end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{11}& =& \sum _{i=1}^m\frac{{\xi }_i{\left(\psi \left({\eta }_i\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Gamma }({\gamma }_1+\beta )},{\mathrm{\Omega }}_{12}=\sum _{i=1}^m\frac{{\xi }_i{\left(\psi \left({\eta }_i\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Gamma }\left({\gamma }_2\right)},\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{21}& =& \sum _{j=1}^n\frac{{\mu }_j{\left(\psi \left({\lambda }_j\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -{\varphi }_j-1}}{\mathrm{\Gamma }({\gamma }_1+\beta -{\varphi }_j)},{\mathrm{\Omega }}_{22}=\sum _{j=1}^n\frac{{\mu }_j{\left(\psi \left({\lambda }_j\right)-\psi \left(a\right)\right)}^{{\gamma }_2-{\varphi }_j-1}}{\mathrm{\Gamma }({\gamma }_2-{\varphi }_j)}.\hfill \end{array}$$

(9)

Proof. 

Suppose that $u\in \mathcal{E}$ is the solution of (6). Taking ${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }$ into both sides of (6) via Lemma 2, we obtain

$${}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\alpha ;\psi }h\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1-1}}{\mathrm{\Gamma }\left({\gamma }_1\right)}{c}_1+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1-2}}{\mathrm{\Gamma }({\gamma }_1-1)}{c}_2,$$

(10)

where $c_1$, $c_2\in \mathbb{R}$.

From the boundary condition ${}^H{\mathfrak{D}}_{0^{+}}^{\beta ,\rho ;\psi }u\left(a\right)=0$, we get $c_2=0$. Taking ${\mathcal{I}}_{a^{+}}^{\beta ;\psi }$ into (10) via Lemma 2 again, it follows that

$$\begin{array}{ccc}\hfill u\left(\tau \right)& =& {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Gamma }({\gamma }_1+\beta )}{c}_1\hfill \\ & & +\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Gamma }\left({\gamma }_2\right)}{c}_3+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-2}}{\mathrm{\Gamma }({\gamma }_2-1)}{c}_4,\hfill \end{array}$$

(11)

where $c_3$, $c_4\in \mathbb{R}$. From condition $x\left(a\right)=0$, it is implied that $c_4=0$. So,

$$u\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Gamma }({\gamma }_1+\beta )}{c}_1+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Gamma }\left({\gamma }_2\right)}{c}_3.$$

(12)

Taking ${}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }$ into (12), then

$${}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }u\left(\tau \right)={\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -{\varphi }_j-1}}{\mathrm{\Gamma }({\gamma }_1+\beta -{\varphi }_j)}{c}_1+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-{\varphi }_j-1}}{\mathrm{\Gamma }({\gamma }_2-{\varphi }_j)}{c}_3.$$

By using boundary conditions in (6), we get

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{11}{c}_1+{\mathrm{\Omega }}_{12}{c}_3& =& {\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left({\eta }_i\right),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_{21}{c}_1+{\mathrm{\Omega }}_{22}{c}_3& =& {\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left({\lambda }_j\right),\hfill \end{array}$$

(14)

where ${\mathrm{\Omega }}_{11}$, ${\mathrm{\Omega }}_{12}$, ${\mathrm{\Omega }}_{21}$, and ${\mathrm{\Omega }}_{22}$ are given by (8) and (9). Solving (13) and (14), we have

$$\begin{array}{ccc}\hfill c_1& =& \frac{1}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,x\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left({\eta }_i\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left({\lambda }_j\right)\right)],\hfill \\ \hfill c_3& =& \frac{1}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }h\left({\lambda }_j\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }h\left({\eta }_i\right)\right)].\hfill \end{array}$$

Hence, the solution u follows by using $c_1$ and $c_3$ in (10). This yields that $u\left(\tau \right)$ verifies (7).

On the other hand, in a direct way, we can show that $u\left(\tau \right)$ is defined by (7) satisfies (6) under nonlinear integral boundary conditions. □

3. Existence Results

Setting the symbol

$${\mathcal{I}}_{a^{+}}^{q;\psi }{\mathcal{F}}_u\left(c\right)=\frac{1}{\mathrm{\Gamma }\left(q\right)}{\int }_a^c{\left(\psi \left(c\right)-\psi \left(s\right)\right)}^{q-1}{\psi }^{\prime }\left(s\right){\mathcal{F}}_u\left(s\right)ds,$$

where ${\mathcal{F}}_u\left(\tau \right)=f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right))$ with $q\in \{\alpha +\beta ,\phi ,\nu ,\alpha +\beta -{\varphi }_j\}$, $c=\{\tau ,\sigma ,\zeta ,{\eta }_i,{\lambda }_j,b\}$, $i=1,2,\dots ,m$, $j=1,2,\dots ,n$. Thanks to Lemma 4, we determine $\mathcal{Q}:\mathcal{E}\to \mathcal{E}$

$$\begin{array}{c}\hfill \begin{array}{ccc}\left(\mathcal{Q}u\right)\left(\tau \right)\hfill & =\hfill & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right)+\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Omega }\mathrm{\Gamma }({\gamma }_1+\beta )}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)]\hfill \\ \hfill & \hfill & +\frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Omega }\mathrm{\Gamma }\left({\gamma }_2\right)}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)].\hfill \end{array}\end{array}$$

(15)

Clearly, $\mathcal{Q}$ has fixed points if and only if problem (3) has solutions. To simplify,

$$\begin{array}{ccc}\hfill {\mathrm{\Psi }}^q(a,v)& =& \frac{{\left(\psi \left(v\right)-\psi \left(a\right)\right)}^q}{\mathrm{\Gamma }(q+1)},\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathrm{\Phi }(A,B)& =& \frac{1}{\left|\mathrm{\Omega }\right|}\left(\left|A\right|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|B\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right),\hfill \\ \hfill \mathrm{\Lambda }\left(q\right)& =& {\mathrm{\Psi }}^q\left(b\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{q-{\varphi }_j}\left({\lambda }_j\right)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & +\mathrm{\Phi }({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^q\left({\eta }_i\right).\hfill \end{array}$$

(18)

3.1. Uniqueness Property via Banach’s Fixed Point Theorem

Lemma 5.

(Banach’s fixed point theorem [56]). Assume that X is a non-empty closed subset of $\mathcal{E}$, where $\mathcal{E}$ is a Banach space. Then, any contraction mapping $\mathcal{Q}$ from $\mathcal{E}$ into itself has a unique fixed point.

Theorem 1.

Assume that $f\in \mathcal{C}(\mathcal{J}\times {\mathbb{R}}^3,\mathbb{R})$ and $k\in \mathcal{C}({\mathcal{J}}^2\times \mathbb{R},\mathbb{R})$ verifies the conditions:

$\left({\mathcal{P}}_1\right)$

There exist constants ${\mathcal{L}}_1$, ${\mathcal{L}}_2$, ${\mathcal{L}}_3>0$ with ${\mathcal{L}}_2<1$ such that

$$\left|f(\tau ,u_1,v_1,w_1)-f(\tau ,u_2,v_2,w_2)\right|\le {\mathcal{L}}_1|u_1-u_2|+{\mathcal{L}}_2|v_1-v_2|+{\mathcal{L}}_3|w_1-w_2|,$$

for any $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$, $\tau \in \mathcal{J}$.

$\left({\mathcal{P}}_2\right)$

There exist constants ${\mathcal{H}}_1^{*}$, ${\mathcal{G}}_1^{*}>0$ such that

$$\left|\mathcal{H}(\tau ,u_1)-\mathcal{H}(\tau ,u_2)\right|\le {\mathcal{H}}_1^{*}|u_1-u_2|\mathrm{and}\left|\mathcal{G}(\tau ,u_1)-\mathcal{G}(\tau ,u_2)\right|\le {\mathcal{G}}_1^{*}|u_1-u_2|,$$

for any $u_i\in \mathbb{R}$, $i=1,2$, $\tau \in \mathcal{J}$.

If

$${\Delta }_1+{\Delta }_2<1,$$

(19)

where

$$\begin{array}{ccc}\hfill {\Delta }_1& =& \mathrm{\Lambda }(\alpha +\beta ){\mathcal{L}}_1+\mathrm{\Lambda }(\mathrm{\theta }+\alpha +\beta ){\mathcal{L}}_2{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta ){\mathcal{L}}_3{w}_1^{*},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\Delta }_2& =& \mathrm{\Phi }({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}+\mathrm{\Phi }({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*},\hfill \end{array}$$

(21)

then the ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3) has a unique solution $u\in \mathcal{E}$.

Proof. 

The problem (3) will transform to $u=\mathcal{Q}u$, where $\mathcal{Q}$ is given by (15). Clearly, the fixed points of $\mathcal{Q}$ are the possible solutions of (3). By applying Lemma 5, we will guarantee that $\mathcal{Q}$ has a unique fixed point, which implies that (3) has a unique solution. Define a bounded, closed, and convex subset ${\mathcal{B}}_{r_1}:=\{u\in \mathcal{E}:\parallel u\parallel \le r_1\}$ with

$$r_1\ge \frac{\mathrm{\Lambda }(\alpha +\beta ){\mathbb{F}}_1+\mathrm{\Phi }({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathbb{G}}_1+\mathrm{\Phi }({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathbb{H}}_1}{1-\left({\Delta }_1+{\Delta }_2\right)},$$

(22)

where ${\Delta }_i$ for $i=1,2$ are given by (20) and (21). Assume that ${sup}_{\tau \in \mathcal{J}}\left|f(\tau ,0,0,0)\right|:={\mathbb{F}}_1<\infty$, ${sup}_{\tau \in \mathcal{J}}\left|\mathcal{H}(\tau ,0)\right|:={\mathbb{H}}_1<\infty$, and ${sup}_{\tau \in \mathcal{J}}\left|\mathcal{G}(\tau ,0)\right|:={\mathbb{G}}_1<\infty$.

Step I. $\mathcal{Q}{\mathcal{B}}_{r_1}\subset {\mathcal{B}}_{r_1}$.

Let $u\in {\mathcal{B}}_{r_1}$, $\tau \in \mathcal{J}$. Then,

$$\begin{array}{c}\hfill \begin{array}{ccc}\left|\right(\mathcal{Q}u\left)\right(\tau \left)\right|\hfill & \le \hfill & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left(b\right)|+\frac{{\left(\psi \left(b\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }({\gamma }_1+\beta )}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,u\left(\sigma \right))\right|\hfill \\ \hfill & \hfill & +\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_x\left({\eta }_i\right)\left|\right)+|{\mathrm{\Omega }}_{12}|\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,u\left(\zeta \right))\right|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_u\left({\lambda }_j\right)\right|\right)]\hfill \\ \hfill & \hfill & +\frac{{\left(\psi \left(b\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }\left({\gamma }_2\right)}[\left|{\mathrm{\Omega }}_{11}\right|\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,u\left(\zeta \right))\right|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_u\left({\lambda }_j\right)\right|\right)\hfill \\ \hfill & \hfill & +|{\mathrm{\Omega }}_{21}|\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,u\left(\sigma \right))\right|+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_u\left({\eta }_i\right)\right|\right)].\hfill \end{array}\end{array}$$

(23)

By using (i) in Proposition 1, we get

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{q;\psi }\left|u\left(\tau \right)\right|& =& \frac{1}{\mathrm{\Gamma }\left(q\right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{q-1}{\psi }^{\prime }\left(s\right)\left|u\left(s\right)\right|ds\hfill \\ & \le & \frac{{\left(\psi \left(\tau \right)-\psi \left(a\right)\right)}^q}{\mathrm{\Gamma }(q+1)}∥u∥={\mathrm{\Psi }}^q\left(\tau \right)∥u∥.\hfill \end{array}$$

(24)

Thanks to (24) with $k_1^{*}={sup}_{(\tau ,s)\in \mathcal{J}\times \mathcal{J}}\left\{\right|k(\tau ,s)\left|\right\}$ and $w_1^{*}={sup}_{(\tau ,s)\in \mathcal{J}\times \mathcal{J}}\left\{\right|w(\tau ,s)\left|\right\}$, this yields that

$$\begin{array}{ccc}\hfill \left|\right(\mathcal{K}u\left)\right(\tau \left)\right|& \le & \frac{1}{\mathrm{\Gamma }\left(\theta \right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{\theta -1}{\psi }^{\prime }\left(s\right)\left|k(\tau ,s)\right|\left|u\left(s\right)\right|ds\le k_1^{*}{\mathrm{\Psi }}^{\theta }\left(\tau \right)∥u∥,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill \left|\right(\mathcal{W}u\left)\right(\tau \left)\right|& \le & \frac{1}{\mathrm{\Gamma }\left(\delta \right)}{\int }_a^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{\delta -1}{\psi }^{\prime }\left(s\right)\left|w(\tau ,s)\right|\left|u\left(s\right)\right|ds\le w_1^{*}{\mathrm{\Psi }}^{\delta }\left(\tau \right)∥u∥.\hfill \end{array}$$

(26)

From the conditions $\left({\mathcal{P}}_1\right)$, $\left({\mathcal{P}}_2\right)$ and (24)–(25), we can estimate

$$\begin{array}{c}\hfill \begin{array}{ccc}\left|{\mathcal{F}}_u\left(\tau \right)\right|\hfill & \le \hfill & \left|f\right(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right))-f(\tau ,0,0,0\left)\right|+\left|f\right(\tau ,0,0,0\left)\right|\hfill \\ \hfill & \le \hfill & {\mathcal{L}}_1\left|u\left(\tau \right)\right|+{\mathcal{L}}_2\left|\left(\mathcal{K}u\right)\left(\tau \right)\right|+{\mathcal{L}}_3\left|\left(\mathcal{W}u\right)\left(\tau \right)\right|+{\mathbb{F}}_1\hfill \\ \hfill & \le \hfill & {\mathcal{L}}_1\parallel u\parallel +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta }\left(\tau \right)∥u∥+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta }\left(\tau \right)∥u∥+{\mathbb{F}}_1\hfill \\ \hfill & =\hfill & \left({\mathcal{L}}_1+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta }\left(\tau \right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta }\left(\tau \right)\right)\parallel u\parallel +{\mathbb{F}}_1,\hfill \end{array}\end{array}$$

(27)

$$\begin{array}{ccc}\hfill \left|\mathcal{H}(\tau ,u(\tau \left)\right)\right|& \le & |\mathcal{H}(\tau ,u\left(\tau \right))-\mathcal{H}(\tau ,0)|+\left|\mathcal{H}(\tau ,0)\right|\le {\mathcal{H}}_1^{*}\parallel u\parallel +{\mathbb{H}}_1,\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill \left|\mathcal{G}(\tau ,u(\tau \left)\right)\right|& \le & |\mathcal{G}(\tau ,u\left(\tau \right))-\mathcal{G}(\tau ,0)|+\left|\mathcal{G}(\tau ,0)\right|\le {\mathcal{G}}_1^{*}\parallel u\parallel +{\mathbb{G}}_1.\hfill \end{array}$$

(29)

By (27)–(29) via (i) of Proposition 1, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_u\left(b\right)\right|\hfill & \le \hfill & \left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)\parallel u\parallel \hfill \\ \hfill & \hfill & +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right),\hfill \end{array}\end{array}$$

(30)

$$\begin{array}{c}\hfill \begin{array}{ccc}{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_u\left({\eta }_i\right)\right|\hfill & \le \hfill & \left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)\right)\parallel u\parallel \hfill \\ \hfill & \hfill & +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right),\hfill \end{array}\end{array}$$

(31)

$$\begin{array}{c}\hfill \begin{array}{ccc}{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_u\left({\lambda }_j\right)\right|\hfill & \le \hfill & ({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ \hfill & \hfill & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right))\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right),\hfill \end{array}\end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,u\left(\zeta \right))\right|& \le & {\mathcal{H}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\nu }\left(\zeta \right)+{\mathbb{H}}_1{\mathrm{\Psi }}^{\nu }\left(\zeta \right),\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,u\left(\sigma \right))\right|& \le & {\mathcal{G}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\phi }\left(\sigma \right)+{\mathbb{G}}_1{\mathrm{\Psi }}^{\phi }\left(\sigma \right).\hfill \end{array}$$

(34)

Substituting (30)–(34) into (23), we obtain

$$\begin{array}{ccc}& & \left|\right(\mathcal{Q}u\left)\right(\tau \left)\right|\hfill \\ & \le & \left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{G}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\phi }\left(\sigma \right)+{\mathbb{G}}_1{\mathrm{\Psi }}^{\phi }\left(\sigma \right)+\sum _{i=1}^m\left|{\xi }_i\right|\left\{\right({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right))\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\})\hfill \\ & & +|{\mathrm{\Omega }}_{12}\left|\right({\mathbb{H}}_1{\mathrm{\Psi }}^{\nu }\left(\zeta \right)+{\mathcal{H}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\nu }\left(\zeta \right)+\sum _{j=1}^n\left|{\mu }_j\right|\left\{\right({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right))\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\}\left)\right]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{H}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\nu }\left(\zeta \right)+{\mathbb{H}}_1{\mathrm{\Psi }}^{\nu }\left(\zeta \right)+\sum _{j=1}^n\left|{\mu }_j\right|\left\{\right({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right))\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\})\hfill \\ & & +|{\mathrm{\Omega }}_{21}\left|\right({\mathcal{G}}_1^{*}\parallel u\parallel {\mathrm{\Psi }}^{\phi }\left(\sigma \right)+{\mathbb{G}}_1{\mathrm{\Psi }}^{\phi }\left(\sigma \right)+\sum _{i=1}^m\left|{\xi }_i\right|\left\{\right({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right))\parallel u\parallel +{\mathbb{F}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\}\left)\right]\hfill \\ & \le & ({\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_1\parallel u\parallel \hfill \\ & & +({\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_2{k}_1^{*}\parallel u\parallel \hfill \end{array}$$

$$\begin{array}{ccc}& & +({\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_3{w}_1^{*}\parallel u\parallel \hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}\parallel u\parallel \hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}\parallel u\parallel \hfill \\ & & +({\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)){\mathbb{F}}_1\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathbb{G}}_1\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)|+|{\mathrm{\Omega }}_{11}{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)|\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathbb{H}}_1\hfill \\ & \le & \{\left({\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\right){\mathcal{L}}_1\hfill \\ & & +({\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_2{k}_1^{*}+({\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_3{w}_1^{*}\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}\}{r}_1+({\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)){\mathbb{F}}_1\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathbb{G}}_1+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathbb{H}}_1\hfill \\ & =& \{\mathrm{\Lambda }(\alpha +\beta ){\mathcal{L}}_1+\mathrm{\Lambda }(\theta +\alpha +\beta ){\mathcal{L}}_2{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta ){\mathcal{L}}_3{w}_1^{*}+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}\}{r}_1+\mathrm{\Lambda }(\alpha +\beta ){\mathbb{F}}_1+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathbb{G}}_1\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathbb{H}}_1.\hfill \end{array}$$

Then,

$$\left|\left(\mathcal{Q}u\right)\left(\tau \right)\right|\le \left({\Delta }_1+{\Delta }_2\right)r_1+\mathrm{\Lambda }(\alpha +\beta ){\mathbb{F}}_1+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathbb{G}}_1+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathbb{H}}_1,$$

which implies that $\parallel \mathcal{Q}u\parallel \le r_1$. Thus, $\mathcal{Q}{\mathcal{B}}_{r_1}\subset {\mathcal{B}}_{r_1}$.

Step II. $\mathcal{Q}:\mathcal{E}\to \mathcal{E}$ is a contraction.

Assume that u, $v\in \mathcal{E}$, $\tau \in \mathcal{J}$. Then, we obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill & \hfill & \left|\left(\mathcal{Q}u\right)\left(\tau \right)-\left(\mathcal{Q}v\right)\left(\tau \right)\right|\hfill \\ \hfill & \le \hfill & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left(s\right)-{\mathcal{F}}_v\left(s\right)|\left(b\right)+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }|\mathcal{G}(s,u\left(s\right))-\mathcal{G}(s,v\left(s\right))|\left(\sigma \right)\hfill \\ \hfill & \hfill & +\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left(s\right)-{\mathcal{F}}_v\left(s\right)|\left({\eta }_i\right))+|{\mathrm{\Omega }}_{12}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }|\mathcal{H}(s,u\left(s\right))-\mathcal{H}(s,v\left(s\right))|\left(\zeta \right)\hfill \\ \hfill & \hfill & +\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }|{\mathcal{F}}_u\left(s\right)-{\mathcal{F}}_v\left(s\right)|\left({\lambda }_j\right)\left)\right]+\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }|\mathcal{H}(s,u\left(s\right))\hfill \\ \hfill & \hfill & -\mathcal{H}(s,v\left(s\right))|\left(\zeta \right)+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }|{\mathcal{F}}_u\left(s\right)-{\mathcal{F}}_v\left(s\right)|\left({\lambda }_j\right))+|{\mathrm{\Omega }}_{21}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }|\mathcal{G}(s,u\left(s\right))\hfill \\ \hfill & \hfill & -\mathcal{G}(s,v\left(s\right))|\left(\sigma \right)+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left(s\right)-{\mathcal{F}}_v\left(s\right)|\left({\eta }_i\right)\left)\right].\hfill \end{array}\end{array}$$

(35)

By helping $\left({\mathcal{P}}_1\right)$ and $\left({\mathcal{P}}_2\right)$, it is implied that

$$\begin{array}{ccc}\hfill \left|\left(\mathcal{K}u\right)\left(\tau \right)-\left(\mathcal{K}v\right)\left(\tau \right)\right|& \le & k_1^{*}{\mathrm{\Psi }}^{\theta }\left(\tau \right)\parallel u-v\parallel ,\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill \left|\left(\mathcal{W}u\right)\left(\tau \right)-\left(\mathcal{W}v\right)\left(\tau \right)\right|& \le & w_1^{*}{\mathrm{\Psi }}^{\delta }\left(\tau \right)\parallel u-v\parallel ,\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill \left|\mathcal{H}\right(\tau ,u\left(\tau \right))-\mathcal{H}(\tau ,v\left(\tau \right)\left)\right|& \le & {\mathcal{H}}_1^{*}\parallel u-v\parallel ,\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill \left|\mathcal{G}\right(\tau ,u\left(\tau \right))-\mathcal{G}(\tau ,v\left(\tau \right)\left)\right|& \le & {\mathcal{G}}_1^{*}\parallel u-v\parallel ,\hfill \end{array}$$

(39)

and

$$\begin{array}{c}\hfill \begin{array}{ccc}\left|{\mathcal{F}}_u\left(\tau \right)-{\mathcal{F}}_v\left(\tau \right)\right|\hfill & =\hfill & \left|f(\tau ,u(\tau ),(\mathcal{K}u\left)\right(\tau ),(\mathcal{W}u\left)\right(\tau \left)\right)-f(\tau ,v(\tau ),(\mathcal{K}v\left)\right(\tau ),(\mathcal{W}v\left)\right(\tau \left)\right)\right|\hfill \\ \hfill & \le \hfill & {\mathcal{L}}_1|u\left(\tau \right)-v\left(\tau \right)|+{\mathcal{L}}_2\left|\left(\mathcal{K}u\right)\left(\tau \right)-\left(\mathcal{K}v\right)\left(\tau \right)\right|\hfill \\ \hfill & \hfill & +{\mathcal{L}}_3\left|\left(\mathcal{W}u\right)\left(\tau \right)-\left(\mathcal{W}v\right)\left(\tau \right)\right|\hfill \\ \hfill & \le \hfill & \left({\mathcal{L}}_1+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta }\left(\tau \right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta }\left(\tau \right)\right)\parallel u-v\parallel .\hfill \end{array}\end{array}$$

(40)

Hence, by inserting (36)–(40) into (35) and using Proposition (i), which yields that

$$\begin{array}{ccc}& & \left|\left(\left(\mathcal{Q}u\right)\left(\tau \right)-\left(\mathcal{Q}v\right)\left(\tau \right)\right)\right|\hfill \\ & \le & \left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)\parallel u-v\parallel \hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{G}}_1^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel u-v\parallel +\sum _{i=1}^m\left|{\xi }_i\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right))\parallel u-v\parallel )+|{\mathrm{\Omega }}_{12}\left|\right({\mathcal{H}}_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel u-v\parallel \hfill \\ & & +\sum _{j=1}^n\left|{\mu }_j\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right)\hfill \\ & & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right))\parallel u-v\parallel )]+\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{H}}_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel u-v\parallel \hfill \\ & & +\sum _{j=1}^n\left|{\mu }_j\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right)\hfill \\ & & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left(\left({\lambda }_j\right)\right))\parallel u-v\parallel )+|{\mathrm{\Omega }}_{21}\left|\right({\mathcal{G}}_1^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel u-v\parallel \hfill \\ & & +\sum _{i=1}^m|{\xi }_i|\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)\right)\parallel u-v\parallel \left)\right]v\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \{\left({\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Lambda }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\right){\mathcal{L}}_1\hfill \\ & & +({\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_2{k}_1^{*}+({\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)){\mathcal{L}}_3{w}_1^{*}\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}\}\parallel u-v\parallel ,\hfill \end{array}$$

then, $∥\mathcal{Q}u-\mathcal{Q}v∥\le \left({\Delta }_1+{\Delta }_2\right)∥u-v∥$. Thanks to (19), ${\Delta }_1+{\Delta }_2<1$; thus, $\mathcal{Q}$ is a contraction. Hence, by applying Lemma 5, the problem (3) has a unique solution $x\in \mathcal{E}$. □

3.2. Existence Property via Leray-Schauder’s Type

Lemma 6.

(Arzelá-Ascoli theorem [57]). A set of functions in $\mathcal{C}\left(\right[a,b\left]\right)$ is relatively compact if and only if it is uniformly bounded and equicontinuous on $[a,b]$.

Lemma 7.

(Reference [57]). If a set is closed and relatively compact, then it is compact.

Lemma 8.

(Leray-Schauder’s nonlinear alternative [56]) Assume that $\mathcal{E}$ is a Banach space, C is a closed, convex subset of M, X is an open subset of C, and $0\in X$. Assume that $\mathcal{Q}:\overline{X}\to C$ is a continuous, compact (that is, $\mathcal{Q}\left(\overline{X}\right)$ is a relatively compact subset of C) map. Then, either $\left(i\right)$$\mathcal{Q}$ has a fixed point in $\overline{X}$, or $\left(ii\right)$ there is $x\in \partial X$ (the boundary of X in C) and $\varrho \in (0,1)$ with $u=\varrho \mathcal{Q}\left(u\right)$.

Theorem 2.

Suppose that $f\in \mathcal{C}(\mathcal{J}\times {\mathbb{R}}^3,\mathbb{R})$ satisfies the following conditions

$\left({\mathcal{P}}_3\right)$

There exist nondecreasing continuous functions $\mathbb{U}$, $\mathbb{V}$, $\mathbb{W}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, $p_i$, $q_j\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$,

for $i=1,2,3$, $j=1,2$, such that

$$\begin{array}{ccc}\hfill \left|f\right(\tau ,x,y,z\left)\right|& \le & p_1\left(\tau \right)\mathbb{U}\left(\right|u\left|\right)+p_2\left(t\right)\left|v\right|+p_3\left(\tau \right)\left|w\right|,\forall (\tau ,u,v,w)\in \mathcal{J}\times {\mathbb{R}}^3,\hfill \\ \hfill \left|\mathcal{H}\right(\tau ,u\left)\right|& \le & q_1\left(\tau \right)\mathbb{V}\left(\right|u\left|\right),\forall (\tau ,u)\in \mathcal{J}\times \mathbb{R},\hfill \\ \hfill \left|\mathcal{G}\right(\tau ,u\left)\right|& \le & q_2\left(\tau \right)\mathbb{W}\left(\right|u\left|\right),\forall (\tau ,u)\in \mathcal{J}\times \mathbb{R},\hfill \end{array}$$

with $p_i^{*}={sup}_{\tau \in \mathcal{J}}\left\{p_i\left(\tau \right)\right\}$, $q_j^{*}={sup}_{\tau \in \mathcal{J}}\left\{q_j\left(\tau \right)\right\}$, $i=1,2,3$, $j=1,2$.

$\left({\mathcal{P}}_4\right)$

There exists a constant ${\mathcal{M}}^{*}>0$ satisfy

$$\frac{\left[1-\left(\mathrm{\Lambda }(\theta +\alpha +\beta )p_2^{*}{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta )p_3^{*}{w}_1^{*}\right)\right]{\mathcal{M}}^{*}}{\mathrm{\Lambda }(\alpha +\beta )p_1^{*}\mathbb{U}\left({\mathcal{M}}^{*}\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})q_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\mathbb{V}\left({\mathcal{M}}^{*}\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})q_2^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\mathbb{W}\left({\mathcal{M}}^{*}\right)}>1.$$

Then, the ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3) has at least one solution $x\in \mathcal{E}$.

Proof. 

Assume that $\mathcal{Q}$ is given by (15). In the first step, we will prove that $\mathcal{Q}$ maps bounded sets (balls) into bounded sets in $\mathcal{E}$. For any a real constant $r_2>0$, given $B_{r_2}:=\{u\in \mathcal{E}:\parallel u\parallel \le r_2\}$ is a bounded set (ball) in $\mathcal{E}$. From (23) in Theorem 1 with (${\mathcal{P}}_4$), we obtain

$$\begin{array}{ccc}& & \left|\right(\mathcal{Q}u\left)\right(\tau \left)\right|\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left(p_1\left(\tau \right)\mathbb{U}\left(\right|u\left(\tau \right)\left|\right)+p_2\left(\tau \right)\left|\left(\mathcal{K}u\right)\left(\tau \right)\right|+p_3\left(\tau \right)\left|\left(\mathcal{W}u\right)\left(\tau \right)\right|\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left(q_2\left(\sigma \right)\mathbb{W}\left(\right|u\left(\sigma \right)\left|\right)\right)+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }(p_1\left({\eta }_i\right)\mathbb{U}\left(\right|u\left({\eta }_i\right)\left|\right)\hfill \\ & & +p_2\left({\eta }_i\right)|\left(\mathcal{K}u\right)\left({\eta }_i\right)|+p_3\left({\eta }_i\right)|\left(\mathcal{W}u\right)\left({\eta }_i\right)\left|\right))+|{\mathrm{\Omega }}_{12}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left(q_1\left(\zeta \right)\mathbb{V}\left(\right|u\left(\zeta \right)\left|\right)\right)\hfill \\ & & +\sum _{j=1}^n\left|{\mu }_j\right|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left(p_1\left({\lambda }_j\right)\mathbb{U}\left(\right|u\left({\lambda }_j\right)\left|\right)+p_2\left({\lambda }_j\right)|\left(\mathcal{K}u\right)\left({\lambda }_j\right)|+p_3\left({\lambda }_j\right)\left|\left(\mathcal{W}u\right)\left({\lambda }_j\right)\right|\right)\left)\right]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left(q_1\left(\zeta \right)\mathbb{V}\left(\right|u\left(\zeta \right)\left|\right)\right)+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }(p_1\left({\lambda }_j\right)\mathbb{U}\left(\right|u\left({\lambda }_j\right)\left|\right)\hfill \\ & & +p_2\left({\lambda }_j\right)|\left(\mathcal{K}u\right)\left({\lambda }_j\right)|+p_3\left({\lambda }_j\right)|\left(\mathcal{W}u\right)\left({\lambda }_j\right)\left|\right))+|{\mathrm{\Omega }}_{21}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left(q_2\left(\sigma \right)\mathbb{W}\left(\right|u\left(\sigma \right)\left|\right)\right)\hfill \\ & & +\sum _{i=1}^m\left|{\xi }_i\right|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left(p_1\left({\eta }_i\right)\mathbb{U}\left(\right|u\left({\eta }_i\right)\left|\right)+p_2\left({\eta }_i\right)|\left(\mathcal{K}u\right)\left({\eta }_i\right)|+p_3\left({\eta }_i\right)\left|\left(\mathcal{W}u\right)\left({\eta }_i\right)\right|\right)\left)\right].\hfill \end{array}$$

By the same process in Theorem 1, we can estimate

$$\begin{array}{ccc}\hfill \parallel \mathcal{Q}u\parallel & \le & \mathrm{\Lambda }(\alpha +\beta )p_1^{*}\mathbb{U}\left(r_2\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})q_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\mathbb{V}\left(r_2\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})q_2^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\mathbb{W}\left(r_2\right)\hfill \\ & & +\left(\mathrm{\Lambda }(\theta +\alpha +\beta )p_2^{*}{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta )p_3^{*}{w}_1^{*}\right)r_2:={\mathcal{N}}_2.\hfill \end{array}$$

Next, we prove that $\mathcal{Q}$ maps bounded sets into equicontinuous sets of $\mathcal{E}$. Assuming that the point ${\tau }_1$, ${\tau }_2\in \mathcal{J}$, where ${\tau }_1<{\tau }_2$ and $u\in B_{r_2}$, where $B_{r_2}$ is bounded set in $\mathcal{E}$, we have

$$\begin{array}{ccc}& & |\left(\mathcal{Q}u\right)\left({\tau }_2\right)-\left(\mathcal{Q}u\right)\left({\tau }_1\right)|\hfill \\ & \le & \left|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\tau }_2\right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\tau }_1\right)\right|\hfill \\ & & +\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }({\gamma }_1+\beta )}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,u\left(\sigma \right))\right|\hfill \\ & & +\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left({\eta }_i\right)\left|\right)+|{\mathrm{\Omega }}_{12}|\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,u\left(\zeta \right))\right|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_u\left({\lambda }_j\right)\right|\right)]\hfill \\ & & +\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }\left({\gamma }_2\right)}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,u\left(\zeta \right))\right|\hfill \\ & & +\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }|{\mathcal{F}}_u\left({\lambda }_j\right)\left|\right)+|{\mathrm{\Omega }}_{21}|\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,u\left(\sigma \right))\right|+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_u\left({\eta }_i\right)\right|\right)]\hfill \\ & \le & \left(p_1^{*}\mathbb{U}\left(r_2\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta }\left(b\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta }\left(b\right)r_2\right)(\frac{1}{\mathrm{\Gamma }(\alpha +\beta )}{\int }_{{\tau }_1}^{t_2}{\psi }^{\prime }\left(s\right){\left(\psi \left({\tau }_2\right)-\psi \left(s\right)\right)}^{\alpha +\beta -1}ds\hfill \\ & & +\frac{1}{\mathrm{\Gamma }(\alpha +\beta )}{\int }_a^{{\tau }_1}{\psi }^{\prime }\left(s\right)\left|{\left(\psi \left({\tau }_2\right)-\psi \left(s\right)\right)}^{\alpha +\beta -1}-{\left(\psi \left({\tau }_1\right)-\psi \left(s\right)\right)}^{\alpha +\beta -1}\right|ds)\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }({\gamma }_1+\beta )}\left[\left|{\mathrm{\Omega }}_{22}\right|\right(q_2^{*}\mathbb{W}\left(r_2\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\hfill \\ & & +\sum _{i=1}^m\left|{\xi }_i\right|\left(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)r_2\right))\hfill \\ & & +|{\mathrm{\Omega }}_{12}\left|\right(q_1^{*}\mathbb{V}\left(r_2\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right)+\sum _{j=1}^n\left|{\mu }_j\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\hfill \\ & & +p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\left)\right)]+\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }\left({\gamma }_2\right)}\hfill \\ & & \times \left[\right|{\mathrm{\Omega }}_{11}\left|\right(q_1^{*}\mathbb{V}\left(r_2\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right)|+\sum _{j=1}^n\left|{\mu }_j\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\hfill \\ & & +p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\left)\right)+|{\mathrm{\Omega }}_{21}\left|\right(q_2^{*}\mathbb{W}\left(r_2\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right)+\sum _{i=1}^m\left|{\xi }_i\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)r_2\left)\right)]\hfill \\ & \le & \left(2{\left(\psi \left({\tau }_2\right)-\psi \left({\tau }_1\right)\right)}^{\alpha +\beta }+\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{\alpha +\beta }-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{\alpha +\beta }\right|\right)\hfill \\ & & \times \frac{1}{\mathrm{\Gamma }(\alpha +\beta +1)}\left(p_1^{*}\mathbb{U}\left(r_2\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta }\left(b\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta }\left(b\right)r_2\right)\hfill \\ & & +\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_1+\beta -1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }({\gamma }_1+\beta )}\left[\left|{\mathrm{\Omega }}_{22}\right|\right(q_2^{*}\mathbb{W}\left(r_2\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\hfill \\ & & +\sum _{i=1}^m\left|{\xi }_i\right|\left(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)r_2\right))\hfill \\ & & +|{\mathrm{\Omega }}_{12}\left|\right(q_1^{*}\mathbb{V}\left(r_2\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right)+\sum _{j=1}^n\left|{\mu }_j\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\hfill \\ & & +p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\left)\right)]+\frac{\left|{\left(\psi \left({\tau }_2\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}-{\left(\psi \left({\tau }_1\right)-\psi \left(a\right)\right)}^{{\gamma }_2-1}\right|}{\left|\mathrm{\Omega }\right|\mathrm{\Gamma }\left({\gamma }_2\right)}\hfill \\ & & \times \left[\right|{\mathrm{\Omega }}_{11}\left|\right(q_1^{*}\mathbb{V}\left(r_2\right){\mathrm{\Psi }}^{\nu }\left(\zeta \right)|+\sum _{j=1}^n\left|{\mu }_j\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\hfill \\ & & +p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)r_2\left)\right)+|{\mathrm{\Omega }}_{21}\left|\right(q_2^{*}\mathbb{W}\left(r_2\right){\mathrm{\Psi }}^{\phi }\left(\sigma \right)+\sum _{i=1}^m\left|{\xi }_i\right|(p_1^{*}\mathbb{U}\left(r_2\right){\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +p_2^{*}{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)r_2+p_3^{*}{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)r_2\left)\right)].\hfill \end{array}$$

Clearly, the right-hand side of the above inequality tends to zero as ${\tau }_2-{\tau }_1\to 0$, which independent of $u\in B_{r_2}$. Then, by the Arzelá-Ascoli theorem (Lemma 6), $\mathcal{Q}:\mathcal{E}\to \mathcal{E}$ is completely continuous.

Next, we show that there is an open set $\mathcal{D}\subset \mathcal{E}$ with $u\ne \kappa \mathcal{Q}\left(u\right)$ for $\kappa \in (0,1)$ and $u\in \partial \mathcal{D}$. Assume that $u\in \mathcal{E}$ is a solution of $u=\kappa \mathcal{Q}u$ for each $\kappa \in (0,1)$. So, for $\tau \in \mathcal{J}$, we will show that $\mathcal{Q}$ is bounded, and then

$$\begin{array}{ccc}& & \left|u\right(\tau \left)\right|\hfill \\ & =& \left|\kappa \right(\mathcal{Q}u\left)\right(\tau \left)\right|\hfill \\ & \le & \mathrm{\Lambda }(\alpha +\beta )p_1^{*}\mathbb{U}(\parallel u\parallel )+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})q_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\mathbb{V}(\parallel u\parallel )\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})q_2^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\mathbb{W}(\parallel u\parallel )+\left(\mathrm{\Lambda }(\theta +\alpha +\beta )p_2^{*}{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta )p_3^{*}{w}_1^{*}\right)\parallel u\parallel .\hfill \end{array}$$

Taking the norm for $\tau \in \mathcal{J}$, then

$$\begin{array}{ccc}\hfill \parallel u\parallel & \le & \mathrm{\Lambda }(\alpha +\beta )p_1^{*}\mathbb{U}(\parallel u\parallel )+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})q_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\mathbb{V}(\parallel u\parallel )\hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})q_2^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\mathbb{W}(\parallel u\parallel )\hfill \\ & & +\left(\mathrm{\Lambda }(\theta +\alpha +\beta )p_2^{*}{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta )p_3^{*}{w}_1^{*}\right)\parallel u\parallel .\hfill \end{array}$$

Consequently, we obtain

$$\frac{\left[1-\left(\mathrm{\Lambda }(\theta +\alpha +\beta )p_2^{*}{k}_1^{*}+\mathrm{\Lambda }(\delta +\alpha +\beta )p_3^{*}{w}_1^{*}\right)\right]\parallel x\parallel }{\mathrm{\Lambda }(\alpha +\beta )p_1^{*}\mathbb{U}(\parallel u\parallel )+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})q_1^{*}{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\mathbb{V}(\parallel u\parallel )+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})q_2^{*}{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\mathbb{W}(\parallel u\parallel )}\le 1.$$

Thanks to $\left({\mathcal{P}}_5\right)$, there is a constant ${\mathcal{M}}^{*}>0$ such that $\parallel u\parallel \ne {\mathcal{M}}^{*}$. Set

$$\mathcal{D}:=\left\{u\in \mathcal{E}:\parallel u\parallel \le {\mathcal{M}}^{*}+1\right\},\mathrm{and}\mathcal{U}=\mathcal{D}\cup B_{r_2}.$$

Notice that $\mathcal{Q}:\overline{\mathcal{U}}\to \mathcal{E}$ is continuous and completely continuous. By the choice of $\mathcal{D}$, there exists no $u\in \partial \mathcal{D}$ so that $u=\kappa \mathcal{Q}u$ for some $\kappa \in (0,1)$.

Therefore, by Lemma 8, we summarize that $\mathcal{Q}$ has fixed point $x\in \overline{\mathcal{U}}$, which suggests that the problem (3) has at least one solution on $\mathcal{J}$. □

3.3. Existence Property via Krasnoselskii’s Fixed Point Theorem

Lemma 9.

(Krasnoselskii’s fixed point theorem [58]) Let $\mathcal{B}$ be a closed, bounded, convex, and non-empty subset of a Banach space. Let ${\mathcal{Q}}_1$, ${\mathcal{Q}}_2$ be the operators such that $\left(i\right)$${\mathcal{Q}}_{1}u+{\mathcal{Q}}_{2}v\in \mathcal{B}$ whenever u, $v\in \mathcal{B}$; $\left(ii\right)$${\mathcal{Q}}_1$ is compact and continuous; $\left(iii\right)$${\mathcal{Q}}_2$ is contraction mapping. Then, there exists $w\in \mathcal{B}$ such that $z={\mathcal{Q}}_{1}w+{\mathcal{Q}}_{2}w$.

Theorem 3.

Suppose that $f\in \mathcal{C}(\mathcal{J}\times {\mathbb{R}}^3,\mathbb{R})$ satisfies $\left({\mathcal{P}}_1\right)$, $\left({\mathcal{P}}_2\right)$, and

(${\mathcal{P}}_5$)

There exist $f_i$, $g_j$, $h_k\in \mathcal{J},{\mathbb{R}}^{+}$, $i=1,2,3,4$, $j=1,2$, $k=1,2$, such that $\forall (\tau ,u,v,w)\in \mathcal{J}\times {\mathbb{R}}^3$,

$$\begin{array}{ccc}\hfill \left|f\right(\tau ,u,v,w\left)\right|& \le & |f_1\left(\tau \right)|+|f_2\left(\tau \right)\left|\right|u|+|f_3\left(\tau \right)\left|\right|v|+|f_4\left(\tau \right)\left|\right|w|,\hfill \\ \hfill \left|\mathcal{G}\right(\tau ,u\left)\right|& \le & |g_1\left(\tau \right)|+|g_2\left(\tau \right)\left|\right|u|,\forall (\tau ,u)\in \mathcal{J}\times \mathbb{R},\hfill \\ \hfill \left|\mathcal{H}\right(\tau ,u\left)\right|& \le & |h_1\left(\tau \right)|+|h_2\left(\tau \right)\left|\right|u|,\forall (\tau ,u)\in \mathcal{J}\times \mathbb{R}.\hfill \end{array}$$

If

$$\left({\Delta }_1+{\Delta }_2-{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right){\mathcal{L}}_1-{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)k_1^{*}{\mathcal{L}}_2-{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)w_1^{*}{\mathcal{L}}_3\right)<1,$$

(41)

then the ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3) has at least one solution $x\in \mathcal{E}$.

Proof. 

By setting ${sup}_{\tau \in \mathcal{J}}|f_i\left(\tau \right)|=\parallel f_i\parallel$, $i=1,2,3,4$, ${sup}_{t\in \mathcal{J}}|g_j\left(\tau \right)|=\parallel g_j\parallel$, and ${sup}_{\tau \in \mathcal{J}}|h_j\left(\tau \right)|=\parallel h_j\parallel$, $j=1,2$, we consider $B_{r_3}=\left\{u\in \mathcal{E}:\parallel u\parallel \le r_3\right\}$, where

$$r_3\ge \frac{\mathrm{\Lambda }(\alpha +\beta )\parallel f_1\parallel +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_1\parallel +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_1\parallel }{1-{\Delta }_3},$$

with

$$\begin{array}{ccc}\hfill {\Delta }_3& =& \mathrm{\Lambda }(\alpha +\beta )\parallel f_2\parallel +\mathrm{\Lambda }(\theta +\alpha +\beta )k_1^{*}\parallel f_3\parallel +\mathrm{\Lambda }(\delta +\alpha +\beta )w_1^{*}\parallel f_4\parallel \hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_2\parallel +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_2\parallel .\hfill \end{array}$$

Define ${\mathcal{Q}}_1$ and ${\mathcal{Q}}_2:B_{r_3}\to \mathcal{E}$ as

$$\begin{array}{ccc}\hfill \left({\mathcal{Q}}_{1}u\right)\left(\tau \right)& =& {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right),\hfill \end{array}$$

(42)

$$\begin{array}{c}\hfill \begin{array}{ccc}\left({\mathcal{Q}}_{2}u\right)\left(\tau \right)\hfill & =\hfill & \frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)]\hfill \\ \hfill & \hfill & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)].\hfill \end{array}\end{array}$$

(43)

Note that $\mathcal{Q}={\mathcal{Q}}_1+{\mathcal{Q}}_2$. For any u, $v\in B_{r_3}$, it follows that

$$\begin{array}{ccc}& & \left|\left({\mathcal{Q}}_{1}u\right)\left(\tau \right)+\left({\mathcal{Q}}_{2}v\right)\left(\tau \right)\right|\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left(\tau \right)|+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}[\left|{\mathrm{\Omega }}_{22}\right|\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,v\left(\sigma \right))\right|+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_v\left({\eta }_i\right)\right|\right)\hfill \\ & & +|{\mathrm{\Omega }}_{12}|\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,v\left(\zeta \right))\right|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_v\left({\lambda }_j\right)\right|\right)]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}[\left|{\mathrm{\Omega }}_{11}\right|\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left|\mathcal{H}(\zeta ,v\left(\zeta \right))\right|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }\left|{\mathcal{F}}_v\left({\lambda }_j\right)\right|\right)\hfill \\ & & +|{\mathrm{\Omega }}_{21}|\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left|\mathcal{G}(\sigma ,v\left(\sigma \right))\right|+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left|{\mathcal{F}}_v\left({\eta }_i\right)\right|\right)]\hfill \\ & \le & {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left(|f_1\left(b\right)|+|f_2\left(b\right)\left|\right|u\left(b\right)|+|f_3\left(b\right)\left|\right|\left(\mathcal{K}u\right)\left(b\right)|+|f_4\left(b\right)\left|\right|\left(\mathcal{W}u\right)\left(b\right)|\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left(|g_1\left(\sigma \right)|+|g_2\left(\sigma \right)\left|\right|v\left(\sigma \right)|\right)+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }(\left|f_1\left({\eta }_i\right)\right|\hfill \\ & & +|f_2\left({\eta }_i\right)\left|\right|v\left({\eta }_i\right)|+|f_3\left({\eta }_i\right)\left|\right|\left(\mathcal{K}v\right)\left({\eta }_i\right)|+|f_4\left({\eta }_i\right)\left|\right|\left(\mathcal{W}v\right)\left({\eta }_i\right)\left|\right))\hfill \\ & & +|{\mathrm{\Omega }}_{12}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left(|h_1\left(\zeta \right)|+|h_2\left(\zeta \right)\left|\right|v\left(\zeta \right)|\right)+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }(\left|f_1\left({\lambda }_j\right)\right|\hfill \\ & & +|f_2\left({\lambda }_j\right)\left|\right|v\left({\lambda }_j\right)|+|f_3\left({\lambda }_j\right)\left|\right|\left(\mathcal{K}v\right)\left({\lambda }_j\right)|+|f_4\left({\lambda }_j\right)\left|\right|\left(\mathcal{W}v\right)\left({\lambda }_j\right)\left|\right)\left)\right]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\left(|h_1\left(\zeta \right)|+|h_2\left(\zeta \right)\left|\right|v\left(\zeta \right)|\right)+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }(\left|f_1\left({\lambda }_j\right)\right|\hfill \\ & & +|f_2\left({\lambda }_j\right)\left|\right|v\left({\lambda }_j\right)|+|f_3\left({\lambda }_j\right)\left|\right|\left(\mathcal{K}v\right)\left({\lambda }_j\right)|+|f_4\left({\lambda }_j\right)\left|\right|\left(\mathcal{W}v\right)\left({\lambda }_j\right)\left|\right))\hfill \\ & & +|{\mathrm{\Omega }}_{21}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\left(|g_1\left(\sigma \right)|+|g_2\left(\sigma \right)\left|\right|v\left(\sigma \right)|\right)+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\left(\right|f_1\left({\eta }_i\right)|+|f_2\left({\eta }_i\right)\left|\right|y\left({\eta }_i\right)|\hfill \end{array}$$

$$\begin{array}{ccc}& & +|f_3\left({\eta }_i\right)\left|\right|\left(\mathcal{K}y\right)\left({\eta }_i\right)|+|f_4\left({\eta }_i\right)\left|\right|\left(\mathcal{W}v\right)\left({\eta }_i\right)\left|\right)\left)\right]\hfill \\ & \le & \left\{{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\right\}\parallel f_1\parallel \hfill \\ & & +\{{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)\parallel u\parallel +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\parallel v\parallel \hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\parallel v\parallel \}\parallel f_2\parallel +\{{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)\parallel u\parallel \hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)\parallel v\parallel +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\parallel v\parallel \}{k}_1^{*}\parallel f_3\parallel \hfill \\ & & +\{{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\parallel u\parallel +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)\parallel v\parallel \hfill \\ & & +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n|{\mu }_j|{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\parallel v\parallel \}{w}_1^{*}\parallel f_4\parallel +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})({\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_1\parallel \hfill \\ & & +{\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_2\parallel \parallel v\parallel )+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\left({\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_1\parallel +{\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_2\parallel \parallel v\parallel \right)\hfill \\ & \le & \mathrm{\Lambda }(\alpha +\beta )\parallel f_1\parallel +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_1\parallel +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_1\parallel \hfill \\ & & +(\mathrm{\Lambda }(\alpha +\beta )\parallel f_2\parallel +\mathrm{\Lambda }(\theta +\alpha +\beta )k_1^{*}\parallel f_3\parallel +\mathrm{\Lambda }(\delta +\alpha +\beta )w_1^{*}\parallel f_4\parallel \hfill \\ & & +\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21}){\mathrm{\Psi }}^{\phi }\left(\sigma \right)\parallel g_2\parallel +\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11}){\mathrm{\Psi }}^{\nu }\left(\zeta \right)\parallel h_2\parallel )r_3\le r_3,\hfill \end{array}$$

which implies that ${\mathcal{Q}}_{1}u+{\mathcal{Q}}_{2}v\in B_{r_3}$ that assumption (i) of Lemma 9 is verified.

Now, we are going to prove that Lemma 9 (ii) is fulfilled. Assume that a sequence $u_n$ so that $u_n\to u\in \mathcal{E}$ as $n\to \infty$. For $\tau \in \mathcal{J}$, we obtain

$$|\left({\mathcal{Q}}_1{u}_n\right)\left(\tau \right)-\left({\mathcal{Q}}_{1}u\right)\left(\tau \right)|\le {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_{u_n}\left(b\right)-{\mathcal{F}}_u\left(b\right)|\le {\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)\parallel {\mathcal{F}}_{u_n}(·)-{\mathcal{F}}_u(·)\parallel .$$

By continuity of f, we get that ${\mathcal{F}}_u$ is continuous. Hence, by the Lebergue dominated convergent theorem, this yields that $|\left({\mathcal{Q}}_1{u}_n\right)\left(\tau \right)-\left({\mathcal{Q}}_{1}u\right)\left(\tau \right)|\to 0$ as $\tau \to \infty$. Then,

$$\parallel {\mathcal{Q}}_1{u}_n-{\mathcal{Q}}_{1}u)\parallel \to 0\mathrm{as}\tau \to \infty .$$

Therefore, ${\mathcal{Q}}_{1}u$ is continuous. So, ${\mathcal{Q}}_1{B}_{r_3}$ is uniformly bounded as

$$\parallel {\mathcal{Q}}_{1}u\parallel \le {\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)\parallel f_1\parallel +{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)r_2\parallel f_2\parallel +k_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)r_3\parallel f_3\parallel +w_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)r_3\parallel f_4\parallel .$$

Afterward, we show compactness of ${\mathcal{Q}}_1$. Define ${sup}_{(\tau ,u,v,w)\in \mathcal{J}\times {\mathbb{R}}^3}\left|f(\tau ,u,v,w)\right|=f^{*}<+\infty$, for each ${\tau }_1$, ${\tau }_2\in \mathcal{J}$, where ${\tau }_1<{\tau }_2$, we have,

$$\begin{array}{c}\hfill \begin{array}{ccc}|\left({\mathcal{Q}}_{1}u\right)\left({\tau }_2\right)-\left({\mathcal{Q}}_{1}u\right)\left({\tau }_1\right)|\hfill & =\hfill & \left|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\tau }_2\right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\tau }_1\right)\right|\hfill \\ \hfill & \le \hfill & \frac{f^{*}}{\mathrm{\Gamma }(\alpha +\beta +1)}(2{(\psi \left({\tau }_2\right)-\psi \left({\tau }_1\right))}^{\alpha +\beta }\hfill \\ \hfill & \hfill & +\left|{(\psi \left({\tau }_2\right)-\psi \left(a\right))}^{\alpha +\beta }-{(\psi \left({\tau }_1\right)-\psi \left(a\right))}^{\alpha +\beta }\right|).\hfill \end{array}\end{array}$$

(44)

Clearly, the right-hand side of (44) is independent of u and $|\left({\mathcal{Q}}_{1}u\right)\left({\tau }_2\right)-\left({\mathcal{Q}}_{1}u\right)\left({\tau }_1\right)|\to 0$ as ${\tau }_2\to {\tau }_1$. Hence, this implies that ${\mathcal{Q}}_1{B}_{r_3}$ is equicontinuous, and ${\mathcal{Q}}_1$ maps bounded subsets into relatively compact subsets, and this yields that ${\mathcal{Q}}_1{B}_{r_3}$ is relatively compact. Therefore, we summarize that ${\mathcal{Q}}_1$ is compact on $B_{r_3}$ by the Arzelá-Ascoli theorem.

Next, we show that ${\mathcal{Q}}_2$ is contraction. For each u, $v\in B_{r_3}$, $\tau \in \mathcal{J}$, then

$$\begin{array}{ccc}& & |\left({\mathcal{Q}}_{2}u\right)\left(\tau \right)-\left({\mathcal{Q}}_{2}v\right)\left(\tau \right)|\hfill \\ & \le & \frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathcal{I}}_{a^{+}}^{\phi ;\psi }|\mathcal{G}(\sigma ,u\left(\sigma \right))-\mathcal{G}(\sigma ,v\left(\sigma \right))|\hfill \\ & & +\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left({\eta }_i\right)-{\mathcal{F}}_v\left({\eta }_i\right)\left|\right)+|{\mathrm{\Omega }}_{12}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }|\mathcal{H}(\zeta ,u\left(\zeta \right))-\mathcal{H}(\zeta ,v\left(\zeta \right))|\hfill \\ & & +\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }|{\mathcal{F}}_u\left({\lambda }_j\right)-{\mathcal{F}}_v\left({\lambda }_j\right)\left|\right)]+\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{11}\left|\right({\mathcal{I}}_{a^{+}}^{\nu ;\psi }|\mathcal{H}(\zeta ,u\left(\zeta \right))\hfill \\ & & -\mathcal{H}(\zeta ,v\left(\zeta \right))|+\sum _{j=1}^n|{\mu }_j|{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }|{\mathcal{F}}_u\left({\lambda }_j\right)-{\mathcal{F}}_v\left({\lambda }_j\right)|)\hfill \\ & & +|{\mathrm{\Omega }}_{21}|\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }|\mathcal{G}(\sigma ,u\left(\sigma \right))-\mathcal{G}(\sigma ,v\left(\sigma \right))|+\sum _{i=1}^m|{\xi }_i|{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_u\left({\eta }_i\right)-{\mathcal{F}}_v\left({\eta }_i\right)|\right)]\hfill \\ & \le & \{\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)}{\left|\mathrm{\Omega }\right|}\left[\right|{\mathrm{\Omega }}_{22}\left|\right({\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}+\sum _{i=1}^m\left|{\xi }_i\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)\left)\right)+|{\mathrm{\Omega }}_{12}\left|\right({\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}+\sum _{j=1}^n\left|{\mu }_j\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\hfill \\ & & +{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\left)\right)]+\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)}{\left|\mathrm{\Omega }\right|}[\left|{\mathrm{\Lambda }}_{11}\right|({\mathrm{\Psi }}^{\nu }\left(\zeta \right){\mathcal{H}}_1^{*}\hfill \\ & & +\sum _{j=1}^n\left|{\mu }_j\right|\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\right))\hfill \\ & & +|{\mathrm{\Omega }}_{21}\left|\right({\mathrm{\Psi }}^{\phi }\left(\sigma \right){\mathcal{G}}_1^{*}+\sum _{i=1}^m\left|{\xi }_i\right|({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left({\eta }_i\right)\left)\right)\left]\right\}\parallel u-v\parallel \hfill \\ & \le & \left({\Delta }_1+{\Delta }_2-{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right){\mathcal{L}}_1-{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)k_1^{*}{\mathcal{L}}_2-{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)w_1^{*}{\mathcal{L}}_3\right)\parallel u-v\parallel .\hfill \end{array}$$

Hence, by (41), ${\mathcal{Q}}_2$ is a contraction.

Then, due to Lemma 9 being verified, this yields that the problem (3) has at least one solution on $\mathcal{J}$. □

4. Ulam’s Stability

This part analyzes a variety of Ulam’s stability of solutions to the problem (3).

Definition 4.

The problem (3) is said to be $\mathbb{UH}$ stable if there is a constant ${\mathfrak{C}}_f>0$ such that for any $ϵ>0$ and for each solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)-{\mathcal{F}}_z\left(\tau \right)\right|\le ϵ,$$

(45)

there is a solution $u\in \mathcal{E}$ of (3) such that

$$\left|z\left(\tau \right)-u\left(\tau \right)\right|\le {\mathfrak{C}}_fϵ,\tau \in \mathcal{J}.$$

(46)

Definition 5.

The problem (3) is said to be $\mathbb{GUH}$ stable if there is a function $\mathcal{T}\in \mathcal{C}({\mathbb{R}}^{+},{\mathbb{R}}^{+})$ with $\mathcal{T}\left(0\right)=0$ such that, for any solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)-{\mathcal{F}}_z\left(\tau \right)\right|\le ϵ\mathcal{T}\left(\tau \right),$$

(47)

there is a solution $u\in \mathcal{E}$ of (3) such that

$$\left|z\left(\tau \right)-u\left(\tau \right)\right|\le \mathcal{T}\left(ϵ\right),\tau \in \mathcal{J}.$$

(48)

Definition 6.

The problem (3) is said to be $\mathbb{UHR}$ stable with respect to $\mathcal{T}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ if there is a constant ${\mathfrak{C}}_{f,\mathcal{T}}>0$ such that for any $ϵ>0$ and for each a solution $z\in \mathcal{E}$ of (47) there is a solution $u\in \mathcal{E}$ of (3) such that

$$\left|z\left(\tau \right)-u\left(\tau \right)\right|\le {\mathfrak{C}}_{f,\mathcal{T}}ϵ\mathcal{T}\left(\tau \right),\tau \in \mathcal{J}.$$

(49)

Definition 7.

The problem (3) is said to be $\mathbb{GUHR}$ stable with respect to $\mathcal{T}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ if there is a constant ${\mathfrak{C}}_{f,\mathcal{T}}>0$ such that for any a solution $z\in \mathcal{E}$ of

$$\left|{}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)-{\mathcal{F}}_z\left(\tau \right)\right|\le \mathcal{T}\left(\tau \right),$$

(50)

there is a solution $u\in \mathcal{E}$ of (3) such that

$$\left|z\left(\tau \right)-u\left(\tau \right)\right|\le {\mathfrak{C}}_{f,\mathcal{T}}\mathcal{T}\left(\tau \right),\tau \in \mathcal{J}.$$

(51)

Remark 1.

It is clear that

$\left(i\right)$

Definition 4⇒ Definition 5;

$\left(ii\right)$

Definition 6⇒ Definition 7;

$\left(iii\right)$

Definition 6 for $\mathcal{T}\left(\tau \right)=1$⇒ Definition 4.

Remark 2.

A function $z\in \mathcal{E}$ is a solution of the inequality (45) if and only if there is a function $v\in \mathcal{E}$ (where v depends on z) such that:

$\left(i\right)$

$\left|v\right(\tau \left)\right|\le ϵ$, $\forall \tau \in \mathcal{J}$;

$\left(ii\right)$

${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)={\mathcal{F}}_z\left(\tau \right)+v\left(\tau \right)$, $\tau \in \mathcal{J}$.

Remark 3.

A function $z\in \mathcal{E}$ is a solution of the inequality (47) if and only if there is a function $w\in \mathcal{E}$ (where w depends on z) such that:

$\left(i\right)$

$\left|w\right(\tau \left)\right|\le ϵ\mathcal{T}\left(\tau \right)$, $\forall \tau \in \mathcal{J}$;

$\left(ii\right)$

${}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)={\mathcal{F}}_z\left(\tau \right)+w\left(\tau \right)$, $\tau \in \mathcal{J}$.

Remark 4.

For the analysis of $\mathbb{UHR}$ stability and $\mathbb{GUHR}$ stability, we assume the following assumption:

($H_1$)

There is an increasing function $\mathcal{T}\in \mathcal{C}(\mathcal{J},{\mathbb{R}}^{+})$ and there is a constant ${\lambda }_{\mathcal{T}}>0$, such that, for any $\tau \in \mathcal{J}$, we obtain

$${\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }\mathcal{T}\left(\tau \right)\le {\lambda }_{\mathcal{T}}\mathcal{T}\left(\tau \right).$$

(52)

4.1. $\mathbb{UH}$ Stability and $\mathbb{GUH}$ Stability

In this subsection, we construct an essential lemma that will be used in proves on $\mathbb{UH}$ and $\mathbb{GUH}$ stables of the problem (3).

Lemma 10.

Assume that $\alpha \in (3,4]$, $\rho \in [0,1]$, and $z\in \mathcal{E}$ is a solution of (45). Then, $z\in \mathcal{E}$ verifies

$$\left|z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)\right|\le \mathrm{\Lambda }(\alpha +\beta )ϵ,$$

(53)

where

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathcal{Z}\left(\tau \right)\hfill & =\hfill & \frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)]\hfill \\ \hfill & \hfill & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)],\hfill \end{array}\end{array}$$

(54)

with Ω, ${\mathrm{\Omega }}_{ij}$, i, $j\in \{1,2\}$, and $\mathrm{\Lambda }(\alpha +\beta )$ are given in Lemma 4 and (18).

Proof. 

Assume that z is a solution of (45). By Lemma 4 and $\left(ii\right)$ of Remark 2, we get

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)={\mathcal{F}}_z\left(\tau \right)+v\left(\tau \right)\tau \in (a,b),}\hfill \\ {\displaystyle z\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\left(a\right)=0,}\hfill \\ {\displaystyle \sum _{i=1}^m{\xi }_{i}z\left({\eta }_i\right)={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right)),\sum _{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\lambda }_j\right)={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right)),}\hfill \end{array}\right.$$

(55)

and then the solution of (55) can be given as

$$\begin{array}{ccc}\hfill z\left(\tau \right)& =& {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(\tau \right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)]+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left(\tau \right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{22}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left({\eta }_i\right)+{\mathrm{\Omega }}_{12}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }v\left({\lambda }_j\right)\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{11}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }v\left({\lambda }_j\right)+{\mathrm{\Omega }}_{21}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left({\eta }_i\right)\right).\hfill \end{array}$$

Thanks to $\left(i\right)$ of Remark 2, it is implied that

$$\begin{array}{ccc}& & \left|z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)\right|\hfill \\ & =& |{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left(\tau \right)+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{22}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left({\eta }_i\right)+{\mathrm{\Omega }}_{12}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(t\right)}{\mathrm{\Omega }}\left(-{\mathrm{\Lambda }}_{11}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }v\left({\lambda }_j\right)+{\mathrm{\Omega }}_{21}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }v\left({\eta }_i\right)\right)|\hfill \\ & \le & \{{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m\left|{\xi }_i\right|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)\hfill \\ & & +\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\}ϵ\hfill \\ & =& \left\{{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|{\mathrm{\Psi }}^{\alpha +\beta }\left({\eta }_i\right)+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Lambda }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|{\mathrm{\Psi }}^{\alpha +\beta -{\varphi }_j}\left({\lambda }_j\right)\right\}ϵ.\hfill \end{array}$$

The proof of (53) is done. □

Next, we establish $\mathbb{UH}$ and $\mathbb{GUH}$ stables of solutions to the problem (3).

Theorem 4.

Assume that $f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$ is continuous. Suppose that assumptions $\left({\mathcal{P}}_1\right)$–$\left({\mathcal{P}}_3\right)$ and

$${\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)<1.$$

(56)

Then, the ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3) is $\mathbb{UH}$ and $\mathbb{GUH}$ stables.

Proof. 

Assume that $z\in \mathcal{E}$ is a solution of (45), and $u\in \mathcal{E}$ is a unique solution of (3). From Lemma 4, which implies that $u\left(\tau \right)=\mathcal{X}\left(\tau \right)+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right)$, where

$$\begin{array}{c}\hfill \begin{array}{ccc}\mathcal{X}\left(\tau \right)\hfill & =\hfill & \frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)]\hfill \\ \hfill & \hfill & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(t\right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_u\left({\lambda }_j\right)\right)\hfill \\ \hfill & \hfill & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left({\eta }_i\right)\right)].\hfill \end{array}\end{array}$$

(57)

Clearly, if $u\left(a\right)=z\left(a\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\left(a\right)={}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\left(a\right)$, ${\sum }_{i=1}^m{\xi }_{i}u\left({\eta }_i\right)={\sum }_{i=1}^m{\xi }_{i}z\left({\eta }_i\right)$, ${\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))$, ${\sum }_{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }u\left({\lambda }_j\right)={\sum }_{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\lambda }_j\right)$, and ${\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))$, then, we get that $\mathcal{X}\left(\tau \right)=\mathcal{Z}\left(\tau \right)$.

By using Lemma 10 and $|u+v|\le \left|u\right|+\left|v\right|$, for any $\tau \in \mathcal{J}$, yields that

$$\begin{array}{ccc}& & \left|z\right(\tau )-u(\tau \left)\right|\hfill \\ & =& |z\left(\tau \right)-\mathcal{X}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right)|\hfill \\ & \le & |z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)|+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_z\left(\tau \right)-{\mathcal{F}}_u\left(\tau \right)|+|\mathcal{Z}\left(\tau \right)-\mathcal{X}\left(\tau \right)|\hfill \\ & \le & \mathrm{\Lambda }(\alpha +\beta )ϵ+\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)|z\left(\tau \right)-u\left(\tau \right)|,\hfill \end{array}$$

that is $|z\left(\tau \right)-u\left(\tau \right)|\le {\mathfrak{C}}_fϵ$, where

$${\mathfrak{C}}_f:=\frac{\mathrm{\Lambda }(\alpha +\beta )}{1-\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)}.$$

Hence, the problem (3) is $\mathbb{UH}$ stable in $\mathcal{E}$. Moreover, if we take $\mathcal{T}\left(ϵ\right)={\mathfrak{C}}_fϵ$ with $\mathcal{T}\left(0\right)=0$, thus, (3) is $\mathbb{GUH}$ stable in $\mathcal{E}$. □

4.2. $\mathbb{UHR}$ Stability and $\mathbb{GUHR}$ Stability

Next, the result will be applied in the investigation results of $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables.

Lemma 11.

Assume that $\alpha \in (3,4]$, $\rho \in [0,1]$, and $z\in \mathcal{E}$ is a solution of (47). Then, $z\in \mathcal{E}$ verifies

$$\left|z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)\right|\le \Theta ϵ{\lambda }_{\mathcal{T}}\mathcal{T}\left(\tau \right),$$

where

$$\Theta =1+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|,$$

(58)

and $\mathcal{Z}\left(\tau \right)$ is given by (54).

Proof. 

Assume that z is a solution of (47). By applying Lemma 4 and $\left(ii\right)$ of Remark 3, then, the solution of the problem

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{a^{+}}^{\alpha ,\rho ;\psi }\left({}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\right)\left(\tau \right)={\mathcal{F}}_z\left(\tau \right)+w\left(\tau \right)\tau \in (a,b),}\hfill \\ {\displaystyle z\left(a\right)=0,{}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\left(a\right)=0,}\hfill \\ {\displaystyle \sum _{i=1}^m{\xi }_{i}z\left({\eta }_i\right)={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right)),\sum _{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\lambda }_j\right)={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right)),}\hfill \end{array}\right.$$

(59)

is given by

$$\begin{array}{ccc}\hfill z\left(\tau \right)& =& {\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{22}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{12}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)]\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(\tau \right)}{\mathrm{\Omega }}[{\mathrm{\Omega }}_{11}\left({\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))-\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }{\mathcal{F}}_z\left({\lambda }_j\right)\right)\hfill \\ & & -{\mathrm{\Omega }}_{21}\left({\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))-\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left({\eta }_i\right)\right)]+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left(\tau \right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{22}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left({\eta }_i\right)+{\mathrm{\Omega }}_{12}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }w\left({\lambda }_j\right)\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{11}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }w\left({\lambda }_j\right)+{\mathrm{\Omega }}_{21}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left({\eta }_i\right)\right).\hfill \end{array}$$

Thanks to $\left(i\right)$ of Remarks 3 and 4, one has

$$\begin{array}{ccc}& & \left|z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)\right|\hfill \\ & =& |{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left(\tau \right)+\frac{{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{22}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left({\eta }_i\right)+{\mathrm{\Omega }}_{12}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }w\left({\lambda }_j\right)\right)\hfill \\ & & +\frac{{\mathrm{\Psi }}^{{\gamma }_2-1}\left(\tau \right)}{\mathrm{\Omega }}\left(-{\mathrm{\Omega }}_{11}\sum _{j=1}^n{\mu }_j{\mathcal{I}}_{a^{+}}^{\alpha +\beta -{\varphi }_j;\psi }w\left({\lambda }_j\right)+{\mathrm{\Omega }}_{21}\sum _{i=1}^m{\xi }_i{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }w\left({\eta }_i\right)\right)|\hfill \\ & \le & \{1+\frac{1}{\left|\mathrm{\Omega }\right|}\left(|{\mathrm{\Omega }}_{22}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{21}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{i=1}^m\left|{\xi }_i\right|\hfill \\ & & +\frac{1}{\mathrm{\Omega }}\left(|{\mathrm{\Omega }}_{12}|{\mathrm{\Psi }}^{{\gamma }_1+\beta -1}\left(b\right)+\left|{\mathrm{\Omega }}_{11}\right|{\mathrm{\Psi }}^{{\gamma }_2-1}\left(b\right)\right)\sum _{j=1}^n\left|{\mu }_j\right|\}ϵ{\lambda }_{\mathcal{T}}\mathcal{T}\left(\tau \right)\hfill \\ & =& \left\{1+\Phi ({\mathrm{\Omega }}_{22},{\mathrm{\Omega }}_{21})\sum _{i=1}^m|{\xi }_i|+\Phi ({\mathrm{\Omega }}_{12},{\mathrm{\Omega }}_{11})\sum _{j=1}^n\left|{\mu }_j\right|\right\}ϵ{\lambda }_{\mathcal{T}}\mathcal{T}\left(\tau \right).\hfill \end{array}$$

The proof is done. □

This result studies $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables of solutions to the problem (3).

Theorem 5.

Let $f:\mathcal{J}\times {\mathbb{R}}^3\to \mathbb{R}$ be continuous. Assume that $\left({\mathcal{P}}_1\right)$-$\left({\mathcal{P}}_3\right)$, (52) is fulfilled, and

$${\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)<1.$$

(60)

Then, the ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s (3) is $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables.

Proof. 

Assume that $z\in \mathcal{E}$ is a solution of (47), and x is a unique solution of (3). By applying Lemma 11, this yields that $u\left(\tau \right)=\mathcal{X}\left(\tau \right)+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right)$, where $\mathcal{X}\left(\tau \right)$ is given by (57). Similarly, if $u\left(a\right)=z\left(a\right)$, ${}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }u\left(a\right)={}^H{\mathfrak{D}}_{a^{+}}^{\beta ,\rho ;\psi }z\left(a\right)$, ${\sum }_{i=1}^m{\xi }_{i}u\left({\eta }_i\right)={\sum }_{i=1}^m{\xi }_{i}z\left({\eta }_i\right)$, ${\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,u\left(\sigma \right))={\mathcal{I}}_{a^{+}}^{\phi ;\psi }\mathcal{G}(\sigma ,z\left(\sigma \right))$, ${\sum }_{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }u\left({\lambda }_j\right)={\sum }_{j=1}^n{\mu }_j{}^H{\mathfrak{D}}_{a^{+}}^{{\varphi }_j,\rho ;\psi }z\left({\lambda }_j\right)$, and ${\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,u\left(\zeta \right))={\mathcal{I}}_{a^{+}}^{\nu ;\psi }\mathcal{H}(\zeta ,z\left(\zeta \right))$, then $\mathcal{X}\left(\tau \right)=\mathcal{Z}\left(\tau \right)$.

Applying Lemma 11 with triangle inequality, for any $\tau \in \mathcal{J}$, it follows that

$$\begin{array}{ccc}& & \left|z\right(\tau )-u(\tau \left)\right|\hfill \\ & =& |z\left(\tau \right)-\mathcal{X}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_u\left(\tau \right)|\hfill \\ & \le & |z\left(\tau \right)-\mathcal{Z}\left(\tau \right)-{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }{\mathcal{F}}_z\left(\tau \right)|+{\mathcal{I}}_{a^{+}}^{\alpha +\beta ;\psi }|{\mathcal{F}}_z\left(\tau \right)-{\mathcal{F}}_u\left(\tau \right)|+|\mathcal{Z}\left(\tau \right)-\mathcal{X}\left(\tau \right)|\hfill \\ & \le & \Theta ϵ{\lambda }_{\mathcal{T}}\mathcal{T}\left(\tau \right)+\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)|z\left(\tau \right)-u\left(\tau \right)|,\hfill \end{array}$$

where $\Theta$ is given as in (58); thus, $|z\left(\tau \right)-x\left(\tau \right)|\le {\mathfrak{C}}_{f,\mathcal{T}}\mathcal{T}\left(\tau \right)ϵ$ such that

$${\mathfrak{C}}_{f,\mathcal{T}}=\frac{\Theta {\lambda }_{\mathcal{T}}}{1-\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)}.$$

Hence, the problem (3) is $\mathbb{UHR}$ stable in $\mathcal{E}$.

Additionally, if we take $ϵ=1$, in $|z\left(\tau \right)-x\left(\tau \right)|\le {\mathfrak{C}}_{f,\mathcal{T}}\mathcal{T}\left(\tau \right)ϵ$, with $\mathcal{T}\left(0\right)=0$, hence (3) is $\mathbb{GUHR}$ stable in $\mathcal{E}$. □

5. Examples

This section shows some illustrative examples of the exactness and applicability of the main results.

Example 1.

The ψ-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s:

$$\left\{\begin{array}{c}{\displaystyle {}^H{\mathfrak{D}}_{0^{+}}^{\frac{3}{2},\frac{4}{5};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}\left({}^H{\mathfrak{D}}_{0^{+}}^{\frac{6}{5},\frac{4}{5};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}x\right)\left(t\right)=f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right)),\tau \in (0,3/2),}\hfill \\ {\displaystyle u\left(0\right)=0,{}^H{\mathfrak{D}}_{0^{+}}^{\frac{6}{5},\frac{4}{5};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}x\left(0\right)=0,}\hfill \\ {\displaystyle \sum _{i=1}^2\left(\frac{i}{i+1}\right)u\left(\frac{9i-6}{10}\right)={\mathcal{I}}_{0^{+}}^{\frac{6}{5};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}\mathcal{G}\left(\frac{6}{5},u\left(\frac{6}{5}\right)\right),}\hfill \\ {\displaystyle \sum _{j=1}^3\left(\frac{4-j}{6-j}\right){}^H{\mathfrak{D}}_{0^{+}}^{\frac{10-j}{5},\frac{4}{5};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}u\left(\frac{4j-1}{10}\right)={\mathcal{I}}_{0^{+}}^{\frac{3}{2};\frac{1}{2}tan\left(\frac{\pi \tau }{\tau +3}\right)}\mathcal{H}\left(\frac{11}{10},u\left(\frac{11}{10}\right)\right).}\hfill \end{array}\right.$$

(61)

Setting $\alpha =3/2$, $\rho =4/5$, $\psi \left(\tau \right)=0.5tan(\pi \tau /(\tau +3\left)\right)$,$\beta =6/5$, $a=0$, $b=3/2$, ${\xi }_i=i/(i+1)$, ${\eta }_i=(9i-6)/10$, $\phi =6/5$, $\sigma =6/5$, ${\mu }_j=(4-j)/(6-j)$, ${\varphi }_j=(10-j)/5$, ${\lambda }_j=(4j-1)/10$, $\nu =3/2$, $\zeta =11/10$, $i=1,2$, and $j=1,2,3$. From the given all datas, we obtain ${\mathrm{\Omega }}_{11}\approx 0.11786018$, ${\mathrm{\Omega }}_{12}\approx 0.5836819$, ${\mathrm{\Omega }}_{21}\approx 0.94874011$, ${\mathrm{\Omega }}_{22}\approx 0.68483544$, and $\mathrm{\Omega }\approx -0.47304769\ne 0$. We consider $f(\tau ,u(\tau ),(\mathcal{K}u\left)\right(\tau ),(\mathcal{W}u\left)\right(\tau \left)\right)$, $\mathcal{H}(\zeta ,u(\zeta \left)\right)$, and $\mathcal{G}(\sigma ,u(\sigma \left)\right)$ as follows:

(i) 

Given the function

$$\begin{array}{ccc}\hfill f(\tau ,u(\tau ),(\mathcal{K}u\left)\right(\tau ),(\mathcal{W}u\left)\right(\tau \left)\right)& =& \frac{{\tau }^4+2{\tau }^2-6}{5{\tau }^2+3t+4}+\frac{5e^{-2\tau -1}}{4-{sin}^2\pi \tau }·\frac{\left|u\right(\tau \left)\right|}{5+\left|u\right(\tau \left)\right|}\hfill \\ & & +\frac{2\tau +6}{3^{5\tau +2}}\left[\frac{\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|}{4+\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|}+\frac{\left|\right(\mathcal{W}u\left)\right(\tau \left)\right)|}{5+\left|\right(\mathcal{W}u\left)\right(\tau \left)\right)|}\right],\hfill \\ \hfill \mathcal{H}(\zeta ,u\left(\zeta \right))=\frac{2}{6+\left|u\right(\xi \left)\right|},& & \mathcal{G}(\sigma ,u\left(\sigma \right))=\frac{2\left|u\right(\sigma \left)\right|}{4+5\left|u\right(\sigma \left)\right|},\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \left(\mathcal{K}u\right)\left(\tau \right)& =& \frac{1}{\mathrm{\Gamma }\left(0.8\right)}{\int }_0^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{0.8-1}{\psi }^{\prime }\left(s\right)k(\tau ,s)u\left(s\right)ds,\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill \left(\mathcal{W}u\right)\left(\tau \right)& =& \frac{1}{\mathrm{\Gamma }\left(1.7\right)}{\int }_0^{\tau }{\left(\psi \left(\tau \right)-\psi \left(s\right)\right)}^{1.7-1}{\psi }^{\prime }\left(s\right)w(\tau ,s)u\left(s\right)ds,\hfill \end{array}$$

(63)

with

$$k(\tau ,s)=\frac{2sin\left(\pi \tau \right)}{s^2+2\tau +5},w(\tau ,s)=\frac{3(2\tau -2)}{5+cos\left(\pi s\right)}.$$

For $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$, $\tau \in [0,3/2]$, we obtain

$$\begin{array}{ccc}& & \left|f(\tau ,u_1,v_1,w_1)-f(\tau ,u_2,v_2,w_2)\right|\le \frac{1}{3}|u_1-u_2|+\frac{1}{4}|v_1-v_2|+\frac{1}{5}|w_1-w_2|,\hfill \\ & & \left|\mathcal{H}(\tau ,u_1)-\mathcal{H}(\tau ,u_2)\right|\le \frac{1}{3}|u_1-u_2|\mathrm{and}\left|\mathcal{G}(\tau ,u_1)-\mathcal{G}(\tau ,u_2)\right|\le \frac{1}{2}|u_1-u_2|.\hfill \end{array}$$

The conditions $\left({\mathcal{P}}_1\right)$–$\left({\mathcal{P}}_2\right)$ are satisfied with ${\mathcal{L}}_1=1/3$, ${\mathcal{L}}_2=1/4$, ${\mathcal{L}}_3=1/5$, ${\mathcal{H}}_1^{*}=1/3$, ${\mathcal{G}}_1^{*}=1/2$, $k_1^{*}=2/5$, and $w_1^{*}=3/5$. Hence, ${\Delta }_1+{\Delta }_2\approx 0.6077104343<1$. Since, Theorem 1 are fulfilled. Then, the problem (61) has a unique solution on $[0,3/2]$. Moreover, we have

$${\mathfrak{C}}_f:=\frac{\mathrm{\Lambda }(\alpha +\beta )}{1-\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)}\approx 0.55937654>0.$$

From Theorem 4, the problem (61) is $\mathbb{UH}$ and $\mathbb{GUH}$ stables on $[0,3/2]$. Take $\mathcal{T}\left(\tau \right)={(\psi \left(\tau \right)-\psi \left(0\right))}^{1/3}$, and we have

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\mathcal{T}\left(\tau \right)=\frac{\mathrm{\Gamma }(4/3)}{\mathrm{\Gamma }(17/6)}{(\psi \left(\tau \right)-\psi \left(0\right))}^{3/2}\mathcal{T}\left(\tau \right)\le \frac{\mathrm{\Gamma }(4/3){tan}^{3/2}(\pi /3)}{2\sqrt{2}\mathrm{\Gamma }(17/6)}\mathcal{T}\left(\tau \right).$$

The inequality (52) is fulfilled with ${\lambda }_{\mathcal{T}}=\frac{\mathrm{\Gamma }(4/3){tan}^{3/2}(\pi /3)}{2\sqrt{2}\mathrm{\Gamma }(17/6)}>0$ and $\Theta \approx 4.6986661$. Then,

$${\mathfrak{C}}_{f,\mathcal{T}}=\frac{\Theta {\lambda }_{\mathcal{T}}}{1-\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)}\approx 2.08782437>0.$$

Therefore, from Theorem 5, the problem (61) is $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables on $[0,3/2]$.

(ii) 

Given the function

$$\begin{array}{ccc}& & f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right))=\frac{2cos\left(\pi \tau \right)+1}{3^{sin\left(\pi \tau \right)+2}}·\frac{\left|u\right(\tau \left)\right|+3}{2+\left|u\right(\tau \left)\right|}\hfill \\ & & +\frac{4\tau -1}{5^{3\tau +2}}·\left[\frac{\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|+\left|\right(\mathcal{W}u\left)\right(\tau \left)\right|}{4+\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|+\left|\right(\mathcal{W}u\left)\right(\tau \left)\right|}\right],\hfill \\ & & \mathcal{H}(\tau ,u\left(\tau \right))=\frac{4\tau +2}{5-2\tau }·\frac{\left|u\right(\tau \left)\right|}{8+5\left|u\right(\tau \left)\right|},\mathcal{G}(\tau ,u\left(\tau \right))=\frac{\tau sin\left(u\right(\tau \left)\right)}{9},\hfill \end{array}$$

with (62) and (63), where $k(\tau ,s)=2/(5+s^{\tau +1})$ and $w(\tau ,s)=3/(7-2sin(\pi s\tau \left)\right)$.

For u, v, $w\in \mathbb{R}$, and $\tau \in [0,3/2]$, we estimate that

$$\begin{array}{ccc}& & \left|f(\tau ,u,v,w)\right|\le \frac{1+2cos\left(\pi \tau \right)}{3^{sin\left(\pi \tau \right)+2}}·\frac{\left|u\right(\tau \left)\right|+3}{2}+\frac{4\tau -1}{5^{3\tau +2}}·\frac{\left|v\right|+\left|w\right|}{4}\hfill \\ & & \left|\mathcal{H}(\tau ,u)\right|\le \frac{4\tau +2}{5-2\tau }·\frac{\left|u\right|}{8},\left|\mathcal{G}(\tau ,u)\right|\le \frac{\tau }{9}·\left|u\right|.\hfill \end{array}$$

The assumption $\left({\mathcal{P}}_4\right)$ is also valid with $p_1\left(\tau \right)=(1+2cos\left(\pi \tau \right))/\left(3^{sin\left(\pi \tau \right)+2}\right)$, $p_2\left(\tau \right)=(4\tau -1)/(4·5^{3\tau +2})=p_3\left(\tau \right)$, $q_1\left(\tau \right)=(4\tau +2)/(5-2\tau )$, $q_2\left(\tau \right)=\tau /9$, $\mathbb{U}\left(\right|u\left|\right)=\left(\right|u|+3)/2$, $\mathbb{V}\left(\right|u\left|\right)=\left|u\right|/8$ and $\mathbb{W}\left(\right|u\left|\right)=\left|u\right|$. Thus, $p_1^{*}=1/3$, $p_2^{*}=1/20=p_3^{*}$, $q_1^{*}=4$, $q_2^{*}=1/6$, $k_1^{*}=2/5$, and $w_1^{*}=3/5$. There is a positive constant ${\mathcal{M}}^{*}>0.37949755$ verifying (${\mathcal{P}}_5$). Then, Theorem is fulfilled, and we can summarize that the problem (61) has at least one solution on $[0,3/2]$.

For any $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2,$ and $\tau \in [0,3/2]$, one has

$$\left|f(\tau ,u_1,v_1,w_1)-f(\tau ,u_2,v_2,w_2)\right|\le \frac{5}{12}\left|u_1-u_2\right|+\frac{1}{20}\left|v_1-v_2\right|+\frac{1}{20}\left|w_1-w_2\right|.$$

The conditions $\left({\mathcal{P}}_1\right)$-$\left({\mathcal{P}}_2\right)$ are verified with ${\mathcal{L}}_1=5/12$, ${\mathcal{L}}_2={\mathcal{L}}_3=1/20$, ${\mathcal{H}}_1^{*}=1/2$, ${\mathcal{G}}_1^{*}=1/6$, $k_1^{*}=2/5$ and $w_1^{*}=3/5$. Thus, ${\Delta }_1+{\Delta }_2\approx 0.44078217<1$. Hence, the problem (61) has a unique solution on $[0,3/2]$. Moreover, we obtain ${\mathfrak{C}}_f:=0.56437711>0$. Theorem 4 is satisfied, the problem (61) is $\mathbb{UH}$ and $\mathbb{GUH}$ stables on $[0,3/2]$. Take $\mathcal{T}\left(\tau \right)={(\psi \left(\tau \right)-\psi \left(0\right))}^{1/2}$, and we have

$${\mathcal{I}}_{a^{+}}^{\alpha ;\psi }\mathcal{T}\left(\tau \right)=\frac{1}{4\sqrt{\pi }}{(\psi \left(t\right)-\psi \left(0\right))}^{3/2}\mathcal{T}\left(\tau \right)\le \frac{{tan}^{3/2}(\pi /3)}{8\sqrt{2\pi }}\mathcal{T}\left(\tau \right).$$

The inequality (52) is satisfied with ${\lambda }_{\mathcal{T}}=\frac{{tan}^{3/2}(\pi /3)}{8\sqrt{2\pi }}>0$ and $\Theta \approx 4.69866612$. Then,

$${\mathfrak{C}}_{f,\mathcal{T}}=\frac{\Theta {\lambda }_{\mathcal{T}}}{1-\left({\mathcal{L}}_1{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right)+{\mathcal{L}}_2{k}_1^{*}{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)+{\mathcal{L}}_3{w}_1^{*}{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)\right)}\approx 2.10648855>0.$$

Hence, Theorem 5 is true, and the problem (61) is $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables on $[0,3/2]$.

(iii) 

Given the function

$$\begin{array}{ccc}& & f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right))=\frac{e^{3\tau -5}}{ln(5-2\tau )}+\frac{\sqrt{4{\tau }^2+2\tau +4}}{\tau sin\left(\tau \right)+6}sin\left(u\left(\tau \right)\right)\hfill \\ & & +\frac{2\tau }{9-2\tau }·\frac{\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|}{1+2\left|\right(\mathcal{K}u\left)\right(\tau \left)\right|}\hfill \\ & & +\frac{4cos\tau }{3^{6\tau +2}}arctan\left(\left(\mathcal{W}u\right)\left(\tau \right)\right),\hfill \\ & & \mathcal{H}(\tau ,u\left(\tau \right))=\frac{\left|2u\right(\tau )+5|}{{\tau }^2+5},\mathcal{G}(\tau ,u\left(\tau \right))=\frac{2\tau sin\left(u\right(\tau \left)\right)+3}{5+ln(2\tau +5)},\hfill \end{array}$$

with (62) and (63), where $k(\tau ,s)=4/(7+s\tau )$ and $w(\tau ,s)=2/(7+2s{cos}^2\left(\pi \tau \right))$.

For any $u_i$, $v_i$, $w_i\in \mathbb{R}$, $i=1,2$, and $\tau \in [0,3/2]$, we obtain

$$\begin{array}{ccc}& & \left|f(\tau ,u_1,v_1,w_1)-f(\tau ,u_2,v_2,w_2)\right|\le \frac{2}{3}|u_1-u_2|+\frac{1}{2}|v_1-v_2|+\frac{4}{9}|w_1-w_2|,\hfill \\ & & \left|\mathcal{H}(\tau ,u_1)-\mathcal{H}(\tau ,u_2)\right|\le \frac{2}{5}|u_1-u_2|\mathrm{and}\left|\mathcal{G}(\tau ,u_1)-\mathcal{G}(\tau ,u_2)\right|\le \frac{3}{5}|u_1-u_2|.\hfill \end{array}$$

The conditions $\left({\mathcal{P}}_1\right)$-$\left({\mathcal{P}}_2\right)$ are satisfied with ${\mathcal{L}}_1=2/3$, ${\mathcal{L}}_2=1/2$, ${\mathcal{L}}_3=4/9$, ${\mathcal{H}}_1^{*}=2/5$, ${\mathcal{G}}_1^{*}=3/5$, $k_1^{*}=4/7$, and $w_1^{*}=2/7$. Hence, we have

$$\left({\Delta }_1+{\Delta }_2-{\mathrm{\Psi }}^{\alpha +\beta }\left(b\right){\mathcal{L}}_1-{\mathrm{\Psi }}^{\theta +\alpha +\beta }\left(b\right)k_1^{*}{\mathcal{L}}_2-{\mathrm{\Psi }}^{\delta +\alpha +\beta }\left(b\right)w_1^{*}{\mathcal{L}}_3\right)\approx 0.76735591<1.$$

For u, v, $w\in \mathbb{R}$, and $\tau \in [0,3/2]$, we have

$$\begin{array}{ccc}& & \left|f(\tau ,u,v,w)\right|\le \frac{e^{3\tau -5}}{ln(5-2\tau )}+\frac{\sqrt{4{\tau }^2+2\tau +4}}{\tau sin\left(\tau \right)+6}\left|u\left(\tau \right)\right|\hfill \\ & & +\frac{2\tau }{9-2\tau }\left|\left(\mathcal{K}u\right)\left(\tau \right)\right|+\frac{4cos\tau }{3^{6\tau +2}}\left|\left(\mathcal{W}u\right)\left(\tau \right)\right|,\hfill \\ & & \left|\mathcal{H}(\tau ,u)\right|\le \frac{2\left|u\right|}{{\tau }^2+5}+\frac{5}{{\tau }^2+5},\left|\mathcal{G}(\tau ,u)\right|\le \frac{2\tau \left|u\right|}{5+ln(2\tau +5)}+\frac{3}{5+ln(2\tau +5)}.\hfill \end{array}$$

The condition $\left({\mathcal{P}}_5\right)$ is verified with $f_1\left(\tau \right)=e^{3\tau -5}/ln(5-2\tau )$, $f_2\left(\tau \right)=\sqrt{4{\tau }^2+2\tau +4}$$/(\tau sin(\tau )+6)$, $f_3\left(\tau \right)=2\tau /(9-2\tau )$, $f_4\left(\tau \right)=4cos\tau /3^{6\tau +2}$, $h_1\left(\tau \right)=5/({\tau }^2+5)$, $h_2\left(\tau \right)=2/({\tau }^2+5)$, $g_1\left(\tau \right)=3/(5+ln(2\tau +5)$, and $g_2\left(\tau \right)=2\tau /(5+ln(2\tau +5))$. So, Theorem 3 is verified, and we can summarize that the problem (61) has at least one solution on $[0,3/2]$.

In addition, the problem (61) has a unique solution on $[0,3/2]$ with ${\Delta }_1+{\Delta }_2\approx 0.89211721<1$. Moreover, we have that ${\mathfrak{C}}_f:=0.60023816>0$. Then, Theorem 4 is true, and the problem (61) is $\mathbb{UH}$ and $\mathbb{GUH}$ stables on $[0,3/2]$. Take $\mathcal{T}\left(\tau \right)={(\psi \left(\tau \right)-\psi \left(0\right))}^{1/4}$, and we get ${\lambda }_{\mathcal{T}}=\frac{\mathrm{\Gamma }(5/4){tan}^{3/2}(\pi /3)}{2\sqrt{2}\mathrm{\Gamma }(11/4)}\approx 0.45418619>0$ and $\Theta \approx 4.69866612$. Then, we obtain ${\mathfrak{C}}_{f,\mathcal{T}}\approx 2.43827113>0$. From Theorem 5, then, the problem (61), is $\mathbb{UHR}$ and $\mathbb{GUHR}$ stables on $[0,3/2]$.

(iv) 

Consider $f(\tau ,u\left(\tau \right),\left(\mathcal{K}u\right)\left(\tau \right),\left(\mathcal{W}u\right)\left(\tau \right))={\varrho }_1{\left(\psi \left(\tau \right)-\psi \left(0\right)\right)}^{{\varpi }_1}$ and

$$\mathcal{G}(\tau ,u\left(\tau \right))={\varrho }_2{\left(\psi \left(\tau \right)-\psi \left(0\right)\right)}^{{\varpi }_2},\mathcal{H}(\tau ,u\left(\tau \right))={\varrho }_3{\left(\psi \left(\tau \right)-\psi \left(0\right)\right)}^{{\varpi }_3}.$$

By Lemma 4 with ${\varrho }_1=2$, ${\varrho }_2=3$, ${\varrho }_3=4$, ${\varpi }_1=1/7$, ${\varpi }_2=1/5$, and ${\varpi }_3=1/3$, the solution of the problem (61) is given by

$$\begin{array}{ccc}& & x\left(\tau \right)\hfill \\ & =& \frac{2\mathrm{\Gamma }(8/7){\left(\psi \left(\tau \right)-\psi \left(0\right)\right)}^{1/7+\alpha +\beta }}{\mathrm{\Gamma }(8/7+\alpha +\beta )}+\frac{{\left(\psi \left(\tau \right)-\psi \left(0\right)\right)}^{{\gamma }_1+\beta -1}}{\mathrm{\Omega }\mathrm{\Gamma }({\gamma }_1+\beta )}\hfill \\ & & \times [{\mathrm{\Omega }}_{22}\left(\frac{3\mathrm{\Gamma }(6/5){\left(\psi \left(\sigma \right)-\psi \left(0\right)\right)}^{7/5}}{\mathrm{\Gamma }(12/5)}-\sum _{i=1}^m\frac{2\mathrm{\Gamma }(8/7){\xi }_i{\left(\psi \left({\eta }_i\right)-\psi \left(0\right)\right)}^{1/7+\alpha +\beta }}{\mathrm{\Gamma }(8/7+\alpha +\beta )}\right)\hfill \\ & & -{\mathrm{\Omega }}_{12}\left(\frac{4\mathrm{\Gamma }(4/3){\left(\psi \left(\zeta \right)-\psi \left(0\right)\right)}^{11/6}}{\mathrm{\Gamma }(17/6)}-\sum _{j=1}^n\frac{2\mathrm{\Gamma }(8/7){\mu }_j{\left(\psi \left({\lambda }_j\right)-\psi \left(0\right)\right)}^{1/7+\alpha +\beta -{\varphi }_j}}{\mathrm{\Gamma }(8/7+\alpha +\beta -{\varphi }_j)}\right)]\hfill \\ & & +\frac{{\left(\psi \left(t\right)-\psi \left(0\right)\right)}^{{\gamma }_2-1}}{\mathrm{\Omega }\mathrm{\Gamma }\left({\gamma }_2\right)}\left[{\mathrm{\Omega }}_{11}\right(\frac{4\mathrm{\Gamma }(4/3){\left(\psi \left(\zeta \right)-\psi \left(0\right)\right)}^{11/6}}{\mathrm{\Gamma }(17/6)}\hfill \\ & & -\sum _{j=1}^n\frac{2\mathrm{\Gamma }(8/7){\mu }_j{\left(\psi \left({\lambda }_j\right)-\psi \left(0\right)\right)}^{1/7+\alpha +\beta -{\varphi }_j}}{\mathrm{\Gamma }(8/7+\alpha +\beta -{\varphi }_j)})\hfill \\ & & -{\mathrm{\Omega }}_{21}\left(\frac{3\mathrm{\Gamma }(6/5){\left(\psi \left(\sigma \right)-\psi \left(0\right)\right)}^{7/5}}{\mathrm{\Gamma }(12/5)}-\sum _{i=1}^m\frac{2\mathrm{\Gamma }(8/7){\xi }_i{\left(\psi \left({\eta }_i\right)-\psi \left(0\right)\right)}^{1/7+\alpha +\beta }}{\mathrm{\Gamma }(8/7+\alpha +\beta )}\right)].\hfill \end{array}$$

A graph displaying of $u\left(\tau \right)$ for the problem (61) under $\alpha =1.65,1.70,\dots ,2.00$ and $\beta =1.86,1.88,\dots ,2.00$ with $\psi \left(\tau \right)={\tau }^{\sqrt{\alpha }+\sqrt{\beta }}$, ${(sin\tau )}^{\sqrt{\alpha }+\sqrt{\beta }}$, ${(\alpha +\beta )}^{\frac{\tau }{2}}$, ${(ln(\tau +1))}^{\sqrt{\alpha +\beta }}$, is shown in Figure 1, Figure 2, Figure 3 and Figure 4.

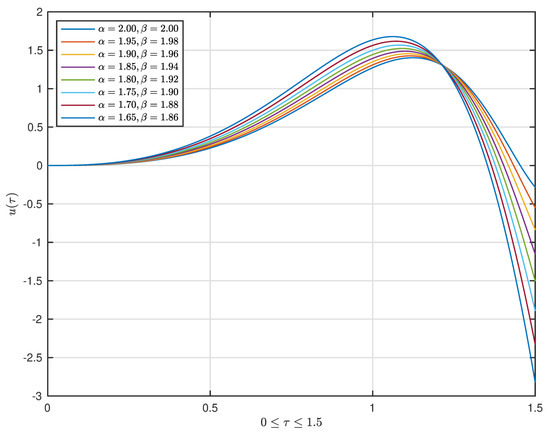
Figure 1. The graph displaying of $u\left(\tau \right)$ for (61) with $\psi \left(\tau \right)={\tau }^{\sqrt{\alpha }+\sqrt{\beta }}$ for $\tau \in [0,3/2]$.

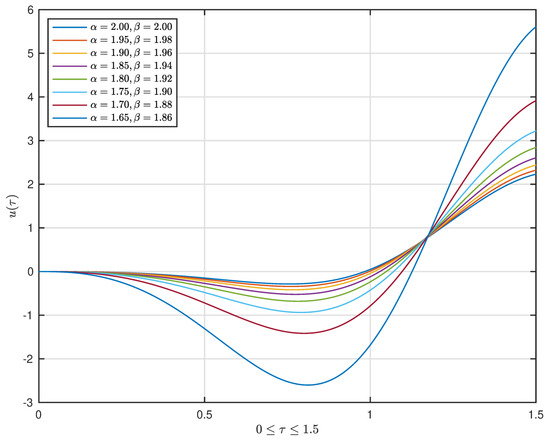
Figure 2. The graph displaying of $u\left(\tau \right)$ for (61) with $\psi \left(\tau \right)={(sin\tau )}^{\sqrt{\alpha }+\sqrt{\beta }}$ for $\tau \in [0,3/2]$.

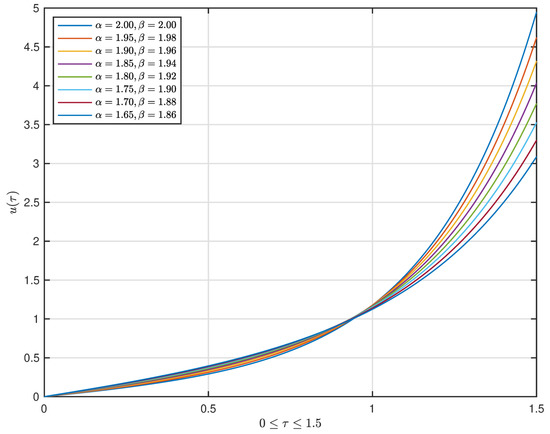
Figure 3. The graph displaying of $u\left(\tau \right)$ for (61) with $\psi \left(\tau \right)={(\alpha +\beta )}^{\frac{\tau }{2}}$ for $\tau \in [0,3/2]$.

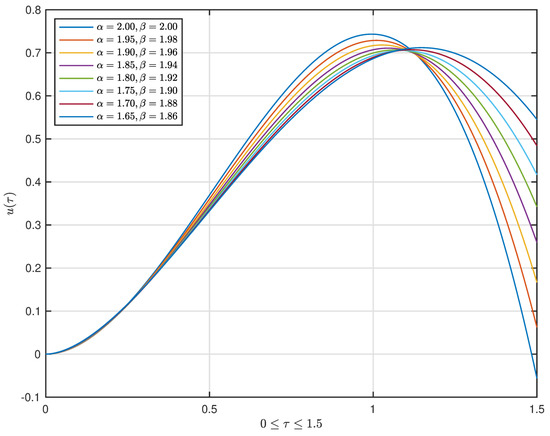
Figure 4. The graph displaying of $u\left(\tau \right)$ for (61) with $\psi \left(\tau \right)={(ln(\tau +1))}^{\sqrt{\alpha +\beta }}$ for $\tau \in [0,3/2]$.

6. Conclusions

The main aims of this study have been accomplished. Firstly, the uniqueness result for a nonlinear $\psi$-Hilfer $\mathbb{FBVP}$ describing Navier model with $\mathbb{NIBC}$s was analyzed by helping Banach’s fixed point theorem. Afterward, the existence results were established by applying fixed point theory of Leray-Schauder’s and Kransnoselskii’s types, while the guarantee of the existence of solutions was shown by the powerful techniques, such as Ulam’s stability, including $\mathbb{UH}$, $\mathbb{GUH}$, $\mathbb{UHR}$, and $\mathbb{GUHR}$ stables. Finally, we ensured the theoretical results via some illustrates in the special cases of $\psi$ are polynomial, trigonometry, exponential, and logarithm functions. This paper has considered different methods and is attractive for researchers who are interested in the work of the integro-differential equation describing Navier model under $\psi$-Hilfer fractional operators. We will concentrate on examining the qualitative theories of solutions to nonlinear equations or systems of real-world models with boundary conditions in the context of other fractional calculus in the future. It also remains to extend the results obtained to new Hilfer-type operators; see, for example, Reference [59].