1. Introduction
In December 2019, the coronavirus disease 2019 (COVID-19) was first identified in Wuhan and rapidly invaded the whole of China and the world [
1]. This disease was officially named COVID-19 by the World Health Organization (WHO) on 11 January 2020; then it was announced as a global health emergency on 11 March 2020 [
2,
3]. Since then, many studies have been done to investigate this global pandemic. As a part of these efforts, we here aim to develop a mathematical model to describe and simulate the interactions between SARS-CoV-2 molecules and the immune system within a two dimensional cellular space. In the following, we present a brief overview of SARS-CoV-2 in terms of its spreading properties, viral replication and mechanism of infection.
Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is a novel virus that has a genetic similarity to SARS-CoV, which is responsible for SARS disease, while the new virus (SARS-CoV-2) causes coronavirus disease 19 (COVID-19) [
4]. Both SARS-CoV and SARS-CoV-2 have a common link in terms of mechanism of infection where both of them use the spike proteins (S-protein) to bind Angiotensin-converting enzyme 2 (ACE2), which in turn helps them to reach and attack the cells [
4]. Despite this similarity, it has been found that SARS-CoV-2 binds to ACE2 slower than the old virus (SARS-CoV) where this slow binding causes a longer incubation period. Hence, this time delay of onset symptoms of COVID-19 leads to a faster spread of the pandemic around the world [
3].
Although there is a lack of enough experimental studies about immune responses for people who have symptomatic/asymptomatic COVID-19 infections, there are some studies which investigate the interactions between the virus and many components of the immune system including the innate and the adaptive immune responses [
5,
6,
7]. Once coronavirus-2 gains access inside the host cell using its spike protein (S) and the target cell receptor (ACE2) (in the same manner as SARS-CoV), it begins uncovering its genetic materials and producing some essential proteins such as envelope (E), nucleocapsid (N) and also spike (S) for motivating the interactions with target cells as well as assembling and releasing a new virus generation [
8,
9]. The ability of viral replication drives to having a local inflammatory response which motivates the immune system to recognize the virus and start the primary line of defense, that is, the activation of neutrophils, natural killer cells, naive T and B cells and the secretion of chemokine [
10,
11]. As long as the infection persists for a certain period of time, T cells pass through many stages including their proliferation, activation, migration, and differentiation, ultimately they come in the form of the effector T cells involving both helper (CD4+) and cytotoxic T cells (CD8+), and the regulatory T cells (Treg) [
10]. Besides the cellular immunity, B cells play a key role in humoral immunity, especially after their transformation into plasma B cells (via the assistance of the armed/follicular helper T cells [
10,
12,
13]). These types of cells have the ability to produce antibodies specific to SARS-CoV-2, such as IgA, IgG, and IgM, in order to neutralize the virus at the infection site [
4,
8,
14]. Antibodies specific to SARS-CoV-2 are mostly a very essential tool for neutralizing the virus via decreasing its binding ability to ACE2, but we should take into account its potential threat of enhancing the immunopathogenesis [
15]. However, there is biological evidence that shows that the antibody levels are going to be decreased over time through infection with SARS-CoV-2, while particular components of the immune system, such as the memory T/B cells, will maintain at a high level for almost 6 to 8 months [
6].
One major obstacle that creates difficulties for dealing with SARS-CoV-2 infection is the quick activation and migration of T cells to the site of viral replication, which in turn leads to releasing a huge amount of inflammatory cytokines such as IL-1, IL-6, and IFN-
. This storm of cytokines causes the cytokine release syndrome resulting in serious damage to vital organs such as lungs as well as causing viral sepsis [
11,
16]. On other hand, there is no clue so far suggesting that the evolution of B cells over time will participate in this pathogenesis. However, we cannot generalize this scenario because it has been found that some of infected patients with SARS-CoV-2 who were treated in the ICU or who died have low levels of T cells as well as B cells [
7].
Over the past decades, mathematical modeling of immune responses to viral infections has developed in terms of either realizing the biological concepts or improving the mathematical techniques to obtain better outputs [
17,
18,
19,
20]. Since the outbreak of COVID-19, many mathematical research projects have been performed, but the majority of these mathematical models focus on the temporal dynamics only (ODE models) which either use the so-called SIR-models (compartmental models) to predict the population progress between compartments such as [
21,
22,
23,
24,
25], or describe the within host dynamics to investigate immune responses to SARS-CoV-2 particles within the cellular scale as proposed in [
22,
26,
27]. However, these within host models were being built on previous studies for similar infectious diseases such as influenza [
18,
28] and hepatitis B [
29]. To our knowledge, we could not find any spatio-temporal model for describing the spatial distribution of the immune responses to SARS-CoV-2 within a two dimensional cellular space. Nevertheless, there are a few preprint mathematical studies using PDEs to describe the spread of the population compartments with respect to time and their physical locations at different regions which means these mathematical approaches are still a type of the compartmental class models. Therefore, in
Section 2, we present a first attempt for deriving a new mathematical model, which is based on a coupled system of partial differential equations to obtain a reasonable description for the interaction between coronavirus-2 and its response to the components of immune system.
The rest of this paper is summarized as follows.
Section 3 includes model calibration and developing a computational framework to compute the coupled reaction diffusion system within two spatial dimensions.
Section 4 involves a comparison of our numerical results with a few cases collected from recent clinical studies. Lastly, in
Section 5 we present a discussion on a few key points including hints at future works.
2. Modeling Framework
Building on some biological observations and mathematical models (temporal approaches) [
7,
8,
10,
11,
12,
13,
16,
22,
28,
30,
31,
32,
33,
34,
35,
36], we develop a new spatio-temporal mathematical model to explore the interactions between the most essential components of the immune system and SARS-CoV-2 particles within a cellular perspective. This dynamical interaction occurs on a spatial domain
over a time interval
and it involves the healthy host cells
, viral-infected cells
, SARS-CoV-2 molecules
, chemokines
, the effector T cells
, the regulatory T cells
, B-lymphocytes cells
and antibodies
. In a similar manner to the modeling derivation method under a continuum approach and the conservation law as detailed in [
37], we assume that
is a fixed (random) volume surrounded entirely by a smooth surface
. Then, the appearance or disappearance of any component within
is expressed by the flux of that component through the boundary
and the proliferation and/or degradation of that component. In other words, we suppose that
represents the concentration of a component at a fixed time
t and a position
,
denotes the net flow of a component and
stands for the proliferation and/or the degradation of a component. Hence, we have the following conservation equation:
where
. Now, using the divergence theorem, we can differentiate to get the following conservation equation for each component of a system, namely,
The above method has been used to model many biological applications such as [
34,
38,
39,
40]. Thus, we can denote the resulting
8D-reaction-diffusion-chemotaxis operator
by the following expression:
where the differential operator
of order 2 will be explained in detail in the following context.
Host & Infected cells Following biological observations and spatio-temporal mathematical approach that have been taken from various experimental studies for similar infectious diseases such as [
31,
32], we suppose that both type of cells are exercising a random motility on the spatial domain
ℵ at rates
and
, respectively. The density of the host cells is assumed to be produced logistically at a rate
, while the decay of its density comes from many reasons at a rate
. At the same time, the infected cells are produced when SARS-CoV-2 virus binds the host cells by the S protein at a rate
through the targeted receptor, namely, ACE2 [
11]. Moreover, the density of infected cells is decreased over time due to two main factors, namely, effector T cells
at a rate
[
10,
33] and natural deaths at a rate
. These assumptions can be formalised mathematically through the following expressions:
SARS-CoV-2 As mentioned in [
8], SARS-CoV-2 has the ability to motile inside the respiratory system, therefore, we assume that coronavirus-2 diffuses randomly through
ℵ at a random motility rate
. Furthermore, the interactions between immune cells and viruses increase the secretion level of chemokines, which in turn impacts virus movement [
8]. Adopting this assumption, we suppose that SARS-CoV-2 migration is directed towards a higher concentration of a chemical gradient at a rate
. Moreover, coronaviruses are capable of viral replication actively within throat for at least 5 days (depending on the duration of the onset of symptoms) as detailed in the clinical studies [
41,
42], where this viral replication occurs due to the existence of the gene (ORF1) [
36]. Hence, we take into account its replication within infected cells at a rate
. However, besides the natural decay of SARS-CoV-2 density at a rate
, the antibodies (produced by B cells) play a key role in restricting or preventing virus entry inside the host cells [
10], hence SARS-CoV-2 particles are assumed to be decreased due to antibodies increasing level at a rate
. These words can be mathematically expressed via the following equation:
Chemokine Concentration Chemokines are small proteins secreted by many cells where they have the ability to direct the surrounding cells chemotaxically towards the source of the chemokines [
43]. Besides the homeostatic function of chemokines [
43], chemokines have been found in many COVID-19 patients [
8,
10] for attracting immune cells towards the inflammatory sites [
8]. Thus, it is assumed to be produced proportionally to the viral-infected cells and T cells at a rate
, with taking into consideration its natural decay at a rate
. Moreover, we suppose that chemokines can move randomly through the tissue at a random motility coefficient rate
. Therefore, we have the following equation:
The effector and the regulatory T cells In general, T cells are one of the most important components of immune system un which they play a key role in the initiation of the adaptive immune responses during the immunity cycle [
10]. Regardless of the complexity of T cells functions and multi-stage processes including naive, helper, cytotoxic and memory T cells, it ultimately turns into the effector T cells
[
10]. Additionally, we also account for the dynamics of the regulatory T cells
due to its significant role in immune homeostasis and in controlling the proliferation of effector T cells [
30]. Biological evidence shows that the efficiency of T cells depends on its motility pattern, spatial distribution and motility major obstacles [
33]. Therefore, we take into account the random movement on the spatial domain for both T cells (effector and regulatory) with motility rates
and
, respectively [
7,
34]. In addition to that, the directional migration of T cells is assumed to be in the form of chemotaxis towards gradients of the secreted chemokines (with the chemotaxic rates
) [
7,
8,
33,
34]). Building on relevant studies [
28,
35], this specific study [
22] proposes a model describing the proliferation form of T cells in the context of COVID-19. Thus, we assume that the proliferation of the effector T cells arises naturally at a rate
and its growth depends on the virus distribution with taking into consideration the maximum carrying capacity
. Furthermore, the proliferation rate of the regulatory T cells keeps track of the production of the effector T cells at a rate
with a carrying capacity rate
. However, both types of T cells are supposed to be decreased naturally at rates
and
, respectively. Besides this, the regulatory T cells regulate the immune system and also suppress the proliferation of effector T cells before damage occurs [
30]. Consequently, this interaction between the two types of T cells leads to a decay in the overall density of the effector T cells at a rate
. Hence, the evolution of the effector and the regulatory T cells are represented by the following equations:
B-lymphocytes cells & Antibodies During the early stages of infection with the SARS-CoV-2 virus, T cells (armed/follicular helper T cells) and their released cytokines during activation play an important role in the activation process of B cells [
12,
13,
16] including the early responses of B cells against the N protein [
8]. Therefore, we suppose that the production level of T cells increases the activation level of B cells at a rate
. Moreover, the proliferation of B cells is caused via virus growth tracking at a rate
with a maximum carrying capacity
. Meanwhile, its density decay is naturally occurring at a rate
. Furthermore, we account for the produced antibodies by B cells at a rate
[
7,
10]. However, the density of antibodies is assumed to be degraded due to inhibition induced via binding with SARS-CoV-2 as well as by natural reasons at a rate
[
7,
10]. Both B cells and antibodies are assumed to exercise a random motility on the spatial domain at diffusion coefficients
and
, respectively. We also take into account the chemotaxis directional movement of B cells towards inflammatory concentration [
8,
10] at a rate
. The above assumptions are formalised mathematically by the following equations:
Considering the above modeling hypotheses, the full model is written as follows:
Each of the above coupled dynamics are followed by initial and boundary conditions which will be given in detail in
Section 3.2.
4. A Comparison of Computational and Clinical Results
In this section, we aim to investigate numerically the dynamics of host cells
, infected cells
, SARS-CoV-2 particles
, chemokines
, the effector T cells
, the regulatory T cells
, B-lymphocytes cells
and antibodies
. These dynamics are computed at each discretized spatio-temporal node
within a computational domain of size
which equals to a physical domain
. For time steps, we run the numerical simulation for 120 stages (120,000
), which equals approximately 333.34 h. However, SARS-CoV-2 particles may remain in the body for more than 60 days or sometimes reaching 150 days as discussed in [
5,
19,
48], which corresponds to 259,200
650,000
(in non-dimensionalised time step). Moreover, we choose the following initial values for the variables those defined in
Section 3.1 based on some biological and mathematical observations [
19,
20,
27],
. In the following context, we discuss the validation of the suggested model (
8) with regards to experimental observations in terms of the viral load of SARS-CoV-2 during time. As mentioned in
Section 1, there are a bunch of studies that discuss a within host modeling of SARS-CoV-2 interactions with immune system components, but these studies consider only the temporal dynamics of this interaction. Hence, there is a lack of both computational and experimental data for the spatial distribution of SARS-CoV-2 within the cellular scale. However, we still wish that our suggested spatio-temporal model (
8) will stimulate experimental works to validate our numerical findings.
Now, in order to check the validation of our modeling assumptions, we first select a list of values for the model parameters as presented in
Table 1 which mainly based on the following published studies [
19,
22,
26,
27,
34,
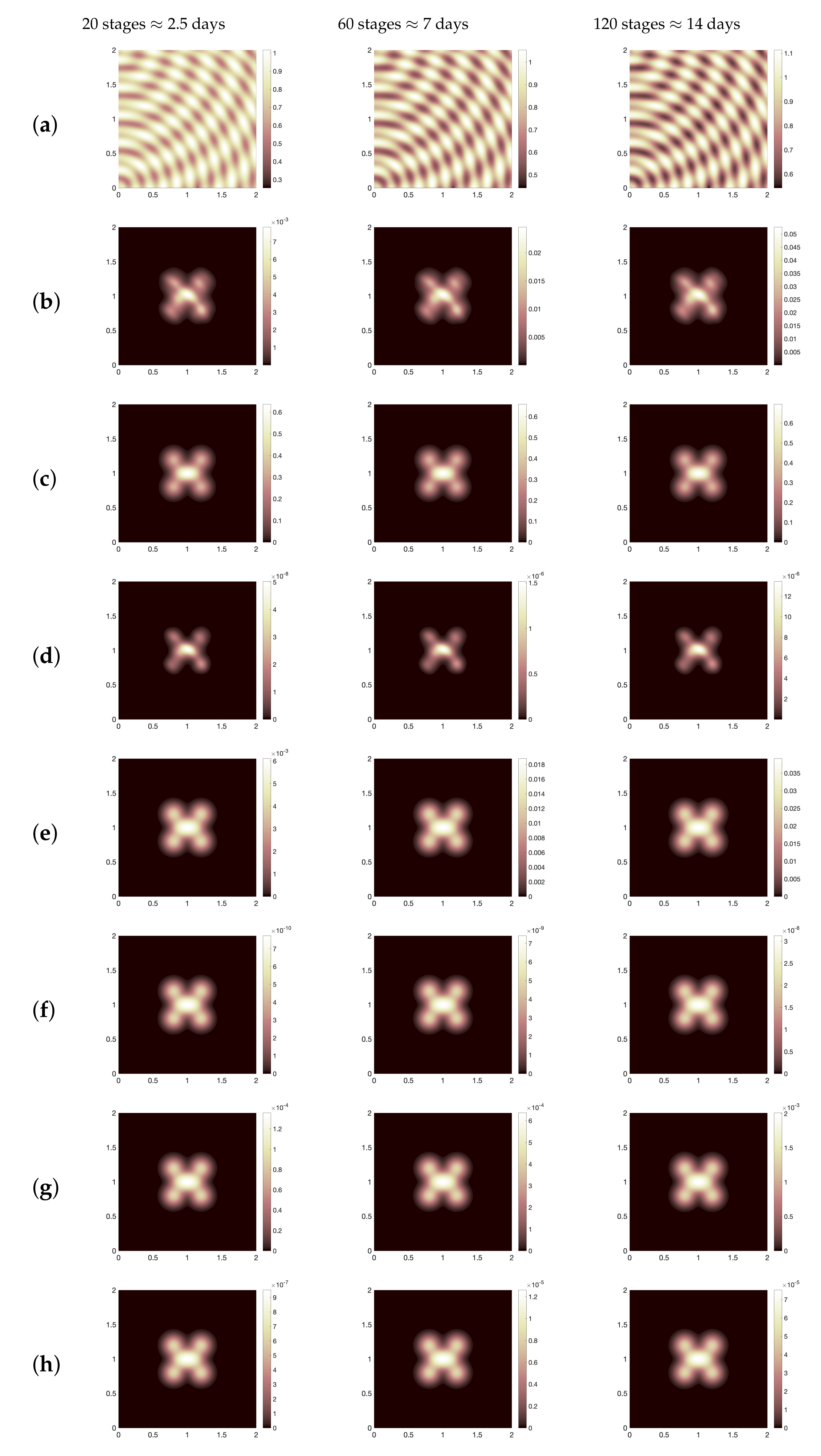
44]. Using this baseline values, we show the spatial distribution for all dynamics as illustrated in
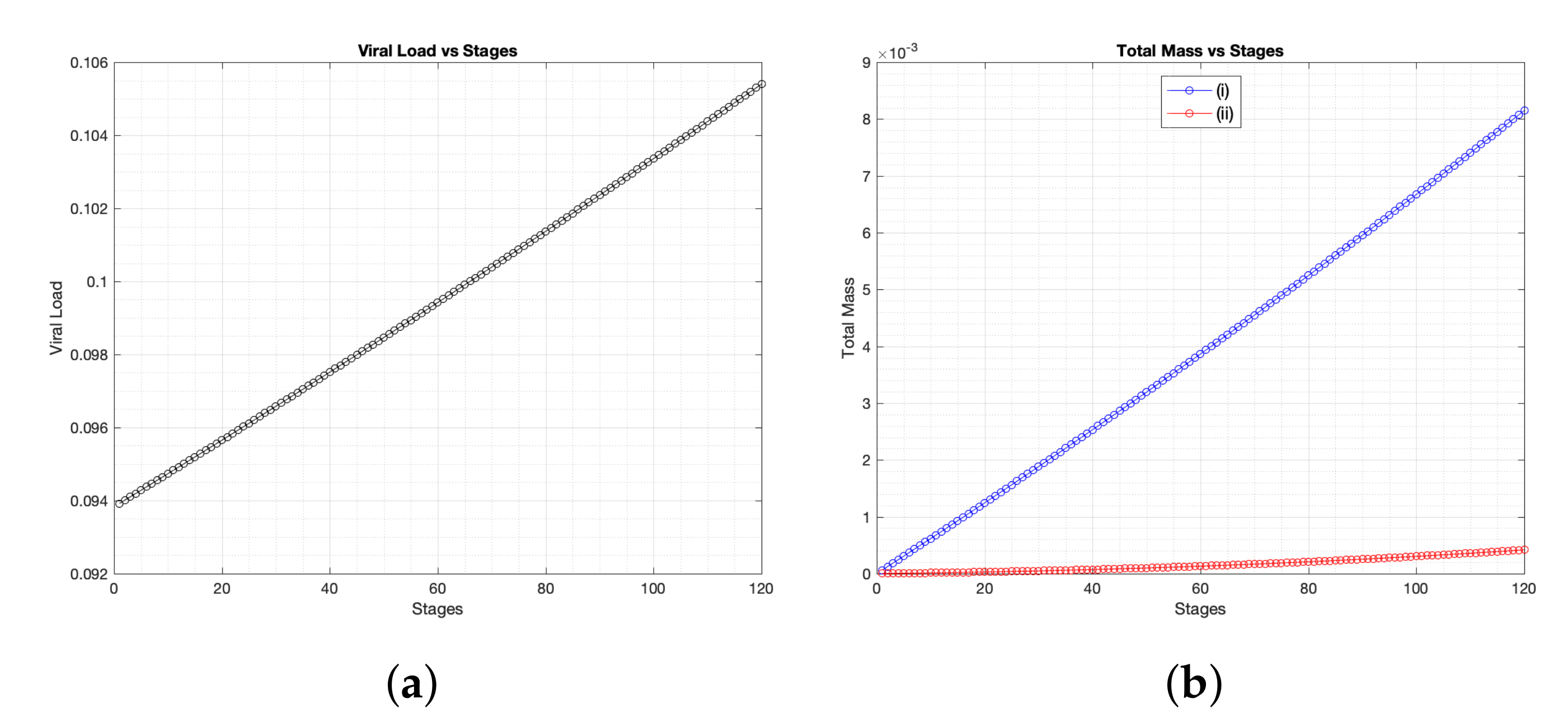
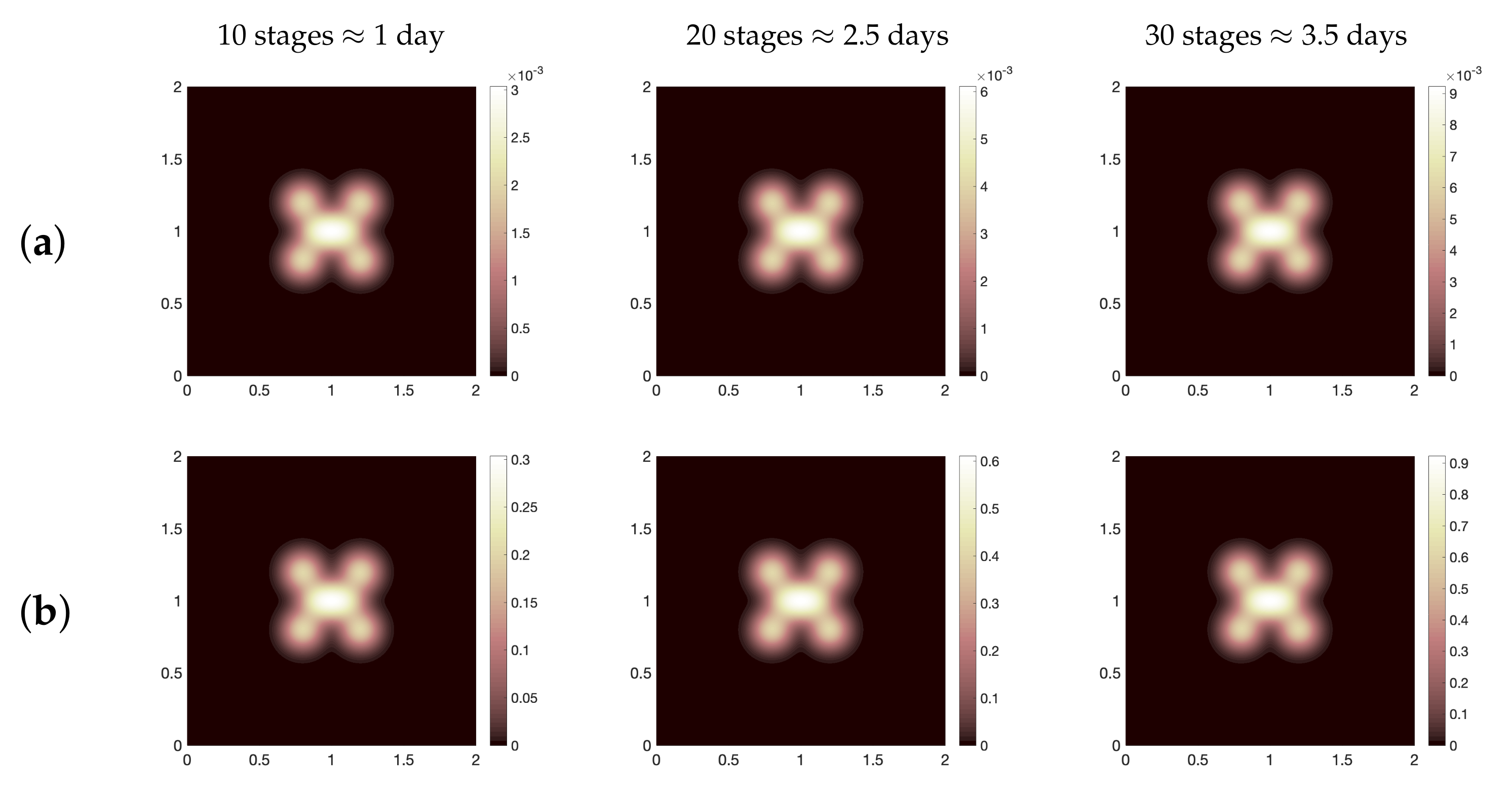
Figure 2 where we present (for three different time periods, namely, ≈2.5 days, 7 days, 14 days): healthy cells (a), infected cells (b), SARS-CoV-2 particles (c), chemokines (d), the effector T cells (e), the regulatory T cells (f), B-lymphocytes cells (g) and antibodies (h). It is obvious to see that the spatial distribution of immune components follows the same distribution patterns of virus. Moreover, for the parameter regimes that we have selected as a starting point for the computational investigation, we find that the total viral load of SARS-CoV-2 increases since day one of infection. This increase of virus occurs due to the slow growth of T and B cells over time (see
Figure 3a,b). However, comparing our computational result with patients data for the whole clinical course that have been considered in [
49], we conclude the following, in the clinical data, the average virus load in swab test was about
copies per mL on the day 5 which equals to
in non-dimensional values, while numerically, the viral load on the day 5 is almost equal to
, that is,
(see
Figure 4a–i). Nevertheless, the baseline scenario of the numerical simulation represents a failure of immune responses to infection with SARS-CoV-2 because it is clearly to see that the density of infected cells increases from day one of infection until 14 days. This immunity failure probably occurred due to the late response of T cells (especially for asymptomatic cases) as presented in
Figure 5 where we compare the effector T cells evolution at early time stages for two cases of immune responses to SARS-CoV-2, namely, baseline scenario and a better case of immunity responses (it will be explained in detail in the next context). Further, the slow response of T cells is negatively reflected on B cells growth and the activation process of antibodies.
In the following, we investigate the impact of variation of parameters on the level of SARS-CoV-2 viral load over a certain period of time. To that end, we first denote the virus domain
to be a sub-domain located entirely within our computational domain, that is,
. Then, we define a new function
which enables increasing or decreasing the level of all system components exclusively at each grid point containing a non-zero solution of virus i.e., at every
. Accordingly,
is expressed as follows:
where
is the topological closure of
and the percentage variable
is given by the following choices:
Thus, the system (
8) can be rewritten in the following form:
Just to note that the system (
12) is only computed by using one of the functions
, for example, if we plug the function
into system (
12), the other function
will be implemented as a matrix of ones during computations. Based on that, we can divide the parameters into two main groups, namely, (A) parameters that, if increased, would decrease the overall viral load over time (motivation occurs at a rate
) and (B) parameters that, if increased, would increase the level of viral load (that occurs at a rate
).
Now, we start the sensitivity analysis using the percentage variable
to explore the impact of parameters defined in group (A) upon the overall result. In general, increasing this group of parameters leads to a proportional decay on the overall viral load of SARS-CoV-2 over time. In other words, increasing the percentage variable
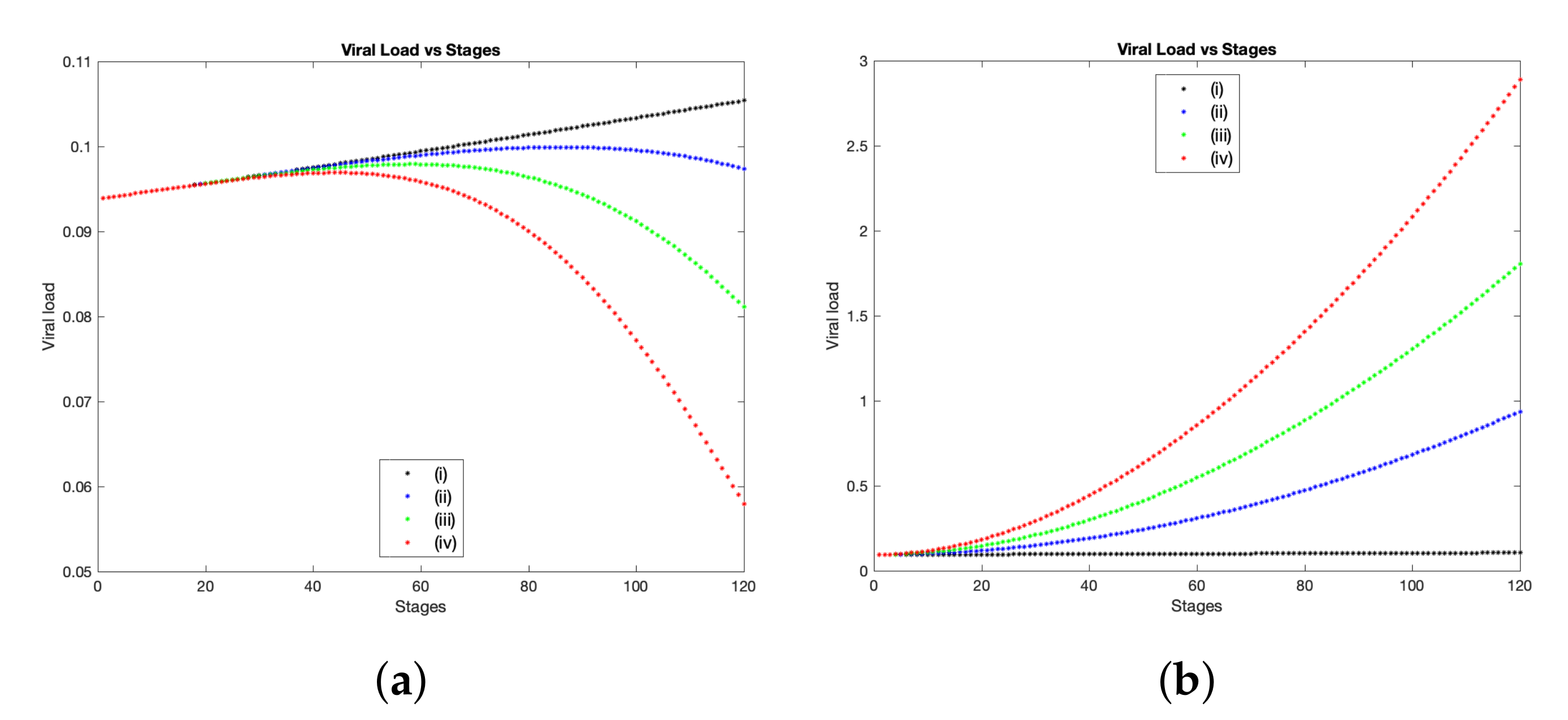
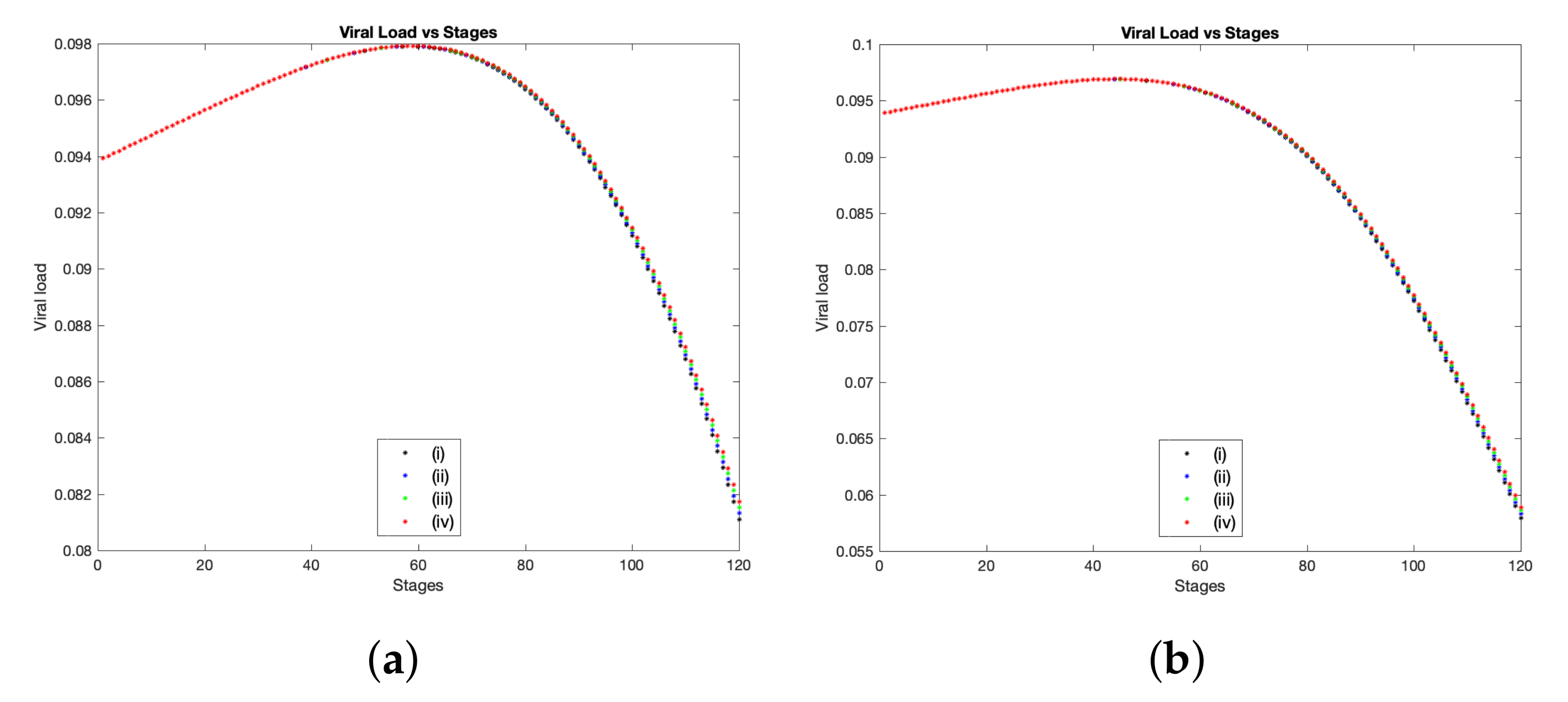
brings a clear influence towards controlling the infection with SARS-CoV-2. This result is obvious in
Figure 4a, where we show the total viral load of SARS-CoV-2 over 120 stages which corresponds to approximately 14 days. The black curve represents the basic scenario using the baseline values presented in
Table 1, while the blue, green and red curves illustrate the same case, but with employing the percentage variable
,
and
respectively. The experimental study [
41] shows the amount of viral load of SARS-CoV-2 for more than 80 patients over 12 to 15 days. The peak of viral load occurs between 5 to 6 or 7 days post symptom onset. However, the median time of symptom onset was varying from 2 to 7 days according to [
22]. Here, we mainly focus on two patients from Beijing where their daily clinical samples were collected from throat swabs, urine, stool and sputum as presented in [
41]. The first patient has a peak of viral load in throat swap in almost 7 days, while the second patient has that peak by the day 5. Hence, in order to compare our computational findings with the above samples results, we find that in the case when
, simulations show that the peak of viral load takes place at stage 43 which corresponds to the day 5 where this result coincides with clinical samples collected from the throat swabs for the second patient (see
Figure 4a(iv)). Moreover, the viral load copies (per mL) at the peak point is ranging from
to
as collected from clinical data [
41,
49], while in our numerical results, when
, the viral load (on the day 5) is equal to
copies per ml (≈
—dimensional value). However, in the case when
, the peak of viral load appears at stage 80 and 54 (which corresponds to the day 9.25 and the day 6.25) with concentrations of
and
copies per ml (which equals to
and
), respectively. Consequently, for both cases of
, the viral load tends to peak within the same time range compared to data collected from clinical trials. Further, in
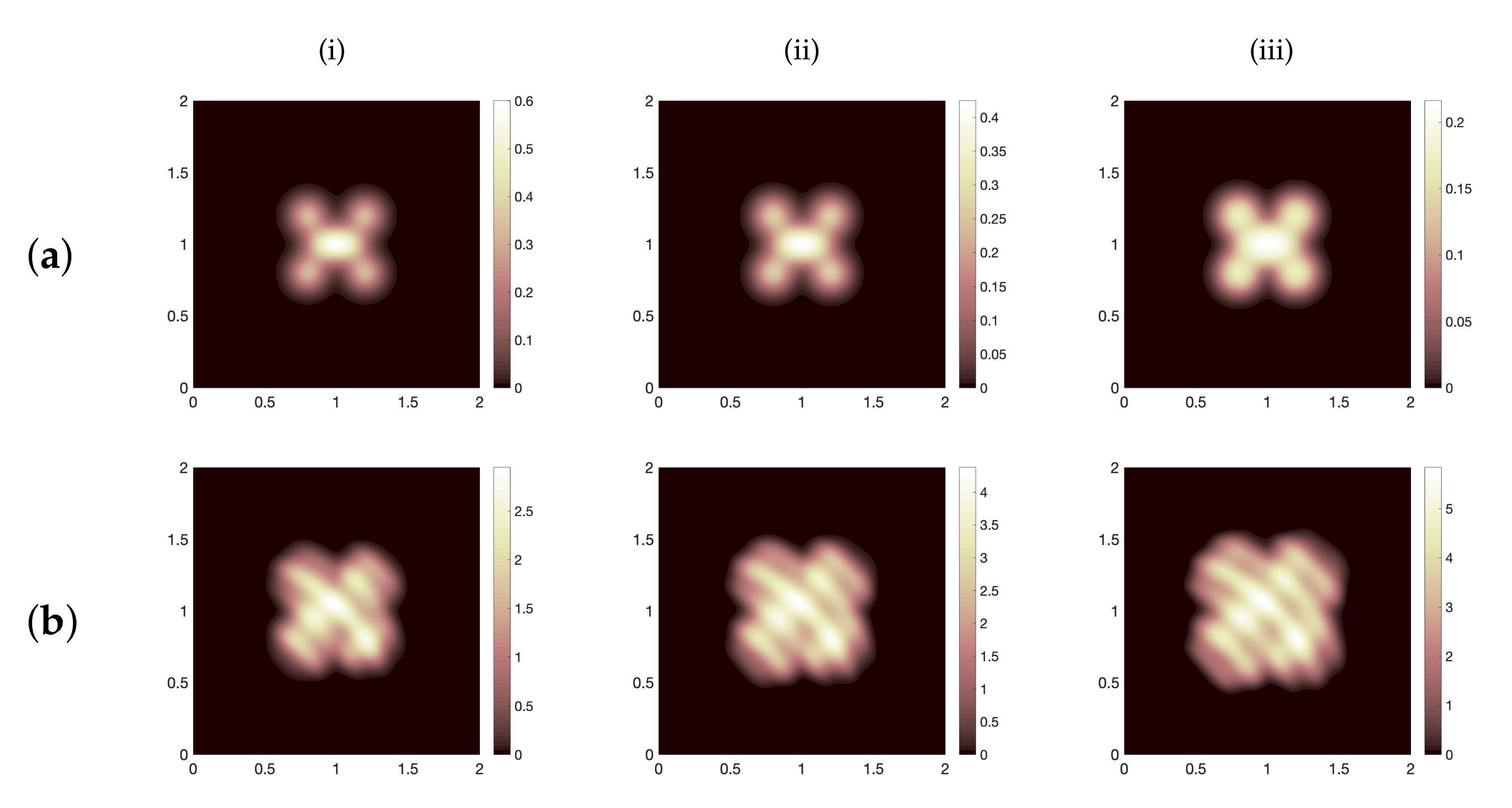
Figure 6a, we show the spatial distribution of virus particles at the final stage (14 days) for the three cases of
, namely,
(i)
, (ii)
and (iii)
. Thus, this result confirms that increasing the parameter values specified in group (A) leads to a better scenario with regards to infection with SARS-CoV-2.
On other hand, to observe the impact of the parameters defined in group (B) on the overall virus spatial expansion and the total viral load during interactions between virus and immune components, we first let
be denoted by the formula defined in (
10), while substituting the function
by one into model (
12)
. Then, using parameters values presented in
Table 1 and changing
by percentages determined in (
11), we show a comparison of viral load of SARS-CoV-2 for the above scenario starting from 2.78 h (stage 1) to 14 days (stage 120). Numerically, we obtain a higher viral load and more expansion of spatial distribution on the computational domain whenever
is increased (see
Figure 4b and
Figure 6b). This undesirable growth of virus can be explained by the fact that both rates of infection and viral replication have been considered within group (B), therefore increasing these rates by
will mostly cause more viral load over time. Following similar scenarios from clinical findings for died patients as presented in [
41], the viral load on the day 8 was at least equal to
for nasal swab and
for sputum sample. Hence, in a comparison to our simulations, the viral load on the day 8 (at stage 69) is greater than
(copies per mL) in dimensional values for all cases of
, namely, when
: viral load is
(non-dim) which equals to ≈
(dim); when
: viral load is
(non-dim) ≈
(dim); when
: viral load is
(non-dim) ≈
(dim). Thus, rising the parameters defined in group (B) drives to a serious situation of infection with SARS-CoV-2.
Another factor that affects SARS-CoV-2 infection is the variation of random motility rates for cells, virus and chemokines on the spatial domain. To check this, we decide to duplicate, triplicate and quadruplicate the diffusion rates for all system components using best outcomes in regards to viral load control, namely, substituting the function
as defined in (
10) into system (
12) with
, while
(these cases are illustrated in
Figure 4a(iii,iv)). Accordingly, in
Figure 7 we show the evolution of viral load of SARS-CoV-2 over 14 days using three values of random motility rates for all system components i.e.,
where
Figure 7a represents the viral load evolution in the case when
, while
Figure 7b shows the same case but when
. In general, numerical results show that there is a viral load growth whenever diffusion coefficients are increased. This result could be explained as follows, fast spatial diffusion of system components (especially infected cells and virus particles) within the tissue (our computational domain
ℵ) could expand the area of the dynamical interaction as well as transfer the virus to respiratory system which that may drive to have a late and a huge immune responses causing the cytokine release syndrome and leading to serious damage of vital organs and death in the worst cases [
8,
11,
16].
5. Discussion
In contrast to the temporal mathematical models (either between-host or within-host models) as presented in [
21,
22,
23,
24,
25,
26], we here suggested a new spatio-temporal (within-host) mathematical model to describe the interactions at the cellular scale between healthy cells, viral infected cells, SARS-CoV-2 particles and the main parts of immune system, namely, effector and regulatory T cells, B-lymphocytes cells and antibodies in the presence of chemokines concentration. Modeling assumptions and settings were carefully selected building on recent biomedical and mathematical studies as detailed in
Section 2. The numerical simulations provided reasonable outcomes for the within-host infection scenario which harmonized with data collected from clinical samples. However, we have faced many challenges regarding data availability as well as investigating the model outputs in a comparison with observations collected from clinical studies.
To investigate the model validation, we have improved a part of the computational framework introduced in [
50] and then extended in [
39]. Besides the implementation process of the finite difference method including approximations of the diffusion and chemotaxis terms, we have inserted additional strategies involving predict-evaluate-correct mode (see
Section 3.3) with taking into account a multi-site of infection on the computational domain and assuming a heterogeneous initial condition for host cells (see
Section 3.2) as well as applying certain conditions such as increasing the density of system components exclusively on the virus domain
. We investigated numerically multiple scenarios compared to the baseline parameter regimes presented in
Table 1 where the majority of these values are selected from [
19,
22,
26,
27,
34,
44]. However, simulation results using these values showed a failure case of immune responses to SARS-CoV-2 as presented in
Figure 4a(i). Hence, we decided to define the functions
(which exercise their role exclusively at
) in order to study the sensitivity of solutions using three choices of the percentage variable
. Based on that, we conclude the following, increasing the production rates of some immune components, namely, (
) by a size of
leads to a clear decay in the total viral load during time, conversely, rising the parameters (
) by a quantity of
encouraged the viral replication and reduced T cells production which in turn caused a growth of the total viral load. Additionally, in the case when
is considered into model (
12), we have found that staying at the peak of viral load differs as the percentage variable changes, for example, when
, the viral load reaches the peak after passing 9.25 days and remains on peak for another 36 h and 6.6 min, then decreases on the day 10.5 (for the other cases of
, see
Table 2). Furthermore, increasing the motility rates for system components would play a central role on the growth of the viral load over time. In general, for all cases of (
), our numerical results almost fit clinical outcomes for some patients data collected from [
41,
49] in terms of the amount of viral load on peaks (in dimensional values—copies per ml) as well as the time of the peak of viral load.
In this work, we have mainly presented a mathematical framework for modeling the immune responses to SARS-CoV-2 using a system of partial differential equations. We have developed a computational approach in order to simulate some scenarios of viral infection at a cellular level. Numerically, we have obtained a better control of SARS-CoV-2 infection in the case when the production level of T cells increases, and B cells and antibodies are exclusively in the spatial domain of the virus. From an immunological perspective, the ability to generate a strong immune response varies between people due to multiple factors. Therefore, we hope that the assumptions formulated in this work will stimulate suitable experimental studies that would investigate the production level of immune components at the infection site. However, in the future, we aim to provide further insight into the other factors such as the resulting pathological damages caused by either virus interactions with surrounding components or the cytokine storm caused by immune system. Moreover, questions regarding the qualitative behavior of the model, the local existence and uniqueness remain an open problem which could be investigated in a later work. Further, topics of COVID-19 are one of the most important research priorities nowadays; therefore, mathematical works should keep track of these efforts which require further improvement and future work. Thus, the proposed modeling framework and the computational technique can be extended to follow new findings from the forthcoming experimental studies.